0 引 言
地基雷达由于其稳定可控且可长期重复观测的特点,近年来已成为探测露天矿边坡形变、城区沉降、山体滑坡等领域的重要应用方向。本文主要针对山体滑坡监测的关键技术,即地基雷达成像进行研究。现有两大典型成像系统应用在山体滑坡监测领域:意大利的Joint Research Centre研制的LISA(Linear SAR)成像系统[1]、佛罗伦萨大学和意大利IDS公司合作研制的GBInSAR(Ground Based InSAR)系统IBIS(Image By Interferometry Survey)[2]。这些成像系统通过雷达天线在水平直轨道运动获得较高的方位向分辨率,但是天线运动的同时会影响测量的精度,也限制了雷达数据的采集速度。MIMO雷达利用其多发多收体制形成的虚拟天线阵元替代实际天线阵元[3],可以很好地解决合成孔径的问题。然而传统的成像算法,如距离多普勒算法和CS(Chirp Scaling)算法由于雷达结构的特殊性不再适用。文献[4]基于MIMO雷达成像在标准BP(Back Projection)算法和TCC(Time-Delayed Curve Correction)-BP算法基础上,提出一种高运算效率的改进MIMO雷达BP成像算法。文献[5]在山体滑坡监测模型中设计一种逆傅里叶变换和波束形成的地基MIMO雷达成像算法,提高了成像算法效率,但需要的天线数目仍然较多。从现有的文献来看,在山体滑坡监测雷达领域,采用的仍是经典的均匀线性布阵方式,稀疏阵列下的地基MIMO雷达成像技术仍待进一步研究。
近年来,压缩感知理论由于能够有效重建稀疏信号,不少学者将其应用于稀疏数据成像中。文献[6]根据压缩感知理论设计了一套采用稀布MIMO阵列和稀疏频率信号的探地雷达成像方案。文献[7]基于稀疏阵列模型,通过二维CZT坐标转换,结合压缩感知理论,提出了一种快速高分辨率的成像方法。本文利用压缩感知技术的降维思想,基于时分地基MIMO雷达的稀疏阵列模型,提出一种距离向逆傅里叶变换脉冲压缩和方位向混合匹配追踪算法的成像方法。通过数值仿真验证,该方法能够在实现目标成像高质量并改善多目标伪影点问题的情况下,减少比传统均匀阵列一半的天线数目,进一步节省了硬件成本,降低了数据处理复杂度。
1 稀疏阵列时分地基MIMO雷达信号模型
基于时分地基MIMO雷达成像系统的原理框架如图1所示。整个雷达系统在系统同步单元的控制和协调下,由信号产生单元产生步进频连续波信号,经过数模转换后送入信号调制单元调制到雷达工作频段,然后通过射频前端放大单元将信号功率放大。再由MIMO发射天线阵列按分时工作模式将信号发射出去,同时MIMO接收天线阵列分时接收雷达回波信号。信号的分时发射和接收均在天线分时选择器的协调和控制下进行。回波信号接收后经过低噪声放大单元将回波信号放大再进行正交解调,然后对回波信号进行采集。最后将采集好的雷达数据送入信号处理单元进行后续的成像处理。

图1 基于时分地基MIMO雷达成像系统原理框架
传统MIMO雷达系统是由M发N收的均匀阵列组成,接收天线间隔为λ/2,发射天线间隔为N(λ/2),λ为信号波长。在实际成像中,阵元数过大会提高系统硬件成本和计算复杂度,为了解决阵元数过大引起的问题,本文采用稀疏布阵进行MIMO雷达成像。
为了发射信号彼此之间正交,通常发射天线数要远小于接收天线数,所以本文对数目较多的接收天线进行稀疏布置:从原始N个接收天线中随机选取N′个,为保证阵列孔径长度足够大,第一个和最后一个接收天线位置不变,接收阵列稀疏比例定义为η=N′/N。根据得到的N′个稀疏接收阵元和M个均匀的发射阵元,利用多项式理论[8]得到MN′个虚拟阵元。
为了获取高的距离向分辨率,本文采取步进频连续波技术。则第m个发射天线发射的一组脉冲信号为Sm(t),表达式为
Sm(t)=![]()
m∈(1,2,3,…,M)
(1)
式中,fi=f0+iΔf,f0为脉冲起始频率,Δf为频率步进量,rect(t)为单位矩形函数,Tr为发射信号脉冲宽度,Q为子脉冲个数,Am为第m个发射信号的能量。
雷达信号分时发射到监测区域后,回波信号被接收天线分时接收。假设第n′个接收阵元接收到第m个发射阵元发射信号的回波,并将该通道称为第mn′个观测通道,将该观测通道回波信号幅度放大并经过解调采样后为
![]() Amn′δexp(j2πfi(-τmn′))
Amn′δexp(j2πfi(-τmn′))
i∈(0,1,2,…,Q-1)
(2)
式中,δ为目标散射系数,τmn′为该观测通道的时延,(x0,y0),(xn′,0),(xm,0)分别为目标和收、发天线的坐标,c为光速。
2 MIMO雷达稀疏成像方法
2.1 雷达数据距离向压缩及近似相位补偿
本文采用时分MIMO雷达体制,通过时分方式发射和接收信号,各通道数据可以被很好地分离开来,可以避免传统MIMO雷达接收端的复杂匹配滤波,但是距离向雷达数据还没有进行压缩处理。步进频连续波是一个频域信号,变换到时域可以形成一个sinc函数信号,即可以形成一个窄脉冲。斜距不同的目标窄脉冲出现的位置也不一样,从而在距离向分离出不同目标。
由第1节所述,雷达采集完数据后得到一个原始雷达数据矩阵I[MN′,Q],Emn′,i为矩阵I第mn′行i列的元素,表示为
Emn′,i=Amn′δexp(j2π(f0+iΔf)(-τmn′))
(3)
在小间距布阵条件下,MIMO雷达阵列长度远小于监测区域目标到阵列的距离,距离徙动不明显,因此,距离向只需要进行逆傅里叶变换(IFFT)即可得到较为准确的压缩数据。对I[MN′,Q]矩阵按行分别进行IFFT得到第mn′行数据为
Sr(tk,xmn′)=![]() exp(-j2πf0τmn′)·
exp(-j2πf0τmn′)·
sinc(πB(tk-τmn′))
(4)
式中,tk∈k/B,B为信号带宽。
将式(4)所示的时延曲线按幂级数展开,省略高方次项。为方便表达,把完成距离向压缩后的雷达数据变换到极坐标下表示,监测区域目标(x0,y0)的波达角设为θ,进一步可得回波数据的相位为
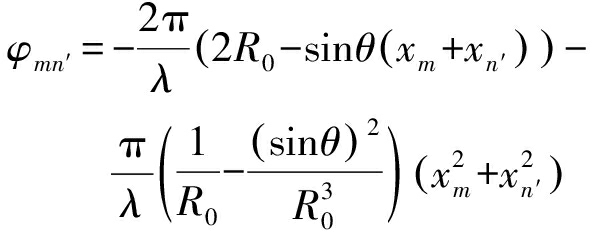
(5)
式中,![]()
根据真实滑坡监测区域的几何特点推出θ很小,sin2θ值非常小,sin2θ/R0的值更小,可以忽略不计,式(5)将合理的近似为
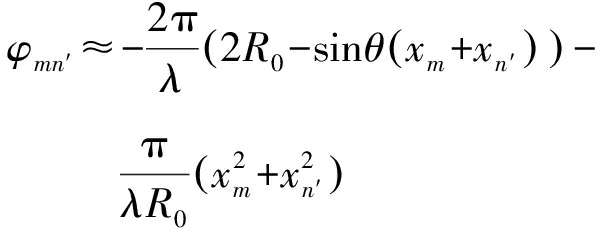
(6)
对比传统的线性阵列,MIMO天线阵列稀疏布置的情况下会存在相位不连续现象,为提高雷达数据方位向压缩的质量,在方位向压缩之前进行预处理,即采用相位相乘的方法消除式(6)的第二项。因为R0是个变量,会造成算法的运算量巨大。所以对式(6)的第二项进行近似的校正,把式(6)第二项中的R0替换为R1,R1表示监测区域中心到雷达天线阵列坐标中心的距离,为一常量。由此可得校正因子为
(7)
因此对式(4)乘以校正因子Sjiao,mn′完成方位向压缩预处理,那么得到
![]()
![]()
sinc(πB(tk-τmn′))
(8)
2.2 基于时延补偿因子稀疏基的压缩感知方位向压缩
若等效的虚拟收发天线是均匀布置的,利用文献[4]方法在方位向用波束形成算法进行数据压缩,即可得到高分辨率的图像。但本文等效的虚拟收发天线是稀疏布置的,直接运用文献[4]方法就会导致旁瓣很高。由于对山体滑坡监测区域目标成像时,聚焦性强的目标只占据监测区域的极小部分,满足压缩感知理论的稀疏性要求,稀疏阵列可认为是原始均匀阵列的低维观测。因此本文结合压缩感知理论[9]对方位向数据进行压缩处理,针对多目标的伪影点问题,引入混合匹配追踪(Hybrid Matching Pursuit,HMP)算法[10],既保证了基信号选择的正交性,又对支撑集选取过程进行回溯优化,大大改善了传统正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[11]的成像质量。
由2.1节处理得到的所有观测通道数据集合![]() 可看作一个大小为Q×MN′的矩阵,其中Q为距离单元数,MN′为等效稀疏收发天线个数。假设等效均匀收发天线得到的回波数据矩阵记为Y,那么X的每一行均可看作Y每一行的低维观测,具体到第q个距离单元可表示为
可看作一个大小为Q×MN′的矩阵,其中Q为距离单元数,MN′为等效稀疏收发天线个数。假设等效均匀收发天线得到的回波数据矩阵记为Y,那么X的每一行均可看作Y每一行的低维观测,具体到第q个距离单元可表示为
![]()
(9)
式中,观测矩阵Φ={φu,v}为广义单位阵,且
(10)
Φ矩阵由MN′行MN列元素构成,矩阵的每一行除了第δu个元素为1外,其余的全为0,δu由等效稀疏收发天线位置决定。
对应地,原始均匀阵列得到的回波数据Y可由稀疏变换矩阵变换为
Yq=ΨΘq
(11)
式中,Θq为第q个距离单元的目标散射点信息,Ψ为稀疏变换矩阵。
根据滑坡监测区域几何形状,得出监测区域波达角的覆盖范围,雷达监测区域距离向从ymin到ymax,方位向从-x到x,则波达角的范围为(-arctan(x/ymin),arctan(x/ymin)),将其均分为MN份,得θl如下式:
θl=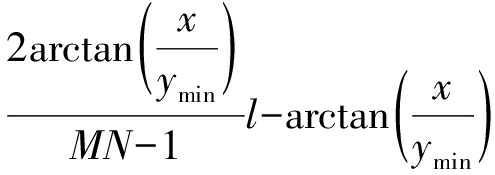
l∈(0,1,2,…,MN-1)
(12)
令Wl,mn=exp(-j2πf0sinθl(xm+xn)/c),由Wl,mn组建MN行MN列时延补偿因子矩阵如下式:
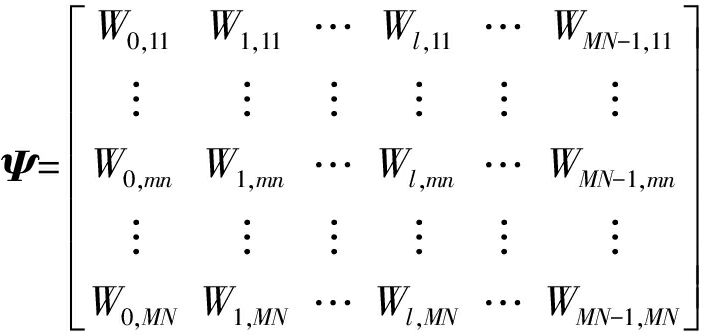
(13)
时延补偿因子与信号本身在某种程度上存在一一对应的关系,很全面地反映了散射点的特征信息,故可以把其作为稀疏变换的稀疏基进行后续的数据压缩处理。
本文在构造稀疏接收阵列时,接收天线是随机选取的,等效的虚拟收发阵元的位置也是随机的,满足广义单位阵Φ与Ψ不相干的要求,因此ΦΨ满足RIP(Restricted Isometry Property)条件[9]。由以上构造的稀疏变换矩阵和观测矩阵,利用正交匹配追踪算法对X的第q行求解以下问题:
Θ=argminΘ0满足![]()
(14)
然后对所有的q=1,2,…,Q求解式(14)问题,即可得到二维像。
事实上直接运用OMP算法对多点目标成像时会有伪影点出现,因为OMP算法在支撑集选择时只能扩充不能去除不良基信号,针对此问题,引入一种混合匹配追踪算法,通过将两种贪婪恢复算法结合起来,利用OMP算法选择基信号的正交性和子空间追踪(Subspace Pursuit, SP)算法[12]支撑集选择的回溯策略,来重构出高分辨且没有伪影的图像。
对X的第q个距离单元获得稀疏解![]() 具体流程如表1所示。
具体流程如表1所示。
表1 方位向数据压缩算法流程

输入:回波采样向量xq,恢复矩阵T=ΦΨ,稀疏度K;输出:稀疏解σ~。初始化:定义初始支撑集为Λold=max_ind(δomp,K),定义函数max_ind(y,P)表示:返回P索引,找到向量y中幅值最大的元素所在的位置。其中δomp=omp(xq,T,K)为标准OMP算法的输出结果。残差初始化γold=xq-TΛold((TΛold)HTΛold)-1(TΛold)Hxq1) 支撑集扩充至2K个:Λtemp=Λold∪max_ind(δnomp,K)式中,δnomp=omp(γold,T,K)2) 支撑集更新新的支撑集为Λnew=max_ind((TΛtemp)HTΛtemp[]-1(TΛtemp)Hxq,K) 3) 残差更新:γnew=xq-TΛnew((TΛnew)HTΛnew)-1(TΛnew)Hxq4) 迭代终止判断。当残差满足范数关系γold22>γnew22时,则令γold=γnew和Λold=Λnew,然后跳回1)进行迭代;否则,迭代停止,计算和输出σ~:σ~Λold=(TΛold)HTΛold[]-1(TΛold)Hxq
然后再分别对X的q=1,2,…,Q个距离单元分别按照表1的算法流程求解,即可得到目标的二维信息。从表1算法流程来看,HMP算法中的每次支撑集确定过程是通过OMP算法得到的,这样就使得在基信号选择时保证了正交性。与此同时,HMP算法中的支撑集回溯选择过程与SP算法的相同,这样就使得HMP算法可以去掉在前面的迭代过程中被选择的病态索引,向支撑集中添加新的潜力高的索引。所以,HMP算法的处理流程结合了OMP算法和SP算法的优点,使得多目标成像的性能会更好。
3 仿真实验
为了验证算法的正确性,在本节进行数值仿真实验。雷达发射步进频信号,载频为15 GHz,带宽为300 MHz,子脉冲数为4 096个。这里按照第1节稀疏布阵方法布置6发25收的阵列,均匀接收阵元的间隔为λ/2,发射阵元的间隔为50×(λ/2),阵列稀疏度为50%。根据山体滑坡的实际成像场景设置雷达仿真参数。雷达成像区域为距离向从1 000 m到2 000 m,方位向为-150 m到150 m。点目标的散射系数都设为1,附加噪声为加性高斯白噪声,信噪比为10 dB。
首先分析单点目标成像,目标方位向为0 m,距离向为1 500 m,图2给出了文献[5]方法、OMP算法以及本文提出的算法成像结果。从图2看出,3种方法均对单点聚焦正确成像,但是图2(a)有低幅度值的旁瓣,图2(b)和图2(c)没有这种情况,且图2(a)的分辨率低于图2(b)和图2(c)。表明对于单点目标成像,OMP算法和本文方法成像效果一致,明显优于文献[5]方法,OMP算法对于单点目标成像没有伪影点出现。
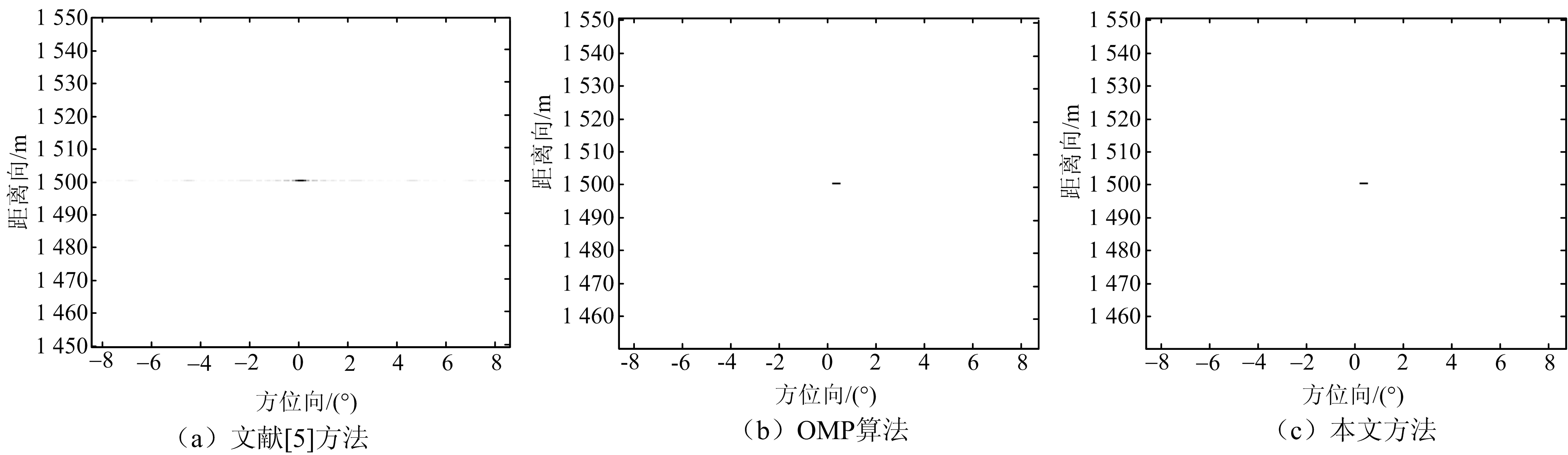
图2 单点目标稀疏阵列成像对比
其次图3分析了多点目标成像,目标点位置信息为tg1-(0,1 500),tg2-(-25,1 505),tg3-(25,1 505),tg4-(0,1 510),tg5-(-50,1 520),tg6-(50,1 520),tg7-(0,1 520)。仿真结果如图3所示,图3(a)给出了文献[5]方法的成像效果图,图3(b)给出了OMP算法的成像效果图,图3(c)给出了本文方法成像效果图。为了更加清晰地比较3种方法成像质量,图4给出了距离向为1 510的方位向切面曲线图。可以看出,图3(a)中由于阵元的缺失,不能很好地处理欠采样数据,呈现出的7个点目标图像模糊,只能大致辨别几个目标点的不同位置信息,且旁瓣水平比单点目标成像恶化明显。图3(b)和图3(c)表明了OMP算法和本文方法在稀疏阵列下多点目标聚焦成像的效果优于文献[5]。但观察图4和对比图3(b)、图3(c)可发现,OMP算法在目标点周围存在多个伪影点,影响多个目标之间的区分,这是由于OMP算法在基信号选择时只能扩充而不能去除的策略造成的。本文方法与OMP算法不同之处在于迭代过程中结合了SP算法,去除了在前面迭代过程中被选择的病态索引,因此本文方法的成像效果更好。为进一步分析本文方法的成像质量,表2分别给出了文献[5]方法、OMP算法、本文方法的分辨率和目标杂波比(TCR)指标对比分析。目标杂波比对应用来衡量目标在背景杂波中的凸显程度,其值越大,聚焦度越高,以dB的形式定义为
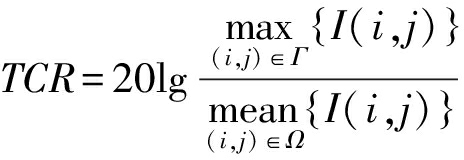
(15)
式中,Γ为目标区域,Ω为杂波区域。分析表2可知,3种方法的距离向分辨率基本相同,这是因为距离向分辨率只与发射信号带宽有关。OMP算法和本文方法的方位向分辨率明显优于文献[5]方法,这是因为阵列的稀疏先验信息用在压缩感知理论可以大大改善成像的质量。从表2可以看出,本文方法的TCR值最高,点目标的散射特性保存最好,比OMP算法的TCR值高4 dB左右,极大地改善了多目标成像的伪影点问题。
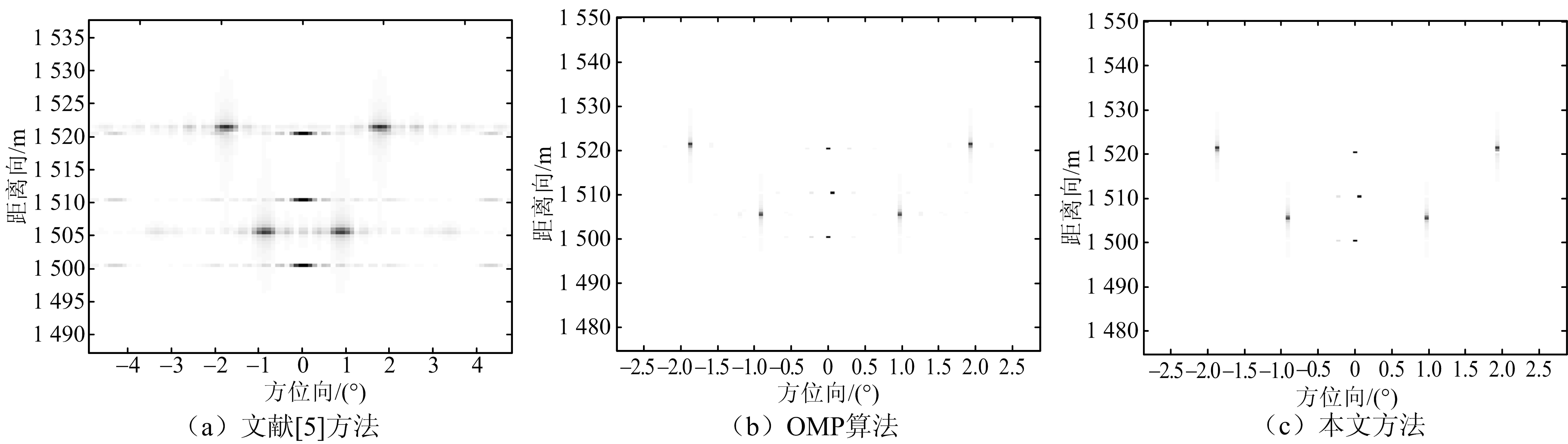
图3 多点目标稀疏阵列成像对比
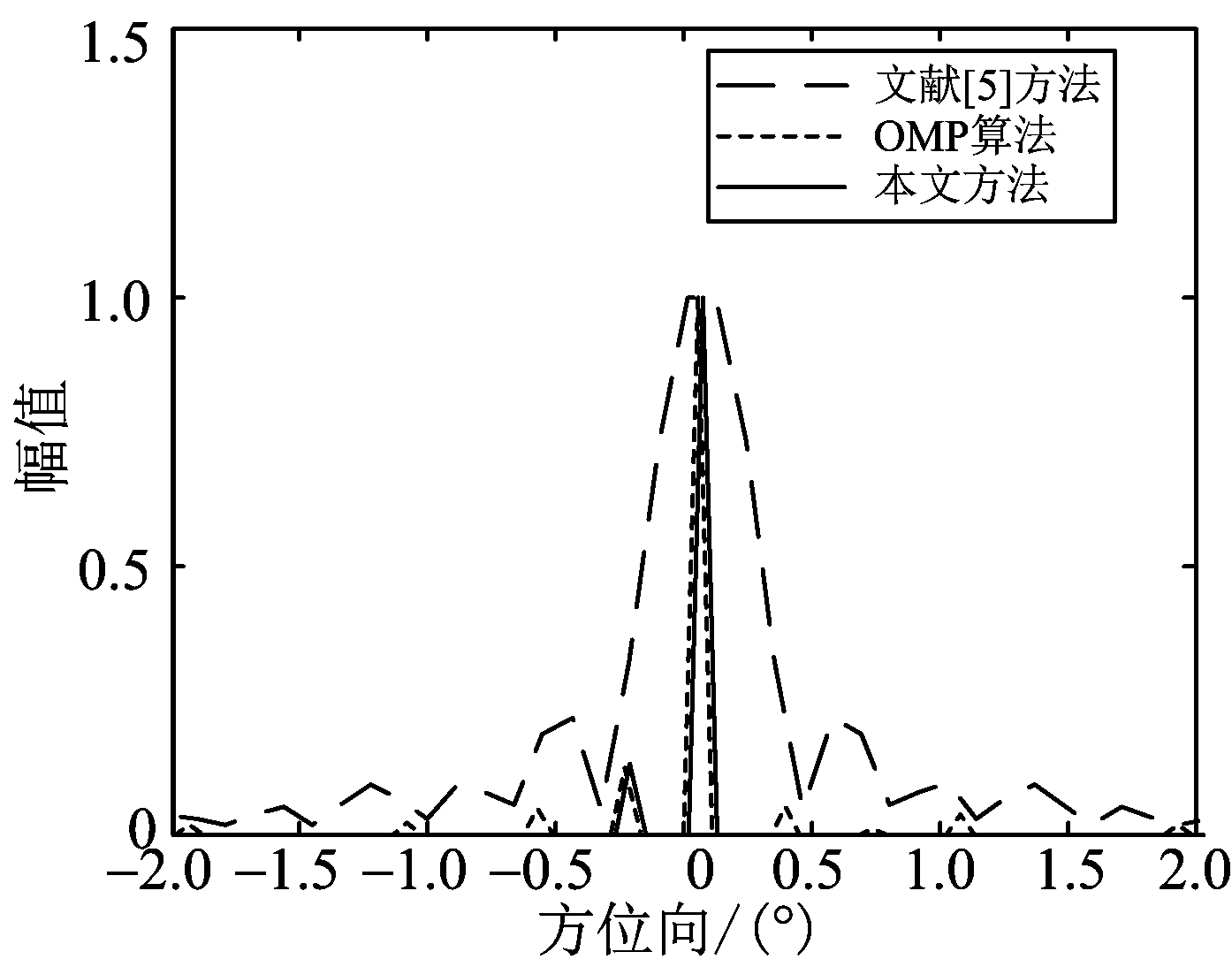
图4 方位向切面曲线图
表2 不同成像方法的分辨率和目标杂波比
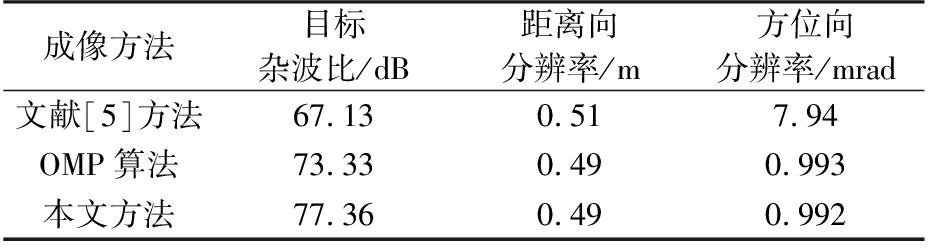
成像方法目标杂波比/dB距离向分辨率/m方位向分辨率/mrad文献[5]方法67.130.517.94OMP算法73.330.490.993本文方法77.360.490.992
下面分析本文方法对应不同稀疏比的阵列天线的重构效果。图5给出了稀疏比分别为50%, 30%,20%,对应的接收阵元依次为25, 15, 10的成像效果对比。从图5的3幅图中看出,随着阵列天线稀疏比的降低,多点目标的重构效果在逐渐变差,且在20%的比例下成像质量恶化严重。为了更准确地评价本文方法在不同稀疏比情况下的成像质量,在此使用均方根误差(RMSE)来比较重建图像的质量。使用理想场景的图像作参考,设置稀疏比从10%到50%分别进行对比,具体结果如表3所示,RMSE值越小代表重建质量越高。从表3中看出,随着稀疏比不断下降,RMSE的值在逐渐升高,对应的多目标成像质量在逐渐变差。所以,只要接收阵列保证稀疏比例在20%以上,均可以运用压缩感知理论实现多点目标的准确重构。
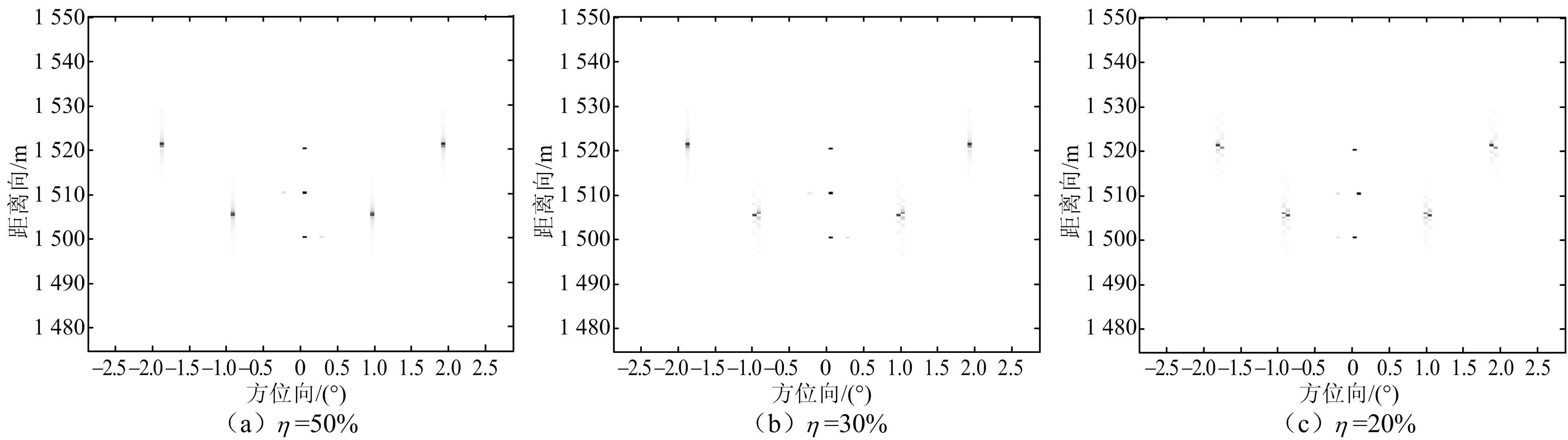
图5 不同阵列稀疏比本文方法成像效果对比
表3 不同阵列稀疏比成像结果均方根误差对比
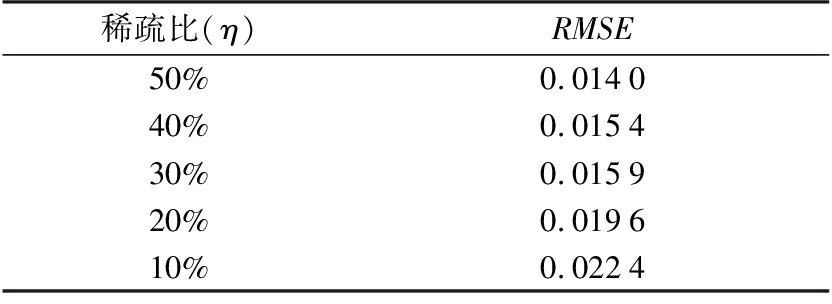
稀疏比(η)RMSE50%0.014040%0.015430%0.015920%0.019610%0.0224
为了说明本文方法的抗噪性,图6给出了接收阵列稀疏比例分别为50%, 30%, 20%的多目标重构误差随信噪比变化的情况。信噪比设置-40 dB到20 dB,把均方根误差值作为衡量成像效果的标准。从图6看出,多目标重构的均方根误差在不同的稀疏比例下均随信噪比的提高而减小。当信噪比大于-20 dB时,不同稀疏比例得到的多目标重构均方根误差均趋于平稳。通过图中误差对比可知,稀疏比例值越高,整体的均方根误差值越小,抗噪性能越好。综上所述,只要信噪比在一定范围内,重构图像的质量整体保持在稳定的高分辨率状态。
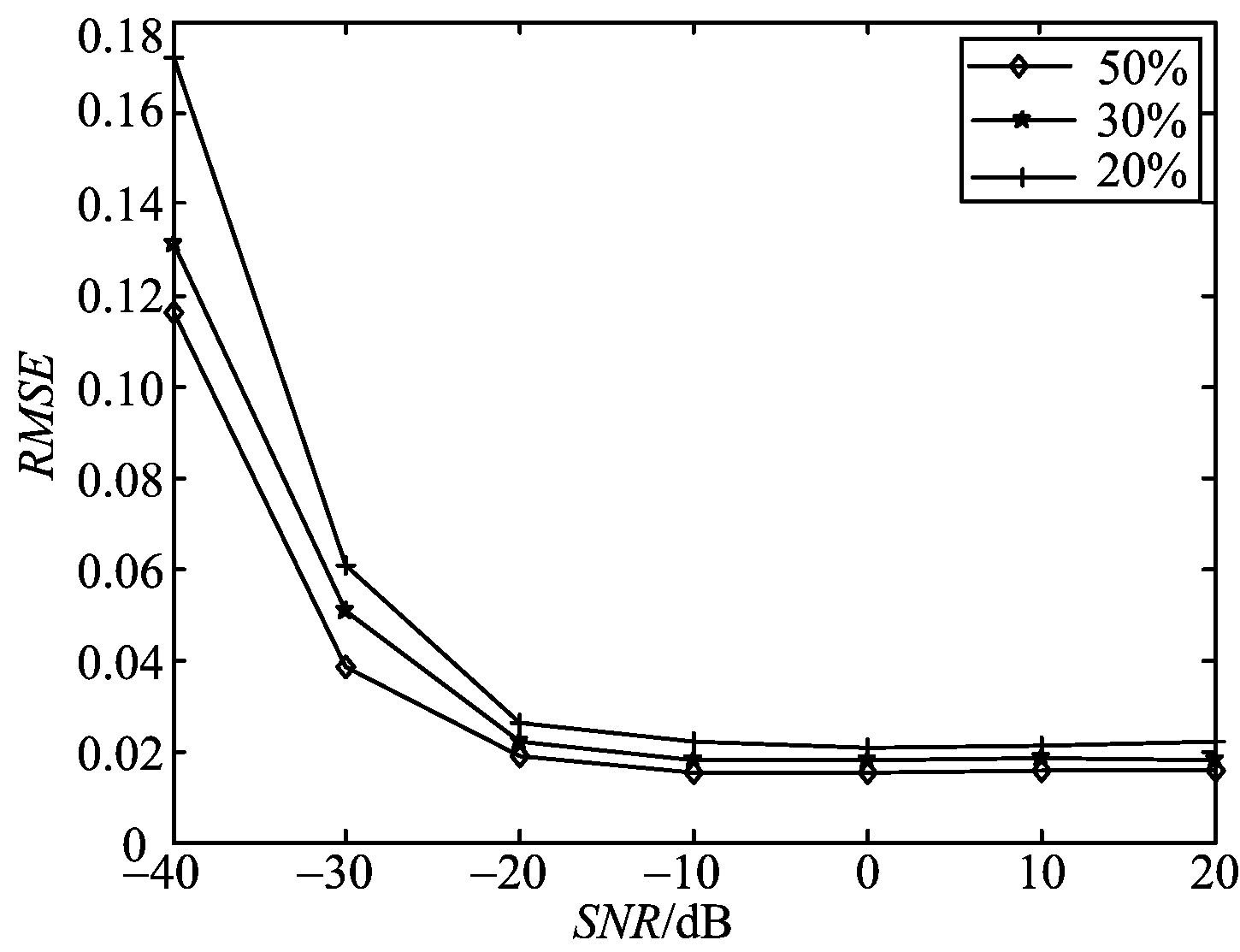
图6 几种阵列稀疏度随信噪比变化的均方根误差比较
4 结束语
将传统MIMO雷达阵列运用在山体滑坡监测方面可解决合成孔径雷达天线运动的精度问题和数据采集速度慢的问题,但需求天线数多,增加系统复杂度和硬件成本。为了解决以上问题,提高系统性能,本文研究了稀疏阵列下的时分MIMO地基雷达成像技术,提出一种逆傅里叶变换结合压缩感知的方法,并针对多目标伪影点问题引入混合匹配追踪算法实现高质量的成像。最后通过数值仿真验证,本文方法在一定的阵列稀疏比例范围下可以实现较为理想的成像结果。总体来说,本文在基于时分MIMO雷达的山体滑坡监测体系下引入稀疏阵列保证多点目标成像的有效性,为山体滑坡监测系统的实物研制提供理论支撑,具有一定的实际应用价值。
[1] HU Cheng, DENG Yunkai, WANG Rui, et al. Two-Dimensional Deformation Measurement Based on Multiple Aperture Interferometry in GB-SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(2):208-212.
[2] HAKOBYAN A, MCGUIRE P, POWER D, et al. Applications and Validation Tests of Ground-Based Coherent Radar for Deformation and Vibration Measurements in Canada’s Atlantic Region[C]∥ IEEE 28th Canadian Conference on Electrical and Computer Engineering, Halifax, NS, Canada: IEEE, 2015:638-642.
[3] PHAM M N, JACOB A F. High-Performance MIMO Imaging Radar with Hybrid Transmit and Receive Arrays[J]. International Journal of Microwave and Wireless Technologies, 2016, 8(4/5):807-813.
[4] 王伟,马跃华,王咸鹏. 一种高运算效率的MIMO雷达BP成像算法[J]. 系统工程与电子技术, 2013, 35(10):2080-2085.
[5] 蒋留兵,杨涛,车俐. 基于时分MIMO的地基雷达高分辨率成像研究[J]. 电子与信息学报, 2016, 38(5):1055-1063.
[6] YANG Jungang, JIN Tian, HUANG Xiaotao, et al. Sparse MIMO Array Forward-Looking GPR Imaging Based on Compressed Sensing in Clutter Environment[J]. IEEE Trans on Geoscience and Remote Sensing, 2014, 52(7):4480-4494.
[7] 赵小茹,童宁宁,胡晓伟,等. 二维CZT的稀疏阵列MIMO雷达快速极坐标格式成像算法[J]. 空军工程大学学报(自然科学版), 2017, 18(2):32-36.
[8] GU Shuainan, LI Ke, REN Xiukun, et al. Antenna Array Design in MIMO Radar Using NSK Polynomial Factorization Algorithm[J]. International Journal of Antennas and Propagation, 2016, 2016:4580479.
[9] 金坚,谷源涛,梅顺良. 压缩采样技术及其应用[J]. 电子与信息学报, 2010, 32(2):470-475.
[10] LI G, BURKHOLDER R J. Hybrid Matching Pursuit for Distributed Through-Wall Radar Imaging[J]. IEEE Trans on Antennas and Propagation, 2015, 63(4):1701-1711.
[11] ZHANG Dong, ZHANG Yongshun, HU Xiaowei, et al. Fast OMP Algorithm for 3D Parameters Super-Resolution Estimation in Bistatic MIMO Radar[J]. Electronics Letters, 2016, 52(13):1164-1166.
[12] DAI W, MILENKOVIC O. Subspace Pursuit for Compressive Sensing Signal Reconstruction[J]. IEEE Trans on Information Theory, 2009, 55(5):2230-2249.

