0 引 言
SAR系统可实现全天候、全天时、高增益的地面静止目标成像。然而在很多军事应用情况下，观测场景中不仅存在静止目标，也存在运动目标。利用SAR系统获取运动目标参数与成像结果已成为当前的研究热点[1-3]。然而随着分辨率的不断提高，SAR系统的数据量和脉冲重复频率(Pulse Repetition Frequency, PRF)不断增大。庞大的数据量对系统的存储能力提出了很高的要求，同时对数据信道的传输能力也是一个很大的挑战。并且较高的PRF会导致SAR系统的成像测绘带宽变小，进而降低了SAR系统的预警探测范围和信息获取能力。因此为了减少回波数据量和实现宽测绘带成像，SAR成像系统采用较低的PRF采集回波数据。由SAR成像原理可知，较低的PRF容易导致方位Doppler模糊。对于地面静止场景成像而言，已有研究学者利用零点控制[4]、空域滤波[5]等方法完成解模糊处理。但是对于场景中运动目标的参数估计而言，传统的多普勒域参数估计方法等非平稳信号处理方法将无法有效应用。因此在低PRF条件下如何进行运动目标参数的准确估计对于SAR动目标成像与检测技术的发展具有重要意义。
考虑到地面静止目标和杂波对消处理后的回波数据中只有运动目标信号，并且观测场景中的运动目标数量是有限的，因此运动目标回波信号满足稀疏性的要求[6]。基于该稀疏特性，文献[7]采用压缩感知理论对低PRF条件下的运动目标回波信号进行参数估计处理。该方法将需要搜索的所有多普勒调频率和方位位置同时考虑进来，随着运动参数估计精度要求的提高，会导致运算量和计算复杂度呈几何级数增加。文献[8]提出了基于参数化稀疏表征的目标参数估计方法，但是该方法的收敛域和收敛空间无法确定，容易产生局部最优解。本文针对低PRF条件下的SAR系统动目标参数估计方法进行研究。首先对距离脉压之后的数据利用DPCA方法进行对消处理，获得只有运动目标信息的回波数据。其次采用Hough变换[9]估计运动目标的跨航向维速度和位置信息，并利用估计结果校正距离单元走动。然后对沿航迹维运动参数进行估计，构造离散的FRFT矩阵作为稀疏基矩阵并建立压缩感知模型，通过对模型进行优化求解获得FRFT的最优阶数，进而估计动目标沿航迹维的速度和位置，完成对目标运动参数的估计。
1 回波信号模型和杂波对消处理
本文的天线结构采用单发双收配置方式，即由3个天线组成，其中天线A发射信号，天线B和C同时接收回波信号。天线A, B, C和运动目标的几何位置关系如图1所示，SAR雷达系统工作在正侧视模式，O为起始点，雷达载机沿X轴方向飞行，速度为va，点目标Pn表示场景中的第n个运动目标，其坐标为(xn,Rn)，垂直于航向和平行于航向的速度分别为vny和vnx，R0为雷达平台离观测场景中心点的距离，RAn为通道A与Pn的距离，RBn为通道B与Pn的距离，RCn为通道C与Pn的距离，d为通道A和B之间的距离。
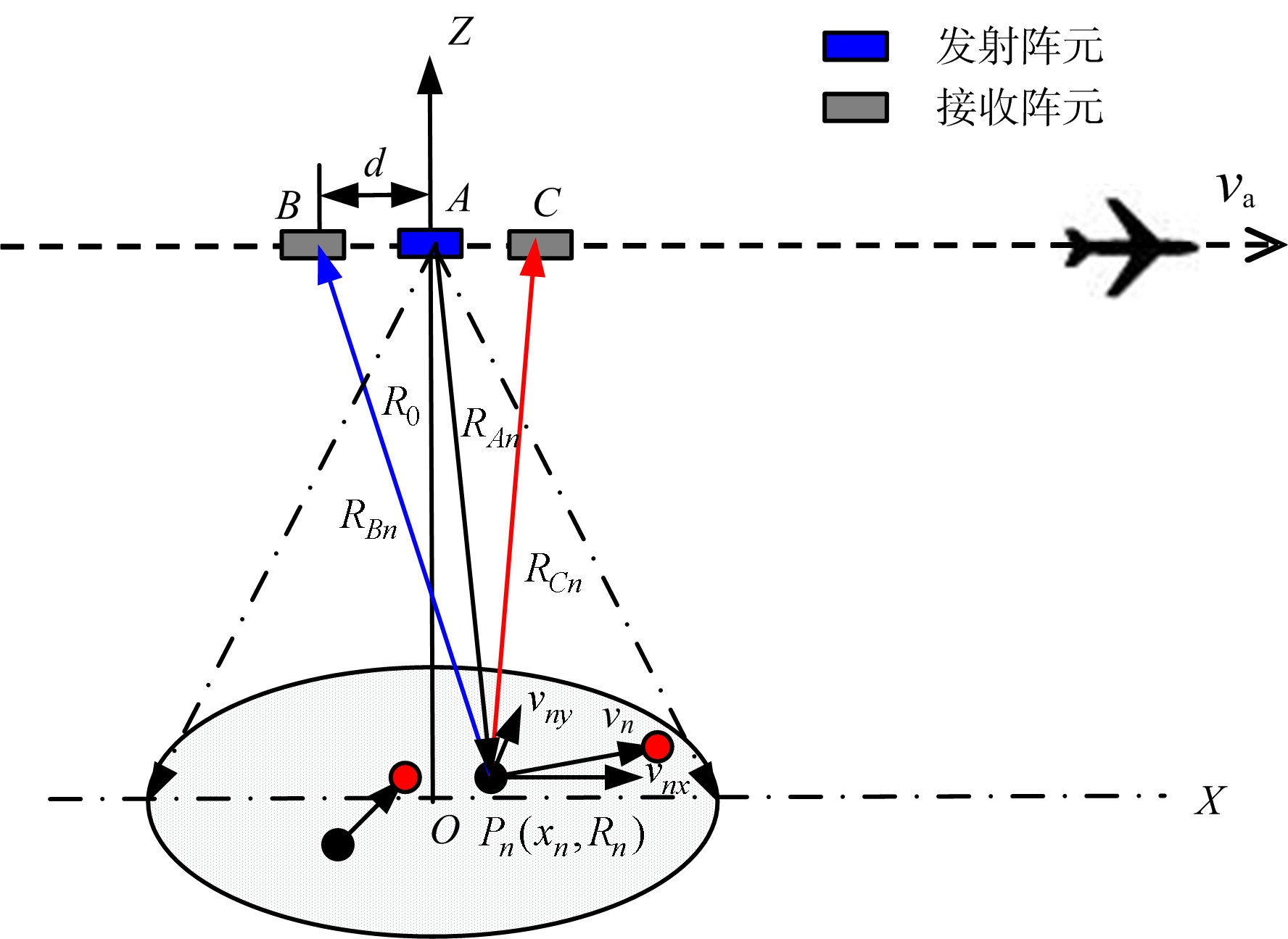
图1 天线A, B, C和运动目标的几何关系
雷达发射信号为线性调频信号，其表达式为
(1)
式中，当-1/2≤t≤1/2时，rect(t)=1，γ为调频率，Tp=1/PRF为发射脉冲宽度，PRF为脉冲重复频率，f0为载频，t为全时间，
为快时间，tm为慢时间。假设场景中的目标散射点数为L，其中运动目标的数目为N，则通道C接收到的基频回波信号为
exp[-j2π(RA l(tm)+RC l(tm))/λ+
(2)
式中，σl为点目标Pl的反射系数，λ为发射信号波长。RAl(tm)和RCl(tm)分别为tm时刻天线阵元A和C与点目标Pl的距离，可表示为
RA l(tm)=
RA l-vlytm+[(va-vlx)tm-xl]2/(2RA l)
(3)
RC l(tm)=
RC l-vlytm+[(va-vlx)tm+d-xl]2/(2RC l)
(4)
式中，
回波信号
进行基于匹配滤波的距离脉冲压缩处理，得到
exp(-j2π(RA l(tm)+RC l(tm))/λ)
(5)
式中，B=γTp为发射信号带宽。为了利用DPCA方法实现杂波对消处理，假设tm+τ时刻通道B运动到tm时刻的通道A处，那么对通道B和C距离脉压之后的信号进行DPCA处理，处理之后的运动目标数据相位信息保持不变。因此DPCA处理之后的信号，可表示为
exp(-j2π(RAn(tm)+RCn(tm))/λ)
(6)
至此完成了地面杂波的对消处理，得到的信号
中只有运动目标的信息。从式(6)、式(3)以及式(4)可见，运动目标的距离走动包括了线性分量和二次分量，为了讨论问题的方便，暂不考虑二次分量对回波信号的影响。因此式(6)可进一步写为
exp(-j4πRCn(tm)/λ)
(7)
从式(7)可见，在距离慢时间域表示为直线，其斜率与运动目标的垂直航向速度vny有关，截距与目标的距离向位置有关。因此如果能够根据信号的包络项估计出斜率和截距，进一步计算即可得到运动目标的垂直航向速度和距离位置。当雷达系统采用低于Nyquist采样定理所需的PRF采样率进行采集时，主要影响方位向处理，距离向处理不受其影响。本文利用Hough变换估计信号的包络项斜率和截距。
2 跨航向速度估计与距离走动补偿
Hough变换的本质是从图像空间到参数空间的映射，其基本思想是把解析曲线从图像空间映射到以参数为坐标的参数空间，根据参数空间的一些标识反过来确定曲线的参数值。假如图像空间里有两条直线，那么Hough变换后参数空间里将有两个峰值点，这两个峰值点所在位置的坐标就确定了这两条直线的参数。
信号在距离多普勒平面内的斜率利用Hough变换进行检测，可以有效获得目标的跨航向速度和距离维位置。进一步能够完成距离徙动校正处理，得到的结果为
exp(-j2π[(va-vnx)tm+d-xn]2/(RCnλ))
(8)
式(8)的相位项可简化为关于慢时间tm的Chirp信号形式，即
exp(-j4πRCn/λ)·
(9)
式中，
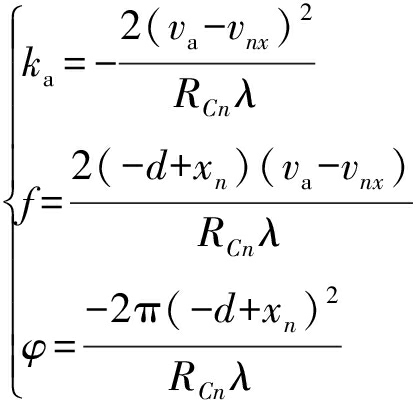
(10)
进一步，存在运动目标的第n个距离单元的信号可简化为
(11)
从式(11)可以看出，经过DPCA处理的地面运动目标回波数据可看作多个Chirp信号叠加。
3 基于离散FRFT的压缩感知方法
分数阶傅里叶变换是处理Chirp信号的一种有效工具。由于SAR系统运动目标的方位向信号可近似为Chirp信号，因此利用FRFT可实现运动目标的成像与运动参数估计[10]。但是需要注意的是，由于本文主要研究的是低PRF条件下的回波数据，利用传统的FRFT处理方法将无法实现Chirp信号的能量聚集。主要利用离散的FRFT矩阵构造稀疏基矩阵，然后再通过求解压缩感知优化问题获得FRFT的最优阶数，并根据最优阶数估计出运动目标方位向的运动参数。
FRFT是传统Fourier变换的推广，信号x(t)角度为α的FRFT定义为
Xα(u)=Fp[x(t)]=
x(t)Kα(t,u)dt
(12)
式中：p为FRFT的阶数，可以为任意实数；α=pπ/2；Fp[·]为FRFT的算子符号，Kα(t,u)为FRFT的核函数。若SAR系统运动目标方位信号是满采样的，那么即可利用传统的FRFT处理对其进行聚焦处理，将满采样的某个距离单元的方位信号记为
传统的FRFT处理过程用公式表示为
(13)
若经搜索得知，在旋转角度为α0时可以获得分数阶域的能量峰值，则回波信号的多普勒调频率和中心频率的估计值[11]为
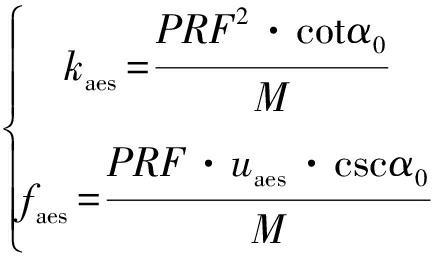
(14)
式中，M为DPCA信号方位向多普勒单元数，PRF2/M和PRF/M为量纲归一化引入的尺度因子。将上述FRFT处理过程用矩阵形式表示，首先需要构造旋转角度为α的离散FRFT矩阵，使得其与信号
矩阵相乘得到的结果仍然与直接利用传统FRFT处理得到的结果一致。
将旋转角度为α的离散FRFT矩阵记为Ψα，满采样的方位信号记为
记为Yα，这样可得
(15)
旋转角度为α的FRFT矩阵Ψα构造有多种方式，根据文献[10]中提出的基于特征分解的构造方式，由于原始回波数据的多普勒单元数为M，那么矩阵Ψα的大小为M×M，其具体表示为
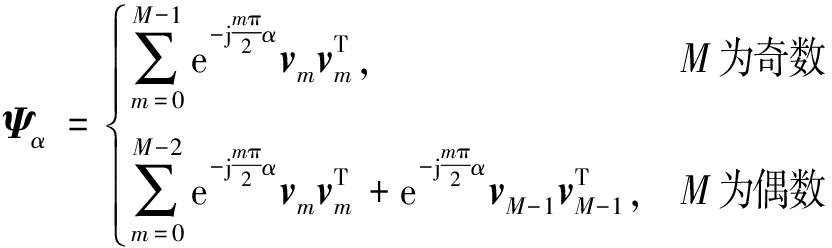
(16)
式中，vm是利用矩阵Ξ得到的特征向量，矩阵Ξ的表达式为
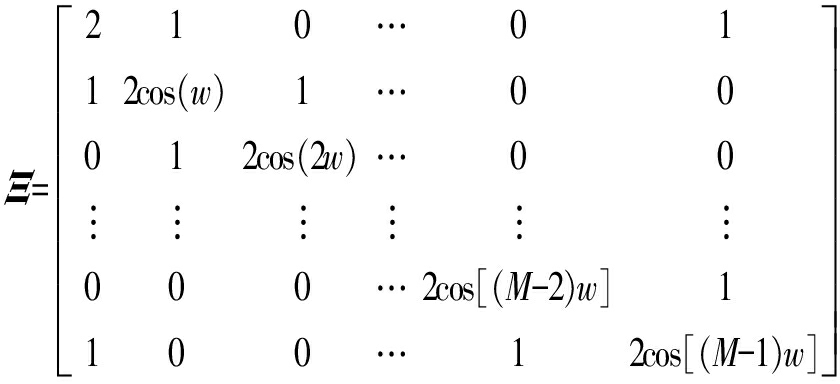
(17)
式中，w=2π/M。这样通过不同旋转角度的设定，可获得聚焦性能最好的变换结果，即为地面运动目标成像结果，同时利用得到的最优旋转角度可进行运动参数的估计。但是对于降采样的回波数据直接利用FRFT进行处理，会产生多普勒模糊。考虑到运动目标相对于观测场景具有一定的稀疏性，因此对于降采样的回波数据引入压缩感知理论进行参数估计处理。
降采样观测矩阵记为Φ，大小为M′×M。降采样的距离单元数据
记为
这样降采样过程可用下述表达式表示：
(18)
稀疏基矩阵
是FRFT矩阵Ψα的逆变换，由于Ψα满足正交特性，因此其逆变换矩阵同样满足正交性，因此其与观测矩阵的乘积
满足RIP性质。这样根据压缩感知理论，利用
通过求解下式得到Yα：
(19)
由于运动目标的参数信息是未知的，必须通过搜索才能够获得最优的旋转角度。因此对于不同的旋转角度均需要进行式(19)的求解，从而获得对应的Yα。根据上述分析得知，当得到的Yα聚焦性能最好的时候，所对应的旋转角度即为最优的旋转角度αaes，由于熵值越小，能量的聚焦性越好，因此选用最小熵对FRFT变换结果的归一化功率谱进行判决，将熵值最小的结果作为最优的旋转角度，也就是FRFT的最优阶数。所提方法与文献[8]相比，不同之处在于，文献[8]的方法存在收敛域和收敛空间的问题，某些情况只能够获得局部的最优值而无法获得全局的最优值，而所提方法能够获得一个全局的最优结果。这两种方法对目标运动参数的估计精度基本相当，均能实现对运动目标状态的准确描述。
4 仿真实验
为了验证本文方法的有效性，进行仿真验证并对仿真结果进行分析。雷达正侧视工作，载机的速度va为150 m/s，载机航线到地面成像中心的距离R0为10 km，发射信号载频f0为10 GHz(波长0.03 m)，脉冲宽度Tp为1.2 μs，带宽B为150 MHz，那么获得的距离向分辨率为1 m。成像积累时间Ta=2 s，PRF=512 Hz以及通道A和B之间的间隔d=5·va·PRI。设定地杂波服从瑞利分布，观测场景中有两个运动目标分别为P1和P2。令运动目标P1和P2的初始位置分别为(10 050, 0) m和(9 975, 30) m，运动速度分别为(5,20) m/s和(-10,-10) m/s。
全采样的回波数据方位向单元数是1 024，设定随机降采样的回波数据的方位向采样率为256，降采样率γ=1/4。对接收到的回波数据进行基于匹配滤波的脉压和地杂波对消处理，图2(a)为通道C所接收的回波信号在距离慢时间域的幅度图，图2(b)为DPCA处理后信号的幅度图。由图2(a)可见，通道A的回波信号中同时包含地杂波和运动目标信号，无法分辨出运动目标。经DPCA对消处理后，图2(b)中已经没有杂波信息，仅剩运动目标信息。对剩余的信号进行后续的运动目标参数估计处理。图2(c)为利用Hough变换估计运动目标的跨航迹维速度和距离位置，得到运动目标P1的跨航迹维速度为5.4 m/s，距离向位置为10 050 m。运动目标P2的跨航迹维速度为 -10.6 m/s，距离向位置为9 976 m。利用获得的运动目标跨航迹维信息对回波数据进行距离走动校正处理，得到的校正结果如图2(d)所示。可以看出，回波数据的距离走动已准确校正。
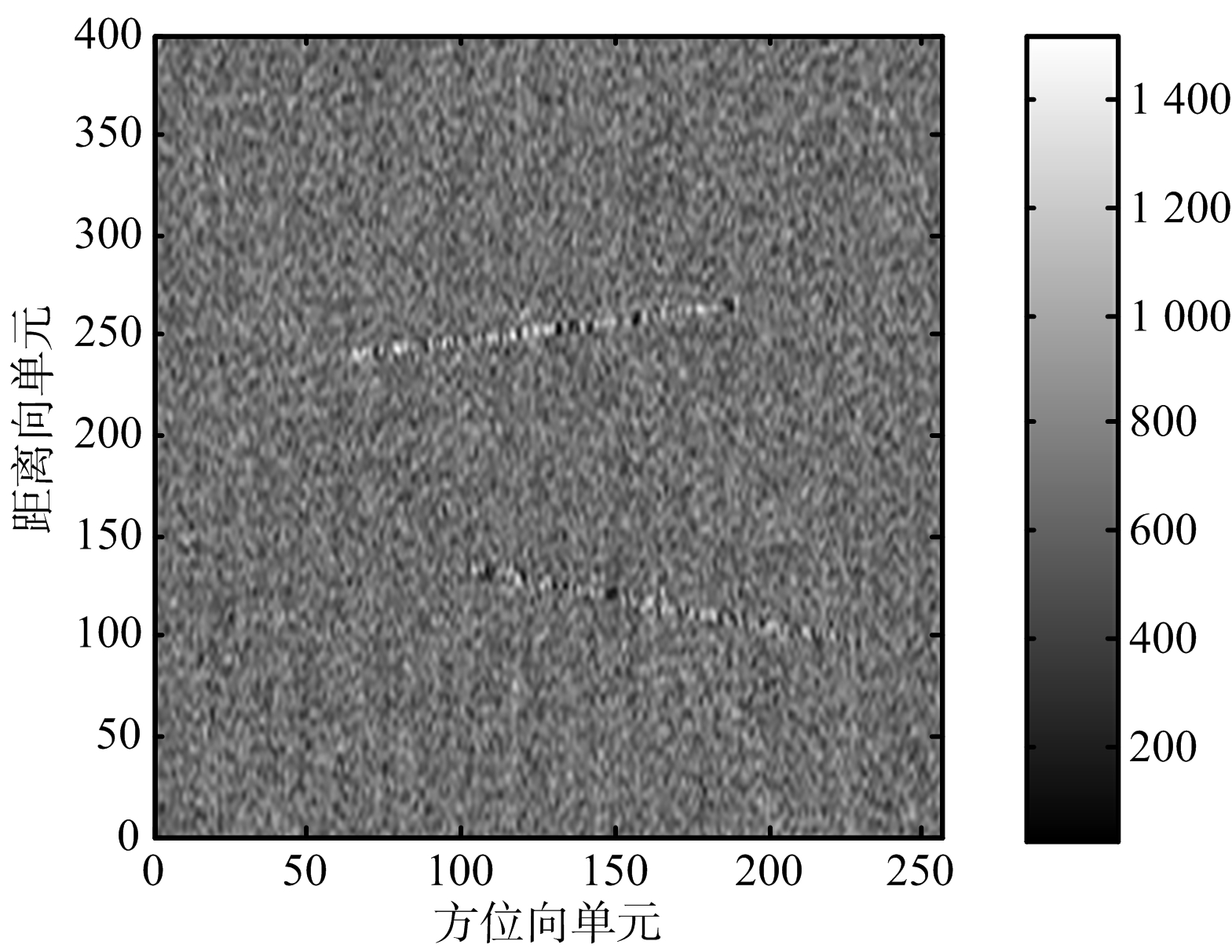
(a) 通道A回波信号幅度
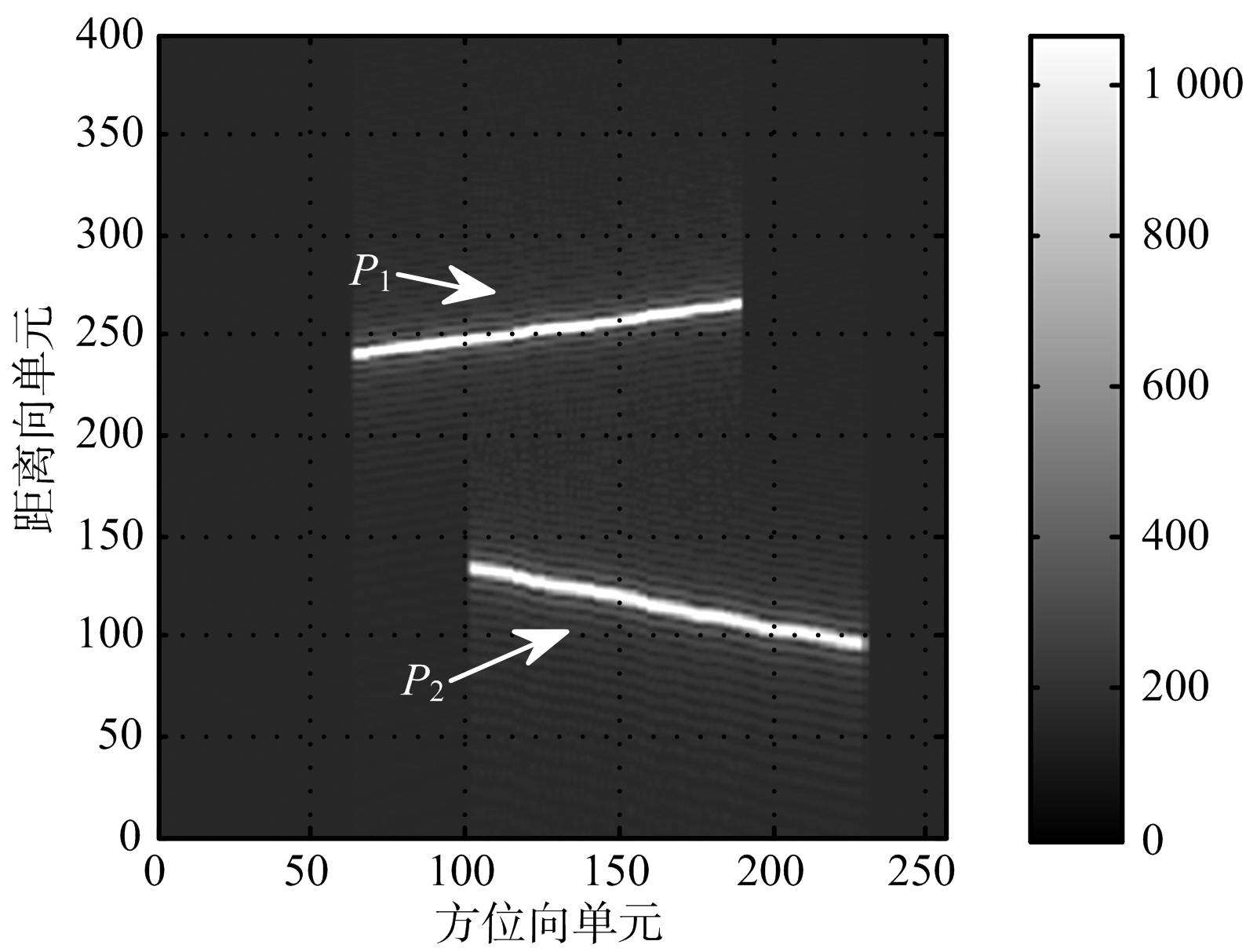
(b) DPCA对消后回波信号幅度
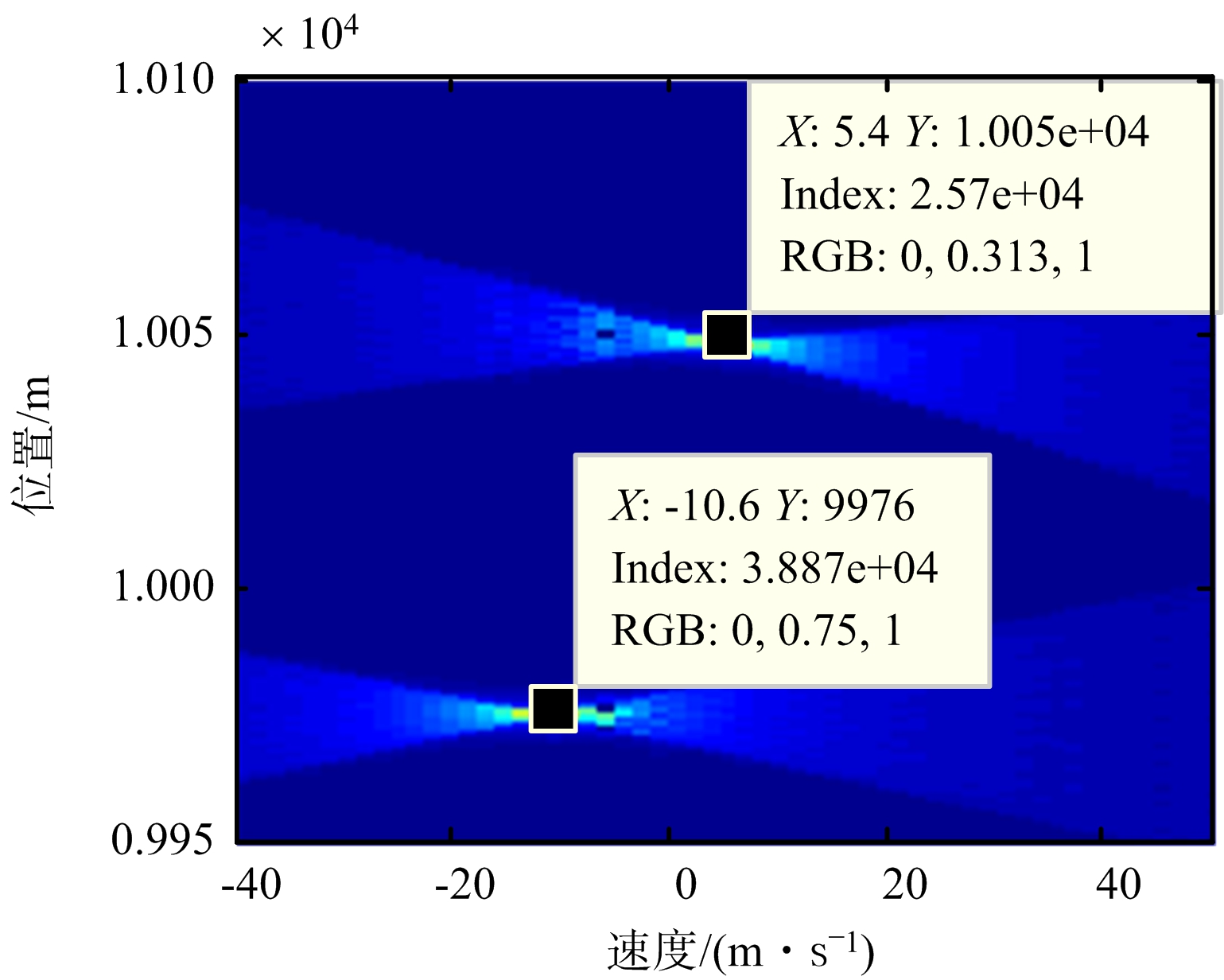
(c) Hough变换结果
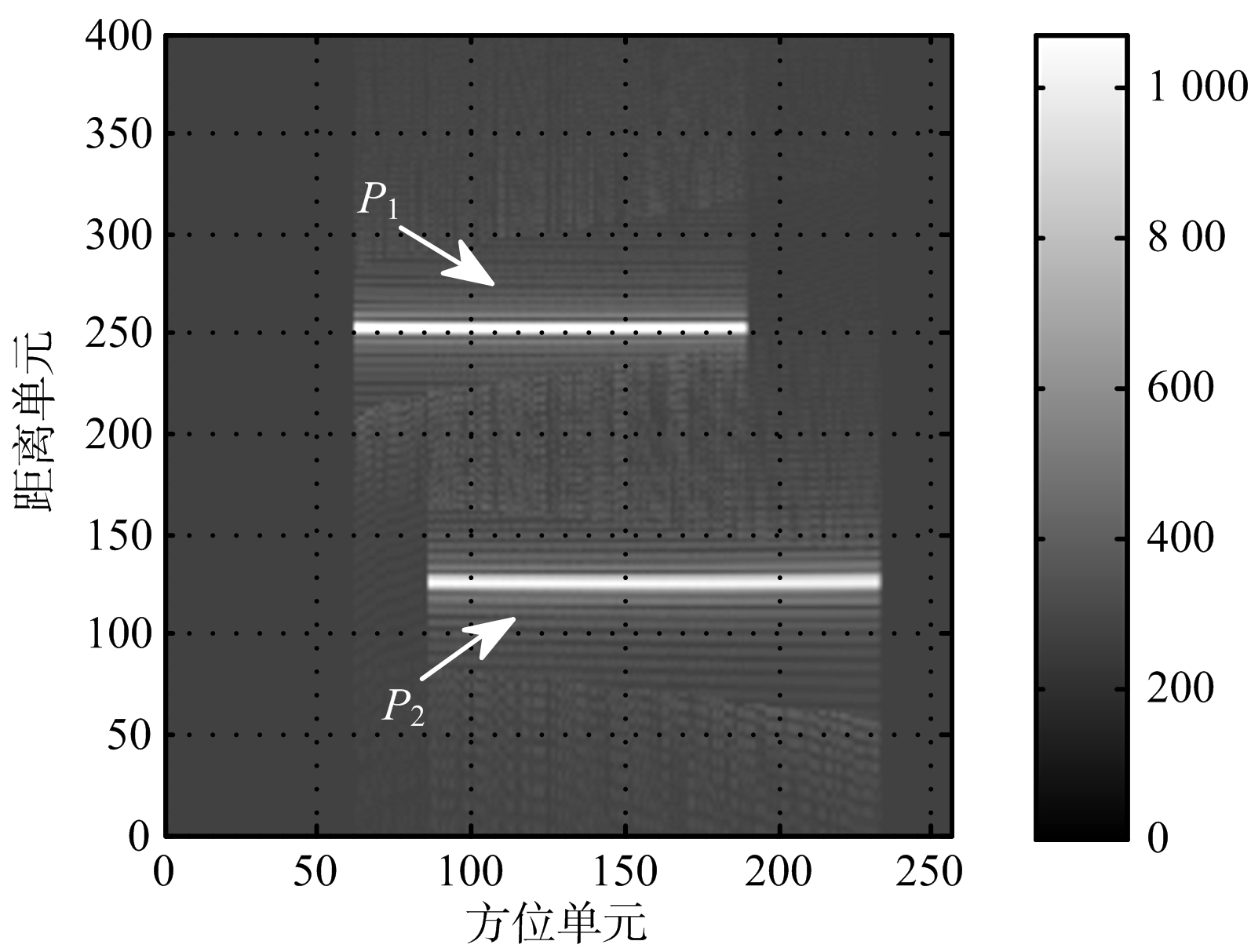
(d) 距离走动校正之后结果
图2 回波数据幅度与DPCA处理
进一步对距离走动校正后的数据进行方位维处理。对于随机降采样的回波数据，利用所提的离散FRFT方法进行处理。降采样率同样设为 γ=1/4。对如图2(d)所示的回波数据进行方位维处理。图3(a)是对运动目标P1所在的距离单元进行搜索得到的结果，图3(b)是对运动目标P2所在的距离单元进行搜索得到的结果。
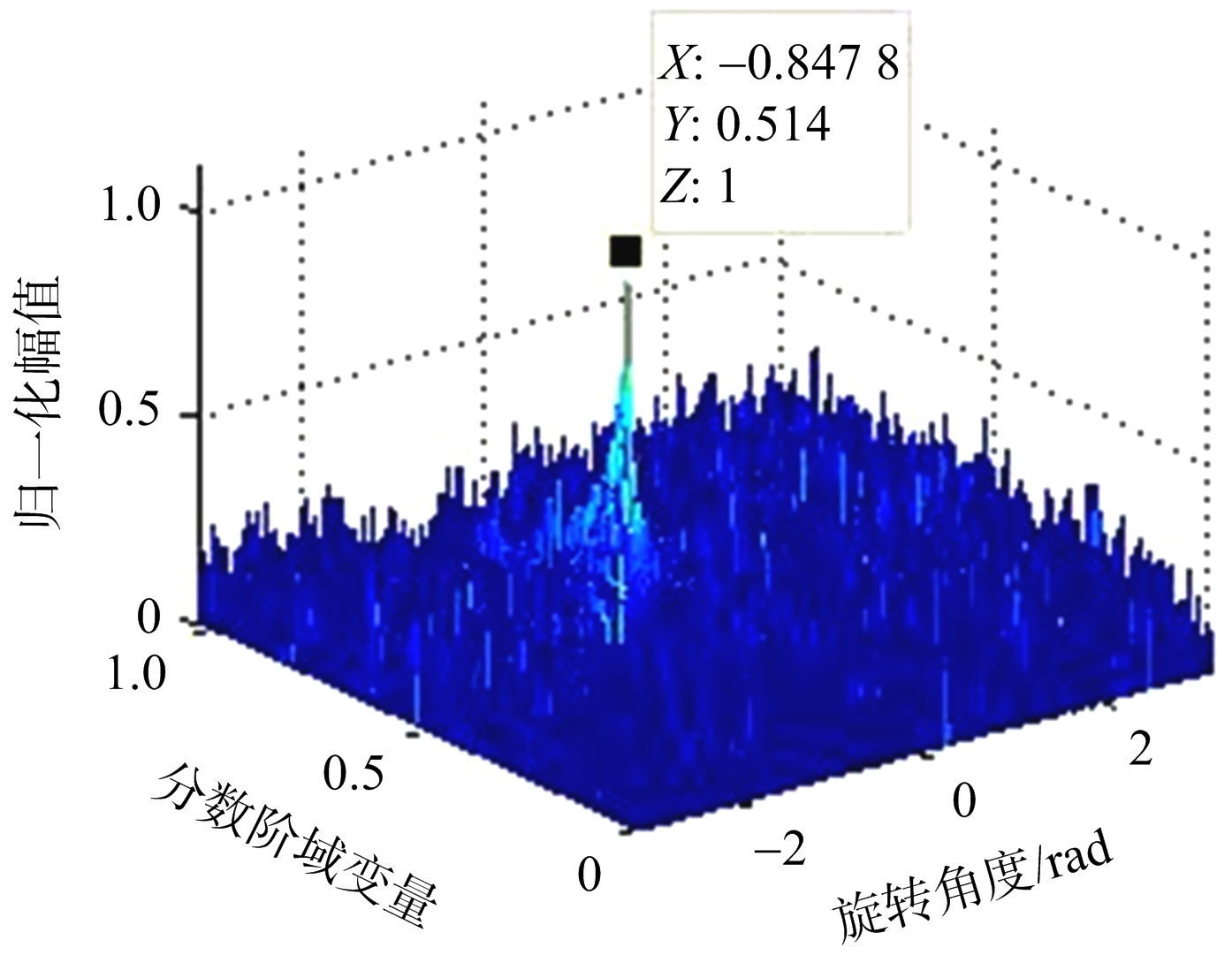
(a) P1最优角度搜索
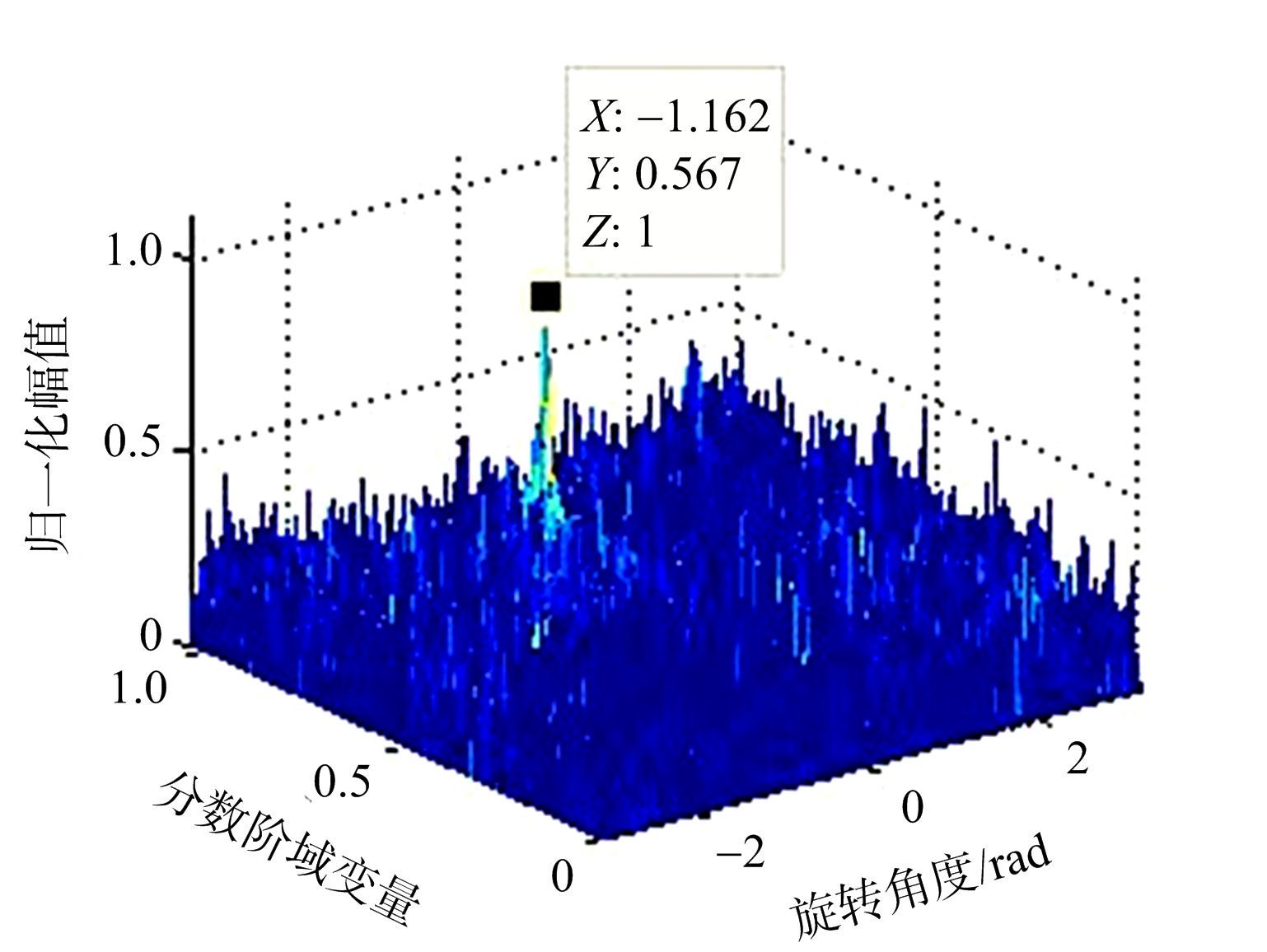
(b)P2最优角度搜索
图3 运动目标成像结果
利用上述搜索获得FRFT的最优阶数，进行运动目标的沿航迹维运动参数估计。由最优阶数和分数阶傅里叶域值可以获得：运动目标P1的中心频率为1.65 Hz，方位向信号的调频率为-115.59 Hz/s2；运动目标P2的中心频率为33.50 Hz，方位向信号的调频率为-168.16 Hz/s2。进一步通过式(10)的求解，地面运动目标沿航迹维运动参数的估计结果如表1所示。可以看出，估计得到的运动目标沿航迹维速度和位置的误差都比较小，能够对动目标的运动状态进行描述。
表1 运动目标的真实值与所提方法的估计结果对比
运动参数真实值估计值相对误差P1方位向速度vx/(m·s-1)2017.9910.02%P1方位向位置x1/m00.37—P2方位向速度vx/(m·s-1)-10-8.812%P2方位向位置x2/m3030.10.3%
5 结束语
本文针对低PRF条件下SAR系统运动目标参数估计问题进行研究。首先利用Hough变换估计了目标跨航向维的速度和位置信息，其次重点分析了基于离散FRFT矩阵的压缩感知模型构建与求解方法，实现了在低PRF条件下的地面运动目标参数估计处理，从而有望提高SAR系统预警探测范围和信息获取能力。
[1] ZHANG Yuan, SUN Jinping, LEI Peng, et al. High-Resolution SAR Based Ground Moving Target Imaging with Defocused ROI Data[J]. IEEE Trans on Geoscience and Remote Sensing, 2016, 54(2):1062-1073.
[2] CHEN Yichang, LI Gang, ZHANG Qun, et al. Refocusing of Moving Targets in SAR Images via Parametric Sparse Representation[J]. Remote Sensing, 2017, 9(8):795.
[3] 胡瑞贤,潘勉. 基于压缩感知的快速运动目标测速方法[J]. 雷达科学与技术, 2015, 13(3):284-290.
HU Ruixian, PAN Mian. Velocity Estimation Method of Fast Moving Target Based on Compressed Sensing Theory[J]. Radar Science and Technology, 2015, 13(3):284-290.(in Chinese)
[4] KRIEGER G, GEBERT N, MOREIRA A. Unambiguous SAR Signal Reconstruction from Nonuniform Displaced Phase Center Sampling[J]. IEEE Geoscience Remote Sensing Letters, 2004, 1(4):260-264.
[5] CALLAGHAN G D, LONGSTAFF I D. Wide-Swath Space-Borne SAR Using a Quad-Element Array[J]. IEE Proceedings: Radar, Sonar and Navigation, 1999, 146(3):159-165.
[6] WANG Weiwei, LIAO Guisheng, ZHU Shengqi, et al. Compressive Sensing-Based Ground Moving Target Indication for Dual-Channel SAR[J]. IET Radar, Sonar and Navigation, 2013, 7(8):856-866.
[7] LIU Yan, WU Qisong, SUN Guangcai, et al. Parameter Estimation of Moving Targets in the SAR System with a Low PRF Sampling Rate[J]. Science China: Information Sciences, 2012, 55(2):337-347.
[8] GU Fufei, ZHANG Qun, CHEN Yichang, et al. Parametric Sparse Representation Method for Motion Parameter Estimation of Ground Moving Target[J]. IEEE Sensors Journal, 2016, 16(21):7646-7652.
[9] 张振杰,郝向阳,刘松林,等. 基于Hough一维变换的直线检测算法[J]. 光学学报, 2016, 36(4):0412005.
[10] TAO Ran, ZHANG Feng, WANG Yue. Progress in the Discretization of Fractional Fourier Transform[J]. Science in China Series F: Information Sciences, 2008, 51(7):859-880.
[11] 邓彬,秦玉亮,王宏强,等. 一种改进的基于FrFT的SAR运动目标检测与成像方法[J]. 电子与信息学报, 2008, 30(2):326-330.
