0 引 言
近年来提出的多输入多输出(Multiple Input and Multiple Output, MIMO)雷达系统是一种新体制雷达，由于其存在诸多优点[1]，已经成为雷达领域的研究热点。MIMO雷达发射的信号是相互正交的，在接收端经过匹配滤波后能够分离出各发射信号。因此，MIMO雷达可以产生大量的虚拟阵元，扩展虚拟阵列孔径[2]，提高参数估计的性能。
波达方向角(Direction of Arrival, DOA)估计是阵列信号处理和雷达应用领域一项重要的研究内容，现如今有关MIMO雷达的DOA估计方法已经数不胜数，例如多重信号分类(Multiple Signal Classification, MUSIC)算法[3-4]、基于旋转不变技术的信号参数估计(Estimation of Signal Parameters via Rotational Invariance Technique, ESPRIT)算法[5-6]等。随着复杂的电磁环境以及信号的实时处理都将对硬件提出更为苛刻的要求，传统的MIMO雷达DOA估计方法已不能满足实际应用的需求。而压缩感知理论[7]的出现使得这一问题得以缓解，该理论指出：若信号可压缩或具有稀疏性，便能够以远低于Nyquist的采样频率，用随机采样获得的数据通过非线性重建算法高概率地恢复出原信号[8]。使用该理论不仅可以减少传输和存储的成本，降低采样数，而且能够提高参数估计的精度，克服了传统DOA估计方法的不足。在稀疏理论的框架下，MIMO雷达的DOA估计问题可以转化为求解l0范数最小化问题。由于该问题是一个非确定性多项式(NP-hard)问题，可将其转化为l1范数最小化问题来进行求解。文献[9]通过建立稀疏重构模型，采用二阶锥规划的方法构造出阵列流型的冗余字典，结合l1范数凸优化方法和奇异值分解(Singular Value Decomposition, SVD)，提出了l1-SVD算法。加权l1-SVD[10]算法通过降维和SVD分解降低了稀疏信号重构的复杂度，并且构造加权矩阵提高了多测量向量问题中MIMO雷达DOA估计的精度。然而l1范数最小化问题是凸优化问题，通常采用线性规划进行求解，这使得加权l1-SVD算法的计算量巨大，进行实时处理较为困难。文献[11]则将l0范数最小化问题转化为平滑函数极值求解问题，提出了一种平滑l0范数(Smoothed l0 Norm, SL0)算法，该算法的运算效率较高，在保证相同精度的条件下，能够比基追踪算法的重构速度快2～3倍。因此，文献[12]提出了一种基于加权SL0算法的MIMO雷达DOA估计方法，该方法对降维后的协方差矩阵进行矢量化运算，并利用噪声和信号子空间的正交性理论来构造加权向量，从而将MIMO雷达DOA估计问题转化为加权平滑函数极值求解问题。然而，在信号传播的过程中，由于同频干扰和多径效应会导致入射到阵列中的信号存在相干信号源，相干信号源的存在将会导致数据协方差矩阵的秩产生退化。因此，利用加权SL0算法来对MIMO雷达的相干信源进行DOA估计时，协方差秩的退化会导致稀疏重构模型存在一定误差，构造的加权向量无法提取出有效的噪声子空间，从而影响加权SL0算法的DOA估计性能。
针对加权SL0算法处理相干信源的不足，本文提出一种基于协方差匹配SL0算法的MIMO雷达DOA估计方法。该方法根据协方差匹配准则建立目标函数，并将其转化为半正定规划问题，利用凸优化方法进行求解，使得协方差矩阵恢复Toeplitz特性，利用修正后的协方差矩阵进行MIMO雷达的DOA估计，以达到解相干的目的。此外，利用协方差逆矩阵的高阶幂来近似噪声子空间，在计算加权向量时无须预知信源数目。仿真分析表明，本文算法能够有效地对相干信源进行DOA估计。
1 相干信源下的MIMO雷达信号模型
假设系统为窄带单基地MIMO雷达系统，该系统有M个发射阵元和N个接收阵元，阵元间距分别为dt和dr，为形成最大孔径的低冗余虚拟阵列，本文选取dt=Nλ/2，dr=λ/2，其中，λ为工作波长。假设有P个远场相干信源，其入射角度分别为θ1,θ2,…,θp。MIMO雷达的接收阵列信号经匹配滤波后，在t次快拍时的接收信号为
x(t)=[at(θ1)⊗ar(θ1),…,at(θp)⊗ar(θp)]·
s(t)+n(t)
(1)
式中：at(θp)=[1,ejπsin(θp),ejπ2sin(θp),…,ejπ(M-1)sin(θp)]T∈CM×1为发射阵列的导向向量，其中，(·)T为矩阵转置；ar(θp)=[1,ejπsin(θp),ejπ2sin(θp),…,ejπ(N-1)sin(θp)]T∈CN×1为接收阵列的导向向量；⊗为Kronecker积；发射信号s(t)=
∈CP×1,其中，sp(t)(p=1,2,…,P)为相干信号源；n(t)∈CMN×1为高斯白噪声向量。令阵列流型矩阵为A=[at(θ1)⊗ ar(θ1),…,at(θp)⊗ar(θp)]∈CMN×P,取J个快拍的接收信号矩阵为
X=AS+N
(2)
式中：X=[x(1),x(2),…,x(J)]∈CMN×J为接收信号矩阵；S=[s(1),s(2),…,s(J)]∈CP×J为信号矩阵；N=[n(1),n(2),…,n(J)]∈CMN×J为高斯白噪声矩阵。由式(2)可以得到信号的协方差矩阵为
RX=E(XXH)=ARSAH+RN
(3)
式中：(·)H为共轭转置运算；E(·)为取数学期望；RS为信源的自相关矩阵；RN为噪声的自相关矩阵。在实际应用中，通常选取有限的采样点，接收数据的协方差矩阵采取近似估计，即
(4)
式中：J为采样数据的快拍数；
为RX的估计值。
若所有的信源都不相干时，信号的相关矩阵RS是一个对角阵，其秩与信源数目相等，而当存在相干信源时，RS的秩将会退化，从而影响矩阵RX的秩，即协方差矩阵的秩将少于信源数目。此时，若采用加权SL0算法[12]进行MIMO雷达DOA估计时，将会使得MIMO雷达的稀疏重构模型失配，同时由于无法有效提取噪声子空间而使得加权向量计算失效，从而导致该算法的DOA估计性能恶化。
2 基于协方差匹配SL0算法的MIMO雷达DOA估计方法
为了解决加权SL0算法在估计MIMO雷达相干信源DOA估计时的问题，本文采用协方差匹配准则对协方差矩阵进行处理。基于协方差匹配准则的目标函数[13]为
f=
=
(5)
式中：‖·‖F为Frobenius范数；(·)-1为求逆；tr(·)为求迹；RX为信号协方差的理论值。文献[14]指出，若信号与噪声是不相关的，则RX可写为
RX(θ,ξ,τ)=E(XXH)=
A(θ)RS(ξ)AH(θ)+RN(τ)=
D(θ,ξ)+RN(τ)
(6)
式中：θ=[θ1,θ2,…,θP]；RN(τ)=E(NNH)=diag(τ)为噪声的协方差矩阵，其中，
为噪声功率构成的1×MN维矢量，diag(τ)为由矢量τ构成的对角矩阵；D(θ,ξ)=A(θ)RS(ξ)AH(θ)，其中，RS(ξ)= E(SSH)为信号的协方差矩阵，由于相干信源的存在，E(SSH)不再是对角矩阵，若信源完全相干，其秩将退化为1，导致信源数目大于信号子空间的维数。为了使得协方差矩阵D(θ,ξ)恢复满秩，实现解相干，故令D(θ,ξ)=A(θ)RS(ξ)AH(θ)= A(θ)diag(ξ)AH(θ)，其中，
为由信号功率构成的1×P维矢量，D(θ,ξ)为Hermitian Toeplitz矩阵。由式(6)可知，协方差矩阵的理论值RX是关于未知参数θ，ξ和τ的非线性函数，根据协方差匹配准则，可得
(7)
式中，
为(θ,ξ,τ)的估计值。将式(6)和式(7)代入式(5)，则未知参数的估计可以等效为
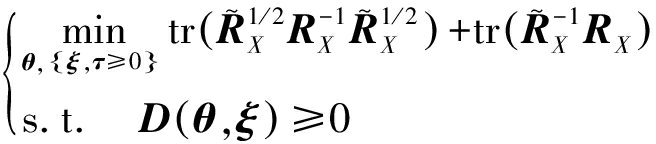
(8)
式中，{ξ,τ≥0}为向量ξ和τ中的元素都大于等于零。式(8)是非线性函数，故不能直接对其进行求解，可将其转化为半正定规划问题：
f⟺
⟺
(9)
式中，Y为一个大小为MN×MN的矩阵。采用凸优化工具包求解式(9)，可直接求得信号协方差矩阵的估计值
此时，
为一个Hermitian Toeplitz矩阵。
根据向量化运算的性质，将协方差矩阵
转化为
y=
(A*⊗A)vec(RS)+vec(RN)
(10)
式中：vec(·)为对矩阵向量化；(·)*为矩阵共轭；⊗为Kronecker积。由文献[12]可知，式(10)可进一步转化为
y=(A*⊙A)ys+yn
(11)
式中：⊙为Khatri-Rao积；
CP×1；yn=vec(RN)∈C(MN)2×1。根据稀疏重构理论，将搜索空域[-90°,90°]按等角度间隔划分，L为划分总单元数，构造一个冗余字典
其中Aθ=[at(θ1)⊗ar(θ1),…,at(θL)⊗ar(θL)]∈
表示空域内所有可能的来波方向。这样，可将MIMO雷达的DOA估计问题转化为一个最优化问题，其求解模型为
(12)
式中，
为l0范数，即向量非零元素的个数。
对协方差矩阵
进行特征分解，可以得到
(13)
式中：US,UN分别为信号子空间和噪声子空间；ΛS=diag[λ1,λ2,…,λP]为由信号特征值构成的对角矩阵；τ2为噪声功率；I为相应阶次的单位矩阵。对求逆，可得
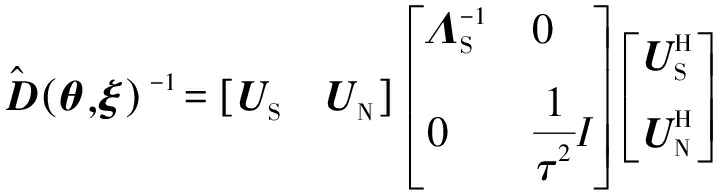
(14)
进一步推导，得
(15)
式中：m为任意正整数；λi(i=1,2,…,P)为信号特征值。由文献[15]知，式(15)中τ2/λi<1，因此，当m→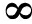
时，有
所以当m趋近无穷大时，式(15)趋近于噪声子空间。于是，本文采用如下的加权向量：
rw=
(16)
式中：rw=[rw1,rw2,…,rwL]T为加权向量, rwi(i=1,2,…,L)为矢量rw中的第i个加权系数。加权SL0算法通过构造加权平滑函数来逼近式(12)中的l0范数，即
(17)
式中：
为函数的变量；σ为函数的形状参数。由文献[12]可知，式(12)可采用下式近似求解：
(18)
式中，
其中，σ的大小可以用来调节
的平滑程度及近似
的程度。σ越大，则函数越平滑，所包含的局部极大值越少，近似的精度越低；反之，函数越不平滑，所包含的局部极大值越多，近似的精度越高。因此，为了避免获得局部极大值，选择一组合适的递减序列[σ1,σ2,…,σK]。对序列中的每一个σ值采用最速上升法求解的最大值，然后将该最大值投影到可行集上。
本文算法步骤总结如下：
步骤1 利用MIMO雷达的虚拟阵列输出信号X来计算协方差矩阵
步骤2 为了恢复MIMO雷达协方差矩阵的秩，采用协方差匹配准则重构协方差矩阵，得到估计值
并将其向量化，即
计算过完备字典
步骤3 根据式(16)计算加权向量
并构造连续函数
构造稀疏表示模型：
步骤4 采用SL0算法求解稀疏表示模型：
初始化：
1) 设初始值v0=BT(BBT)-1y；
2) 选取一组合适的序列[σ1,σ2,…,σK],且σk+1=ρσk,0<ρ<1，σ1=4max{|v0|}。
算法迭代：
For k=1,2,…,K
1) 令σ=σk；
2) 进行Q次迭代求解
的全局最大值，并将该最大值投影到可行集上
a) 令
b) For q=1,2,…,Q
(a) 计算
(b) 计算
其中u为步长
(c) 将
投影到可行集上，
c) 令
最终解
步骤5 通过搜索的谱峰位置确定目标的DOA。
3 仿真结果及分析
为验证本文算法的有效性，本节设计了几组MUSIC算法、m-CAPON算法、加权SL0[12] (Reweighted Smoothed l0 Norm, RSL0)算法、加权 l1-SVD(Reweighted l1-SVD, RL1-SVD)算法[10]和本文算法的对比试验。在仿真中，MIMO雷达的发射阵元数和接收阵元数均为4，发射阵元间隔dt=Nλ/2，接收阵元间隔dr=λ/2，在空间角度范围[-90°,90°]进行等间隔划分，其中角度间隔为0.05°。DOA估计的均方根误差定义为
其中，P为远场窄带信号的数目，
为真实目标θp在第i次蒙特卡罗实验中的目标DOA的估计值，Z为总的蒙特卡罗实验次数。在本文算法以及加权SL0算法中，选取σ1=4max{|v0|}，σoff=0.000 4，内循环次数L=5，步长u=2，衰减因子α=0.7。本文方法在计算加权向量时以及m-CAPON算法中，选取m=4。
仿真实验1 设置两个相干信源的DOA分别为-30°和20.6°，信噪比为0 dB。图1为本文算法、MUSIC算法、m-CAPON算法以及加权SL0算法的谱估计图，其中，快拍数J=50。由图1可知，本文算法在真实目标角度处存在较尖的谱峰，因此本文方法能有效实现相干信源的DOA估计，而其他算法均无法估计相干信源的DOA。
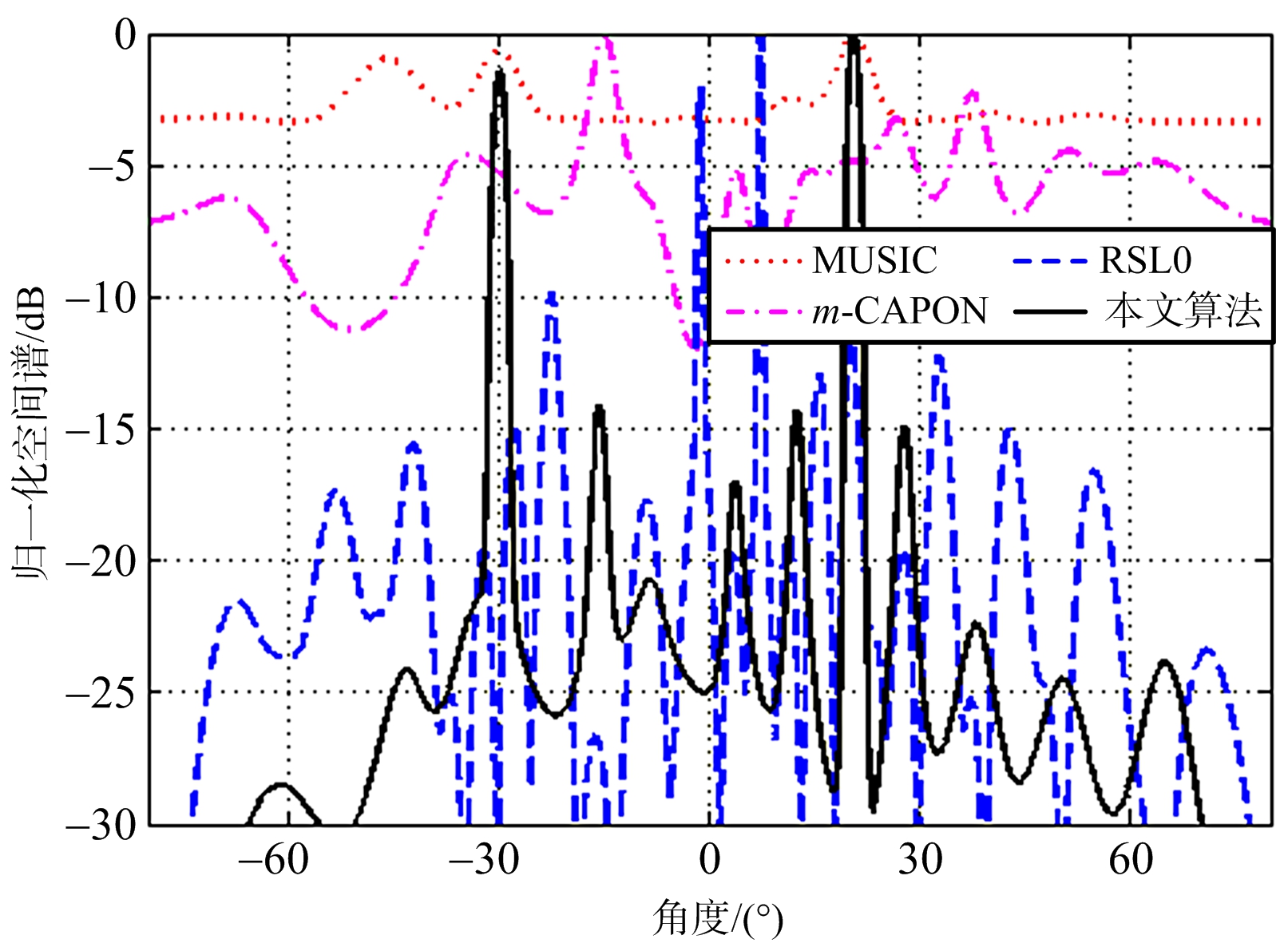
图1 各种算法的DOA估计谱图
仿真实验2 图2为各种算法的均方根误差与信噪比的变化关系，其中，CRB[16]是DOA估计方法有效性能的一种评价标准，是任何无偏方向估计方差的下界。设置两个相干信源的DOA分别为-30°和20.6°，令信噪比由-5～20 dB变化，进行200次蒙特卡罗实验，快拍数J=300。由图2可知，本文算法通过协方差匹配技术把相干信源的协方差矩阵的秩进行了恢复，达到了解相干的目的，因此其DOA估计精度明显高于其他算法，且其估计性能最为接近CRB。
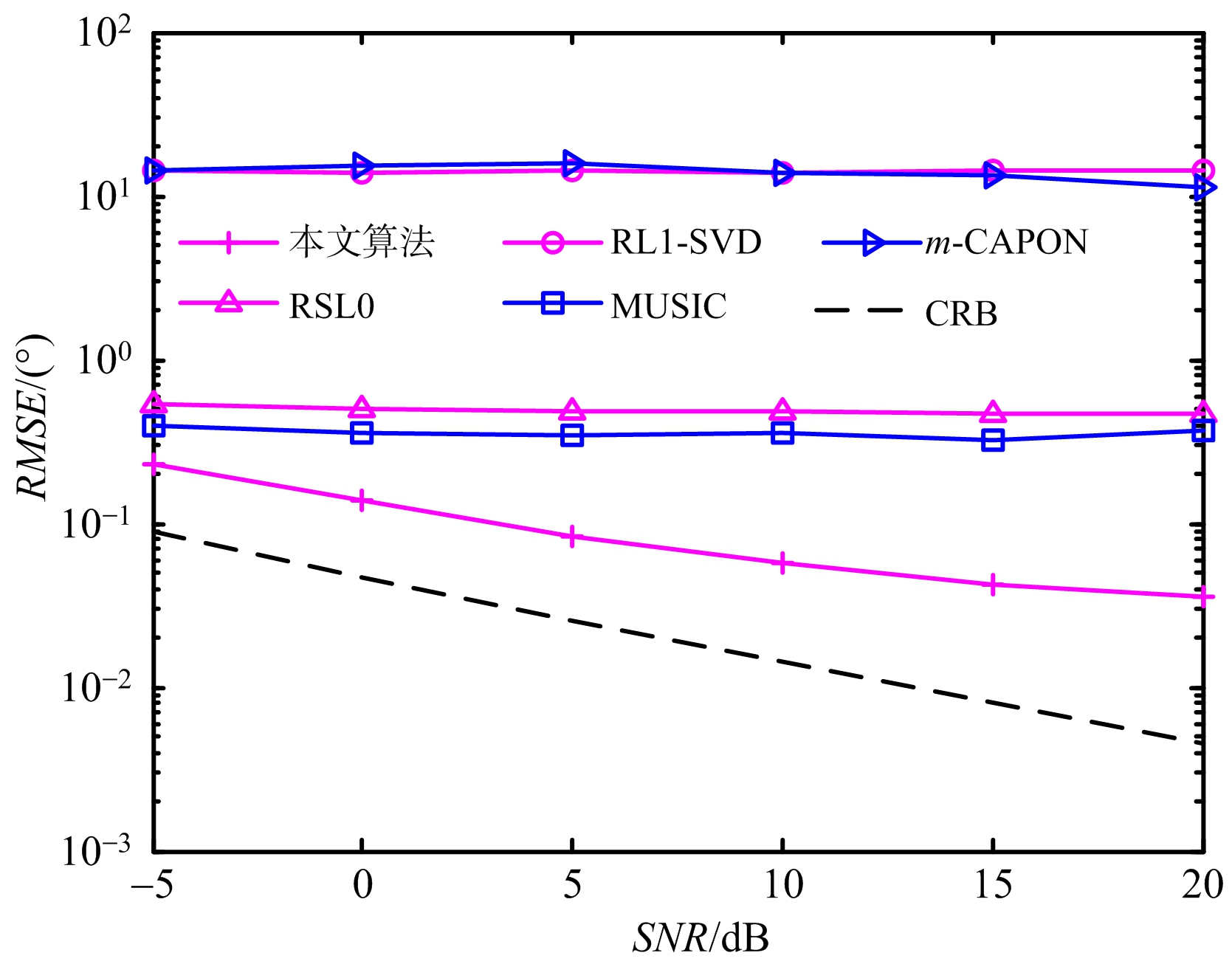
图2 各种算法的DOA估计均方根误差与信噪比的变化关系
仿真实验3 图3为各种算法的均方根误差随快拍数的变化关系。设置两个相干信源的DOA分别为-30°和20.6°，信噪比为5 dB，进行200次蒙特卡罗实验，快拍数J由50～350变化。由图3可知，随着快拍数的增加各算法的DOA估计精度均有不同程度的提高，而本文算法的DOA估计性能始终保持最优，表明其具有良好的相干信号处理能力。
图3 各种算法的DOA估计均方根误差随快拍数的变化关系
4 结束语
在相干信源的条件下，MIMO雷达协方差矩阵的秩将退化，即信号子空间的维数少于信源数目，使得稀疏重构模型失配以及加权向量计算失效，从而导致加权SL0算法的DOA估计性能恶化。本文提出了一种基于协方差匹配SL0算法的MIMO雷达DOA估计方法，该方法通过协方差匹配技术估计出新的满秩协方差矩阵，达到了解相干的目的，同时不再采用特征值分解而采用协方差逆矩阵的高阶幂构造加权向量。仿真分析表明，本文算法可以有效地解决MIMO雷达相干信源的DOA估计问题。
[1] 朱丽芳,任翠霞,李军,等. 一发多收MIMO雷达的目标关联特性[J]. 雷达科学与技术, 2016, 14(4):387-392.
ZHU Lifang, REN Cuixia, LI Jun, et al. Association Characteristics of MIMO Radar with Single Transmitting Station and Multiple Receiving Stations[J]. Radar Science and Technology, 2016, 14(4):387-392. (in Chinese)
[2] 梁浩,崔琛,余剑. 基于ESPRIT算法的十字型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2016, 38(1):80-89.
[3] ZHOU Ming, ZHANG Xiaofei. Joint Estimation of Angle and Polarization for Bistatic MIMO Radar with Polarization Sensitive Array Using Dimension Reduction MUSIC[J]. Wireless Personal Communications, 2015, 81(3):1333-1345.
[4] 刁鸣,李永潮,高洪元. 酉求根MUSIC算法在双基地MIMO雷达中的应用[J]. 哈尔滨工程大学学报, 2016, 37(9):1292-1296.
[5] 窦道祥,李茂,何子述. 单基地MIMO雷达降维Power-ESPRIT算法[J]. 雷达科学与技术, 2015, 13(1):76-80.
DOU Daoxiang, LI Mao, HE Zishu. Reduced-Dimensional Power-ESPRIT Algorithm for Monostatic MIMO Radar[J]. Radar Science and Technology, 2015, 13(1):76-80. (in Chinese)
[6] WANG Wei, WANG Xianpeng, SONG Hongru, et al. Conjugate ESPRIT for DOA Estimation in Monostatic MIMO Radar[J]. Signal Processing, 2013, 93(7):2070-2075.
[7] DONOHO D L. Compressed Sensing[J]. IEEE Trans on Information Theory, 2006, 52(4):1289-1306.
[8] 康乃馨,何明浩,王冰切,等. 基于压缩感知的多径LFM信号参数估计[J]. 雷达科学与技术, 2016, 14(3):291-296.
KANG Naixin, HE Minghao, WANG Bingqie, et al. Parameter Estimation of Multipath LFM Signal Based on Compressive Sensing[J]. Radar Science and Technology, 2016, 14(3):291-296. (in Chinese)
[9] MALIOUTOV D, CETIN M, WILLSKY A S. A Sparse Signal Reconstruction Perspective for Source Localization with Sensor Arrays[J]. IEEE Trans on Signal Processing, 2005, 53(8):3010-3022.
[10] WANG Xianpeng, WANG Wei, LIU Jing, et al. A Sparse Representation Scheme for Angle Estimation in Monostatic MIMO Radar[J]. Signal Processing, 2014, 104:258-263.
[11] MOHIMANI H, BABAIE-ZADEH M, JUTTEN C. A Fast Approach for Overcomplete Sparse Decomposition Based on Smoothed l0 Norm[J]. IEEE Trans on Signal Processing, 2009, 57(1):289-301.
[12] LIU Jing, ZHOU Weidong, JUWONO F H, et al. Reweighted Smoothed l0-Norm Based DOA Estimation for MIMO Radar[J]. Signal Processing, 2017, 137:44-51.
[13] 冯明月,何明浩,韩俊,等. 基于协方差拟合旋转不变子空间信号参数估计算法的高分辨到达角估计[J]. 上海交通大学学报, 2017, 51(9):1145-1152.
[14] OTTERSTEN B, STOICA P, ROY R. Covariance Matching Estimation Techniques for Array Signal Processing Applications[J]. Digital Signal Processing, 1998, 8(3):185-210.
[15] 张涛麟,刘颖,廖桂生. 一种未知信源数的高分辨DOA估计算法[J]. 电子与信息学报, 2008, 30(2):375-378.
[16] STOICA P, NEHORAI A. Performance Study of Conditional and Unconditional Direction-of-Arrival Estimation[J]. IEEE Trans on Acoustics, Speech and Signal Processing, 1990, 38(10):1783-1795.
