0 引 言
阵列信号处理在无线通信、雷达信号处理、水声探测、医学诊断等领域都有广泛的应用[1-2]。例如在空地双基地雷达中,雷达系统由无人机搭载发射器,如果采用传统的脉冲追赶方式[2],要求比较高的时间准确度和空间定位精度。但在实际情况中,由于空中平台的稳定度较低,发射波束指向不稳定,导致来波方向无法与实际情况相符,造成一定的空域覆盖损失。而盲波束形成算法只需要一定的先验信息而不需要训练数据,是阵列天线在复杂环境中有效工作的迫切要求。
现有的盲波束形成算法中,最常见的比如利用信号的恒模特性[3]、循环平稳特性[4]、高阶统计量特性[5]等。但是其主要适用于窄带信号的分析中。国内分析宽带信号的文献较少。其思路一般是将其理解为卷积混合盲源分离问题[6-7],再利用盲解卷积算法进行求解。盲解卷积算法主要包括时域算法和频域算法两大类[8]。时域算法需要设计FIR滤波器达到解卷积的目的,而滤波器阶数上升会造成计算量大幅增加,并且系统的稳定性也是必须考虑的问题。频域算法主要是利用傅里叶变换,将时域问题转换为频域问题,将一个卷积混合问题转化为瞬时混合问题,利用时域上的盲分离算法如H-J扩展算法即可完成波束形成。但是由于各频点输出独立,存在子带输出排序上的模糊问题,导致性能下降。
文献[9-11]将时频分析理论应用到盲波束形成算法中,通过在时频域上的分析估计出导向矢量,在性能方面较之传统的波束形成有一定的优势,但是计算过于繁琐。本文从宽带信号的特性出发,利用分数阶模型分析提取信号。理论分析和仿真实验表明,在快拍数较少、信噪比较低的情况下,所提算法具有更好的有效性和稳健性。
1 信号模型
1.1 宽带信号模型
有M阵元的均匀线阵,以第一个阵元为参考原点,阵元间隔是d。假设有Q个线性调频信号入射到平面上,第m个阵元的输出为
(1)
式中,τm,q=(k-1)dsinθq/C,sq(t)=ejπ(2fq0t+μqt2), C为光速,τm,q为第q个信号关于参考阵元的延时,fq0为第q个信号的初始频率,μq为第q个信号的调频率,nm(t)为与信号无关的高斯白噪声,θq为第q个信号的入射角度。
写成向量的形式:
(2)
式中,第q个信号的导向矢量是
aq(t)=[1 e-j2π(fq0+μqt)τ1,qejπμq(τ1,q)2…
e-j2π(fq0+μqt)τM,qejπμq(τM,q)2]T
(3)
1.2 信号的分数阶域模型
对于线性调频信号,找到适当的分数阶参数,可以得到较好的能量聚集特性[12]。对于sq(t)进行分数阶傅里叶变换![]() 表示最优阶次,代入αq0可得
表示最优阶次,代入αq0可得

(4)
式中,T为观测时间长度。为了能在离散域进行计算,采用Ozaktas的离散算法[12],得到离散的分数阶傅里叶变换。以采样率Fs对sq(t)完成时域上的离散:
s1,q(n)=ejπ(2fq0(n/Fs)+μq(n/Fs)2)
(5)
对其进行分数阶傅里叶变换,对应最优阶数αq0=-cot-1(μq):
(6)
对每个阵元的接收数据进行最优阶次分数阶傅里叶变换,可得
Sm,q(αq0,km,q)=Am,q(τm,q)S1,q(αq0,k)
(7)
Am,q(τm,q)=ejπ/Nτm,q(-2kq0Fscscαq0)ejπ/N(τm,q)2(-Fs2sinαq0cosαq0)
(8)
综合所有阵元的输出可得
(9)
由于线性调频信号在最优阶的变换下除峰值点以外其他取值比较小,可以把它看作干扰项略去。改写为
X(αq0,km,q)=Aq,m(τm,q)Sq(αq0,kq0)+
Nm(αq0,km,q)
(10)
提取每个阵元上的Q个峰值点,组成新的空时频输出矩阵![]() 的输出:
的输出:

(11)
考虑到模型建立与实际情况的关系,下面的分析中做出以下3点假设:
1) 调频率不一样,可以将其分离;
2) 信号的来向不同,也就是导向矢量之间是相互独立的;
3) 采集到的信号是一个脉冲内的信号。
2 基于分数阶傅里叶域滤波的盲波束形成算法
对于线性调频信号而言,分数阶傅里叶变换具有独特的优势。在最优阶的变换下具有最好的能量聚集性。据此可以把信号的能量集中于很小的一个部分,通过滤波的方式获得信号的大部分能量,根据这些信息便可以很好地估计出实验需要的导向矢量,再根据波束形成算法对特定的方向完成接收和抑制的作用。
2.1 分数阶傅里叶域峰值滤波
通过上述分析可知,在最优阶数下,线性调频信号在分数阶域会出现能量的聚集效应,也就是会出现单峰值点,这个峰值就是线性调频信号在分数阶域的表示,它包含了线性调频信号的所有信息,如图1所示。据此,可以构造一个峰值滤波器,最大限度地分离特征不同的信号,并且滤除噪声。

(a) 有用信号在不同阶下的幅值分布

(b) 干扰信号在不同阶下的幅值分布
图1 不同信号的幅值分布图
2.2 导向矢量的估计
对每个阵元接收到的信号作峰值滤波后可以得到如式(11)所示的空时频输出矩阵,对于每一个信号而言,对应![]() 中某一M×1维的列向量,其中
中某一M×1维的列向量,其中
(12)
可以从中看出,![]() 仅与延时τm,1=(k-1)·dsinθ1/C有关(式中1表示信号1的相关参数)。推广可得
仅与延时τm,1=(k-1)·dsinθ1/C有关(式中1表示信号1的相关参数)。推广可得
(13)
由式(13)可得每个信号的估计导向矢量,其中q表示第q个信号,m表示第m个阵元。
2.3 干扰协方差矩阵
滤波后得到的干扰信号同样对其作分数阶域的峰值滤波,得到与有用信号导向矢量估计相似的干扰导向矢量估计,而对其作协方差的运算即可得到MVDR准则中的关于分数阶域的空时频输出矩阵协方差矩阵:
(14)
式中,![]() 表示除去有用信号一列的空时频输出矩阵。
表示除去有用信号一列的空时频输出矩阵。
计算时为了提高整个系统的稳健性,采用文献[13]中提到的对角加载技术改造协方差矩阵,如下式:
(15)
式中,load表示加载系数,具体数值根据环境中的信噪比确定。
2.4 波束形成
根据MVDR波束形成理论,得到导向矢量和干扰协方差矩阵,如下式计算权值:

(16)
根据Lagrange乘数法,可以得到最终需要的最优权矢量,通过最优权矢量便可以形成所需要的波束:
(17)
2.5 算法分析
本小节为更清晰地展示计算过程,将计算步骤按顺序列出,如表1所示。
文献[8]的运算主要集中在时频变换的计算上,本文算法的计算量主要集中在分数阶域滤波上,利用FFT算法可以极大程度地减少运算量,提高运算效率。具体运算量对比如表2所示。
通过分析可知,文献[8]算法随着N的增大快速增加,而本文算法利用FFT算法可以很好地降低运算量,且FFT算法在工程实践中已经有成熟的算法,所以该算法在工程实践中有更好的应用前景。
表1 本文算法

初始化:阵列接收数据X(t) 1) 对参考阵元上的数据做阶次p(步长是0.01,范围是0到-1)的FRFT,寻找单峰值点(αq0,kq0),提取前K个单峰值点作为信号个数,即K=Q。对每个信号作峰值滤波后分离得到不同的信号。2) 对其他阵元作变换阶次为pq0的FRFT,得到不同的峰值点(αqm,kqm),由式(10)得到各阵元的空时频输出。3) 根据式(11)构造出阵列的空时频输出矩阵输出。4) 提取X的每一列,由式(13)估计出第q个信号的导向矢量a^lq,同时根据式(14)和式(15)估计协方差矩阵R^。5) 根据式(17)得到最优权矢量wopt,据此形成波束。 结果:最优权矢量wopt估计导向矢量a^lq
表2 运算量对比分析

算法运算量文献[8]算法KM2N2+(O(M3)+1)N本文算法O(PMN(log2N))
注:P表示需要做P次(本文取100次)的分数阶傅里叶变换,M表示阵元数,N表示采样点数。
3 实验仿真结果与分析
考虑有8个阵元的均匀线阵,阵元间距是信号最小波长λmin的一半,为了不失一般性,有两个远场信号射入。假设一个是宽带信号s1,入射角是-25°,调频范围是90~100 MHz,中心频率是95 MHz,相对带宽满足宽带条件。另一个是宽带信号s2,入射角是0°,中心频率是142.5 MHz,调频范围是135~150 MHz,相对带宽满足宽带条件。输入干噪比等于输入信噪比。设置不同的仿真条件,假设s1是有用信号,s2是干扰信号,进行100次蒙特卡罗实验,将本文算法与频域[8]以及时频域[9]算法进行对比,分析总结算法性能。
实验一 不同输入信噪比下的输出信干噪比
实验条件是信噪比由-20~20 dB,步长是 5 dB,采样频率是400 MHz的情况下。比较本文算法与频域[8]算法以及时频域[9]算法的输出信干噪比随输入信噪比的变化趋势。仿真结果如图2所示。
如图2所示,在信噪比较低的时候,由于分数阶傅里叶变换具有较好的能量聚集性,本文算法可以较好地识别信号。而频域和时频域的方法由于受到噪声的影响更大,恢复性能有较大限制。

图2 输出信干噪比与输入信噪比的关系
实验二 不同快拍数下的形成质量
在同样的信噪比(SNR=10 dB)下,设置不同的采样率从100~400 MHz,快拍数分别是80,120,160,200,240,280,320。比较时频域[9]的算法和本文算法在不同快拍数下的区别,仿真结果如图3所示。

图3 不同快拍数下的输出信干噪比
如图3所示,在低快拍数的情况下本文算法具有较好的性能,时频域算法的性能要略差一些。
实验三 波束形成的鲁棒性仿真分析
在导向矢量误差为1°的情况下,设置信噪比是-40~40 dB,步长是5 dB,采样频率是400 MHz。比较本文算法与频域[8]、时频域[9]算法的输出信干噪比随输入信噪比的变化趋势,仿真结果如图4所示。
通过图4可以看出,当估计导向矢量1°的误差时仿真的3种算法性能都有所下降,但是本文算法能随着输入信噪比的提高能较快地趋向最优,说明本文算法的鲁棒性较好。
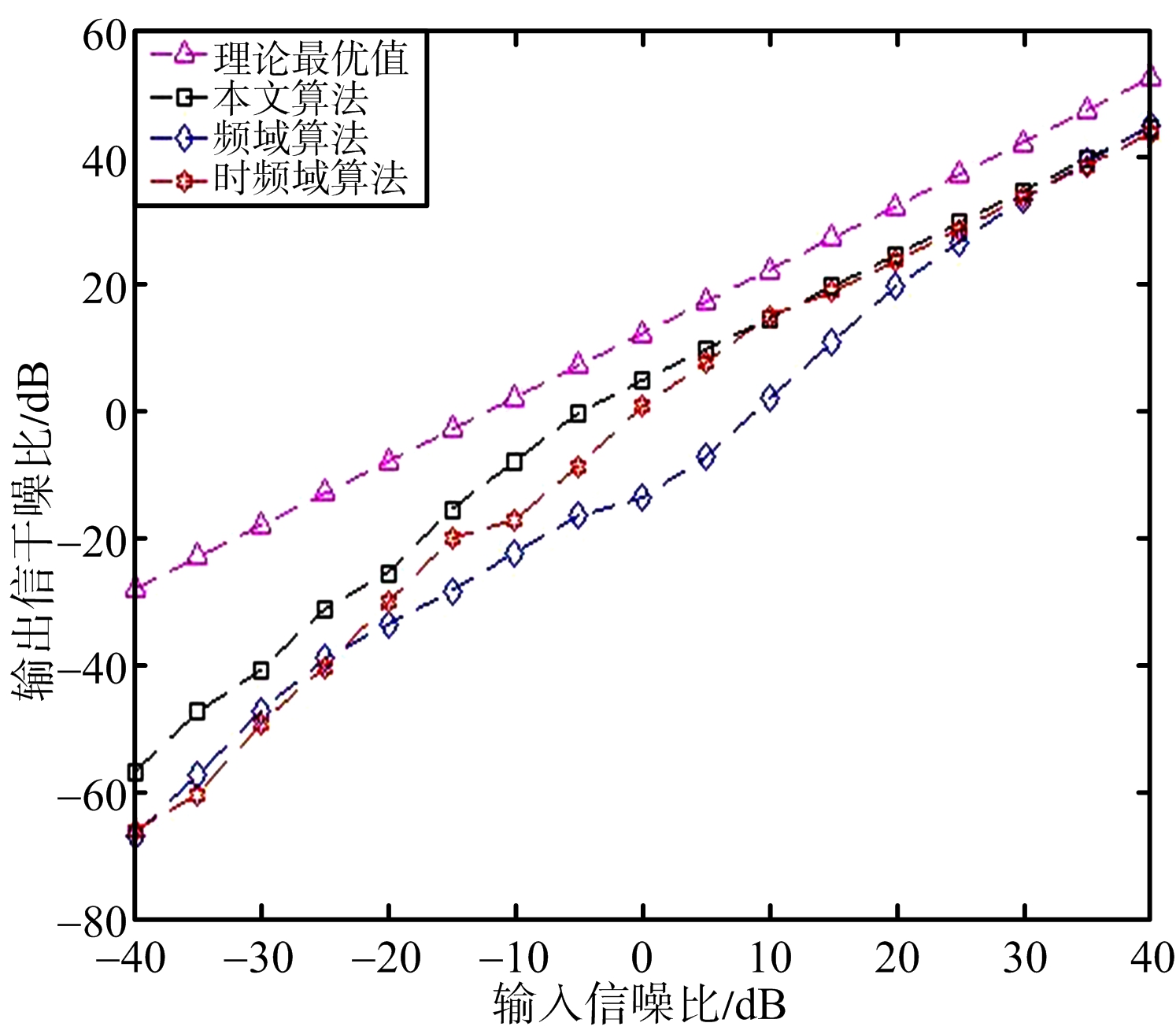
图4 导向矢量误差1°时的输出信干噪比
实验四 一定条件下的波束形成图
在信噪比(SNR=10 dB)下,设置采样率是400 MHz,入射角是-25°,调频范围是90~100 MHz,中心频率是95 MHz。根据本文方法计算波束图。
通过图5可以看出,本文方法形成的波束指向较为稳定,可以较好地接收信号。但是副瓣电平较高,接近-10 dB,对波束形成的稳定性造成了不良影响。

图5 波束形成图
4 结束语
波束形成算法中传统的时频分析方法计算量较大,当需要快速探测时,会有较大的迟滞。本文利用线性调频信号在分数阶傅里叶域具有能量聚集的特性,采用峰值滤波的方式构造空时频输出矩阵,并估计导向矢量,实现宽带信号的波束形成。实验结果表明,本文算法在低信噪比、计算量较少的情况下,可得到较好的输出性能。但是波束的旁瓣较高,需要进一步提高波束的稳定性,这也成为下一步的研究重点。
[1] 刘振,孙超,刘雄厚,等.一种加权稀疏约束稳健Capon波束形成方法[J].物理学报,2016,65(10):104303.
[2] 马彦恒,宋瑶,董健.空地双基地雷达空间同步研究[J].雷达科学与技术, 2015, 13(1):65-69.
[3] 刘可,钱华明,马俊达.一种基于导向矢量约束的恒模盲波束形成算法[J].哈尔滨工业大学学报, 2016, 48(9):151-156.
[4] 史公正,陈建春,耿富录.基于循环平稳性的盲波束形成改进算法[J].西安电子科技大学学报(自然科学版), 2003, 30(3):370-373.
[5] 沈怡平,滕升华.基于四阶累积量的稳健盲波束形成算法[J].电波科学学报, 2008, 23(6):1056-1060.
[6] 王颖翠,陈励军.宽带盲波束形成与卷积混合盲源分离[J].声学技术,2003,22(1):40-43.
[7] 臧传霞.盲源分离频域算法研究[D].沈阳:沈阳理工大学,2014.
[8] 梅铁民.盲源信号分离时域与频域算法研究[D].大连:大连理工大学, 2006.
[9] 刘亚奇,赵拥军,刘成城.宽带恒定束宽盲波束形成算法[J].信号处理,2015,31(7):784-793.
[10] ATCHESON M, JAFARI I, TOGNERI R, et al.On the Use of Contextual Time-Frequency Information for Full-Band Clustering-Based Convolutive Blind Source Separation[C]∥ IEEE International Conference on Acoustic, Speech and Signal Processing, Florence, Italy: IEEE, 2014:2114-2118.
[11] MALIK S, BENESTY J, CHEN J D.A Bayesian Framework for Blind Adaptive Beamforming[J].IEEE Trans on Signal Processing, 2014, 62(9):2370-2384.
[12] OZAKTAS H M,ARIKAN O, KUTAY M A,et al.Digital Computation of the Fractional Fourier Transform [J].IEEE Trans on Signal Processing,1996,44(9):2141-2150.
[13] LI J,STOICA P,WANG Z.On Robust Capon Beamforming and Diagonal Loading [J].IEEE Trans on Signal Processing,2003,51(7):1702-1715.
