0 引 言
近程微波雷达系统已广泛应用于军事、环境、卫生和商业系统的监测领域[1]。与宽带雷达[2-3](如调频连续波雷达、步进频率雷达和超宽带雷达(UWB))相比，双频雷达由于其复杂度低、成本低等优点，成为移动目标定位的首选解决方案[4-5]。此外，由于在双频雷达中只使用多普勒信号的相位测量，所以它不受静止目标的杂波干扰。
尽管文献[4-7]中对双频雷达作了一些研究，但这些方法都是基于远场假设的，然而双频雷达大部分应用于短距离定位。在实际情况中，远场假设可能会导致其定位性能恶化。本文提出了一种简单的基于菲涅耳模型[8]的单站双频雷达近场定位新方法。现有文献[9-10]中对近场定位的研究主要针对被动定位，而双频连续波雷达属于主动定位系统，因此现有近场定位方法[9-10]不能直接运用于双频雷达。此外，现有方法需要对距离和波达方向(DOA)进行联合二维搜索或者需要复杂的矩阵运算，例如奇异值分解和矩阵求逆。当前近场定位算法由于具有很高的计算负担，很难应用于嵌入式系统中。本文提出的方法只需简单的代数运算，并提供闭式解。该算法主要应用于单站近场低成本动目标定位领域，如室内定位、安保监控、高速车辆定位等。与其他宽带雷达相比，本算法所采用的双频雷达技术成本更低、频率带宽资源占用更少。此外，本文还推导了克拉美罗下界(CRLB)作为性能评估的基准。
1 信号模型
双频雷达是一种近程雷达，主要用于安全和监控领域[4]。与远程军用雷达不同，双频雷达的主要考虑因素是低成本和低复杂度。大多数近程雷达的商业产品(如K-MC，IVQ系列[11])采用由一个发射天线和两个接收天线组成的最小系统设计。因此，本文使用了双频雷达的最小系统结构，如图1所示。它工作在两个连续波(CW)频率f1和f2上，由两个本地振荡器(LO)产生。两个CW频率同时组合并传输。频率差f2-f1用于确定最大不模糊距离。对于每个接收天线，都有两个接收信道对应于两个CW频率f1和f2，采用零中频技术获得基带信号。
图1 单站双频雷达的结构
由于零中频技术只保留了回波信号中的多普勒分量，因此可以采用较低的采样频率，同时使得双频雷达基带回波没有杂波。每个接收信道的下转换信号被低通滤波和数字化。FFT方法用于区分不同的动目标，并获得每个接收信道的相位估计。波达方向和距离可以由每个多普勒频率分量的相位差的不同组合确定。最后，根据估计的波达方向(DOA)和距离就可以计算得动目标的位置。
1.1 距离估计
假设φi1和φi2是第i个接收天线对应于两个CW频率的两个相位，r是雷达与动目标之间的真实距离，φij和r的关系[4-7]可以写为
(1)
式中，c为光速，λ1和λ2分别为对应于两频率f1和f2的波长，注意相位是在[0,2π]范围内测量的。最大不模糊距离rmax=λj/2非常小。例如，对于一个200 MHz单频雷达来说，rmax为0.75 m。为了增大不模糊距离，在双频雷达中采用频率差f2-f1。从式(2)中可以看出，通过相位差φi2-φi1可以获得距离估计[4-7]：
(2)
式中，a=c/(2π(f2-f1))，最大不模糊距离为
(3)
其取决于频率差f2-f1，适当的选择f2-f1可以提供足够范围的不模糊距离。与单频雷达rmax=0.75 m相比，当双频雷达的f2-f1=10 MHz时，最大不模糊距离增大到15 m。
从图1和式(2)可以看出，每个天线都可以得到一个距离估计。因此，距离估计最终为
(4)
1.2 波达方向(DOA)估计
DOA可由接收天线1和2的相位差决定。设DOA为θ，接收天线间距为d，两个接收天线之间的距离差可以用远场假设来近似[4-6]：
dr=dcosθ
(5)
为了避免角度模糊，d通常设置为半波长。由式(5)中的距离差引起的两个接收天线之间的相位差为
(6)
DOA可以估计为
(7)
动目标的位置(x,y)可以由r和θ估计：
x=rcosθ, y=rsinθ
(8)
2 近场定位方法
从式(4)、式(5)可以看出，到目前为止，现有文献[4-6]对双频雷达的DOA和距离估计都是假设动目标在阵列的远场中。远场假设导致平面波在阵列通常转化为相位随天线位置线性变化的信号。然而双频雷达大部分应用于短距离定位。在实际情况中，远场假设可能会导致定位性能的恶化。
本文提出了一种简单的基于菲涅耳模型的单站双频雷达近场定位新方法。为了便于说明，在二维平面上进行研究。本文算法可以很容易扩展到三维平面。如图2所示，假设在二维平面内有一线性阵列。
图2 二维平面定位
假设待估计的动目标的位置为(x,y)，已知第i个天线的坐标为(xi,yi)，其中发射天线和两个接收天线的坐标分别为(x0,y0)=(-d0,0)，(x1,y1)=(0,0)，(x2,y2)=(d1,0)。d1为半波长，ri为第i个天线到动目标的真实距离。发射角为θ0，(x1,y1)的到达角为θ1。在第i个接收天线的两个CW频率上测量的相位差可以建模为
(9)
式中，li=r0+ri是发射天线与第i个接收天线之间的传播距离。
比较式(4)和式(9)可知，传统的方法是基于远场假设的，即r0, r1和r2相等，这与近场信道是不符合的。不同天线之间的相位差可以建模为
(10)
由式(10)，dr21=r2-r1可以如下计算：
(11)
利用三角形定理，dr21为
(12)
式(12)的一阶近似为
dr21=r2-r1≈-d1cosθ1
(13)
将式(13)代入式(11)，保留式(7)。显然，基于远场模型的传统方法是利用泰勒展开的一阶近似来近似信道。这可能不足以描述近场目标。这里采用基于泰勒展开的二阶近似的菲涅耳模型来提高定位精度。
采用二阶近似，式(12)变为
(14)
由于(sinθ1)2=1-(cosθ1)2，式(14)可以写为
e(cosθ1)2+fcosθ1+g=0
(15)
式中，
注意到|cosθ1|≤1，由式(15)可以得到cosθ1：
(16)
然而，无法由式(16)直接解得θ1，因为e和g中含有未知量r1。为了求解问题，有必要进一步近似。
基于图1所示的几何拓扑，下面的等式保持不变：
l1=r0+r1, l2=r0+r2
dr21=r2-r1, dr10=r1-r0
(17)
由式(17)可解得r1：
(18)
式中，li和dr21可分别由式(9)和式(11)得到。利用远场假设dr10≈dr21，式(18)变为
(19)
将式(19)代入式(16)，θ1可以如下估计：
(20)
可由r1和θ1得到(x,y)的第一步估计：
x=r1cosθ1,y=r1sinθ1
(21)
注意到式(19)是基于远场假设的，利用近场模型可以进一步获得r1和θ1的改进估计。
利用二阶近似，dr10为
(22)
式中，cosθ0和r0可以利用(x,y)的第一步估计得到：
(23)
将式(22)代入式(18)，可以更新r1。将式(18)和式(20)代入式(21)可以最终获得动目标位置(x,y)的第二步解。
3 克拉美罗界
众所周知，克拉美罗界(CRLB)为对任何未知参数进行无偏估计的方差或协方差矩阵的下限[12]，这部分推导了在单站双频雷达系统中进行动目标定位的CRLB，这可以为任何一个无偏估计器提供性能评估基准。
以
代表{*}的有噪声测量值，设
为一相位测量向量，其包括
未知参数向量θ为动目标位置
CRLB矩阵定义为Fisher信息矩阵(FIM)的逆矩阵Jθ：
(24)
式中，
为对θ的估计。
FIM定义为
(25)
φij的相位测量可以建模为
(26)
式中，nij表示零均值方差为
的高斯测量噪声。
由式(26)，概率密度函数
可以写为
(27)
式中，
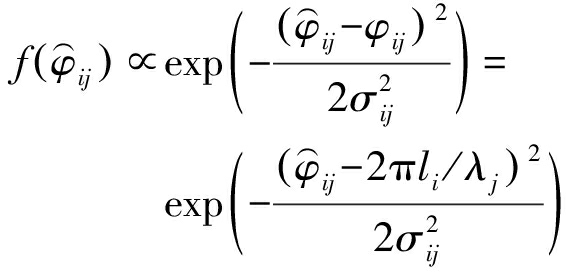
(28)
将式(27)、式(28)代入式(25)，得到
Jθ=HQ-1HT
(29)
式中，
(30)
最终得到的CRLB为
CRLB=trace{(HQ-1HT)-1}
(31)
4 仿真结果
在仿真中，雷达的载波频率为433 MHz，频率差为10 MHz，所以由分析可得最大不模糊距离为15 m。d0=d1设为半波长。积累时间设置为T=1 s，由多普勒频率定义
可知dfd=1 Hz，其中fs为采样速率，N为采样点个数，T为累积时间。速度分辨率dv=λ/(2T)=0.35 m/s。即在实际定位过程中，目标最小径向速度大于0.35 m/s系统即可探测，多目标的径向速度差别大于0.35 m/s，系统可以区分多目标。设RMSE表示以m为单位定义为
的标准误差，为2 000次独立仿真结果取平均值所得。
图3记录了不同相位测量标准差下提出的新方法的性能。r1为10波长，θ1=70°。图4为不同距离下的RMSE。θ1=70°，相位噪声标准差为0.5°，距离由5波长变化到20波长。图5画出了不同波达方向下的RMSE，DOA变化范围为30°～150°，r1为10波长，相位噪声标准差为0.5°。图3～图5表明所提出的方法具有比传统方法式(8)更好的性能。
图3 不同相位噪声下的RMSE
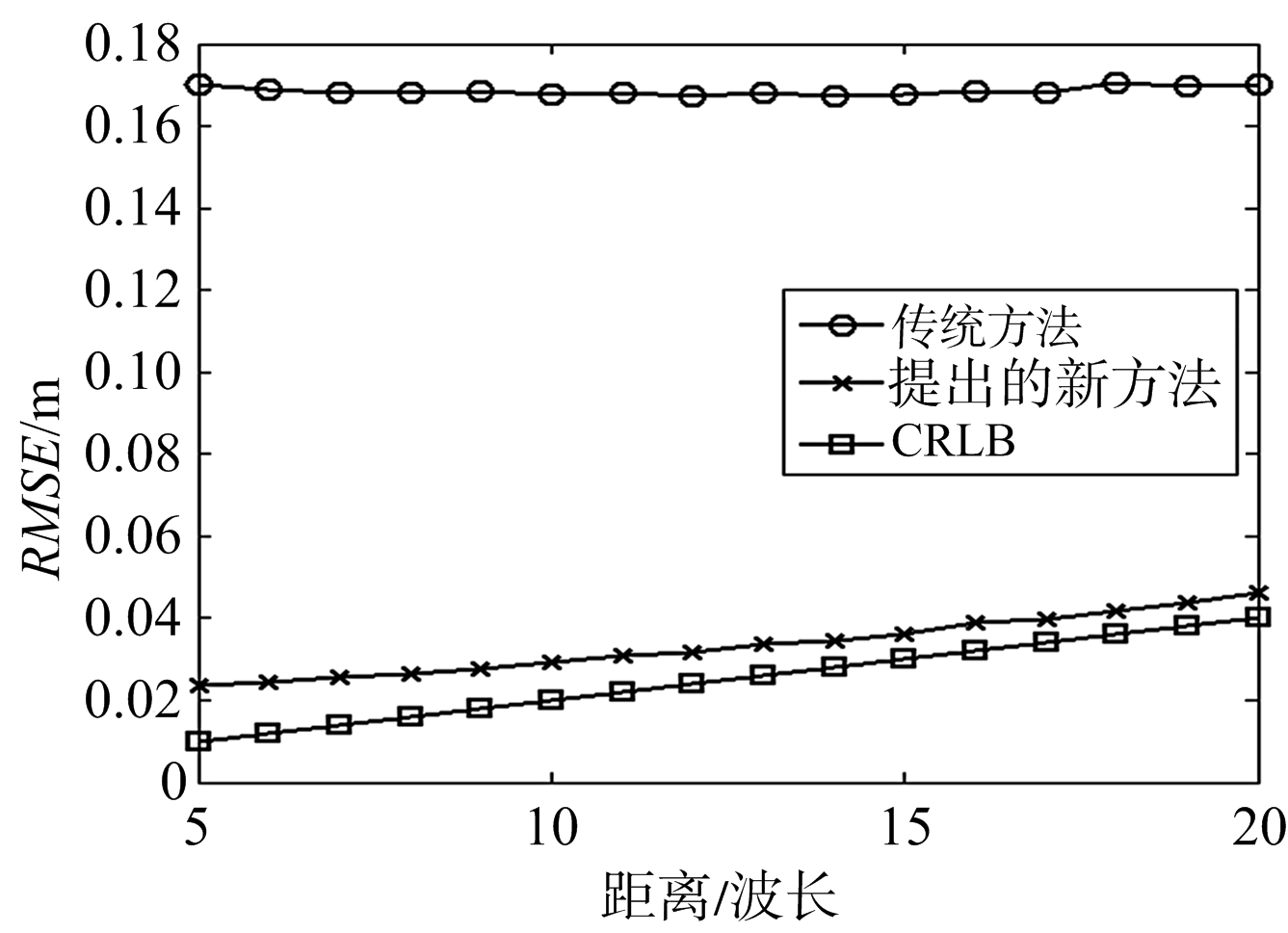
图4 不同距离下的RMSE
图5 不同波达方向下的RMSE
从仿真中可以看出本项目定位精度能达到0.03 m，这种精度足以满足大多数高精度近场定位要求。对于相同的定位精度，宽带雷达则需要多达5 G的带宽和复杂的调制形式，而双频雷达仅仅需要几兆的带宽。
5 结束语
本文针对单站双频雷达系统，提出了一种基于简单代数转换的近场定位新方法。该算法采用的双频雷达复杂度低、成本低，且不受静止目标的杂波干扰。由于不需联合二维搜索或者复杂的矩阵运算，很大程度上减少了计算负担，可以应用于低成本动目标定位领域。此外，本文还推导了在单站双频雷达系统中进行动目标定位的CRLB作为性能评估基准。仿真结果表明，该方法比基于远场模型的传统方法具有更好的性能。且与其他宽带雷达相比，本算法所采用的双频雷达技术成本更低、频率带宽资源占用更少。
[1] LI C Z, PENG Z Y, HUANG T Y, et al. A Review on Recent Progress of Portable Short-Range Noncontact Microwave Radar Systems[J]. IEEE Trans on Microwave Theory and Techniques, 2017, 65(5):1692-1706.
[2] ANGHELA, VASILE G, CACOVEANU R, et al. Short-Range Wideband FMCW Radar for Millimetric Displacement Measurements[J]. IEEE Trans on Geoscience and Remote Sensing, 2014, 52(9):5633-5642.
[3] SVECOVA M, KOCUR D, URAMOVA N, et al. TOA Complementing Method for Target Localization by UWB Radar Systems[C]∥ 16th International Radar Symposium, Dresden, Germany: IEEE, 2015:949-954.
[4] DING Yipeng, SUN Kehui, XU Xuemei. Hough-MHAF Localization Algorithm for Dual-Frequency Continuous-Wave Through-Wall Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2016, 52(1):111-121.
[5] AMIN M, ZEMANY P, SETLUR P, et al. Moving Target Localization for Indoor Imaging Using Dual Frequency CW Radars[C]∥ Fourth IEEE Workshop on Sensor Array and Multichannel Processing, Waltham, MA: IEEE, 2006:367-371.
[6] LIN A, LING H. Location Tracking of Indoor Movers Using a Two-Frequency Doppler and Direction-of-Arrival (DDOA) Radar[C]∥ IEEE Antennas and Propagation Society International Symposium, Albuquerque, NM: IEEE, 2006:1125-1128.
[7] AHMAD F, AMIN M G, ZEMANY P D. Dual-Frequency Radars for Target Localization in Urban Sensing[J]. IEEE Trans on Aerospace and Electronic Systems, 2009, 45(4):1598-1609.
[8] GAGE K S, ECKLUND W L, BALSLEY B B. A Modified Fresnel Scattering Model for the Parameterization of Fresnel Returns[J]. Radio Science, 1985, 20(6):1493-1501.
[9] STARER D, NEHORAI A. Passive Localization of Near-Field Sources by Path Following[J]. IEEE Trans on Signal Processing, 1994, 42(3):677-680.
[10] YUEN N, FRIEDLANDER B. Performance Analysis of Higher Order ESPRIT for Localization of Near-Field Sources[J]. IEEE Trans on Signal Processing, 1998, 46(3):709-719.
[11] INNOSENT GMBH. Data Sheet IVQ-3005[DB/OL].[2018-01-10]. http:∥www.innosent.de/fileadmin/media/dokumente/DATASHEETS_2016/Datenblatt_IVQ-3005.pdf.
[12] BAR-SHALOM Y, WILLETT P. A Survey of Some Recent Results on the CRLB for Parameter
Estimation and its Extension[C]∥ 19th International Conference on Information Fusion, Heidelberg, Germany: IEEE, 2016:528-535.
