0 引 言
随着军事技术和武器装备的发展，空中军事目标也呈现出一些新特点和新发展[1]，如具有隐身性能、高速机动、目标周围有虚假干扰等。而导弹在现代军事对抗过程中有速度快、射程远、精度高、威力大等优点，因此其相关研究在现代战争中日益受到重视[1-3]。
除了在时域、频域来对目标进行识别，极化域的目标检测识别方法也越来越受到学者们的重视[4-6]。由于传统的分时全极化测量体制雷达在测量运动特别是高速运动目标时会出现时间去相关，因此这种测量体制不适合对目标动态散射矩阵测量。 Giuli等于1993年提出了同时全极化测量体制雷达[7]，这种体制雷达可以克服分时全极化雷达的上述问题。随后，国内外都在积极研究该技术并应用于实际中。目前已经研制出来的同时全极化雷达有法国的MERIC雷达、荷兰的PAR-SAX雷达、国防科学技术大学的KD-IPR雷达等。
目前从公开发表文献看国内外许多学者都对该体制雷达的误差源和系统模型进行了分析，其中Titin-Schnaider等讨论了同时全极化雷达两路发射信号的延迟误差，但没有考虑目标运动参数对散射矩阵测量的影响[8]。常宇亮从线性调频信号的时间模糊函数提出通过模糊函数矩阵来校正运动目标的回波延时和多普勒频移对匹配滤波的影响[9]。何密、赵峰等提出了运动参数估计方法[10-11]。但是没有考虑到当运动参数的估计出现误差时，极化散射矩阵测量结果也会出现误差。
本文分析了同时全极化雷达系统模型，并给出了匹配滤波失真矩阵的物理意义，用匹配滤波器引入的等效极化串扰和极化通道不平衡来描述发射波形不正交和目标运动对系统极化矩阵散射矩阵测量的影响，与分时全极化雷达系统模型统一。提出了运动估计误差矩阵，利用该矩阵对同时全极化雷达测量中运动估计误差对测量结果的影响进行了定量仿真分析。
1 同时全极化雷达系统模型及误差影响机理
同时全极化雷达系统能够在同一个脉冲重复周期内同时发射两路不同极化且波形正交的信号，再同时接收两路信号进行测量，通过匹配滤波器实现不同极化信号的分离，从而获得目标散射矩阵测量结果。多个脉冲重复测量，即可获得目标动态散射矩阵。然而在匹配滤波处理时，由于发射信号非点频信号，无法做到波形完全正交[8]，这样不同极化信号不能完全分离。同时全极化雷达系统原理框图如图1所示。
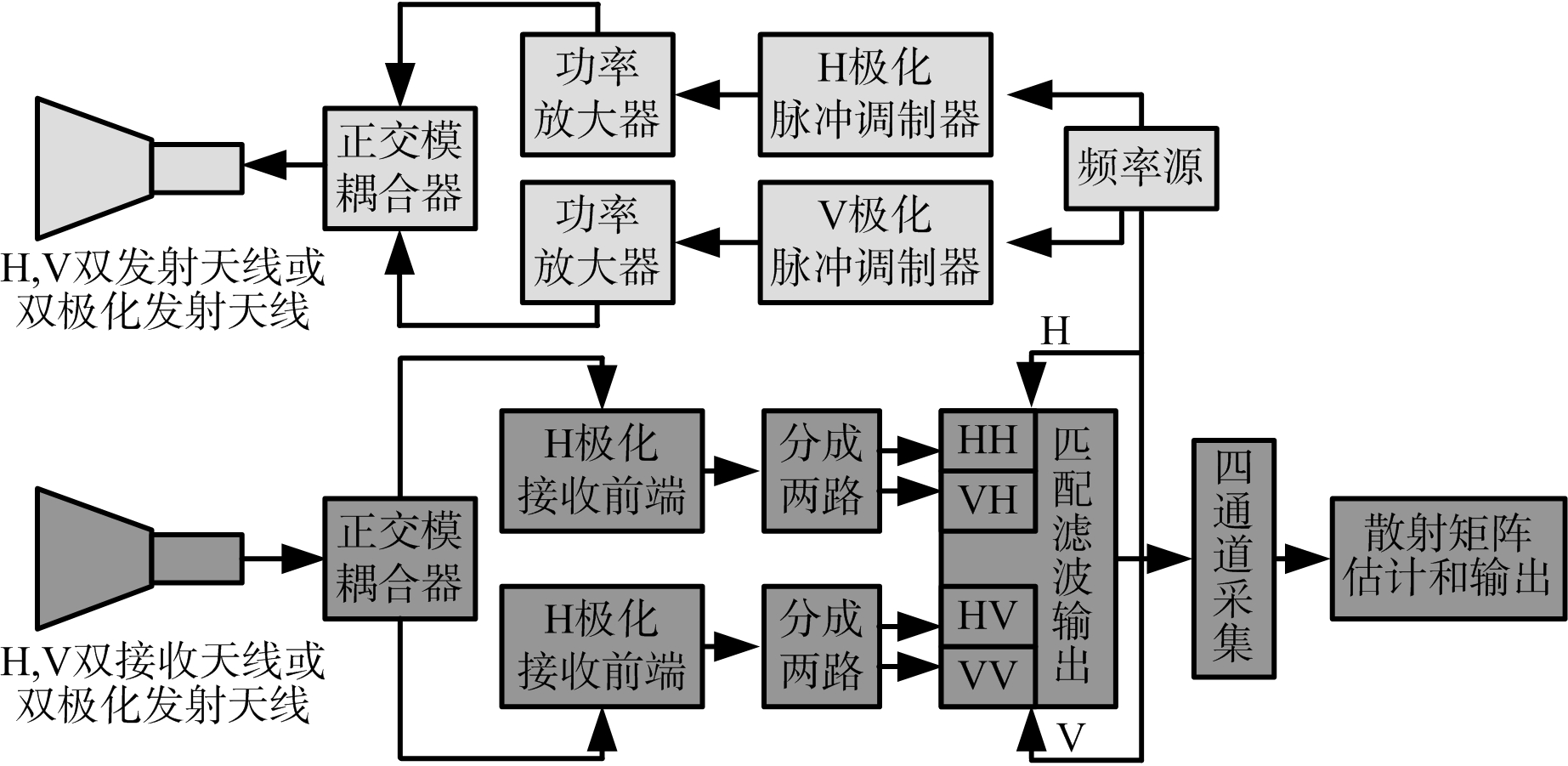
图1 同时全极化雷达系统原理框图
根据同时全极化雷达系统原理框图，同时全极化雷达与分时全极化雷达系统相比，硬件上的重要区别之一是除了发射通道和接收通道外，增加了匹配滤波器，即同时全极化雷达系统可分为三大组成部分：1) 发射通道；2) 接收通道；3) 匹配滤波器。因而目标散射矩阵测量结果主要受系统这3个部分的影响。分时全极化雷达系统建模中将发射通道和接收通道的对散射矩阵测量的影响分别建模为发射失真矩阵T和接收失真矩阵R，通过对应的隔离度参数和极化通道幅相不平衡参数来表征。这里借鉴分时全极化雷达系统的模型，类似的匹配滤波器对散射矩阵测量的影响也可以建模为类似的匹配滤波器失真矩阵H。于是，同时全极化雷达系统模型结合Van Zyl的系统模型[12]可以表示为
M=HRST
(1)
式中，M为测量所得目标极化散射矩阵，S为目标极化散射矩阵。为了便于讨论匹配滤波失真矩阵H，设R，S，T三个矩阵的乘积为S′，即矩阵
(2)
式中，
为RST矩阵相乘后对应位置元素值，δ1，δ2为接收通道串扰，δ3和δ4为发射通道串扰，f1和f2分别为接收和发射的极化通道幅相不平衡，Shh，Shv，Svh和Svv分别为目标真实散射矩阵元素。
这样式(1)简写为
M=HS′
(3)
根据文献[9-10]匹配滤波器失真矩阵可表示为
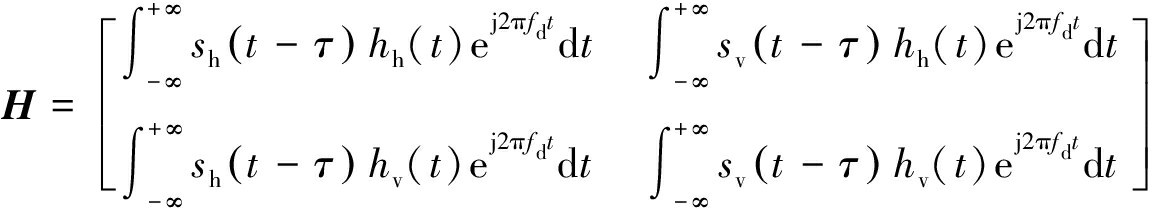
(4)
式中，sh(t-τ)和sv(t-τ)分别为经过目标延时后的水平极化和垂直极化发射信号，hv(t)为垂直极化发射参考信号，hh(t)为水平极化发射参考信号。
当发射信号接为正负线性调频信号时，可以推出
sh(t-τ)hh(t)ej2πfdtdt=
ejπτfd(Tp-|τ|)sinc(π(fd+kt)(Tp-|τ|))
(5)
sv(t-τ)hv(t)ej2πfdtdt=
ejπτfd(Tp-|τ|)sinc(π(fd-kt)(Tp-|τ|))
(6)
sv(t-τ)hh(t)ej2πfdtdt=
(7)
sh(t-τ)hh(t)ej2πfdtdt=
(8)
式中，C(x)=
cos
cos
分别为菲涅耳余弦函数、菲涅耳正弦函数，τ为时延，Tp为脉宽，fd为多普勒频率，k为线性调频斜率。
对于运动目标该矩阵是目标延时和目标径向运动速度的函数，可以写为H(τ，v)。
对H的影响可以分两种情况来讨论：
1) 当目标静止时由发射波形与匹配滤波参考信号不正交引入的匹配滤波失真矩阵的等效串扰误差，以及这一部分误差不会随物体运动参数变化而变化，将其定义为波形非正交串扰误差矩阵W=H(0，0)。该矩阵数值上等于匹配滤波失真矩阵H各个运动参数为0时的结果。
2) 当目标运动时发射波形经过收发延时接收后，由于多普勒效应造成的回波信号与匹配滤波参考信号失配造成的误差，将这一部分定义为运动调制矩阵A，A=H(τ，v)H-1(0，0)。A矩阵中的值与运动目标有关。这样
H(τ，v)=AW=H(τ，v)H-1(0，0)H(0，0)
(9)
当然，在目标运动条件下，计算匹配滤波失真矩阵时，可直接计算H(τ，v)，不需要分开计算W和A。
由于在极化散射矩阵测量中一般不考虑绝对幅度和相位，因此将H矩阵对HH极化归一化，这样仿照R，T矩阵，对匹配滤波失真矩阵H重新定义：
(10)
式中，δh1，δh2为匹配滤波处理时匹配滤波处理引入的极化通道间串扰，fh为匹配滤波处理时的极化通道不平衡。需要注意δh1，δh2，fh由于运动调制矩阵的存在会随目标运动参数变化而变化。
在同时全极化系统中，当发射信号为正负线性调频信号时，除了通过匹配滤波进行处理还能使用De-chirp处理，此时容易得到对应H矩阵为
(11)
同样将H对HH极化归一化，与前面匹配滤波处理一样可以写成
下面相关分析都只针对匹配滤波处理，对De-chirp处理不进行讨论。
对于分时全极化雷达系统，由于系统没有匹配滤波器，此时对应的
2 运动参数估计误差对测量结果影响
由观测矩阵M得到目标极化散射矩阵S需要进行两步校正处理来得到最终测量结果，根据式(1)，第一步数据校正将H的影响校正，第二步将R，T矩阵的影响校正，单独考虑H矩阵影响，即匹配滤波器造成的影响。为求得测量值
对式(2)两边乘以估计所得H矩阵的逆：
(12)
式中，
为运动目标的时延估计值，
为径向速度估计值。现有的目标运动参数估计方法，如线性调频信号的时延估计法、时延多普勒联合估计方法[10-11]等，都会存在一定误差，即
测量值
与真实值S′之间的关系可以根据式(12)推出：
H-1(τ+Δτ，v+Δv)M=
H-1(τ+Δτ，v+Δv)H(τ，v)S′
(13)
为分析运动参数估计误差对散射矩阵测量的影响，定义运动估计误差矩阵E=H-1(τ+Δτ， v+Δv)H(τ，v)。这样测量结果与真实值之间的关系简写为
(14)
同样将E矩阵归一化：
(15)
式中，δe1, δe2为数据处理过程中运动估计误差所带来的极化通道间串扰，fe为数据处理过程中运动估计误差所带来的极化通道不平衡。当各运动参数估计误差都为0时，E矩阵转化为单位矩阵，此时
3 仿真试验与结果分析
根据Giuli等提出的目标极化散射矩阵同时测量方法，参数设置如表1所示，为便于分析，下面仿真中运动估计误差矩阵E各元素幅值采用dB为单位，相位采用rad为单位。参照一般极化定标中对R，T矩阵定标要求，极化间串扰精度优于 -30 dB，极化通道的幅度不平衡小于0.5 dB，相位不平衡小于5°的要求，当运动误差估计矩阵对应的极化串扰和极化通道幅相不平衡满足上述精度时，第一步数据校正中运动参数估计误差不会对后续的数据校正或系统定标产生影响。
表1 仿真参数设置
参数名称参数值极化散射矩阵10.1+0.1i0.1+0.1i0.5+0.4i[]径向初始距离100km径向速度3km/s载频15GHz脉宽100μs信号带宽3MHz信号波形正负线性调频信号
3.1 运动估计误差矩阵E的变化特性
仿真得到的δe1，δe2，fe幅度与相位随Δτ(时延估计误差)变化的关系图如图2所示。
(a) 时延估计误差引起的δe1，δe2，fe幅度变化
(b) 时延估计误差引起的fe相位变化
图2 时延估计误差影响
当速度估计准确、时延估计存在误差时，为保证δe1，δe2的值小于-30 dB，fe绝对值小于0.5 dB，相位不平衡小于5°，其时延估计误差应小于18 ns。
图3展示了当时延估计误差为零时速度估计误差对第一步数据校正处理结果的影响，为保证δe1，δe2的幅值小于-30 dB，fe幅度小于0.5 dB，相位小于5°，其速度估计误差应小于20 m/s。
(a) 速度估计误差引起的δe1，δe2，fe幅度变化
(b) 速度估计误差引起的fe相位变化
图3 速度估计误差影响
在实际测量高速运动的物体时，时延与速度是耦合在一起的，因此对速度的估计精度势必会影响到时延的估计精度，而这一部分的误差会对高速运动物体的极化散射矩阵第一步数据校正处理结果也会产生影响。当速度与时延都估计准确时才能正确地得到校正结果。
图4展示了E矩阵各元素受到速度估计误差与时延估计误差联合影响关系。为使得δe1，δe2的幅值小于-30 dB，fe幅度小于0.5 dB，相位小于5°，对仿真结果进行定量分析。从结果得出，只有当时延估计误差小于18 ns，速度估计误差应小于20 m/s时，测量结果才能忽略该校正步骤的影响。
(a) 速度、时延估计误差引起的δe1幅度变化
(b) 速度、时延估计误差引起的δe2幅度变化
(c) 速度、时延联合估计误差引起的fe幅度变化
图4 速度、时延估计误差联合影响
3.2 运动估计误差对最终测量结果的影响
为了直观得到交叉通道的误差，将三面角角反射器作为测量目标，第一步数据校正处理后的测量结果S′的交叉项有一定误差，该误差经过发射系统极化串扰矩阵T、接收系统极化串扰矩阵R传递后会增大。
对第一步数据校正后得到的测量结果进行计算，设发射、接收端交叉极化通道存在-30 dB误差，校正后交叉通道串扰误差在-40～-20 dB之间变化。再将S′中发射、接收系统极化串扰进行校正，最终三面角角反射器散射矩阵元素Shv，Svh观测结果如图5所示。
图5 运动估计误差引入的误差对最终测量结果S的影响
从图中可以看出，当第一步数据校正残留 -30 dB误差时，经过R，T两个矩阵传递后，交叉通道测量结果变为了-29.85 dB，这样最终测量精度下降了0.15 dB。在加性噪声、乘性噪声的影响下，该部分误差会增到更大，因此在实际操作过程中可能需要将第一步数据校正和后续校正联合处理。
4 结束语
本文根据同时全极化雷达物理模型推导了完整的同时全极化雷达误差模型，重点分析了匹配滤波失真矩阵的组成机理。研究了第一部数据校正处理过程中，运动参数估计误差Δτ，Δv对测量结果的影响。通过仿真模拟了延时估计误差、速度估计误差对第一步数据校正结果的影响。最后对运动估计误差引入的测量结果的误差对后续极化校正的影响作了分析。为数据测量或系统定标过程中运动参数估计精度要求提供了参考。
[1] 王雪松. 雷达极化技术研究现状与展望[J]. 雷达学报, 2016, 5(2):119-131.
[2] 赵春雷,王亚梁,阳云龙,等. 雷达极化信息获取及极化信号处理技术研究综述[J].雷达学报,2016,5(6):620-638.
[3] SUKHAREVSKY O I, VASILETS V A, ZALEVSKY G S. Electromagnetic Wave Scattering by Aerial and Ground Radar Objects[C]∥ IEEE Radar Conference, Arlington, VA: IEEE, 2015:162-167.
[4] 宗志伟. 弹道中段目标极化雷达识别方法[D]. 长沙: 国防科学技术大学, 2016.
[5] 代大海,廖斌,肖顺平,等. 雷达极化信息获取与处理的研究进展[J]. 雷达学报, 2016, 5(2):143-155.
[6] 宋新景. 基于极化特征的雷达目标识别技术[J]. 雷达科学与技术, 2016, 14(1):39-44.
SONG Xinjing. Radar Target Recognition Based on Polarization Feature[J]. Radar Science and Technology,
2016, 14(1):39-44. (in Chinese)
[7] GIULI D, FOSSI M, FACHERIS L. Radar Target Scattering Matrix Measurement Through Orthogonal Signals[J]. IEE Proceedings F: Radar and Signal Processing, 1993, 140(4):233-242.
[8] TITIN-SCHNAIDER C, ATTIA S. Calibration of the MERIC Full-Polarimetric Radar: Theory and Implementation[J]. Aerospace Science and Technology, 2003, 7(8):633-640.
[9] 常宇亮. 瞬态极化雷达测量、检测与抗干扰技术研究[D]. 长沙: 国防科学技术大学, 2010.
[10] 何密. 同时极化测量体制雷达的校准方法研究[D]. 长沙: 国防科学技术大学, 2012.
[11] 赵锋,王雪松,肖顺平. 高耦合系数条件下径向速度估计的新方法[J]. 电子学报, 2005, 33(9):1571-1575.
[12] VAN ZYL J J. Calibration of Polarimetric Radar Images Using only Image Parameters and Trihedral Corner Reflector Responses[J]. IEEE Trans on Geoscience and Remote Sensing, 1990, 28(3):337-348.
