0 引 言
单站无源定位技术在电子侦察、远距离预警探测等应用领域中具有重要意义，受到广泛关注[1-2]。其中采用干涉仪[3-4]两阵元间相位差变化率(Rate of Phase Difference Changes，RPDC)的单站无源定位方法一直是无源定位技术理论和工程实践的研究热点。
文献[5]提出了采用角度、长基线干涉仪相位差变化率相结合进行测距定位。文献[6]通过相位差变化率对目标实现定位，并且通过机载平台机动，使干涉仪产生快速的姿态变化，能够带来定位精度的大幅提高。文献[7]研究了利用旋转多普勒的单站无源定位体制，重点分析了干涉仪姿态变化影响定位精度的原理，推导了定位误差的克拉美罗下限(CRLB)，并通过典型场景下的定位误差计算结果对分析结论进行了验证。
在文献[7]的基础上，本文对干涉仪基线自身不断旋转情况下的定位性能进行了研究分析。针对观测平台机动，干涉仪基线自身以一定角速度旋转这一过程建立旋转基线干涉仪[8-10]定位模型，分析其定位过程中的定位误差，并对典型机动场景进行仿真试验，试验证明此定位方法有着较好的定位性能。
1 旋转干涉仪定位模型
如图1所示，在二维平面上，E1和E2为运动观测平台上的两个接收天线，构成基线长度为d的干涉仪，其基线矢量方向为E1指向E2的方向，O′为基线中心，目标辐射源T固定在xT=[xT,yT]，发射频率为f0的电磁波。在某一时刻，观测平台运动到x0=[x0,y0]，速度为
以x轴正向为基准，规定逆时针方向为矢量角正值方向，基线矢量角为θ，旋转基线角速度为
目标视向角为γ，观测平台到目标辐射源的距离为
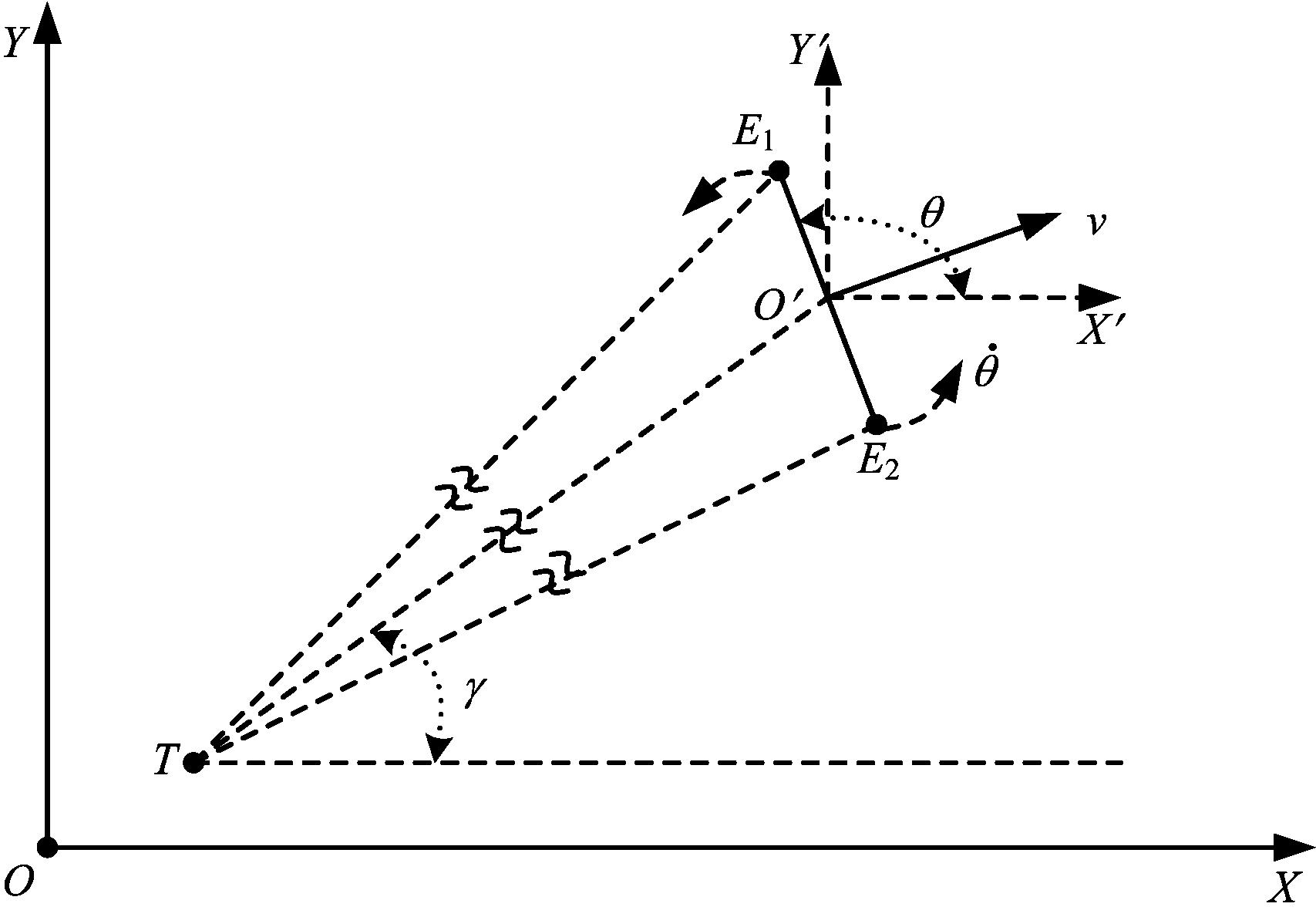
图1 干涉仪接收来波信号相位差示意图
假设某一时刻，目标辐射源发射初始相位为φ0的电磁信号，传播到干涉仪中心O′的距离为r0，传播到E1阵元的距离为r1，所需时间为t1，E1阵元处多普勒频率为fd1，E1阵元接收到的电磁信号相位为φ1，目标辐射源发射的电磁信号传播到E2阵元的距离为r2，所需时间为t2，E2阵元处的多普勒频率为fd2，E2阵元接收到的电磁信号相位为φ2，则有
φ1= 2π·(f0+fd1)·t1+φ0=2π·(f0+fd1)·(r1/c)+φ0
φ2= 2π·(f0+fd2)·t2+φ0=2π·(f0+fd2)·(r2/c)+φ0
(1)
式中，
为电磁波传播速度，vr1为沿r1方向的径向速度，vr2为沿r2方向的径向速度。
则相位差φ为
φ=φ2-φ1=k·[(c+vr2)·r2-(c+vr1)·r1]
(2)
式中，k=2πf0/c2，则相位差变化率
为
(3)
式中，阵元E1的旋转速度
cosθ]，速度v1=(vω1+v)，阵元E2的旋转速度vω2=
速度为
分别为观测平台上两阵元E1,E2到目标辐射源的距离变化率。
由d≪r0，则
目标辐射源视线方向上的单位向量e为e=[cos(γ), sin(γ)]。
则阵元E1径向速度为vr1=v1·e，阵元E2径向速度为vr2=v2·e：
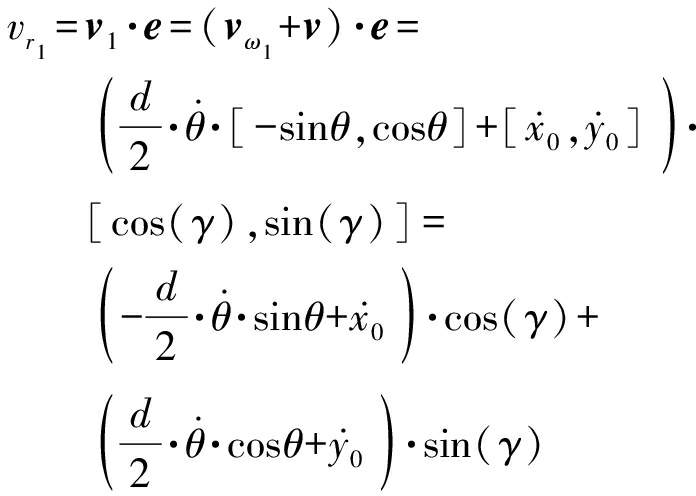
(4)
vr2=v2·e=(vω2+v)·e=
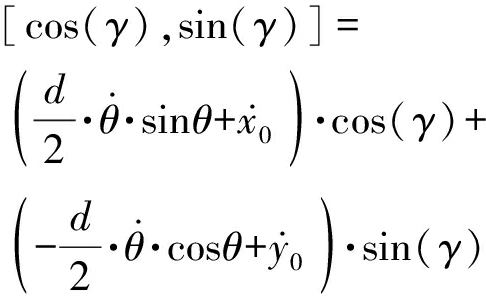
(5)
则
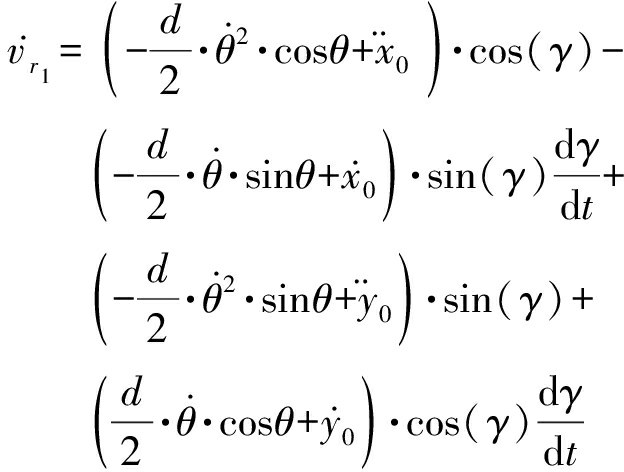
(6)
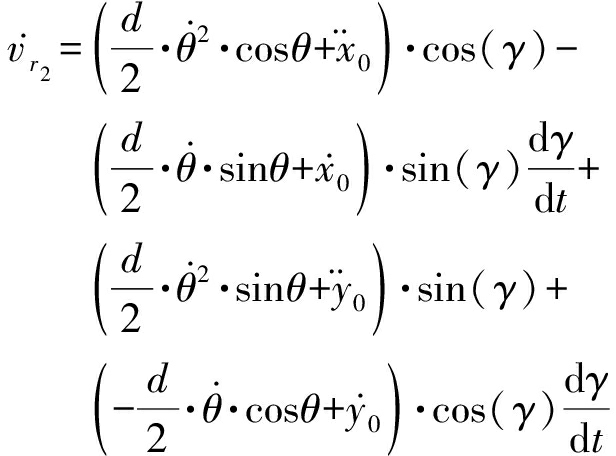
(7)
式中，
由
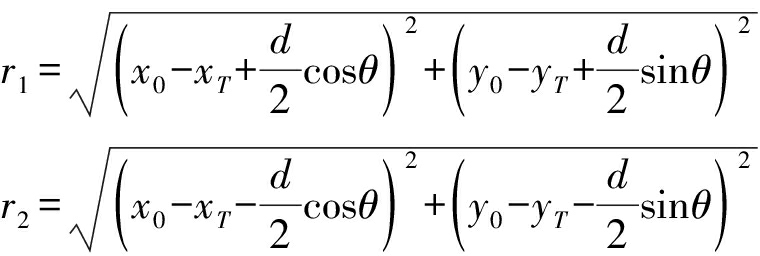
(8)
则
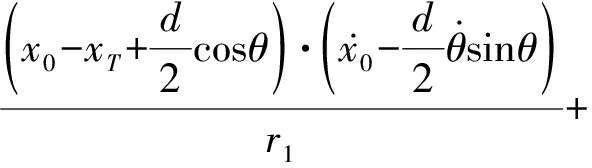
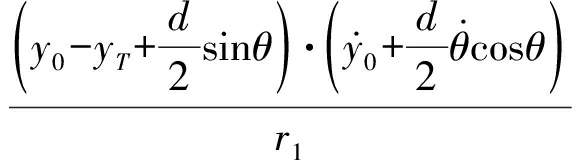
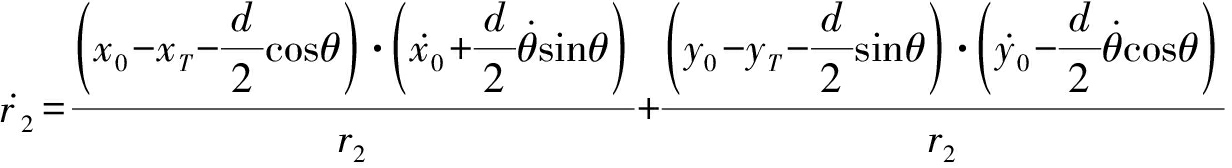
(9)
代入相位差变化率
中可得
k·[n1+n2]
(10)
式中，k=2πf0/c2，由r1≈r2≈r0，则
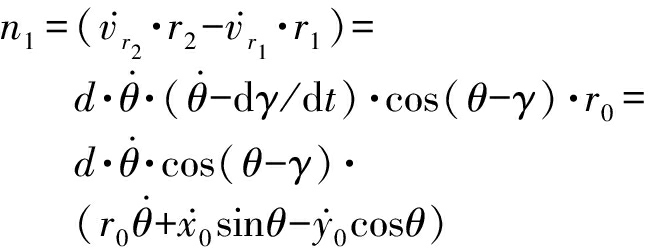
(11)
n2=
m1+m2
(12)
式中，
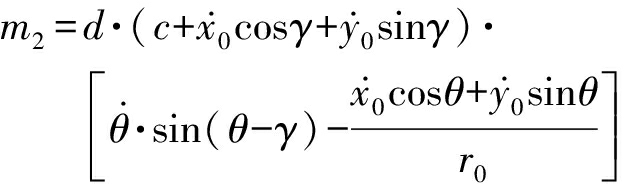
(13)
可知，相位差变化率只与
有关。在一段观测时间内，通常可以测得多个相位差变化率，从而得到多个定位观测方程，结合观测平台位置、速度以及干涉仪姿态角、姿态角变化率等信息，利用非线性最小二乘，扩展卡尔曼滤波等方法即可估计出目标位置。
2 定位性能CRLB分析
为了解在有相位差变化率测量误差下的定位误差及其分布，需要计算相位差变化率定位误差的CRLB[6]。假定得到K个相位差变化率测量
测量误差ε1,ε2,…,εk,…,εK为独立零均值高斯白噪声，方差为
则所有时刻的相位差变化率误差的方差相同且相互之间独立，即有
其联合概率密度函数可写为
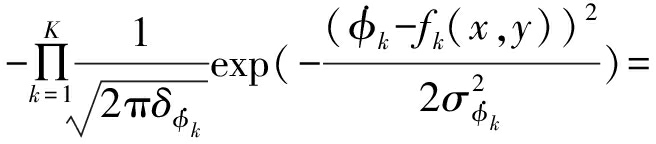
(14)
式中，fk(x,y)为第k次观测的相位差变化率真值，令X=[x,y]T,根据CRLB的定义，则
(15)
而
式中，Mx
可得
(16)
由于
∀i≠j，则
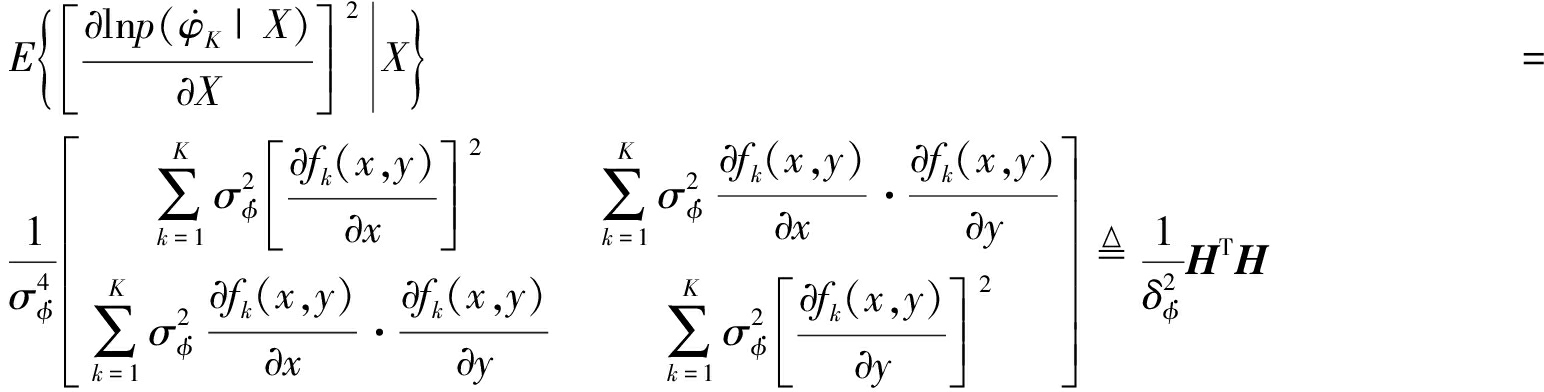
(17)
式中，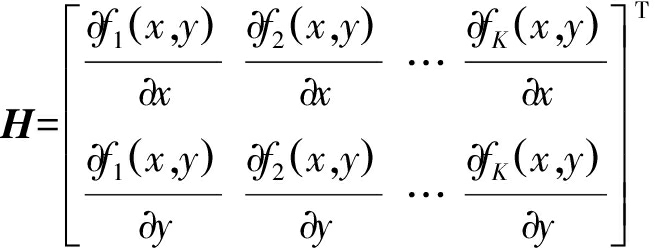
为每一个时刻测量函数对目标位置的偏导数。
某一时刻k，目标辐射源的位置(x,y)，观测器的位置是(xk,yk)，则对应的
(18)
(19)
式中，
则
可以得到
计算平面内每点(x,y)的CRLB，可以得到GDOP为
(20)
3 典型场景定位误差仿真
本节通过典型场景下定位仿真分析，揭示干涉仪基线转动对定位的影响，并比较不同转速下的定位性能。
仿真参数：干涉仪基线长d=10 m，天线旋转基线在观测平台上转动，目标辐射源发射的信号频率为3 GHz，观测间隔为0.1 s，总观测时间为20 s，相位差变化率测量误差为10°/s。
观测平台5种运动方式[7]分别为：
1) 以速度200 m/s从坐标原点开始沿x轴正向匀速直线运动，干涉仪旋转基线转速为0.1 rad/s；
2) 以速度200 m/s从坐标原点开始沿x轴正向匀速直线运动，干涉仪旋转基线转速为1 rad/s；
3) 以速度200 m/s从坐标原点开始沿x轴正向蛇形机动，机动周期10 s，机动半径5 km，且平台转动角速度为0.04 rad/s，观测平台矢量角变化范围分别为[-11.5°，11.5°]，干涉仪旋转基线转速为1 rad/s；
4) 以速度200 m/s从坐标原点开始沿x轴正向蛇形机动，机动周期10 s，机动半径5 km，且平台转动角速度为0.04 rad/s，观测平台矢量角变化范围分别为[-11.5°，11.5°]，干涉仪旋转基线转速为5 rad/s；
5) 以速度200 m/s从坐标原点开始沿x轴正向蛇形机动，机动周期10 s，机动半径1 km，且平台转动角速度为0.2 rad/s，观测平台矢量角变化范围分别为[-57.3°，57.3°]，干涉仪旋转基线转速为5 rad/s。
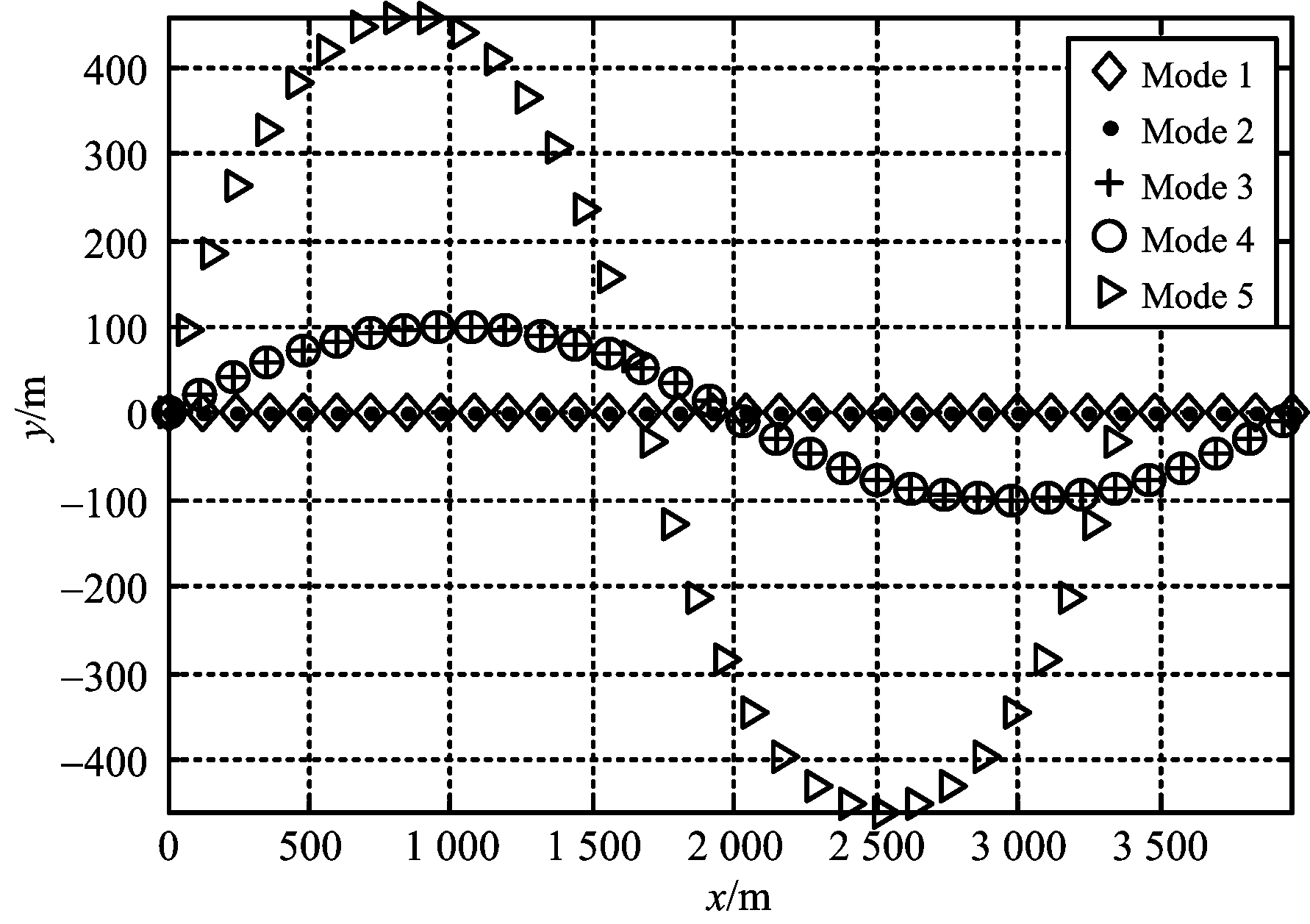
图2 观测平台运动轨迹
5种观测平台运动轨迹如图2所示。观测平台在5种运动场景下定位误差分布图分别如图3～图7所示。
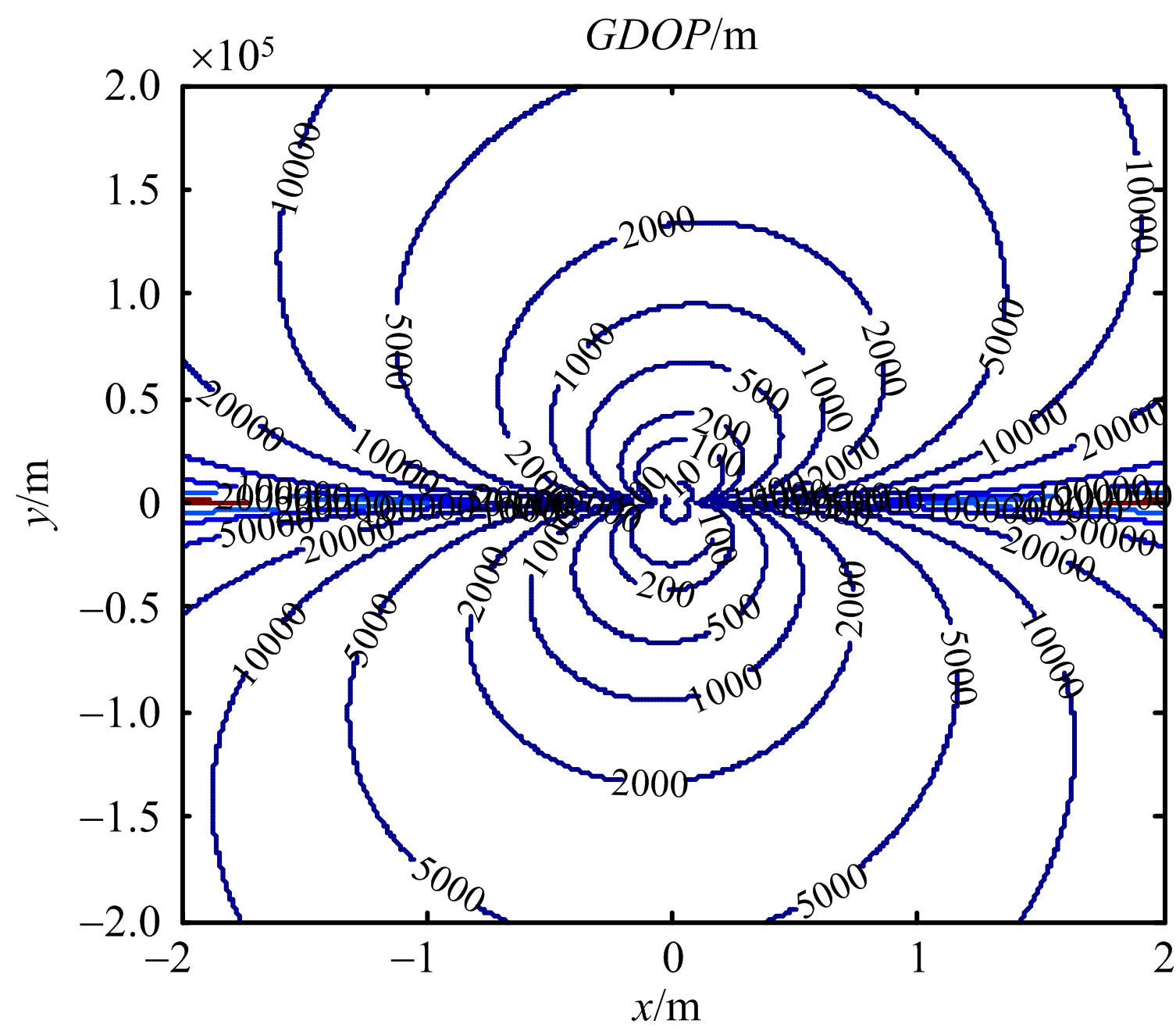
图3 运动场景1)下的GDOP分布图
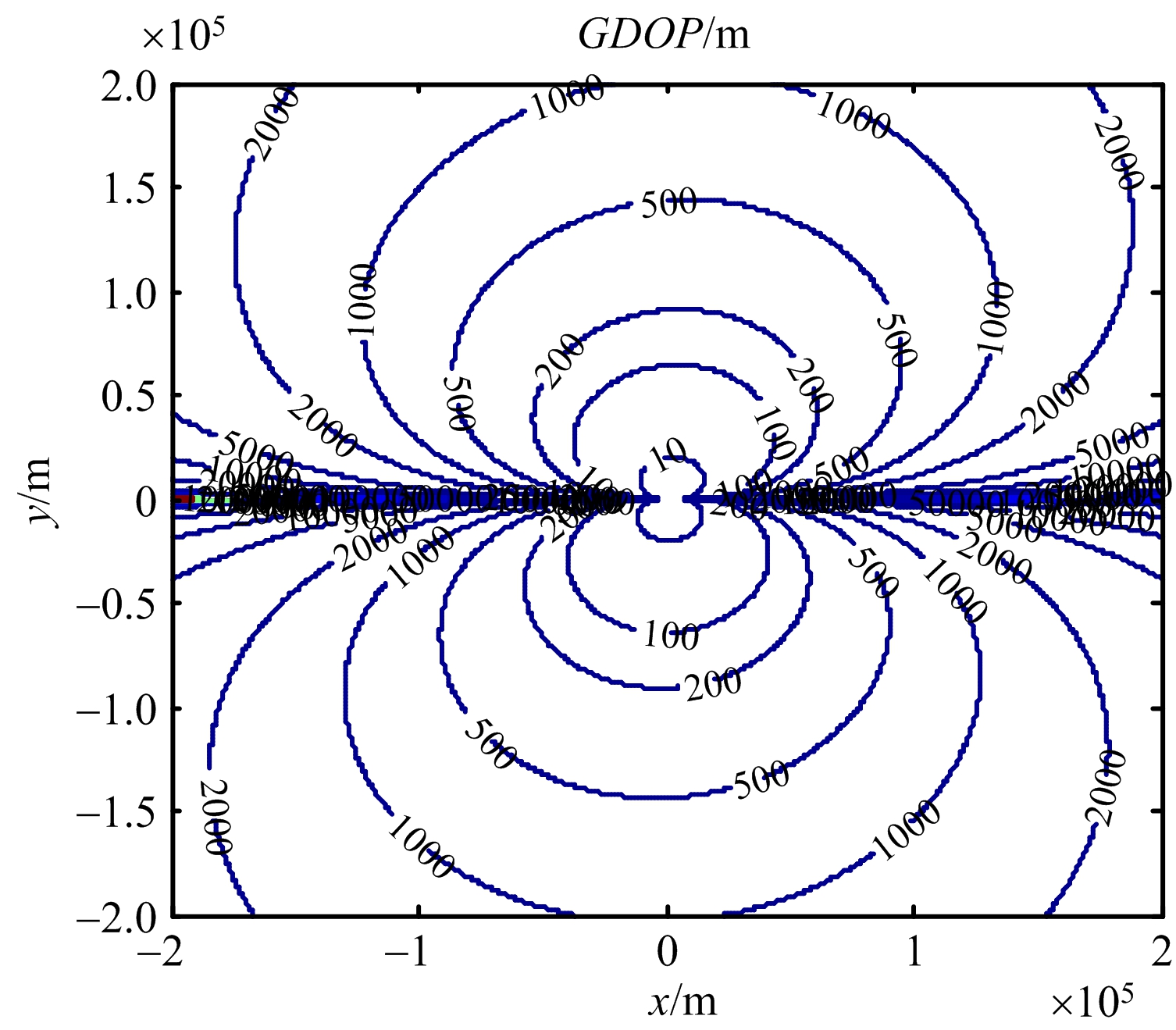
图4 运动场景2)下的GDOP分布图
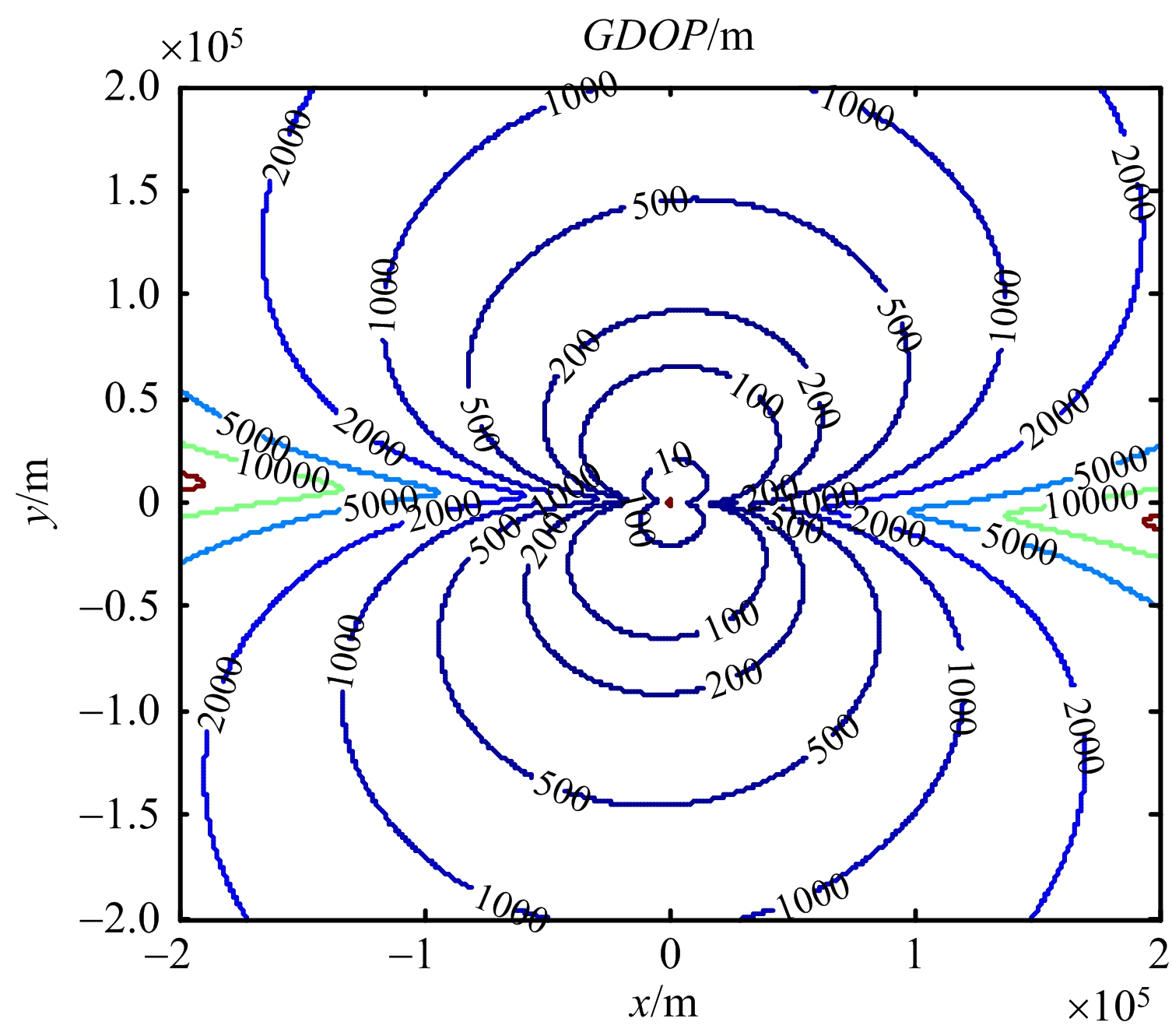
图5 运动场景3)下的GDOP分布图
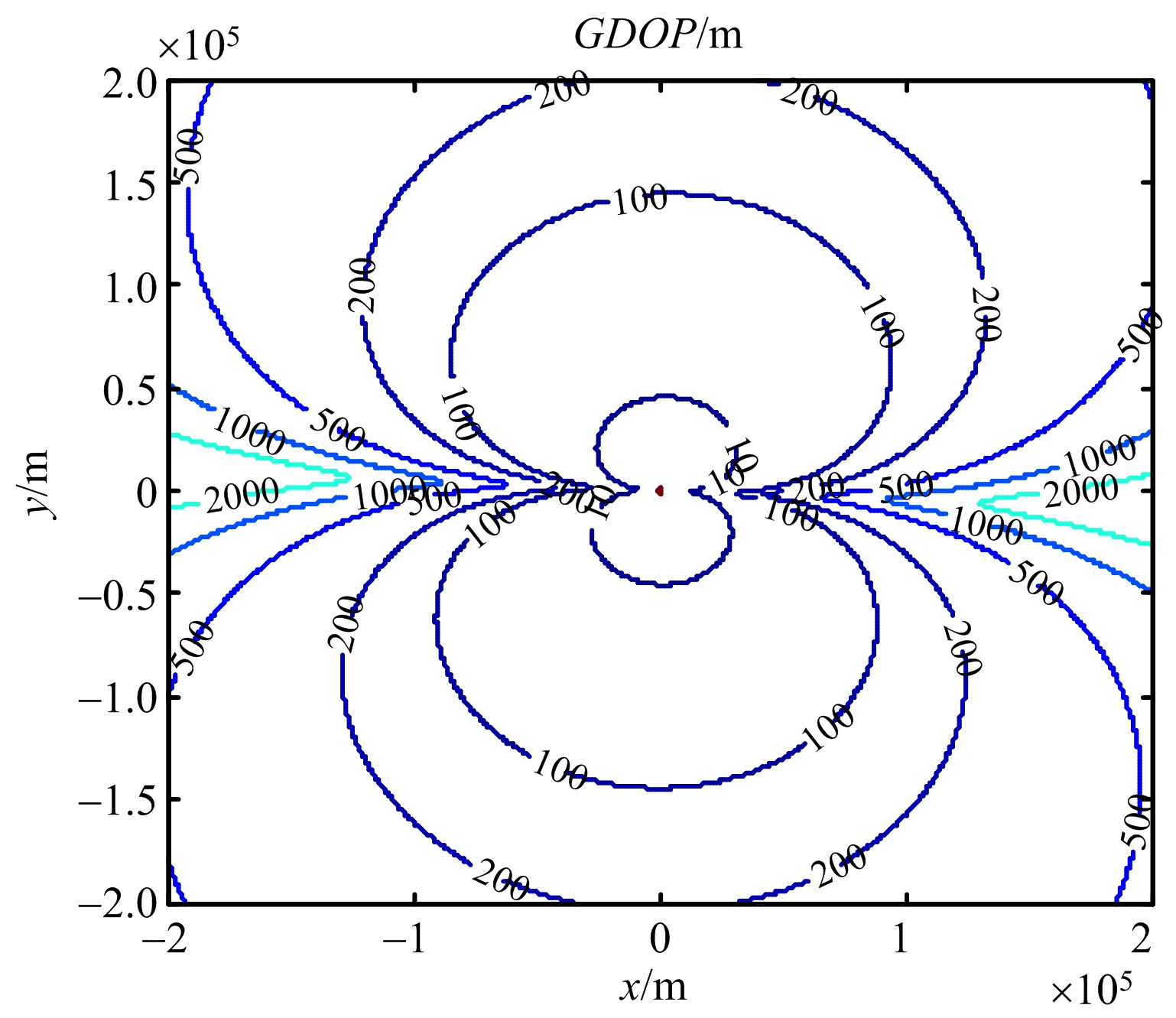
图6 运动场景4)下的GDOP分布图
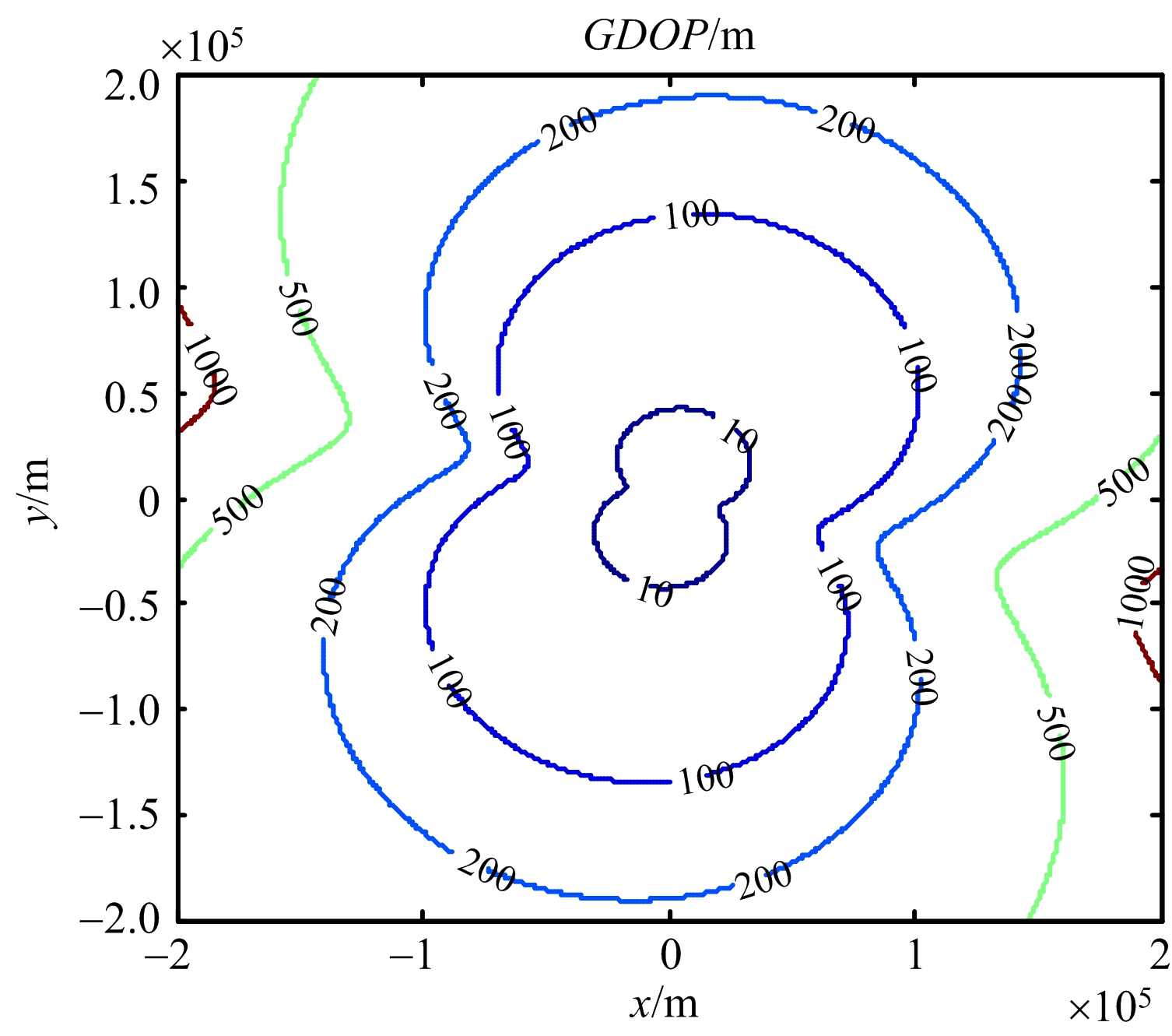
图7 运动场景5)下的GDOP分布图
从图3和图4、图5和图6可以看出，观测平台在相同的匀速直线机动或蛇形机动下，旋转基线旋转速度越快，其定位精度越高，误差越小，说明在同种机动形式下，提高旋转基线的转速能大大提高定位性能；从图4和图5可以看出，由于观测平台的蛇形机动，提高了观测站在水平方向上的定位精度，再一次验证文献[7]中，采取不同的机动能减少某一方向上的定位误差，改善定位效果；从图6和图7可以看出，在相同转速下，提高观测平台的机动程度(如减小转弯半径)，能较好地提高定位精度，验证了文献[6]中的载机采取某种机动，使姿态发生变化从而均取得较好的定位效果；本文中定位方法较优于文献[6-7]中给出的定位效果，因此选取合适的转速，能有效地提高定位精度。
4 结束语
通过对仅用相位差变化率的长基线旋转干涉仪的研究，分析了观测平台运动过程中干涉仪进行旋转情况下的定位效果，可以得出如下结论：在干涉仪旋转的情况下，较高的旋转速度能提高观测站的定位精度，同时观测平台在运动过程中采用某种机动能进一步减少定位误差。因此单站旋转基线定位过程中，旋转基线选择合适的旋转速度，配合观测平台的某种机动，从而具有很好的定位性能。
[1] 游文江. 星载单站无源定位技术研究[D]. 西安: 西安电子科技大学, 2017.
[2] XI Wei, YU Bianzhang, WANG Songshan. Theoretical Analysis of Direct-Finding Targets with Rolling-Airframe Passive Radar by Phase Interference Technique[C]∥CIE International Conference on Radar, Shanghai: IEEE, 2006:1-4.
[3] 刘满朝,刘乐. 二维干涉仪测向技术研究[J]. 现代雷达, 2018, 40(2):44-48.
[4] 陆安南,尤明懿. 相位干涉仪测向模糊与误差统计分析[J]. 中国电子科学研究院学报, 2018,13(1):42-46.
[5] 许耀伟,孙仲康. 利用相位差变化率对固定辐射源的无源被动定位[J]. 系统工程与电子技术, 1999, 21(3):34-37.
[6] WANG Qiang, GUO Fucheng, ZHOU Yiyu. A Single Observer Passive Location Method and Accuracy Analysis Using Phase Difference Rate of Change Only[C]∥ IEEE International Conference on Information and
Automation, Changsha: IEEE, 2008:1030-1033.
[7] 李腾,郭福成,姜文利. 利用旋转多普勒的单站无源定位性能分析[J]. 宇航学报, 2010,31(10):2388-2394.
[8] 张金秀,陶海红,王渊. 一种基于双基线旋转的改进干涉仪定位算法[J]. 北京理工大学学报, 2018, 38(3):320-324.
[9] 马菁涛,陶海红,谢坚,等. 基于旋转干涉仪的近场源参数估计算法[J]. 雷达学报, 2015, 4(3):287-294.
[10] 吴癸周,张敏,郭福成. 旋转长基线干涉仪的系统偏差联合估计方法[J]. 系统工程与电子技术, 2015, 37(11):2454-2459.
