0 引 言
穿墙雷达成像在城市巷战反恐、灾难救援、医学监测等领域都产生了巨大的应用价值[1-4]。
穿墙雷达成像主要应用在建筑物内隐藏目标探测和建筑物布局成像两个领域，确定墙内隐藏目标位置的前提条件是确定建筑物的内部结构，而实际应用中建筑物的布局结构通常是未知的。利用建筑物布局成像可以为建筑物内隐藏目标的相对位置提供辅助参考，且建筑物布局成像可以显示出其内部构造，为执法和救援人员顺利进入建筑物内提供路径、争取时间。
因此，建筑物布局成像在许多国内外科研机构中开展研究。ARL的Nguyen 等采用后向投影算法(Back Projected Algorithm，BP)进行成像，通过获得的建筑物两个方向的单视角图像进行非相干求和得到建筑物布局图像[5]。斯洛伐克科希策理工大学的Aftanas 等采用后向投影算法成像，对获得两个视角的图像进行图像融合、边缘检测等一系列流程获得建筑物布局的图像[6]。但传统的算术相加融合将不同视角的不同部分综合后，却同时将相同部分进行重复的叠加，从而造成图像产生冗余，影响成像质量。国内电子科技大学同样采用后向投影算法形成多幅包含部分建筑物的单视角图像，采用MNK检测器融合成像[7]。虽然都能大致显示出建筑物的内部结构，但在单一尺度域下的图像融合，效果不理想，会出现一定程度的空洞残缺和毛刺。因为图像在不同层次的轮廓和细节信息会在图像的不同尺度上体现，而单一尺度融合方法不能完全体现图像的信息。
本文提出一种基于多方位多尺度的建筑物布局成像的方法，利用多方位二维匹配滤波器抑制墙体的旁瓣、栅瓣和杂波等，再结合多尺度域的非下采样Contourlet变换(Nonsubsampled Contourlet Transform，NSCT)变换，将变换后的高频分量和低频分量采用相应的融合规则进行融合。低频采用平均加权法，高频采用能量的倒数加权法，最后将融合后的低频和高频图像通过NSCT反变换得到最终建筑物布局全景图。
1 成像模型
如图1所示，采用MIMO雷达从建筑物的多个视角进行探测，天线阵列平行于墙体，沿墙体垂直方向进行探测，获取建筑物墙体各个方向的回波从而形成一幅完整的建筑物布局全景图。
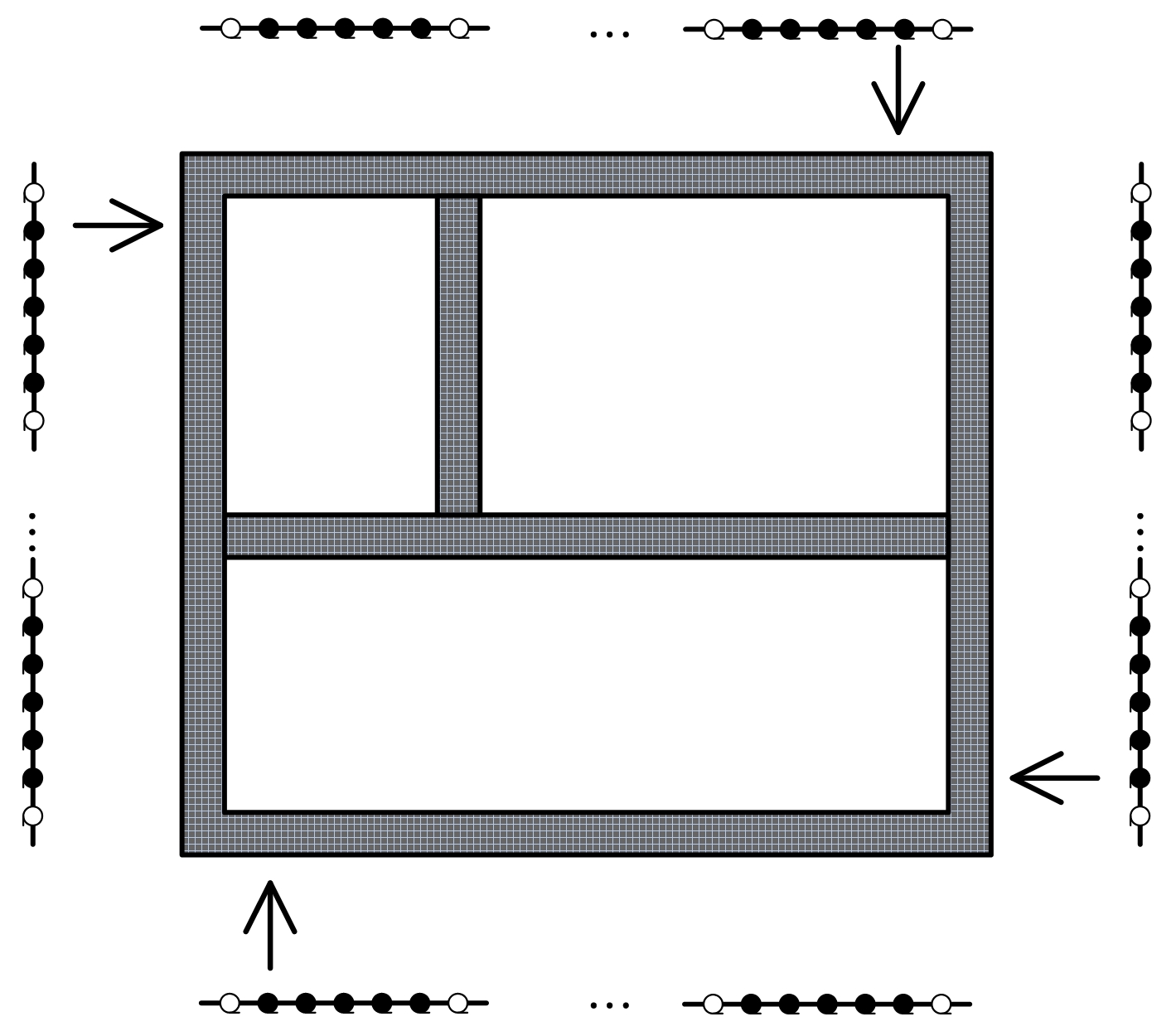
图1 稀疏观测模式
雷达天线采用M发N收的MIMO阵列，发射信号的步进频率为
fq=f0+qΔf,q=0,2,…,Q-1
(1)
式中，q=0,2，…，Q-1代表步进频的阶数，f0代表起始频率，Δf代表步进频率。
以第k个探测视角为例，第m个发射通道发射频率为fq信号时，第n个接收通道的回波信号可以表示为
(2)
式中，A代表散射幅度，τmn代表墙体到第m个发射天线和第n个接收天线的信号传播时长。根据文献[8]的延时求和成像算法，位于建筑物成像区域(xi,yj)处像素单元的像素值为
Ik(xi,yj)=
k=1,…,K
(3)
式中，τmn,ij表示为
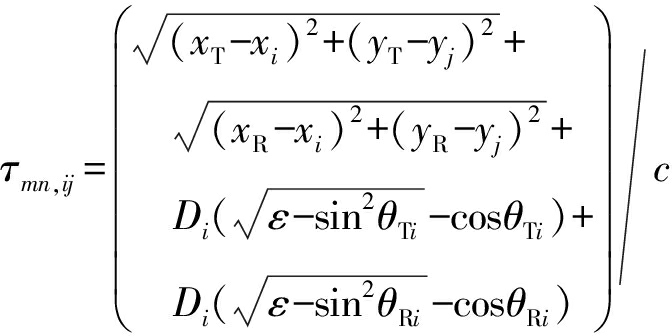
(4)
式中，(xT,yT)为第m个发射天线的位置，(xR,yR)为第n个接收天线的位置，θTi为第m个发射天线发射的电磁波穿透墙体产生折射时的出射角，θRi为电磁波穿透墙体折射到第n个接收天线的入射角，Di为墙体厚度，ε为介电常数，c为电磁波传播速度。
2 算法描述
2.1 多方位二维匹配滤波
采用高斯模板的多方位二维匹配滤波器[9]，由于墙体大多都是垂直或水平方向，仅检测方位向和距离向上所有存在的墙体，消除旁瓣、栅瓣以及其他干扰信号对目标墙体信号的干扰，增强图像细节信息，提高图像清晰度。模板的核函数为
(5)
式中，d为像素点到中心点的欧氏距离，σ为表征该点亮度的方差。由于G(d;σ)的拖尾较长，需要截断，必须选取邻域U，即U={(u,v)||u|≤3σ,|v|≤L/2}，σ，L为常数，这里(u,v)坐标是由(x,y)坐标旋转
四个角度得到。
因为匹配滤波器只有在与墙体垂直时才能取得峰值，高斯旋转矩阵在方位向和距离向上旋转角度为θl时的高斯旋转矩阵
为
(6)
则在该旋转角度θl上的点变为
Dl=(u,v)=(x,y)*
(7)
根据式(5)得到的第l个高斯模板系数为
hl(x,y)=-exp(-μ2/(2σ2))
(8)
则第l个高斯核函数的平均值为
(9)
式中，Q表示第l个高斯核函数中的元素个数。考虑均值等因素的影响，最终使用的是减去均值后的高斯匹配滤波器，表示为
(10)
确定了式(10)给出的高斯模板以后，需要将模板与得到的建筑物布局的成像进行卷积，以达到增强图像的作用。则用l个高斯模板对获得的成像增强后得到的图像公式表示为
(11)
2.2 NSCT分解
NSCT是一种将图像变换到不同尺度域上的图像分析工具[10]，其平移不变性是建筑物成像特征提取中重要的特性，可以可靠地表示成像各个方向的信息，提高建筑物图像融合的质量。
NSCT以非下采样塔形分解(Nonsubsampled Pyramid，NSP)来获取多尺度特征，而由非下采样方向滤波器组(Nosubsampled Directional Filter Bank，NSDFB)来进行方向滤波。一般情况下，源图像经NSP分解得到低频子带和高频子带，然后NSP继续分解每一尺度的低频子带，最后高频子带经过NSDFB分解得到不同的方向子图，其结构框图如图2所示。
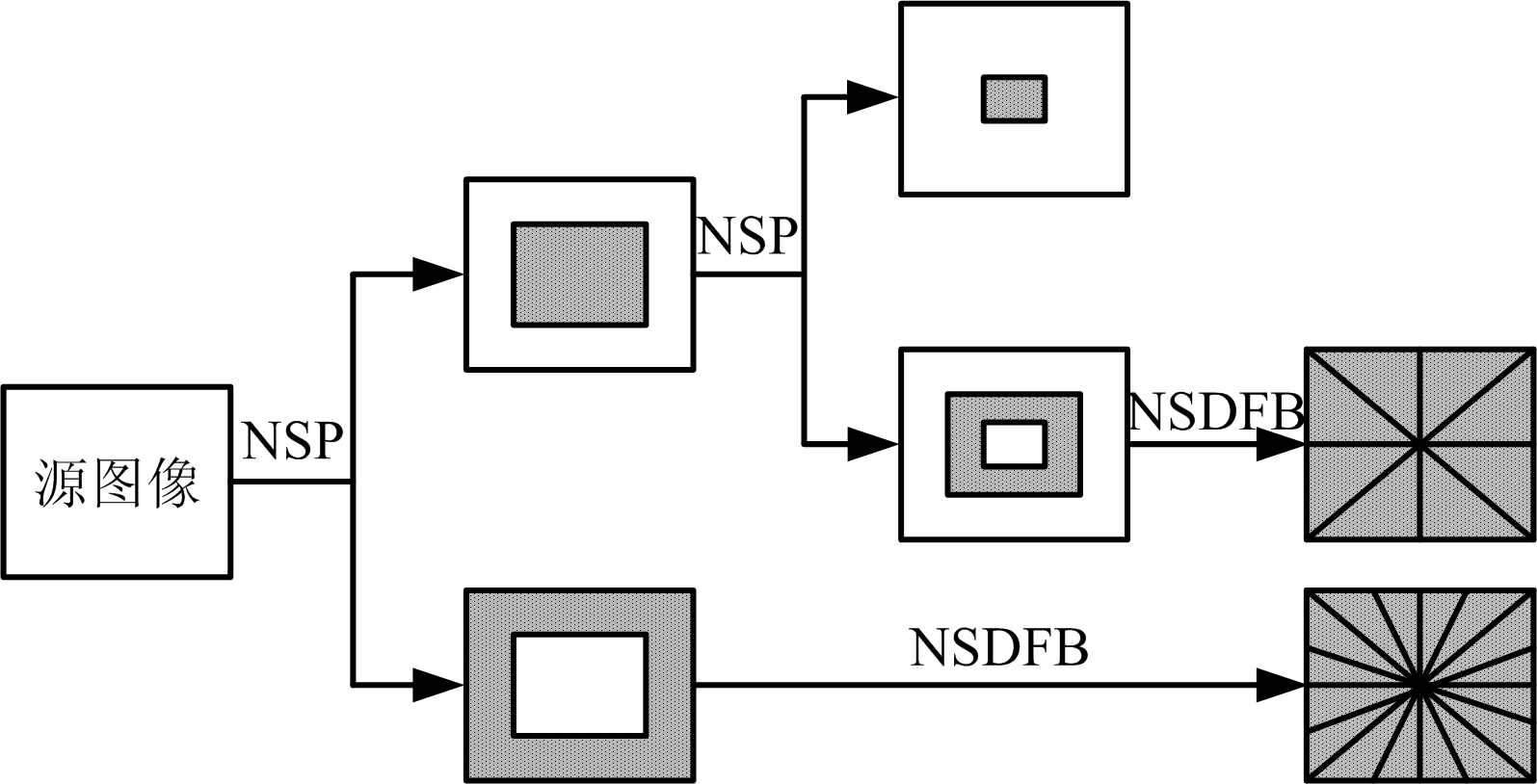
图2 NSCT分解示意图
将第k个视角的图像
经NSCT分解后，最终会产生
个与源图像大小相同的子图像，则第k个视角下图像的NSCT过程可表示为
(12)
式中，
表示k视角下第r尺度上的低频子图像，lr表示在第r个尺度上的方向分解数，
表示k视角下第r个分解尺度上第z个方向的子图像。
2.3 多视角融合过程
不同视角下的图像经NSCT分解后，获得在不同尺度下的多方向子带系数，包括低频系数和高频系数，低频系数体现建筑物成像的轮廓信息，高频系数则表示成像的细节信息。对各子带系数进行区域特征信息分析，综合区域信息和实际应用，本文对低频采用平均加权的融合规则，对高频采用能量倒数加权的融合规则。低频平均加权融合规则表示为
(13)
式中，K代表视角数目，If代表低频分量。而高频的融合规则表示为
(14)
式中，IF代表高频分量，
代表相应的权重，则权重的选取规则为
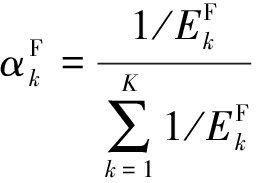
(15)
式中，
代表高频分量的能量，即
(16)
因为干扰成分越多，
在高频的值就越大，所以利用的倒数来计算权重
就越小，起到抑制干扰的作用越好。
经多方位匹配滤波和多尺度变换后的多视角图像按低频和高频采用相应的融合规则融合后，利用NSCT反变换得到一幅全景图像，即
I(x,y)=NSCT(If,IF)
(17)
综上所述，以两个视角为例，算法流程如图3所示。
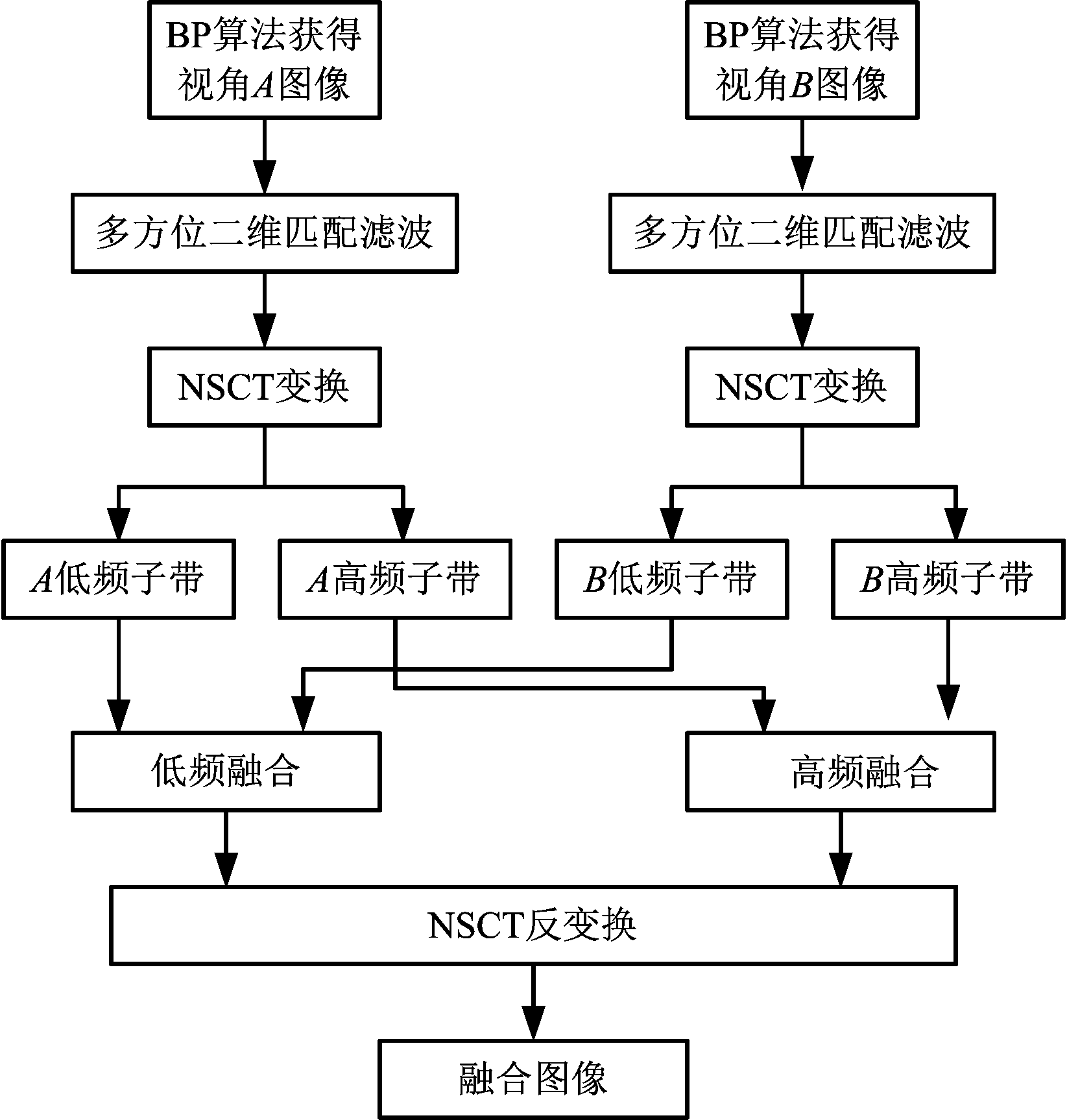
图3 算法流程
3 仿真实验及实测结果
3.1 仿真实验结果
仿真场景如图1所示。采用MIMO脉冲天线沿平行于建筑物墙体的4个视角(K=4)进行探测，天线距离墙体1 m，选用两发十四收的MIMO阵列，接收天线间隔0.2 m，发射天线与之相邻的接收天线间隔0.2 m。墙体厚度为0.2 m，介电常数为4.5。
图4为4个视角获得的回波数据经过后向投影算法成像的结果。采用多方位二维匹配滤波处理对应视角的结果如图5所示。对比两图，图5中经多方位匹配滤波获得的图像比图4的后向投影成像的各视角成像有了较清晰的墙体轮廓。
图6给出了不同融合方法的处理结果，图6(a)为对BP算法的各视角图像采用算术融合算法得到的融合后图像，图6(b)为文献[7]的方法获得的融合后的图像，图6(c)为经过本文算法得到的融合后的建筑物布局图像。可以看出，本文算法相较于BP算法的算术融合方法，可以有效消除MIMO天线阵列成像时的旁瓣栅瓣和其他干扰信息对建筑物真实目标的干扰，提高了成像质量。采用文献[7]的MNK方法融合后的图像出现了毛刺和不连贯的现象，本文算法与之相比增强了图像细节信息，对建筑物墙体的恢复更完整。
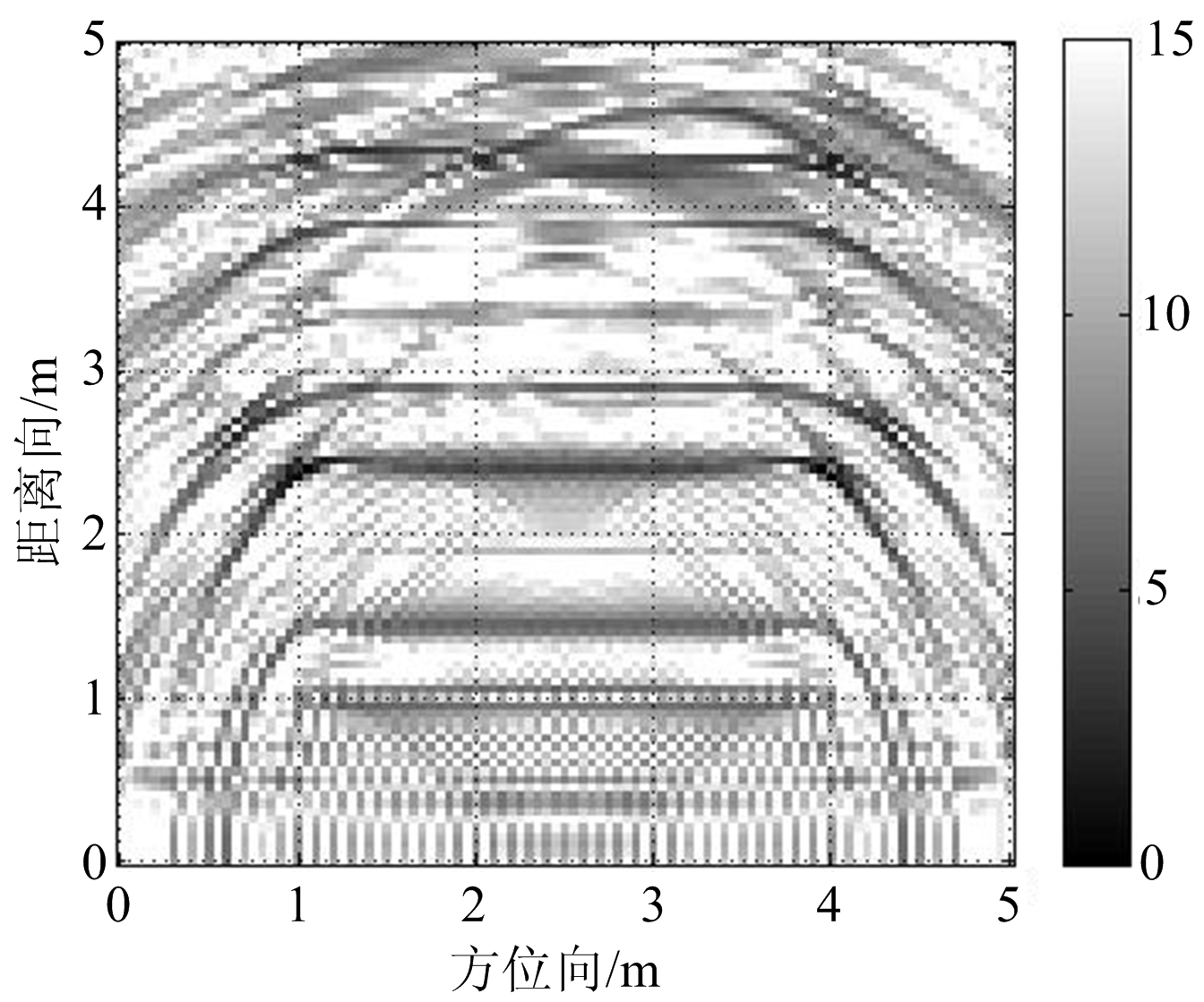
(a) 视角1
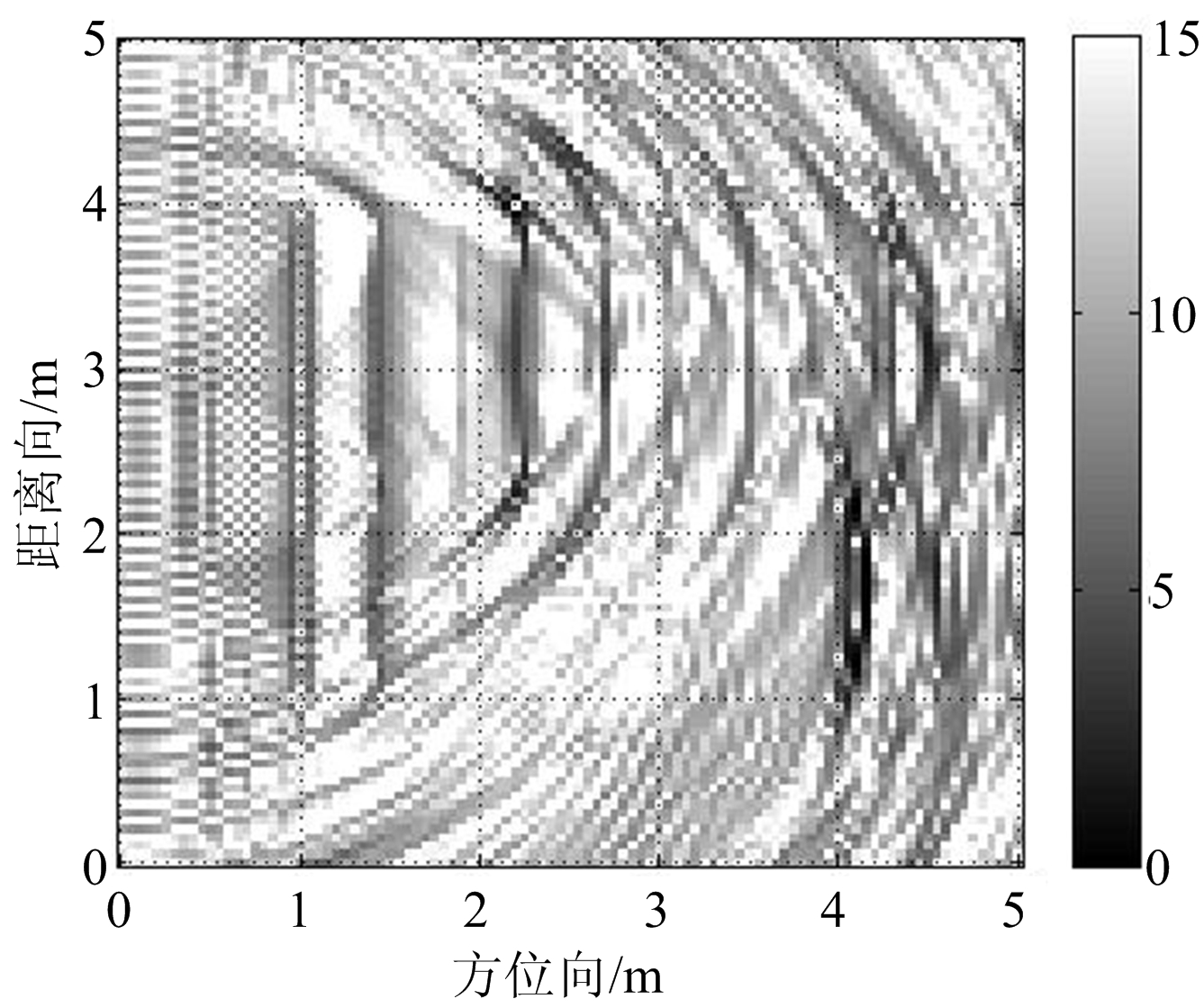
(b) 视角2
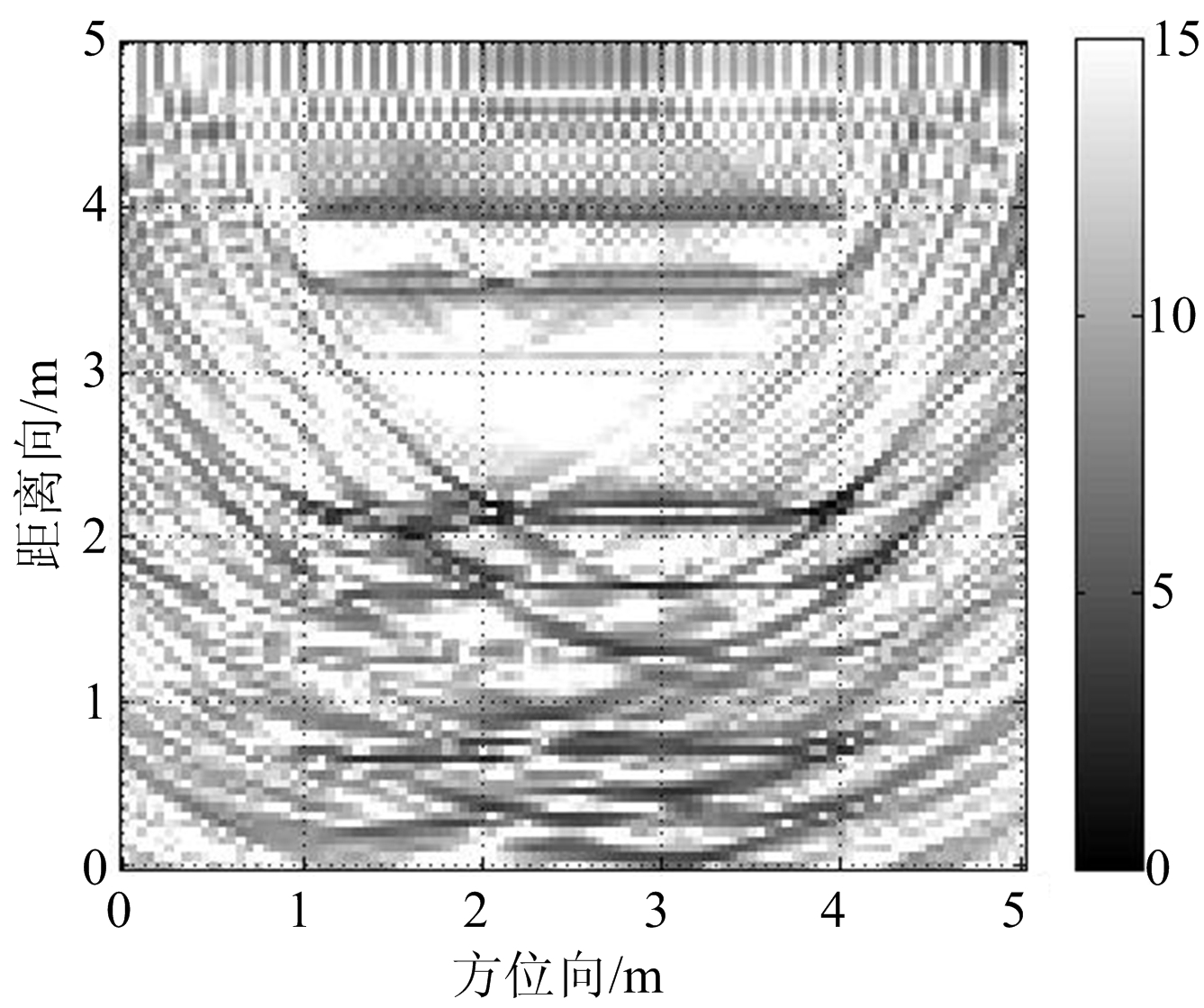
(c) 视角3
(d) 视角4
图4 多视角BP成像
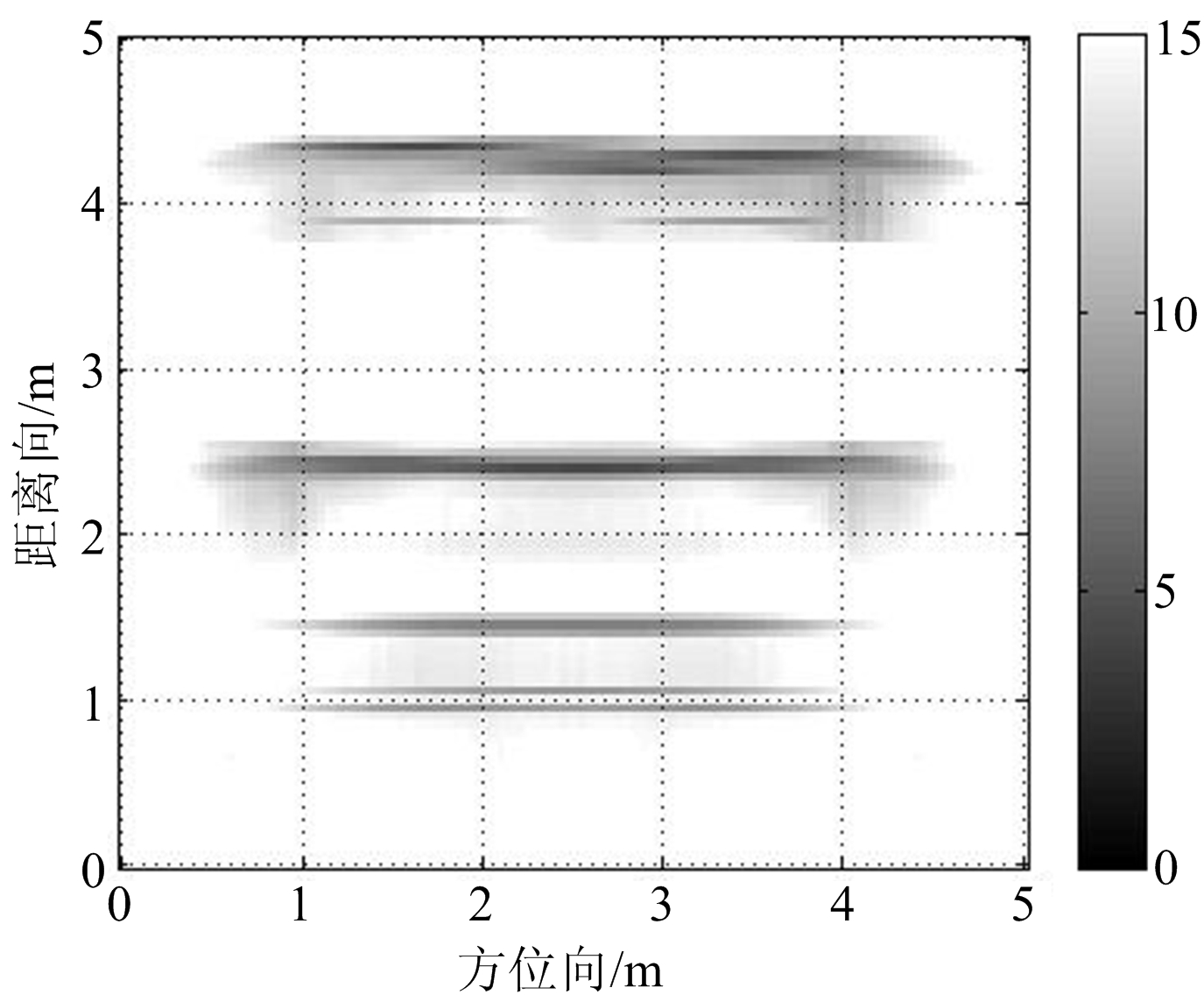
(a) 视角1
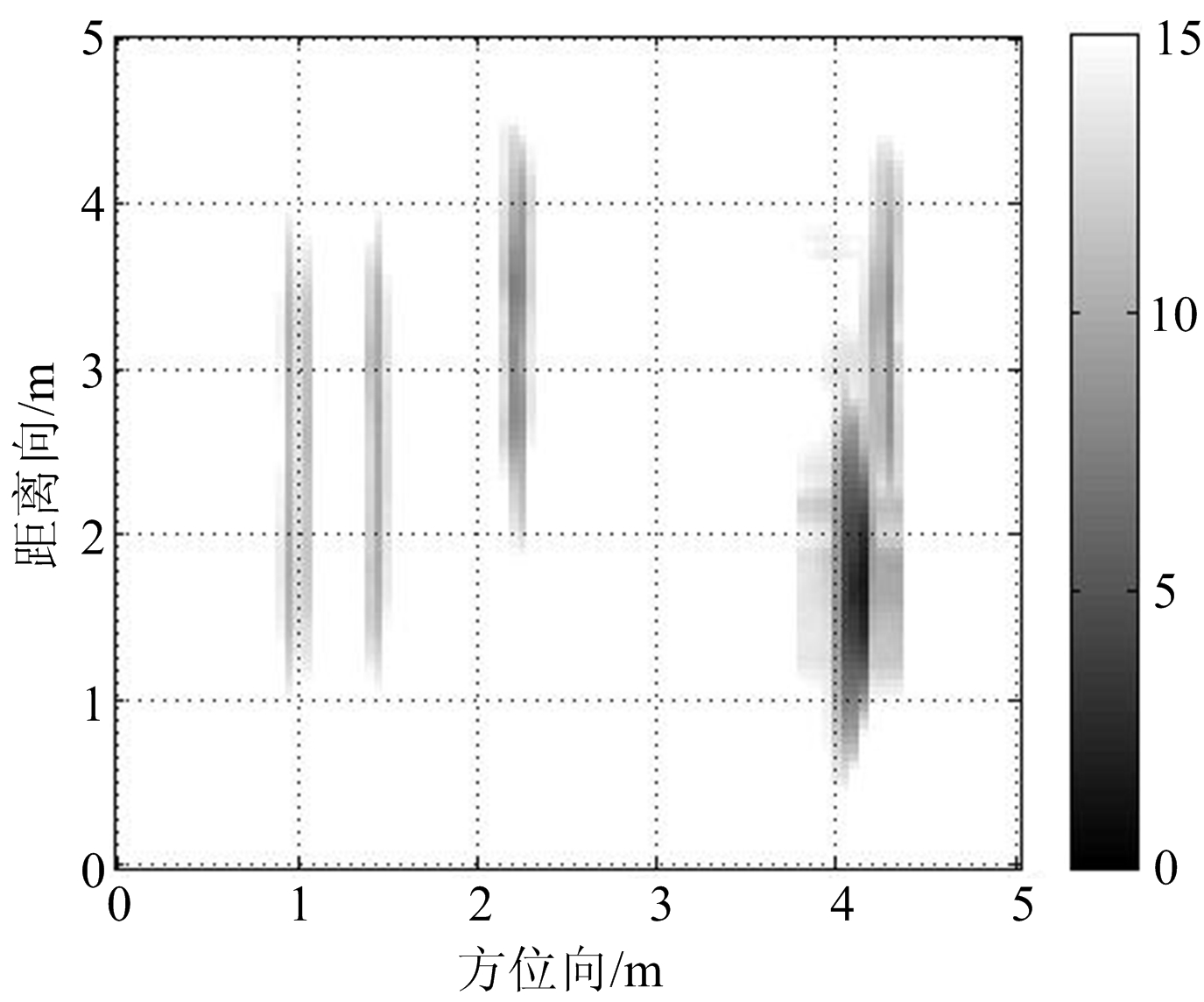
(b) 视角2
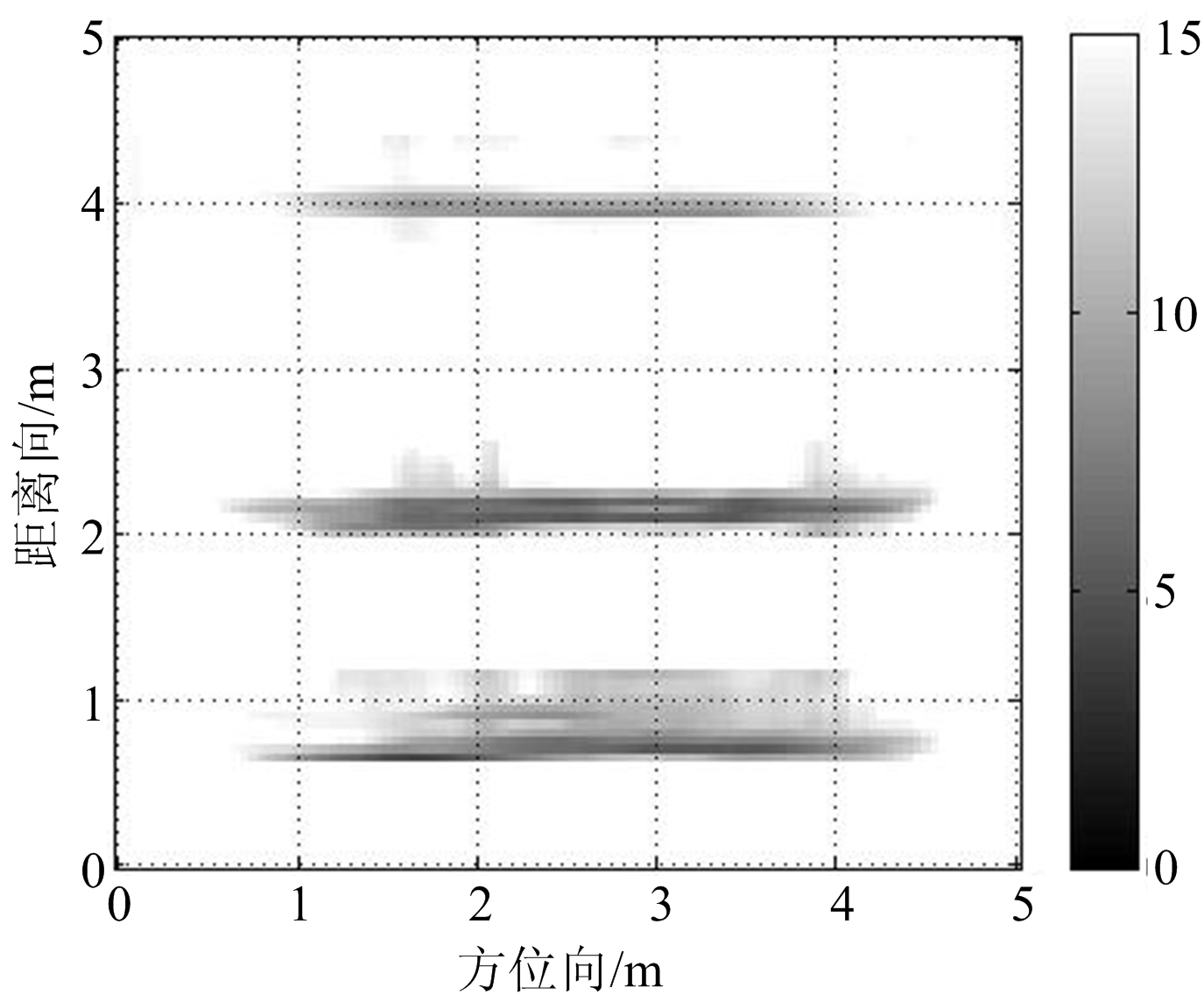
(c) 视角3
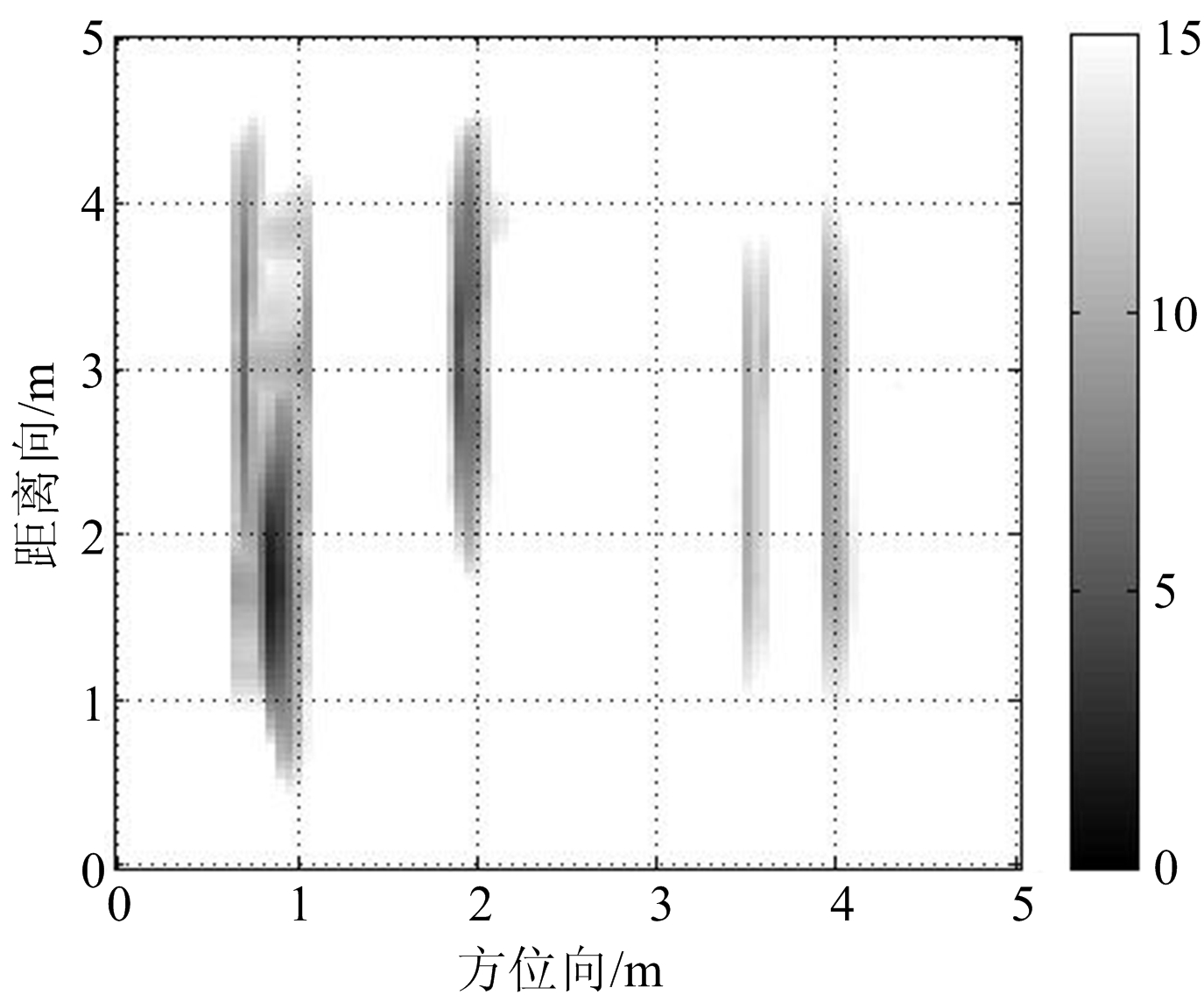
(d) 视角4
图5 多视角多方位二维匹配滤波处理结果
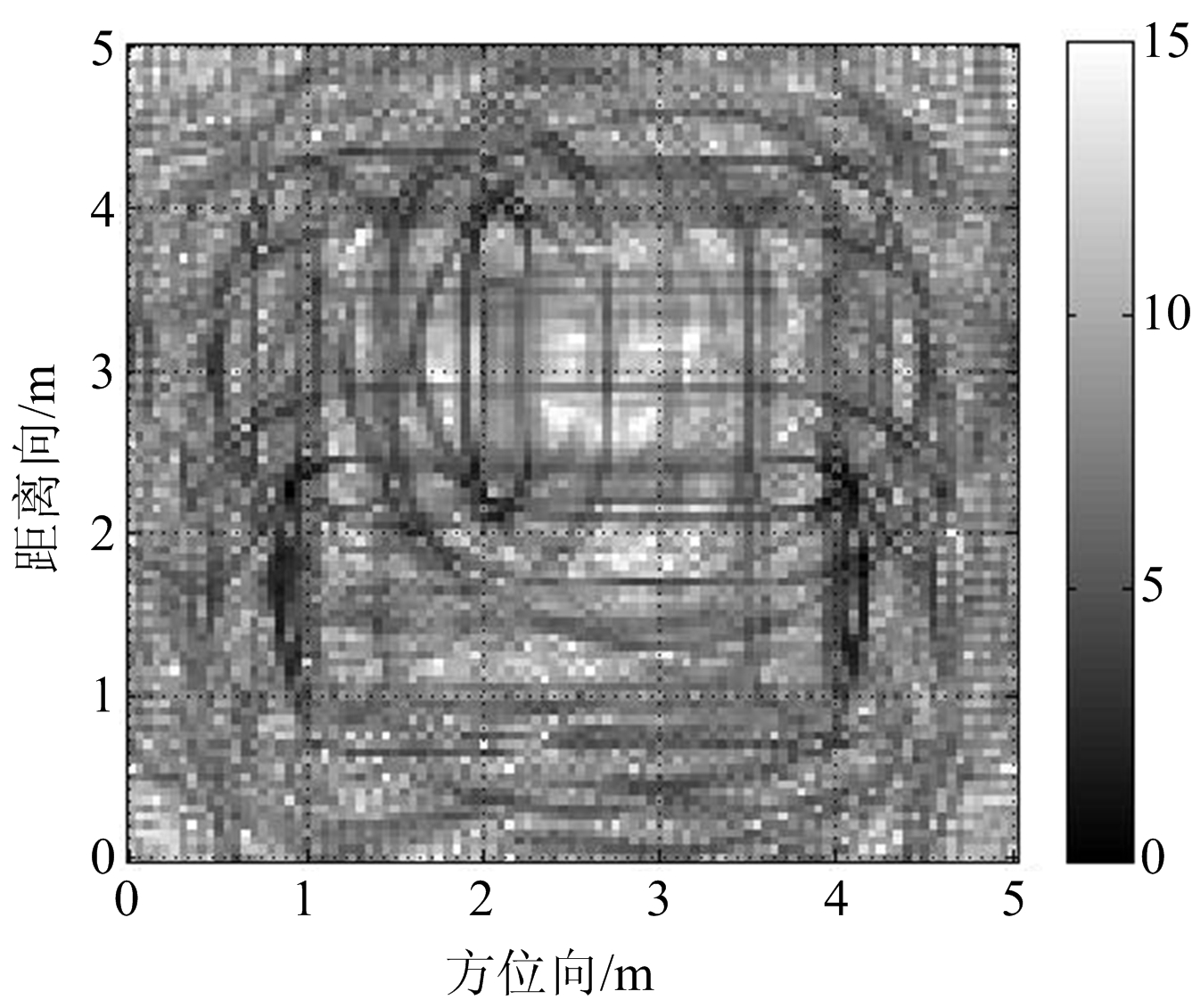
(a) 算术融合方法
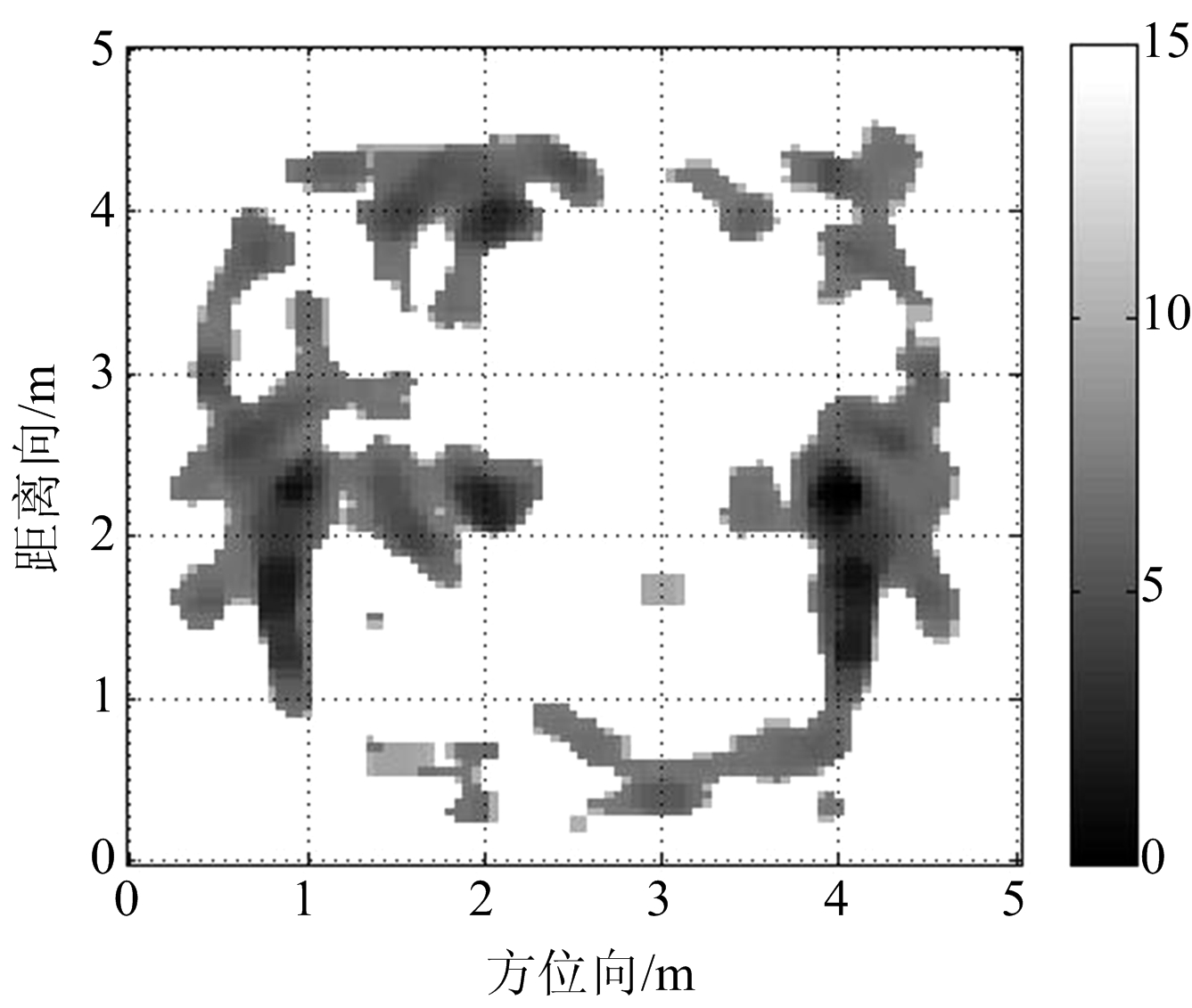
(b) MNK融合方法
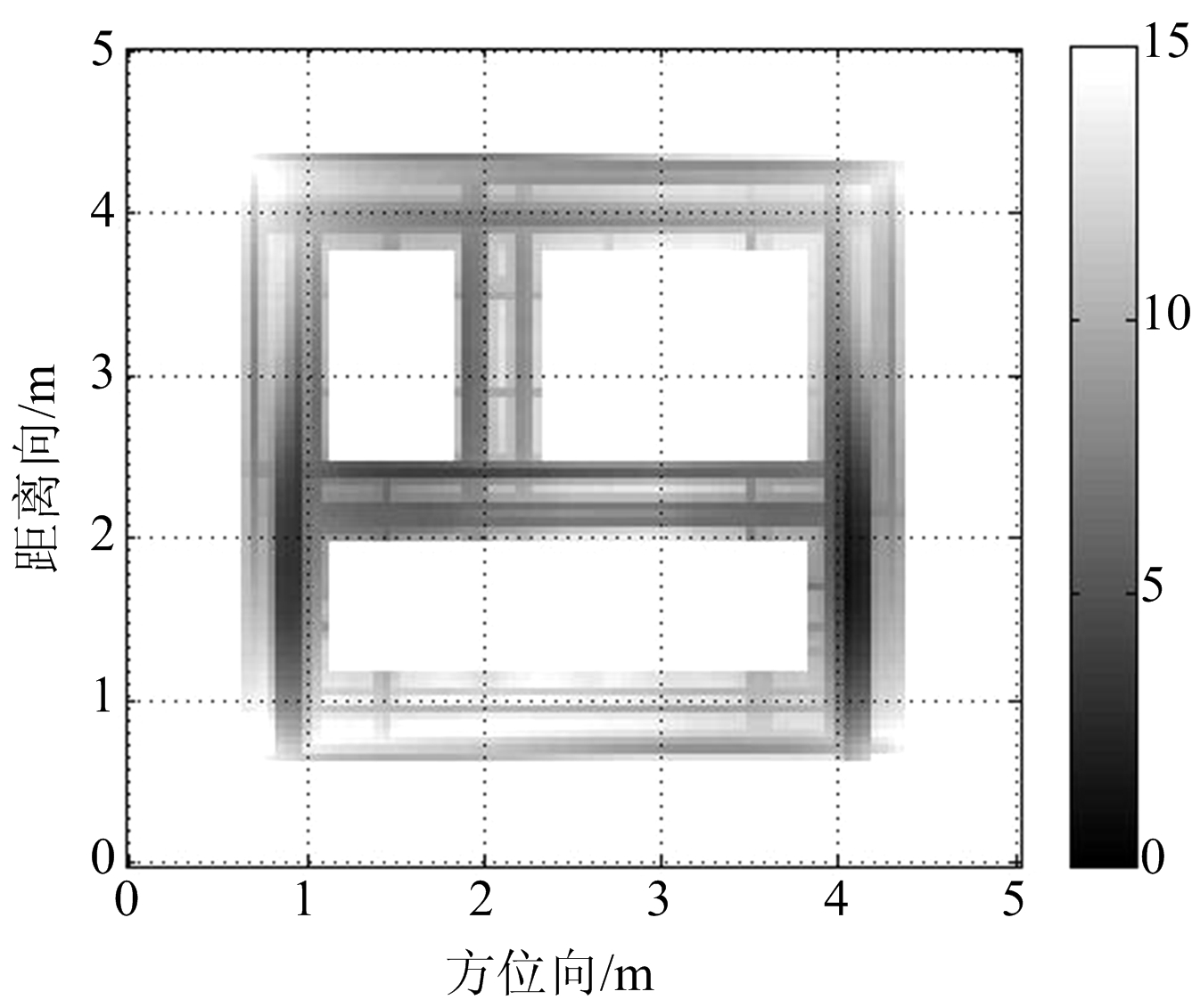
(c) 本文方法
图6 不同融合方法处理结果的比较
3.2 实测数据结果
实测场景如图7所示，这里从视角A和视角B两个视角平行于建筑物墙体进行探测。雷达探测系统采用自行搭建的基于矢量网络分析仪(VNA)的步进频MIMO穿墙雷达实验平台，如图8所示。系统的工作频率范围为1～2 GHz，中心频率为1.5 GHz。MIMO天线阵列采用两发五收的工作模式，相邻天线间的距离从左至右依次为0.37,0.35,0.25,0.35和0.37 m,天线距离墙1.5 m。实验场景中的墙体厚度为0.3 m，相对介电常数为6.5。
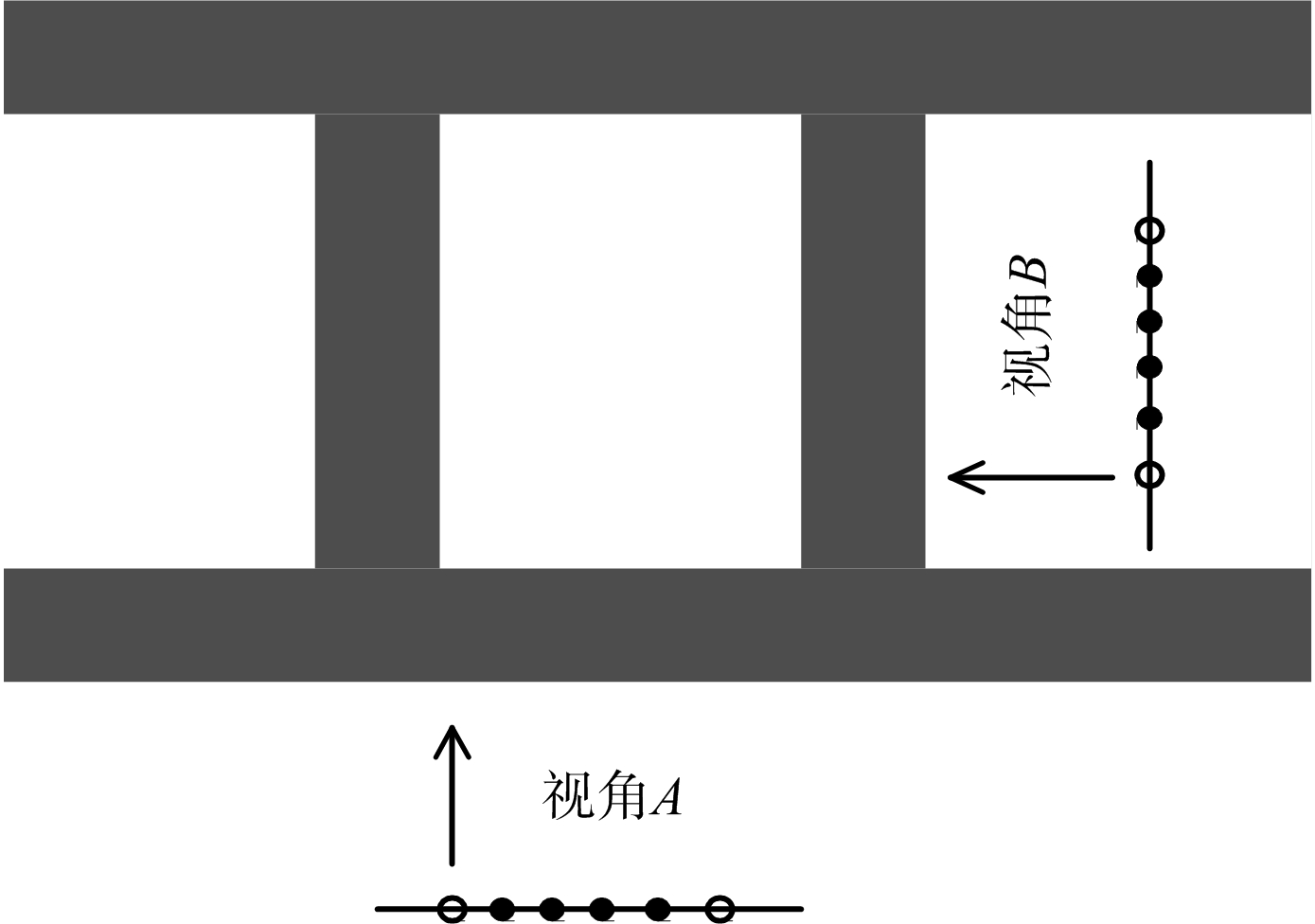
图7 实测场景
图8 步进频MIMO雷达实验平台
图9为不同的融合算法对实测数据处理成像的结果。从这些实测数据的处理结果来看，本文方法获得的建筑物布局成像图，相较于其他两种方法在成像质量上有所提高，没有毛刺、断层和旁瓣栅瓣等干扰信息，墙体的边缘细节信息有一定程度的增强，对建筑物布局的恢复更加理想。
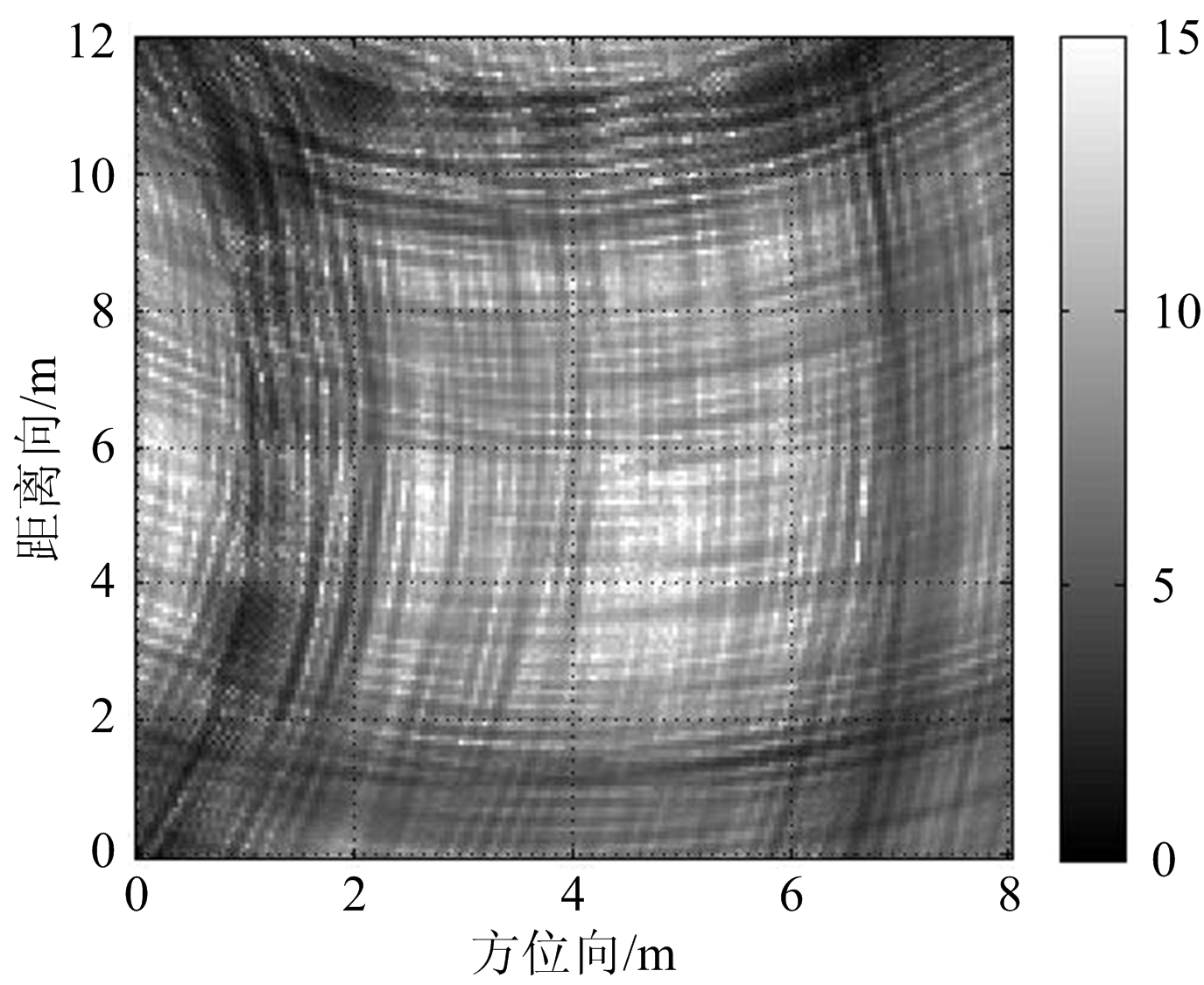
(a) 算术融合方法
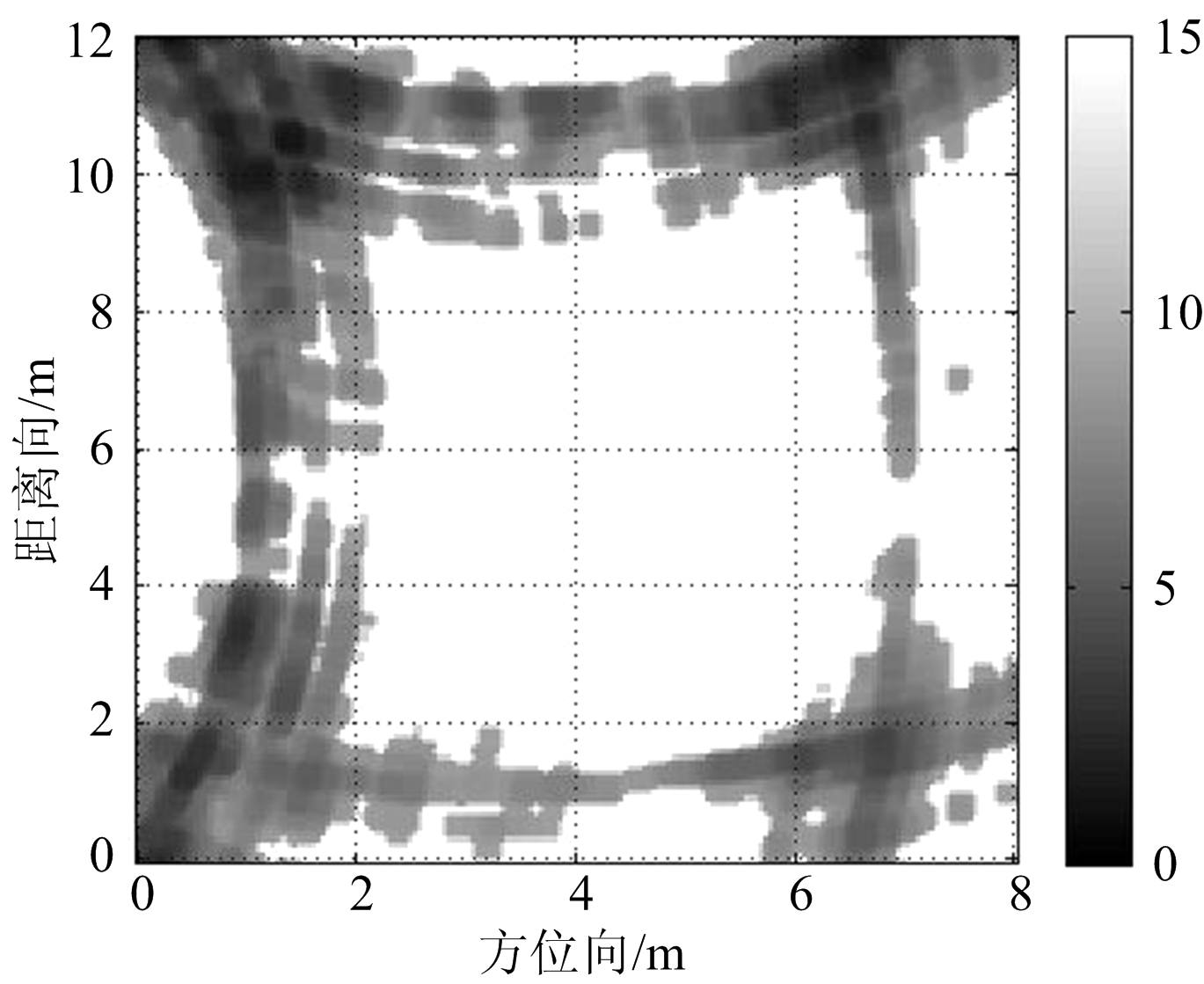
(b) MNK融合方法
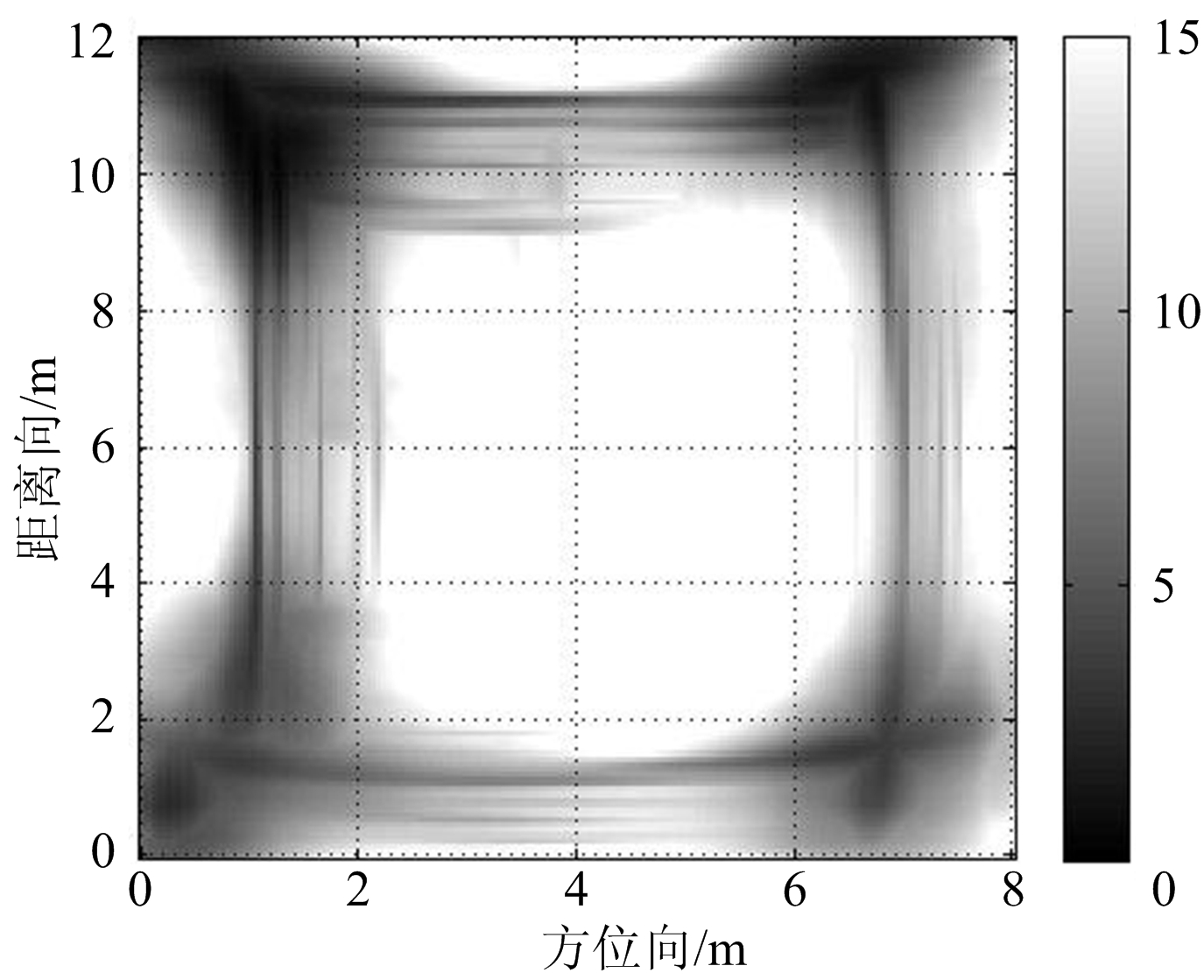
(c) 本文方法
图9 不同融合方法处理的实测数据结果
4 结束语
提出的基于多方位多尺度的图像融合方法增强了建筑物墙体的轮廓和细节信息，所得到的最终融合图像中墙体像突出，边缘轮廓清晰，整体的细节信息保留良好。图像融合的质量均比算术融合方法和文献[7]给出的MNK融合方法有较大的提高，为后续包括建筑物墙角和门窗等散射体在内的融合方法做铺垫。
[1] ODEDO V C, YAVUZ M E, COSTEN F, et al. Time Reversal Technique Based on Spatio-Temporal Windows for Through the Wall Imaging[J]. IEEE Trans on Antennas and Propagation, 2017, 65(6):3065-3072.
[2] YILMAZ B, ÖZDEMIR C. Design and Prototype of Radar Sensor with Vivaldi Linear Array for Through-Wall Radar Imaging: An Experimental Study[J]. Journal of Applied Remote Sensing, 2016, 10(4):046012.
[3] ZOOFAGHARI M, TAVAKOLI A, DEHMOLLAIAN M. Imaging Through a Wall with Corrugated Surfaces[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(3):394-398.
[4] ZHANG W, HOORFAR A, THAJUDEEN C, et al. Full Polarimetric Beam-Forming Algorithm for Through-the-Wall Radar Imaging[J]. Radio Science, 2011, 46(5):1-17.
[5] NGUYEN L, WONG D, RESSLER M, et al. Obstacle Avoidance and Concealed Target Detection
Using the Army Research Lab Ultra-Wideband Synchronous Impulse Reconstruction (UWB SIRE) Forward Imaging Radar[C]∥ Defense and Security Symposium: Detection and Remediation Technologies for Mines and Minelike Targets XII, Orlando, FL: SPIE, 2007:1-8.
[6] AFTANAS M, DRUTAROVSKY M. Imaging of the Building Contours with Through the Wall UWB Radar System[J]. Radioengineering, 2009, 18(3):258-264.
[7] 贾勇,孔令讲,马静,等. 穿墙雷达多视角建筑布局成像[J]. 电子与信息学报, 2013, 35(5):1114-1119.
[8] LAGUNAS E, AMIN M G, AHMAD F, et al. Determining Building Interior Structures Using Compressive Sensing[J]. Journal of Electronic Imaging, 2013, 22(2):021003.
[9] 顾晓峰,朱宏擎. 一种基于二维匹配滤波器的掌纹识别算法[J]. 华东理工大学学报(自然科学版), 2017, 43(1):90-96.
[10] DA CUNHA A L, ZHOU J, DO M N. The Nonsubsampled Contourlet Transform: Theory, Design, and Applications[J]. IEEE Trans on Image Processing, 2006, 15(10):3089-3101.
