0 引言
机载雷达具有探测距离远、覆盖范围大且具有较强的机动性和灵活性等优点，因此，在军事和民用领域应用越来越广泛[1]。相控阵体制雷达的收发天线阵列紧密排布，各阵元发射相关信号，在空间同向叠加，可以获得较高的天线增益[2]。为了使目标波达方向(Direction of Arrival，DOA)的估计不模糊，通常要求阵列阵元间距满足空间采样定理，即阵元间距小于等于波长的一半[3]。当要求天线阵列具有很高的角度分辨率时，就需要较大的阵列孔径，此时，传统阵列需要的阵元个数较多，而在空间欠采样情况下，可大大减少所需阵元数，不仅减少了系统成本而且削弱了天线间的互耦效应[4]。但空间欠采样会使天线方向图出现栅瓣或高旁瓣问题，影响角度估计性能。所以研究空间欠采样下的DOA估计技术就显得十分重要[3]。
经典的DOA估计算法都以点目标信号源为模型来简化算法，降低分析的复杂性[5]。然而，由于复杂环境下的散射、反射、衍射及折射等原因导致大量的多径现象，从而造成信号源在空间发生一定的角度扩展[6]，这类发生角度扩展的信号源统称为分布式信号源[7]。因此，当信号源的空间分布特性不能忽略时，点信号源模型往往不能准确描述阵列观测数据，那么用点源为模型的DOA估计方法的性能会恶化，甚至得不到正确的估计结果[7-8]。
目前，分布式目标的DOA估计方法有MUSIC算法[9]、TLS-ESPRIT算法[10]和最大似然算法[11]等，但以上算法均是在阵列满足空间采样定理下实现的。针对空间欠采样的情况，本文提出了一种基于PSO-MUSIC算法的分布式目标波达方向估计方法。该方法首先建立分布式目标信号模型，然后利用粒子群优化算法优化天线阵元间距，改善空间欠采样情况下天线方向图的栅瓣和高旁瓣问题，最后利用分布式目标导向矢量结合MUSIC算法得到目标信号功率谱，从而估计空间欠采样下分布式目标的中心波达方向。
1 信号模型
任意线阵阵列示意图如图1所示。假设第一个阵元为参考阵元，那么N个阵元的阵元间距为
且阵元间距
(n=1,2,…,N-1，λ为雷达波长)，相干处理脉冲数为M，天线发射脉冲重复频率(PRF)为fr。图中，θ为分布式目标的中心波达方向。
图1 任意线阵阵列示意图
分布式目标为一群满足一定统计分布特性的散射体的集合[6]。那么分布式目标回波即为波束范围内所有散射点回波的叠加。考虑远场空间有一个分布式目标信号源入射到N元线阵上，阵列观测信号数据x表示为
(1)
式中：n表示噪声；Q, αi分别表示分布式目标中的散射粒子总数和第i个散射粒子的幅度；θ表示分布式目标的中心DOA；θi表示第i个散射粒子与中心DOA的角度偏差，为随机变量，满足一定的概率分布，如高斯分布、均匀分布、三角分布等； b(θ+θi)表示分布式目标第i个散射粒子的导向矢量，且
b(θ+θi)=a(θ)⊙g(θi)
(2)
式中，⊙表示Hadamard积，a(θ)表示分布式目标中心DOA方向上的导向矢量，g(θi)表示具有确定性角密度函数(高斯分布、均匀分布、三角分布等)的分布式目标在中心DOA上的扩展。本文采用角密度函数为高斯分布的分布式目标，Δ为扩展角度，则a(θ)和g(θi)可表示为
a(θ)=
(3)
g(θi)=
exp
(4)
2 分布式目标中心DOA估计方法
阵元稀疏布置(即阵元间距d>
可以减少天线单元，从而降低天线系统工程成本，而且具有更大自由度在阵列孔径上布置阵元，可以获得更加优越的天线性能[12]。对于相同的天线数目，稀疏阵比传统均匀阵更易获得较窄的主瓣，但高旁瓣电平会随着阵元数的减少而升高，为了降低旁瓣电平就需要优化阵列阵元间距。本文首先利用粒子群优化算法得到最高旁瓣电平最小情况下的阵元间距，根据该阵元间距可得到相应的阵列流形，然后在该阵列流形下接收回波数据，最后利用MUSIC算法构造代价函数，从而获得分布式目标的中心DOA估计。
2.1 粒子群优化算法优化阵元间距
粒子群优化算法(PSO)是一种新的全局优化算法，它源于对鸟类捕食行为的模拟[13]。本文利用PSO算法对N元线阵的阵元间距
进行优化，首先定义一个粒子总群，该总群中粒子个数为Z，每个粒子位置的搜索空间为N-1维(也即是未知参数个数)，为了寻找使得适应度函数最小的粒子位置(也即是最优的阵元间距)，需要对总群中所有粒子位置进行更新迭代，在第r次迭代中，总群中第k(k=1,2,…,Z)个粒子的位置表示为
其中
表示第n个阵元与第n+1个阵元的阵元间距)，那么整个总群的位置可表示为
PSO算法是根据适应度函数来评价粒子位置“好坏”程度的，那么适应度函数的选取很关键。本文的优化问题为寻找天线方向图高旁瓣电平最小情况下的阵元间距，因此适应度函数可设为
(5)
式中，
k=1,2,…,Z
(6)
式中，
为阵元间距，也是本文中需要优化的参数，In为天线阵列加权，φ为入射波与阵列法线的夹角，φ0为天线方向图主瓣方向角，Fmax= 
为最大方向图，S表示天线方向图的旁瓣区域，可表示为
(7)
式中，φw为天线方向图的主旁瓣分界角度。
本文将寻找天线方向图高旁瓣电平最小时的阵列阵元间距转化为在粒子群优化算法搜索使得适应度函数最小的粒子位置。以第k个粒子为例，在第r次迭代中适应度函数有如下关系：
⟺
k=1,2,…,Z
(8)
在第r次迭代中，将总群中第k个粒子的位置和该粒子上一次迭代选择出的使得适应度函数最小的粒子位置(记为个体极值)
代入到适应度函数中，根据适应度函数值的大小选择出本次迭代的个体极值：
(9)
在第r次迭代中，从总群所有粒子位置的个体极值中选择出使得适应度函数最小的粒子位置记为全局极值
其位置选择表达式如下：
(10)
当前后两次迭代的适应度函数值小于门限值时满足迭代终止条件，得到的全局极值Pg即为PSO算法优化后的阵列阵元间距。
粒子每次迭代更新速度和位置都是与个体极值和全局极值相关的，更新规则如下：
(11)
(12)
式中：
表示第r次迭代中第k个粒子位置更新的速度，为了避免粒子位置跳离 搜索空间，一般需要对粒子每一维的速度 Vkj(j=1,2,…,N-1)进行限定，即 Vkj∈[-Vmax,Vmax]；c1，c2表示学习因子，通常c1=c2=2；rand表示0到1之间的随机数；w表示关于迭代次数的惯性权重，为了防止粒子群优化算法在解空间内搜索时，粒子位置在某个全局极值附近震荡，因此使得惯性权重的取值随着迭代的进行由最大惯性权重wmax减小到最优惯性权重wmin，表示如下[14]：
(13)
式中，a表示当前迭代次数，T表示总的迭代次数，即为迭代终止条件满足时的次数。
2.2 估计分布式目标中心DOA
根据PSO算法优化后的阵元间距得到相应的阵列流形，在该阵列流形下接收数据，并得到其协方差矩阵表示如下：
R=E[xxH]=Rs+Rn
(14)
由于信号与噪声相互独立，接收数据协方差矩阵可分解为信号、噪声相关的两部分。其中Rs为分布式目标的协方差矩阵，Rs为噪声协方差矩阵。对协方差矩阵R进行特征分解有
(15)
式中，(·)H表示共轭转置，Us表示由大特征值对应的特征矢量张成的子空间即信号子空间，Un表示小特征值张成的子空间即噪声子空间。在理想情况下，信号子空间与噪声子空间正交，即
(16)
其中，分布式目标信号角密度函数已知，且能够通过式(2)得到广义的分布式目标导向矢量 b(ψ)。利用式(16)的特点，可得到MUSIC算法的谱估计公式为
(17)
那么本文中所求分布式目标中心DOA的代价函数如下：
(18)
3 算法流程
PSO-MUSIC算法主要步骤如下：
1) 在给定范围内随机初始化总群中所有粒子的位置和速度；
2) 计算每个粒子的适应度函数值；
3) 每个粒子所得到的适应度函数值与上一次迭代选择出的个体极值的适应度函数值比较，如果较好，则替换当前个体极值；
4) 每个粒子所得到的适应度函数值与整个总群中选择出的全局极值的适应度函数值比较，如果较好，则替换当前全局极值；
5) 根据式(11)、式(12)更新粒子速度和位置；
6) 如果满足终止条件，则输出最优位置，否则返回步骤2)继续运行直到满足终止条件为止；
7) 由PSO优化后的阵列接收数据并得到数据协方差矩阵，对协方差矩阵进行特征分解，确定信号子空间和噪声子空间，根据信号子空间与噪声子空间的正交性构造有关DOA的代价函数；
8) 最后通过寻找代价函数的最小值得到分布式目标的中心DOA估计结果。
4 仿真结果及分析
4.1 分布式目标仿真
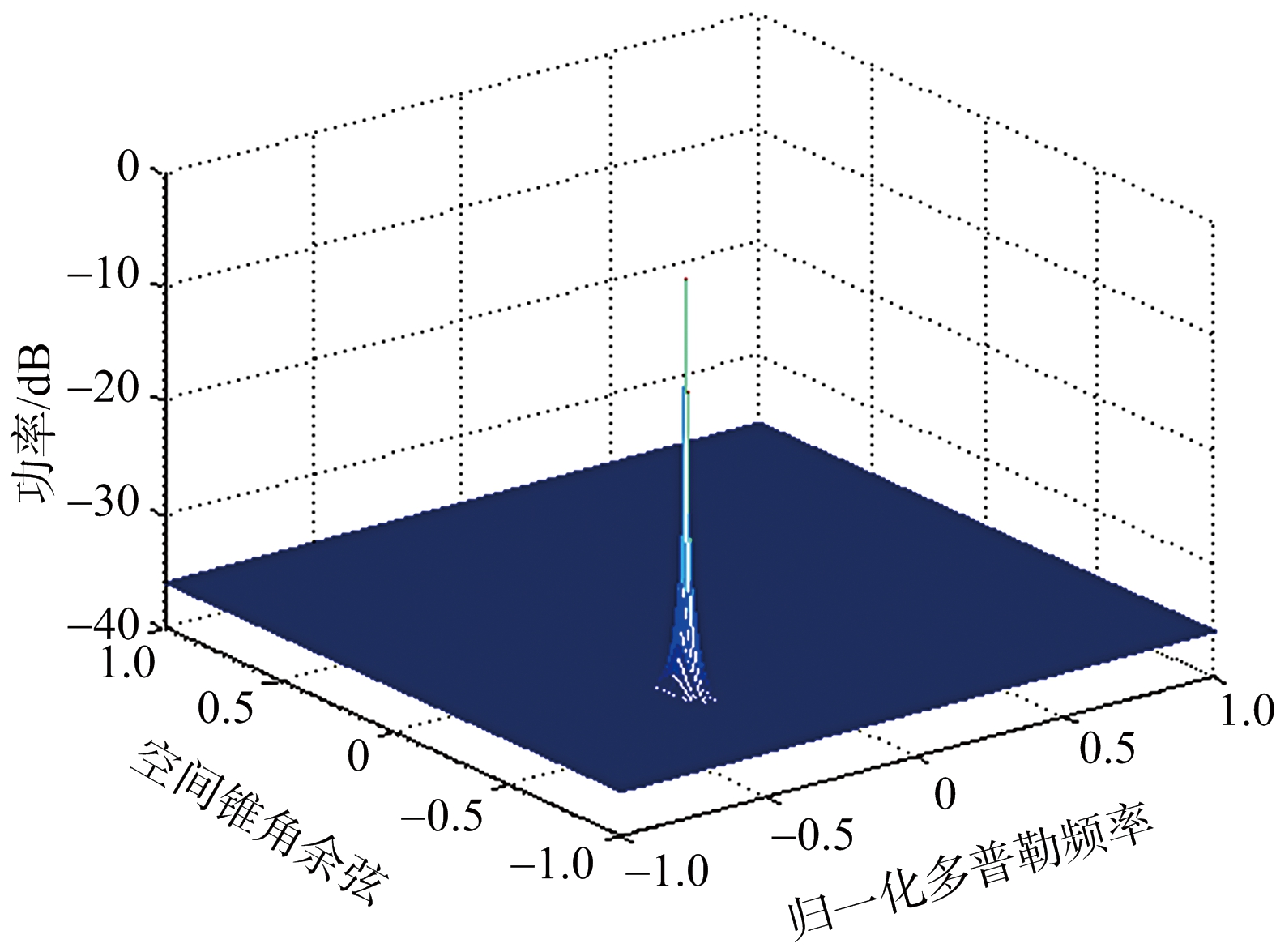
图2 点目标模型
图2为传统的点源信号模型，图3为本文采用的分布式目标信号模型，目标的中心DOA为60°，角度扩展为2°。从图中可以看出，分布式目标在空间上会有一定的扩展，不再是一个单纯的点源，因此其阵列观测矢量也与点目标不同。
图3 分布式目标模型
4.2 粒子群优化算法优化阵元间距
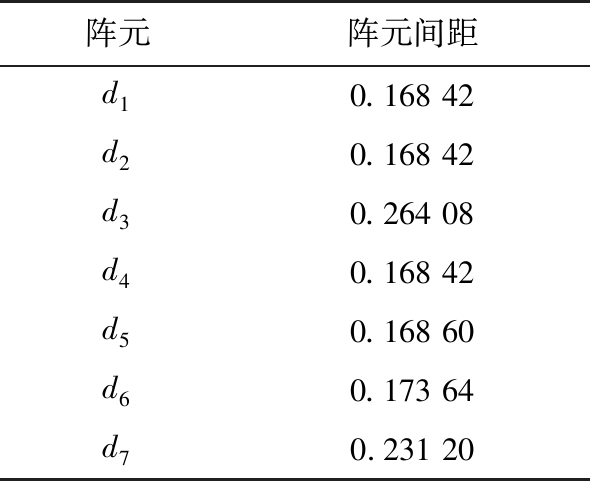
考虑一个8阵元线阵，那么PSO算法的空间维度为7(相邻阵元间距的个数)，群体初始化大小为300，迭代次数为500，最大惯性权重wmax=0.9，最小惯性权重wmin=0.4，最大速度vmax=1，优化的阵元间距在
到λ，且λ=0.32 cm。在此条件下，PSO算法优化后的阵元间距如表1所示。
表1 PSO优化后阵元间距
阵元阵元间距d10.168 42d20.168 42d30.264 08d40.168 42d50.168 60d60.173 64d70.231 20
空间欠采样可以利用较少的阵元数得到更大的阵列孔径，但是均匀欠采样下天线方向图会出现栅瓣，如图4所示，非均匀欠采样下天线方向图的旁瓣电平较高，如图5所示，不利于分布式目标的DOA估计。图6为PSO算法优化的阵列天线方向图，可以看出PSO算法优化后的阵列可以消除栅瓣，得到旁瓣电平较低情况下的天线方向图，有利于提高目标的参数估计性能。图7为粒子群优化算法的收敛曲线，即为PSO算法随着迭代的进行适应度函数的变化情况，可以看出本文选取的迭代次数满足终止条件。
图4 均匀稀疏阵天线方向图
图5 随机非均匀阵天线方向图
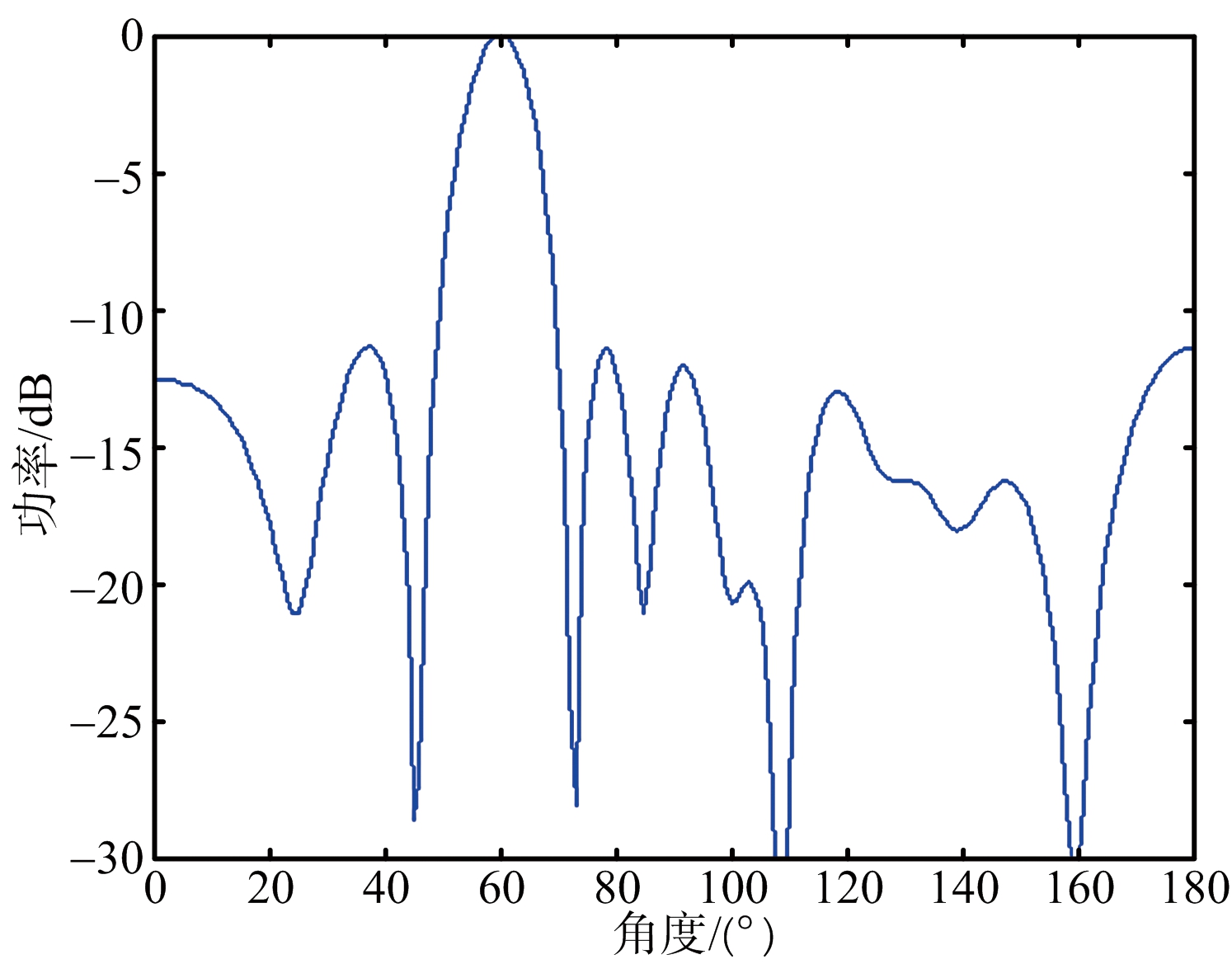
图6 PSO算法天线方向图
图7 PSO算法收敛曲线
4.3 基于PSO-MUSIC算法的DOA估计
图8为本文算法的分布式目标中心DOA估计结果图，从图中可以看出，PSO-MUSIC算法的DOA估计中没有出现伪峰，可以得到较准确的分布式目标DOA估计结果。
图8 MUSIC算法DOA估计结果
5 结束语
针对空间欠采样情况下目标DOA估计的多值问题，本文提出了一种基于PSO-MUSIC算法的分布式目标DOA估计方法。该方法首先利用粒子群优化算法优化阵元间距，得到天线方向图高旁瓣电平最小情况下的阵元间距，然后利用该阵元间距得到阵列流形并接收回波数据，最后通过MUSIC算法得到阵列回波功率谱，并通过功率谱的最大值，能够获得空间欠采样下分布式目标中心DOA的准确估计。仿真结果表明，在空间欠采样情况下，本文方法能够获得准确的分布式目标中心DOA估计。
[1] 丁鹭飞,耿富录. 雷达原理[M]. 3版. 西安:西安电子科技大学出版社, 2002:1-24.
[2] 柳艳. 稀疏阵雷达正交波形设计与角度估计研究[D]. 南京:南京理工大学, 2013.
[3] 曾操. 空时欠采样下的参数估计及硬件实现[D]. 西安:西安电子科技大学, 2004.
[4] RAHARDJO E T, SANDI E, ZULKIFLI F Y. Design of Linear Sparse Array Based on the Taylor Line Source Distribution Element Spacing[C]∥ IEEE Asia Pacific Microwave Conference, Kuala Lumpar, Malaysia: IEEE, 2017:61-64.
[5] 林晓帆,韦岗. 一种获取非相干分布源空间分布的算法[J]. 电子与信息学报, 2014, 36(2):260-265.
[6] HASSANIEN A, SHAHBAZPANAHI S, GERSHMAN A B. A Generalized Capon Estimator for Localization of Multiple Spread Sources[J]. IEEE Trans on Signal Processing, 2004, 52(1):280-283.
[7] 姚晖. 分布式信号源参数估计技术研究[D]. 郑州:解放军信息工程大学, 2013.
[8] BESSON O, STOICA P. Decoupled Estimation of DOA and Angular Spread for a Spatially Distributed Source[J]. IEEE Trans on Signal Processing, 2000, 48(7):1872-1882.
[9] WAN Liangtian, HAN Guangjie, JIANG Jinfang, et al. DOA Estimation for Coherently Distributed Sources Considering Circular and Noncircular Signals in Massive MIMO Systems[J]. IEEE Systems Journal, 2017, 11(1):41-49.
[10] SHAHBAZPANAHI S, VALAEE S, BASTANI M H. Distributed Source Localization Using ESPRIT Algorithm[J]. IEEE Trans on Signal Processing, 2001, 49(10):2169-2178.
[11] SIESKUL B T, JITAPUNKUL S. An Asymptotic Maximum Likelihood for Estimating the Nominal Angle of a Spatially Distributed Source[J]. AEU:International Journal of Electronics and Communications, 2006, 60(4):279-289.
[12] 但庚元. 稀布阵列方向图综合优化算法研究[D]. 成都:电子科技大学, 2015.
[13] KENNEDY J, EBERHART R. Particle Swarm Optimization[C]∥ International Conference on Neural Networks, Perth, WA, Australia: IEEE, 1995:1942-1948.
[14] 侯志荣,吕振肃. 基于MATLAB的粒子群优化算法及其应用[J]. 计算机仿真, 2003, 20(10):68-70.
