0 引言
不同于传统的激光、电视和红外等制导体制下的导引头[1-3]，主动式雷达导引头可实现目标的自主攻击[4-5]，可实现“发射后不管”的功能，大幅度提升了导弹发射平台和飞行员的安全。此外，其可在恶劣的气候条件下使用，可全天时、全天候作战[6-8]。
导引头的性能指标对弹上控制系统的设计以及导弹的命中精度起着至关重要的作用。比如，对于末制导采用比例导引攻击目标的导弹而言，精确的导引头视线角速度是导弹准确命中目标的关键[9-11]。然而由于存在各种非理想的系统误差，如天线罩瞄准线的误差斜率、导弹加速度和各种噪声的存在，使得导引头自身输出的视线角速度无法描述视线角速度的真实值。因此评估导引头输出的视线角速度是否满足制导算法的需求至关重要。为保证导引头的作战使用性能，尤其是造价昂贵的毫米波导引头，其性能指标除了在实验室进行考核验证以外，还需要进行外场的高塔试验和跑车试验等，但是这些试验无法模拟导弹的飞行环境。因此进一步的挂飞试验是必不可少的。通过将导引头挂装在飞行平台上，平台模拟数字仿真弹道飞行，最大程度地模拟导引头的作战使用环境。在挂飞试验中，如何评估毫米波导引头的性能指标至关重要，为保证导弹的命中精度和毁伤效能，寻求精确的导引头性能指标外场评估方法亟待解决。
针对此问题，本文提出了一种基于载波相位差分技术(Real-Time Kinematic, RTK)[12-13]的毫米波导引头性能评估方法。RTK技术具有定位精度高、测量时间短、全天候作业等优点，可利用全球定位系统(Global Position System, GPS)实时高精度获取目标的位置坐标[14-15]。通过将利用GPS数据计算出的导引头性能指标和导引头的自身输出进行对比，实现毫米波导引头的性能评估。实测的毫米波导引头挂飞数据验证了所提方法的有效性，与惯性导航系统测量数据的对比进一步验证了所提方法的优越性。
1 RTK定位原理
RTK技术是在GPS技术基础上发展而来的载波相位差分测量技术，是一种以载波相位测量与数据传输技术相结合的实时差分GPS测量技术，它在测量过程中可以实时提供目标厘米级精度的三维坐标[12-13]。在测量过程中不受通视条件限制、速度快、精度高，各测量结果之间误差不累积。
RTK系统利用两台GPS接收机同时接收卫星信号，其中一台安置在已知坐标点上作为基准站，另一台作为流动站用来测定未知点的坐标。基准站根据该点的准确坐标求出其他卫星的距离改正数，并将这一改正数发给移动站，移动站根据这一改正数来修正其定位结果。它能够实时地提供移动站所在测试点的三维定位结果，并达到厘米级精度。RTK的工作原理示意图如图1所示。
图1 RTK定位的工作原理
2 基于RTK的导引头参数计算
2.1 构型设置
首先构造基于RTK的毫米波导引头性能评估系统构型。在保证RTK的正常工作范围内，结合导弹的数字仿真弹道，规划载机的运动航线和确定GPS系统主站和各子站的安装位置。固定GPS的主站后，根据RTK正常工作的距离范围，将两个GPS的子站接收端分别固定在载机平台和目标上。毫米波导引头性能评估系统构型的示意图如图2所示。载机模拟数字仿真弹道飞向目标，当载机飞行至毫米波导引头的有效作用距离时，毫米波导引头开始发射电磁波搜索目标，同时载机上的GPS接收端实时测量并记录下毫米波导引头的位置坐标，目标上的GPS接收端实时测量并记录下目标所在位置的坐标。一般而言，RTK的有效工作范围为4 km[12-13]，对于本文所讨论的直升机载空地导弹而言，毫米波导引头的解锁(即解除锁定模式，开始发射电磁波扫描搜索目标的动作)距离通常小于4 km，因而此系统构型可以保证RTK的定位精度，由于GPS的定位精度而导致的参数计算误差将在后文进行详细的讨论。
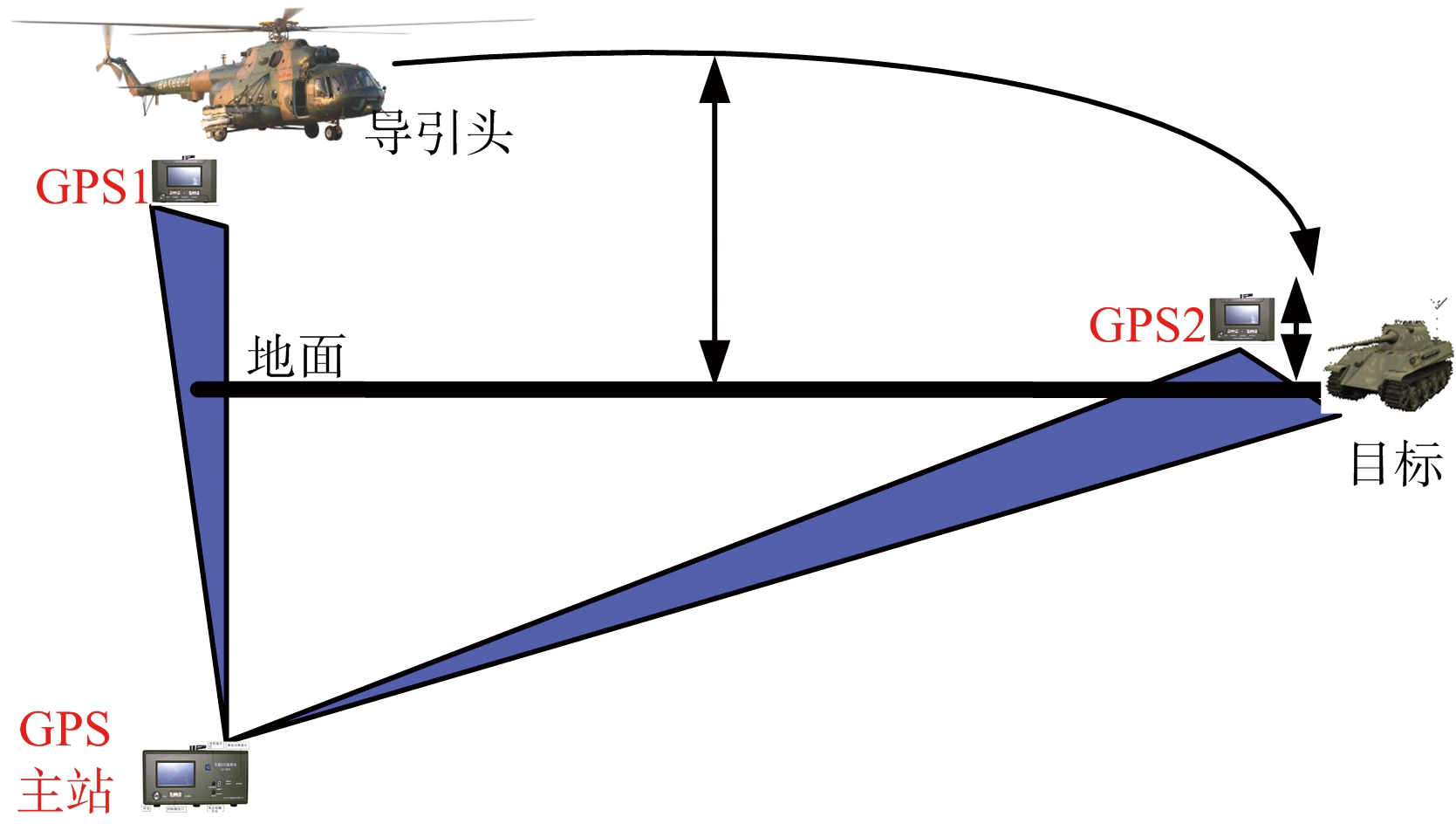
图2 基于RTK的导引头评估系统构型图
根据GPS测量得到的毫米波导引头位置和目标位置，即可实时计算出导引头的诸多重要参数，例如导弹与目标之间的距离(后文简称为弹目距离)、俯仰视线角速度以及偏航视线角速度等。通过将这些参数与导引头自身输出的参数进行实时对比分析，即可实时评估毫米波导引头准确捕获与跟踪目标等性能。
2.2 参数计算
在图2所示系统构型下，利用GPS测量的位置信息，可计算获得诸多毫米波导引头的重要性能参数。这里以弹目距离和比例导引算法所需的视线角速度为例(包括俯仰视线角速度和偏航视线角速度)，介绍基于RTK技术的导引头参数计算方法。在挂飞试验中，可实时获取毫米波导引头位置和目标位置的GPS数据，首先将实时获得的目标位置(λt,φt,ht)和导引头位置(λa,φa,ha)转换到空间直角坐标系。其中，λ表示经度，φ表示纬度，h表示高度，下标t和a分别表示目标位置和毫米波导引头位置。将(λt,φt,ht)和(λa,φa,ha)由角度转换为弧度后，分别得到(λt0,φt0,ht0)和(λa0,φa0,ha0)。
利用目标的经度、纬度、高度信息，目标在空间直角坐标系中的位置坐标可表示为[16]
(1)
式中，
表示第一偏心率，a=6 378 160 m为地球的长半轴长，b=6 356 774 m为地球的短半轴长。
毫米波导引头位置坐标为
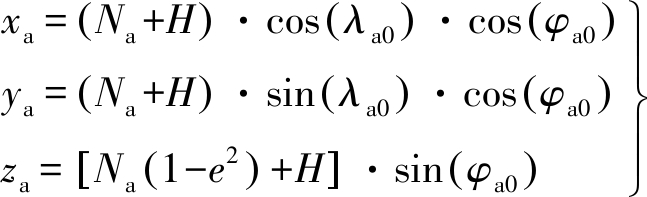
(2)
式中，
将地球直角坐标系的原点平移到毫米波导引头位置，即(xt-xa,yt-ya,zt-za)。将上述坐标系转换到北天东导航坐标系，可得到目标在北天东导航坐标系下的位置坐标(xT,yT,zT)为
(3)
至此，可以求得毫米波导引头与目标之间的距离，即弹目距离：
(4)
图3给出了导引头俯仰视线角与偏航视线角的计算示意图。根据导引头与目标的几何位置关系，挂飞过程中，假设挂飞平台飞行平稳，即导引头没有滚转方向的运动。图3中，OP为弹目距离连线，OP′为OP在导航坐标系xoy平面内的投影，毫米波导引头的俯仰视线角θn0和偏航视线角φn0可分别表示为
(5)
(6)
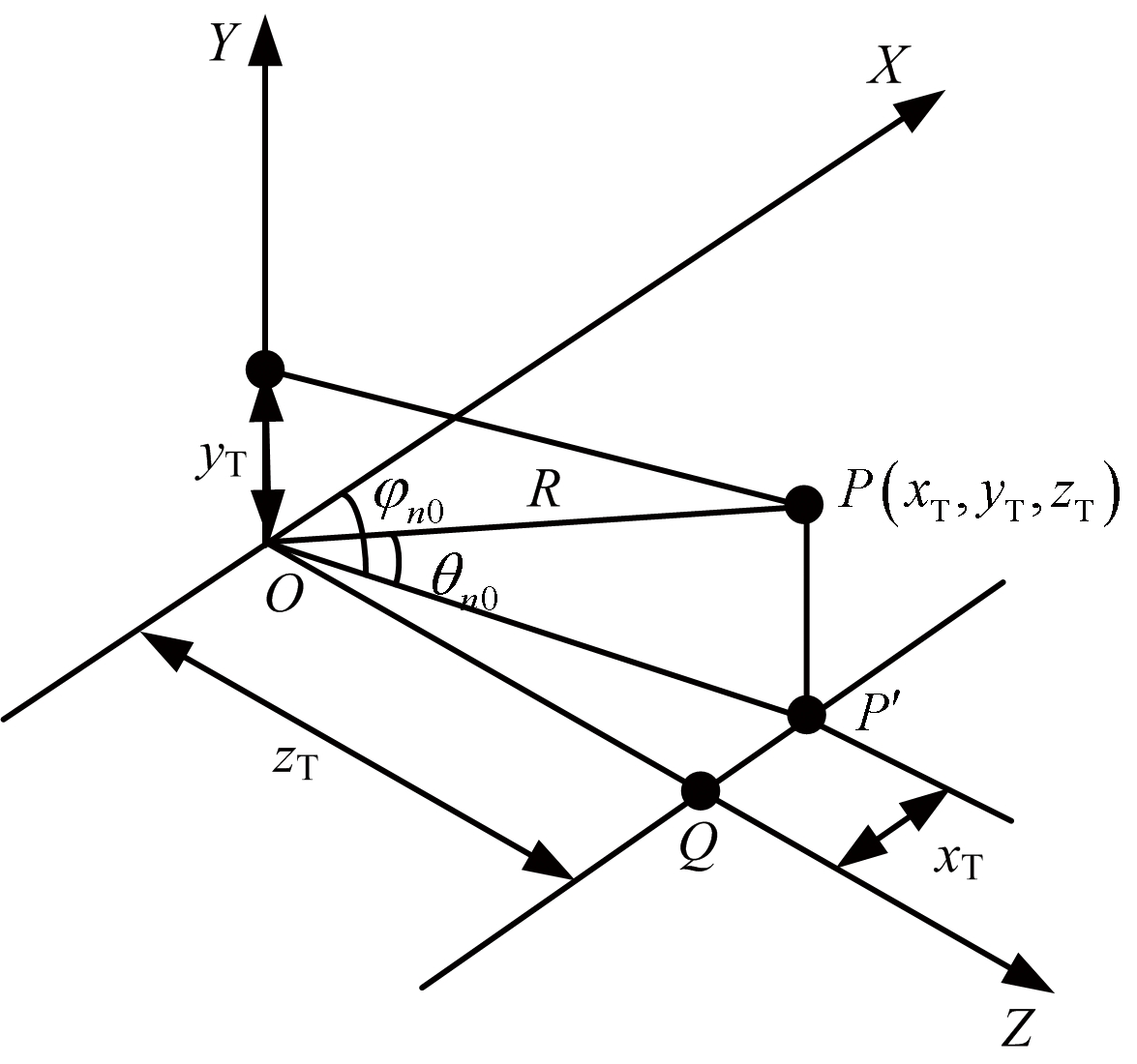
图3 导引头俯仰视线角和偏航视线角的示意图
对θn0和φn0分别取微分后，即可获得毫米波导引头相对于目标的俯仰视线角速度
和偏航视线角速度
将通过差分GPS获得的弹目距离、俯仰视线角速度、偏航视线角速度与导引头自身输出的弹目距离和视线角速度进行对比，即可评估毫米波导引头输出的参数是否满足要求。
2.3 误差分析
GPS的定位结果将不可避免地存在误差[14-15]，接下来讨论GPS的测量误差对毫米波导引头性能评估的影响，假设由GPS测量引入的x向、y向和z向的误差分别为ΔxT，ΔyT和ΔzT。在RTK的正常工作范围内，可保证|ΔxT|，|ΔyT|和|ΔzT|的取值范围为厘米级。
在不同的应用条件下，测量误差对导引头性能参数的影响不尽相同。以某直升机载毫米波空地导弹为例，对各误差源对测量精度的影响进行分析，若弹目距离dTA=2.5 km时，导引头开始进行目标搜索，假设载机的飞行高度为H=150 m，则
理想条件下弹道没有侧向偏差，即zT=0。
以某10 km射程小型毫米波空地导弹为例，在距离目标2.5 km处毫米波导引头开始扫描搜索，毫米波导引头由远及近靠近目标，然而挂飞过程中无法实现比例导引段弹道的全部模拟。首先，雷达导引头在进入盲区后，将无法实现参数的有效输出，以80 m盲区为例，有效数据截止到盲区对应时刻41.11 s。此外，为保证载机和目标区的安全，载机不可能像导弹一样无限接近目标，而是必须保证一定的安全距离，通常情况下，当载机高度为40 m左右时，飞行员就会执行载机拉升操作。以40 m高度为例，有效数据截止到40.04 s。因而在本例中，真正有效的基于RTK的导引头性能评估参数范围为从导引头工作开始到40.61 s，挂飞过程中，毫米波导引头解锁后的有效X向和Y向的弹道曲线如图4所示。
(a) X向
(b) Y向
图4 毫米波导引头的有效挂飞曲线
下面给出基于GPS测量数据计算毫米波导引头参数的误差分析。只有保证了测试系统的高精度，才可能实现毫米波导引头性能指标的准确评估。此处以弹目距离和视线角速度为例进行误差分析。
2.3.1 弹目距离
考虑GPS测量误差后，弹目距离的计算公式应更新为
(7)
将弹目距离dTA进行泰勒级数展开，有
dTA=dTA0+ΔdTA0
(8)
式中，
(9)
如前所述，理想条件下导弹的侧向偏离zT=0，此时上式可简化为
(10)
GPS测量误差ΔxT对弹目距离测量精度的影响如图5(a)所示，ΔyT对弹目距离测量精度的影响如图5(b)所示。由图5可见，当GPS三个方向的定位误差从2 cm增加到10 cm时，GPS的测量误差对弹目距离的影响逐渐增大，但是即使是误差达到10 cm时，3个方向中误差幅度的最大值也小于0.1 m，这个量级的误差对于毫米波主动制导模式的导引头而言是完全可以容忍的。
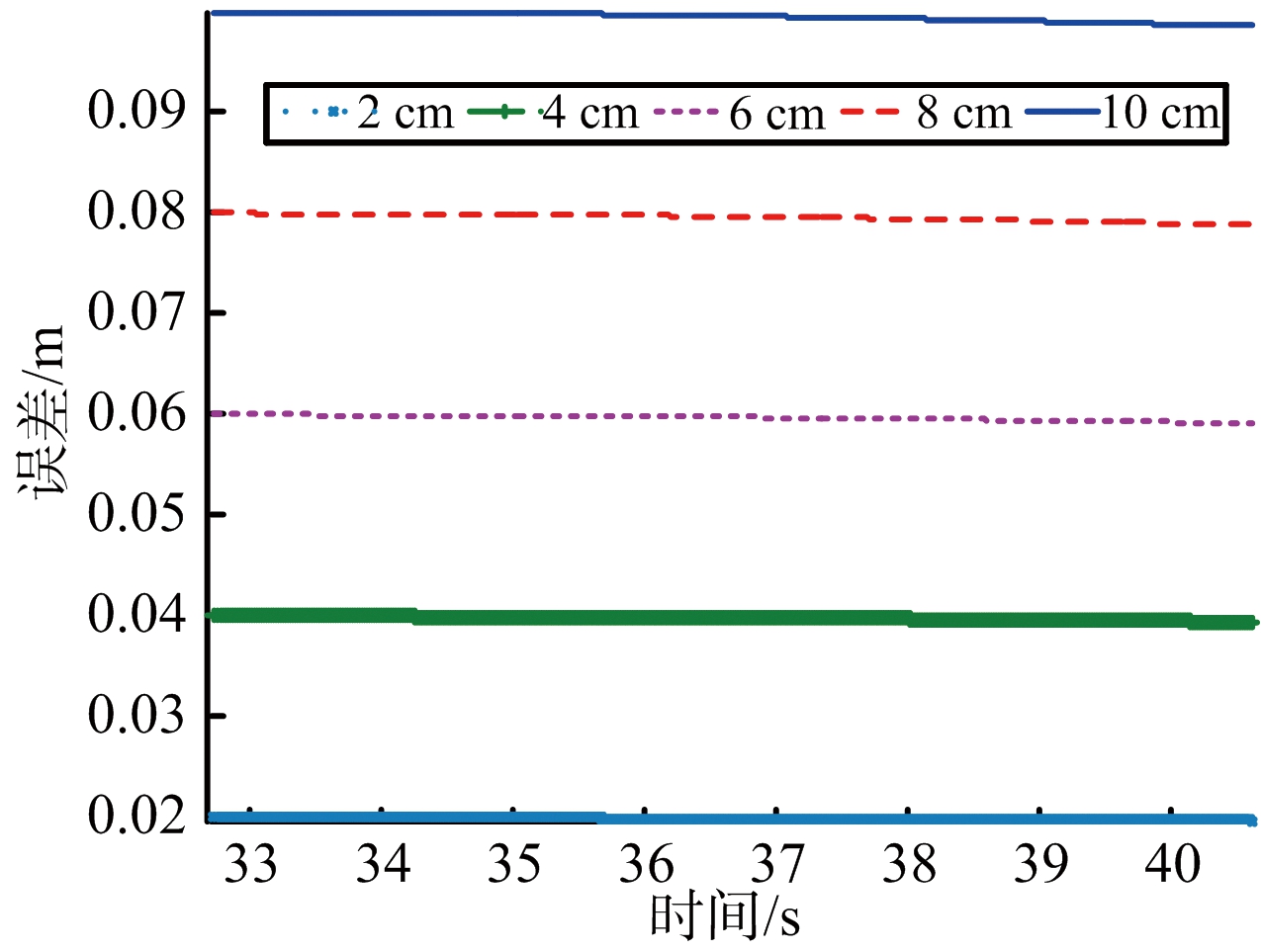
(a) X向测量误差对弹目距离精度的影响
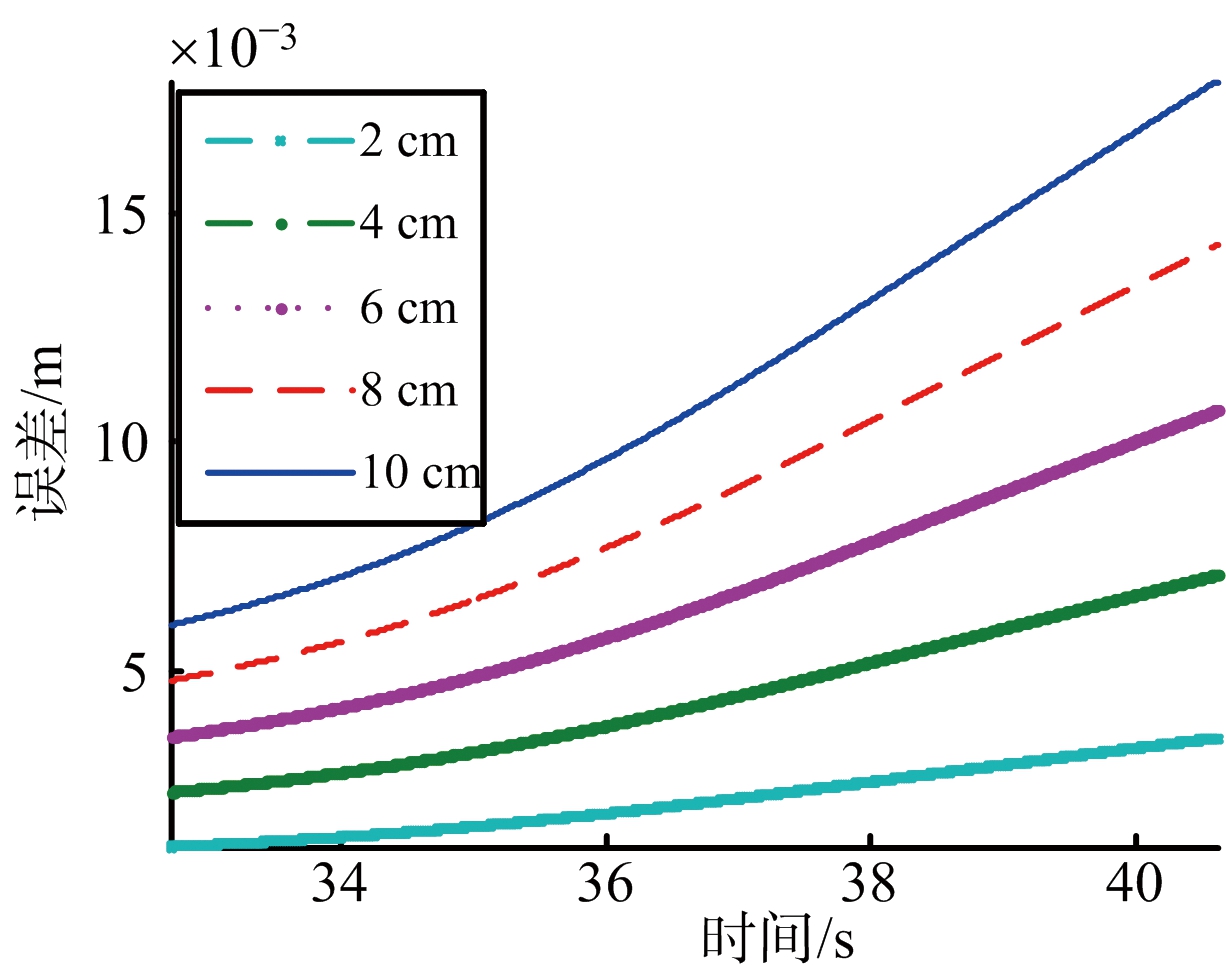
(b) Y向测量误差对弹目距离的影响
图5 GPS测量误差对弹目距离精度的影响
2.3.2 俯仰视线角
考虑测量误差后的俯仰视线角可表示为
θn=arctan(yT+ΔyT)/
(11)
同样将俯仰视线角θn进行泰勒级数展开，可得
θn=θn0+Δθn
(12)
式中，
Δθn=
(13)
如前所述，理想条件下导弹的侧向偏离zT=0，因而，上式可简化为
(14)
同样采用上述参数误差范围评估GPS测量误差对俯仰视线角测量精度的影响，结果如图6所示。由图6可见，GPS测量误差对俯仰视线角误差的影响量级为10-4，该测量误差对该参数测量的影响可以忽略。
(a) X向
(b) Y向
图6 GPS测量误差对俯仰视线角精度的影响
2.4 偏航视线角
下面给出GPS测量误差对偏航视线角精度的影响，考虑测量误差后的偏航视线角可表示为
φn=arctan[(zT+ΔzT)/(xT+ΔxT)]
(15)
同样将偏航视线角φn进行泰勒级数展开，有
φn=φn0+Δφn
(16)
式中，
(17)
同样地，理想条件下上式可简化为
(18)
ΔzT的测量误差对偏航视线角的精度影响如图7所示。
图7 Z向测量误差对偏航视线角精度的影响
可见，由于GPS测量导致的误差对俯仰角和偏航角的影响非常小，误差的量级为10-4～10-5，由GPS带来的测量误差对参数精度的影响完全可以忽略。
3 实验结果与分析
以国内某研究所录取的毫米波导引头实测数据验证本文所提方法对毫米波导引头性能评估的有效性。试验中，GPS主站固定在已知位置，分别将两个GPS流动站安装在毫米波导引头所在的直升机载体以及目标位置上。设置毫米波导引头评估系统构型，保证RTK的有效工作半径，GPS接收机所用型号为LD-HD60，实时存储双频差分定位数据。直升机模拟弹道飞行，毫米波导引头在2.5 km处开始进行目标搜索，当捕获并稳定跟踪目标后，输出比例导引算法所需的俯仰和偏航视线角速度，同时毫米波导引头实时输出弹目距离等参数。采用本文所提方法，根据获得的GPS测量数据进行毫米波导引头性能参数计算，图8给出了毫米波导引头输出以及利用GPS数据计算出的弹目距离对比图，图9和图10分别给出了毫米波导引头输出以及利用GPS数据计算得到的偏航视线角速度和俯仰视线角速度的对比结果。
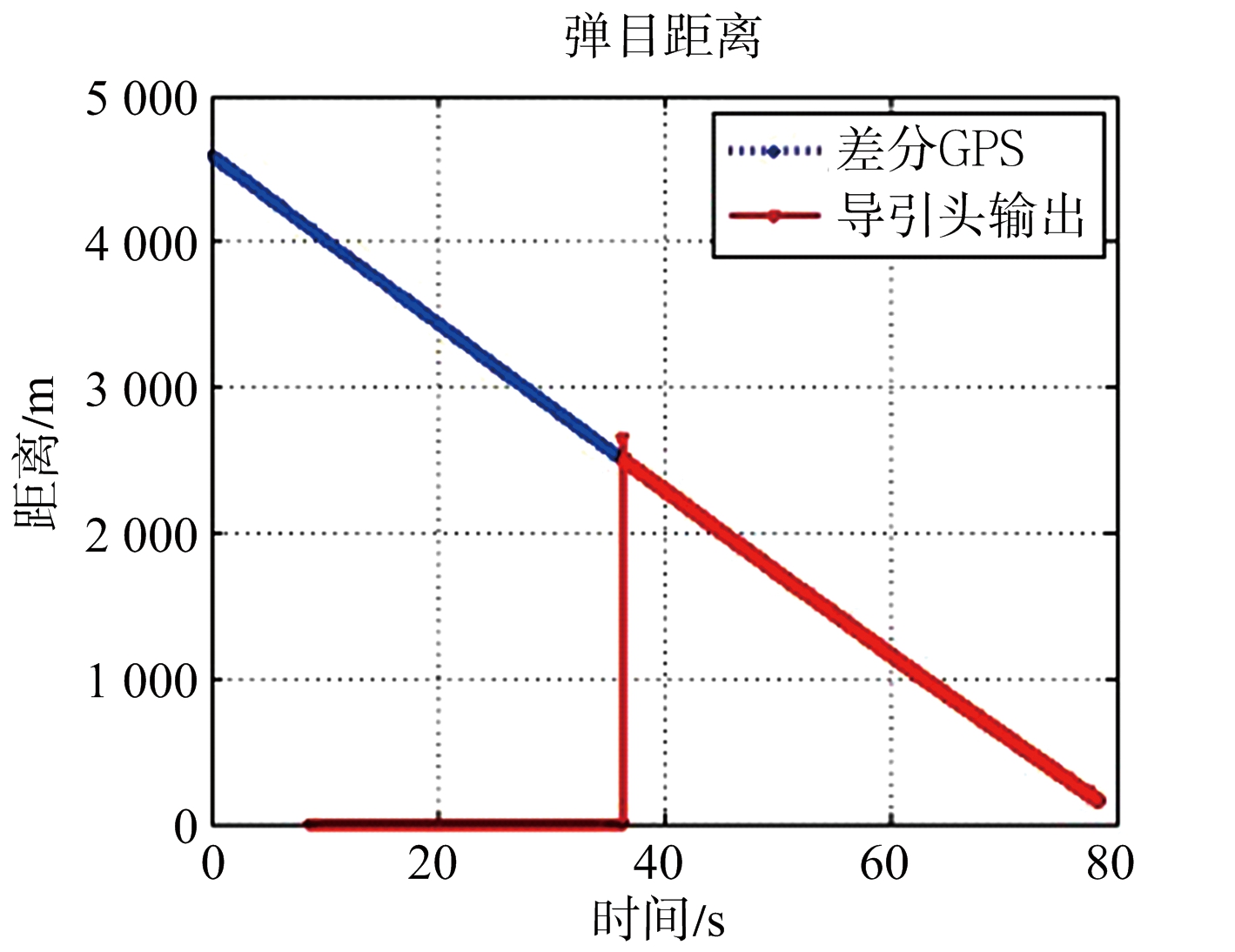
(a) 全过程结果
(b) 局部放大结果
图8 导引头输出以及差分GPS计算的弹目距离
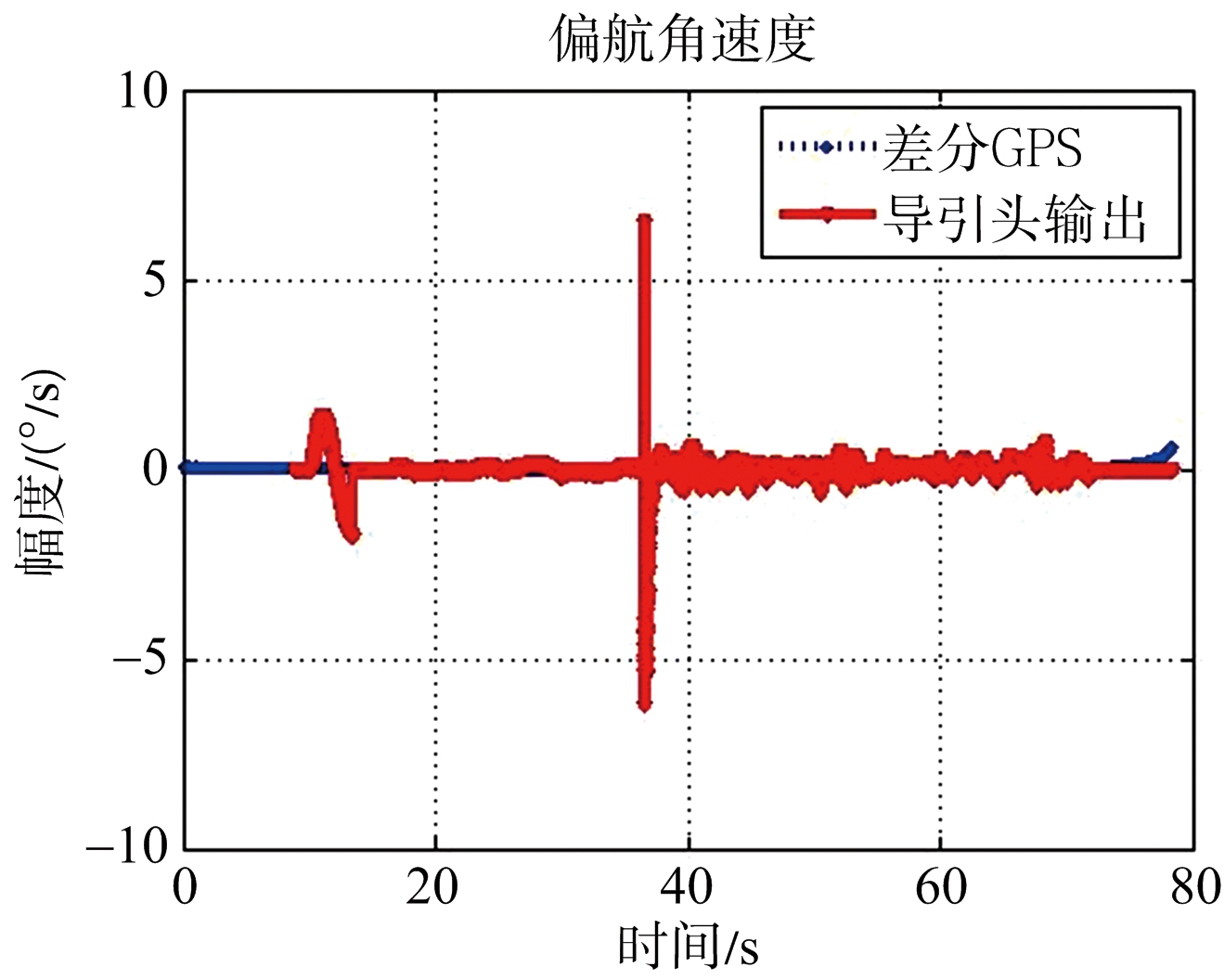
(a) 全过程结果
(b) 局部放大结果
图9 导引头输出以及差分GPS计算的偏航视线角速度
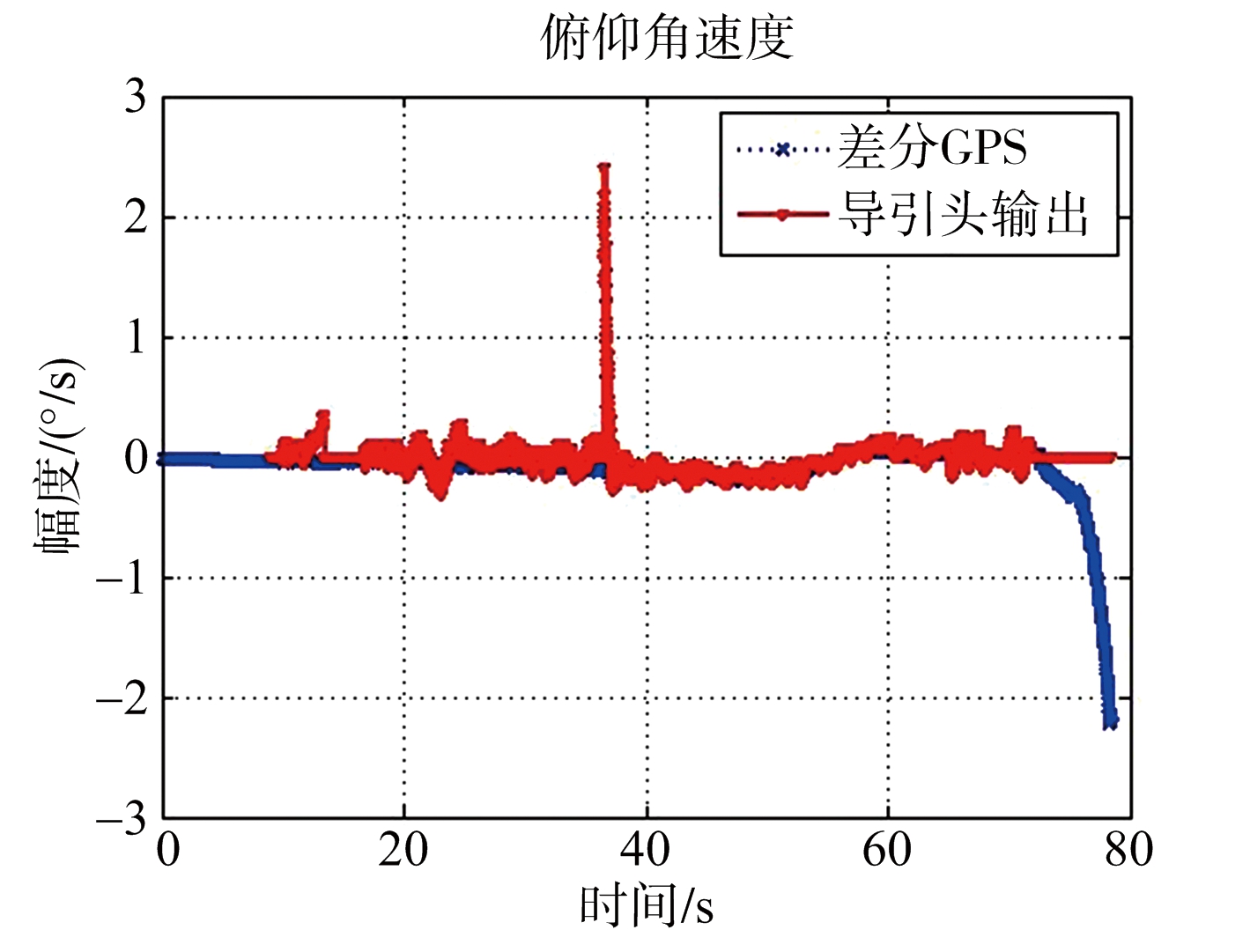
(a) 全过程结果
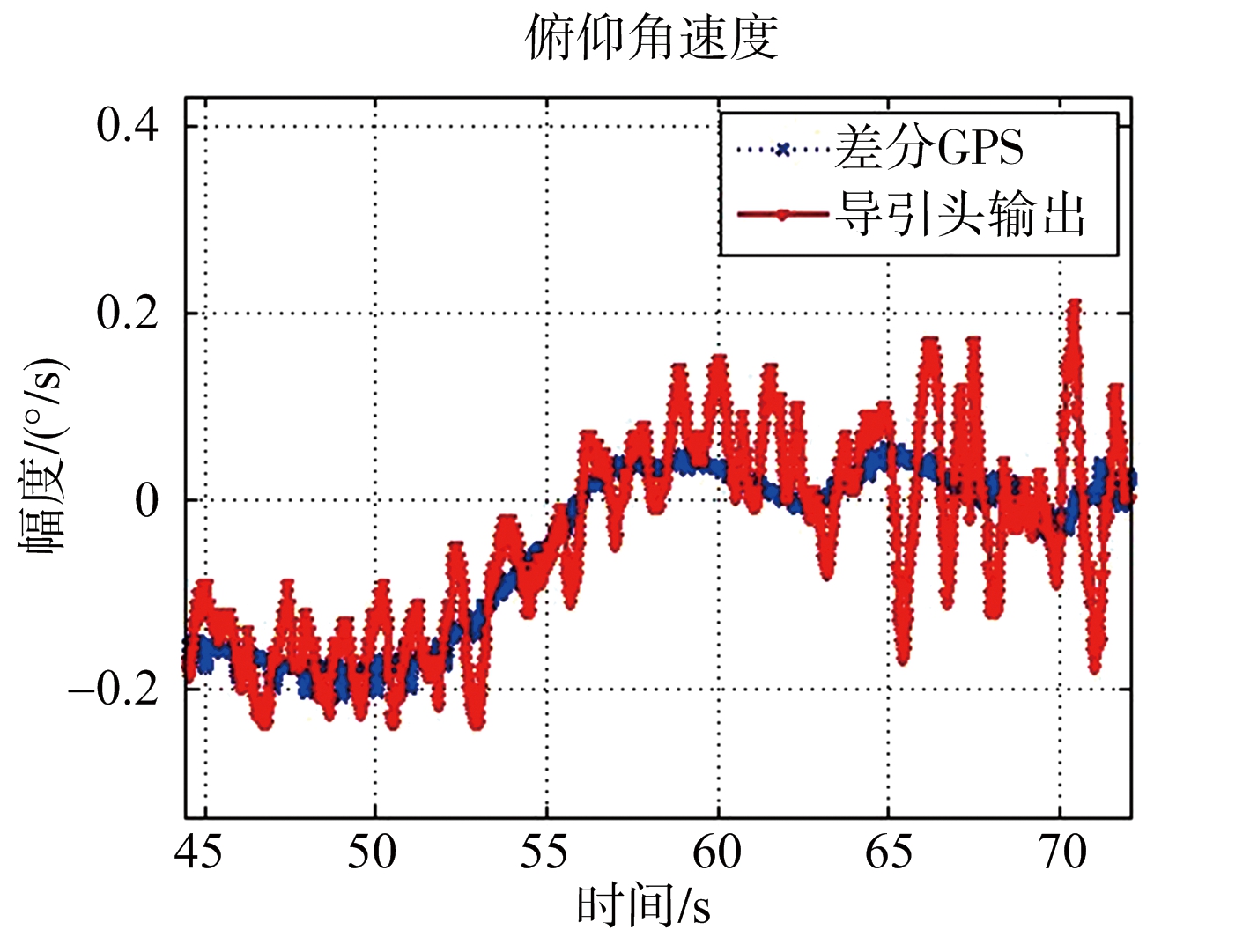
(b) 局部放大结果
图10 导引头输出以及差分GPS计算的俯仰视线角速度
由图8～图10的结果可见，毫米波导引头的各参数输出结果与基于RTK技术的计算结果基本吻合。两种途径下弹目距离的差异小于1 m，偏航视线角速度相差大约为±0.4°，俯仰视线角速度相差大约为±0.15°。
为进一步验证所提算法的优越性，对比了基于组合导航数据的参数计算结果，以视线角速度为例，图11给出了基于组合导航数据的计算结果和本文所提的基于RTK技术计算结果的对比。可见，基于组合导航数据的计算结果明显要差于本文所提方法的计算结果，尤其对于俯仰方向，误差接近10°，无法实现毫米波导引头性能指标的准确评估。造成这种结果的原因在于，组合导航的误差漂移较大，尤其对于高程测量，误差更大。此外，组合导航测量产生的各误差项随着时间的增大，累计误差也会逐步累计放大。因此，基于组合导航数据的参数计算方法无法适应长时间的毫米波导引头性能参数评估。
(a) 偏航视线角速度
(b) 俯仰视线角速度
图11 基于差分GPS和组合导航数据的计算结果对比
4 结束语
本文提出了一种基于RTK技术的毫米波导引头参数计算方法，实现导弹飞行试验前毫米波导引头的性能评估。通过视线角速度和弹目距离等参数的对比分析，评估毫米波导引头输出参数的精度，达到评估毫米波导引头性能的目的。该方法可考核评估毫米波导引头的性能，保证导弹飞行时毫米波导引头视线角速度的高精度输出，为实现后续的制导控制和精确打击提供支持。
[1] 赵乾,刘志国,王仕成,等. 高重频激光对激光导引头解码干扰的研究[J]. 红外与激光工程, 2015, 44(5):1438-1443.
[2] 韦卓,杨卫华,姚德龙,等. 基于火箭橇的激光导引头抗干扰试验方法研究[J]. 激光与红外, 2017, 47(2):221-224.
[3] 刘仲宇,张涛,王平,等. 红外导引头稳定平台主框架拓扑优化设计[J]. 红外与激光工程, 2016, 45(2):208-212.
[4] 郝英振,秦玉亮,李彦鹏,等. 毫米波导引头港口舰船目标识别技术[J]. 雷达科学与技术, 2009, 7(3):180-183.
HAO Yingzhen, QIN Yuliang ，LI Yanpeng, et al. Recognition Technology of Warship Targets for Millimetre Guidance Radar Seeker[J]. Radar Science and Technology, 2009, 7(3):180-183.(in Chinese)
[5] 莫翠琼,戴幻尧,陈秋菊,等. 基于扩展目标的单脉冲多普勒雷达导引头相干干扰[J]. 电波科学学报, 2016, 31(4):731-736.
[6] 杨勇,冯德军,王雪松,等. 低空雷达导引头海面目标检测性能分析[J]. 电子与信息学报, 2011, 33(8):1779-1785.
[7] HAN S, RA W, WHANG I, et al. Geometric Joint Probabilistic Data Association Approach to Ballistic Missile Warhead Tracking Using FMCW Radar Seeker[J]. IET Radar, Sonar & Navigation, 2016, 10(8):1422-1430.
[8] WEN Qiuqiu, LU Tianyu, XIA Qunli, et al. Beam-Pointing Error Compensation Method of Phased Array Radar Seeker with Phantom-Bit Technology[J]. Chinese Journal of Aeronautics, 2017, 30(3):1217-1230.
[9] 王广帅,林德福,范世鹏,等. 一种适用于红外制导弹药的偏置比例导引律[J]. 系统工程与电子技术, 2016, 38(10):2346-2352.
[10] 黄诘,张友安,刘永新. 一种有撞击角和视场角约束的运动目标的偏置比例导引算法[J]. 宇航学报, 2016, 37(2):195-202.
[11] JEON I, LEE J. Impact-Time-Control Guidance Law with Constraints on Seeker Look Angle[J]. IEEE Trans on Aerospace and Electronic Systems, 2017, 53(5):2621-2627.
[12] JUAN J M, SANZ J, HERN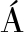
NDEZ-PAJARES M, et al. Wide Area RTK: A Satellite Navigation System Based on Precise Real-Time Ionospheric Modelling[J]. Radio Science, 2012, 47(2):1-14.
[13] AGHILI F, SALERNO A. Driftless 3-D Attitude Determination and Positioning of Mobile Robots by Integration of IMU with TWO RTK GPSs[J]. IEEE/ASME Trans on Mechatronics, 2013, 18(1):21-31.
[14] DAS S, MAJUMDER S, CHAKRABORTY R, et al. Simplistic Approach for Water Vapour Sensing Using A Standalone Global Positioning System Receiver[J]. IET Radar, Sonar & Navigation, 2014, 8(8):845-852.
[15] RUNGRAENGWAJIAKE S, SUPNITHI P, SAITO S, et al. Ionospheric Delay Gradient Monitoring for GBAS by GPS Stations Near Suvarnabhumi Airport, Thailand[J]. Radio Science, 2015, 50(10):1076-1085.
[16] 宋玉珍, 刘炼. MEMS-IMU/GPS组合导航系统仿真研究[J]. 雷达科学与技术, 2010, 8(4):301-305.SONG Yuzhen, LIU Lian. Simulation of MEMS IMU and GPS Integrated Navigation System[J]. Radar Science and Technology, 2010, 8(4):301-305. (in Chinese)
