0 引言
近太空双基地雷达利用飞艇等平台的滞空时间长、定点能力弱等特点[1-3]，从近太空对重要地区和目标实施长时间凝视侦察监视。由于系统兼具高度优势和精度优势，另外凝视侦察大大降低了环境杂波回波的复杂程度，因此有效提高了双基地雷达系统的作战效能，具有良好的发展前景。
目标三维坐标定位精度是双基地雷达的一个重要技术指标，各类精确制导武器的发展也对雷达的探测定位精度提出了更高的要求。近太空双基地雷达由于静止悬停实施长时间凝视侦察监视[1-2]，因此无须像机载双基地雷达一样采用卫星导航定位系统对站址进行实时定位，但是飞艇的弱定点特性决定了其在长滞空时间内必然存在一定幅度的波动漂移。此外，战时敌方可能对卫星导航定位系统进行干扰，影响站址定位精度，这都将影响系统的目标定位精度。因此，研究站址误差对目标三维定位精度的影响可以促进近太空双基地雷达的研制部署、提高系统GPS干扰条件下的定位精度和双基地雷达系统的作战性能，具有多重意义。
1 近太空双基地雷达目标三维定位
双基地雷达收、发基站与目标三者之间存在一定的空间几何关系，如图1所示，利用双基地之间的空间几何关系，T-R 型两坐标双基地雷达也具备三维定位能力[4-6]。
图1 近太空双基地雷达空间几何关系
建立图1所示的三维直角坐标系，T为发射站，位置坐标为(xT,yT,zT)，R为接收站，位置坐标为(xR,yR,zR)。T与R间距为基线L，RT和RR分别为目标到T站和R站的距离，RT和RR在xoy平面内的投影分别为
和
和θR分别为发射波束和接收波束的方位角。由于收、发站都是两坐标雷达，系统直接测量为θT，θR和R，根据三角形正弦定理，如式(1)所示，利用双基地雷达空间几何关系，采用解析几何法求得目标高度和相对T站距离如式(2)、式(3)所示：
(1)
(2)
(3)
以发射站为解算基站，求得空间目标的三维坐标为
(4)
2 近太空平台站址误差对目标三维定位精度的影响
近太空双基地雷达有地发空收、空发地收和空发空收三种布站模式。对于地发空收模式，T站位于地面，站址具有较高的定位精度，R站位于近太空，由于R站平台波动，造成近太空双基地雷达探测目标时的真实站址位置以及探测三角形，与解算时用到的站址位置和几何三角形不一致，从而造成目标定位误差。
系统对目标的三维定位精度可用目标空间位置的均方根误差(Root Mean Square, RMS)来表示,即用定位误差方差的平方根来表示。由于RMS与目标及T站和R站的相对几何位置有关,因此又称为定位精度的几何分布[7-8](Geometrical Dilution of Precision, GDOP)。对于本文，双基地站址误差主要通过基线距离来影响系统的目标定位精度，因此，由站址误差引起的目标定位误差可由目标位置坐标对L求偏微分计算得到，计算公式如下：
GDOP=
(5)
对于两坐标近太空双基地雷达系统，对式(4)求关于L的偏微分，如式(6)所示：
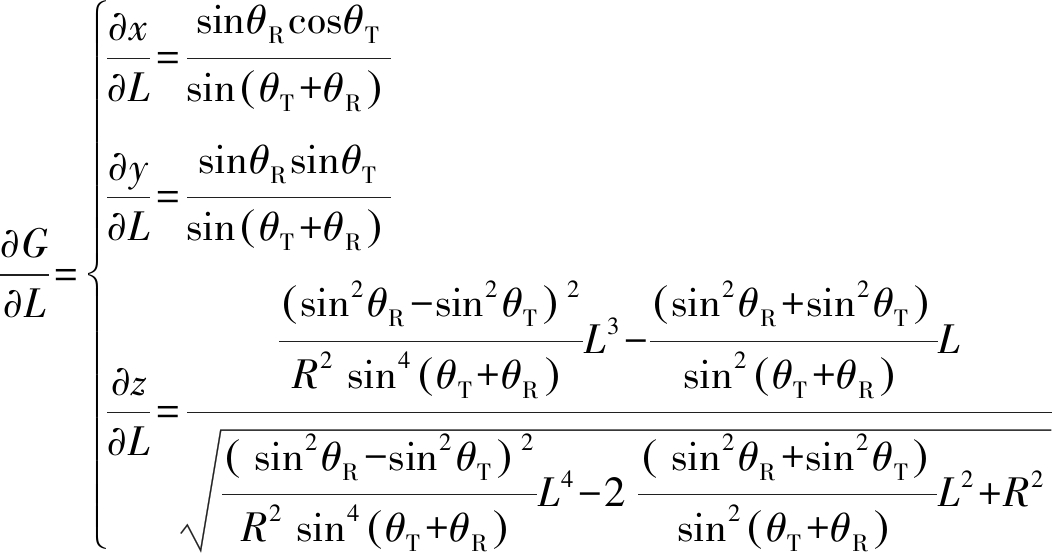
(6)
将式(6)代入式(5)，即可解算近太空双基地雷达采用(R,θT,θR)法定位时站址误差引起的目标定位误差。
3 仿真结果分析
3.1 站址误差对目标定位精度影响比分析
T站位于地面坐标原点没有站址漂移，设其站址误差为零。R站位于近太空，站址坐标为(100，0，0)，设其站址误差为(0.1，0.1，0.1)km。忽略其他测量误差因素[9-10]，限制双基地雷达目标距离和R= 500 km，根据式(5)、式(6)仿真两坐标近太空双基地雷达目标三维定位误差，如图2所示。
图2 站址误差引起的目标定位误差
图2反映了θR分别为1°,21°,…,161°，θT在取值范围内以1°为步长进行扫描时的目标定位精度。图中θT的值越小，表示目标距离基线越近，高度越高，θT的值越大，表示目标距离基线越远，高度越低。从图2可以得到以下结论：
1) 两坐标近太空双基地雷达对于近距离高空目标的定位精度较高，对于远距离低空目标的定位精度较低。
2) 对比图2第1行的3幅图和第3行的3幅图的最大定位误差值，可以发现近太空双基地雷达对从T站一侧来袭的目标定位精度稍高于从R站一侧来袭的目标的定位精度。
由于3个坐标轴分量对于基线距离L的贡献不一样，下面分别讨论站址的单个坐标轴坐标分量误差对目标定位精度影响。对于x坐标误差，假设Δx=0.1 km，Δy=0，Δz=0，将站址误差代入式(6)、式(7)，仿真结果如图3所示。对比图2和图3不难发现，单独Δx=0.1 km引起定位误差与Δx=Δy=Δz=0.1 km引起的定位误差大小基本一致，这是由于x轴与基线平行，x坐标误差对基线距离的影响最大所致。
y轴与基线L垂直，假设x，z坐标无定位误差， y轴分量误差Δy=0.1 km，仿真目标定位误差分布如图4所示。
图3 R站x坐标误差引起的目标定位误差
图4 R站y坐标误差引起的目标定位误差
图3所示误差曲线形状与图2完全一样，大小也基本相同，图4所示误差曲线形状也与图2完全一样，但大小只有大约10-4倍，这是由于y轴与基线L垂直，其坐标误差对于基线距离的影响要比x分量误差小很多的原因。同理，z轴也垂直于基线L，对基线距离L贡献与y轴相同，因此z坐标误差引起的目标定位误差曲线与图4相同。
图2、图3和图4所示3条目标定位误差曲线形态完全相同，只有量的差别。这表明不同坐标轴的坐标误差对于目标定位精度的影响性质上是一样的，大小取决于其对基线距离L的贡献大小。因此，可以通过合理布站和建立合适的坐标系来降低站址误差对于目标定位精度的影响。
3.2 站址误差与角度误差对目标定位精度影响对比分析
角度测量误差等因素也会造成目标定位误差，为了更清楚认识站址误差对于目标定位精度的影响，下面将站址误差和θR误差进行对比分析，以期得到更多有用的结论。
θR误差引起的目标定位误差可由式(7)求得，式中目标位置对θR的偏导数可以仿照式(6)求得:
为了更深入地分析站址误差对目标定位精度的影响，将目标的三维定位误差(GDOP)分成水平误差分量(HGDOP)和高度误差分量[11](VGDOP)，二者的计算公式如下：
(8)
(9)
假设站址定位无误差，R站方位角测量误差ΔθR=0.1°，根据式(7)、式(8)、式(9)，仿真ΔθR引起的目标定位误差如图5所示。
图5 θR误差引起的GDOP，HGDOP和VGDOP
图5中θR代表目标来袭方位，θT代表目标来袭距离和高度，并且θT的值小，目标距离基线近，目标高度高，θT的值大，目标距离基线远，目标高度低。红色实线代表HGDOP，黑色虚线代表VGDOP，蓝色点划线代表GDOP。图中还将各幅小图的y轴底部另外进行了放大显示，以便观察其细节特征。依据图5可以得到以下结论。
图5中各幅分图θT与目标定位误差的变化关系显示：系统对远距离低空超低空的目标定位精度较差，水平定位精度好于高度定位精度；系统对于中、近距离中高空目标的定位精度较高，且高度定位精度好于水平定位精度。
图5中θR与目标定位误差的变化关系显示系统对于侧向来袭目标的定位精度比正向来袭目标差，特别是对于侧向远距离低空目标，系统无法对其定位。另外，图6(i)显示，当目标从R站侧向来袭时，不论目标高低远近，系统基本失去定位能力。
因此当系统角度测量精度较低时，系统将失去对侧向来袭目标和远距离低空目标的定位能力，造成系统不能定位的原因是高度定位误差过大。
当R站站址误差Δx=Δy=Δz=0.1 km时，忽略其他误差因素，目标的GDOP，HGDOP和VGDOP误差仿真如图6所示。
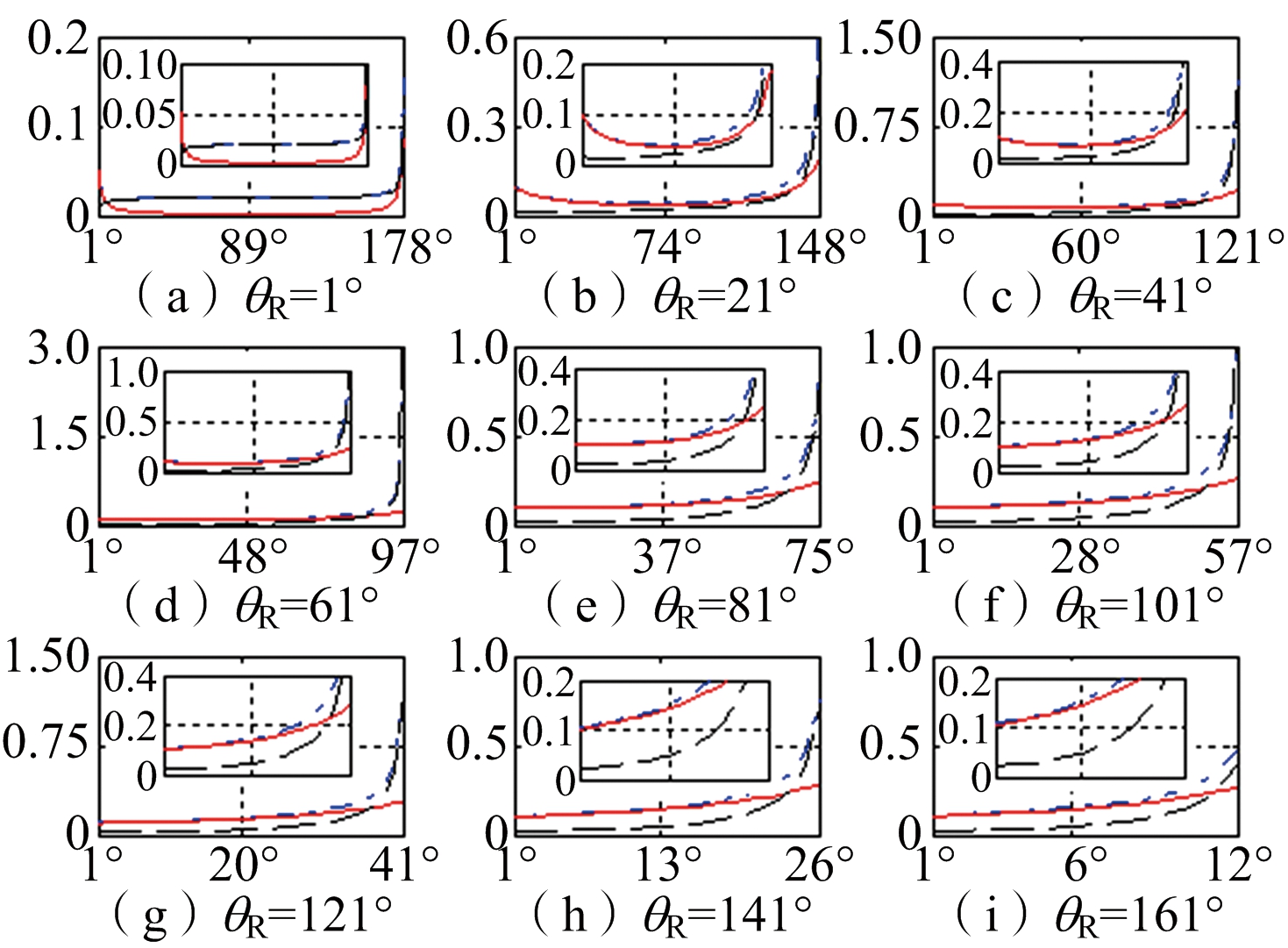
图6 站址误差引起的HGDOP，VGDOP和GDOP
图6中红色实线代表HGDOP，黑色虚线代表VGDOP，蓝色点划线代表GDOP。图中还将各幅小图的y轴底部另外进行了放大显示，以便观察其细节特征。θR=1°表示目标位于基线附近，θT从1°向最大值变化表示目标距离由近及远，目标高度由高到低变化。图6中θT，θR与目标定位误差的变化关系显示在整个探测空域内，HGDOP变化缓慢且变化幅度很小，VGDOP在中近距离中高空区域较小，且明显小于HGDOP，而在远距离低空超低空区域和基线附近，VGDOP较大且明显大于HGDOP，说明HGDOP对目标空间几何位置不敏感而VGDOP对目标空间几何位置敏感。
对比图6和图5看到,在整个探测空域内，站址误差引起的目标定位误差小于角度误差引起的目标定位误差，尤其是对远距离低空超低空目标，站址误差引起的定位误差仍较小，而θR误差却导致系统无法对目标进行定位，二者在此有本质的区别。
4 结束语
对于讨论的两坐标近太空双基地雷达系统，在R-θR-θT法下，角度误差是影响目标定位精度的主要因素，其对目标的来袭方位、距离、高度等因素，即对目标的空间几何位置敏感。
在整个探测空域内，站址误差造成的目标三维定位误差的绝对值较小，明显小于角度误差引起的目标定位误差，而且目标定位误差主要是由对基线距离起主要贡献的坐标分量(对于本文是x坐标)造成的。因此，控制平台在这一坐标分量上的定点精度，可大大降低站址波动对系统定位精度的影响，提高整个探测空域内目标的三维定位精度。
[1] 吴洋. 临近空间太阳能无人机飞行平台的特点及发展前景[J]. 科技创新导报, 2016(33):11-13.
[2] 阎啸,唐博,张天虹,等. 临近空间飞行器信息系统一体化载荷平台[J]. 航空学报, 2016, 37(S1):S127-S133.
[3] 王庚,袁俊泉,王力宝,等. 天空双基地预警雷达空间同步技术研究[J]. 雷达科学与技术, 2017, 15(4):449-456.
WANG Geng, YUAN Junquan, WANG Libao, et al. Research on Spatial Synchronization Technique of Space-Air Based Bistatic Early Warning Radar[J]. Radar Science and Technology, 2017,15(4):449-456. (in Chinese)
[4] ZHAO Yongsheng, ZHAO Yongjun, ZHAO Chuang. Joint Delay-Doppler Estimation for Passive Bistatic Radar with Direct-Path Interference Using MCMC Method[J]. IET Radar, Sonar & Navigation, 2018, 12(1):130-136.
[5] 杨振起,张永顺,骆永军. 双(多)基地雷达系统[M]. 北京: 国防工业出版社, 1998.
[6] 马艳霞,刘二小. 靶场测量中双基地雷达定位与定位精度分析[J]. 数字技术与应用, 2015(1):211-212.
[7] 邓兵,孙正波,杨乐,等. 存在站址误差时的线性校正TDOA定位算法[J]. 西安电子科技大学学报(自然科学版), 2017, 44(4):106-111.
[8] 支双双. 双基地雷达两种目标定位方法误差分析与仿真[J]. 西安工程大学学报, 2015, 29(2):209-214.
[9] 白桂明,李晓东. 收/发异地配置雷达探测系统探测精度[J]. 火力指挥与控制, 2003, 28(6):70-72.
[10] 张正言,张剑云. 双基地MIMO雷达多目标高精度跟踪算法[J]. 系统工程与电子技术, 2018, 40(6):1241-1248.
