0 引言
脉冲压缩是解决雷达探测距离与分辨率之间矛盾的一种有效手段,常用的脉冲压缩信号有线性调频(LFM)信号和非线性调频(NLFM)信号[1-2]。LFM信号脉冲压缩结果一般副瓣较高,为了降低副瓣,通常采用窗函数加权,但是加权实际上是对信号进行失配处理[3],会引起信噪比的损失和主瓣展宽等问题[4-5]。而NLFM信号进行脉冲压缩时无需进行加权,具有低副瓣的优点[6],且没有信噪比损失,因此NLFM信号被广泛使用,其中最常用的就是S型NLFM信号。
S型NLFM信号采用S型调频曲线来设计,由于默认NLFM信号脉压为匹配处理[7],因此通常采用传统方法设计S型NLFM信号时,认为S型调频函数的最优调频因子只受时宽带宽影响,只要时宽带宽一定,就可以确定出最优S型NLFM信号。但是通过研究发现,在实际工程中,脉冲压缩都是通过数字方式实现的,因此存在一定的离散采样误差,这将会导致雷达回波与滤波器之间发生失配,从而会带来信噪比损失。由信号理论可知,离散采样误差与采样频率有关,因此设计S型NLFM信号时,采样频率也是影响S型NLFM信号优劣的一个非常重要的参数。文献[8]中也提到,采样频率对NLFM信号脉冲压缩结果是有影响的,理论上采样频率越高越好,但是增加采样频率会加大运算量,实际系统中的采样频率通常只有1~3倍的带宽,此时脉压结果受离散采样误差影响较大,采用传统方法设计的S型NLFM信号就不是最优的。
本文将针对离散采样误差对S型NLFM信号进行优化,使得所设计的信号在实际系统常用的采样频率下也有较好的脉压结果,这种优化方法具有较强的实用性,可直接应用于雷达波形设计领域,具有一定的指导意义。
1 传统S型调频信号设计方法
1.1 基本原理
S型NLFM信号相当于LFM信号与正弦调频信号的组合,其群延时函数的表达式为

(1)
式中,f0为信号中心频率,T为矩型调制脉冲的时宽,B为调频带宽,K为调频因子,是个常数,可通过调整其大小来控制非线性程度。
由于采用的是数字方法产生信号,故可以采用插值或迭代逼近求值的方法得到S型NLFM信号的调频函数,即群延时函数的反函数:
f(t)=t-1(f)
(2)
进而得到信号的相位函数:
φ(t)=2π![]() f(x)dx,0≤t≤T
f(x)dx,0≤t≤T
(3)
从而综合得到基带NLFM信号:
s(t)=exp[jφ(t)],0≤t≤T
(4)
值得说明的是,群延时函数中的调频因子K会影响脉冲压缩的结果,传统的S型NLFM信号设计方法就是在给定采样频率下,在一定范围内对K值进行搜索,利用穷举法搜索出最大的主副比对应的K值(即最优K值),据此K值设计信号即可。
1.2 设计举例
基于上述原理对S型NLFM信号进行数字脉压仿真,这里认为回波和滤波器完全匹配,仿真参数:时宽T=40 μs,带宽B=2 MHz,采样频率fs=2B,此时穷举法搜索到的最优K值为0.091。据此设计出的S型NLFM信号如图1和图2所示,匹配脉压结果如图3所示,脉压主副比为33.552 4 dB,该采样频率下,除最优K值之外任意K值设计的S型NLFM信号的脉压主副比都小于33.552 4 dB,例如,当K值取0.080时,脉压结果如图4所示,此时脉压主副比为32.759 4 dB。
图1 S型调频信号实部信号
图2 S型调频信号虚部信号

图3 脉冲压缩结果(K=0.091)

图4 脉冲压缩结果(K=0.080)
在本例中,在设计S型NLFM信号时,认为信号与脉冲压缩滤波器完全匹配,但实际上,回波信号与滤波器之间往往存在一定的失配现象,所以按照传统方法搜索出来的K值并不是最优的。
1.3 失配现象分析
实际工程中,由于离散采样误差的存在,有时采样得到的回波脉冲前沿正好对准采样时刻,这时回波信号与脉冲压缩滤波器完全匹配,脉压结果主瓣幅度大,副瓣幅度小,主副比大;但也有回波脉冲前沿正好落在两个采样时刻中间,这时回波与脉冲压缩滤波器失配,导致脉压主瓣幅度有衰减,副瓣有抬升,主副比就会减小。
下面仿真对比匹配时和失配时的脉压结果,这里选择最差的失配情况,即回波脉冲前沿恰好落在两个采样时刻中间(后文仿真中的失配情况均指这种情况)。当时宽T=40 μs,带宽B=2 MHz,采样频率fs=2B时的匹配与失配情况下的脉压结果如图5和图6所示。

图5 主瓣对比

图6 副瓣对比
由仿真结果得到,匹配时的脉压主副比为 33.553 4 dB,失配时的脉压主副比为29.637 9 dB,由此可见失配现象确实对脉冲压缩结果有一定影响,而且这种影响在实际工程中不能忽略。
1.4 采样频率对S型调频信号脉冲压缩的影响
由1.3节可知离散采样误差给脉冲压缩结果带来的影响较大,而离散采样误差又与采样频率有关,因此在S型调频信号脉冲压缩时,采样频率是一个很重要的参数。
先在不同采样频率下按传统方法设计S型调频信号,然后对比不同采样频率下的匹配脉压主副比和失配脉压主副比,图7为不同采样频率下传统法设计S型信号时的最优K值,图8为不同采样频率下匹配和失配脉压主副比。对于复信号,采样频率应不小于复信号带宽,图7和图8的仿真起始频率为3 MHz,其余仿真参数同1.2节。

图7 K值随采样频率变化曲线
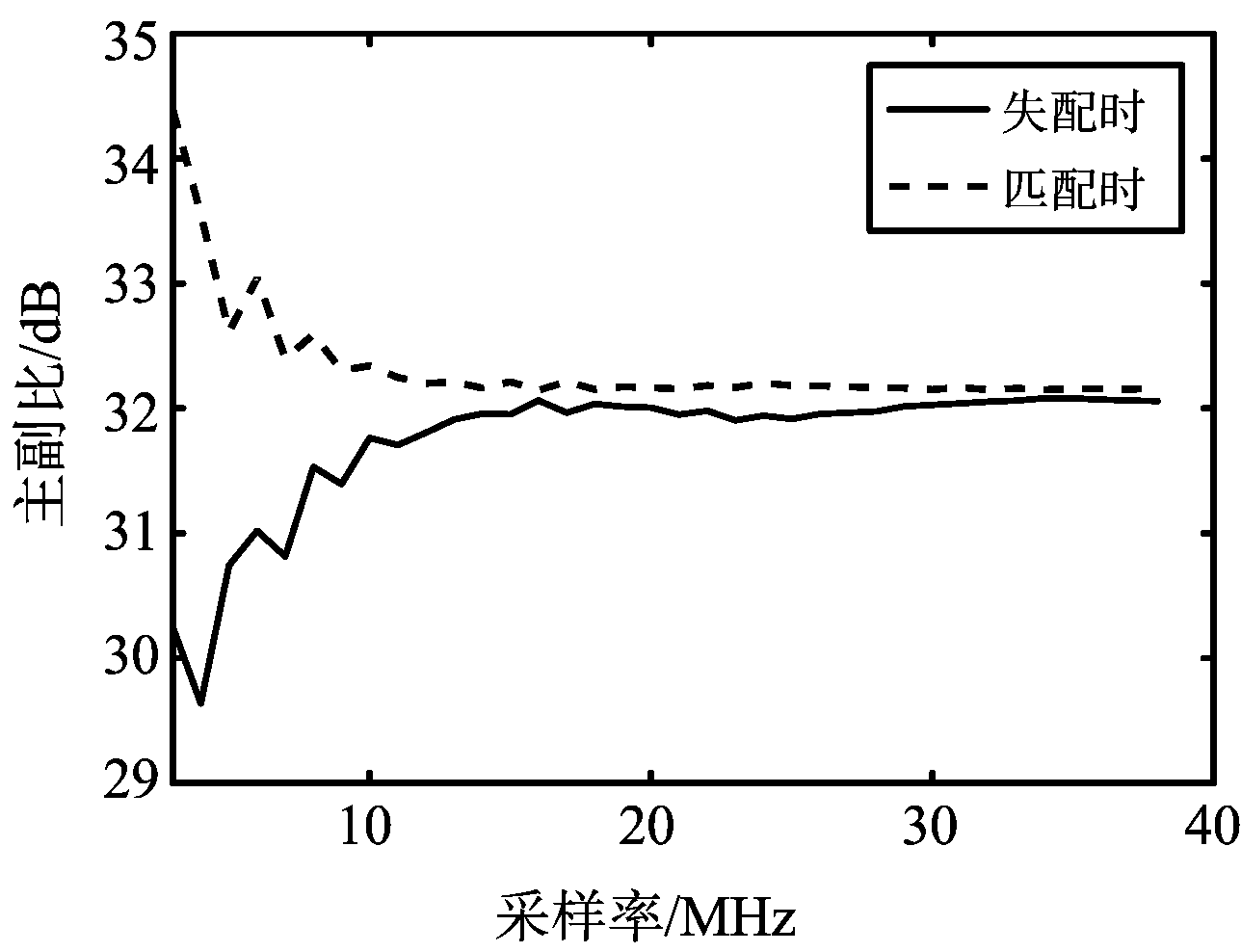
图8 主副比随采样频率变化曲线
由结果可以看出,当采样频率为3~10 MHz时最优K值的搜索结果变化幅度比较大,匹配脉压主副比和失配脉压主副比差距很大,最大可达到4.14 dB,表明采样频率比带宽高的不是很多时,失配现象对脉压结果带来的影响很大,如果实际回波采样中恰好出现这种情况,将会导致脉压主副比变小而影响目标的检测;当采样频率大于12 MHz时,穷举法搜索出的最优K值趋于一个稳定值,匹配主副比和失配主副比也非常接近,表明采样频率越高,失配现象对脉压结果影响越小。
但是,实际工程中采样频率一般都不会很大,因此需要对S型NLFM信号进行优化,使得在实际系统常用的采样频率下也能降低失配现象给脉压带来的影响。
2 S型NLFM信号的优化方法
2.1 基本原理
实际回波采样中存在多种延迟情况,就会有多种离散采样误差,由概率论的知识可知,离散采样误差是一个连续型的随机变量,可以用X来表示,则X在区间[0,Ts](其中Ts=1/fs为离散采样间隔)上服从均匀分布,其概率密度函数为
(5)
由于不同的离散采样误差对应着不同的脉冲压缩主副比(用变量RMS来表示),因此RMS可视为随机变量X的函数,可将RMS表示为G(X),则RMS的期望为

(6)
期望越大,表明各种失配情况下的脉冲压缩主副比均值越高,即脉压结果越好。为了计算简单,将上述公式离散化,则式(6)可以写为
(7)
式中,M表示回波离散采样误差的个数。只要找到使得RMS的期望(即脉压主副比均值)最大的K值,即可认为是最优K值。
简而言之,这种优化方法的基本思想就是尽可能将离散采样误差的各种情况都考虑进去,对所有失配情况的回波脉压主副比取均值,根据穷举法找出最优K值,这种优化方法综合考虑了回波的多种可能情况,所以可以降低离散采样误差给脉压结果带来的影响。
2.2 具体设计步骤
1) 确定K值的搜索范围与搜索间隔;
2) 选择初始K值,根据前面S型调频信号的产生原理得到基带信号:
s(t)=exp[jφ(t)]
(8)
3) 根据匹配滤波理论,得到匹配滤波器:
h(t)=s*(t0-t)
(9)
4) 根据采样频率得到采样时间间隔,记为Δt,将步骤2)中得到的基带NLFM信号分别延时0,0.1Δt,0.2Δt,…,0.9Δt,即在[0,Δt]上均匀地取了10个离散采样误差,于是得到10个NLFM信号:
sk(t)=exp[jφ(t+Δk(t))], k=0,1,…,9
(10)
5) 将式(10)得到信号sk(t)分别用步骤3)得到的滤波器进行脉冲压缩;
6) 对步骤4)得到的10个脉压结果进行分析,找出每一个脉压结果的主副比,进行求和取均值;
7) 对搜索范围的所有K值均执行上述操作,将所有主副比均值进行比较,最大主副比均值所对应的K值即可认为是最优K值,依据此K值设计S型NLFM信号即可。
2.3 仿真分析
根据2.2节的设计步骤设计S型NLFM信号,其余仿真参数和1.4节相同,得到K值随采样频率变化曲线如图9所示,匹配和失配时的脉压主副比随采样频率变化曲线如图10所示。

图9 K值随采样频率变化曲线

图10 主副比随采样频率变化曲线
由结果可以看出匹配与失配情况的误差最大为2.76 dB,当采样频率大于5 MHz时,K值曲线起伏已基本趋于稳定,匹配主副比和失配主副比已经非常接近。而由图7、图8可得,用传统方法设计S型NLFM信号时,采样频率大于12 MHz时,才能达到这种效果,因此优化后的信号在较低采样频率时可以降低离散采样误差给脉压带来的影响。
由于回波的离散采样误差情况是随机的,所以脉压主副比也是随机的,因此选择脉压主副比的均值作为衡量脉压结果好坏的依据。现对传统方法设计的S型信号在多种失配情况下的主副比进行取均值,然后和优化方法的主副比均值进行比较,观察其随采样频率的变化曲线,结果如图11所示。显然,在采样频率低时,优化方法的主副比均值高于传统法,因此这种优化方法是有效的。
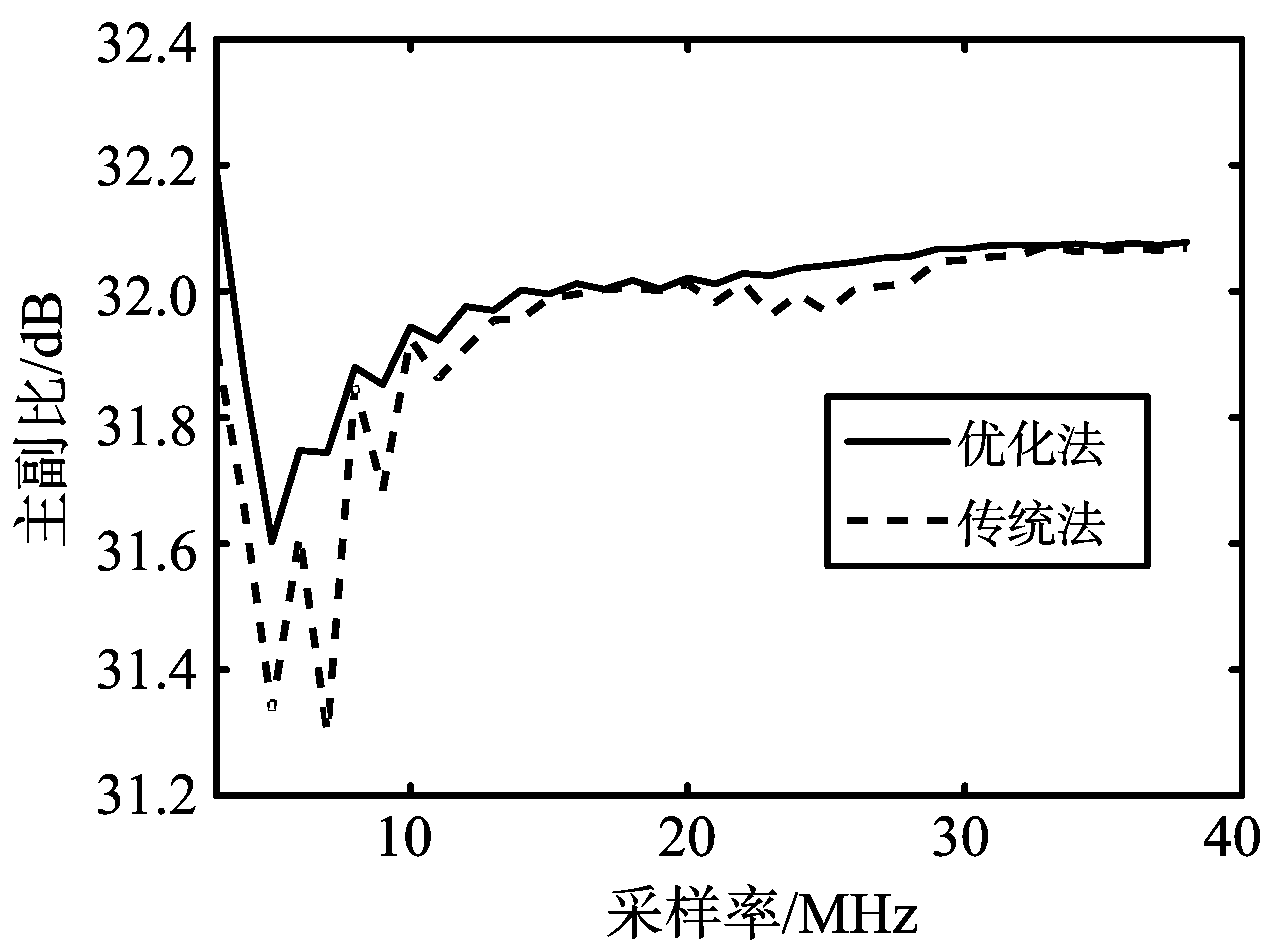
图11 主副比均值随采样频率变化曲线
实际系统中常采用过二采样,即采样频率为2倍带宽,下面在过二采样下对多种BT组合下用传统设计法和优化方法搜索出的K值、匹配与最大失配脉压主副比之差以及主副比均值进行统计对比,统计表如表1所示。
表1 优化法与传统法对比统计表

BT组合方法K值RMS差值/dBARMS/dB80100160200传统法0.09103.915531.6578优化法0.10402.760031.8665传统法0.07002.089732.3268优化法0.10601.456533.1431传统法0.06702.248835.4063优化法0.09000.821536.1392传统法0.06301.704536.6450优化法0.08200.784437.5350
表1中,RMS差值表示匹配与最大失配脉压主副比之差,ARMS表示主副比均值。由表中结果可以看出,优化方法可以减小匹配主副比与失配主副比之差,同时提高主副比均值,且BT值越大时改进效果越明显,当BT值为200时,可将主副比均值提高将近1 dB,可见优化方法在实际系统常用的采样频率下可以大大降低离散采样误差给脉压带来的影响,证明了这种优化方法是有效的。
3 结束语
本文分析论证了S型信号的设计不仅受时宽、带宽影响,采样频率也是一个非常重要的因素,基于此对S型NLFM信号进行了优化。该优化方法综合考虑了实际中多种回波失配情况,使得在实际系统常用采样频率下就能设计出较好的信号,降低了实际工程中的失配现象对脉压结果带来的影响,而且能提高主副比。仿真结果表明,此方法具有一定的优越性,对S型NLFM信号脉冲压缩的工程实现有一定的指导意义。
[1] 刘萍,邹林,周云,等. 基于NLFM的超低副瓣脉冲压缩方法研究[J]. 雷达科学与技术, 2014, 12(5):527-531.
LIU Ping, ZOU Lin, ZHOU Yun, et al. An Ultra-Low Sidelobe Pulse Compression Method Based on Nonlinear Frequency Modulation Signal[J]. Radar Science and Technology,2014,12(5):527-531.(in Chinese)
[2] 王侠,王进军,杨战社. 基于三次样条插值的非线性调频雷达信号设计[J]. 山西大学学报(自然科学版), 2017,40(4):797-803.
[3] 李红霞. 雷达信号数字脉冲压缩技术分析及MATLAB仿真[J]. 信息化研究, 2018, 44(1):69-73.
[4] 刘萍. 低旁瓣脉冲压缩技术研究[D]. 成都: 电子科技大学, 2015.
[5] ROHMAN B P A, INDRAWIJIYA R, KURNIAWAN D, et al. Sidelobe Suppression on Pulse Compression Using Curve-Shaped Nonlinear Frequency Modulation[C]∥1st International Conference on Information Technology, Information Systems and Electrical Engineering, Yogyakarta, Indonesia: IEEE, 2017:49-53.
[6] 彭志刚,杨志国,彭世蕤. 一种非线性调频信号数字脉压性能分析[J]. 空军雷达学院学报, 2003, 17(3):51-53.
[7] 付启众,陈忠先. 一种超低副瓣非线性调频脉压信号的性能分析[J]. 雷达科学与技术, 2007, 5(1):60-64.
FU Qizhong, CHEN Zhongxian. Performance Analysis of an Ultra-Low Side Lobe Non-Linear Frequency Modulation Signal for Pulse Compression[J]. Radar Science and Technology,2007,5(1):60-64.(in Chinese)
[8] YUE Wenzhen, ZHANG Yan. A Novel Nonlinear Frequency Modulation Waveform Design Aimed at Sidelobe Reduction[C]∥ IEEE International Conference on Signal Processing, Communications and Computing, Guilin: IEEE, 2014:613-618.
