0 引言
油库储油罐感知层由温度、压力、流量、液位等信息传感器组成,雷达液位计是储油罐油量的非接触式测量装置,采用发射—反射—接收的工作模式探测液位高度,具有安全可靠、精度高、寿命长、适应各种工作环境的特点,广泛应用于石化、仓储行业,是储油罐的核心传感器[1]。
雷达液位计的发展是从20世纪80年代开始的,雷达液位计主要由调频连续波(FMCW)雷达、脉冲雷达两类[2],一般工作在C,X,K波段。众所周知,雷达的测距精度主要取决于信号的带宽和信噪比,脉冲雷达液位计由于受脉冲宽度和高速计时器件的限制,测量精度一般在3 m~10 mm,主要用于过程控制,为中低端雷达液位计。与脉冲雷达相比,FMCW雷达液位计通过测量发射和目标反射的FMCW信号的频率差来测量距离,可以形成大带宽的FMCW信号且不受脉宽的限制,因此能达到更高的测量精度和分辨率,目前FMCW雷达液位计测量精度可达0.4 m~3 mm,计量级精度则在±1 mm以内,主要用于计量级和商品交易,为中高端应用场合使用[3]。
对于中远程雷达来说,其测距精度一般在米级水平,诸如频率精度、波形线性度、大气温度和压力等因素对精度的影响微乎其微,在设计时这些因素一般不予考虑。而在超近程高精度的雷达液位计中,这些因素则是影响测距精度的主要方面。例如,在雷达液位计中的100 MHz晶振具有10-5的频率精度,经过上行链路10倍频到X或K波段,则频率精度变为10-4,在测量20 m的目标时就有2 mm的误差。因此,计量级高精度测量对雷达液位计的系统设计和处理方法上提出了诸多挑战。本文从FMCW雷达液位计系统角度出发,针对这些因素对测距精度的影响进行了深入研究,并提出了可行的技术手段。
1 系统原理和组成
1.1 FMCW雷达测距原理
线性调频连续波(FMCW)雷达是一种通过对发射FMCW信号及相应的接收处理获得距离与速度信息的雷达体制,一方面发射信号通过天线向外辐射,另一方面作为混频器的基准信号解调回波信号,其得到的差频信号频率与目标的距离成正比,式(1)表示差频信号频率与目标的距离的关系。雷达波形及测距原理如图1所示。

图1 FMCW雷达波形及测距原理图
![]()
(1)
式中,fb为差频信号频率,R为目标距离,B为调频带宽,T为调频周期,c为光速。
1.2 FMCW雷达液位计组成
FMCW雷达液位计由喇叭天线、收发模块、电源模块、信号处理模块、显示模块等单元组成。收发模块产生FMCW信号,经环行器至喇叭天线向外辐射,回波信号由喇叭天线接收经环行器送到接收通道,接收通道对回波信号进行谐波混频、放大、低通滤波后,输出包含距离信息的差频信号,经A/D采样形成数字信号,信号处理模块接收收发模块的差频数字信号进行FFT、杂波抑制、目标检测、频谱估计等处理后,得到高精度的液位数据,通过现场总线送到显示单元和上位机,其原理框图如图2所示。
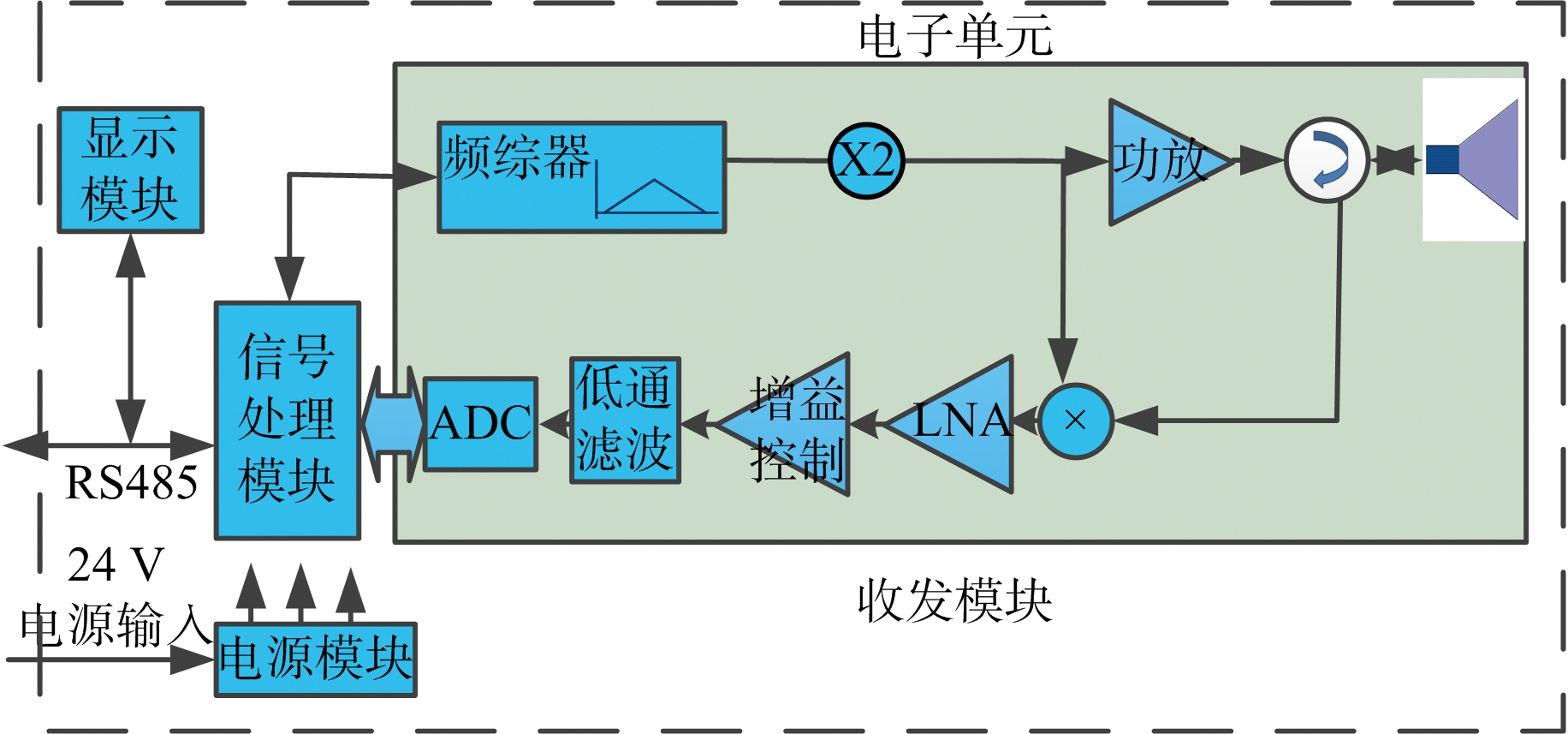
图2 FMCW雷达液位计原理框图
2 测距精度影响因素分析及相应的解决措施
根据FMCW信号测距精度公式[4]:
(2)
测距精度主要取决于信号带宽和信噪比,假定信号带宽B为2 GHz,要达到1 mm的精度,则信噪比(SNR)J=29 dB,式(2)为雷达测距精度的Cramer-Rao界,因此在实际系统中信噪比应大于29 dB。由此看出,要满足1 mm的测距精度,雷达液位计应具有大带宽、高信噪比的特征。
在雷达液位计系统设计满足测距精度情况下,最终得到的距离精度还受其他因素影响,由式(1)变换得
(3)
式中,K=B/T为调频斜率。从式(3)可以看出,差频频率、调频斜率将会影响测距精度,误差表现形式为比例误差,下面对这些因素对测距精度的影响进行分析,并提出相应的技术措施。
2.1 晶振频率
差频频率fb和带宽B的误差的主要来源于晶振频率的误差,该误差主要由中心频率偏差和温度变化引起的频率偏差两部分构成,前者用频率准确度表示,后者用频率温度稳定度表示。对于晶振中心频率偏差,可在雷达系统校正时进行比例修正,尽量选择频率准确度较高的器件,目前晶振的频率准确度(与晶振输出频率的比值)一般在1×10-5以内;对于温度变化引起的频率偏差,为了减小温度变化的影响,需选用恒温晶振,其温度稳定度指标可达1×10-9;考虑到价格因素,也可采用价格便宜的温补晶振,其温度稳定度指标可达5×10-7,可以满足精度要求。
2.2 FMCW调频斜率
FMCW信号的调频斜率的线性度指标直接关系到距离测量精度,早期的FMCW雷达液位计大多采用VCO产生FMCW信号,由于VCO是模拟电压控制频率产生,易受模拟电压非线性和温度变化的影响,FMCW信号的线性度不高,要采用复杂的校正控制电路和温度补偿电路。而数字直接频率合成技术(DDS)采用数字方法产生频率,线性度极高且受温度影响较小,在雷达和通信系统中得到了广泛的应用,且芯片价格已下降到合理的水平。因此,在设计中需采用DDS来产生FMCW信号,以保证FMCW信号的线性度。
DDS具有良好的线性度,其等效线性度在10-6以下,根据线性度误差的经验公式[3]:
δL=4LR
(4)
式中,L为线性度,R为目标距离,设L=10-6,R=20 m,则δL=0.08 mm。
采用DDS后,其调频线性度对测距精度基本没有影响,但DDS的量化误差对测距精度有影响,该影响也可通过系统校正进行比例修正。
2.3 系统校正
晶振频率、调频斜率等的误差对测距精度有较大的影响,其表现形式为比例误差,在系统设计时要进行定量分析,其定量分析数据对系统调试有指导作用,但最终需要通过测量系统来对雷达液位计进行精确的比例校正,考虑到比例误差的影响,式(3)修正为
(5)
式中,g(fr,K)为校正系数,与晶振频率、调频斜率等的误差有关。
雷达液位计测量系统主要由激光跟踪仪、储油罐模拟板、液位计支架(液位计安装车)、监控计算机等组成,放置在满足一定长度要求的暗室内,其原理框图如图3所示。在该系统中,激光跟踪仪测量雷达液位计与目标板之间的距离,并以此距离值为基准,与雷达液位计测量的距离值进行比对来计量雷达液位计的精度,通过设置多个测量点来进行比例校正,具体方法如下:
1) 在量程范围内均匀设置N个测量点;
2) 记录激光跟踪仪的N点测量值Rl,n,n=1,2,…,N,计算N-1点距离差分值:
ΔRl,n=Rl,n+1-Rl,n,n=1,2,…,N-1
3) 记录雷达液位计的N点测量值Rr,n,n=1,2,…,N,计算N-1点距离差分值:
ΔRr,n=Rr,n+1-Rr,n,n=1,2,…,N-1
4) 计算比例校正系数:
gn=ΔRl,n/ΔRr,n,n=1,2,…,N-1
5) 计算比例校正系数的均值,代入式(5),完成比例校正。
由于雷达液位计内部的射频电路和电缆在传输信号时有一定的延时,因此雷达液位计基准面的距离值不等于零,存在固定误差,该固定误差可通过雷达液位计测量系统进行测量,在系统计算时予以消除。

图3 雷达液位计测量系统
3 高精度频谱估计技术
从前面的分析可知,要达到1 mm的测量精度,雷达液位计需要具备大带宽、高信噪比的特点。传统测量方法通过数字化和FFT计算得到距离量化值,但是FFT的分辨率是显然不能满足测量精度要求的。例如,假定信号带宽为2 GHz,则FFT的距离分辨率为75 mm。这是因为检测频谱上的高点不一定是回波信号频谱的实际峰值,直接采用FFT的离散频谱点来计算距离会有较大的误差。因此,需要通过高精度频谱估计来找到两离散频谱高点中间的峰值位置,以得到高精度的距离测量值。
为了满足高精度测量需求,学者们提出了多种提高FMCW雷达距离测量精度的方法。例如:
1) 利用DFT频谱相位信息实现高精度测距[5],该方法运算量大,对硬件要求高,工程化实现难度较大;
2) 结合Chirp-Z变换,“由粗到细”逐步找到频谱实际峰值的位置[6],该方法的本质是通过增加采样点的方式提高精度,增加了运算量;
3) 找到频谱主瓣内最大和次大谱线,使用插值法求出中心频率[7],该方法原理简单,计算量小,易于工程实现,但其提高仿真精度的能力有限。
针对上述问题,本文提出一种基于迭代插值的高精度谱估计算法,该算法首先采用FFT粗测差频信号的频率,然后在FFT峰值附近取两条谱线进行频率细化。其核心思想为:找到回波序列 x(n)的频谱X(k)幅度最大值A和次大值B,及其所在的位置k1, k2;若A=B,则目标真实位置所对应的频率就在k1, k2的中心。其原理如图4所示。
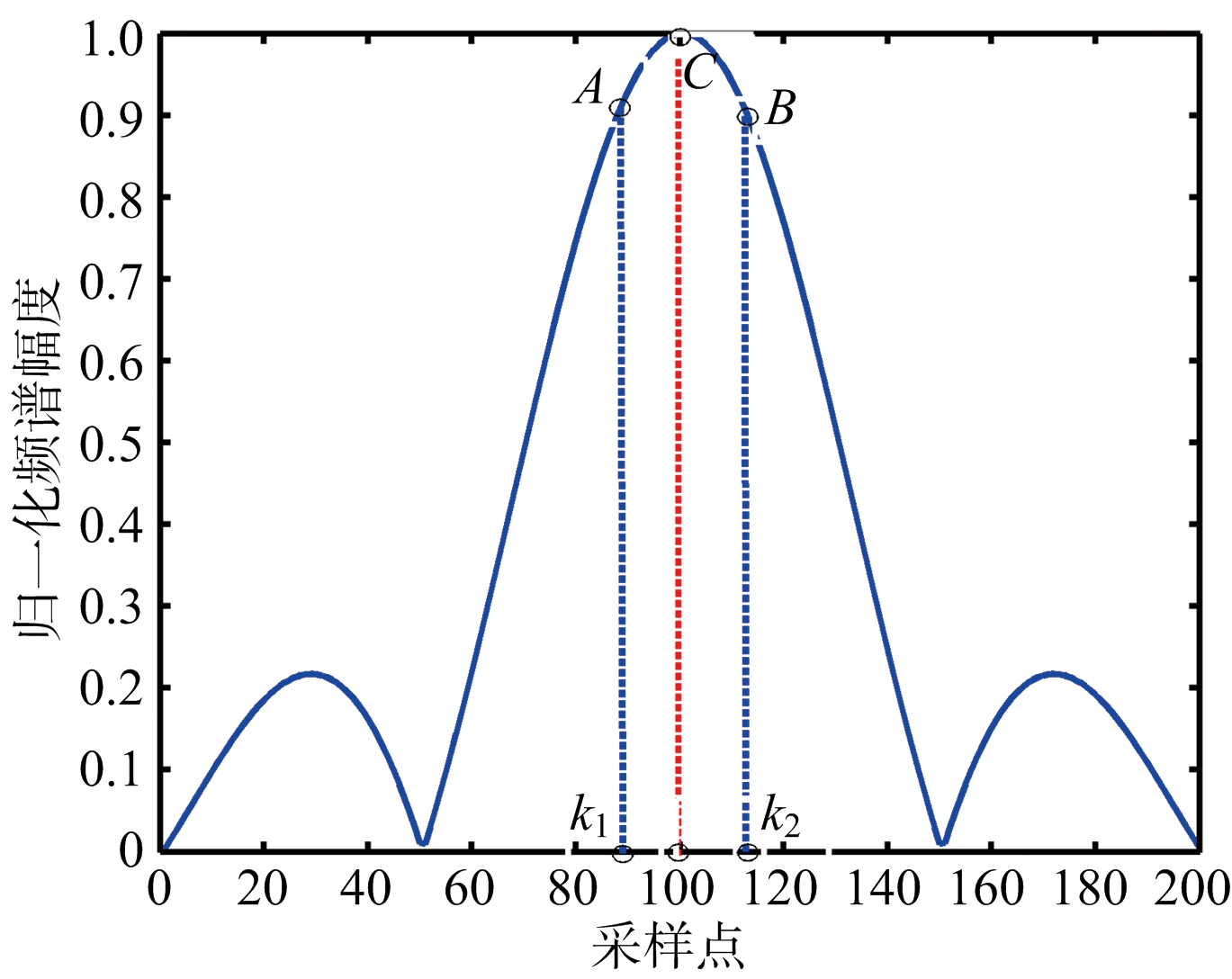
图4 高精度谱估计算法示意图
实现方法为:找到X(k)幅度最大值所对应的位置k1,选出k1左右两点中幅度较大的那个点位置记为k2,即k2=k1+1或k2=k1-1;根据这两个分量,利用式(8)计算出第一次迭代结果![]()
(6)
式中,用上标来表示迭代序号。根据式(8)计算出的位置,利用式(9)可以进一步确定一组新的![]()
(7)
通过式(10)计算![]() 这两点对应的频率分量的幅度值,分别为
这两点对应的频率分量的幅度值,分别为
(8)
得到![]() 和
和![]() 之后,继续利用式(8)计算出k(2),按照同样的步骤,迭代3次,最后得到
之后,继续利用式(8)计算出k(2),按照同样的步骤,迭代3次,最后得到![]() 而最优频率分量对应的位置k*由式(11)计算得到:
而最优频率分量对应的位置k*由式(11)计算得到:
(9)
这种方法测量精度高,而且最大的优点是运算量小,单次测量只需进行6次DFT。
设定一组仿真参数:带宽B=2 GHz,频率调制时间T=5.12 ms,采样率fs=200 kHz,信噪比SNR=29 dB。使用上述算法进行仿真,对20.8~21 m以1 mm采样间隔得到的距离进行测试,得到误差统计结果,如图5所示。

图5 本文算法测距误差统计结果
从图5可知,利用本文提出的基于迭代插值的高精度谱估计算法进行测距,不同距离的测量误差都控制在1 mm以内。经统计,误差绝对值的最大值为0.153 2 mm,误差绝对值的最小值为 2.987 8×10-5 mm;误差均值为0.001 2 mm,标准差为0.045 8 mm;误差绝对值的均值为0.036 4 mm,误差绝对值的标准差为0.027 7 mm;证明了该算法可以满足高精度测距的要求。
4 结束语
本文从FMCW雷达液位计系统设计角度出发,根据计量级测量精度的要求,分析得出雷达液位计应具有大带宽高信噪比的特点;在此基础上,对诸如晶振频率、调频斜率、工作环境等影响测量精度的因素进行了分析,提出了相应的技术措施,得到了其影响为比例误差的结论;通过设计雷达液位计测量系统,对比例误差进行校正,给出了具体的测试方法;最后研究了一种高精度频谱估计算法。本文研究的FMCW雷达液位计高精度测量技术在实际的雷达液位计得到了应用,并通过了1 mm精度的国家计量认证,验证了该技术的有效性。
[1] 谭梦奇,王辉. 雷达液位计在原油储油罐上的应用[J]. 油气田地面工程, 2015, 34(4):43-44.
[2] 张庆庆. 导波雷达液位计测量技术研究[J]. 仪器仪表用户, 2017, 24(3):23-27.
[3] 高红博. 浅析雷达物位计的应用[J]. 中国仪器仪表, 2016(9):43-46.
[4] Skolnik M I. 雷达系统导论[M]. 3版. 左群声,徐国良,马林,等译. 北京:电子工业出版社, 2014:244.
[5] 齐国清,贾欣乐. 基于DFT相位的正弦波频率和初相的高精度估计方法[J]. 电子学报, 2001, 29(9):1165-1167.
[6] 候庆文,陈先中,王小攀,等. 改进的FMCW信号加权补偿校正相位差法[J]. 仪器仪表学报, 2010, 31(4):721-726.
[7] 陈亚培,李明,左磊. 利用插值法提高PD雷达测距测速精度[J]. 雷达科学与技术, 2011, 9(5):447-452.
CHEN Yapei, LI Ming, ZUO Lei. Improving Range and Velocity Measurement Precision of PD Radar with Interpolating Method[J]. Radar Science and Technology, 2011, 9(5):447-452.(in Chinese)
