0 引言
通常对发射源的定位一般采用基于两步处理的定位方法：首先，从观测信号中估计得到与位置相关的参数，如到达时间/时间差(TOA/TDOA)、到达角(AOA)、多普勒频率等[1-3]；然后，利用已估计参数和雷达以及目标之间的几何约束进一步确定目标位置。从估计理论的角度来看，该方法是次优的，原因是第一步中的参数估计是在各接收基站独立进行的，它忽略了所有观测信号对应同一个目标这一客观约束。而直接定位(Direct Position Determination, DPD)[4-6]方法充分利用了这一客观约束，直接联合所有原始回波信号构建依赖于目标位置的代价函数，通过优化代价函数进行一步参数估计便能直接提取目标的位置，具有较传统两步定位方法更优的估计性能。
多重信号分类(Multiple Signal Classification, MUSIC)算法[7]能将高维搜索问题转化为低维参数估计问题，且具有高精度的参数估计能力。在文献[5]中，结合MUSIC算法，通过计算感兴趣区域内频谱峰值点来确定发射未知信号的多个发射源的位置。该方法的计算复杂度相比于基于全局最优的最大似然估计器的方法大大减小。在文献[6]中，目标数目是利用恒虚警率(Constant False Alarm Rate, CFAR)的方法来确定的，却忽略了目标提取的这一关键步骤，而若无法成功提取目标，目标位置也难以确定，相应地，后续定位性能的分析也会受到阻碍。文献[8]中给出了一种目标提取及位置估计的方法，通过消除已定位目标的影响，按照目标强度依次定位出监测区域的目标，直至满足一定停止准则时算法停止。
图像膨胀(Image Expansion, IE)算法的应用可基于像素复制、双线性插值、三次插值以及基于Canny边缘化的方法[9-10]，一般被用于处理图像方面的问题以及提取局部极值。提出定位方法利用IE算法来提取目标，相比于文献[8]中通过依次进行门限处理来获取目标位置的方法，该方法更为简单且能达到很好的效果。
在本文中，首先由AIC确定模型阶数，再利用基于MUSIC的DPD算法来获得用于定位的代价函数，并通过计算感兴趣区域所有网格点的代价函数值得到代价函数平面，之后利用IE算法来提取代价函数平面的局部最大值即可获取目标个数以及位置的估计值。仿真验证提出方法(IE-DPD-MT)可以有效提取并定位多个发射源，且进一步分析了影响目标提取有效性的主要因素。
1 基本原理
1.1 信号模型建立
考虑监测区域内的G个静止目标，位置坐标为pg=(xg,yg),g=1,2,…,G，G的值固定且未知。在二维笛卡尔坐标系下，L个在时间上同步的接收基站位于(xl,yl),l=1,2,…,L，每个接收基站接收端是包含N个阵元的均匀线阵(Uniform Linear Array, ULA)。接收基站l截获的回波信号复包络为
rl(t)=
t0,g)+wl(t), 0≤t≤T
(1)
式中：rl(t)表示与时间相关的N×1维向量；αlg表示信号在第g个发射源与第l个接收站之间的通道的复衰减系数；T表示观测时间；αl(pg)表示由位置pg的发射源发射的信号在第l个接收站的阵列响应，为N×1维向量；xg(t-τl(pg)-t0,g)表示第g个发射源在时刻t0,g发射并经过时延 τl(pg)之后的信号波形；wl(t)表示基站l处的阵列天线观测到的噪声和干扰。
为了分离出信号波形中的延时项，这里在频域上对信号进行分析。为便于准确估计观测信号的协方差矩阵，这里将观测时间T分为K个部分，每个部分的长度为T/K≥max
。τl(pg)表示位置pg的发射源发射的信号传输到第l个接收站的时延：
(2)
式中，c为光速。
式(1)中接收信号的第k部分的傅里叶变换可表示为
rl(m,k)=
wl(m,k), m=1,2,…,M
k=1,2,…,K
(3)
式中，rl(m,k)，xg(m,k)以及wl(m,k)分别表示接收信号、发射信号以及噪声在第k部分第m个频点上的傅里叶系数。
首先定义以下向量及变量：
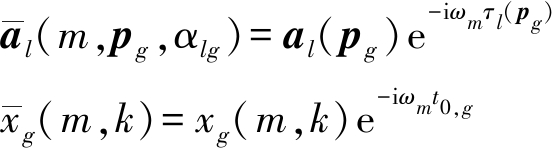
(4)
则式(3)可写成
rl(m,k)=
wl(m,k)
(5)
由以上分析可知，目标的位置信息只包含在
中，可进一步将式(5)表示为如下形式：
(6)
式中，
(7)
进一步地，将联合了L个接收站的所有信息表示为
(8)
式中，
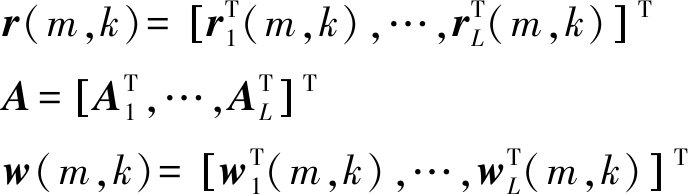
(9)
未知的参数包括复信号
复反射系数αlg和发射源的位置pg，其中，反射系数满足
针对于多发射源的情况，按照MLE的方法则需要进行高维搜索才能完成对多个发射源位置的确定。为了避免高维空间搜索所带来的指数式增长的计算量，本文方法采用MUSIC算法对高维估计问题进行降维处理。
1.2 膨胀算法原理
膨胀算法通常用来处理二值图像，简单来说就是用结构元素作为模板在原始二值图像上遍历一遍，扫描图像的每一个像素，用结构元素中的每一个元素与其覆盖的二值图像作“或”运算(假设结构元素都为1)，如果结果为1，则二值图像中对应结构元素原点位置的像素值为1，否则为0。
膨胀操作其实将图像与核进行卷积。核也称作结构元素，可以是任何的形状和大小，它拥有一个单独定义出来的参考点，多数情况下，核是一个小的中间带有参考点和实心正方形或者圆盘，而膨胀算法用于本文算法实则是用来求局部最大值，将核与图像卷积，即计算核覆盖区域的像素点的最大值，并把这个最大值赋值给参考点指定的所有像素。膨胀操作后，图像中会表现出高亮区域逐渐增长。
2 基于膨胀算法提取目标的多目标直接定位算法
2.1 基于MUSIC的直接定位算法
MUSIC算法是基于信号空间与噪声空间的谱估计分析方法，首先根据式(8)中的信号模型求得接收信号的协方差矩阵：
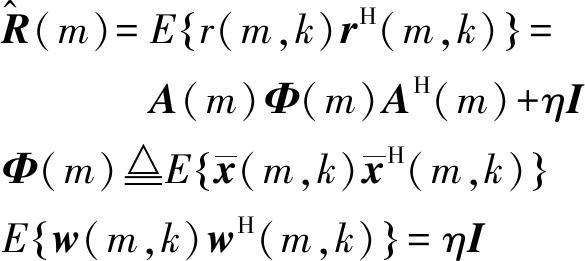
(10)
然后，利用信号空间与噪声空间的正交性[12]，求得相应代价函数：
F1(p,α)≜
(11)
式中，
(12)
Qs(m)是由
的G个最大特征向量组成的NL×G维矩阵，p和α表示发射源位置和衰减系数。
由于应用MUSIC算法时需要已知目标数目，而本文假设目标个数是未知的，所以这里利用AIC定阶方法[13]来确定目标的个数。由式(11)可知，F(p,α)的最大值取决于p和α，需要对参数空间进行2(L-1)+D维搜索才能得到确定。该问题可以采用一定的矩阵变换进一步地降维，其具体思路如下：
首先重新表示矩阵
(13)
式中，
(14)
式中，Λ(m)是以接收基站对应的阵列响应为对角元素的对角矩阵，IL是L×L维单位矩阵，1N是全1的N×1维向量，⊗是克罗尼克乘积。
上述过程可将发射源位置参数与衰减系数进行解耦合并分离，以用于后续的降维处理，式(11)中的代价函数可重新表示为
(15)
从上式可以看出，F2(p,b)的最大值对应于矩阵Z(p)的最大特征值，Z(p)定义如下：
Z(p)≜
(16)
式中，数据矩阵Z(p)包含与目标位置的相关的信息。根据假设
再利用瑞利商理论，式(15)中的估计问题可转化为
F3(p)≜λmax[Z(p)]
(17)
上式表示位置p处对应的代价函数值为矩阵 Z(p)的最大特征值。因此，由上式可知，对感兴趣区域进行二维网格搜索，计算并保存每个网格点代表的位置坐标对应的代价函数值，即可获得代价函数平面。
2.2 应用膨胀算法提取目标
当目标发射波形未知时，应用基于MUSIC的直接定位算法可得到代价函数平面，由于MUSIC算法具有较高的分辨率，能直观地从该代价函数平面上看出目标的大概个数及大致位置区域。但是，只有成功估计出目标个数并确定目标的位置，才能进一步从误差角度分析针对每个目标算法的定位性能。
根据膨胀原理，当参考点在局部极大值位置时，参考单元内的所有值都相同且为最大值，此时局部极大值所在的区域亮度将增长。在得到进行膨胀操作处理后的图像(亦是一个矩阵，矩阵的元素即代价函数平面每个网格点处保存的代价函数值)后，将该图像和原图像进行对比，两者相匹配的多个像素点即为代价函数平面上目标的位置。膨胀操作的输入为代价函数平面，输出设定为目标位置的横纵坐标。由于膨胀算法应用于实际场景中时是基于一定虚警概率的，所以同时可得到目标数目以及位置的估计值。
总结应用膨胀算法提取目标的多目标直接定位算法(IE-DPD-MT)流程图如图1所示。
图1 算法流程图
3 算法性能分析
3.1 仿真场景设置
假设阵列雷达系统中有3个接收基站，每个接收基站配备4个天线单元且阵列间距为半波长的ULA。发射信号为窄带高斯随机信号，定位结果基于10个频点上的100个快拍。接收端衰减系数幅度设定为服从均值为1、方差为0.1的正态分布的随机数，相位衰减分布服从[-π,π]均匀分布。目标发射机以及接收基站位置分布情况如图2所示，发射源的坐标为(-3,-1;0,5;3,1.5)km，接收基站的位置为(-6,-6;-2,-6;2,-6;6, -6) km。信噪比取值为-15∶3∶15(dB)，对每一个信噪比取值点，所执行的蒙特卡洛仿真迭代次数为200次。应用膨胀算法所选参考单元大小为2个网格点，虚警概率为1×10-5。
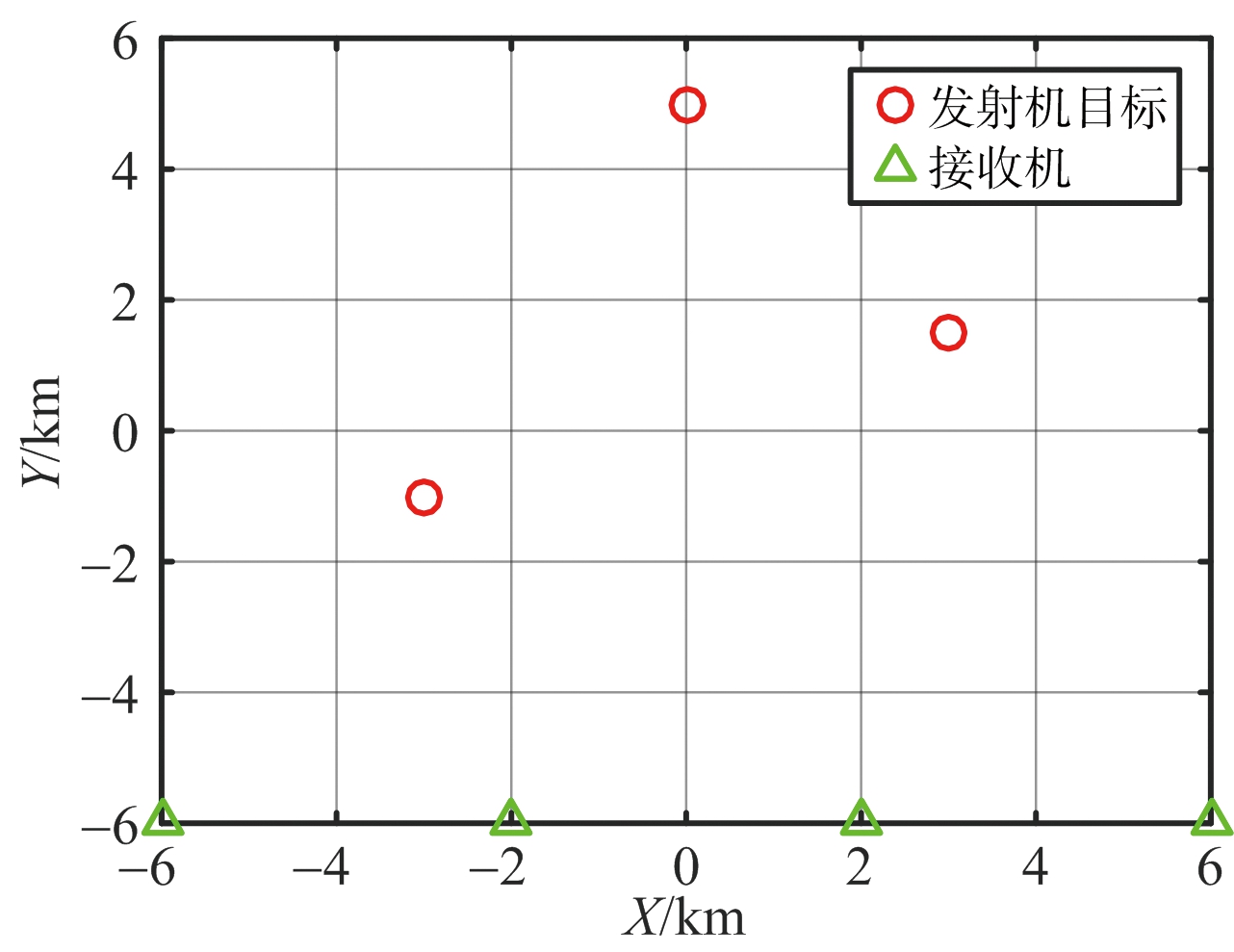
图2 定位场景图
算法性能由目标有效提取率Pr和目标均方根误差(Root Mean Square Error, RMSE)两个指标评价，定义如下：
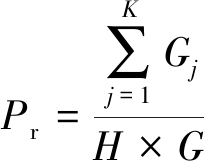
(18)
(19)
式中，H为蒙特卡洛仿真次数，xj,yj为第j次实验得到的目标位置估计值，Gj为第j次实验提取得到目标位置落在真实目标位置指定范围内的目标个数。目标有效提取率为在N次独立的定位实验中，有效提取得到的目标总数与真实目标总数的比值。有效提取率越高，定位准确的目标数越多，即定位算法越有效。
3.2 应用膨胀算法提取目标的定位算法有效性验证实验
图3中颜色较深的红色区域表示该区域的目标代价函数值较大，其中颜色较深的3块区域里的最大值分别对应3个目标的位置。对图3(a)中的代价函数平面进行膨胀处理，能得到图3(b)所示高亮度区域增长的平面，再将基于门限处理后的平面与原始代价函数平面作对比，只有原始平面上局部极大值的位置在两个平面上的值是相同的，提取出这些位置，即得到目标个数及对应位置的估计值，如图3(c)所示。
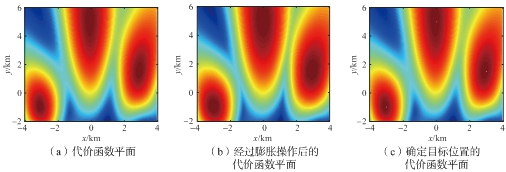
图3 基于膨胀算法的目标提取过程分析图
统计在每个信噪比值下每次蒙特卡洛实验中得到的目标个数及位置的估计值后，基于统计的概念，利用式(18)和式(19)可得单个信噪比值下目标有效估计率与位置均方根误差。
在图2所示定位场景下，利用提出的IE-DPD-MT方法得到的目标有效提取率Pr以及各目标位置估计的RMSE随信噪比变化关系分别如图4和图5所示。
图4 目标有效提取率Pr随SNR变化曲线
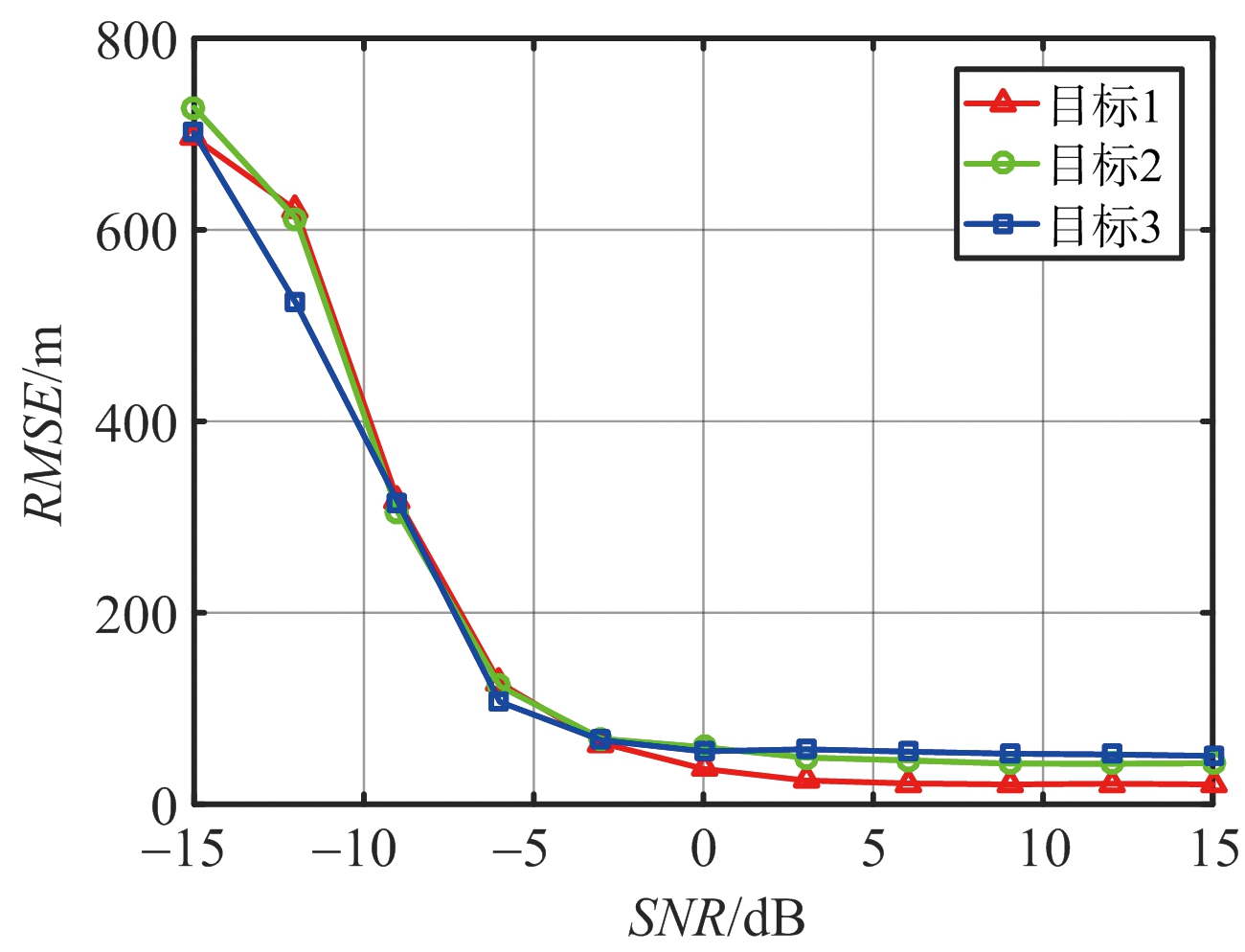
图5 目标位置估计的RMSE随SNR变化曲线
从图4可以看出，在信噪比较高时，利用膨胀算法能有效地提取目标并估计出目标的个数，而在信噪比较低时，由于利用AIC确定模型阶数时也给造成一定估计误差，进一步地，目标提取也会不太准确。当目标位置估计值得到后，根据式(19)可以得到如图5所示的各目标位置估计的RMSE随信噪比的变化趋势，从图中可看出，随着信噪比增大，目标的RMSE呈下降趋势，当信噪比高于0 dB左右，定位误差趋于稳定。
3.3 临近目标提取有效性影响因素分析实验
考虑到对于临近目标的定位问题，都会面临在信噪比较低、天线阵元数目较少、干扰较强的情况下，所有目标都成功提取的难度加大，研究此时膨胀算法的应用的可行性及有效性具有很大的必要性及价值。下面将考虑目标的个数、天线阵列阵元的数目，膨胀算法应用时参考单元的大小对目标有效提取的影响情况。
对比场景：考虑多个沿一条平行于横坐标的直线均匀相隔1 km放置的发射机目标。中心目标的位置坐标为(0,-1) km，其他的参数同上文所述。
3.3.1 目标数目对目标有效提取性能的影响
考虑目标数目对目标有效提取率的影响，其他参数与前述相同。目标个数分别为1,3,5,7时，目标提取率随信噪比变化曲线如图6所示。
从图6可以看出，在目标数目不同时，目标有效提取率都随信噪比提高而增大。而目标个数增多使得在信噪比较高时，Pr才能收敛到1，同时，当目标个数过多时，目标提取率在信噪比很高时也无法收敛到1，即此时不是每次实验都能准确提取并定位所有目标，原因是临近目标数目过多导致目标之间干扰增强，目标函数平面上目标所属区域相互影响，使得目标提取时也出现阻碍。
图6 目标数目不同时目标有效提取率随SNR变化曲线
3.3.2 阵元个数对目标有效提取性能的影响
考虑阵元数目对目标有效提取率的影响，其他参数与前述相同。阵元个数分别为2,3,5,8, 12时，目标提取率随信噪比变化曲线如图7所示。
图7 阵元个数不同时目标有效提取率随SNR变化曲线
从图7可以看出，在阵元数目不同时，目标有效提取率都随信噪比提高而增大。阵元数目越多，基于MUSIC的应用，代价函数平面对应的目标所在位置的区域越集中，即此时利用提出算法提取目标的优势越明显，表现为目标有效提取率就越大。
3.3.3 参考单元大小对目标有效提取性能的影响
考虑参考单元大小对目标有效提取率的影响，其他参数与前述相同。参考单元大小分别为1,2,7,10,15,18个网格点时，目标提取率随信噪比变化曲线如图8所示。
从图8可以看出，在应用膨胀算法选取的参考单元大小不同时，目标有效提取率都随信噪比提高而增大，而参考单元在一定范围内增大时，对有效提取率的影响基本可忽略，此时单个目标的中心未被其余目标经过膨胀后的中心区域覆盖；而参考单元进一步增大使得在信噪比较低时，出现了覆盖的现象，当增大到一定值时，一个或多个目标的中心被其他目标膨胀后的中心区域覆盖，此时这些目标无法成功提取而后得到目标位置，导致在信噪比较高时目标有效提取率无法收敛到1。
图8 参考单元大小不同时目标有效提取率随SNR变化曲线
4 结束语
为解决有效定位多个发射未知信号的发射机目标的定位问题，本文方法结合DPD技术与MUSIC算法，能实现同时准确提取目标并进一步确定目标位置。首先，基于MUSIC算法，可以获得基于特征分析的关于目标位置的代价函数；然后，利用图像膨胀算法处理代价函数平面，得到目标个数及位置的估计值；之后，根据膨胀处理的结果分析了定位精度受信噪比的影响情况；最后，进一步分析了影响提取有效性的主要因素。仿真结果表明，提出算法可以有效地提取并确定多个发射机目标的位置。
[1] AMAR A, WEISS A J. Localization of Narrowband Radio Emitters Based on Doppler Frequency Shifts[J]. IEEE Trans on Signal Processing, 2008, 56(11):5500-5508.
[2] 朱新权,俞志强,蒋晓宇,等. 时差定位无源雷达探测威力量化分析研究[J]. 雷达科学与技术, 2015, 13(1):55-59.
ZHU Xinquan, YU Zhiqiang, JIANG Xiaoyu, et al. Quantitative Analysis of TDOA Passive Radar Detection Coverage[J]. Radar Science and Technology, 2015, 13(1):55-59. (in Chinese)
[3] 苏峰, 王昌海, 徐征. 基于最小二乘的时差定位算法[J]. 雷达科学与技术, 2013, 11(6):621-625.
SU Feng, WANG Changhai, XU Zheng. TDOA Location Algorithms Based on the Least Squares[J]. Radar Science and Technology, 2013, 11(6):621-625. (in Chinese)
[4] WEISS A J. Direct Position Determination of Narrowband Radio Frequency Transmitters[J]. IEEE Signal Processing Letters, 2004, 11(5):513-516.
[5] WEISS A J, AMAR A. Direct Position Determination of Multiple Radio Signals[J]. EURASIP Journal on Advances in Signal Processing, 2005, 2005:653549.
[6] TIRER T, WEISS A J. High Resolution Direct Position Determination of Radio Frequency Sources[J]. IEEE Signal Processing Letters, 2016, 23(2):192-196.
[7] SCHMIDT R. Multiple Emitter Location and Signal Parameter Estimation[J]. IEEE Trans on Antennas and Propagation, 1986, 34(3):276-280.
[8] YI Wei, CHEN Zhenhua, HOSEINNEZHAD R, et al. Joint Estimation of Location and Signal Parameters for an LFM Emitter[J]. Signal Processing, 2017, 134:100-112.
[9] SCHULTZ R R, STEVENSON R L. Improved Definition Image Expansion[C]∥ IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA: IEEE, 1992:173-176.
[10] 邓仕超,黄寅. 二值图像膨胀腐蚀的快速算法[J]. 计算机工程与应用, 2017, 53(5):207-211.
[11] VAN TREES H L. Optimum Array Processing:
Part IV of Estimation, Modulation Theory[M]. New York: John Wiley and Sons Inc, 2002:293-303.
[12] 何子述,夏威. 现代数字信号处理及其应用[M]. 北京: 清华大学出版社, 2009.
[13] WAX M, KAILATH T. Detection of Signals by Information Theoretic Criteria[J]. IEEE Trans on Acoustics Speech and Signal Processing, 1985, 33(2):387-392.
