0 引言
如今，多类应用需要目标定位算法，如无线传感网络[1-2]、雷达系统[3-4]。常利用测量技术实现目标定位，如接收信号强度(Received Signal Strength, RSS)、到达时间(Time of Arrival, TOA)和到达角度(Angle of Arrival, AOA)，其中基于TOA测量是常用的测距技术。在基于TOA测量的测距技术中，每个基站以自己离目标节点的距离为半径以自己为圆心构建一个圆。理论上，由多个基站所形成的多个圆的共同交点就是目标节点位置。
如果TOA信号是沿直线传输，则可较准确地测量基站离目标节点的距离。然而，噪声会影响TOA信号，降低了测距准确性。换言之，如果TOA信号是通过反射达到的，测量距离将超过真实距离。这种情况也称为非视距(Non Line of Sight, NLOS)问题，其能引起较大的测距误差。NLOS误差也总会加大测距值，而不是缩小测距值。
通常，可通过使用大量传感节点提高定位精度。如文献[5]引用大量传感节点测量电脉冲信号的始端。在大量传感节点系统中，NLOS问题也称为源误差。然而，基于测量数据识别NLOS情况是非常耗时，且耗时量随基站数呈指数关系。因此，如何识别NLOS情况成为无线传感网络的研究热点。
近期，研究人员提出不同的算法消除或识别NLOS误差[6]。如文献[6]提出残差加权算法(RWGH)。RWGH算法能够有效地处理大型定位系统中的节点定位问题。然而，节点数的增加，不仅增加了计算复杂度，但定位误差也会增加。此外，文献[7]采用环境扫描算法消除NLOS误差。类似地，文献[8]采用SRNI算法降低复杂度，并采用稀疏恢复技术[9]消除NLOS问题。
为此，提出基于特征矢量的NLOS误差检测的定位(Eigenvector-Based NLOS Error Identification Localization, E-NIL)算法。E-NIL算法先利用测距数据的统计特性建立测距模型，再通过寻找相关值的特征向量识别NLOS误差。然后，将NLOS误差值从观察数据中删除。最后，依据这些无NLOS误差的观察数据估计移动基站位置。实验数据表明，提出的E-NIL算法有效地提高定位精度，并降低定位误差。
1 问题描述
考虑一个二维(Two-Dimensional, 2-D)定位场景，N个基站(Base Station, BS)随机分布于区域内。利用N个BS估计一个移动基站(Mobile Station, MS)的位置，且N个BS的位置表示为 si=[xi,yi]T,i=1,…,N。而MS的真实位置表示为u=[x,y]。
在NLOS的环境下，第i个BS获取的观测数据：
(1)
式中:ωi为测量噪声，假定ωi为独立零均值的高斯分布变量，且方差为σ2；ni为非零常数，表示NLOS值；ri为MS离第i个BS间的真实距离，其定义如式(2)所示：
(2)
当无NLOS存在时，就可利用最小二乘法(Least Square, LS)算法估计MS位置：
(3)
从式(3)可知，式(3)是MS位置的非线性函数。因此，任何非NLOS模型的求解均会导致较大的估计误差。而识别NLOS位置，并处理相关的测距值是处理NLOS问题的有效方式。
2 E-NIL算法
2.1 寻找NLOS误差
本文考虑加性噪声的NLOS，并利用统计特性识别NLOS。首先，将式(1)进行矩阵化，如式(4)所示：
(4)
式中，r=[r1,r2,…,rN]T,ρ=n+ω，n=[n1,n2,…,nN]T，ω=[ω1,ω2,…,ωN]T。
再计算ρ的自相关值Rρ，如式(5)所示：
Rρ=E(n+ω)(n+ω)H=
EnnH+EnωH+EωnH+EωωH
(5)
由于ω是零均值的高斯白噪声变量，且方差为σ2，式(5)可转换成
Rρ=nnH+σ2I
(6)
对式(6)两边乘以矢量n，可得
(7)
式中，
为特征向量n的特征值。在对称矩阵中，所有特征向量呈正交关系。假定e是Rρ的任意一个特征向量。由于e与n正交，对式(6)两边同时乘以e可得
Rρe=nnHe+σ2e=σ2e
(8)
比较式(7)和式(8)，不难发现Rρ的最大特征值所对应的特征向量是n。因此，如果确定Rρ，则可通过寻找最大特征值和相应的特征向量，识别NLOS。
为此，对ρ进行M次测量，并进行近似求解，便可计算Rρ：
(9)
式中，ρl为在第l次观察中的误差矢量。
为了能判断是否存在NLOS误差，先计算σ2，并与最大特征值进行比较。如果此特征值大于σ2，则存在
项，最终可确认存在NLOS误差。依据式(8)，排除最大特征值之外，其他所有特征值应等于σ2。
然而，由于采用式(9)计算Rρ，而不是利用精确的数学式计算，特征值呈随机性、非常数特性。因此，需要一个算法计算Rρ的最大特征值，并分析该特征值内是否存在NLOS项。为此，先引用定理1。
定理1：可利用Marceko规则[10]描述自相关矩阵的特征值。Marceko规则定义了特征值概率密度函数(Probability Density Function, PDF):
(10)
式中，γ表示观察数与抽样率，其控制Marceko分布统一特性，且
(11)
此定理的证明过程可参见文献[10]。
然而，直接计算式(10)的累加分布函数(Cumulative Distribution Function, CDF)是非常复杂的。当γ接近1时，可利用式(12)计算式(11)的CDF。
Fλ(λ)=1-e-αλ
(12)
式中，α为控制参数。
假定λi为Rρ的特征值，且i=1,2,…,N。对N个特征值进行排序，可建立离散函数：
(13)
式中，λ1<λ2<…<λN。
依据式(12)可知，通过控制参数α调整式(12)函数。为此，最初，先对控制参数α进行猜测，然后，再采用梯度下降算法优化控制参数α。据此，最初，令控制参数α的初始值为零，然后，定义式(14)和式(15)的变量：
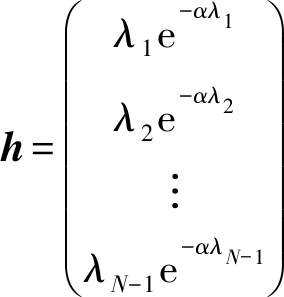
(14)
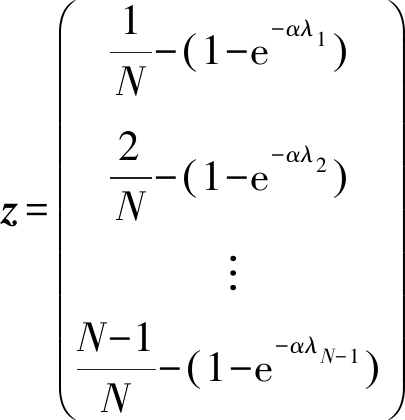
(15)
假定δ表示猜测参数α所导致的误差，其定义如式(16)所示：
δ=[hTh]-1hTz
(16)
然后，将此误差加入控制参数α，再代入式(15)，重复此过程，直到控制参数α收敛于最终值：
α←α+δ
(17)
接下来，定义σ2小于预定阈值Γ的概率τ：
τ=
(18)
将式(12)代入式(18)，便可计算预定阈值Γ，如式(19)所示：
(19)
E-NIL算法的目的就是识别NLOS误差。具体过程如下：先计算Rρ的特征值，并依据式(13)进行排序，然后调整式(12)，再针对任意τ值，并依据式(19)计算预定阈值Γ。最后，判断如果最大特征值大于Γ，则存在NLOS的概率为τ。
综上所述，从N个基站中分辨哪些基站与MS间通信存在NLOS误差的过程，如算法1伪代码所示，本文将其命名NLOS Finder算法。假定λ是包含Rρ矩阵的所有特征值矢量、υ是最大特征值所对应的特征矢量，而引用τ表示检测NLOS误差的概率。
算法1的步骤为：第一步，对所有特征值进行排序，形成式(13)，然后依据式(12)计算α值；第二步，依据式(19)计算阈值Γ；第三步，将阈值Γ与λN值进行比较，如果Γ小于λN，则将最大特征值的下标数赋予NSN,否则为零。由此得到算法1的伪代码为：
输入：λ,τ,υ
输出：NSN
过程NLOS Finder(λ,τ,υ)
步骤1：F←sort(λ)
步骤2：α←fit function(12) to F
步骤3：Γ←equation (19) using α
步骤4：if(Γ>λN)
NSN←index of maximum (υ)
else
NSN←0
end if
返回NSN
结束过程
2.2 基于NLOS识别的定位
先获取N个BS的观测数据。假定
表示第i个BS所观察的测距数，而S表示N个BS的位置集，且第j个BS的位置表示为(xj,yj)。
先利用LS算法估计MS位置，且初始估计的位置表示为(x′,y′)，然后依据(x′,y′)和式(9)计算Rρ。再计算λ和υ。
然后，执行算法NLOS Finder，即NSN←NLOS finder (λ,υ,τ)。再判断NSN是否为零。如果NSN等于零，则退出算法。否则，就相应地将它从S内删除，剔除NLOS误差，再形成
最后，再依据
的数据，并利用LS算法，估计MS的最终位置。整个定位过程伪代码(快速定位算法伪代码)为：
输入：
输出：MS的定位点
过程
while ever do
步骤1：Rρ←equation (9) using (x′,y′)
步骤2：λ←Eigenvalue(Rρ)
步骤3：α←fit function (12) to F
步骤4：υ←Eigenvector(Rρ)
步骤5：NSN←NLOS finder(λ,υ,τ)
if(NSN==0) then exit while
else
eliminate the i station in S,S′←S\i
end if
end while
返回
返回过程
3 性能仿真
3.1 仿真环境
利用Matlab 7.1软件建立仿真平台，分析E-NIL性能，并选择LS[11], RWGH[12]和SRNI[8]算法作为参照，比较它们的均方根误差性能。均方根误差(Root Mean Square Error, RMSE)定义如式(20)所示：
(20)
式中，
表示在第i轮实验中所估计的移动位置，Mc表示总的Monte Carlo实验次数。
在仿真实验中，总运行的Monte Carlo次数Mc=3 000。移动基站MS位于10 000 m×10 000 m内，且基站MS的位置为(200 m,-400 m)，且τ=0.95。
3.2 实验一
首先分析噪声标准方差对RMSE的影响，且σ从0至100 m变化，步长为10 m，假定第一个NLOS误差为500 m。基站数N=15，实验数据如图1所示。
图1 RMSE随σ的变化曲线
从图1可知，σ的增加提高了RMSE值，其原因是噪声方差值的增加，加大测距误差。与LS算法和SRNI算法相比，提出的E-NIL算法的RMSE得到有效控制。这些数据表明：提出的E-NIL算法能够有效地消除NLOS误差，提高了定位精度。
3.3 实验二
实验二分析存在NLOS误差的基站数m对RMSE的影响。σ=10，基站数N=20，且m从1至12变化。实验数据如图2所示。
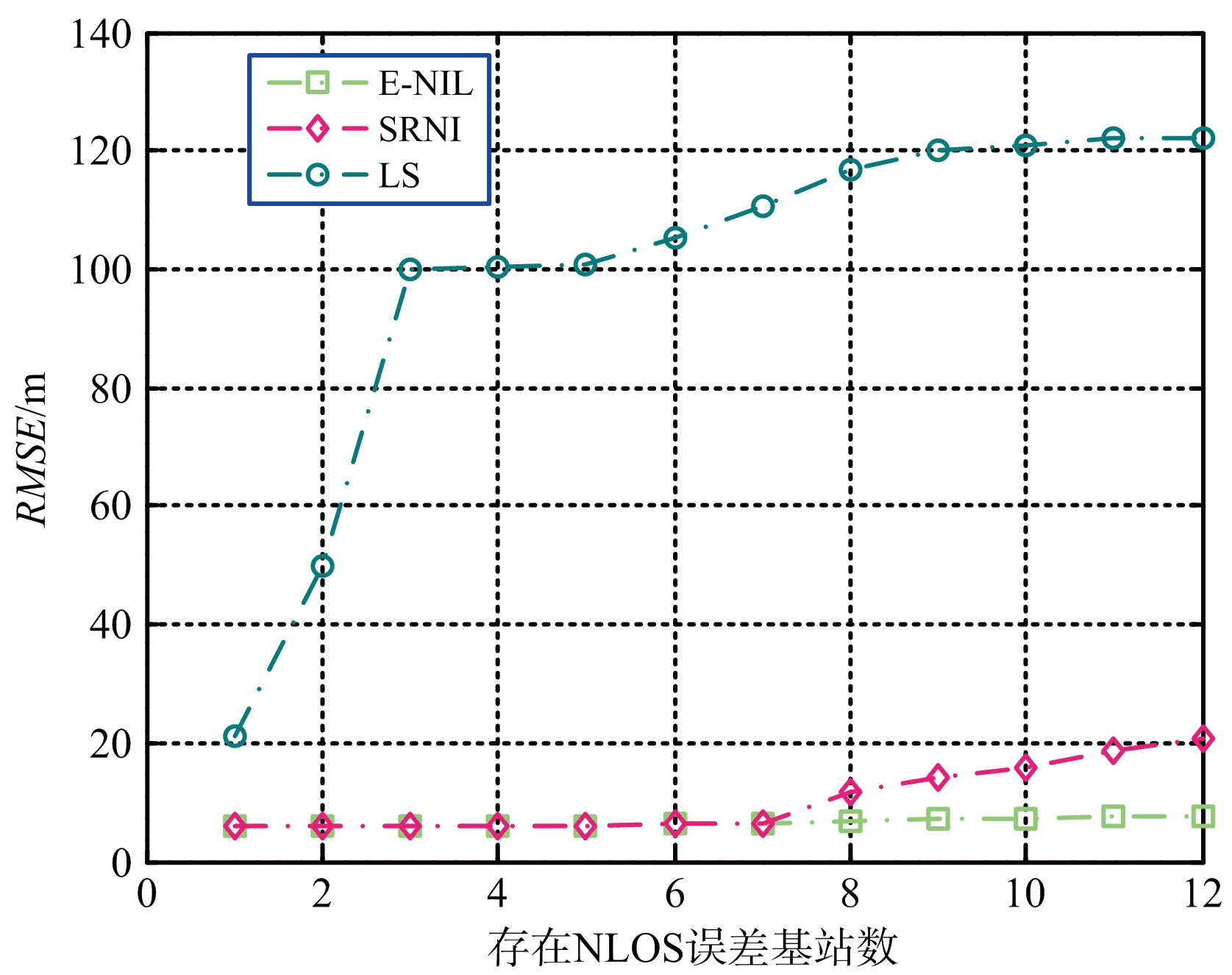
图2 RMSE随存在NLOS误差的基站数的影响
从图2可知，存在NLOS误差的基站数m对RMSE存在影响。当m较少时，SRNI和E-NIL算法的RMSE相同，但随着m的增加(m>7)，SRNI算法的RMSE迅速增加，而E-NIL算法的RMSE并没有提高，保持较稳定。与SRNI和E-NIL算法相比，LS算法的RMSE并没有得到控制，这也说明LS算法并没有消除NLOS误差的影响。
3.4 实验三
本次实验分析算法的复杂度。执行算法的电脑参数为：Inter Core i5, 2.4 GHz CPU。基站数N从5至30变化，噪声方差σ=10 m，实验数据如图3所示。
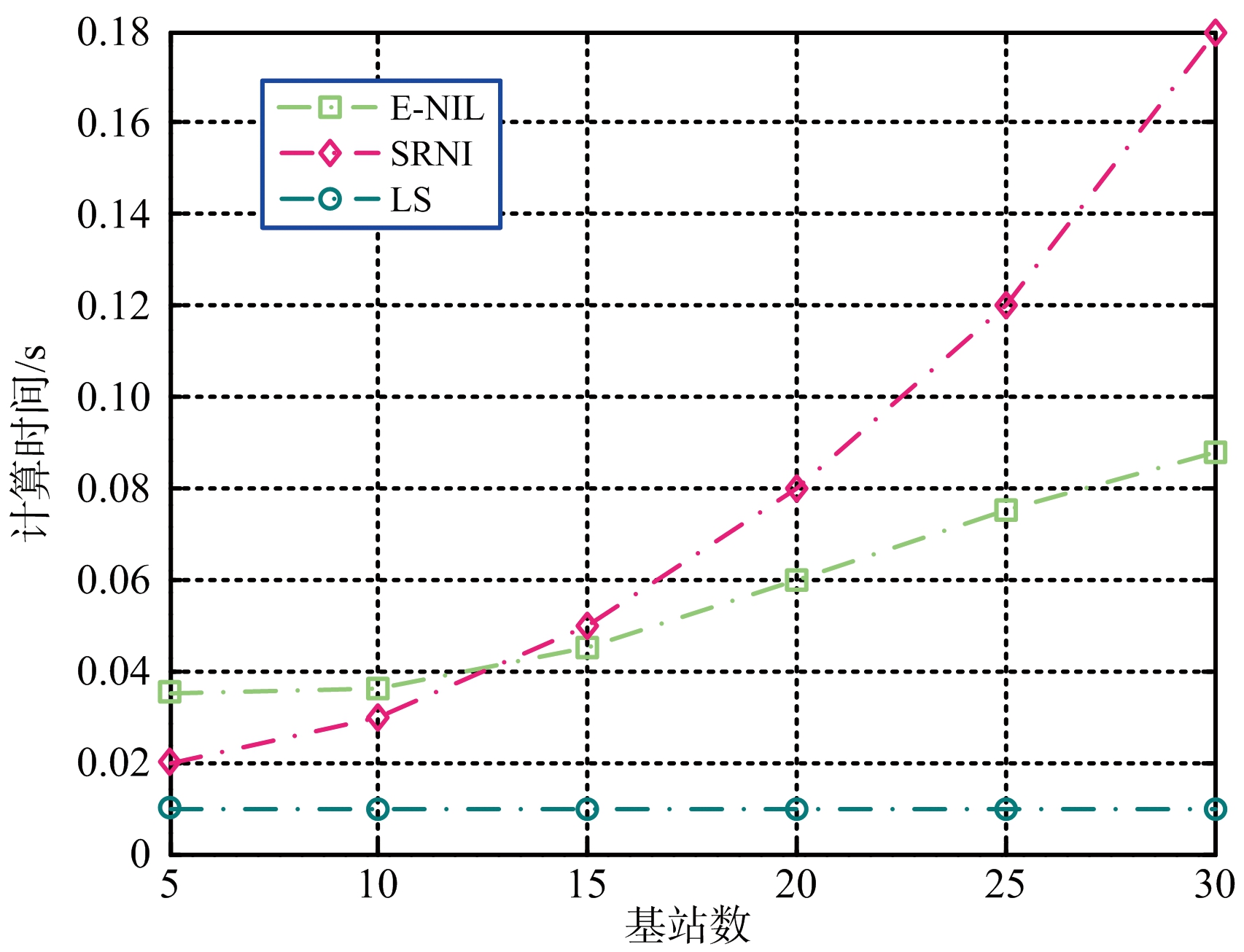
图3 算法的复杂度
从图3可知，LS算法的计算时间最低，远低于E-NIL和SRNI算法。其原因在于：LS算法简单，其低的复杂度换来的是低的定位精度。而提出的 E-NIL算法的复杂度较高。随着基站数的增加，E-NIL算法的执行时间也迅速增加。
4 结束语
本文考虑了NLOS误差对测距的影响，并在正视NLOS误差的情况下，建立测距模型，再提出特征矢量的NLOS误差检测的定位E-NIL算法。E-NIL算法先基于最小二乘估计建立测距模型，再分析特征矢量，并搜索NLOS误差，进而剔除NLOS误差数据，从而提高定位精度。实验数据表明，提出的E-NIL算法有效地提高定位精度，并降低了算法复杂度。
[1] 江禹生,冯砚毫,管芳,等. 无线传感网非测距三维节点定位算法[J]. 西安电子科技大学学报(自然科学版), 2012, 39(5):140-147.
[2] WANG G, CHEN H, LI Y, et al. NLOS Error Mitigation for TOA-Based Localization via Convex Relaxation[J]. IEEE Trans on Wireless Communications, 2014, 13(8):4119-4131.
[3] AMIRI R, BEHNIA F, SADR M A M. Exact Solution for Elliptic Localization in Distributed MIMO Radar Systems[J]. IEEE Trans on Vehicular Technology, 2018, 67(2):1075-1086.
[4] AMIRI R, ZAMANI H, BEHNIA F, et al. Sparsity-Aware Target Localization Using TDOA/AOA Measurements in Distributed MIMO Radars[J]. ICT Express, 2016, 2(1):23-27.
[5] WILL H, HILLEBRANDT T, YUAN Y, et al. The Membership Degree Min-Max Localization Algorithm[C]∥ Ubiquitous Positioning, Indoor Navigation, and Location Based Service, Helsinki, Finland: IEEE, 2012:1-10.
[6] MIURA S, KAMIJO S. GPS Error Correction by Multipath Adaptation[J]. International Journal of Intelligent Transportation Systems Research, 2015, 13(1):1-8.
[7] AL-JAZZAR S, CAFFERY J, YOU H-R. A Scattering Model Based Approach to NLOS Mitigation in TOA Location Systems[C]∥ 55th Vehicular Technology Conference, Birmingham, AL: IEEE, 2002:861-865.
[8] ABOLFATHI A, BEHNIA F, MARVASTI F. NLOS Mitigation Using Sparsity Feature and Iterative Methods[EB/OL]. [2018-01-14]. https:∥arxiv.org/abs/1803.06838.
[9] MARVASTI F, AZGHANI M, IMANI P, et al. Sparse Signal Processing Using Iterative Method with Adaptive Thresholding (IMAT)[C]∥ 19th International Conference on Telecommunications, Jounieh, Lebanon: IEEE, 2012:1-6.
[10] JIANG Tiefeng. The Limiting Distributions of Eigenvalues of Sample Correlation Matrices[J]. The Indian Journal of Statistics, 2014, 66(1):35-48.
[11] CHAN Y T, HO K C. A Simple and Efficient Estimator for Hyperbolic Location[J]. IEEE Trans on Signal Process, 1994, 42(8):1905-1915.
[12] CHEN Pichun. A Non-Line-of-Sight Error Mitigation Algorithm in Location Estimation[C]∥ IEEE Wireless Communications and Networking Conference, New Orleans, LA: IEEE, 1999:316-320.
