0 引言
干涉合成孔径雷达(Interferometric Synthetic Aperture Radar, InSAR)是通过计算两幅配准后的SAR复图像的干涉相位差,结合地表高度和干涉相位差之间的关系,获取地表三维信息的重要遥感技术[1]。传统单频率相位解缠前提是相邻像素的绝对相位差小于π。实际就是要求待解缠的区域比较平缓,没有陡变地形。此外,单频率相位解缠算法计算方法复杂,且噪声敏感性高,误差传递现象严重。因而传统单频干涉SAR无法有效解决某些复杂地区的高程重建问题。为了实现复杂地形的DEM(Digital Elevation Model)反演,提出了多通道InSAR测量技术。
多通道InSAR测量技术[2]包括多频率InSAR测量技术[3]和多基线InSAR测量技术[4]。多频率InSAR通常选取互质的载频波段来增大高度模糊数。多基线InSAR技术则是利用不同的基线来增大高度模糊数。模糊高度数的扩大,有利于得到更为精确的解缠相位信息。
多通道干涉SAR技术发展迅速,高度重建算法种类众多。其中较为早期的一种方法是多通道最大似然估计(Maximum Likelihood Estimation, MLE)算法[5]。该算法利用干涉相位的概率统计特性直接进行高程重建,重建速度快,但受干涉通道数目、基线长度、工作频率、相干系数的影响特别大,抗噪能力弱,在相干系数低的区域需要增加很多的通道数来保证精确度[6-7]。为了解决MLE中过高的通道数要求和重建精度的矛盾,基于Markov随机模型的MRF-MAP(Markov Random Field Based Maximum a Posteriori Estimation)算法被提出来。该方法利用Markov模型作为先验分布,通过估计每个像素的超参数实现高程重建。至今,有许多人提出了改进的MAP算法[8-9]。虽然MRF-MAP提高了反演精度,但该方法需估算每一点的超参数,运算时间过长,设备要求过高[10]。相比之下,ML算法在计算速度上拥有绝对的优势,适合做大数据量的数据处理。但ML估计结果噪声点和噪声聚集成斑块的现象严重,本文提出了ML估计结果噪声斑块去除方法。具体方法是:首先利用聚类分析[11](CA)思想去掉解缠结果中大量出错区域对应的模糊类;再利用变长滑动加权窗口判定并去除噪斑,得到正确的解缠相位。
1 基于MLE的双频干涉高程重建方法
双频系统可以通过两个互质的频率增大高度模糊数,从而实现更复杂地形的高程反演。在基于MLE的高程重建算法中,高程重建问题被转化成了找到高程值h(p)使似然函数达到最大化的问题。
在单通道InSAR中,对于图像的每个像素点(i,j),缠绕的干涉相位φ′与地表高程信息之间的关系为
(1)
式中,λ为载频波长,〈·〉2π为“模2π”处理操作,μ为一个比例系数,由InSAR系统收发模式以及飞行参数确定:
(2)
式中,B⊥为垂直斜距平面的基线分量,r0为该点斜距,θ为该点斜视角。
根据InSAR干涉相位的统计特性,得到干涉相位的概率密度统计特性:
f(φ|φ′)=

(3)
将式(1)代入式(3)可以得到测量干涉相位与高程信息之间的概率密度分布函数:
f(φ|h)=
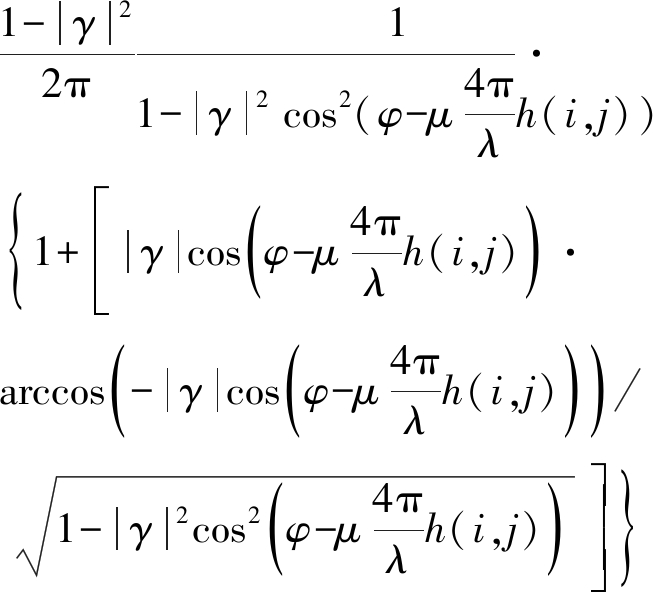
(4)
式中,γ称作干涉图像的相关系数:
(5)
测量所得的干涉相位φ已知。根据式(4)可知 f(φ|h)随着h而变化。只要观测到了干涉图上每个像素对应的φ,式(4)就变成了统计信号处理中的似然函数,对f(φ|h)进行估计便可得估计的高程![]()
(6)
图1给出了给定观测相位和相干系数情况下该似然函数的波形。由图可知,该函数的最大似然解的周期为![]() 有无穷多个:
有无穷多个:
(7)
为了解决无数个最大似然解的问题,增加独立的观测相位,采用双频干涉技术,式(4)中的各个变量加上角标则得到了各个通道对应的似然函数。此时,总的似然函数变成
![]()
(8)
利用联合最大似然估计方法进行高程重建,多频率最大似然估计高程值如下:
![]()
![]()
(9)

(a) 通道1似然函数
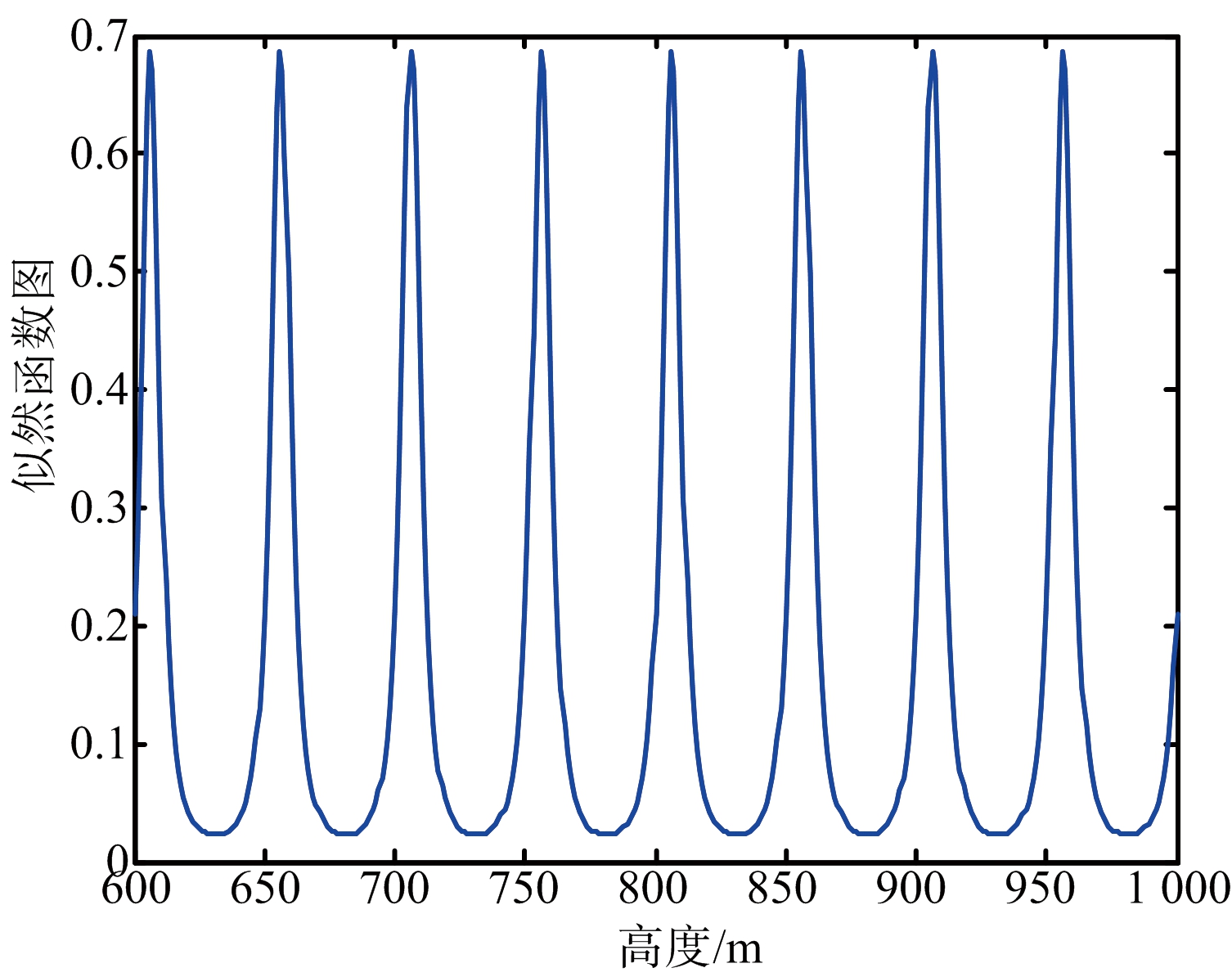
(b) 通道2似然函数

(c) 通道3似然函数
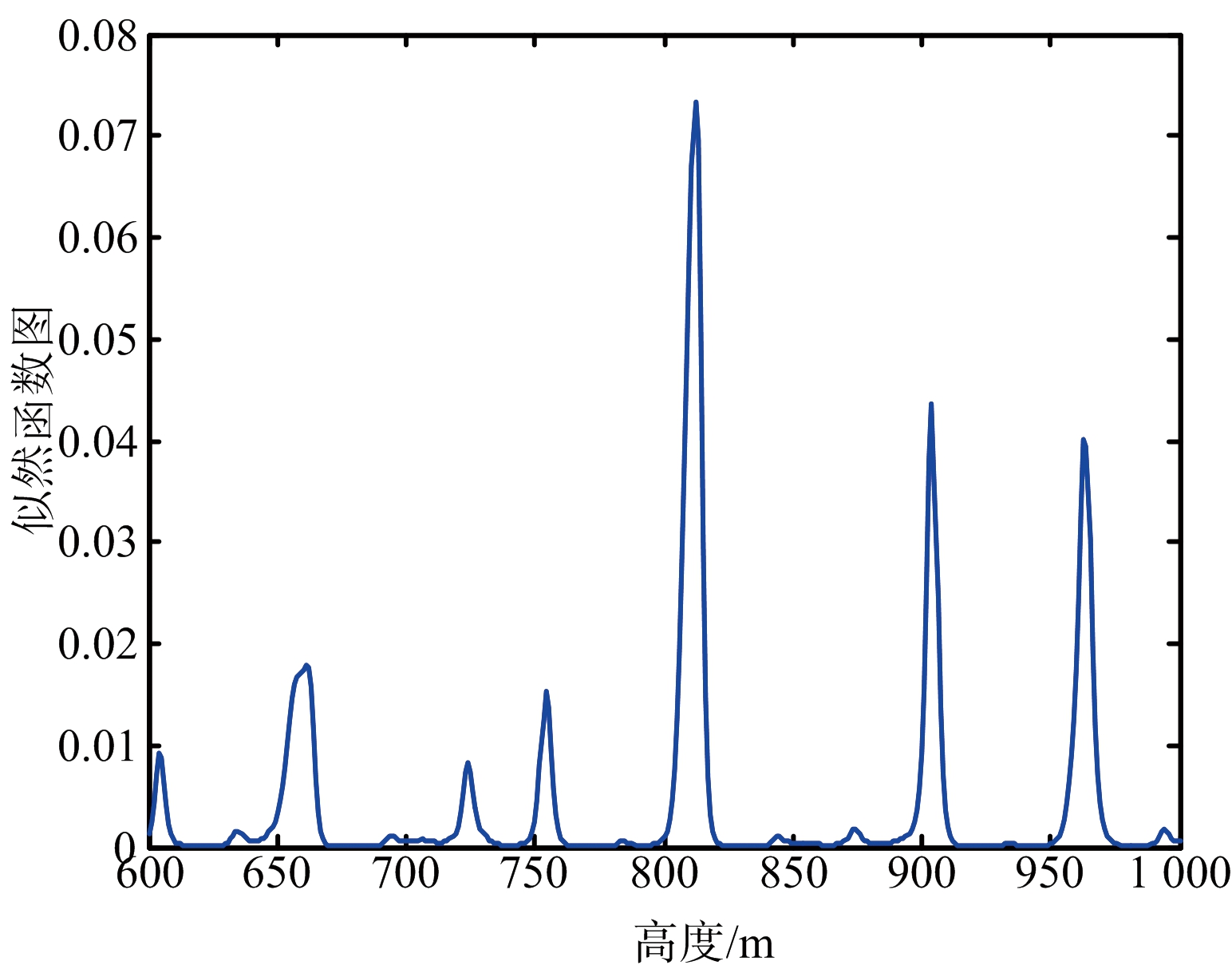
(d) 多频干涉系统似然函数
图1 单频似然函数和多频似然函数示意图
2 MLE重建结果噪斑去除方法
MLE的双频高程重建算法鲁棒性不强,得到的结果中有单点噪声和噪声斑。由文献[6]可知,这些噪点高程都与周围点的高程相差很大。此外,若高程范围选择得当,MLE重建结果中噪声像素所占比例较小。基于这两点,本文提出了一种噪声斑块去除方法。能在保证处理效率的同时,能够提高重建精度。具体去噪方法分为两个部分。
2.1 变邻域错点标记
根据文献[11],将像素的模糊矢量定义为该像素在各个干涉通道下的模糊数所组成的矢量。各个干涉通道下p像素的模糊数为
(10)
式中,⎣·」表示下取整运算。这样,p像素所对应的模糊矢量即为
V(p)=[n1(p),n2(p),…,nk(p)]
(11)
根据聚类分析的思想,将高程值按高度模糊数进行聚类分组。通过执行以下几个步骤来进行错点标记:
1) 构建初始标记矩阵,大小与图像大小相同,初始值均为1。
2) 根据目标地段高度范围粗略计算出高度模糊区间,区间之外的点判定为错点,标识符标记为0。标记出明显出错的解缠坏斑。
3) 若某一个模糊类所对应的像素个数低于预期比例阈值,判定为噪声并将该分组内的像素标识符标记为0。
4) 通过目标点高程与3×3邻域内重建正确点的高程均值的归一化差值来判断该点是否为噪声点。将噪点像素的标记置为0。
当相邻的一片像素点均为坏点时,3邻域均值判定噪点的方法不再起作用。鉴于噪声斑的大小不一,采用可变邻域的判别器来判定突变噪声斑,从而达到将连城小片的噪声斑进行标记的目的。
2.2 非均匀加权滤波
前面的步骤已经将误差较大的错点标记出来。传统均值滤波会将错点带入到加权中使得高程误差变大。此外,MLE解缠结果中解缠错误的部分区域也含有变化的高程信息,解缠出错的区域只是表现为该区域的整体抬高或者降低,不能将错点的像素权值全部设为0,因而采用比例加权的方式计算错点的加权系数。
假设U(p,k)是以p为中心,可调控值k作为宽度的方形邻域。p′是在U(p,k)内除了p点之外的邻域像素。
解缠正确的点的均值为
(12)
解缠错误的点的均值为
(13)
从而计算出错点的归一化加权系数为
(14)
得到错点修正DEM为
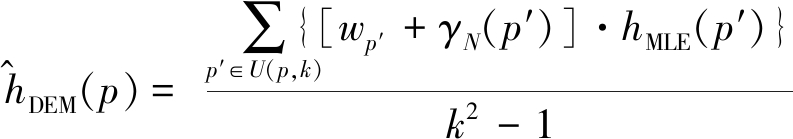
(15)
1) wp′为领域内各点的第一个加权系数。在U(p,k)内,若被标记为解缠错点,则其值为0,若被标记为正确的点,其值为1。
2) γN(p′)为邻域各点的第二个加权系数,将其权值设定为U(p,k)邻域内解缠正确的像素的高程均值和解缠出错像素的高程均值之比。
综合以上两个部分,通过选取合适的模糊类阈值,调节合适的标记窗口和非均匀加权滤波窗口来去除噪声。窗口选择时可以利用小窗口方法去掉斑点噪声,利用大窗口去除噪声斑块。而且由于本文方法不是将带有高程信息的噪斑完全丢掉,如此便可以在保证解缠效率的同时提高重建精度。
3 实验结果与分析
实验分为两个部分,分别是建模验证(3.1节)和实测数据验证(3.2节)。建立的仿真模型为一个城市地形和一个带有悬崖的真实DEM模型,适合验证双频重建算法。仿真模型中的干涉图均为根据舍选法[12]生成的干涉图。实测数据为机载C/X双频干涉SAR数据,比较适合验证双频干涉算法。实验主机平台内存为8 GB,CPU主频为 3.2 GHz。仿真代码为Matlab代码。
3.1 仿真数据处理
仿真数据的参数如表1所示。本节均采用该参数进行仿真。第一个模型最大高程差为250 m,两个通道的相邻像素的相位差分别可达到34.79π和19.58π,适合用双频干涉算法进行处理。第二个模型为美国Isolation Peak的真实地形仿真模型。峭壁的高度差可达137 m。对应的两个通道相邻像素的相位差可达19.07π和10.73π。对模拟数据的处理结果用误差图和归一化均方误差σ2来进行分析。σ2由如下公式给出:
(16)
式中,Fig为每个像素构成的图像,![]() 为点p的高程重建值,hp为点p的真实高程。
为点p的高程重建值,hp为点p的真实高程。
表1 仿真模型主要参数
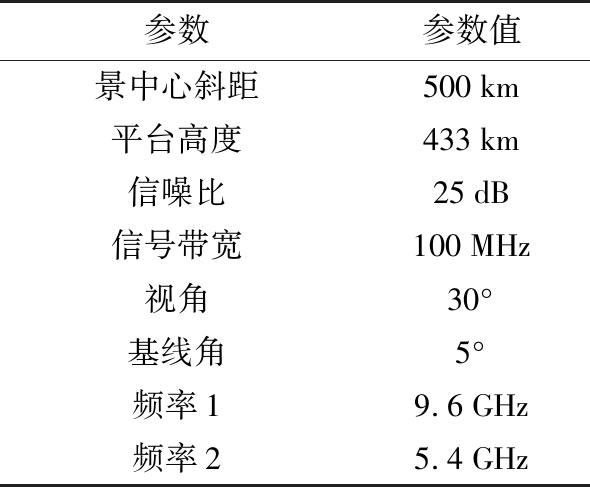
参数参数值景中心斜距500km平台高度433km信噪比25dB信号带宽100MHz视角30°基线角5°频率19.6GHz频率25.4GHz
3.1.1 仿真城市地形
建立的仿真地形DEM投影图如图2(a)所示。其中三棱柱形高度为250 m。舍选法所得的两个通道的干涉图形如图2(b)、图2(c)所示。

(a) 仿真地形投影图
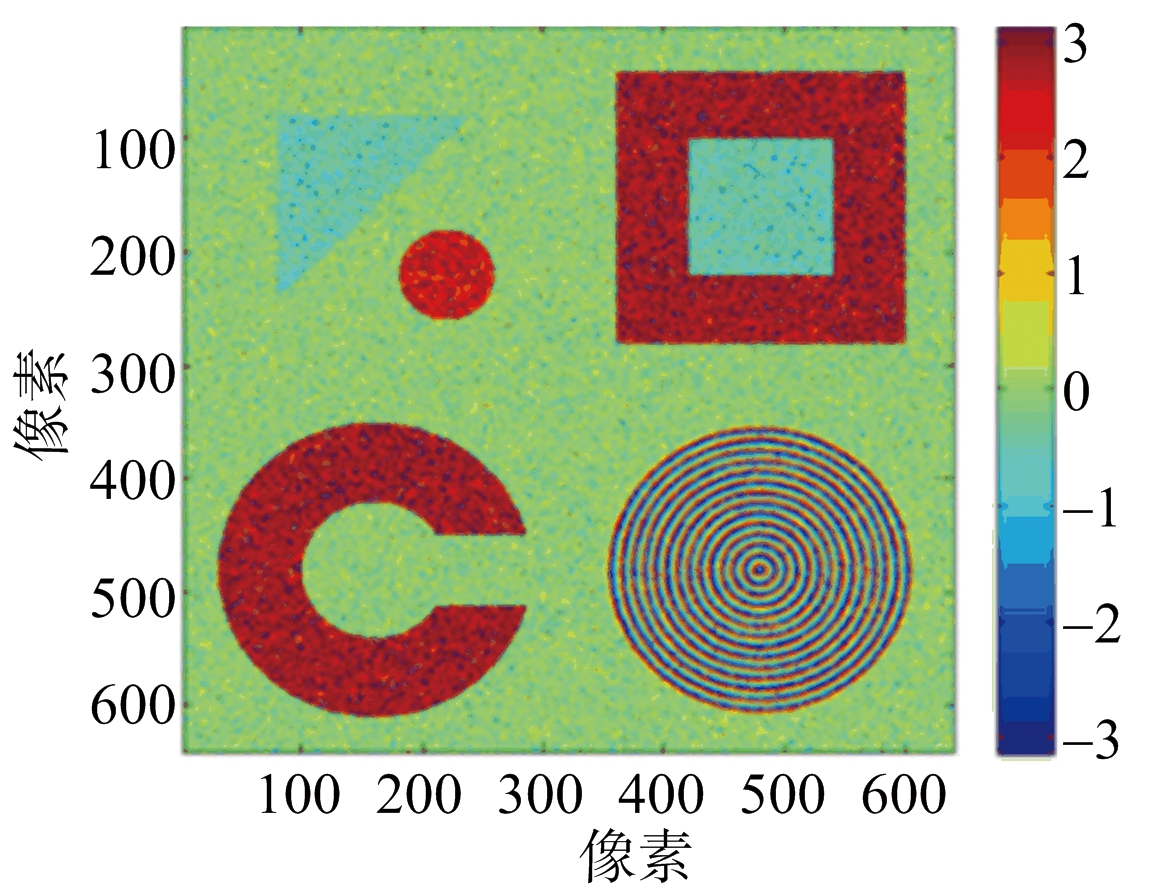
(b) f=9.6 GHz干涉图
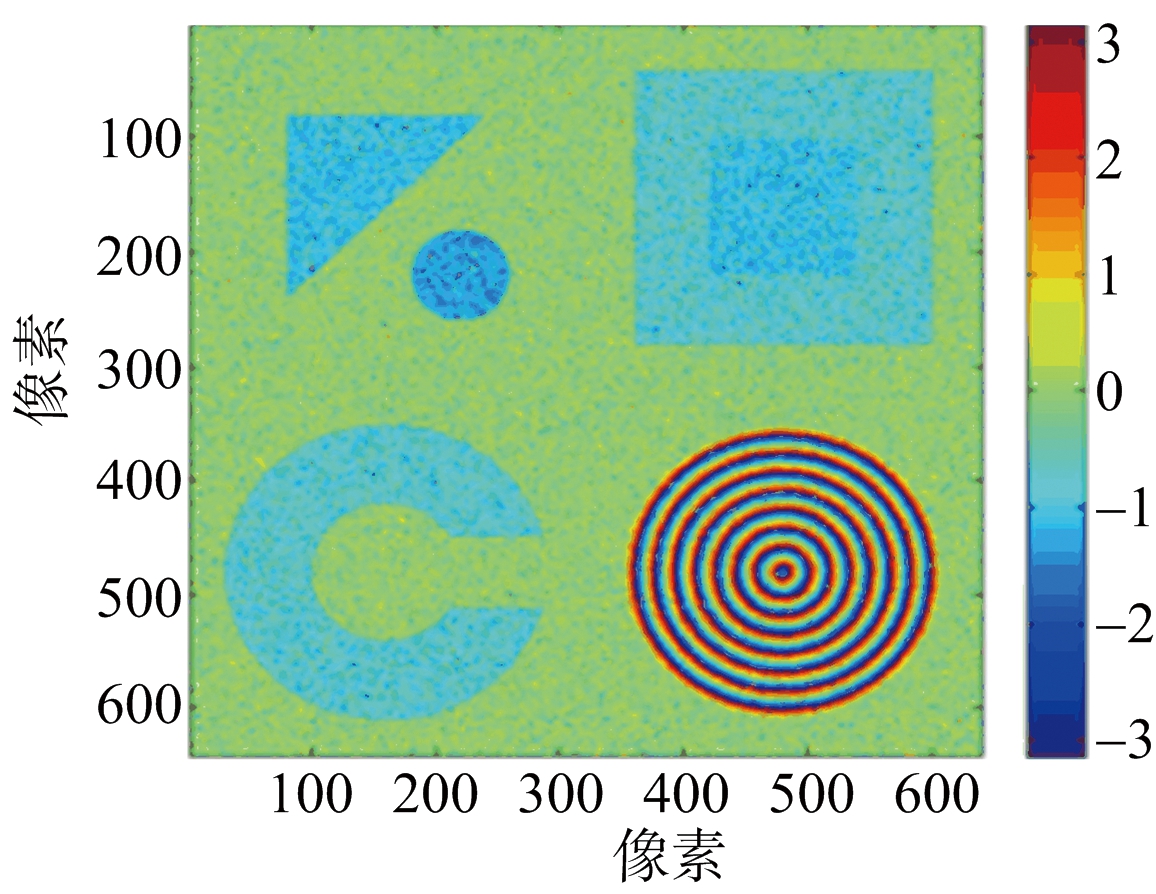
(c) f=5.4 GHz干涉图
图2 仿真城市地形数据
反演所得MLE结果如图3(a)所示,可知MLE结果中含有大量的噪斑。利用本文算法去噪点所得到的结果如图3(b)所示,二次去噪斑结果如图3(c)所示。从结果看出,重建的高程基本将MLE结果中的噪斑去掉。
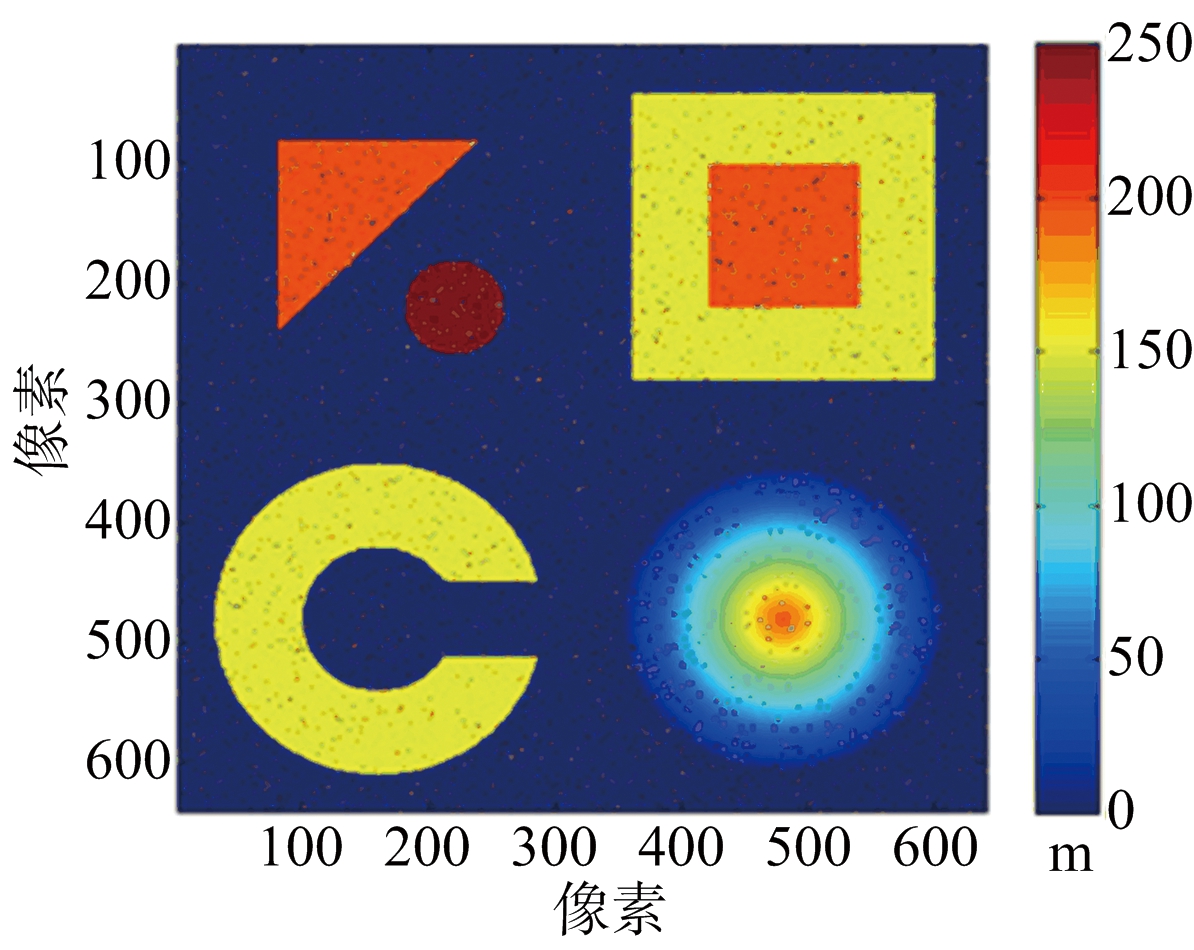
(a) MLE重建结果

(b) 噪点去除结果
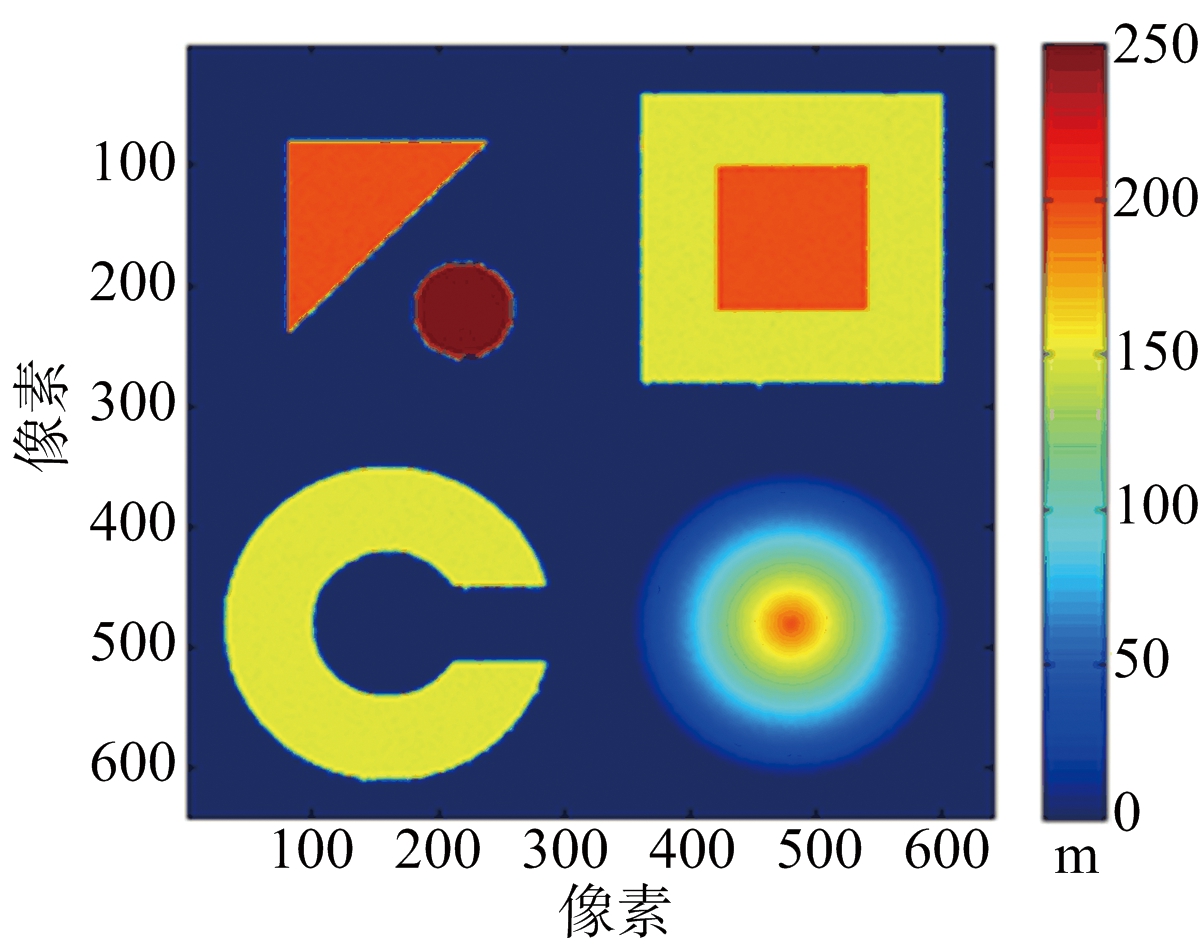
(c) 噪斑去除结果
图3 仿真城市地形去噪斑

(a) 原始DEM投影
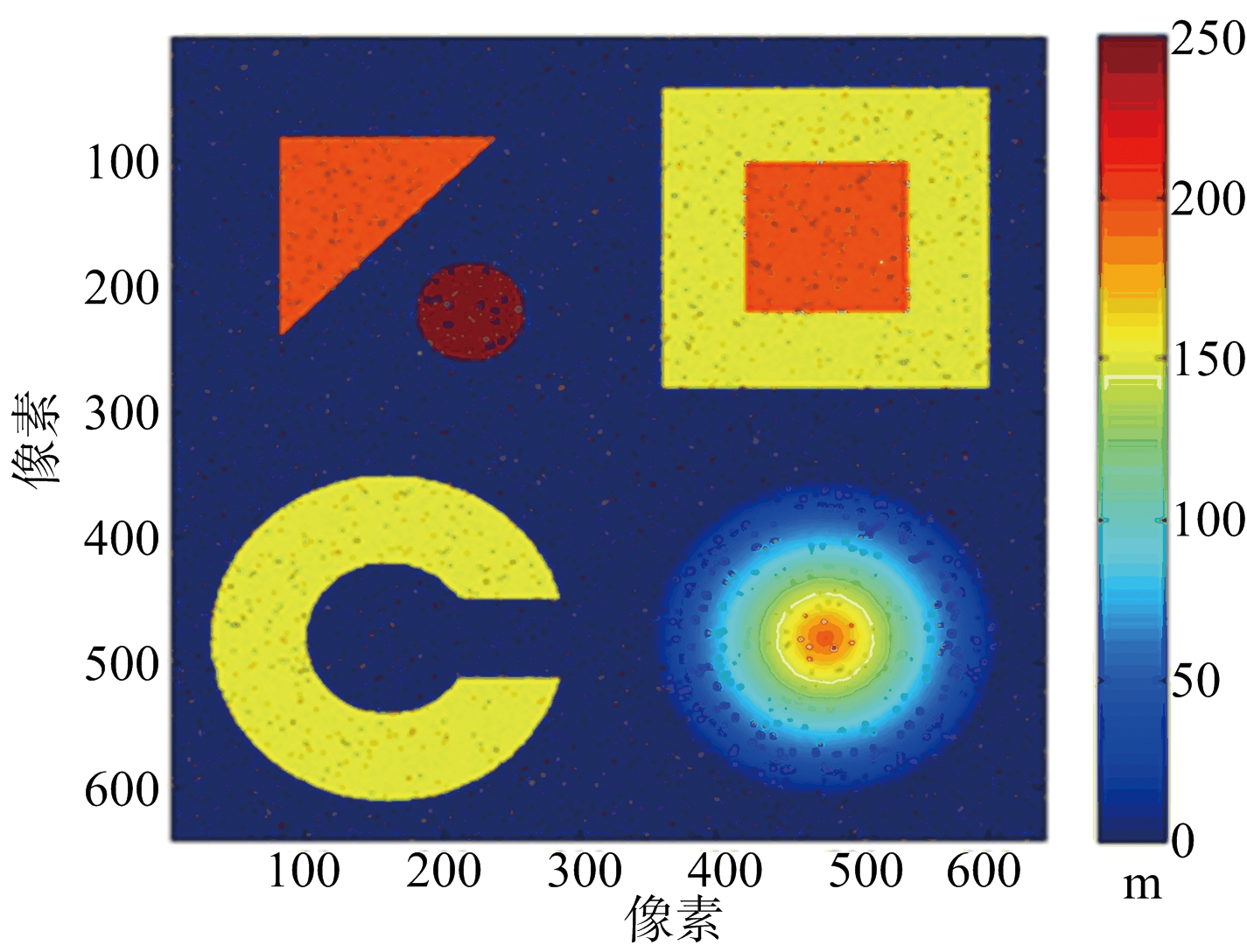
(b) MLE重建DEM投影

(c) MAP重建DEM投影
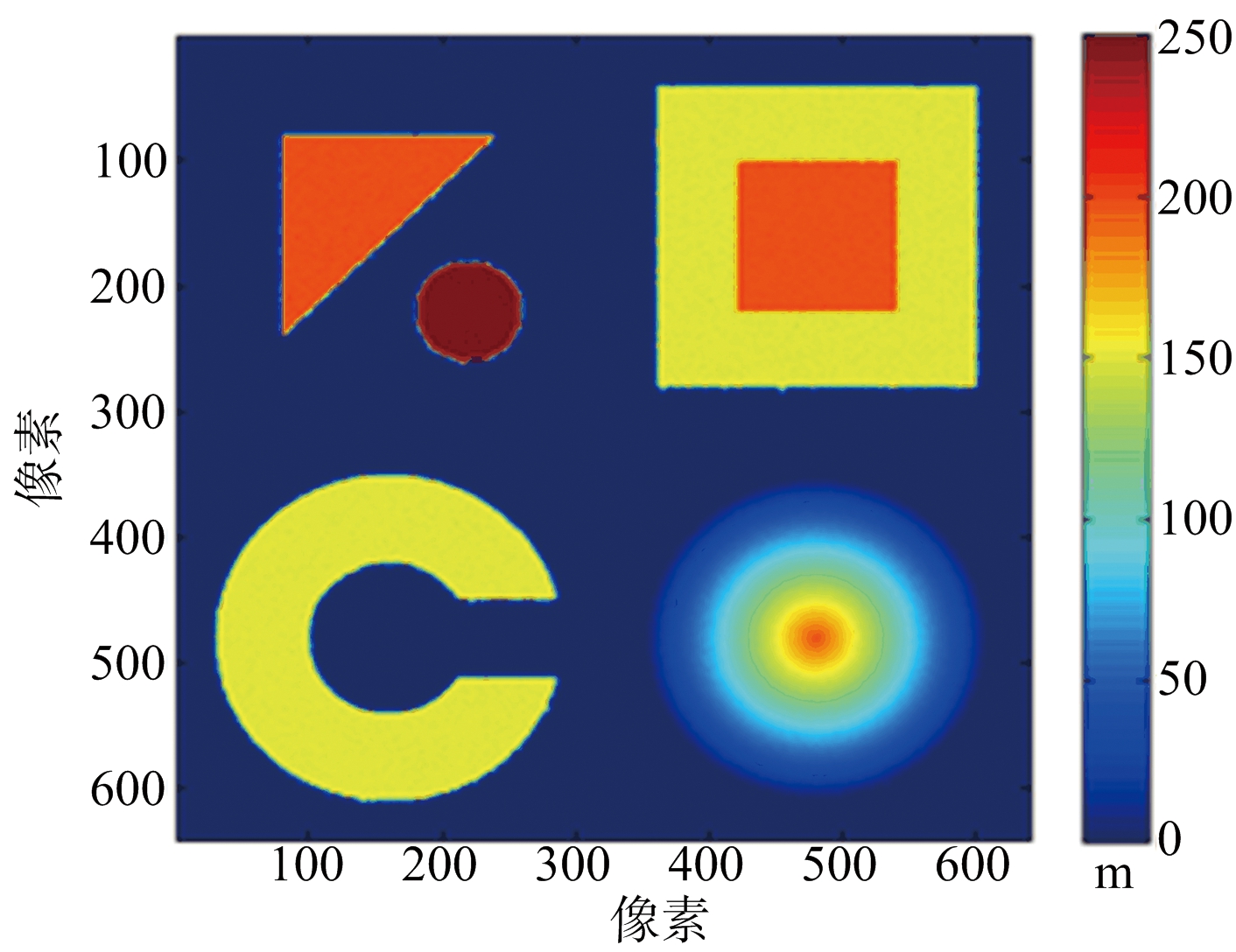
(d) 本文重建DEM投影
图4 仿真城市地形各种重建算法DEM与原始DEM对比
图4分别列出原始DEM、MLE算法DEM、MAP估计DEM、本文算法DEM来进行对比。3种重建算法的误差图分别如图5(a)、图5(b)、图 5(c)所示。统计的各种重建方法归一化均方误差如表2所示。重建耗时上:MLE约13.53 s,本文方法约15.61 s;MAP估计达到1 493.14 s,是本文算法的将近100倍。从归一化误差来看,MLE算法最差,本文方法和MAP估计相近。
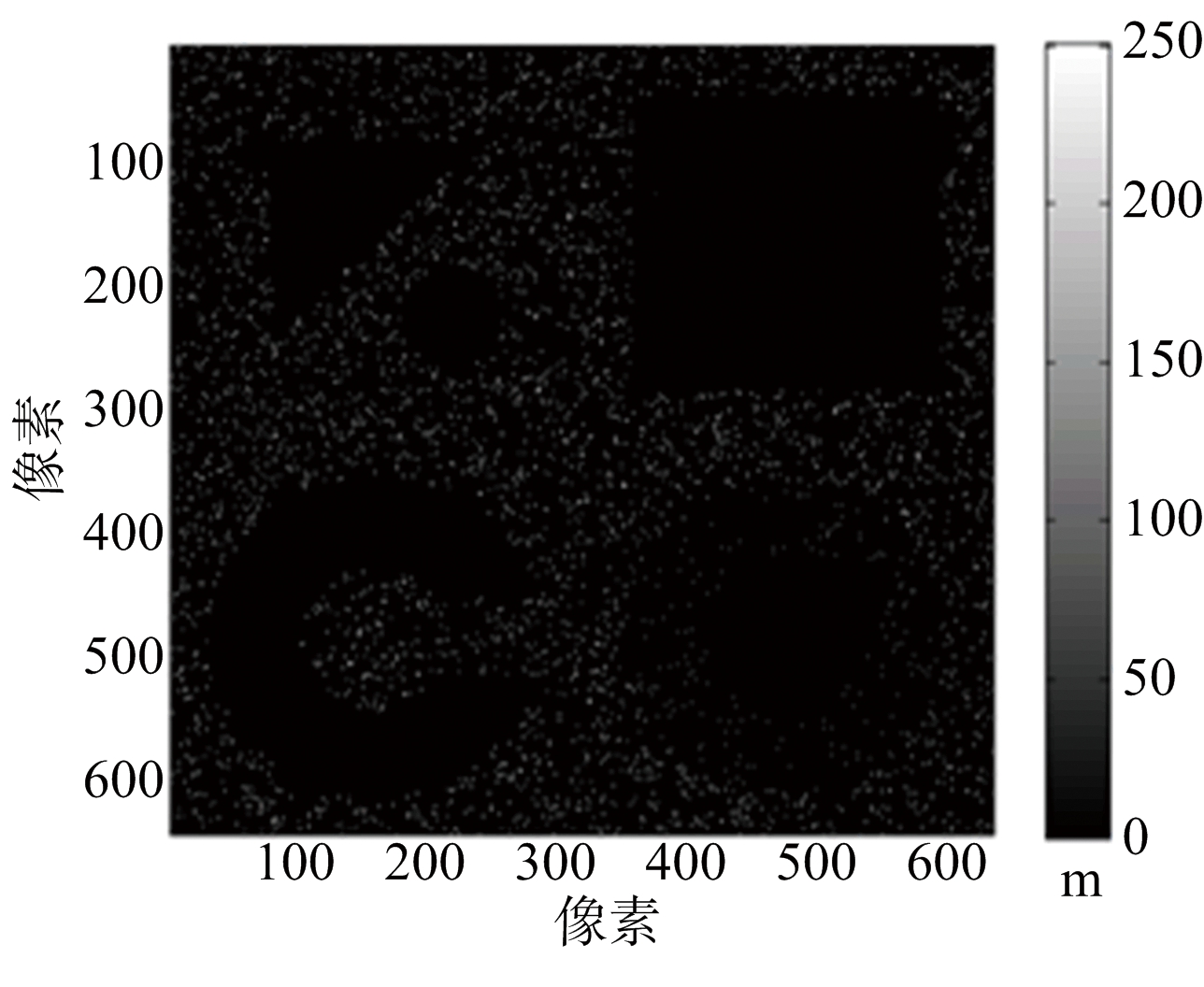
(a) MLE重建误差图
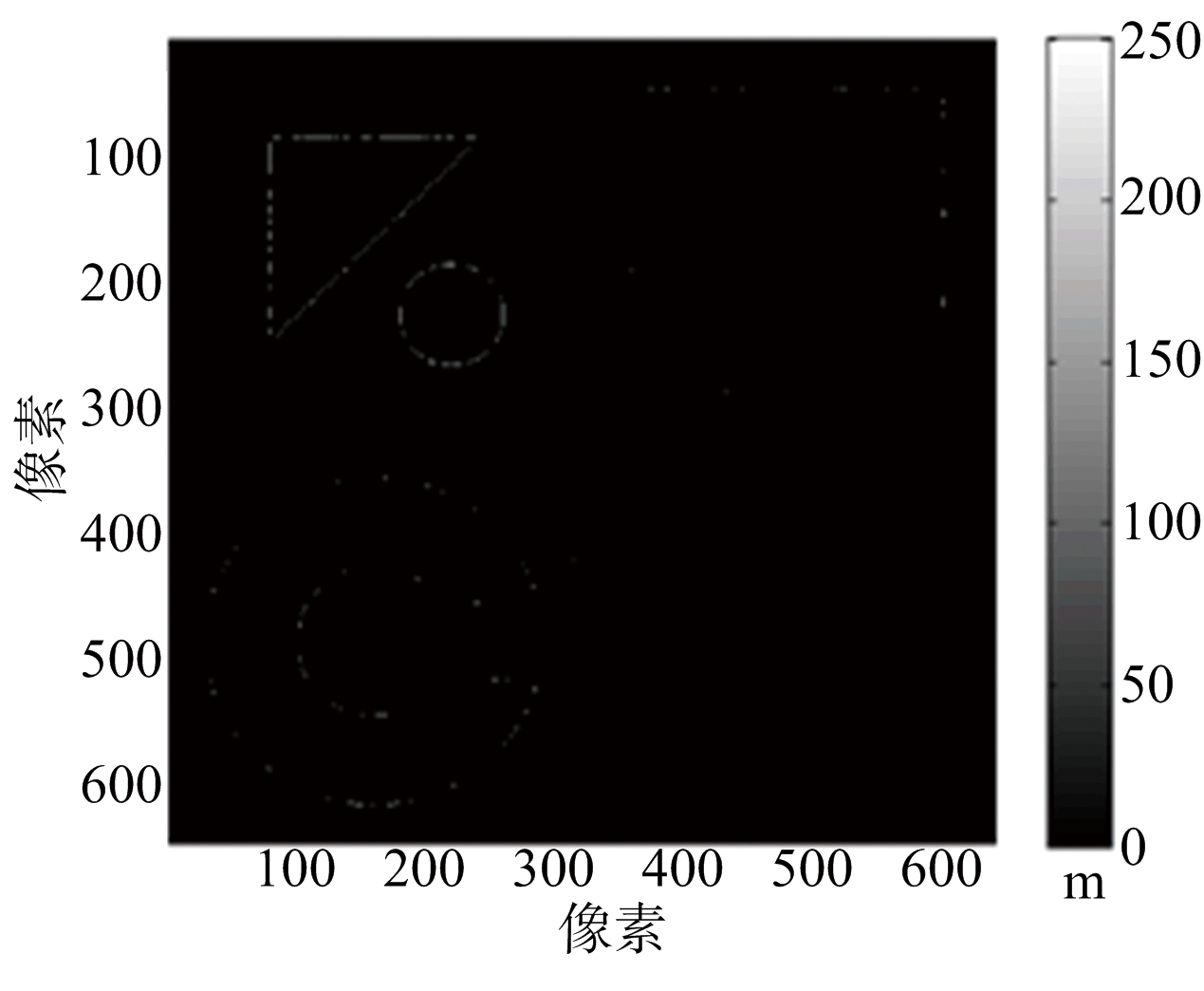
(b) MAP重建误差图
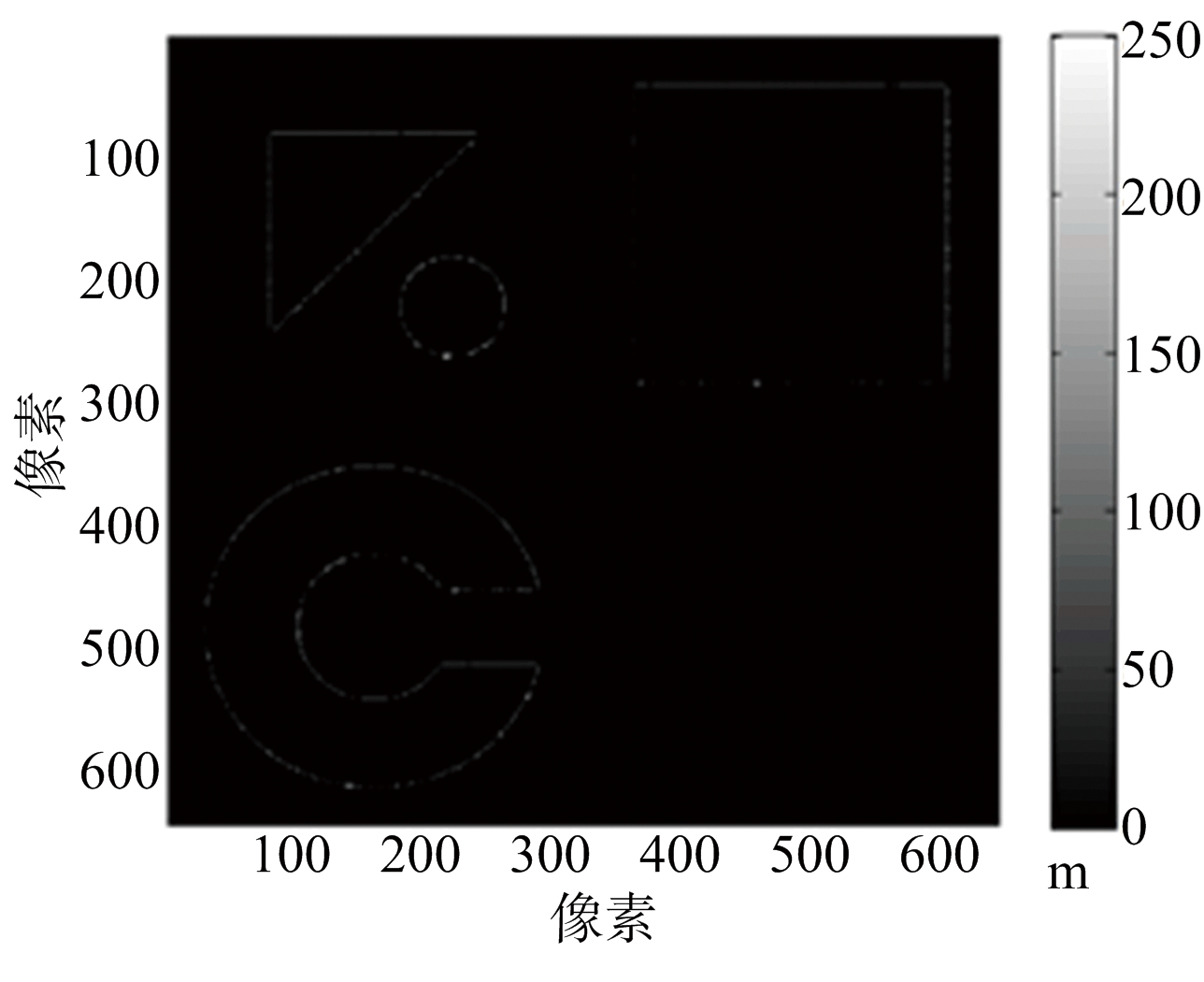
(c) 本文方法重建误差图
图5 仿真城市地形各种重建算法误差图
表2 仿真城市地形重建算法归一化均方误差表

重建方法归一化均方误差MLE0.3268MAP0.0056本文方法0.0064
图6给出各种算法重建结果与原始DEM三维对比。该图证明本算法在精度上表现较为优异。

(a) 原始DEM
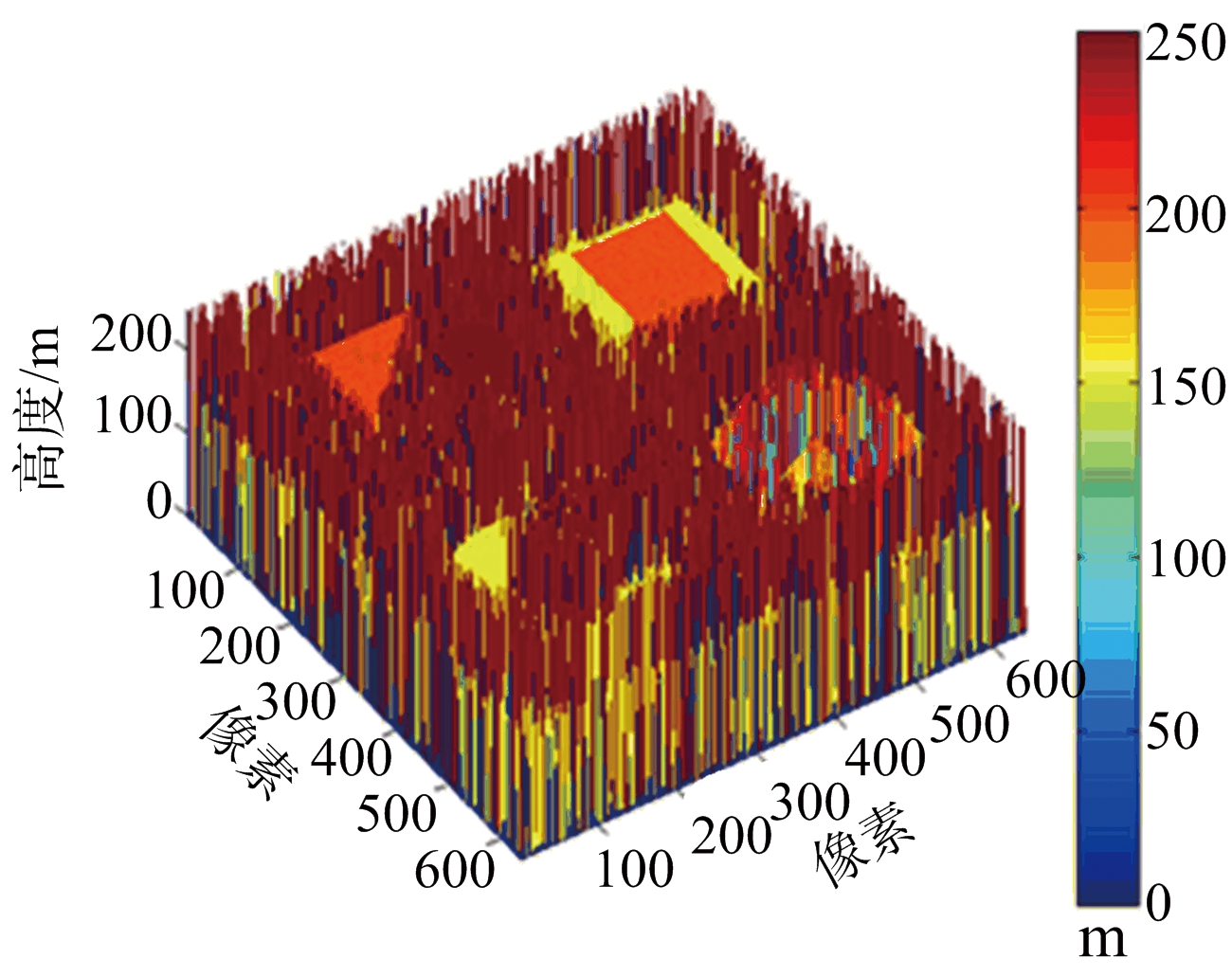
(b) MLE重建DEM

(c) MAP重建DEM
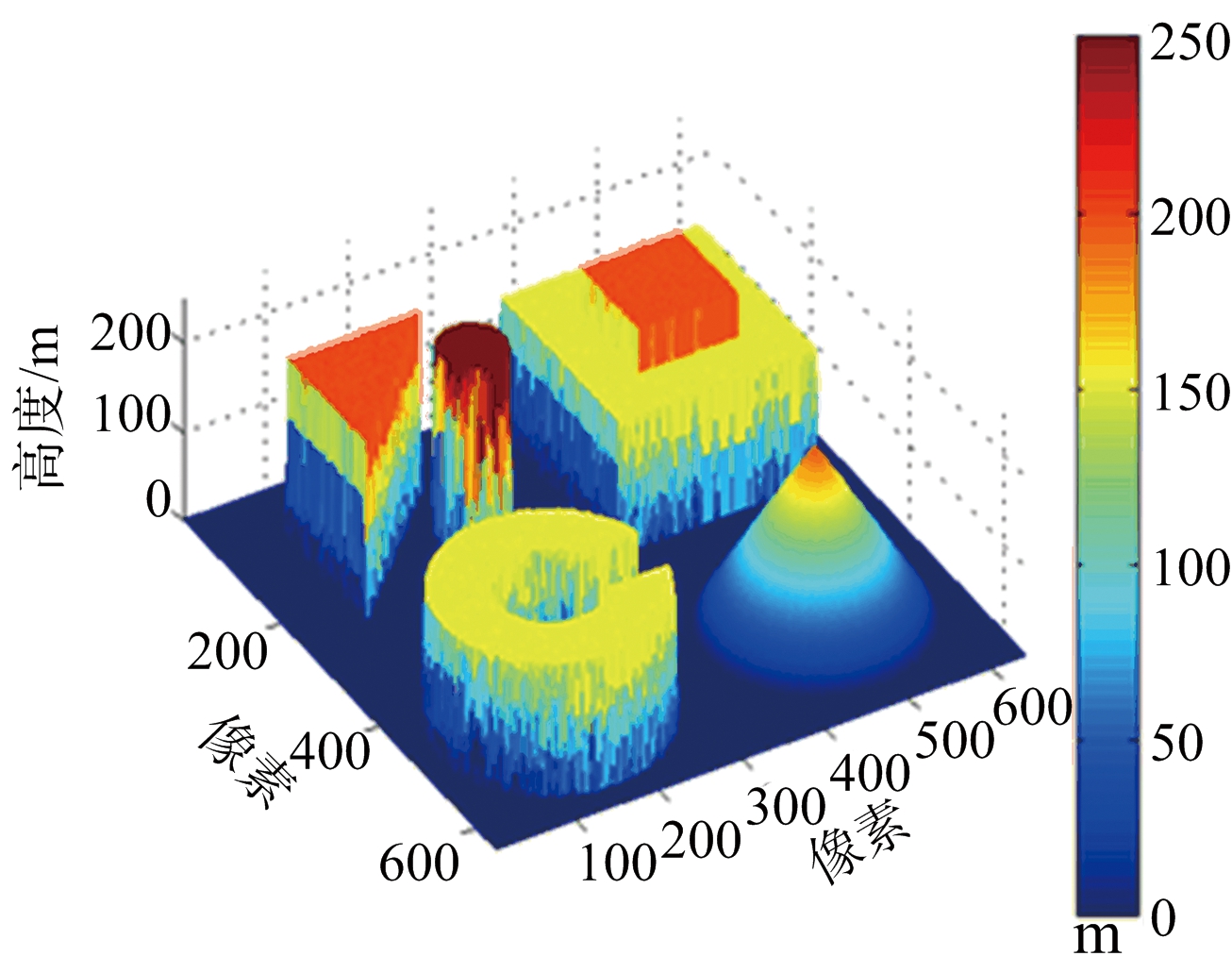
(d) 本文算法重建DEM
图6 各重建结果三维视图
3.1.2 仿真真实地形
美国Isolation Peak国家公园DEM仿真参数如表1所示。图7(a)为该场景的DEM投影图。两个通道的干涉图如图7(b)、图7(c)所示。
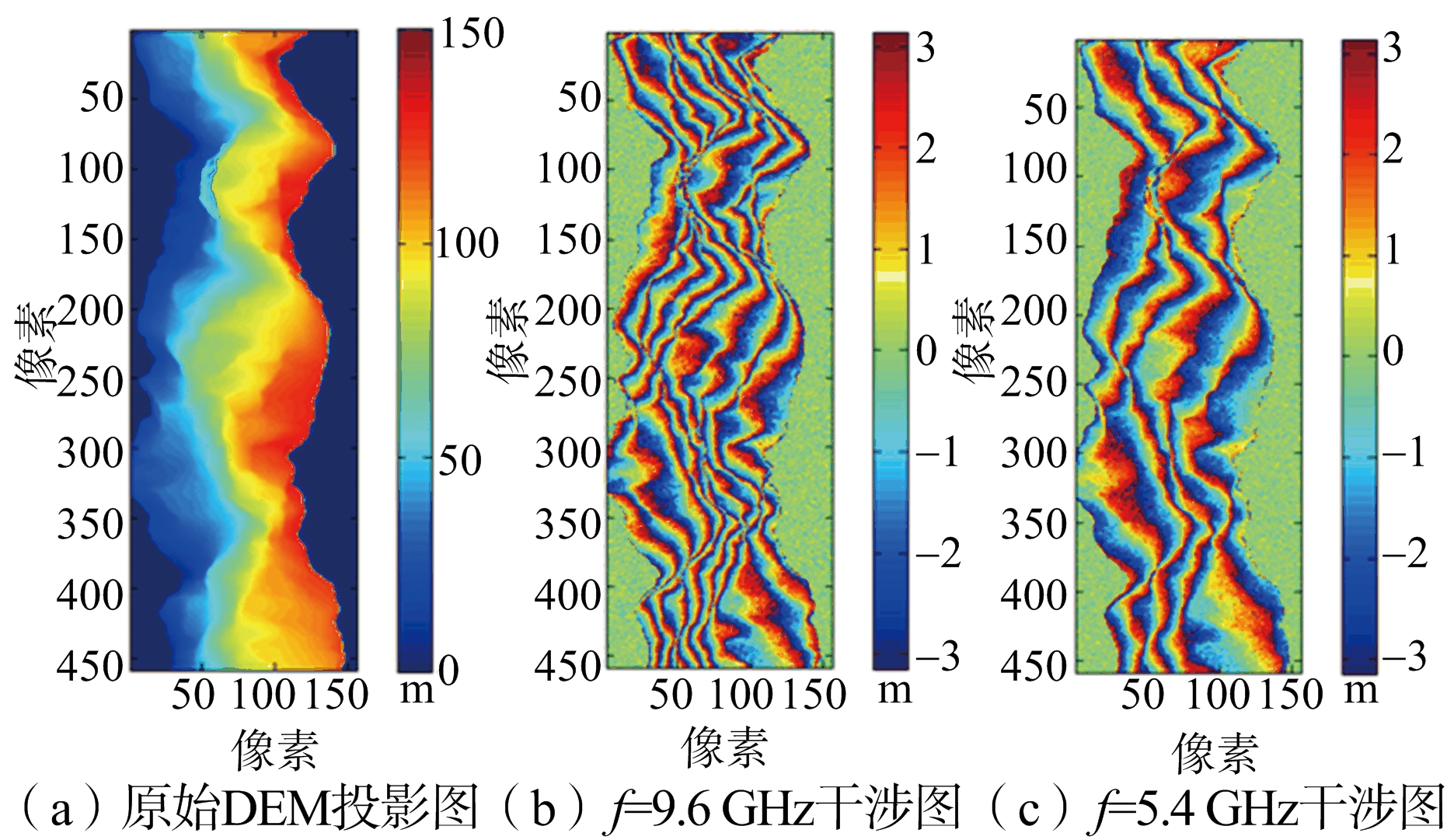
图7 真实地形数据
进行高程反演所得的MLE结果如图8(a)所示。对MLE结果进行噪点去除(结果如图8(b)所示)和噪斑去除(结果如图8(c)所示)。从结果中看出,重建的高程基本将MLE结果中的噪斑去掉。
图9列出了各算法DEM与原始DEM。3种重建算法的误差图分别如图10(a)、图10(b)、图10(c)所示。统计的误差如表3所示。重建时间来看:MLE算法为2.14 s,本文方法为3.08 s,MAP估计法为258.14 s。说明本文方法可以保证重建精度和重建效率。
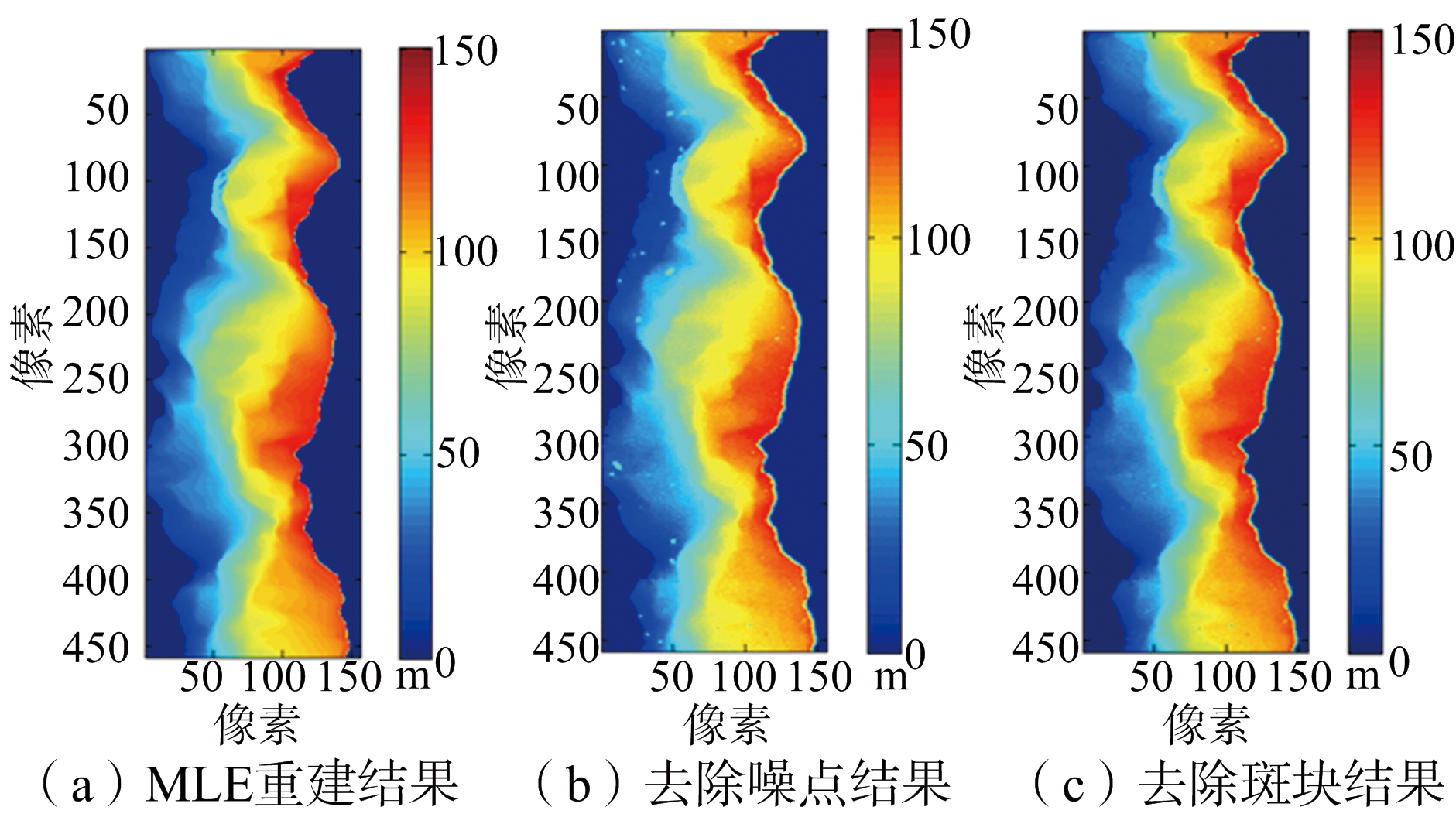
图8 真实地形去噪


图9 真实地形各重建结果与原始DEM对比

图10 仿真城市地形各种重建算法误差图
图11为各重建结果三维视图。算法优劣此处不再赘述。
表3 真实地形重建算法归一化均方误差表

重建方法归一化均方误差MLE0.1036MAP0.0044本文方法0.0046
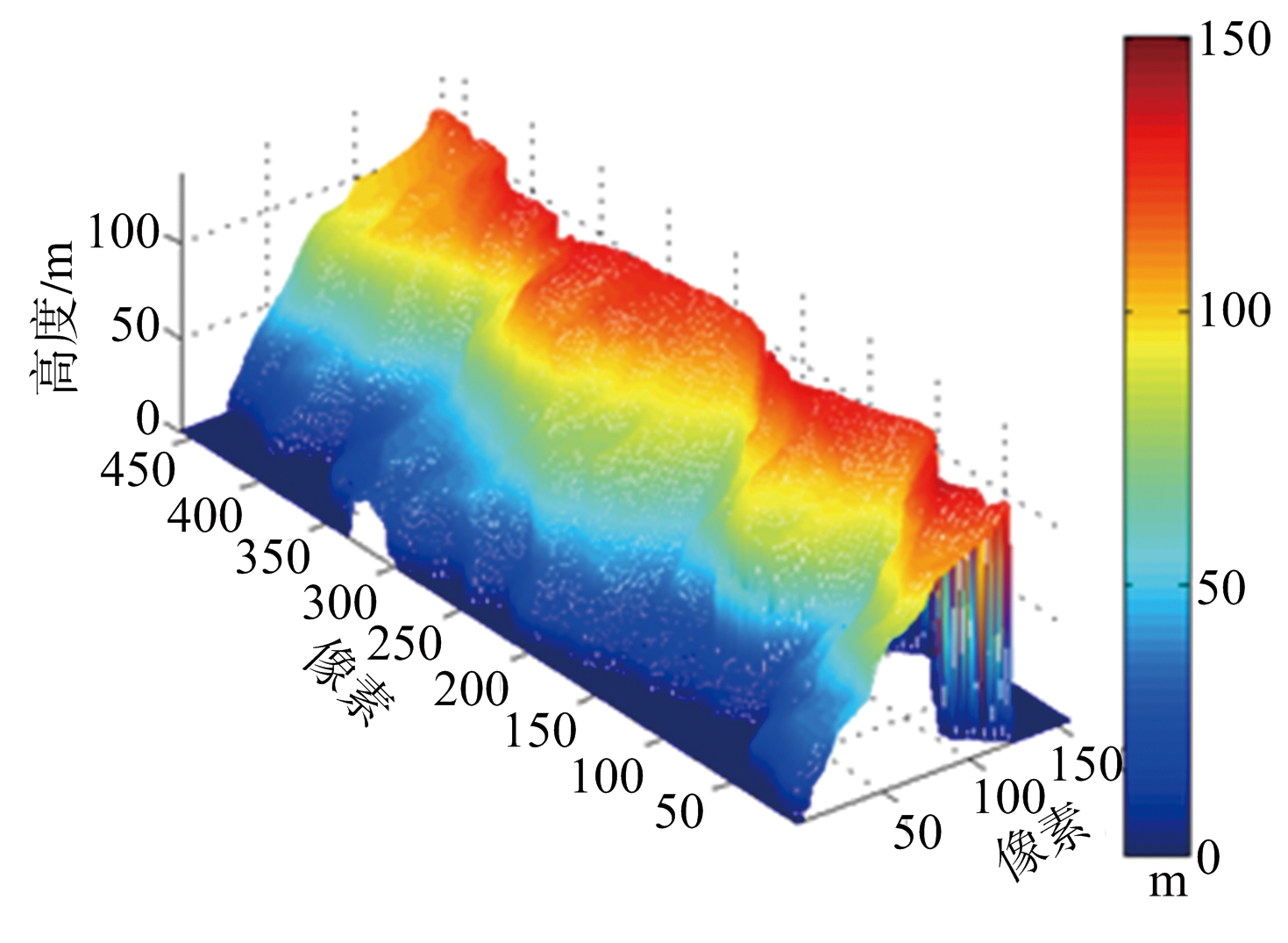
(a) 原始DEM

(b) MLE算法DEM
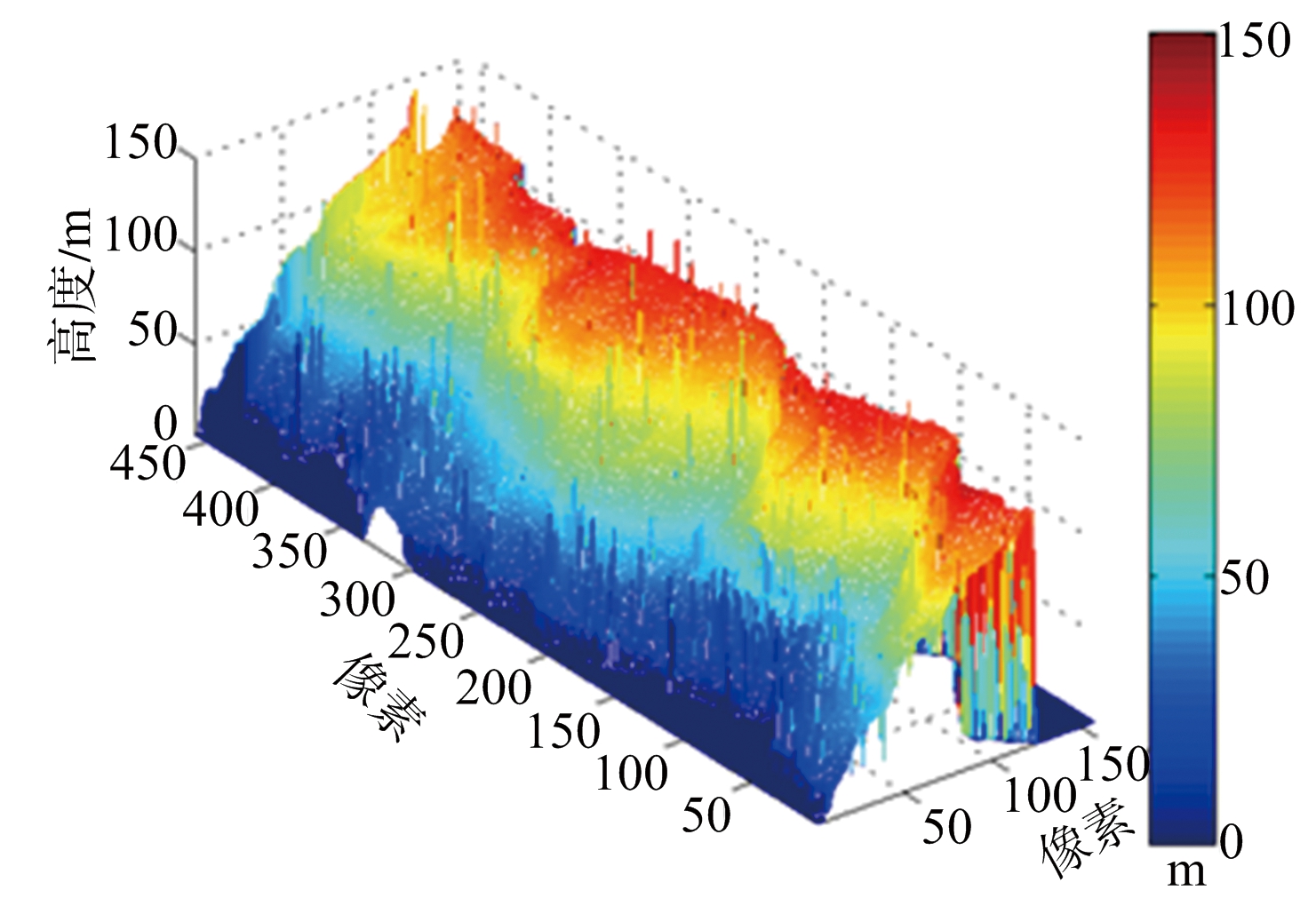
(c) MAP算法DEM
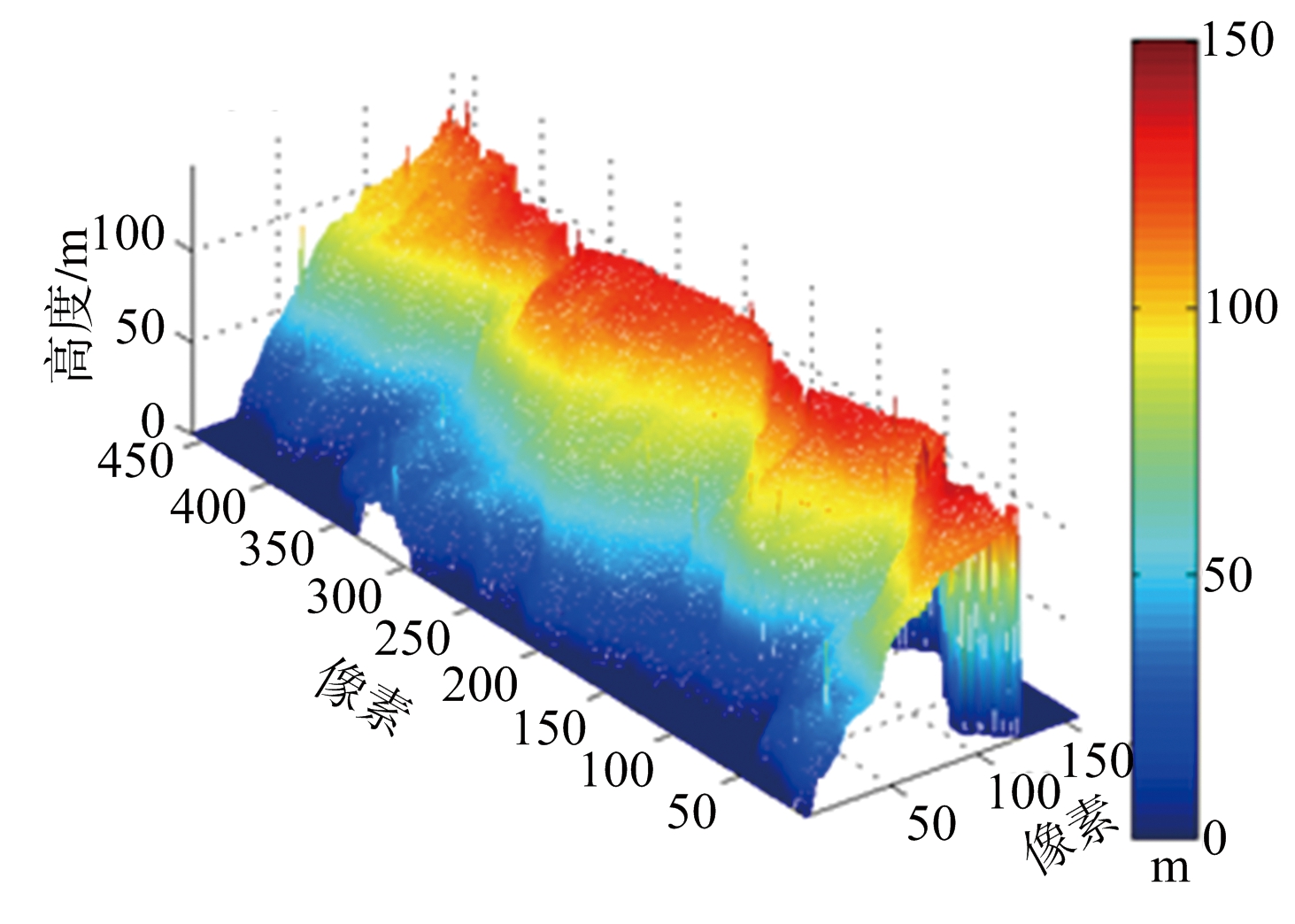
(d) 本文方法DEM
图11 各重建结果三维视图
3.2 实测数据处理
实测数据采用了机载C/X双频干涉SAR测量数据,该机载平台的具体参数如表4所示。第一块实验数据为澄城县城的干涉SAR数据。县城中高楼高度有90~100 m。两个通道相邻像素之间的干涉相位差分别可达3.2π和5.8π。第二块数据为白水县东坡村附近数据,该块数据中有沟壑和高架桥,地形复杂多变。两块数据均适合验证双频干涉处理算法。
表4 机载C/X双频系统主要参数

参数参数值平台高度4127.8m视角45°方位向采样率1503.13Hz基线角0°基线长度2.3m信号带宽210MHz双通道频率C/X5.4GHz/9.6GHz
3.2.1 澄城县实测数据处理
所选取的地域和对应的光学图像如图12所示。图中黄色旗帜所示的点为选取的控制点。对澄城县的两幅C/X波段图像分别进行配准,得到两幅干涉条纹图分别如图13(a)、图13(b)所示,利用轨道法[13]去除平地效应。再将C/X波段得到的干涉图配准。得到配准的去平地干涉相位图如图13(c)、图13(d)所示。MLE算法进行高程重建结果如图14(a)所示,利用本文方法去噪所得结果如图14(b)所示。图15(a)、图15(b)所示为重建结果的三维视图,可以更清楚地看出本文方法的有效性。

图12 澄城县Google Earth光学图像与干涉SAR数据图像

(a) C波段干涉相位图

(b) X波段干涉相位图

(c) C波段去平地干涉相位图

(d) X波段去平地干涉相位图
图13 各个通道去平地前后干涉相位图

(a) MLE重建结果
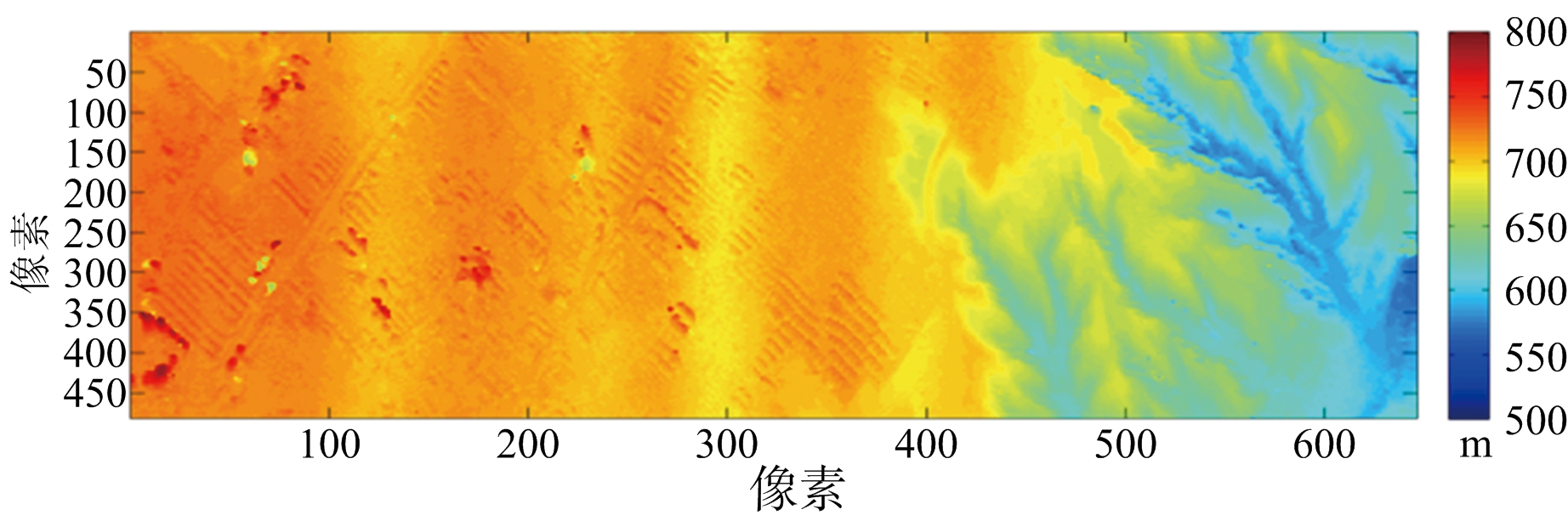
(b) 本文方法结果
图14 MLE算法重建结果与本文方法去噪结果
对图12中所选取的控制点进行高程统计,统计结果如表5所示。从结果中可以看出,MLE算法噪声过多,本文方法反演高度接近于真实高度。由于使用MAP耗时过长,这里没有采用。
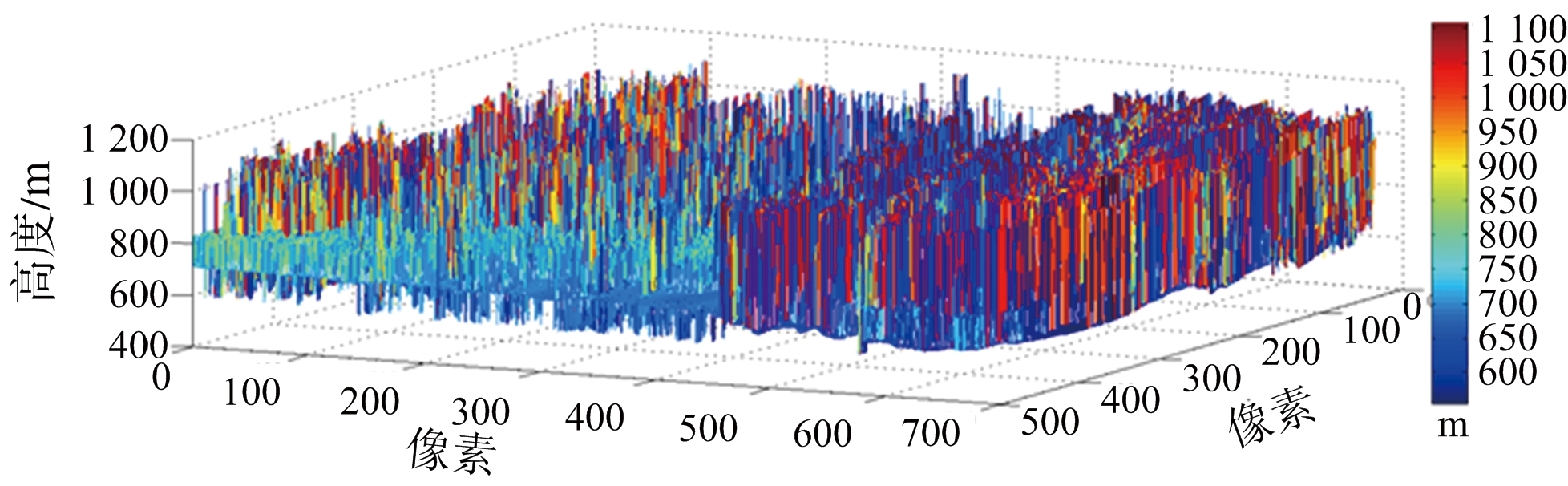
(a) MLE结果三维DEM
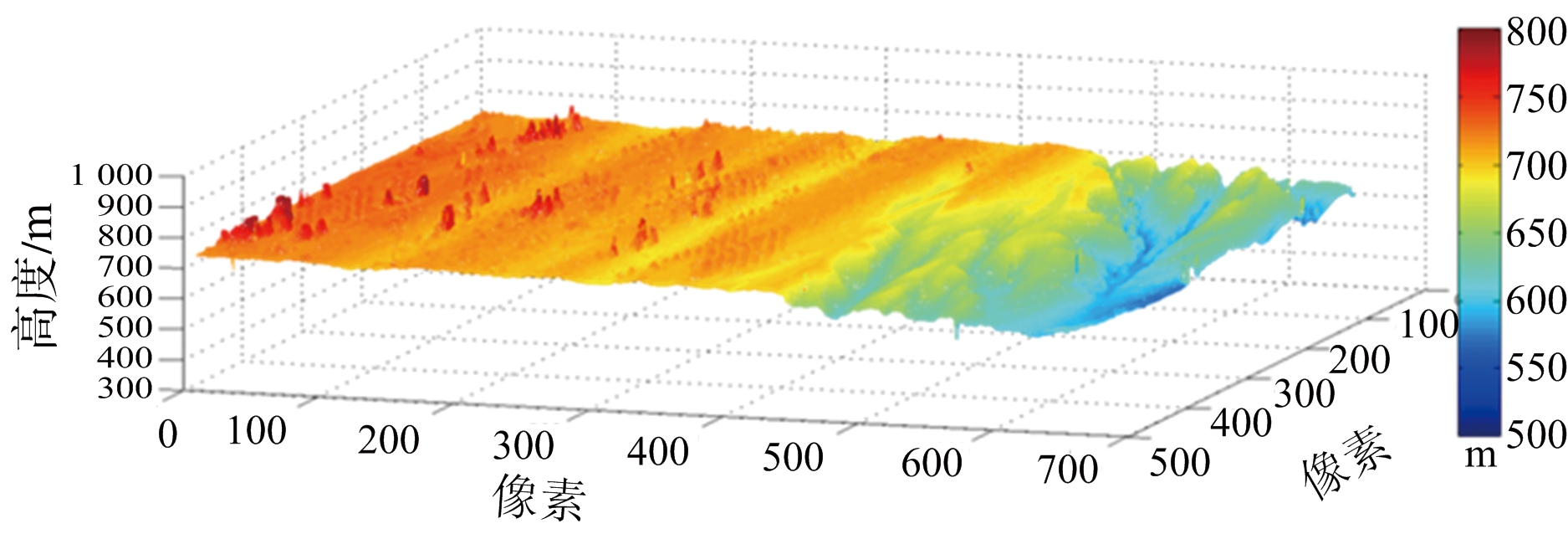
(b) 本文结果三维DEM
图15 MLE算法重建结果与本文方法去噪结果三维视图
表5 控制点高度统计表
m

控制点Google Earth高度MLE重建高度本文方法重建高度1791950.32788.672780791.55785.9537881000.14780.324765790.12772.13
3.2.2 白水县东坡村实测数据处理
首先给出的是光学图像和SAR图像如图16所示。黄色旗帜为误差分析控制点。其中1号点地区为沟壑,2号点白色条状地形为高架桥的影像,3号点地区为平地上的河流。

图16 白水县东坡村附近高架Google Earth光学图像与干涉SAR数据图像
两幅干涉条纹图分别如图17(a)、图17(b)所示,配准的去平地干涉相位图如图17(c)、图17(d)所示。
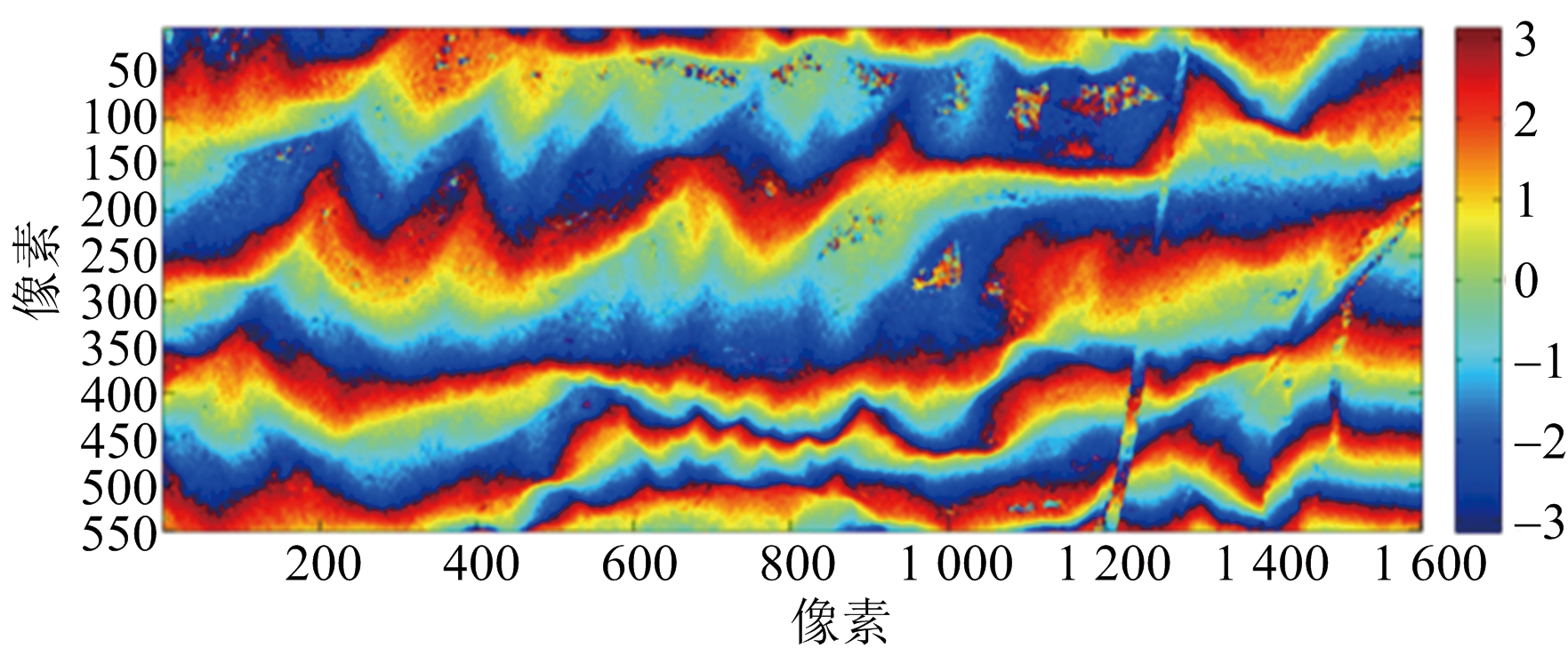
(a) C波段干涉条纹

(b) X波段干涉条纹

(c) C波段去平地干涉相位

(d) X波段去平地干涉相位
图17 各个通道去平地前后干涉相位图
MLE算法重建结果如图18(a)所示,利用本文方法进行重建结果如图18(b)所示。可见噪斑去除效果明显,具有良好的重建性能。
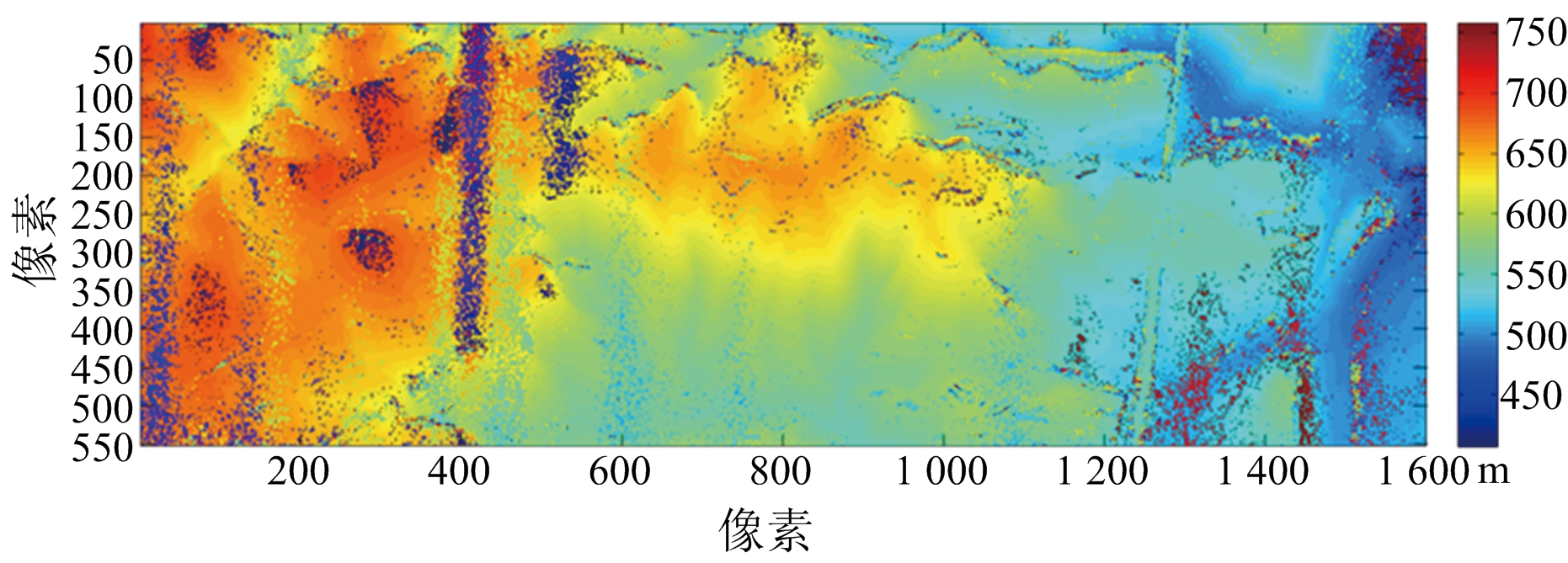
(a) MLE重建结果
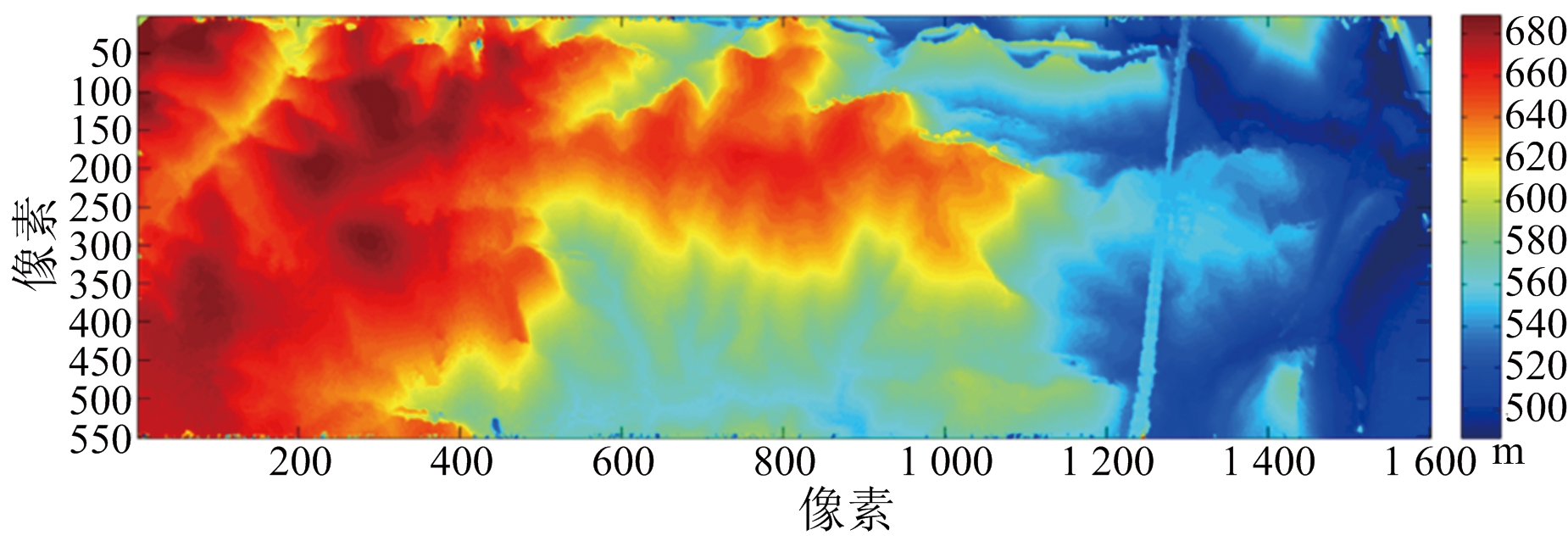
(b) 本文方法重建结果
图18 MLE算法重建结果与本文方法去噪结果
控制点高程统计结果如表6所示。在某些地带MLE算法噪声过大,例如本例中的3号控制点河流部分,高架边缘部分。统计结果表明,本文方法有效提高了重建精度。
表6 控制点高度统计表 m

控制点Google Earth高度MLE重建高度本文方法重建高度1615624.15619.542560580.22569.803512720.53505.26
图19(a)、图19(b)列出了MLE和本文方法的重建结果三维视图。为了减少内存消耗,在生成三维图形时,在方位向作了降采样处理,因而三维视图中方位向点数变少。

(a) MLE重建结果
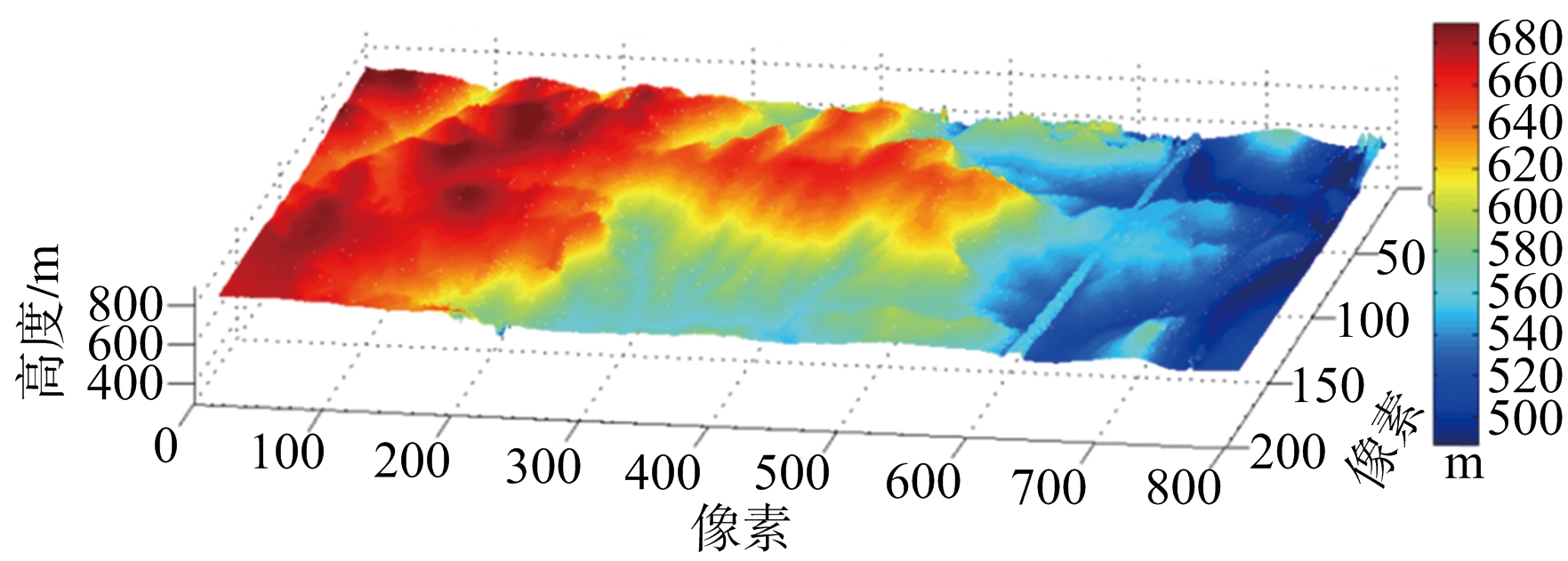
(b) 本文方法重建结果
图19 MLE算法重建结果与本文方法去噪结果三维视图
4 结束语
本文对传统的基于MLE的双频重建算法进行了改进,可以去除MLE重建结果中的噪点和噪声斑块,在保证重建效率的同时提高重建精度。基于上文模拟模型的论证分析,本文的方法在精度上与MAP估计相近,但是在重建效率上要远远优于MAP估计。上文中的实测数据处理结果表明,本文提出的方法可以用在大规模数据处理过程中,拥有较为良好的处理效果。但是本文方法也存在不足,例如阈值的选取和加权窗口的选取一般都是选取经验值,后期需要添加自适应的阈值控制方法来降低后处理的难度。此外,更加合理的去噪权值应该为越临近所求像素点的权值越大,越远的像素点权值越小,这也是以后工作中一个要调整的方面。
[1] YU Hanwen, XING Mengdao, BAO Zheng. A Fast Phase Unwrapping Method for Large-Scale Interferograms[J]. IEEE Trans on Geoscience and Remote Sensing, 2013, 51(7):4240-4248.
[2] AMBROSINO R, BASELICE F, FERRAIOLI G, et al. Extended Kalman Filter for Multichannel InSAR Height Reconstruction[J]. IEEE Trans on Geoscience and Remote Sensing, 2017, 55(10):5854-5863.
[3] ZENG Tao, LIU Tiandong, DING Zegang, et al. Phase Unwrapping Method Based on Multi-Frequency InSAR in Highly Sloped Terrain[J]. Electronics Letters, 2016, 52(12):1058-1059.
[4] YU Hanwen, LAN Yang. Robust Two-Dimentional Phase Unwrapping for Multi-Baseline SAR Interferogr-Ams: A Two-Stage Programming Approach[J]. IEEE Trans on Geoscience and Remote Sensing, 2016, 54(9):5217-5225.
[5] PASCAZIO V, SCHIRINZI G. Multi-Frequency InSAR Height Reconstruction Through Maximum Likelihood Estimation of Local Planes Parameters[J]. IEEE Trans on Image Processing, 2002, 11(12):1478-1489.
[6] MAGNARD C, FRIOUD M, SMALL D, et al. Analysis of a Maximum Likelihood Phase Estimation Method for Airborne Multibaseline SAR Interferometry[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(3):1072-1085.
[7] SCHMITT M, STILLA U. Maximum-Likelihood Estimation for Multi-Aspect Multi-Baseline SAR Interferometry of Urban Areas[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 87:68-77.
[8] 李泓宇. 干涉合成孔径雷达高程测量关键技术研究[D]. 北京:中国科学院大学, 2016:75-85.
[9] SHABOU A, TUPIN F. A Markovian Approach for DEM Estimation from Multiple InSAR Data with
Atmospheric Contributions[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4):764-768.
[10] FERRAIUOLO G, MEGLIO F, PASCAZIO V, et al. DEM Reconstruction Accuracy in Multichannel SAR Interferometry[J]. IEEE Trans on Geoscience and Remote Sensing, 2009, 47(1):191-201.
[11] 斯奇,王宇,邓云凯,等. 一种基于最大后验框架的聚类分析多基线干涉SAR高度重建方法[J]. 雷达学报, 2017, 6(6):640-652.
[12] 袁志辉. 多通道干涉SAR关键技术研究[D]. 北京:中国科学院大学, 2013:35-43.
[13] 花奋奋,张继贤,邓喀中,等. 几种机载InSAR平地效应去除方法的比较研究[J]. 遥感信息, 2010(5):58-61.

