0 引言
导弹弹道一般分为助推段、中段和再入段,中段是飞行时间最长的阶段,由于具有充足的时间进行目标识别和反导拦截,所以弹道中段是反导拦截的关键阶段,因此越来越多的防空识别和反弹拦截系统工作在中段,比如美国宙斯盾海上中段反导拦截技术。逆合成孔径雷达(ISAR)是弹道中段目标识别的重要传感器,通过对目标回波进行二维压缩处理,能获得目标的尺寸、形状、结构、姿态等信息,在雷达目标识别领域发挥着极其重要的作用,已成为弹道目标识别的主要途径之一[1]。随着弹道目标中段生存概率不断下降,研究弹道中段目标对ISAR的干扰是十分有必要的。
弹道目标为了突防,通常会释放主动干扰机和弹头伴飞,以产生虚假的回波信号[2]。基于主动干扰机,文献[3]研究了空中目标伴飞式干扰,可以产生不同姿态角的假目标,其思想可以借鉴于导弹目标中段突防。文献[4]把干扰机接收信号和雷达实时信号的相位差调制进干扰信号中进行补偿,产生逼真假目标。目前,已有文献中有源伴飞式干扰都是采取的固定方式释放干扰机,鲜有文献对干扰机的释放方式进行探讨。
1 ISAR成像原理
目前ISAR信号分析、补偿方法都得到了长足发展,并在目标分类和识别实践中已经进行了运用,对空中目标ISAR成像技术已经相当成熟。ISAR对目标散射信号进行SRTETCH处理或者匹配滤波得到一维距离像序列,通过对多个距离像进行积累,实现方位聚焦[5]。其基本原理为:
设雷达发射的LFM信号为
(1)
式中,![]() 为快时间,tm为慢时间,
为快时间,tm为慢时间,![]() 为全时间,fc为载频,k为调频率。回波表达式为
为全时间,fc为载频,k为调频率。回波表达式为
![]()
![]()

(2)
式中,![]() 为目标到雷达的距离,v,a,J分别为径向速度、径向加速度、径向加加速度。经下变频,脉压处理后信号频域表达式为
为目标到雷达的距离,v,a,J分别为径向速度、径向加速度、径向加加速度。经下变频,脉压处理后信号频域表达式为
sr1(f,tm)=![]()
(3)
构造运动补偿:
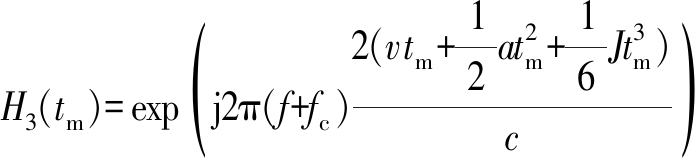
(4)
运动补偿后回波为
sr2(f,tm)=sr1(f,tm)·H3=
(5)
式(5)为目标散射点在ISAR中的成像形式。值得一提的是,对于ISAR来说,目标的方位分辨率为δ=λ/2ψ,ψ为相干时间内目标相对于雷达的转角,但弹道中段目标和空中目标不同,由于不受外力的影响,其运动参数变化相对缓慢,于是想要形成足够清晰的二维像就必须增长相干处理时间,文献[6]中提出了提取目标进动特征来缩短成像时间。但微动特性是一种细微运动,不会对弹头的姿态产生大的影响,因此对于基于微多普勒效应的ISAR成像,本文提出的姿态欺骗方法依然有效。
2 伴飞式ISAR干扰方法
2.1 伴飞干扰原理
伴飞式干扰原理如图1所示,干扰机装载在导弹上,同弹头一起发射,在距地高度100 km时,发动机关闭,进入弹道中段(弹道1),开始进行无推力的平稳飞行状态。干扰机安装两副天线,分别指向雷达(后文称之为前天线)和弹头(后文称之为后天线)。当前天线接收到的是窄带信号时,判断此时雷达处于搜索、跟踪状态,前天线将直接接收雷达信号并进行调制转发,形成传统距离假目标干扰[7],相当于对常规雷达进行自卫干扰。当前天线开始接收到大时宽带宽信号(点A),判断ISAR雷达进入成像阶段,导弹将干扰机以一定角度(θ角)和特定速度释放,根据动量守恒原理,由于速度矢量的改变,弹头将会变轨(弹道2),干扰机被释放后也将有自己的速度矢量,会形成自己的轨道(弹道3)。干扰机进入自己的弹道后,后天线开始接受弹头反射的包含方位信息的回波,然后采样、存储、调制、放大后通过前天线向雷达转发,目的是在ISAR上形成假目标图像。此时雷达、干扰机和弹头等效为双站ISAR,雷达等效为发射站,干扰机等效为接收站,雷达采用干扰机接收到的信号进行成像等效为单站雷达在夹角中线的成像结果[8]。Ra表示雷达位置距离弹头落点距离,弹头在A点的方位角为α。可以看出,干扰机和弹头的角度决定了ISAR所成图像的姿态。通过改变角度,转发形成的假目标图像使雷达判断为真目标,并且该“真目标”弹头的姿态发生了变化。与空中气动目标和海面舰船目标相比,空间轨道目标的运动相对平稳、可预测性强,而且目标姿态通常严格受控,目标相对雷达视线角变化通常可以根据轨道信息精确解算[9]。因此合成孔径雷达与弹头姿态角(雷达视线与弹头轴线夹角ζd)是和轨道信息有关联的。改变了姿态就意味着改变了弹头弹道,可导致雷达对弹头飞行速度、弹道倾角和落点误判,增加弹头突防的概率。
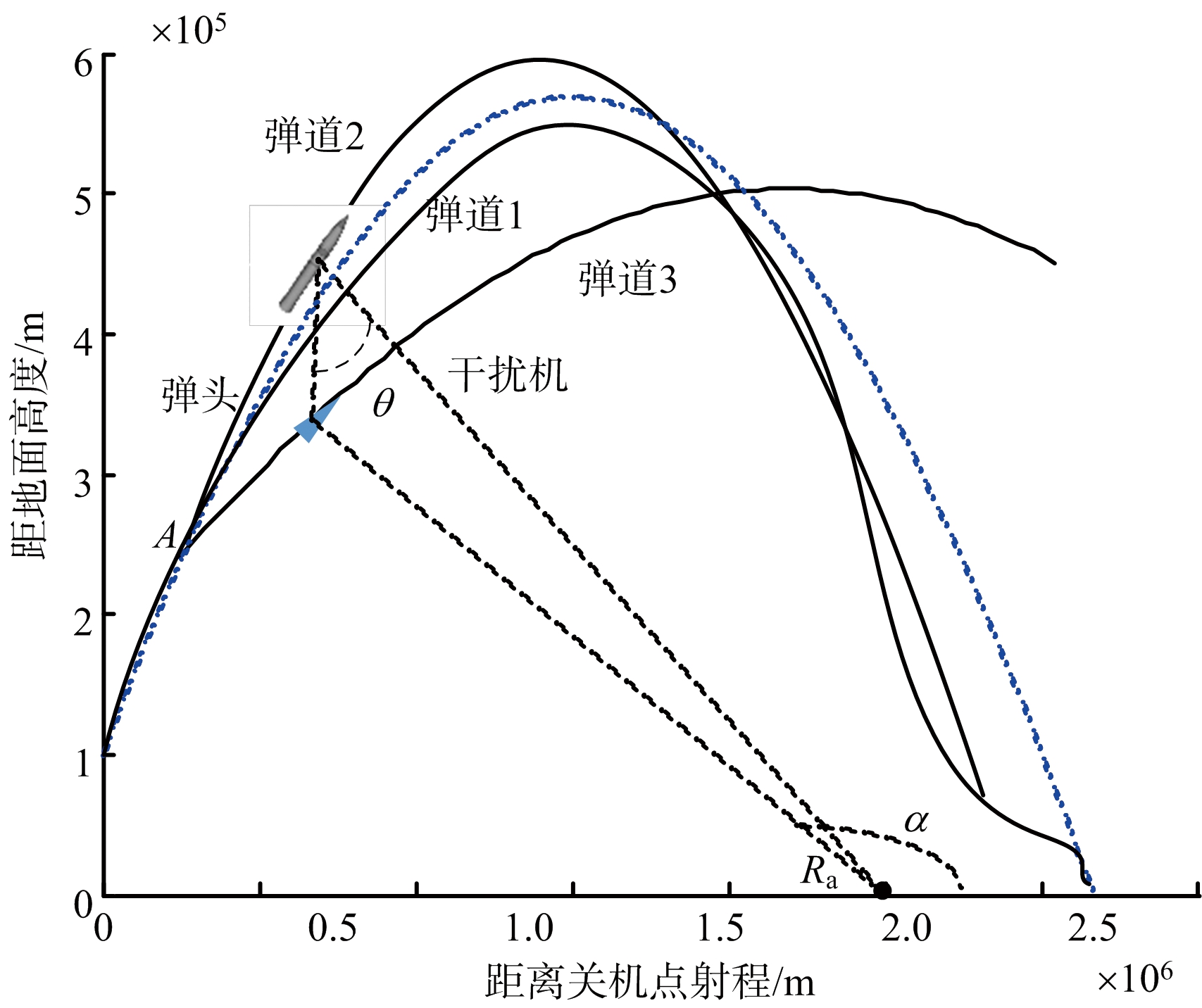
图1 伴飞式干扰原理图
2.2 干扰机和弹头的位置关系
当雷达处于成像模式下,干扰机接收弹头的回波并向雷达放大转发,雷达会接收到弹头回波和干扰回波,要始终使干扰回波大于弹头回波才保证干扰效果,因此有必要分析干扰机与弹头和雷达的位置关系。根据雷达距离方程,雷达接收到的弹头回波为
![]()
(6)
式中,Pt为雷达发射功率,G为雷达主瓣增益,σ为弹头散射截面积,λ为信号波长,R为弹头与雷达之间的距离。干扰机后天线接收到的弹头散射信号功率为
![]()
(7)
式中,Gw为后天线增益,Rw为干扰机与弹头的距离。雷达接收到的干扰信号功率为
![]()
(8)
式中,Rt=R-Rw为干扰机与雷达距离,Gt为干扰机前天线增益。那么,雷达接收机输入端干信比为
(9)
联立式(6)~式(9),得到干扰机前天线发射功率为
(10)
若雷达发射功率为Pt=1 000 kW,天线主瓣增益为G=60 dB,弹头RCS=1 m2,弹头距离雷达R=1 000 km,弹头与干扰机的分离点相对雷达的方位角为α=150°。则在不同干信比下干扰机功率与干扰机距离弹头的关系如图2所示。
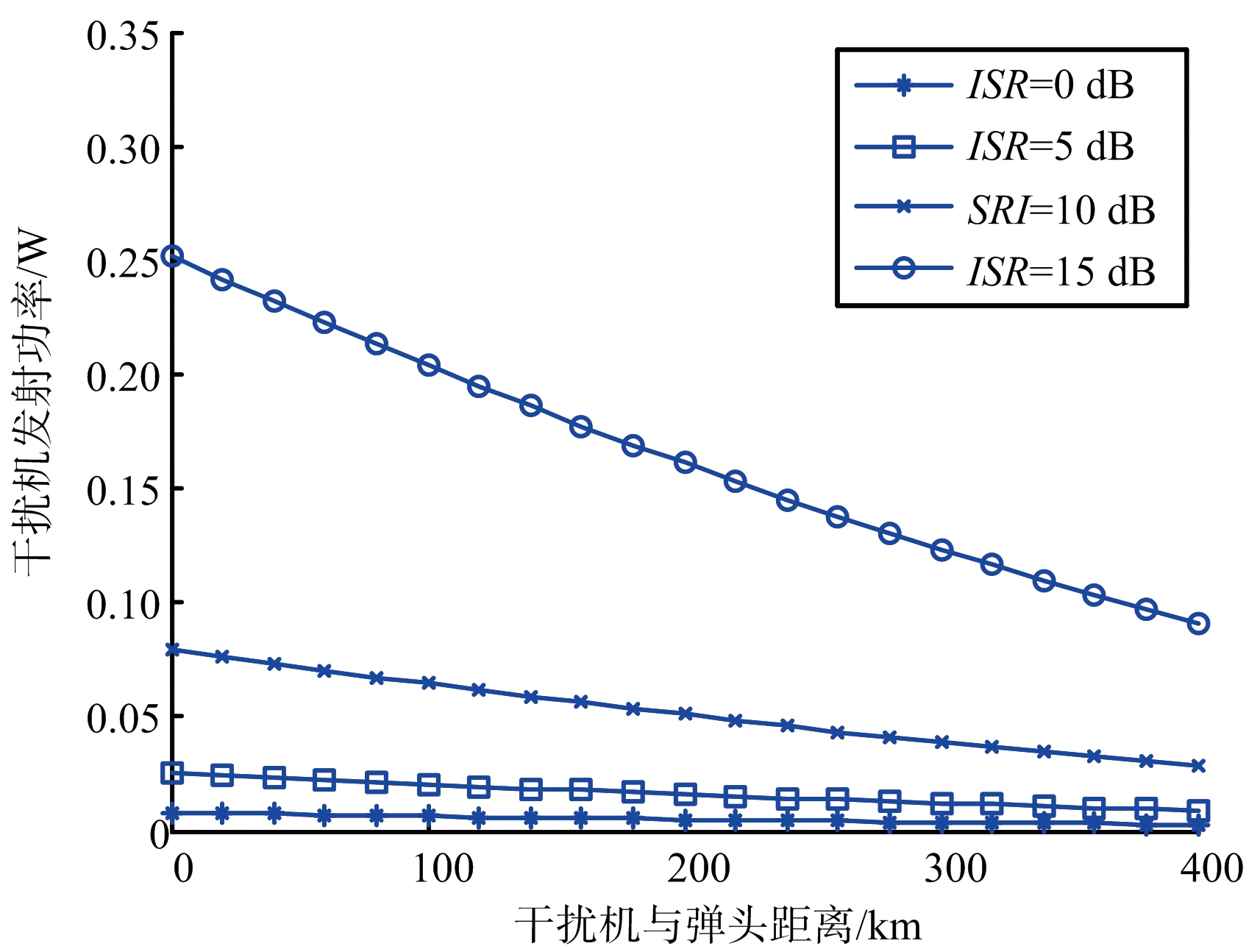
图2 干扰机功率与干扰机与弹头距离关系
从图2可以看出,当雷达接收机ISR=15 dB时,所需最大功率值0.25 W,说明其对干扰机的功率要求不高,因此干扰机和弹头的距离选择比较自由,即干扰机相对弹头的径向轴速度不敏感。
弹头相对于干扰机和雷达的角度θ是产生姿态欺骗的关键参数。为了尽可能使干扰功率得到最大化利用,则干扰机与弹头应同时在雷达波束主瓣内。设雷达发射波束宽度ϑ=1°,弹头距离雷达1 000 km,则干扰机被允许的相对弹头的横向最大位移距离如表1所示。
表1 干扰机距弹头距离
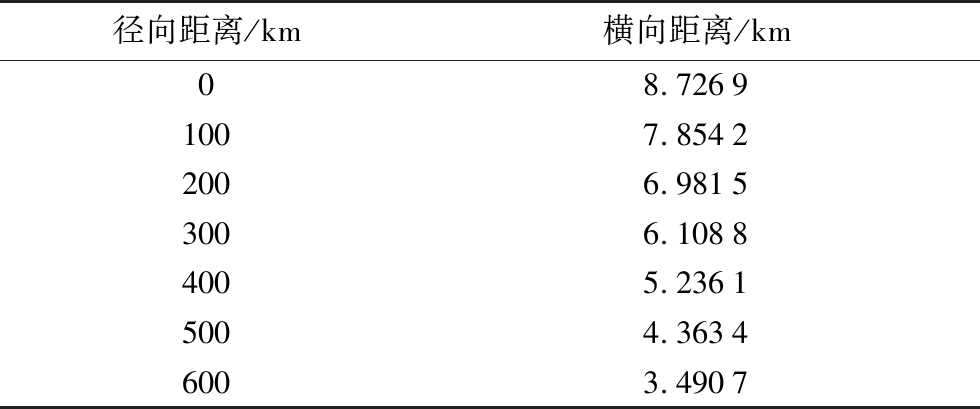
径向距离/km横向距离/km08.72691007.85422006.98153006.10884005.23615004.36346003.4907
从表1可以看出,干扰机发挥干扰作用的横向距离在几公里的范围内,这和弹道中段目标群长度几百米到几千米的范围是吻合的,因此干扰机在弹道中段目标群中的位置是具有一定自由性的,所以改变干扰机释放方式而导致干扰机位置发射变化是依然能产生干扰效果的,是改变干扰机释放方式的理论支撑。
2.3 最佳干扰姿态角推导
当雷达同时接收到弹头回波和干扰信号时,真实回波和干扰信号都会形成ISAR像,要想雷达跟踪干扰像,就得使干扰像比真实像更清晰,更容易分辨出形状。在中段,由于弹道的缓变性,在某一时间段内,弹头的方位角α和弹道倾角θk可以看作是不变,则对于雷达而言,弹头的姿态角ζd=180°-α+θk是恒定的。要通过改变θ寻找使干扰像最清晰的点,必须找到成像最清晰的姿态角。雷达接受的干扰信号包含目标的姿态信息,也包含干扰机和弹头之间的角度信息,干扰信号中的姿态角为ζj=180°-α+θk+θ/2。仿真中,在[0,π]等间隔的取ζj值,进行ISAR成像,比较各角度的图像,选择最清晰的角度值,然后利用ζj和θ的关系求得成像最清晰时的θ,由于篇幅限制,选取几个典型值进行成像。由于弹道目标具有军事敏感性,想要获得真实弹头对ISAR的实际回波是十分困难的。文献[10]指出,可以利用软件设置若干点模拟弹道目标形状,计算机生成仿真数据,用于弹道中段目标ISAR成像研究。计算机设置仿真目标如图3所示。
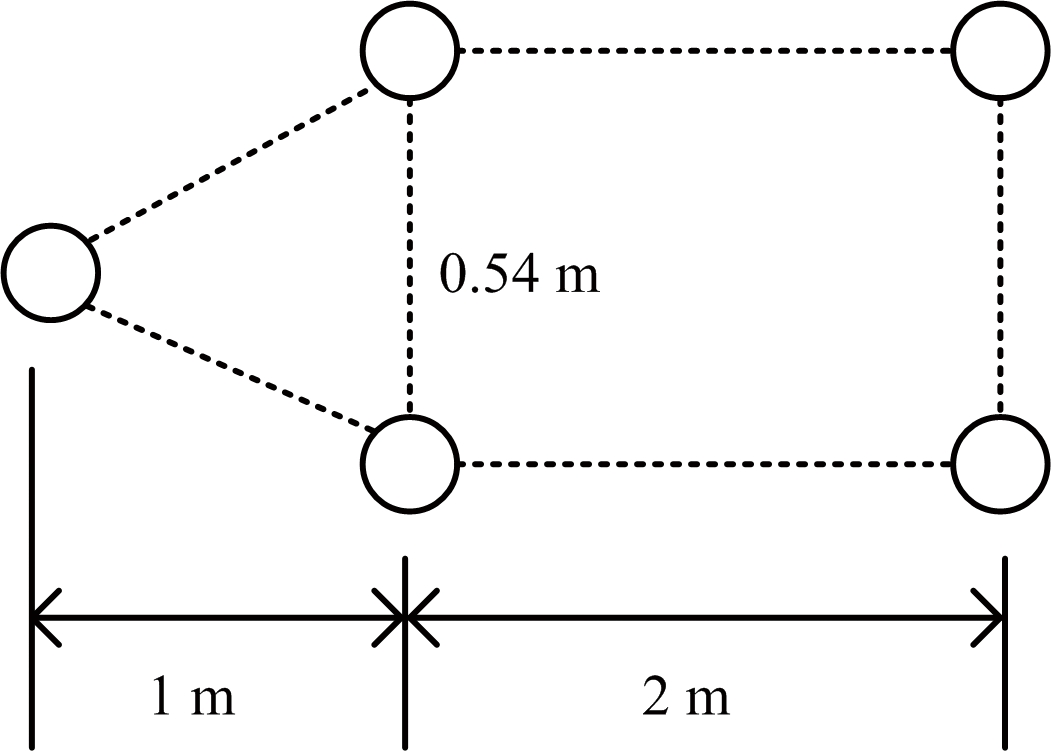
图3 仿真目标结构
弹头构成简单,一般都是柱、球、锥等的组合,表面光滑,于是可由5个模拟散射点构成仿真目标。假设各散射点强度都为1,直径前锥角为30°。仿真条件设置为:信号载频fc=10 GHz,脉冲宽度T=20 μs,脉冲重复频率PRF=100 Hz,信号带宽B=400 MHz,采样频率Fs=800 MHz,调频斜率K=2×1012Hz/s,雷达距离弹头1 000 km。根据式(1)~式(5)进行运动补偿和成像。则不同ζj值对应的干扰图像如图4所示。
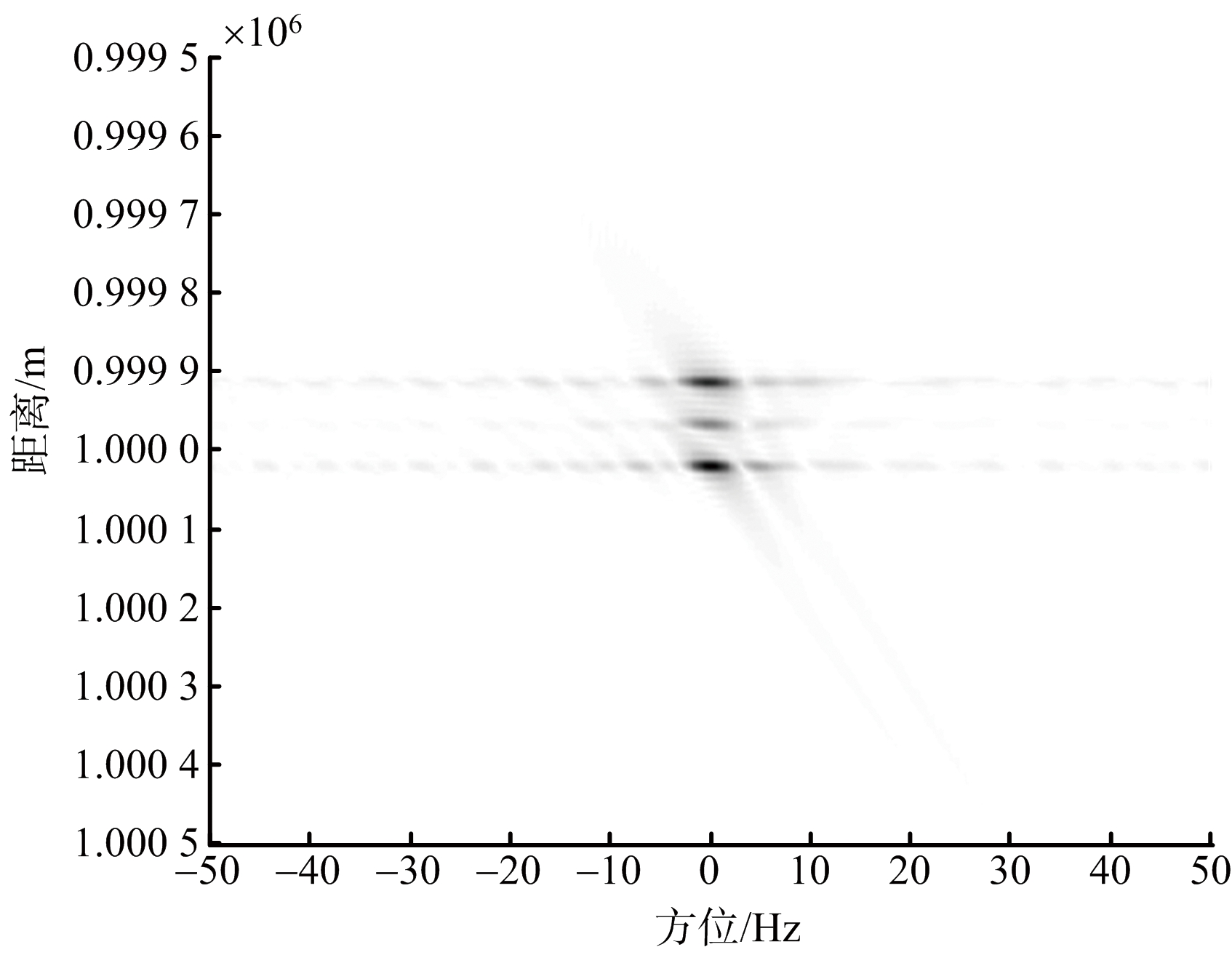
(a) ζj=0°时ISAR干扰像
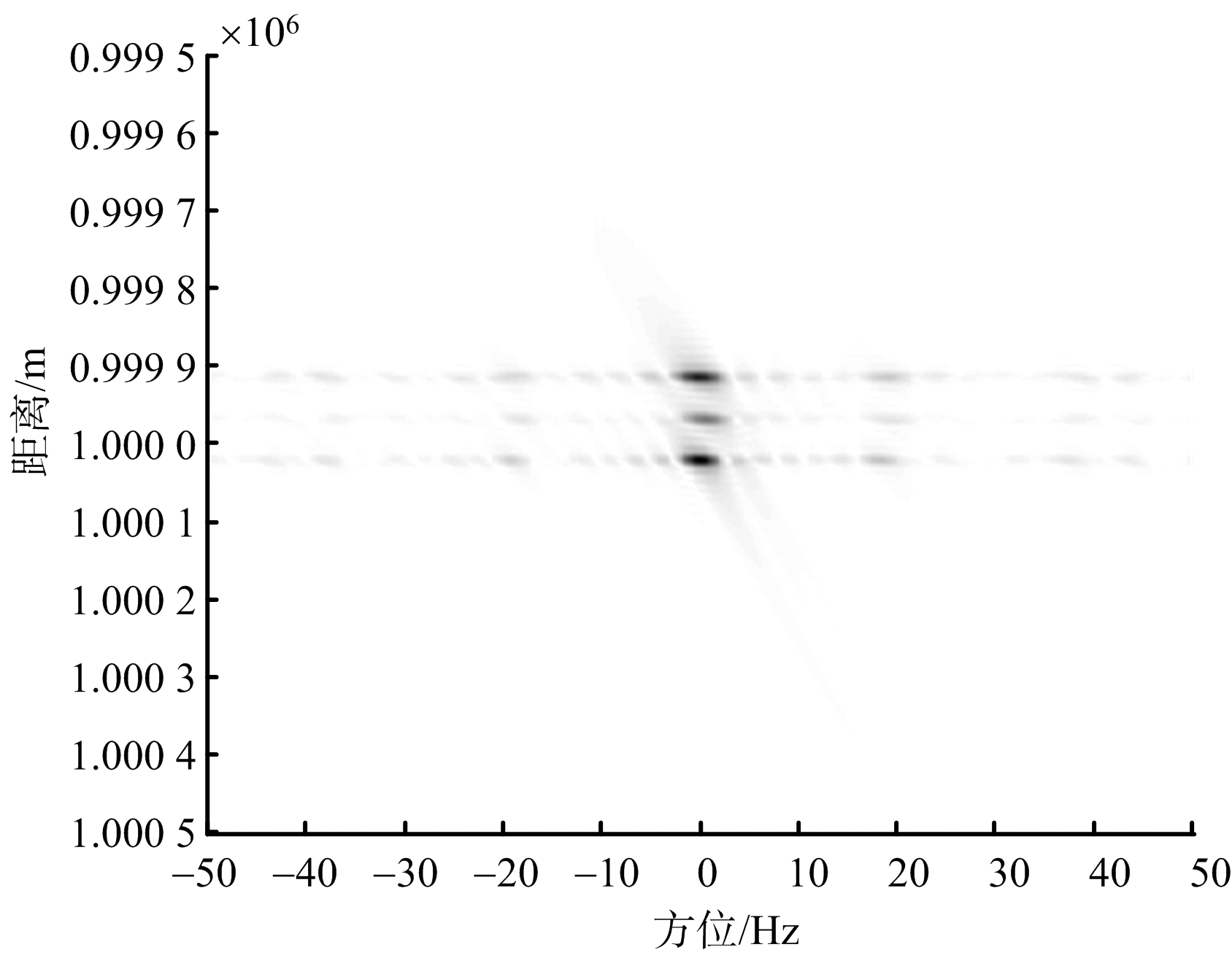
(b) ζj=30°时ISAR干扰像
(c) ζj=75°时ISAR干扰像
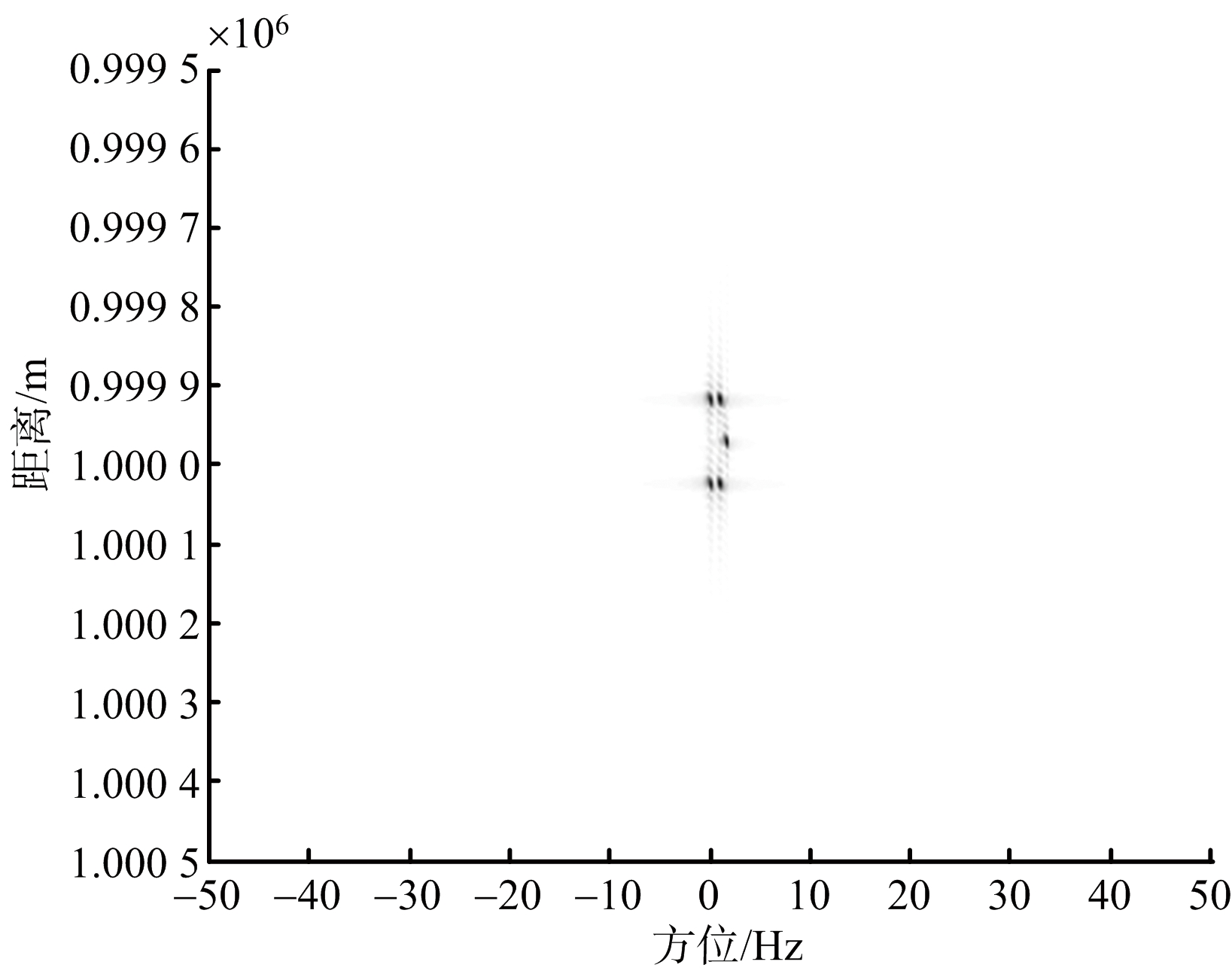
(d) ζj=90°时ISAR干扰像
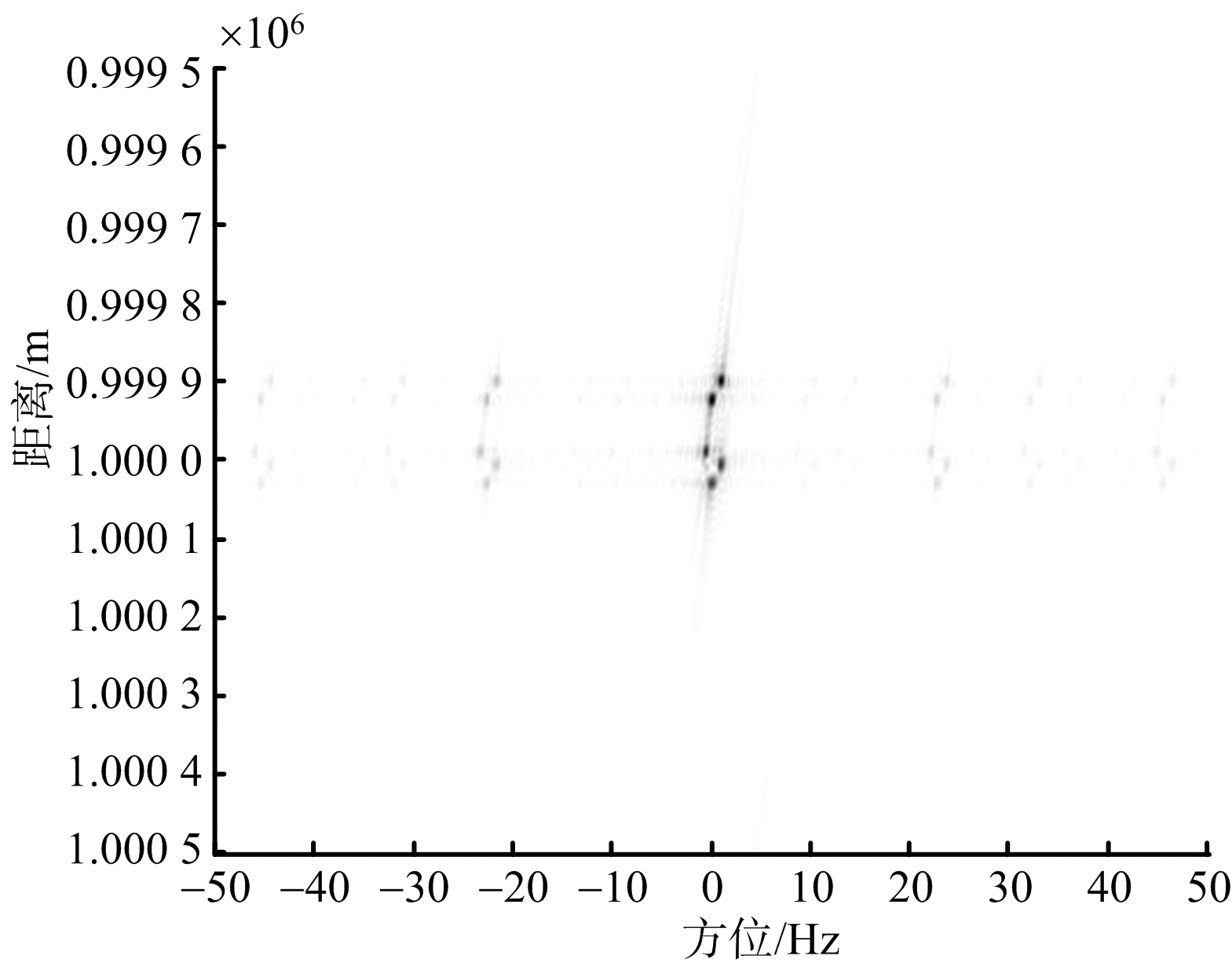
(e) ζj=105°时ISAR干扰像
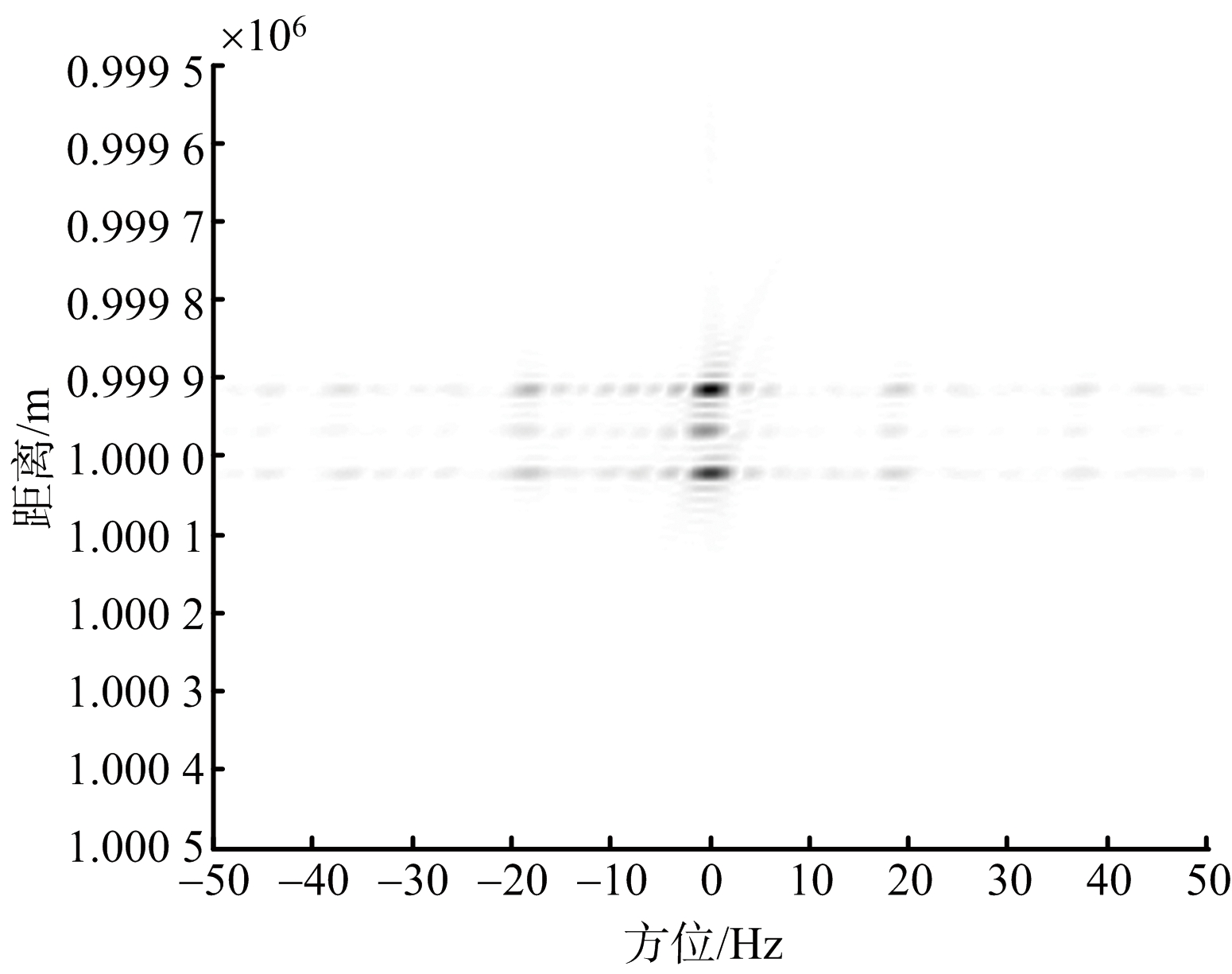
(f) ζj=150°时ISAR干扰像
图4 不同ζj值时形成的干扰像
从图4可以看出,在ζj=90°附近时,在雷达内形成的干扰像图像比较聚拢,形状比较清晰好认。因此,在释放干扰机时,根据实时弹道参数,能产生最好干扰效果的关系表达式为
θ=2α-2θk-180°
(11)
从图4可以看出,当姿态角过小,ISAR像方位向信息显现得十分有限,这是由于姿态角跟弹道目标的方位角和弹道倾角有关,而方位分辨率δy=λ/2ψ,即ISAR图像的方位向分辨率同目标在观测时间内的转过的角度成反比。ψ与姿态角的变化率有关,姿态角变化率为![]() 为姿态角变化率曲线。
为姿态角变化率曲线。
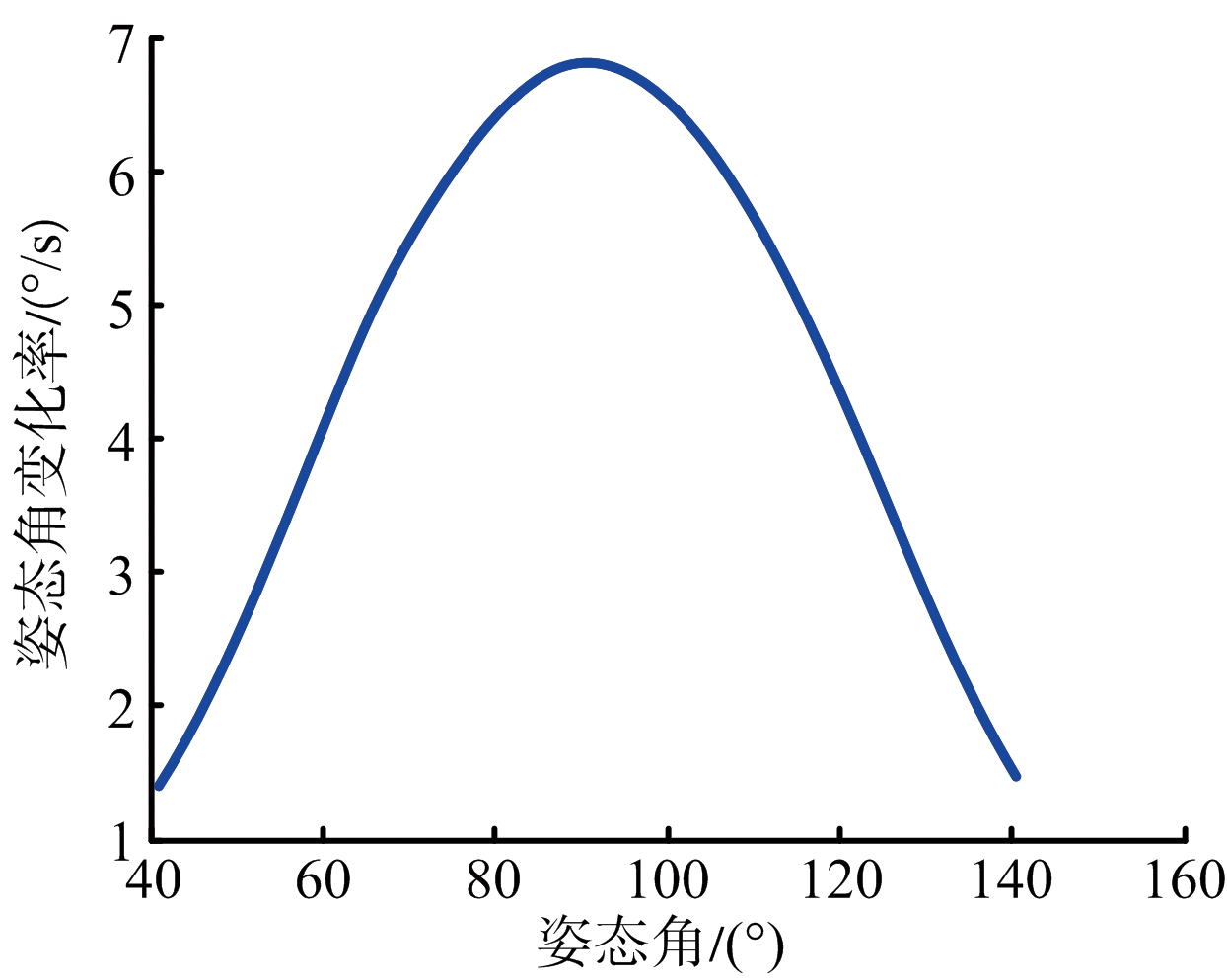
图5 姿态角变化率曲线
从图5可以看出,姿态角变化率呈现中间高两边低的规律,姿态角越接近90°,其变化率越大,相应的相同时间内转过的角度就越大,相干积累效果越好,这就印证了姿态角为90°时干扰成像最好。当姿态角分布靠近两侧时,变化率降低,导致要达到同样分辨率所需要的相干时间增长,相同时间内所能获取方位信息减少,雷达图像变模糊。
3 干扰机释放的初始参数解算
释放干扰机是实现伴飞式干扰的核心过程,最终的干扰效果由θ决定,而干扰机被释放时的初始速度和初始角度决定θ的初值,同时知道θ值后可以反推出初始速度和初始角度。完成分离后,干扰机和弹头的空间位置关系如图6所示,容易得到θ的随时间的变化关系为
θ(t)=α(t)-β(t)+90°
(12)
式中,β(t)=arctan(Δvxt/Δvyt),Δvx,Δvy为弹头和干扰机的水平和垂直的相对速度。从式(12)可以看出,θ主要是受α和β影响,β只与分离完成后的相对速度有关,那么θ受时间的影响主要来源于α。由于方位角α的缓变性,θ同样具有缓变性,说明这种干扰持续时间长,干扰距离远。
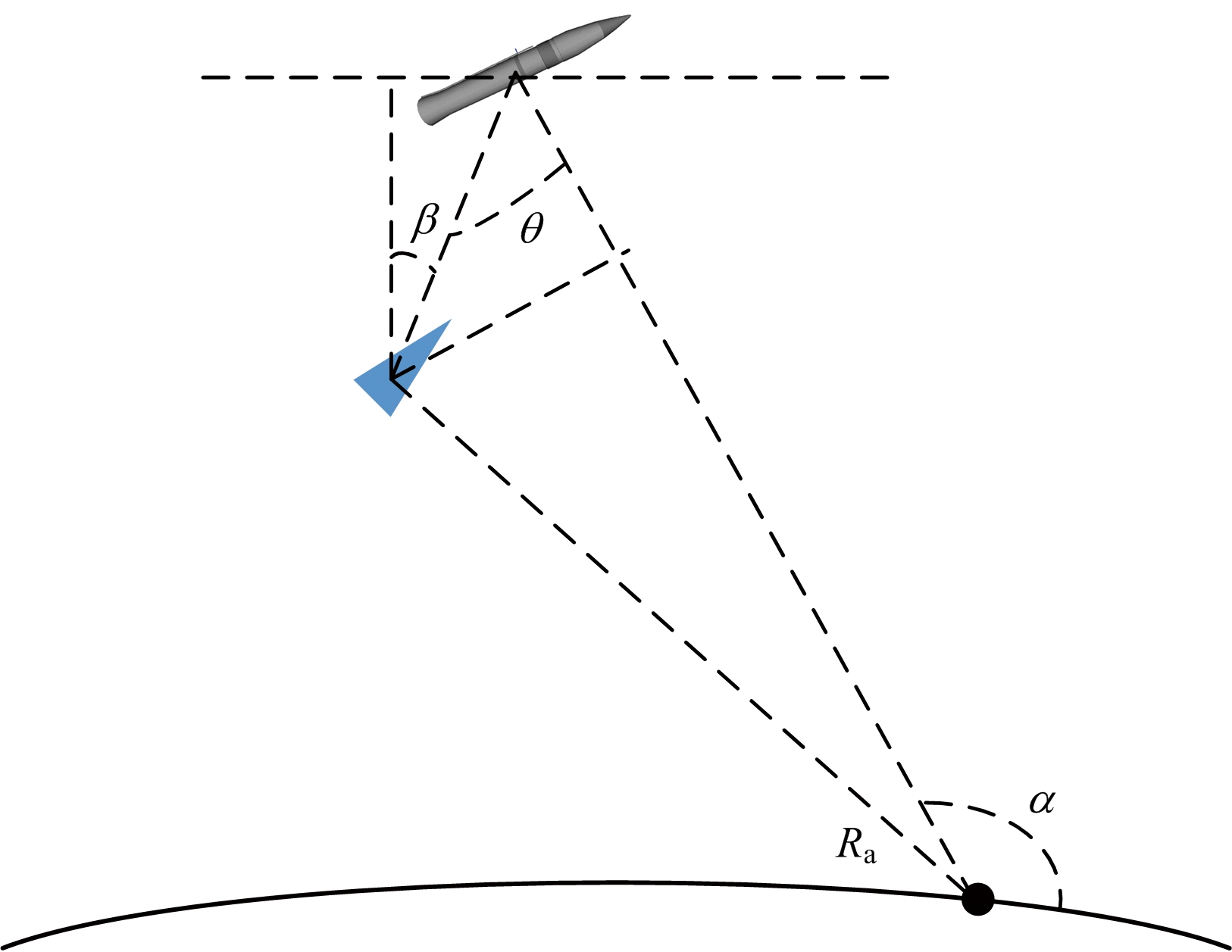
图6 分离完成后θ空间位置关系
为了求得分离后两者的相对速度,以A点为原点建立直角坐标系,在A点进行分离时的速度分解,如图7所示。
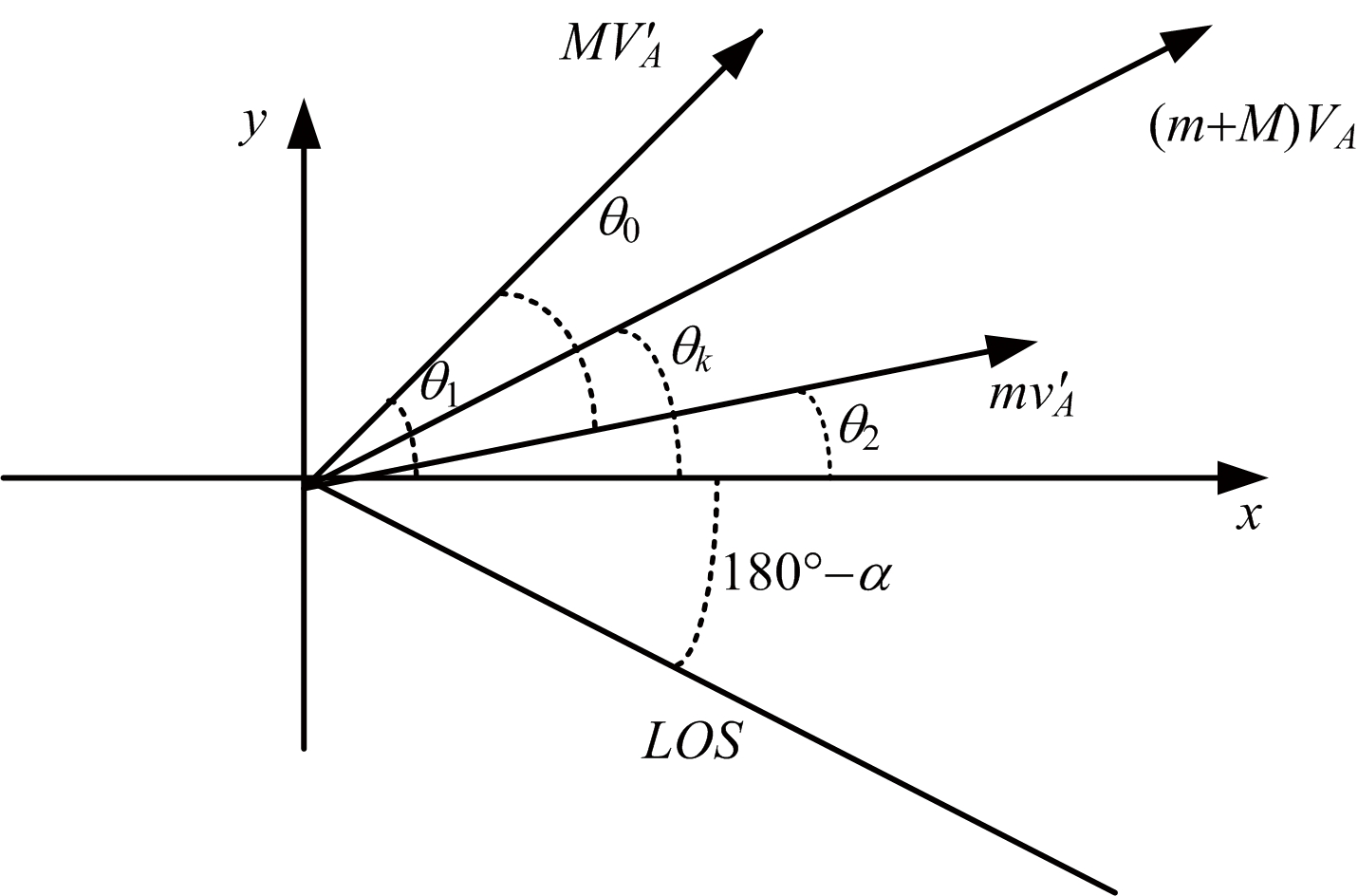
图7 A点的速度分解图
其中M为弹头质量,m为干扰机质量;VA为分解前弹头和干扰机共同速度,![]() 为速度分解后弹头速度,
为速度分解后弹头速度,![]() 为速度分解后干扰机速度,θk为分解前弹道倾角;θ0为干扰机相对弹体的射出角;θ1,θ2分别为完成分离后弹头和干扰机弹道倾角。于是,可以进一步将相对速度表示为
为速度分解后干扰机速度,θk为分解前弹道倾角;θ0为干扰机相对弹体的射出角;θ1,θ2分别为完成分离后弹头和干扰机弹道倾角。于是,可以进一步将相对速度表示为
(13)
根据动量守恒有
![]()
(14)
联立式(13)和式(14)可以建立方程组:
(15)
式中,![]() 是未知参数,非线性方程组方程数目小于未知数个数,因此并不能得到准确解,需要寻求新的约束关系;求解多元非线性方程组需要耗费大量的时间,大大降低了干扰的时效性。一般情况下,弹道目标释放干扰机突防时,考虑到干扰机质量远小于弹头质量,根据动量守恒,弹头速度变化量将会很小,而干扰机在释放后速度一般相对弹头会有一定的初速度,高分辨雷达通常会获取两者的速度差异来识别诱饵和弹头。因此弹头在释放干扰机的过程中,要破坏基于速度差异的识别方法,必须使干扰机相对弹头的初速度很小,则可以认为干扰机被释放时不会被赋予新的速度,即
是未知参数,非线性方程组方程数目小于未知数个数,因此并不能得到准确解,需要寻求新的约束关系;求解多元非线性方程组需要耗费大量的时间,大大降低了干扰的时效性。一般情况下,弹道目标释放干扰机突防时,考虑到干扰机质量远小于弹头质量,根据动量守恒,弹头速度变化量将会很小,而干扰机在释放后速度一般相对弹头会有一定的初速度,高分辨雷达通常会获取两者的速度差异来识别诱饵和弹头。因此弹头在释放干扰机的过程中,要破坏基于速度差异的识别方法,必须使干扰机相对弹头的初速度很小,则可以认为干扰机被释放时不会被赋予新的速度,即
(16)
联立式(15),解四元非线性方程组有
θ0=2arctanρ
θ1=-2arctan(m+M-Mρ2+mρ2)-
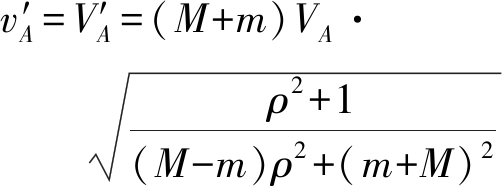
(17)
式中,ρ=1/tan(θ-α)。至此,整个伴飞式干扰过程模型已经建立。式(11)给出了干扰决定因素θ的选取准则;式(17)给出了在θ确定的条件下,弹头释放干扰机时的初始速度和初始角度,以完成弹头和干扰机的分离;式(12)给出了弹体干扰机分离后θ随时间的变化关系,这是进行干扰效果分析的基础。
4 干扰效果分析
进行干扰效果分析时,首先要建立干扰有效准则。如果认为图4(c)和图4(e)已经不具备干扰效果,那么这里建立的准则为:当干扰机和弹头不再同时处于雷达波束之内时,θ的值变化不超过30°。
为了清楚展示伴飞式干扰机的干扰效果,设定一个真实的干扰场景:弹道目标在距离雷达R1=1 000 km处被发现(即点A),雷达开始进入目标成像阶段。此时弹道目标的方位角为α=141.5°,弹道倾角为θk=6.81°,速度为VA=4 022.2 m/s,距关机点射程为l=1 217 km,地心距为rk=6 999 km,距地高度为h=621.6 km。建立有效干扰的θ的范围为[78°,138°];取最好干扰效果时θ=108°,假设弹头重量M=2 000 kg,干扰机重量为弹头重量的1/10;根据式(15),那么干扰机和弹头分离时干扰机的弹道倾角为θ2=-20.58°,速度为![]() 干扰机相对弹体释放角为θ0=30°,则弹头的弹道倾角为θ1=9.41°,弹头速度为
干扰机相对弹体释放角为θ0=30°,则弹头的弹道倾角为θ1=9.41°,弹头速度为![]() 弹头和干扰机分离后,需要根据A点的参数分别建立新的飞行弹道,建立的新弹道如图8所示。
弹头和干扰机分离后,需要根据A点的参数分别建立新的飞行弹道,建立的新弹道如图8所示。
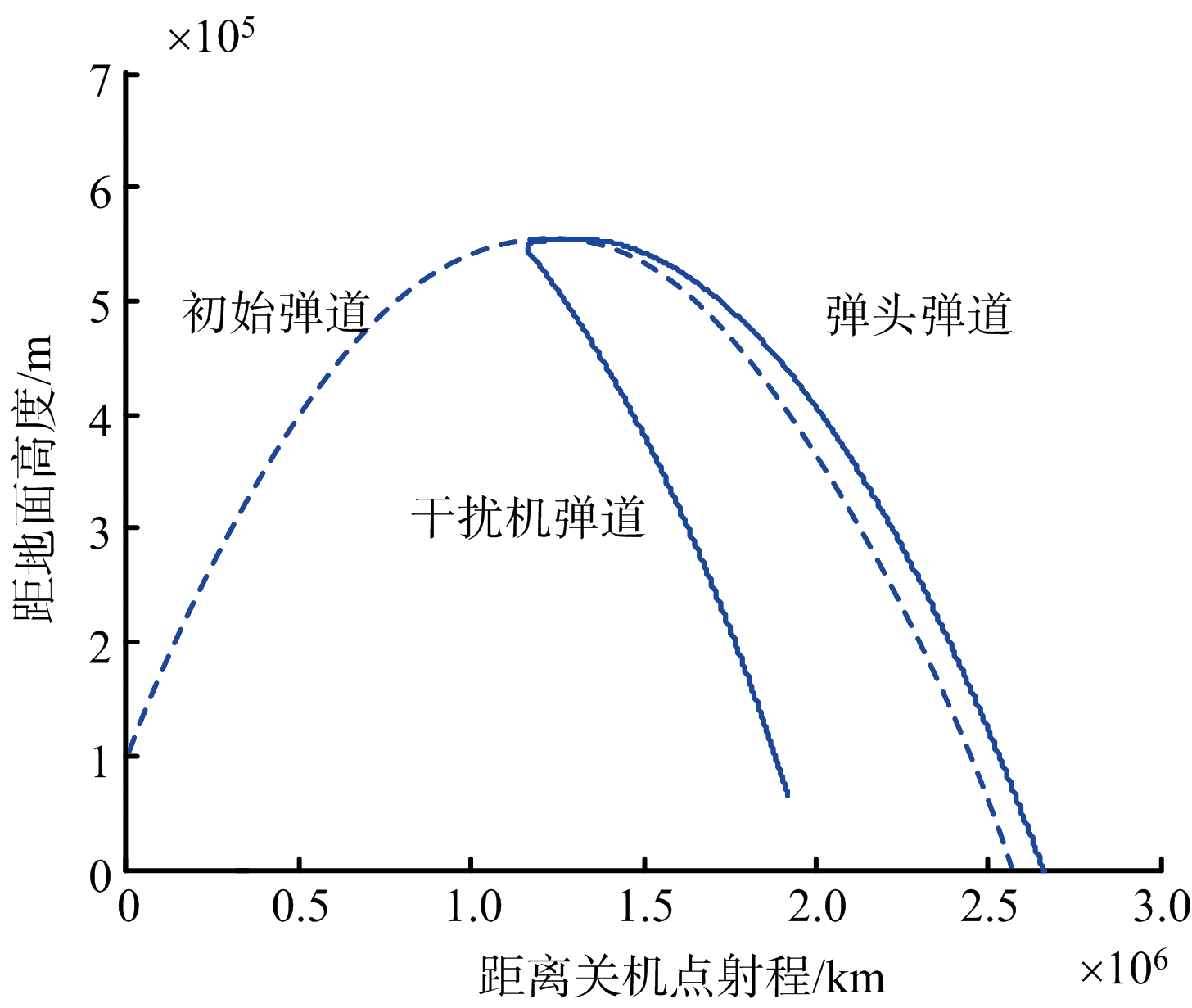
图8 干扰机和弹头弹道
从图8可以看出,弹头在释放干扰机后,弹道会有变化,可能会改变落点的位置,这并不是所希望的,但是由于弹头和干扰机质量比较大,这种偏差往往比较小。弹道目标轨道有偏差时,会有相应的控制算法进行修正[11-12],由于弹道修正不是本文的主要内容,这里不再赘述。释放干扰机会带来弹头速度和弹道倾角的偏差,减小这种偏差的主要途径是增大弹头和干扰机的质量比,以及减小释放干扰机时的抛出角度,使弹头和干扰机分离后速度矢量变化尽可能小。
干扰机被释放后,两者相对速度为:vx= 251 m/s,vy=2 079.4 m/s。相对速度的径向分量和横向分量为:vr=-vxcosα-vysinα,vt=vxsinα-vycosα。雷达波束宽度为1°,则干扰机和弹头刚好不同时处于雷达波束的时间满足![]() 由于干扰持续时间较长,方位角不能再认为是常量,而是关于时间的变量,则方位角为
由于干扰持续时间较长,方位角不能再认为是常量,而是关于时间的变量,则方位角为
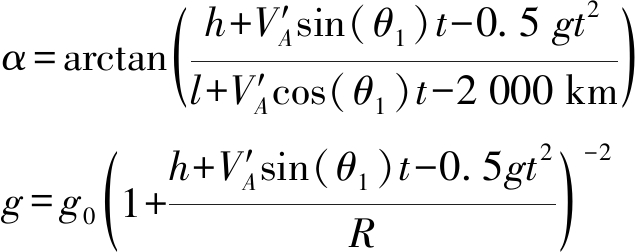
(28)
将数据代入,得到干扰机相对弹头的径向距离和横向距离,并对比表1数据中径向距离和横向距离的约束关系,若其不再满足这种约束关系,则干扰机和弹头不同时处于雷达波束内。得到干扰机和弹头刚好不同时处于雷达波束的时间为t=131 s,弹头的路程为l=535 km,t时间后方位角 α=115°,变化25°,根据式(12),则θ变化为25°,符合建立的干扰有效准则。
在弹头释放干扰机后的131 s内,雷达距离-多普勒域上始终存在形状清晰、姿态变化符合正常弹道目标的干扰像。并且随着时间的推移,干扰像和模糊的真实像距离越拉越大,雷达将会跟着清晰度更好的干扰像,从而把真实弹头从雷达视野拖出来,类似于窄带有源拖引干扰,使真弹头有足够时间和空间突防,因此是完全具有干扰效果的。
5 结束语
利用伴飞式干扰机和弹头的位置关系不同可以改变ISAR中干扰像姿态的特性,提出了一种姿态欺骗的干扰方法。推导了有效干扰时的姿态角,生成的干扰像始终比真实像更加清晰,更容易识别。解出了弹头释放干扰机的初始参数,并建立了干扰有效准则,进行了干扰效果分析。干扰效果分析表明,用该方法生成的干扰像能长时间停留在雷达距离-多普勒域上,造成类似窄带拖引干扰效果。同时,本文提出的干扰方法生成不依赖对地面雷达信号参数的测量,可以大大减少干扰机信号处理单元,因此干扰信号产生相对简单,效果明显,为实际应用提供了参考。
[1] 刘记红,徐少坤,韩国强,等. 基于压缩感知的进动目标ISAR成像方法[J]. 雷达科学与技术, 2017, 15(4):403-409.
LIU Jihong, XU Shaokun, HAN Guoqiang,et al. ISAR Imaging Method for Precession Targets Based on Compressed Sensing[J]. Radar Science and Technology, 2017, 15(4): 403-409. (in Chinese)
[2] 冯德军,王博,王伟. 弹道中段雷达目标识别研究进展综述[J]. 中国电子科学研究院学报, 2013, 8(2):142-148.
[3] 徐乐涛,冯德军,张文明,等. 基于间歇采样转发干扰的ISAR群目标生成方法[J]. 国防科技大学学报, 2013, 35(5):140-145.
[4] PAN Xiaoyi, WANG Wei, LIU Jin, et al. Modulation Effect and Inverse Synthetic Aperture Radar Imaging of Rotationally Symmetric Ballistic Targets with Precession[J]. IET Radar, Sonar & Navigation, 2013, 7(9):950-958.
[5] 胡恩诚. 空间目标ISAR成像算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2017.
[6] 陈津. 空间目标ISAR成像方法与特征分析研究[D]. 北京: 北京理工大学, 2016.
[7] WANG Xuesong, LIU Jiancheng, ZHANG Wenming, et al. Mathematic Principles of Interrupted-Sampling Repeater Jamming (ISRJ)[J]. Science in China(Series F: Information Sciences), 2007, 50(1):113-123.
[8] 张亚标,朱振波,汤子跃,等. 双站逆合成孔径雷达成像理论研究[J]. 电子与信息学报, 2006, 28(6):969-972.
[9] 周叶剑,张磊,王虹现,等. 空间轨道目标的逆合成孔径雷达成像质量分析[J]. 雷达学报, 2017, 6(1):17-24.
[10] 邹飞. 弹道中段目标逆合成孔径雷达成像技术研究[D]. 长沙: 国防科学技术大学, 2012.
[11] 冯燕来,王红杰,李旭,等. 基于外弹道修正理论的导弹落点预测精度评估方法[J]. 指挥信息系统与技术, 2017, 8(4):48-52.
[12] 赵雄飞,吴国东,王志军,等. 一维弹道修正机构优化设计和仿真分析[J]. 兵器装备工程学报, 2017, 38(3):42-45.
