0 引言
地球同步轨道合成孔径雷达(Geosynchronous Earth Orbit SAR,GEO SAR)工作在高度约为 35 786 km的地球同步轨道,每天卫星星下点轨迹相同、覆盖范围大、重访时间短(小时级)、可视时间长,适合进行大范围监测,是近些年国内外星载SAR领域的热门研究课题。
回波仿真是研究GEO SAR的一种重要方法,目前GEO SAR的回波仿真方法还在不断完善中。2009年,文献[1]对8字型轨道的GEO SAR进行了建模与仿真研究,该仿真方法假设地球为圆球体,卫星轨道为正圆,有明显的局限性。2013年,文献[2]提出了精确的坐标数值模型(ACNM)和高阶多普勒模型(DRM-n),但是所提模型没有考虑“Stop-Go”假设误差。2014年,文献[3]提出了一种考虑“Stop-Go”假设误差的等效中点距离模型,该模型是建立在正圆轨道下的,不适用于大偏心率椭圆轨道。2015年,文献[4]对GEO SAR回波的场景模型进行了研究,建立起一种曲面场景模型,但是,该模型是建立在局部球体假设下,可进一步改进。同年,文献[5-6]都提出了基于泰勒级数展开的非“走-停”假设的四阶距离模型,不足的是,这两种模型在一定合成孔径时间下满足成像要求。2016年,文献[7]利用STK软件导出卫星轨道坐标信息,在场景坐标系下建立距离向、方位向两维空时变的斜距模型,能够对大场景点阵目标进行斜视成像,但是,模型没有考虑“Stop-Go”假设斜距误差。
本文在综合考虑已有研究成果基础上,提出了一种改进的GEO SAR回波仿真方法。该方法主要有以下特点:1)适用于小偏心率大倾角和大偏心率小倾角等不同轨道构型;2)考虑了适用于GEO SAR的姿态导引方法;3)考虑了“Stop-Go”假设误差,精确计算雷达与目标的双程斜距;4)在椭球地表布设点阵目标。本文对两种轨道构型的GEO SAR分别进行了点阵目标的回波信号仿真和成像,验证了所提方法的有效性。
1 GEO SAR回波仿真关键步骤
1.1 GEO SAR轨道建模
卫星轨道可以由轨道六根数确定,其中包括轨道半长轴a、偏心率e、轨道倾角i、近地点幅角w、升交点赤经Ω以及过近地点时间tp。本文主要考虑两种轨道构型:8字型轨道和椭圆型轨道,对应的轨道参数特点分别为大倾角小偏心率和大偏心率小倾角。典型轨道参数如表1所示,在地心转动坐标系中典型星下点轨迹如图1所示。
表1 轨道参数

轨道参数8字型轨道椭圆型轨道a42164.1km42164.1kme0.00110.1i53°7.4°w90°90°Ω105°E105°E
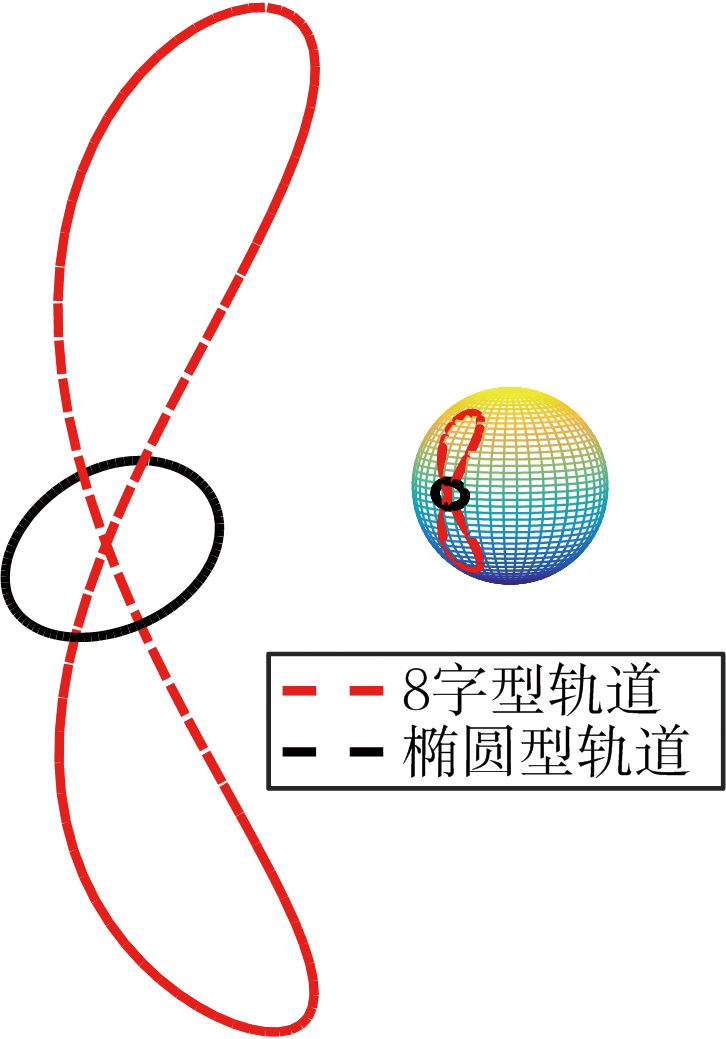
图1 GEO SAR的星下点轨迹
1.2 星地几何关系计算方法
GEO SAR在轨坐标信息可以根据星地几何关系通过坐标旋转得到,其中主要涉及场景坐标系[8]、地心转动坐标系(ECR)、地心不转动坐标系、轨道平面坐标系、卫星星体坐标系、卫星平台坐标系、天线坐标系七个坐标系,各个坐标系之间的转换关系以及转换矩阵在文献[9]中已经给出,本文不再赘述。
为了便于处理,将各个轨道参数统一转换到ECR坐标系下进行表示,基于星地几何关系,以t0为中心的一段时间内,(t0+ta)时刻卫星坐标Sg可以表示为
Sg(t0+ta)=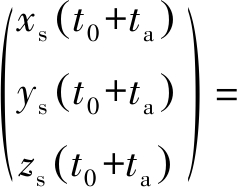
Ago(t0+ta)Aov·
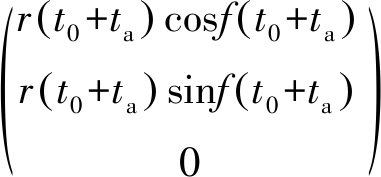
(1)
式中,r为卫星到地心的距离,f为真近心角。在天线坐标系中,设波束指向向量为Ua,将其转换到ECR坐标系下可得
Ug(t0+ta)=Ago(t0+ta)AovAvr(t0+ta)·
Are(t0+ta)Ua
(2)
式中,Ua=[sin(θa)sin(θl),cos(θl),-cos(θa)· sin(θl)]T,θl为天线下视角,θa为方位向角,设卫星与目标的斜距为![]() 波束与地球表面的交点坐标Pg可以表示为
波束与地球表面的交点坐标Pg可以表示为
![]()
(3)
将式(3)代入地球椭球方程,可以通过椭圆二次方程最小根方法求得![]() 的数值[10],根据卫星与目标的坐标可求得斜距信息:
的数值[10],根据卫星与目标的坐标可求得斜距信息:
Rt(ta)=|Sg-Pg|
(4)
将式(4)得到的Rt代入式(5)便可以得到回波信号[10]:
Sr(tr,ta)=![]()
(5)
式中,A0为散射系数,tr与ta分别为距离向和方位向时间,tac为波束中心穿越目标点的时刻,wr为距离向包络,它是一个与发射信号脉冲宽度有关的矩形窗,wa为天线的方位向函数。λ与c分别为波长和光速。
1.3 GEO SAR姿态导引方法
由于椭圆运动轨迹以及地球自转的影响,GEO SAR的相对运动速度方向偏离航迹方向,造成多普勒中心频率不为零,需要采用二维姿态导引来控制雷达波束指向与相对运动速度方向垂直[11],使多普勒中心频率为零。当卫星轨道的偏心率较小时,姿态导引可以将多普勒中心频率调整为零,当卫星轨道的偏心率较大时(如e=0.1),姿态导引会使波束照射到地球表面之外。为了在波束照射到地表的前提下将多普勒中心频率调整为零,文献[12]提出了一种基于最小多普勒平面的姿态导引方法。基于此方法,这里对表1中两种轨道构型的GEO SAR进行了姿态引导仿真,天线的下视角为-5.5°,结果如图2所示。图2(a)、图2(b)、图2(c)为8字型轨道GEO SAR仿真结果,图2(d)、图2(e)、图2(f)为椭圆型轨道GEO SAR仿真结果,其中θS,θP,θT三个角的具体定义见文献[12]。从仿真结果可以看出,当卫星轨道的偏心率较小时(如e<0.001),θS≥θP恒成立,通过二维姿态引导可以将多普勒中心频率调整为零。当卫星轨道的偏心率较大且倾角较小时(如e>0.1,i<20°),θS≥θP只在少数轨道位置处成立,其余轨道位置多普勒中心频率只能调整到最小。而当偏心率为0.1,倾角为7.4°时,θS≥θP只在近地点与远地点处的极短的轨道时间内成立,因此在该轨道构型下,SAR工作在斜视状态下。

图2 GEO SAR姿态导引仿真结果
1.4 双程斜距信息计算方法
通常基于“Stop-Go”假设计算星载SAR的双程斜距,该假设认为在脉冲发射与接收期间,卫星与目标相对静止,用脉冲发射时刻雷达与目标斜距的二倍来计算双程斜距。当卫星轨道高度低且偏心率较小时,这种方法计算得到的斜距误差较小,当卫星轨道较高或偏心率较大时,该方法会产生很大的误差。以偏心率为0.1、倾角为7.4°的GEO SAR来说,雷达与目标的斜距达到42 000 km量级,信号时延达到0.27 s量级,而卫星轨道半径的变化率在赤道附近达到300 m/s,此时“Stop-Go”假设将不再成立。
文献[13]采用二分查找法计算双程斜距信息,该方法计算精度高,可以作为衡量其他方法计算双程斜距精度的依据,但是该方法需要迭代运算,计算量较大。文献[14]提出利用发射时刻卫星与目标的斜距时延替代接收时刻卫星与目标的斜距时延,从而计算双程斜距信息,这里称该方法为“发射时延替代法”。图3给出了在照射时间为1 000 s时,两种轨道构型采用“Stop-Go”假设和发射时延替代法计算双程斜距时所产生的误差。其中图3(a)、图3(b)为8字型轨道仿真结果,图3(c)、图3(d)为椭圆型轨道仿真结果。结果表明,在“Stop-Go”假设下,8字型轨道的斜距误差在赤道附近高达4 m,而椭圆轨道斜距误差在赤道附近高达70 m,而采用发射时延替代法计算斜距,在两种轨道配置下斜距误差降到10-4量级,因此可以采用此方法计算双程斜距信息。
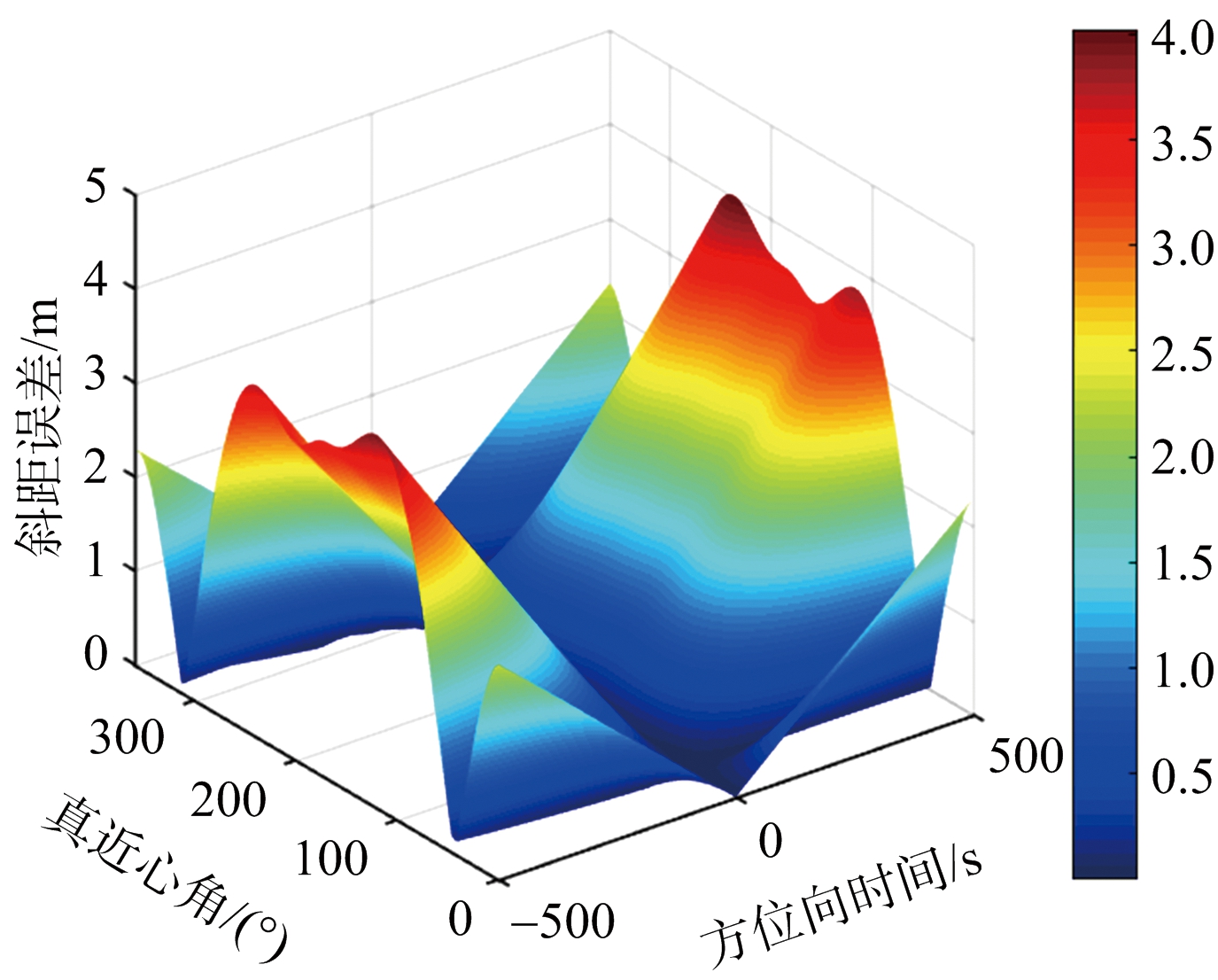
(a) “Stop-Go”假设斜距误差
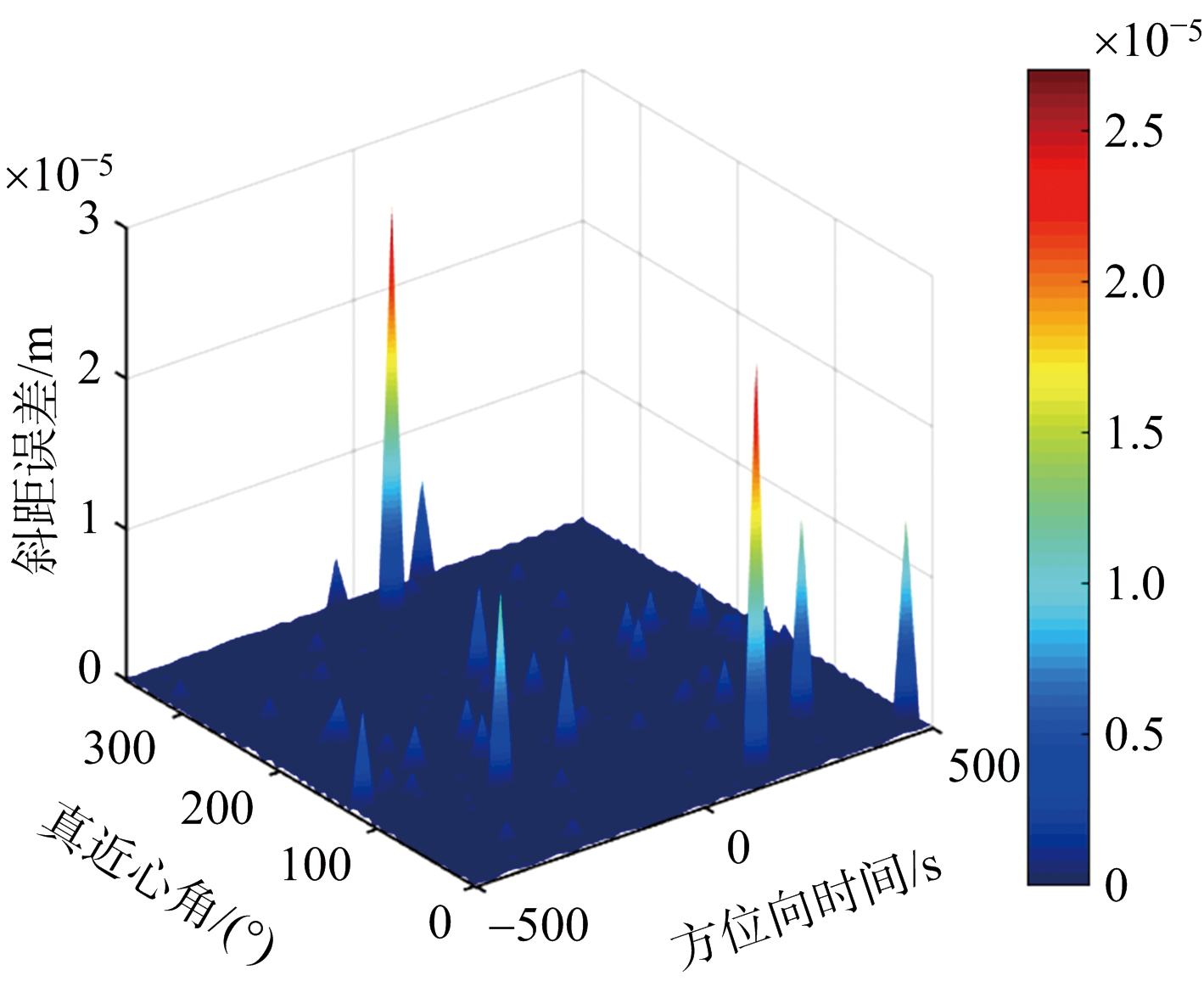
(b) “发射时延替代”斜距误差
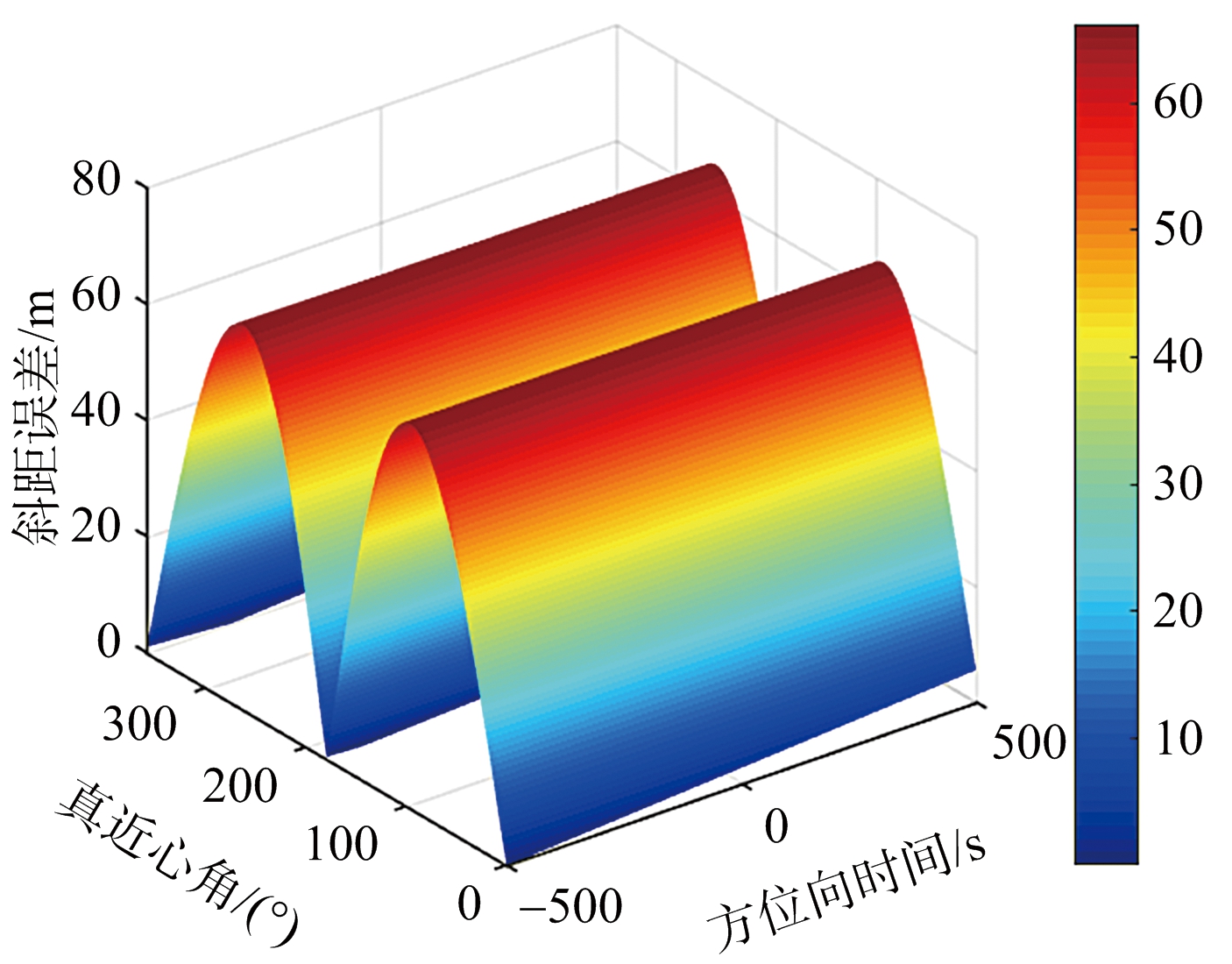
(c) “Stop-Go”假设斜距误差
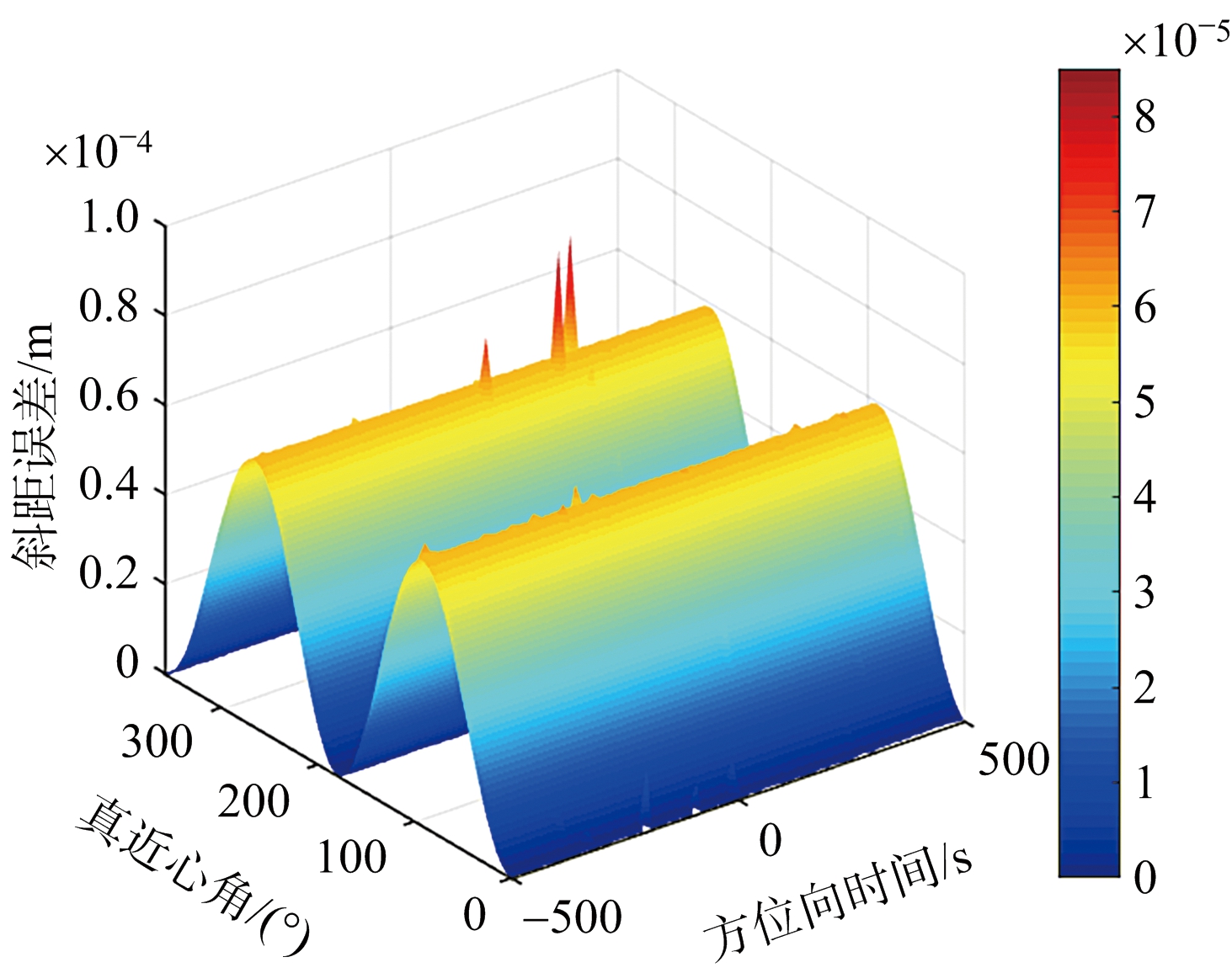
(d) “发射时延替代”斜距误差
图3 GEO SAR斜距计算误差
1.5 曲面场景构建方法
1.5.1 Vinceny公式
为了在大地椭球面上计算两个点目标间的精确距离信息及方位向角,引入Vincenty公式,Vincenty公式能够通过椭球面上目标点的经纬度以及两点间距离方位关系求解大地解算问题[15]。该公式利用贝塞尔球作为辅助球,首先将椭球面上目标点的坐标信息转换到贝塞尔球面上,在贝塞尔球上进行解算,然后利用椭球修正项将贝塞尔球上的解算结果归算到椭球上,从而达到在椭球上进行大地主题解算的目的。基于Vincenty公式的大地主题正算为:已知一个起始点目标的经纬度P1(Φ1,L1)和起始方位向角A12以及两点之间距离S,求解终点目标的经纬度P2(Φ2,L2)和方位向角A21,其中Φ2和L2的表达式为
Φ2=tan-1·
![]()
(6)
L2=L1+Δλ-f(1-C)sinA0σ+Csinσcos(2σm)+
Ccosσ(-1+2cos2(2σm))
(7)
基于Vincenty公式的大地主题反算为:已知起始点目标的经纬度P1(Φ1,L1)和终点目标的经纬度P2(Φ2,L2),求解方位向角A12和A21,以及距离S,其中S和A12的表达式为
S=bK1![]() cos(2σm)+
cos(2σm)+
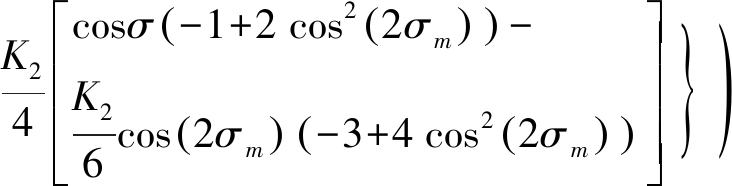
(8)
(9)
这里,式(6)~式(9)中具体参数可参考文献[16]。
1.5.2 波束覆盖区域求解方法
考虑地球为WGS-84椭球,雷达波束为圆锥形,下面给出波束覆盖边界的求解方法。在天线坐标系下,Xa轴与卫星速度方向相同,Ya轴与波束指向方向相同,Za轴满足右手定则。如图4所示,O点为天线相位中心,M点位于沿Y轴距离为S的波束前端界的圆周上,O′为波束前端所在圆的圆心,O′M与Z轴平行,设圆的半径为R,M点的坐标在天线坐标系下可以表示为M=[0,S,R],则任意圆锥形波束上的矢量ON都可以通过O′M沿Y轴旋转θm角得到。ON的表达式为
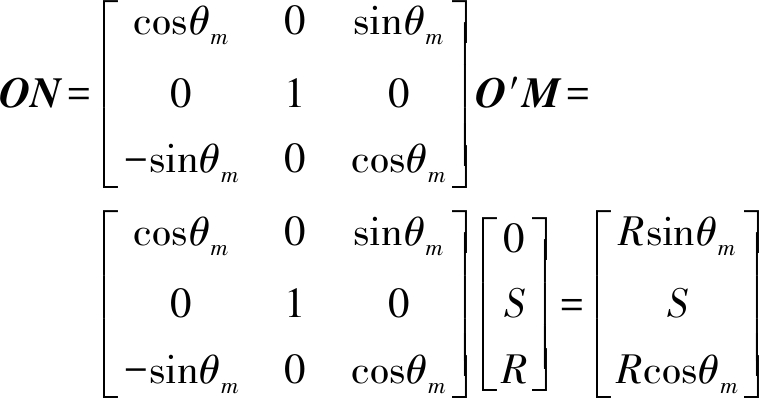
(10)
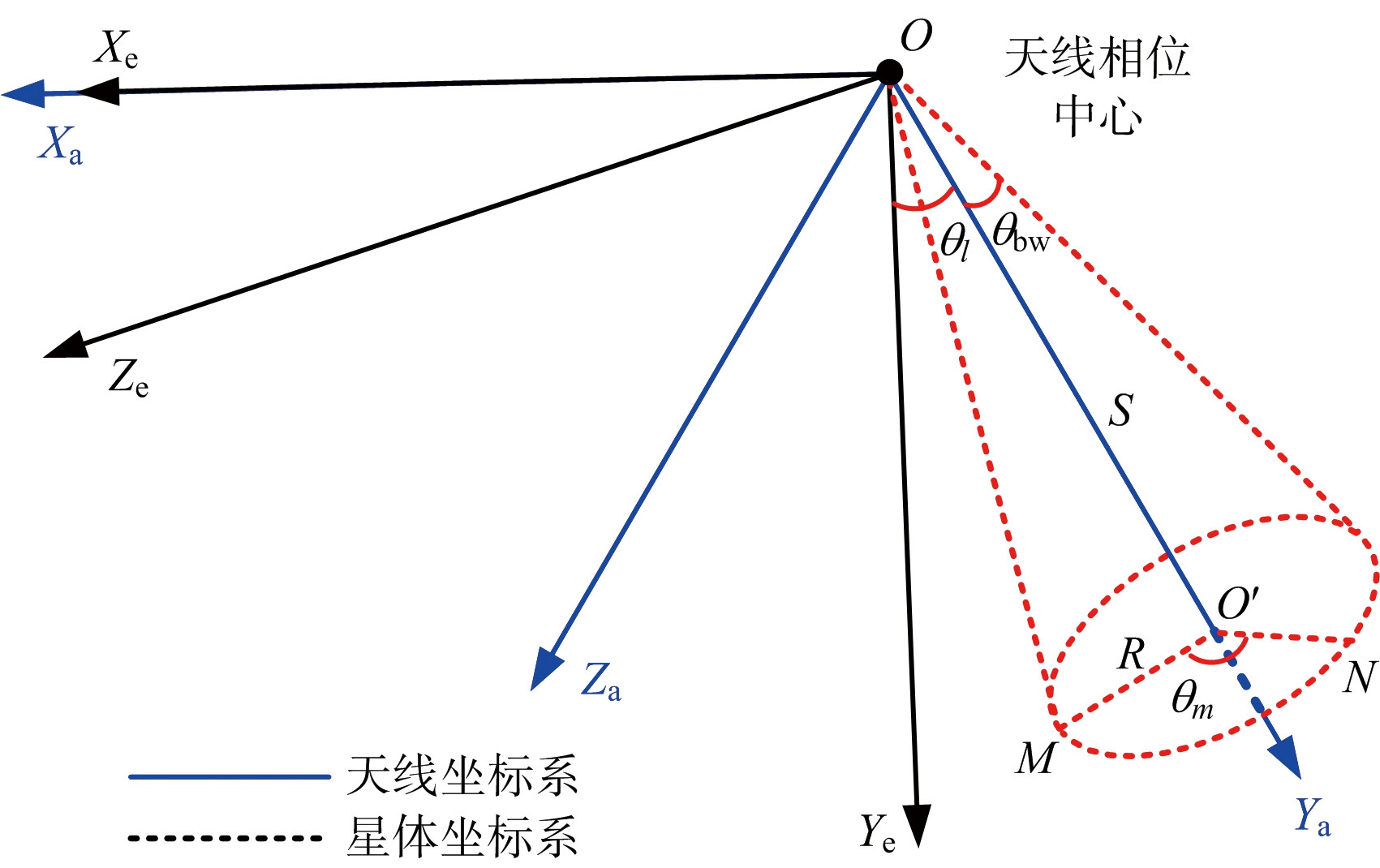
图4 天线坐标系下波束指向几何
设N=[x,y,z]T,则向量ON可以归一化为
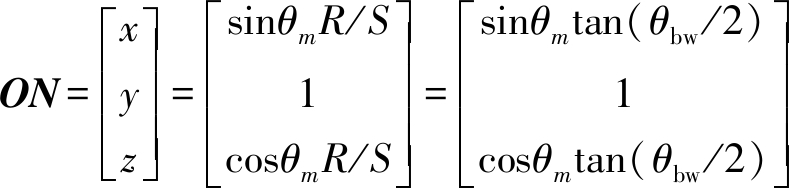
(11)
式中,R/S=tan(θbw/2),θbw为雷达天线3 dB波束宽度。将ON转换到地心转动坐标系下,然后在式(2)中,将Ua用ON替换掉,令θm=2π/N,当θm取遍0~2π上所有值时求解得到的Pg便是波束与地球的交点,即波束覆盖区域边界。图5给出了8字轨道和椭圆轨道波束覆盖区域的仿真结果和STK软件显示结果,其中,波束宽度为0.4°,8字型轨道GEO SAR经过了姿态导引。通过对比可以看出,所提出波束覆盖区域计算方法精确有效。
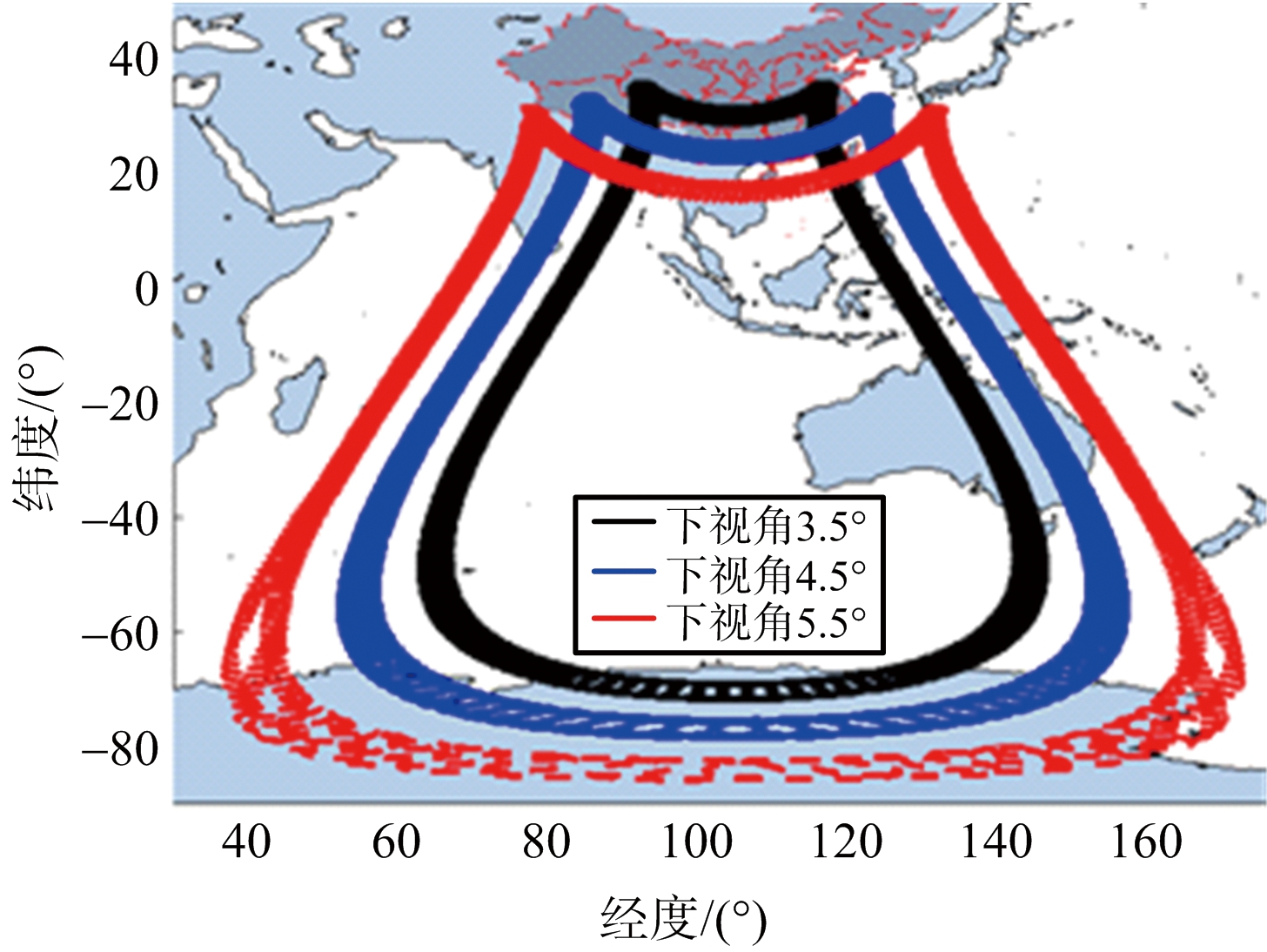
(a) 8字型轨道仿真结果
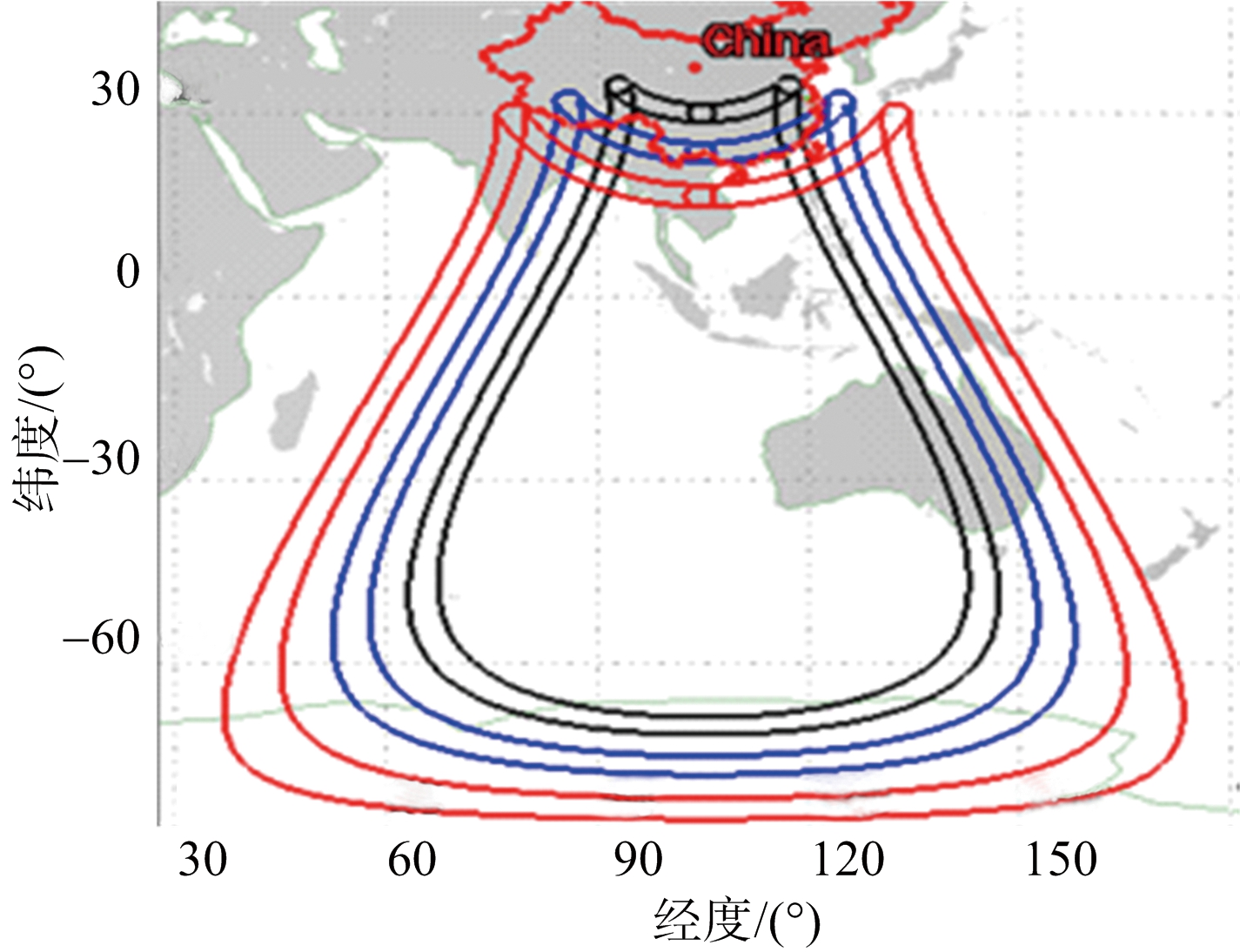
(b) 8字型轨道STK显示结果
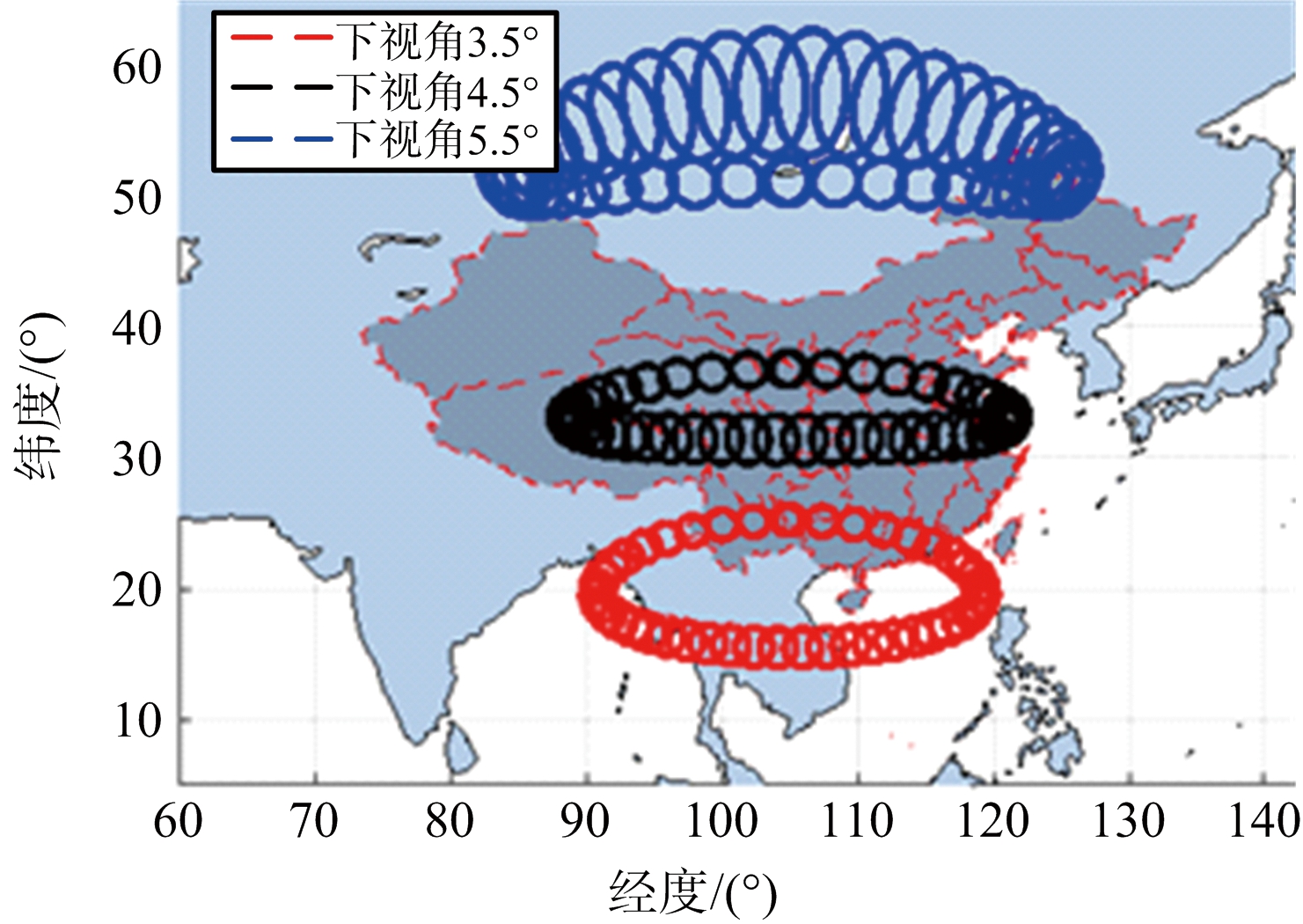
(c) 椭圆型轨道仿真结果
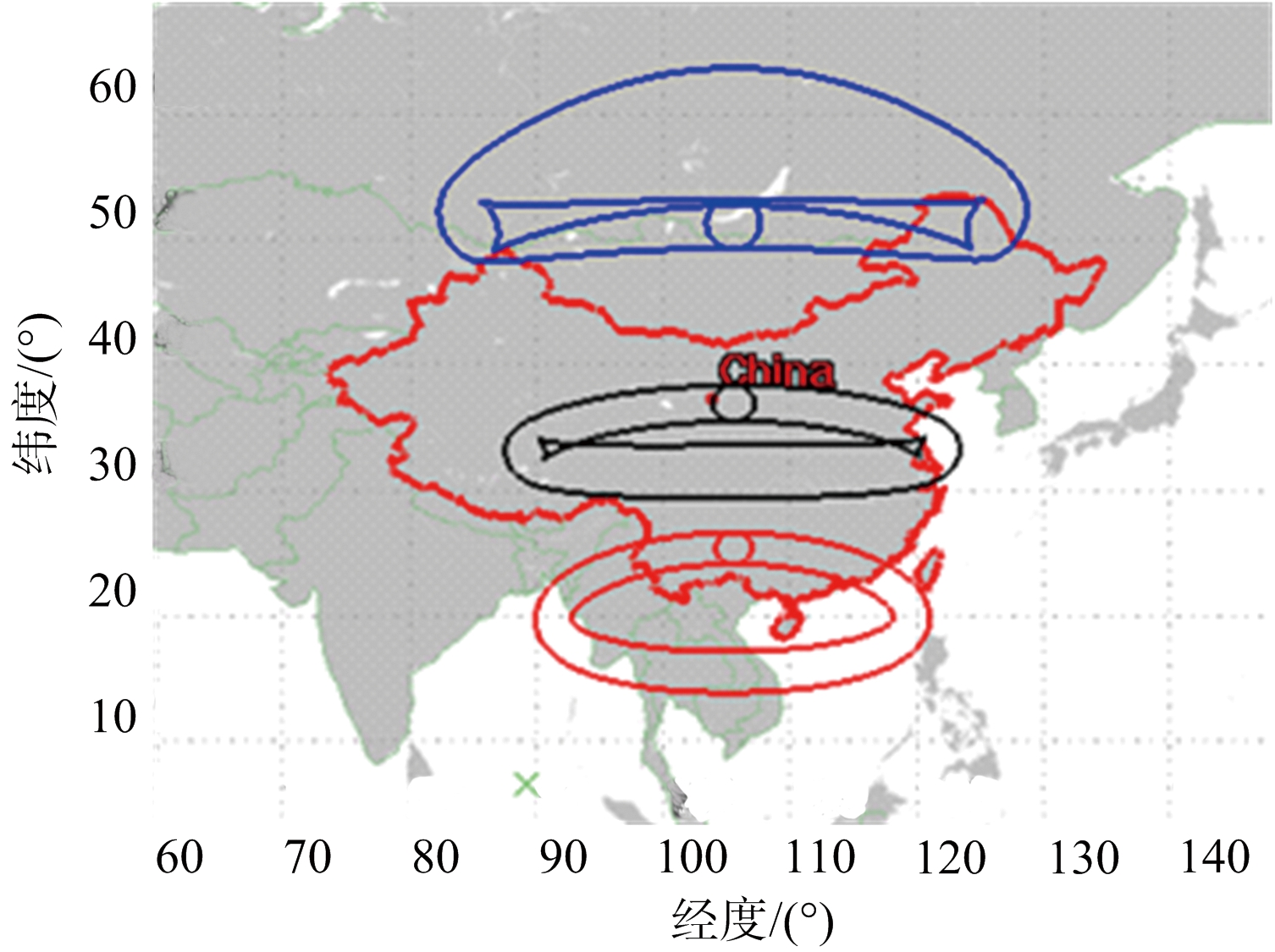
(d) 椭圆型轨道STK显示结果
图5 波束覆盖边界示意图
1.5.3 曲面场景模型构建方法
目前在GEO SAR回波仿真中,成像场景大都是建立在平面上,文献[4]在地球球体假设下对平面场景目标进行修正,给出曲面上点目标高度信息的计算方法。真实情况下地球是椭球体,在平面或者近似曲面上布设场景目标都会带来斜距误差。本文提出一种在椭球面上布设点阵目标的方法,该方法基于Vincenty公式,利用各点目标与参考点的距离和方位向角的相对关系来确定点目标的坐标信息,具体方法步骤如下:
1) 首先通过视角θl和距离向波束宽度θbw确定合成孔径中心时刻波束中心与地球表面交点Os的经纬度,通过最大视角θl+θbw/2、最小视角θl-θbw/2,计算同一方位时刻波束远端点A和波束近端点B的经纬度信息,如图6所示。
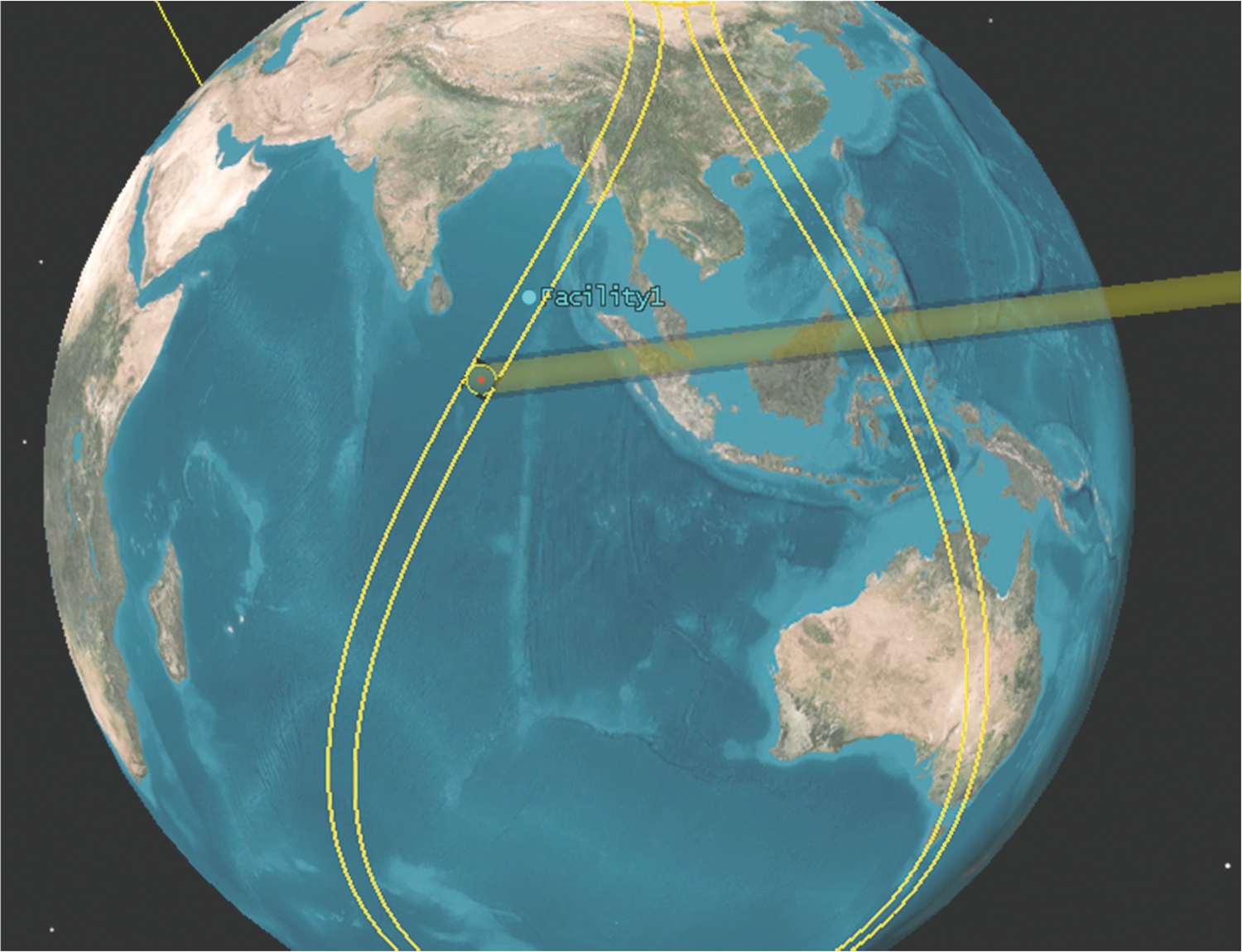
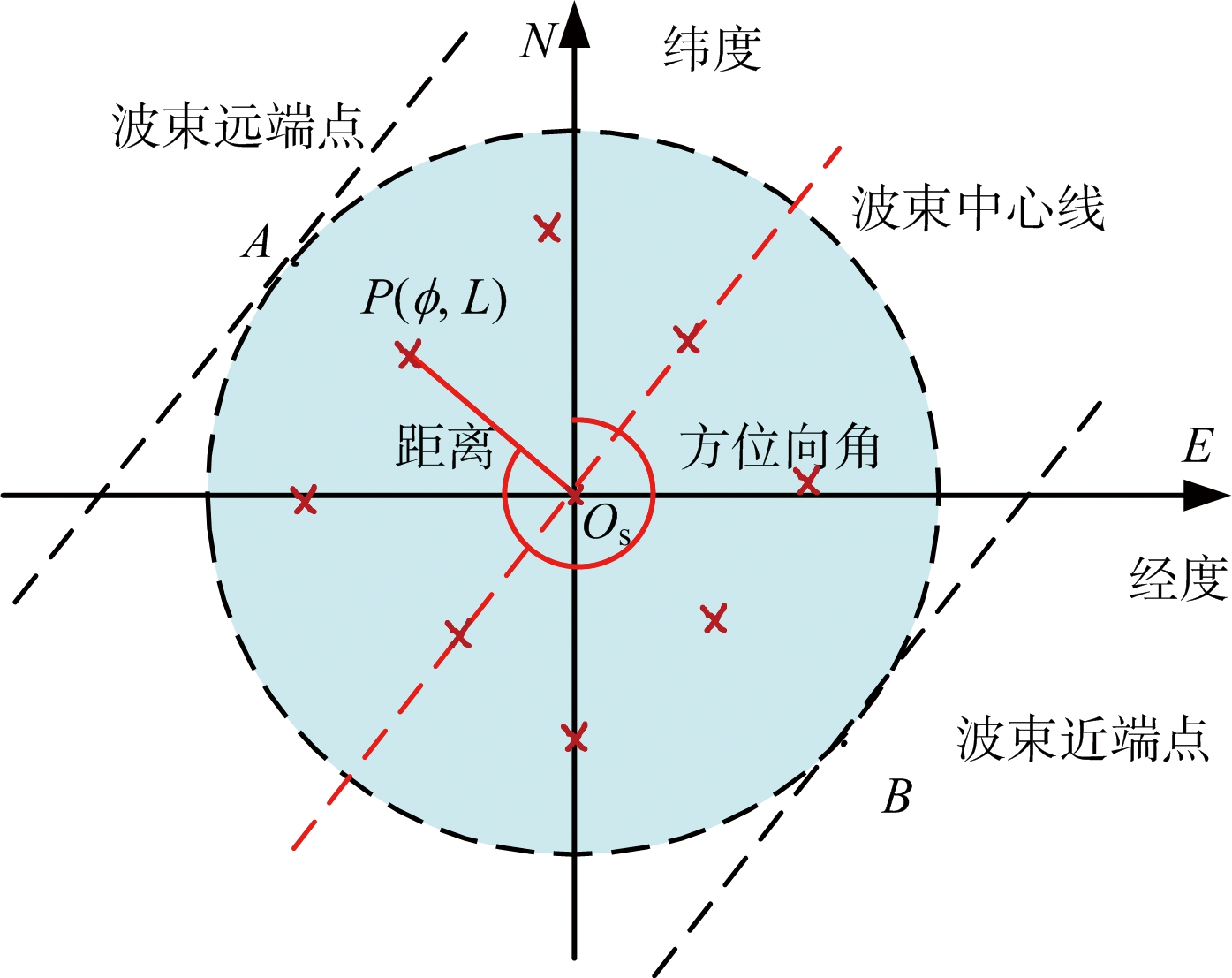
图6 曲面点阵目标构建方法示意图
2) 利用基Vincenty公式的大地主题反算方法计算出A,B,Os之间的方位向角。
3) 已知Os点的经纬度,以及与Os属于同一方位时刻的点目标与Os之间的方位向角,利用基Vincenty公式的大地主题正算方法计算出给定大地线长的目标点的经纬度。
4) 同理,以波束中心穿越Os的时刻为中心时刻,选择不同方位时刻便可以得到一组在同一方位向的点目标的经纬度。
5) 根据目标经纬度将目标位置转换到地心惯性坐标系下,便可以得到三维空间的点阵目标坐标。
基于上述曲面点阵目标的构建方法,给出了8字型轨道GEO SAR在近地点以及离近地点45°两个轨道位置、天线下视角为5.5°时,曲面点阵目标的布设结果。如图7所示,图7(a)、图7(b)为40 km×40 km的小场景点阵目标,其中图7(a)在经纬度坐标系下,图7(b)在场景坐标系下,可以看出不同点目标的高度信息不同,最高达到100 m。类似地,图7(c)~图7(f)给出了200 km×200 km大场景点阵目标,其中点目标高度差最高能达到 2 000 m,可见,考虑地球椭球面时,传统的平面场景布设方法完全不再适用。
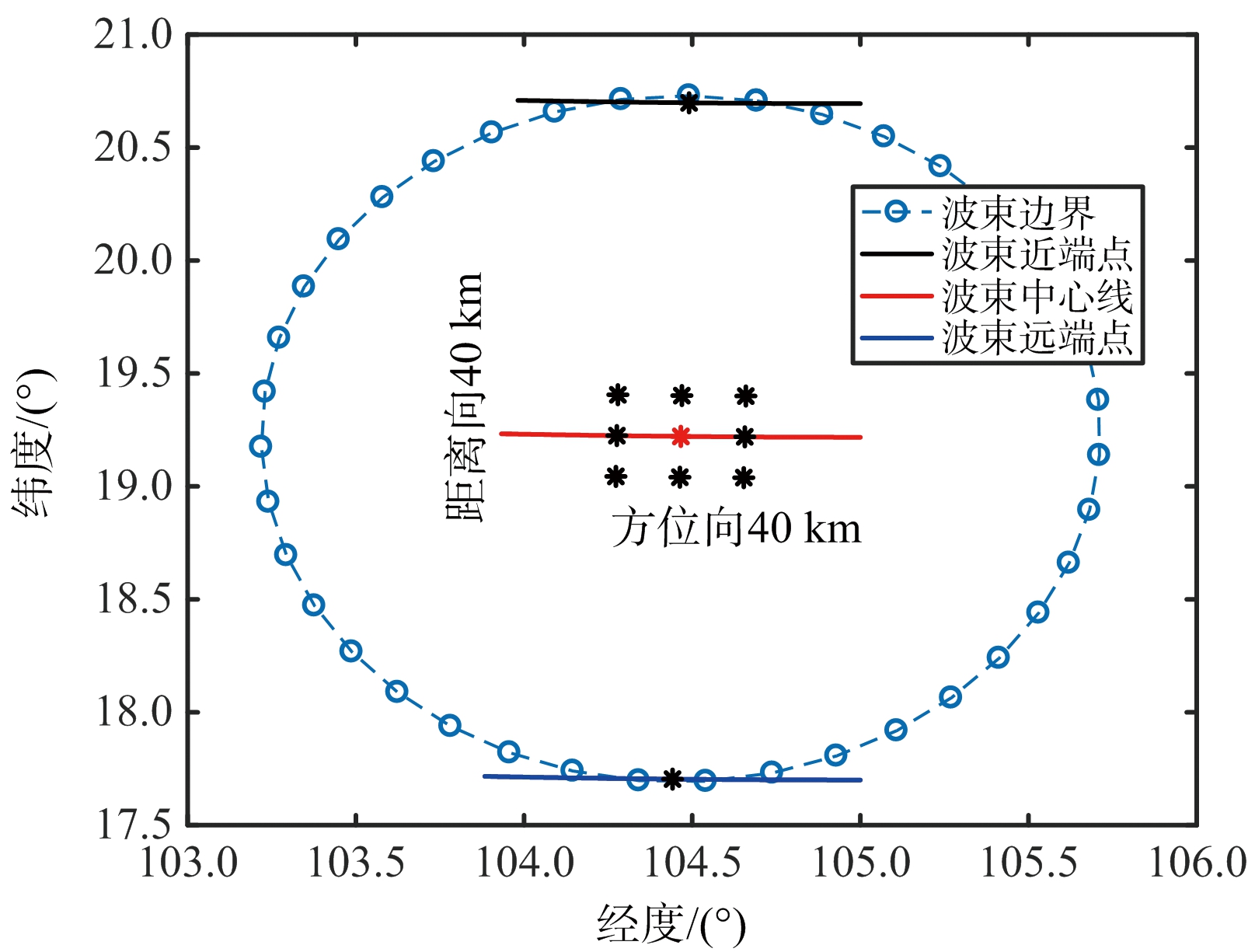
(a) 经纬度坐标系下小场景点阵目标
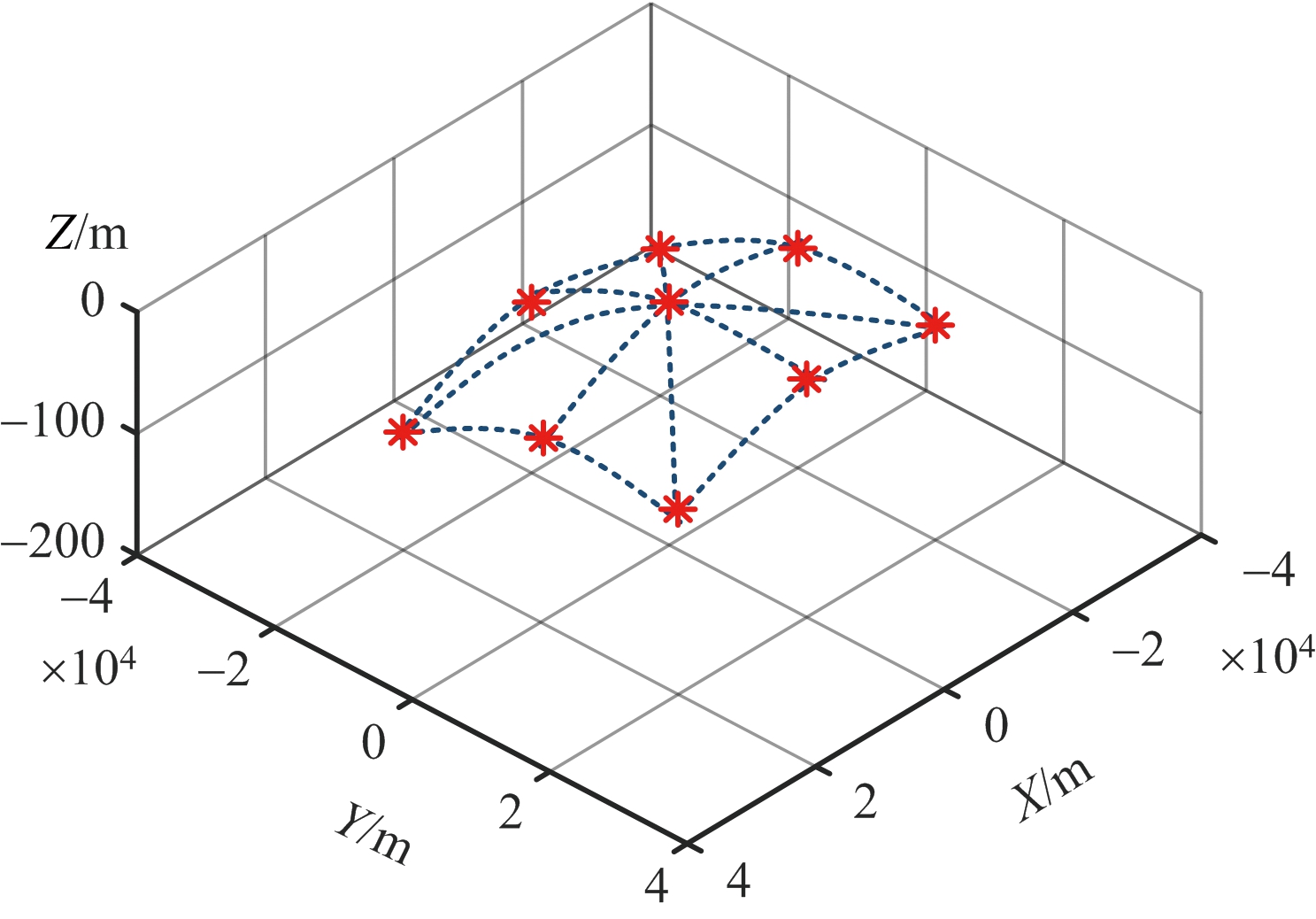
(b) ECR坐标系下小场景点阵目标
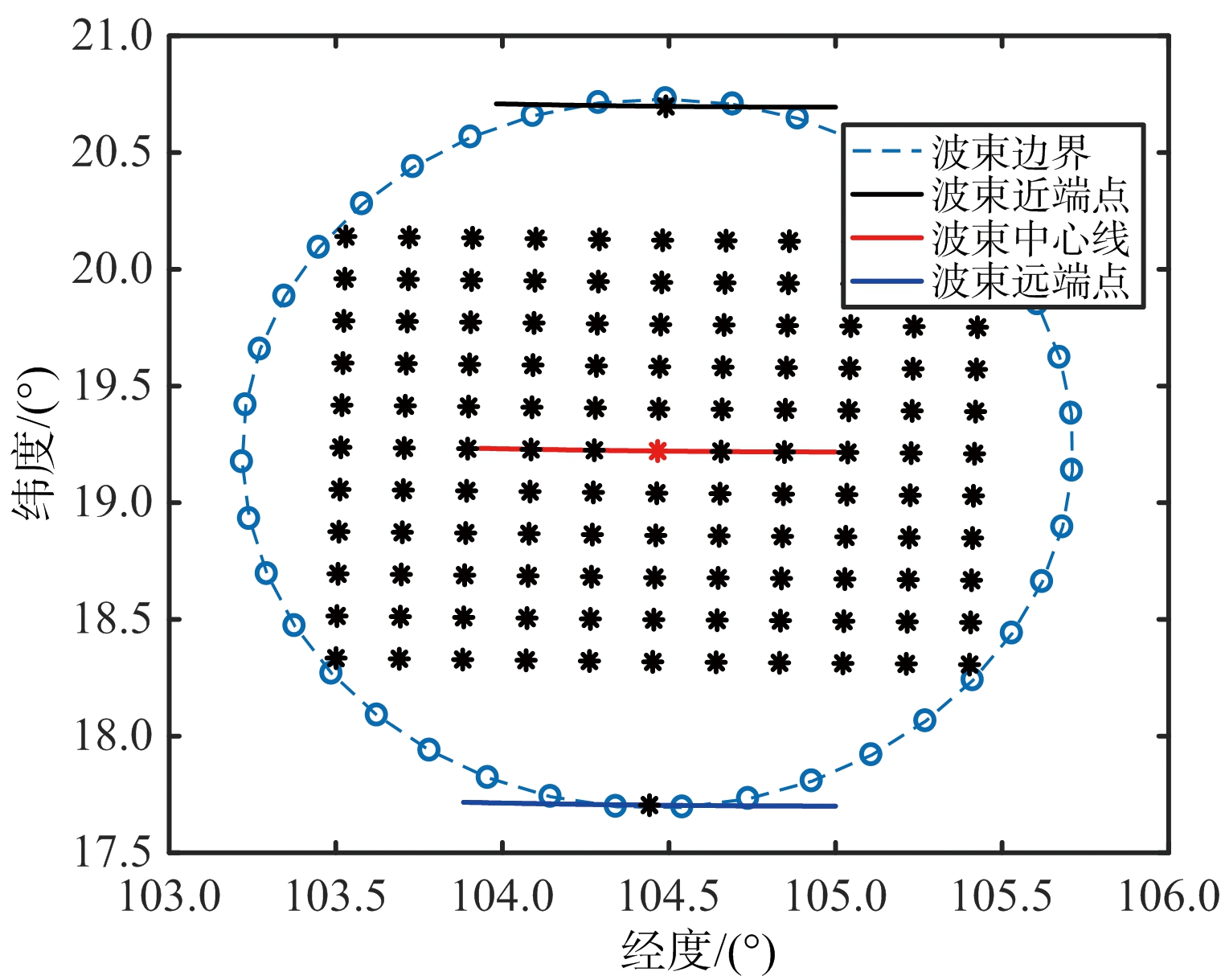
(c) 大场景点阵目标(真近心角0°)
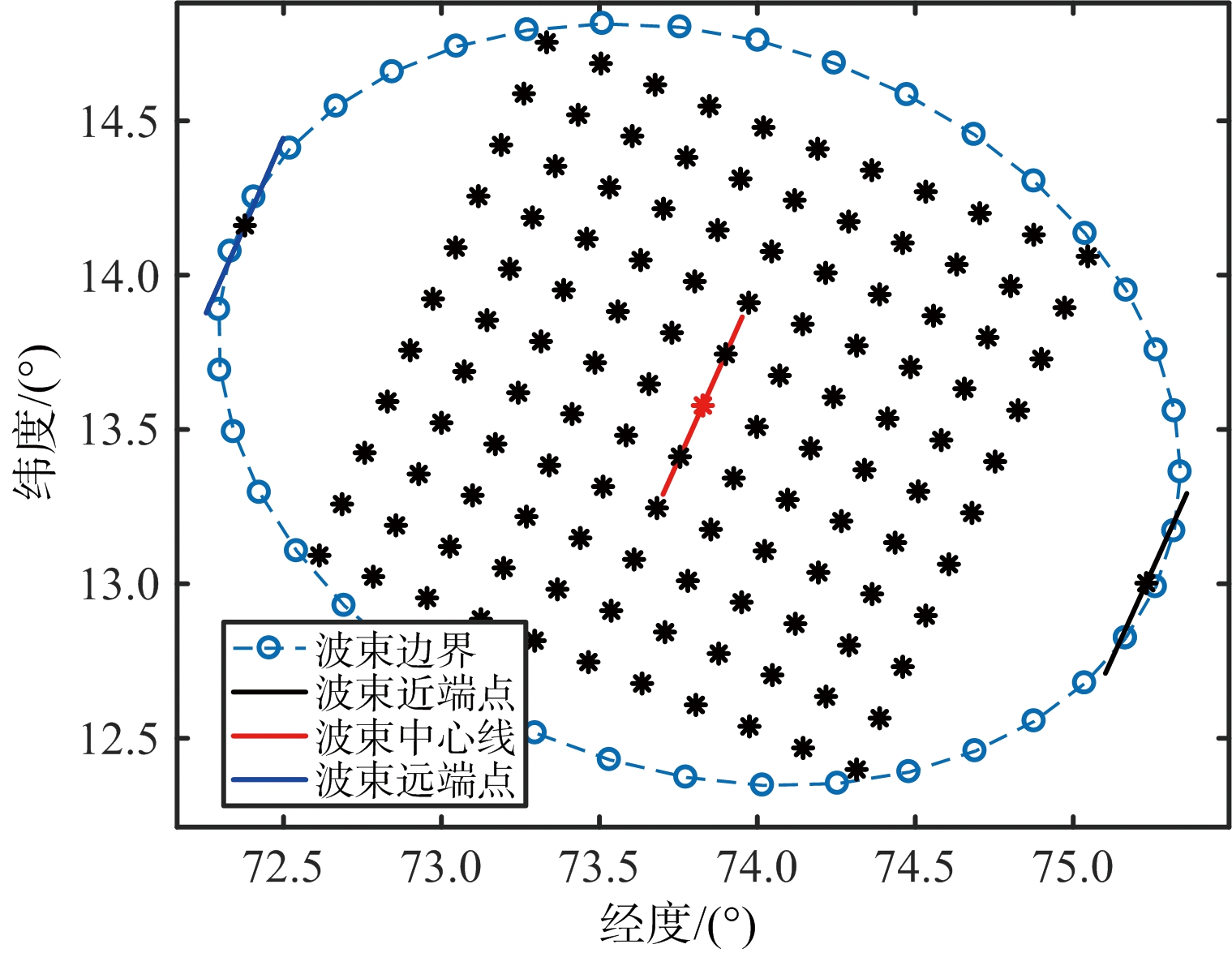
(d) 大场景点阵目标(真近心角45°)
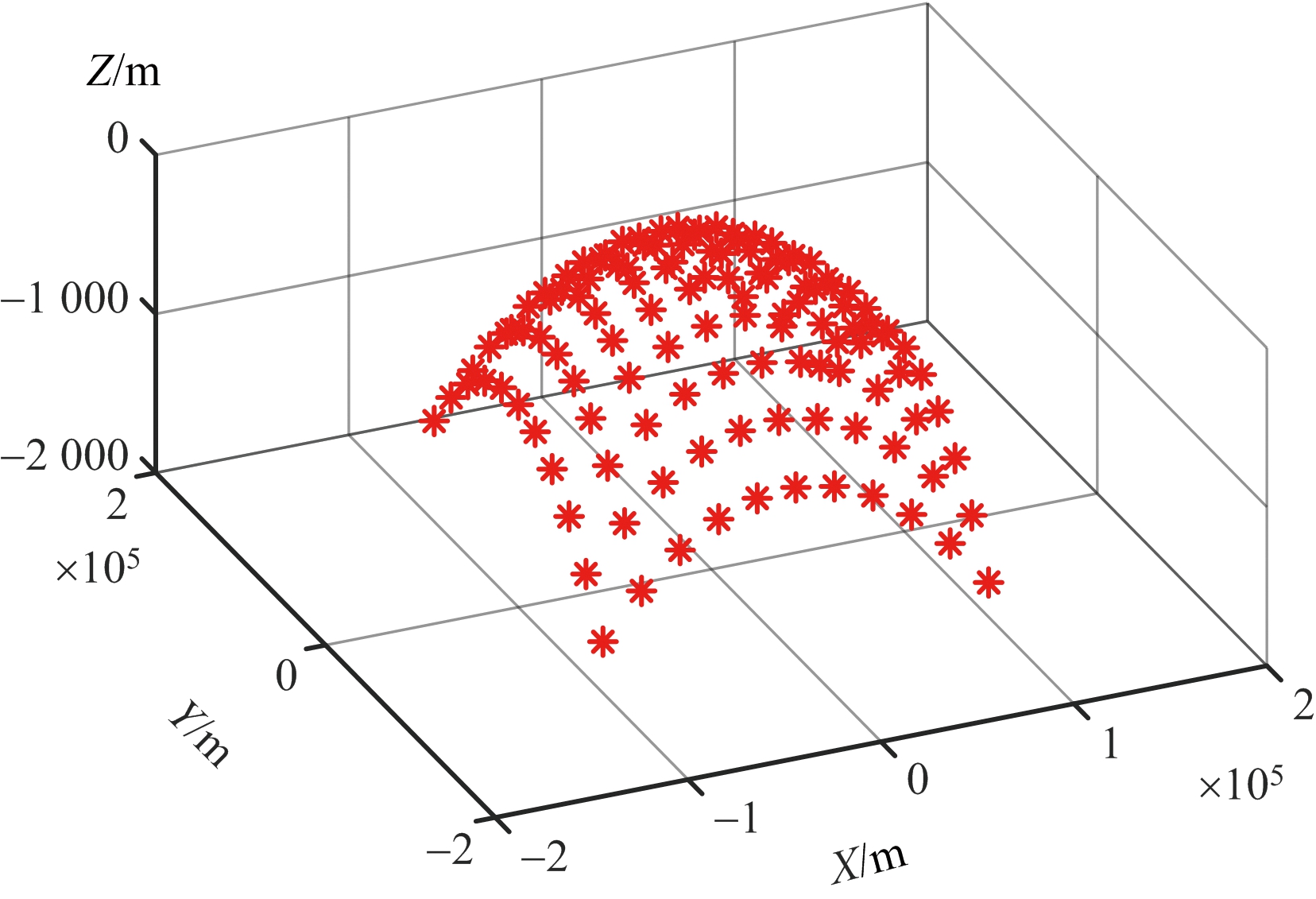
(e) ECR坐标系下大场景点阵目标
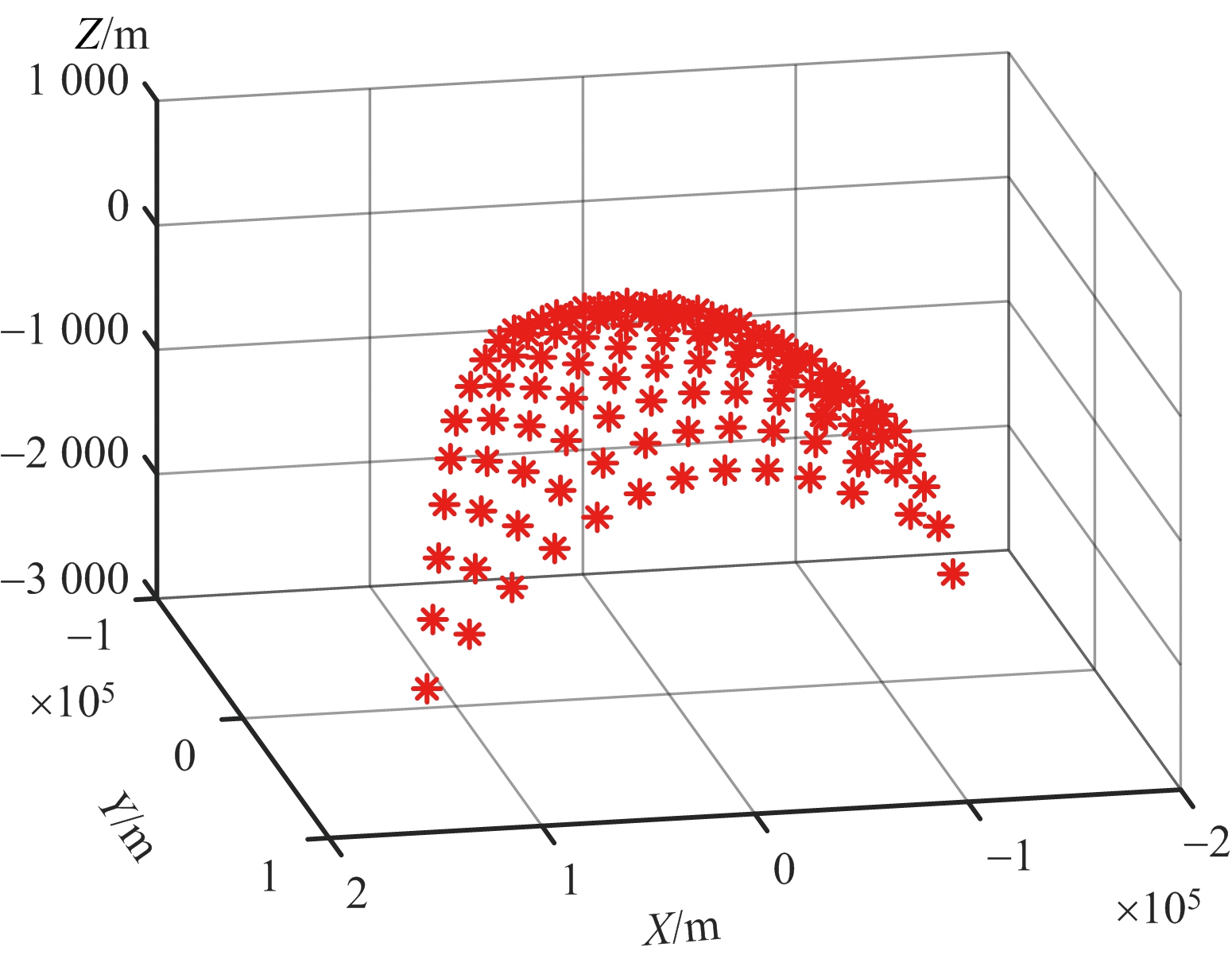
(f) ECR坐标系下小场景点阵目标
图7 曲面场景点阵目标及波束覆盖区示意图
2 回波仿真步骤
前文从轨道模型建立、姿态导引、双程斜距计算以及曲面点阵目标构建等几个方面介绍了GEO SAR回波仿真的关键步骤,下面给出GEO SAR回波仿真的具体步骤:
1) 设置卫星轨道参数、信号带宽、脉宽和采样率等雷达系统参数。
2) 选定卫星过近地点时间(即仿真中心时刻)t0及仿真时间ts,记方位向采样点数为N,则每个方位向采样样本对应的脉冲发射时刻可以表示为
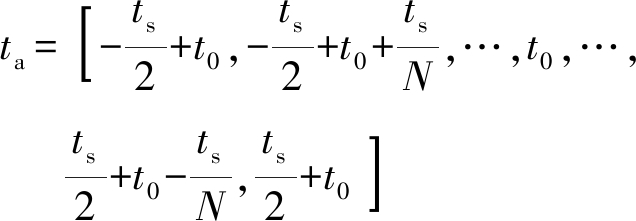
(12)
3) 若要求进行姿态导引,就根据1.3节中的方法计算出相应姿态导引角,否则,进入下一步。
4) 根据第1.5节中提出的场景目标构建方法布设点阵目标。
5) 针对每一个方位向时刻,由式(1)计算卫星在地心转动坐标系下的坐标和速度。
6) 由步骤5)中得到的脉冲发射时刻卫星坐标和步骤4)中布设的目标点的位置坐标计算脉冲发射时刻雷达到目标的单程斜距Rt,脉冲接收时刻可以近似为
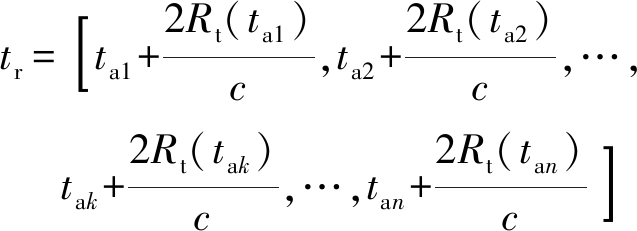
(13)
由tr确定卫星位置,从而求出脉冲接收时刻目标到雷达的斜距Rr,最终求得收发双程斜距:
Rtr=Rt(ta)+Rr(tr)
(14)
7) 由卫星速度矢量以及卫星与点目标的相对位置矢量,计算出每个点目标不同时刻所处的天线方位向角θ,表达式[17]为
(15)
式中,Vs为卫星在ECR坐标系中的速度,fdc为多普勒中心频率。由天线方位向角θ可以算出对应的方位向天线方向图增益为[10]wa(θ)= sinc2(0.886θ/θbw),式中θbw为方位向的波束宽度。
8) 最后,由双程斜距得到时延相位信息及求得天线方位图增益代入式(5)便可以得到精确的回波信息。
3 仿真验证
为了验证本文所提GEO SAR回波仿真方法的有效性,针对表1中两种轨道构型的GEO SAR,分别进行了曲面点阵目标布设,回波仿真和成像,信号带宽为18 MHz,采样率为20 MHz,脉冲宽度为20 μs,脉冲重复频率为100 Hz。仿真结果分别如图8和图9所示。
图8给出了8字轨迹GEO SAR卫星在赤道位置处的回波仿真和成像结果,目标为3×3点阵,目标间隔50 km,场景大小为100 km×100 km;成像中心视角为5.5°,仿真时间为400 s。图8(a)为9个点目标在经纬度坐标系下的坐标,图8(b)为仿真得到的点阵目标回波信号的实部,为方便进行性能评价,方位向天线方向图采用的是矩形窗,矩形窗的时间长度为100 s,图8(c)为使用BP成像算法的成像结果,表2给出了第1,5,9三个点目标的峰值旁瓣(PSLR),积分旁瓣(ISLR),以及地距分辨率(IRW),成像性能接近理论值,证明了所提仿真方法对8字轨迹GEO SAR的有效性。

(c) 成像结果
图8 8字型轨道仿真结果
同理,图9给出了椭圆轨迹GEO SAR的仿真结果。卫星真近心角为25°,目标为间隔20 km点阵,场景大小为40 km×40 km;成像中心视角为5.5°,仿真时间为400 s,矩形窗时间长度为180 s。表3给出了第1, 5, 9三个点目标的峰值旁瓣(PSLR),积分旁瓣(ISLR),以及地距分辨率(IRW),成像性能接近理论值,证明了所提仿真方法对椭圆轨迹GEO SAR的有效性。

(c) 成像结果
图9 椭圆型轨道仿真结果
表2 8字型轨道成像评估结果
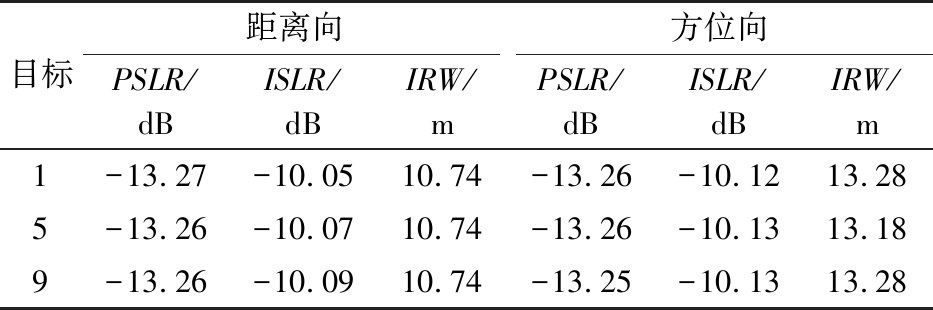
目标距离向方位向PSLR/dBISLR/dBIRW/mPSLR/dBISLR/dBIRW/m1-13.27-10.0510.74-13.26-10.1213.285-13.26-10.0710.74-13.26-10.1313.189-13.26-10.0910.74-13.25-10.1313.28
表3 椭圆型轨道成像评估结果
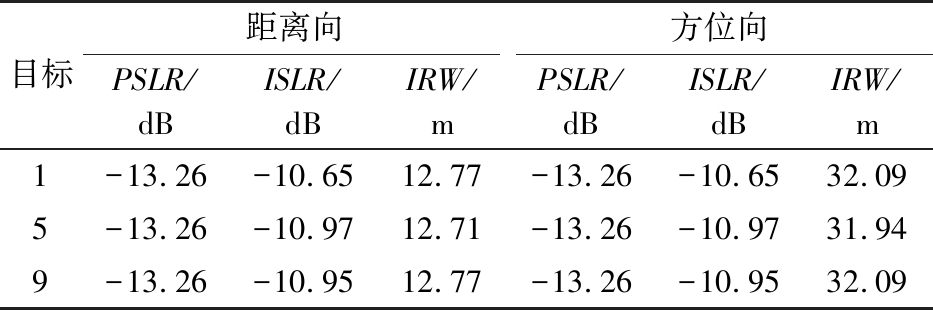
目标距离向方位向PSLR/dBISLR/dBIRW/mPSLR/dBISLR/dBIRW/m1-13.26-10.6512.77-13.26-10.6532.095-13.26-10.9712.71-13.26-10.9731.949-13.26-10.9512.77-13.26-10.9532.09
4 结束语
本文从建立轨道模型入手,针对不同轨道构型GEO SAR,分析了现有姿态导引方法的适用性以及“Stop-Go”假设下斜距计算误差,验证了使用“发射时延替代法”计算双程斜距的可行性,给出了圆锥形波束覆盖区域的计算方法。并提出了一种改进的地球同步轨道SAR回波仿真方法,该方法在椭球地球表面布设点阵目标,更符合实际情况,回波仿真和成像性能评估表明该仿真方法正确有效。
[1] 李财品,张洪太,陈文新. 地球同步轨道SAR回波建模与仿真[J]. 中国雷达, 2009(3):46-50.
[2] 赵秉吉. 地球同步轨道SAR关键技术研究[D]. 北京: 中国科学院大学, 2013:70-88.
[3] TIAN Yurun, GUO Shenglong, WANG Yu, et al. A Novel Geo-SAR Echo Simulation Method[C]∥ 10th European Conference on Synthetic Aperture Radar, Berlin, Germany: VDE, 2014:1-4.
[4] WANG Xiaobei, XU Yinhui, DING Zegang, et al. Research on Echo Simulation of Geosynchronous SAR[C]∥ IET International Radar Conference, Hangzhou: IET, 2015:1-5.
[5] WANG Zhuoqun, JIANG Yicheng, ZHANG Yun. Improved Slant Range Model and Imaging Method for Geosynchronous SAR[C]∥ IET International Radar Conference, Hangzhou: IET, 2015:1-5.
[6] HU Bin, JIANG Yicheng, ZHANG Yun, et al. Accurate Slant Range Model and Focusing Method in Geosynchronous SAR[C]∥ IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy: IEEE, 2015:4464-4467.
[7] 舒博正. 地球同步轨道SAR成像处理算法研究[D]. 北京: 北京理工大学, 2016:10-20.
[8] ZHANG Tianyi, DING Zegang, TIAN Weiming, et al. A 2-D Nonlinear Chirp Scaling Algorithm for High Squint GEO SAR Imaging Based on Optimal Azimuth Polynomial Compensation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(12):5724-5735.
[9] 黄丽佳. 中高轨道SAR成像算法研究[D]. 北京: 中国科学院大学, 2011:14-16.
[10] CUMMING I G, WONG F H. 合成孔径雷达成像:算法与实现[M]. 洪文,胡东辉,等译. 北京: 电子工业出版社, 2012:91-92,374-375.
[11] LONG Teng, DONG Xichao, HU Cheng, et al. A New Method of Zero-Doppler Centroid Control in GEO SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(3):512-516.
[12] CHEN Jianlai, SUN Guangcai, XING Mengdao, et al. A Two-Dimensional Beam-Steering Method to Simultaneously Consider Doppler Centroid and Ground Observation in GEO SAR[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(1):161-167.
[13] ZHANG Xin, HUANG Puming, WANG Weiwei. Equivalent Slant Range Model for Geosynchronous SAR[J]. Electronics Letters, 2015, 51(10):783-785.
[14] 刘娇,李财品,谭小敏,等. GEO SAR非“停走停”特性分析[J]. 现代雷达, 2014, 36(10):38-42.
[15] 李业,任鸿翔,朱耀辉. 一种改进的雷达模拟器回波图像生成算法[J]. 大连海事大学学报, 2016, 42(3):123-128.
[16] WIKIPEDIA. Vincenty’s Formulae[EB/OL]. [2017-05-20]. https:∥en.wikipedia.org/wiki/Vincenty%27s_formulae.
[17] 李财品,何明一. 地球同步轨道SAR方位模糊度研究[J]. 信号处理, 2015, 31(6):694-701.


