0 引言
针对日益严峻的雷达目标探测环境，在电子技术发展的基础上，国外学者将通信领域多输入多输出(Multi-Input Multi-Output, MIMO)思想引入雷达领域建立起MIMO雷达概念。MIMO雷达不同天线可以发射任意波形，相比传统雷达具有更多的自由度，也因此可以进一步提升目标发现、定位等性能，受到雷达界广泛关注，在过去的10多年里一直是研究热点之一[1-5]。
OFDM(Orthogonal Frequency Division Multiplexing)信号具有多个并行正交子载波，Sen研究了各子载波的自适应调制，以提高多径环境中雷达对目标的检测性能[6]，并进一步将OFDM信号应用于集中式MIMO雷达，研究了集中式OFDM-MIMO雷达低空目标跟踪场景下的波形设计问题[7]。文献[8-10]研究了分布式OFDM-MIMO雷达包络对齐、目标的非相参检测、MTI处理以及高速目标的检测前跟踪算法。文献[11]研究了分布式OFDM-MIMO雷达在非高斯杂波下回波信号参差补偿问题。文献[12]研究了集中式OFDM-MIMO雷达对目标的广义似然比检测算法。在研究集中式OFDM-MIMO雷达目标探测问题时，通常没有在算法设计阶段考虑多个频率通道的独立性以及对检测算法性能的理论分析。
我们知道，目标和杂波在不同的频段具有不同的散射特性，OFDM-MIMO雷达通过发射具有一定频率间隔的多频信号探测目标从而获得独立的目标回波，多个独立的频率通道可以获取更多的目标信息，可以提高目标的探测性能[7,13-14]。相比分布式OFDM-MIMO雷达，集中式OFDM-MIMO雷达可以避免包络对齐等问题，具有更好的可实现性，因此本文主要对集中式OFDM-MIMO雷达展开研究。针对集中式OFDM-MIMO雷达在未知杂波中目标检测问题，在给出集中式OFDM-MIMO雷达回波数据模型的基础上，考虑集中式OFDM-MIMO雷达不同频率通道回波数据的独立性，基于一步和两步广义最大似然比准则，给出了两种检测器，并分析了其恒虚警性能。两种检测器利用集中式OFDM-MIMO雷达频率分集特性，降低了杂波协方差矩阵求逆维数，也因此同时降低了杂波协方差矩阵的估计难度。
1 集中式OFDM-MIMO雷达回波模型
如图1所示，假设集中式OFDM-MIMO雷达由L个收发阵元组成一均匀线阵，阵元间距为d，第l个阵元的位置记为(d(l-1),0,0)，其发射信号为sl(t)，相干处理脉冲数为N，脉冲重复周期为TPRI。
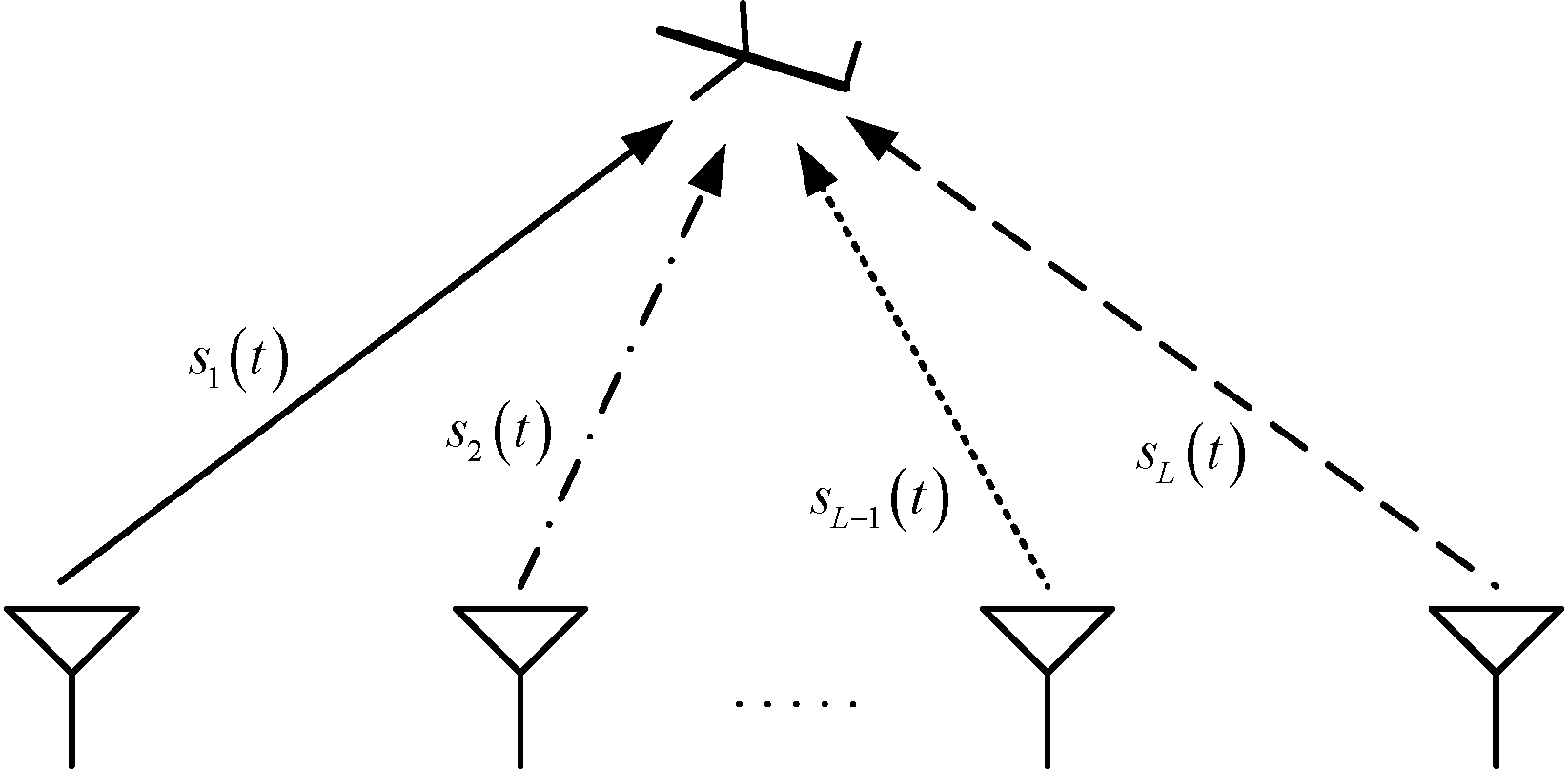
图1 集中式OFDM-MIMO雷达示意图
集中式OFDM-MIMO雷达回波同时由L个阵元接收，通过对每个阵元的接收回波进行L路混频和低通滤波，从而获得L组阵列回波信号，每组阵列回波信号对应一个频率通道，具有L个数据。当Δf满足式(1)[14]：
(1)
不同频率通道回波信号独立，其中D为目标尺寸，c为光速，ε为严格性因子，一般取0.5。此时，集中式OFDM-MIMO雷达可有效实现频率分集增加自由度，从而可以提高雷达性能。
在频率分集条件下，对于第l个频率通道，假设有一个目标，其回波强度为al。该目标所在距离单元回波记为
杂波记为
共有K个参考距离单元，对于第k个参考单元，其回波记为
杂波记为
目标相对雷达角度为θ，速度为v，则目标的归一化空间频率和多普勒频率分
和
则空间导向向量
和时间导向向量
分别为
(2)
(3)
式中，T表示转置。因此，第l个接收通道的信号为
⊗
(4)
式中，⊗表示Kronecker积。
定义如下N1=L2N维列向量：
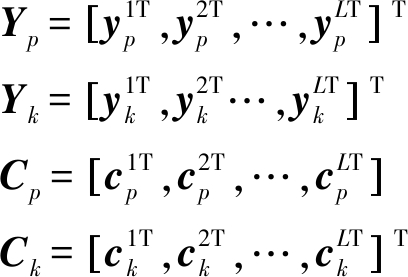
(5)
得到以下集中式OFDM-MIMO雷达目标二元假设检验问题：
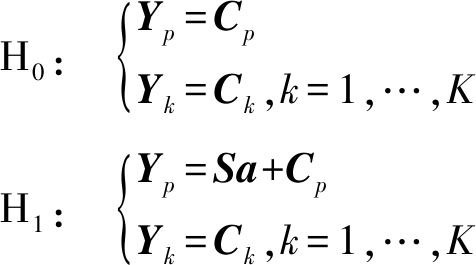
(6)
式中，
(7)
⊗
表示以s1,s2,…,sL为对角元素的对角矩阵。
记各频率通道杂波协方差矩阵
为共轭转置。在频率分集条件下，集中式OFDM-MIMO各频率通道杂波
和
互相独立，杂波协方差矩阵为块对角矩阵，可表示为
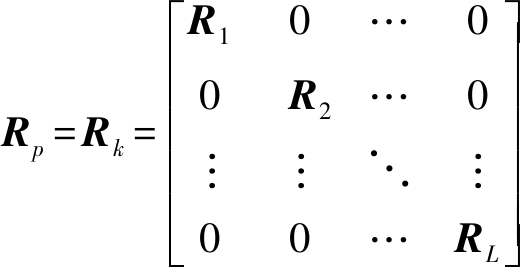
(8)
因此，Yp和Yk的联合概率密度函数为
(9)
(10)
式中，
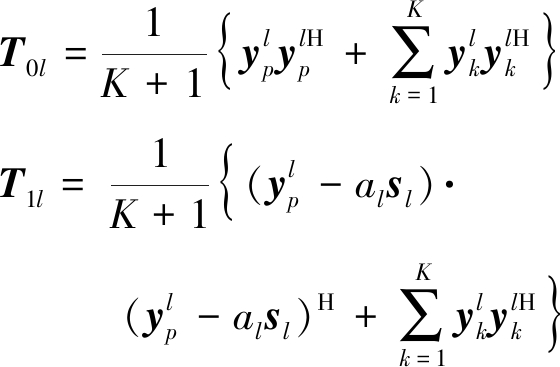
(11)
‖·‖表示矩阵的行列式，tr(·)表示矩阵的迹。
由以上回波模型，当集中式OFDM-MIMO雷达满足通道独立性条件时，各个通道的目标回波强度不同，杂波也相互独立。由于不同频率通道回波数据的独立性，相比于普通集中式MIMO雷达，集中式OFDM-MIMO雷达具有新的目标分集特性以及杂波对抗性能。相比于分布式MIMO雷达，集中OFDM-MIMO雷达避免了不同通道数据包络对齐等难题，实现难度更低。
2 集中式OFDM-MIMO雷达GLRT检测器与AMF检测器
本节首先在式(6)所给出的集中式OFDM-MIMO雷达回波模型基础上，基于一步和两步广义最大似然比准则，给出集中式OFDM-MIMO雷达GLRT检测器[15]和AMF检测器[16]，然后分析这两种检测器的恒虚警特性。
2.1 集中式OFDM-MIMO雷达GLRT检测器
由一步广义似然比准则[15]以及式(6)、式(9)～式(11)，集中式OFDM-MIMO雷达GLRT检测器可表示为
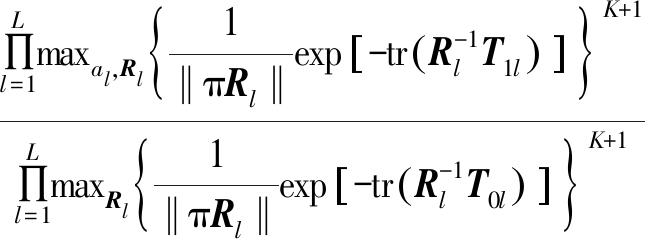
(12)
首先对式(12)分子、分母分别关于Rl最大化：
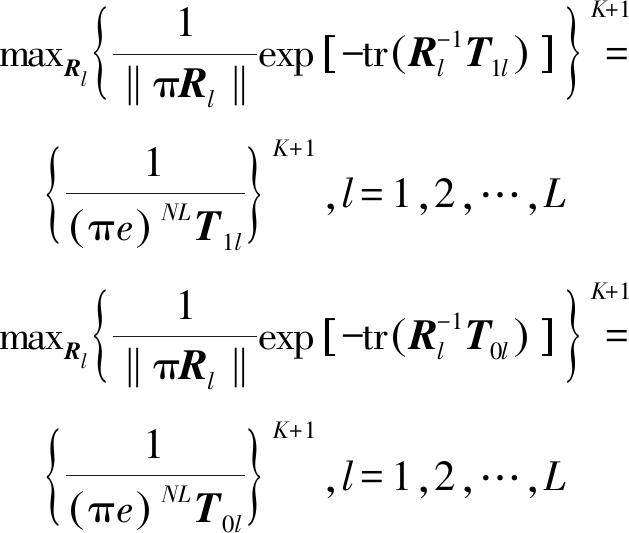
(13)
进而可以将式(12)表示为
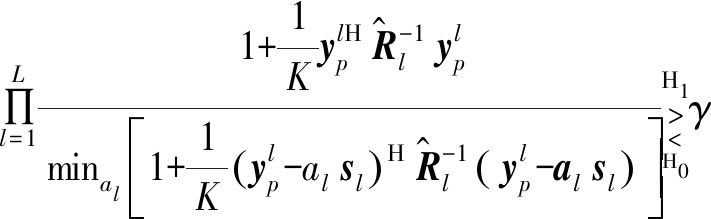
(14)
式中,
进一步对式(14)关于al最大化，可得al的最小二乘估计
最后将
代入式(14)，可得集中式OFDM-MIMO雷达GLRT检测器的表达式：
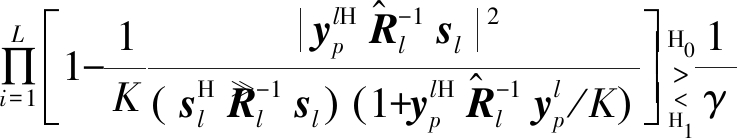
(15)
2.2 集中式OFDM-MIMO雷达AMF检测器
由两步广义似然比准则[16]，以及式(6)、式(9)～式(11)，首先假设杂波协方差矩阵Rl已知，可以将集中式OFDM-MIMO雷达AMF检测器表示为
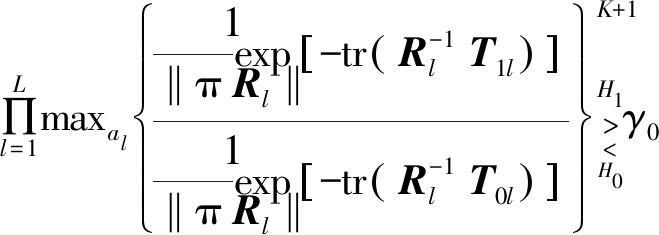
(16)
对式(16)关于al最大化，得到al的最小二乘估计为
进而式(16)可表示为
(17)
最后，用Rl的估计值
代替式(17)中的Rl，得到集中式OFDM-MIMO雷达AMF检测器的表达式：
(18)
2.3 两种检测器恒虚警性能分析
为了方便研究两个检测器的统计特性，首先将式(15)和式(18)分别改写成式(19)和式(20)：
(19)
(20)
式中，
(21)
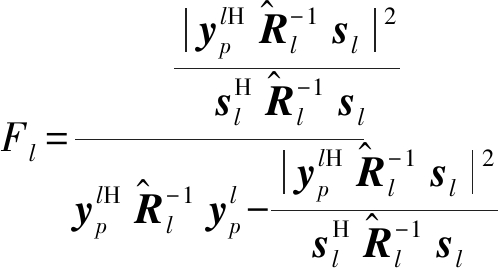
(22)
由文献[17]可知，El和Fl的统计特性分别与式(23)和式(24)两式等效：
(23)
(24)
其中，在H0假设下h3l和
服从复高斯分布，
和
服从参数分别为LN-1，K-LN+1，K-LN+2的中心chi平方分布，
由以上可知，式(23)和式(24)与频率通道数L，脉冲数N以及参考单元数K有关，而与杂波协方差矩阵Rl无关。因此式(15)和式(18)两种集中式OFDM-MIMO雷达检测器相对杂波协方差矩阵具有恒虚警特性。
另外，两种集中式OFDM-MIMO雷达检测器在设计阶段，考虑不同频率通道回波数据独立，进而可以对Rl分别进行估计和求逆运算。这带来两个好处：1) 3 dB参考单元数目要求由2L2N降低为2LN；2) 矩阵求逆运算复杂度由O(L6N3)降低到O(L4N3)。
3 计算机仿真
本节通过计算机仿真，分析研究不同频率分集以及参考单元数量条件下，集中式OFDM-MIMO雷达两种检测器的目标检测性能。
在数值仿真中，不同频率通道的目标回波强度为服从零均值，方差为1的复高斯变量，起伏特性满足第一类起伏模型，即
杂波采用文献[18]所给模型，假设静止雷达平台，各频率通道的杂波谱相同，则可由式(25)表示：
(25)
式中,σfd为杂波多普勒谱峰宽度，σfs为杂波角度谱峰宽度，fcsi为角度谱峰的中心频率，
为各杂波峰的功率，I为杂波峰个数。各频率通道的杂波协方差矩阵Rl可表示为
⊗
(26)
各频率通道的信杂比SCR定义为
(27)
OFDM-MIMO雷达阵元间距为d=0.15 m，f0=1 GHz，Δf=100 MHz，阵元间距为d=0.15 m。相干脉冲数N=5，目标相对雷达速度v=150 m/s，TPRI=0.25 ms，目标相对雷达的方位角度θ=30°。各频率分集通道的杂波谱相同，杂波峰个数I=3，fcsi分别为-0.3，0，0.3，σfd=0.01，σfs=0.025。
仿真1：发射和接收阵元数为4，Pfa=10-4时，不同信杂比不同参考数量情况下，集中式OFDM-MIMO雷达GLRT检测器和AMF检测器的性能。
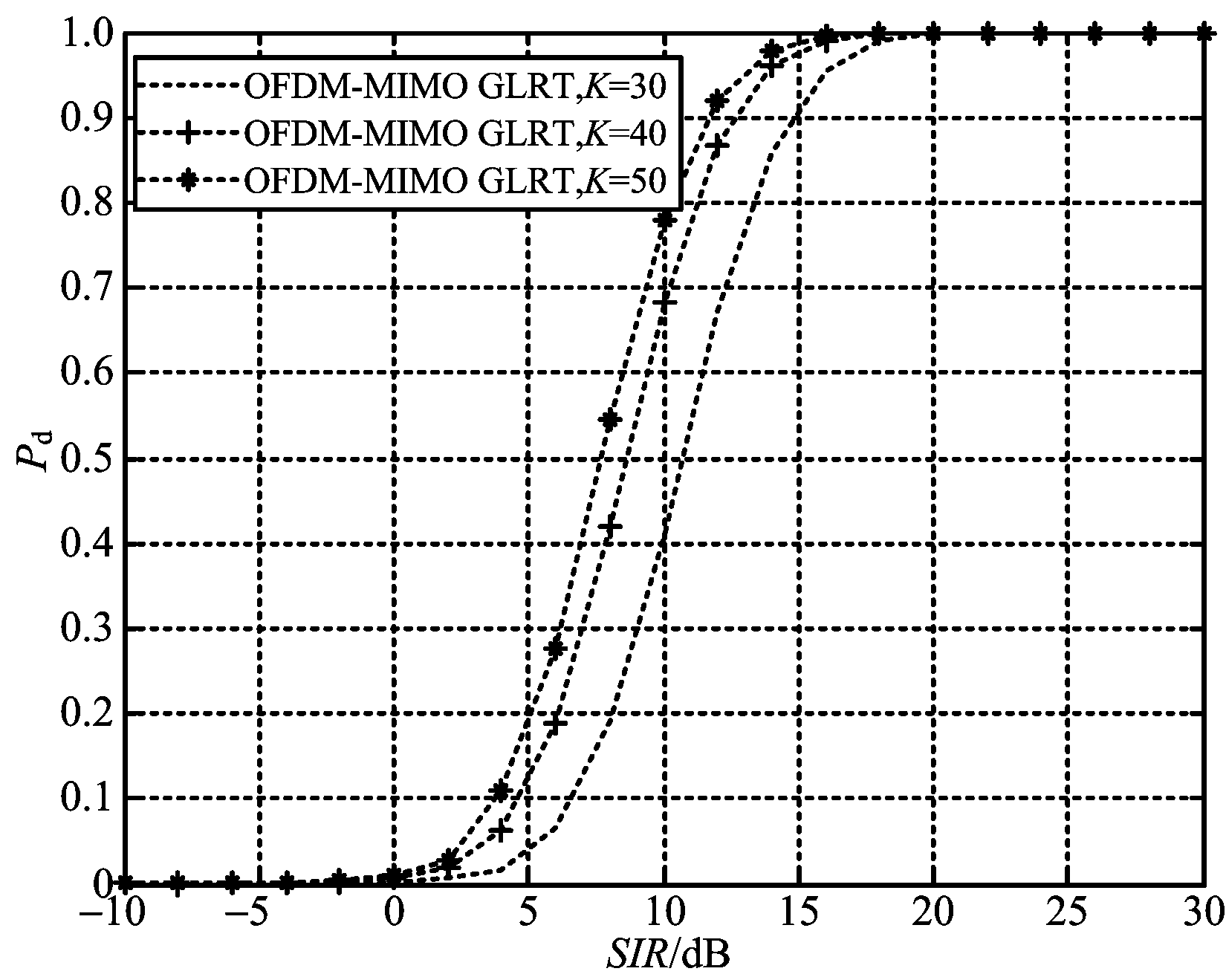
图2 不同参考单元数量GLRT检测器的性能比较
由图2和图3可以看出，随着参考单元数量的提升，两种集中式OFDM-MIMO雷达检测器的性能都不断提高。我们知道，杂波协方差矩阵估计误差引起的性能损失小于3 dB，要求参考单元数K至少为矩阵维数的两倍。在本仿真实验中，集中式OFDM-MIMO雷达总数据维数为80，每个频率通道数据维数为20，因此要求3 dB参考单元数目K≥40。从两图还能看出，K从30到40的性能提升大于K从40到50的性能提升。两种检测器利用OFDM-MIMO雷达通道独立性，降低了对参考单元数量K的要求，即降低了杂波协方差矩阵估计难度，也同时降低了检测器运算量，提高了实用性。另外，对比图2和图3，集中式OFDM-MIMO的GLRT检测器性能要略优于AMF检测器性能。同时也应指出，对比式(15)和式(18)，式(15)的运算量略大于式(18)的运算量，并且AMF检测器更适用于非均匀杂波环境。
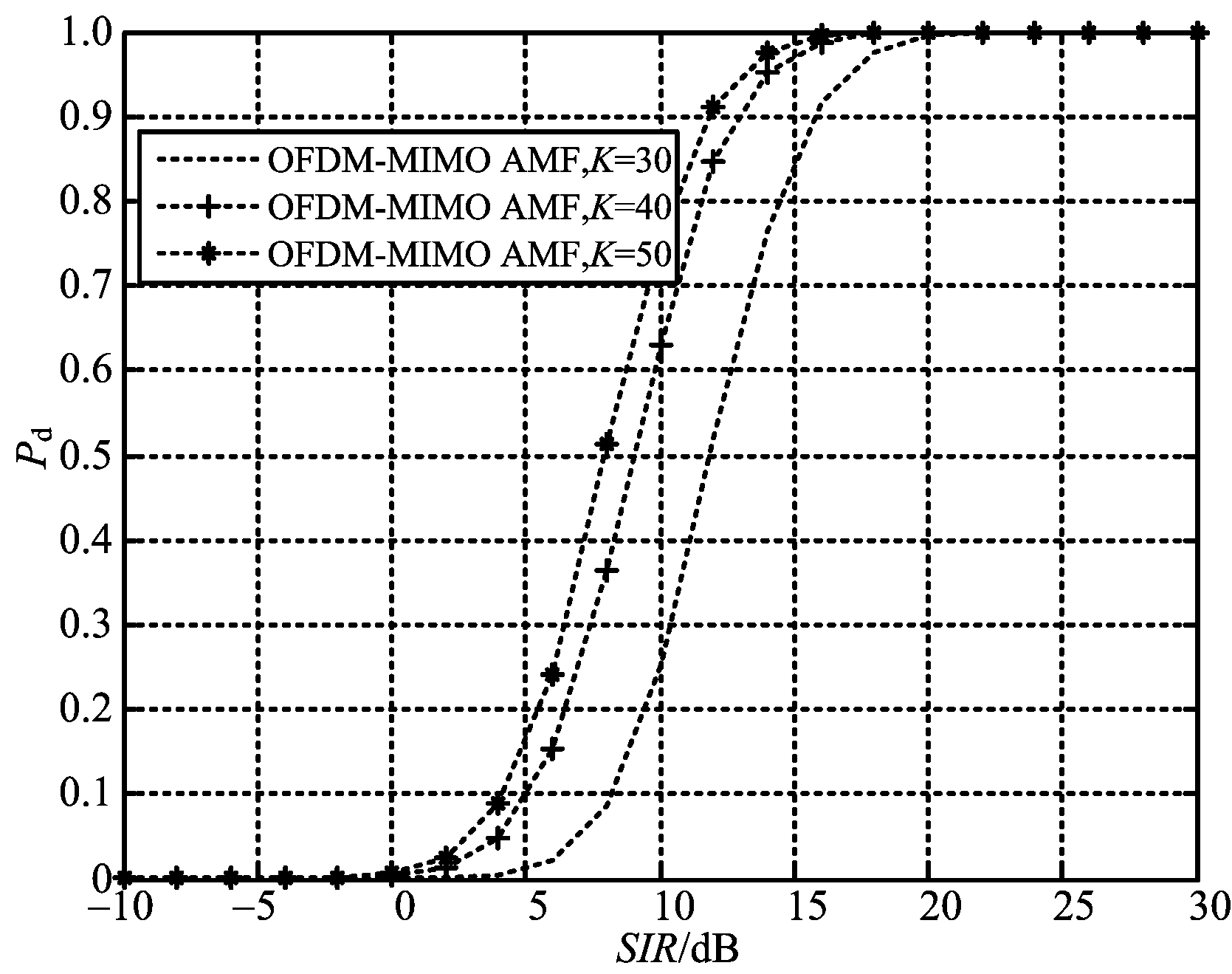
图3 不同参考单元数量AMF检测器的性能比较
仿真2：Pfa=10-4时，不同发射和接收单元数量，即不同频率通道数量条件下，集中式OFDM-MIMO雷达GLRT检测器和AMF检测器的性能。
由图4和图5可以看出，随着频率通道数量的增多，两种集中式OFDM-MIMO雷达检测器的性能不断提升。这是由于目标RCS的闪烁，导致雷达回波信杂比(SCR)波动，不同频率通道获得具有不同SCR的回波，两种集中式OFDM-MIMO雷达检测器综合利用不同频率通道信息，抑制SCR波动，从而提升检测性能，并且频率通道数越多，SCR波动抑制能力越强，检测性能也因此得以提高。
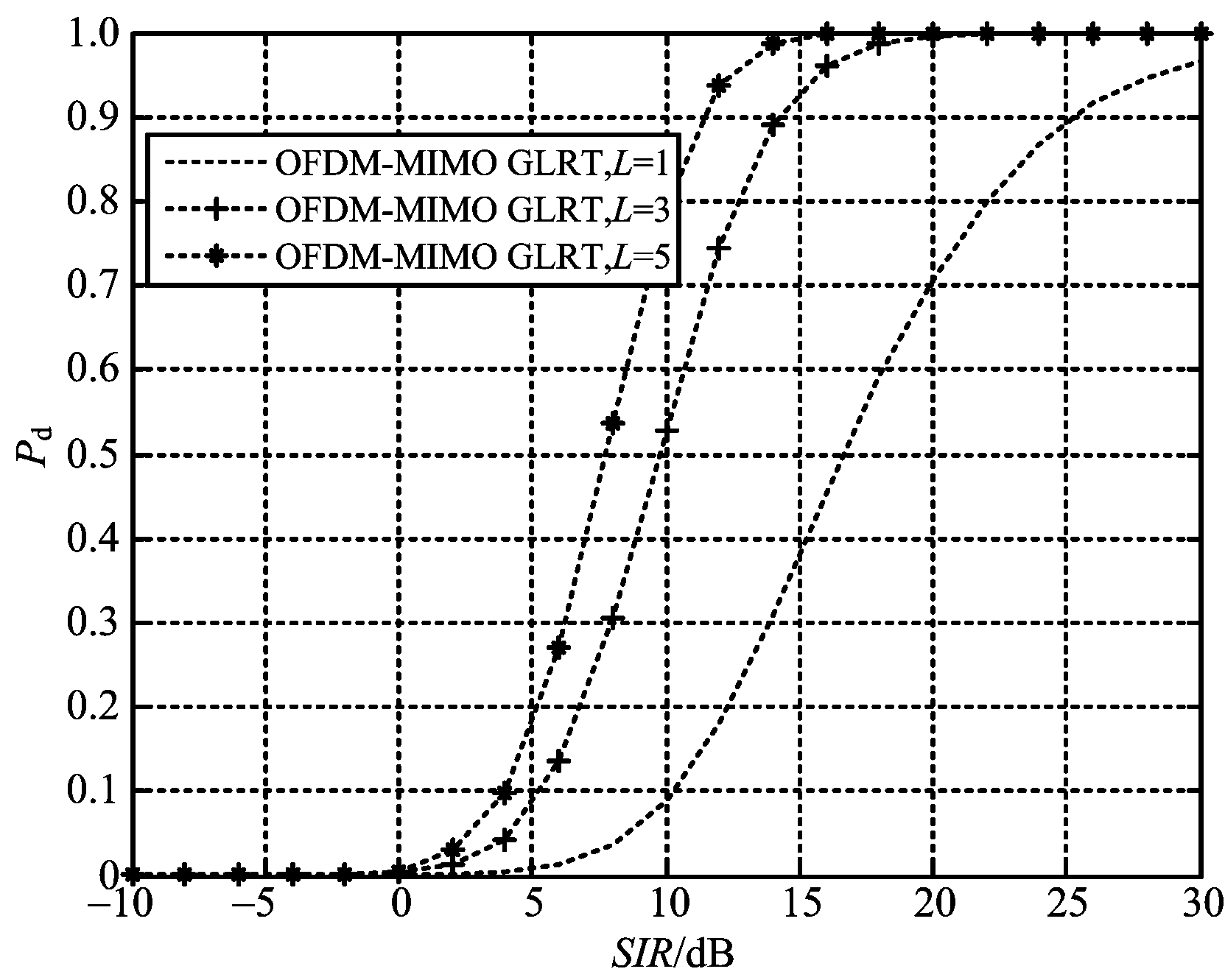
图4 不同频率通道数GLRT检测器的性能比较
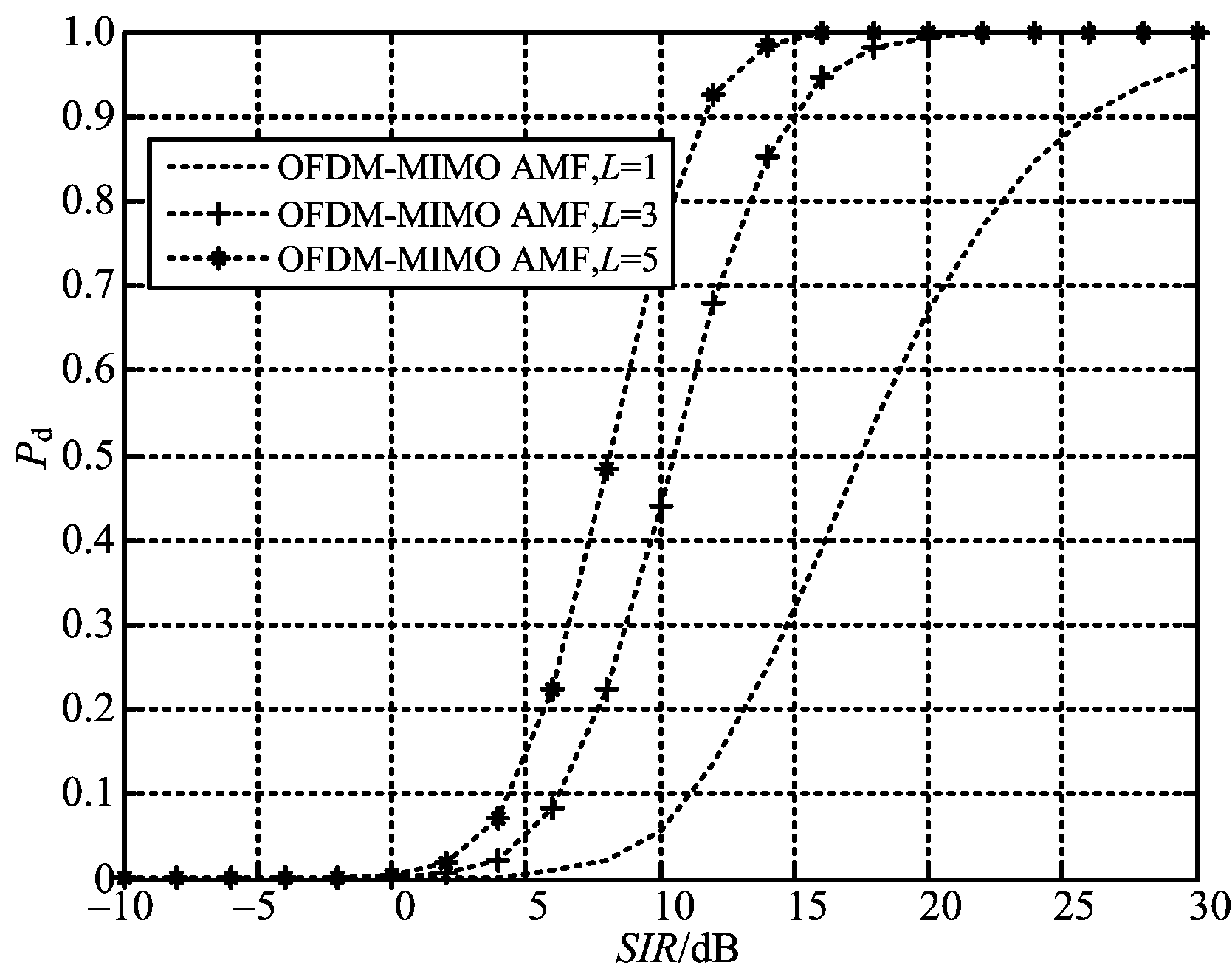
图5 不同频率通道数AMF检测器的性能比较
4 结束语
频率分集条件下，集中式OFDM-MIMO雷达具有目标分集性能，新的杂波特性，同时避免了分布式雷达包络对齐等难题。本文针对集中式OFDM-MIMO雷达在未知杂波中目标检测问题，基于一步和两步广义最大似然比准则，给出了集中式OFDM-MIMO雷达GLRT和AMF两种检测器。两种检测器能有效利用集中式OFDM-MIMO雷达频率分集，抑制SCR波动，提升目标检测性能。同时，两种检测器相对杂波协方差矩阵，具有恒虚警特性，并基于杂波频率通道独立特性，降低了算法复杂度，也降低了参考单元数目要求，具有一定的实用价值。
[1] LI Jian, STOICA P. MIMO Radar with Colocated Antennas[J].IEEE Signal Processing Magazine, 2007, 24(5):106-114.
[2] 陈诚,李洪涛,朱晓华,等.干扰背景下MIMO 雷达部分相关信号设计[J].电子与信息学报,2016,38(2):442-449.
[3] 冯涵哲,严俊坤,刘宏伟.一种用于多目标定位的MIMO 雷达快速功率分配算法[J].电子与信息学报,2016,38(12):3219-3223.
[4] 唐波,张玉,张浩.基于交替投影的MIMO 雷达信号盲分离算法研究[J].电子学报,2017,45(9):2092-2097.
TANG Bo,ZHANG Yu,ZHANG Hao.Blind Separation of MIMO Radar Signals Based on Alternating Projection[J].Acta Electronica Sinica,2017,45(9):2092-2097.(in Chinese)
[5] 李小波,张正言,王珽,等.双基地MIMO雷达相干目标的角度快速估计算法[J].信号处理,2016,32(3):370-377.
[6] SEN S, NEHORAI A. Adaptive OFDM Radar for Target Detection in Multipath Scenarios[J]. IEEE Trans on Signal Processing, 2011, 59(1):78-90.
[7] SEN S, NEHORAI A. OFDM MIMO Radar with Mutual-Information Waveform Design for Low-Grazing Angle Tracking[J]．IEEE Trans on Signal Processing, 2010, 58(6):3152-3162.
[8] 谷文堃,王党卫,马晓岩,等.分布式OFDM-MIMO雷达非相参积累目标检测方法[J].系统工程与电子技术,2015,37(10):2266-2271.
[9] 谷文堃,王党卫,马晓岩.分布式OFDM-MIMO雷达MTI处理[J].系统工程与电子技术,2016,38(8):1794-1799.
[10] 谷文堃,王党卫,郑岱堃,等. 分布式OFDM-MIMO雷达高速微弱目标多帧检测[J].华中科技大学学报(自然科学版),2016,44(2):65-69.
GU Wenkun,WANG Dangwei,ZHENG Daikun,et al.High-Spead Weak Target Multiframe Detection Using Distributed OFDM-MIMO Phased Radar[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2016,44(2):65-69.(in Chinese)
[11] 周豪,胡国平,师俊朋,等. OFDM-MIMO雷达低空目标探测性能研究[J].电波科学学报,2016,31(5):988-995.
[12] 袁海锋,江朝抒.OFDM-MIMO雷达体制的多径抑制性能分析[J].信号处理, 2012, 28(7):1000-1005.
[13] 兰星,李伟,王兴亮,等.频率分集MIMO 雷达信号优化设计[J].信号处理,2015,31(8):1029-1034.
[14] FANTE R L. Multifrequency Detection of a Slowly Fluctuating Target[J]. IEEE Trans on Aerospace and Electronic Systems, 1996, 32(1):495-497.
[15] KELLY E J. An Adaptive Detection Algorithm[J]. IEEE Trans on Aerospace and Electronic Systems, 1986, 22(2):115-127.
[16] ROBEY F C, FUHRMANN D R, KELLY E J, et al. A CFAR Adaptive Matched Filter Detector[J]. IEEE Trans on Aerospace and Electronic Systems, 1992, 28(1):208-216.
[17] KRAUT S, SCHARF L L. MCWHORTER L T. Adaptive Subspace Detectors[J]. IEEE Trans on Signal Processing, 2001, 49(1):1-16.
[18] PARK H, LI Jian, WANG Hong. Polarization-Space-Time Domain Generalized Likelihood Ratio Detection of Radar Targets[J]. Signal Processing,1995, 41(2):153-164.
