0 引言
近年来,球载雷达以预警能力强、生存能力强、留空时间长和效费比高等优势,越来越受到世界各国军队的青睐[1]。但是由于球载雷达探测平台的升高,波束下视,导致雷达波束会直接照射地面,并且球载雷达平台的漂移会使杂波频谱展宽,所以球载雷达工作时面临着很强的地海杂波[2]。另一方面,在实际应用中,球载雷达的探测性能还会受到以云雨杂波为主的气象杂波影响,尤其对于S、C和X波段的雷达,气象杂波对雷达目标探测性能的影响更为严重[3]。特别是在探测低慢小目标(如无人机)时,由于目标雷达散射截面积很小,而且与气象杂波运动速度相近,很容易被杂波淹没,给检测带来了困难。杂波建模是进行杂波抑制研究的一项重要基础工作[4],因此,有必要对球载雷达工作模式下的云雨杂波及其特性进行研究。
目前公开文献中关于气象杂波的建模主要集中在地基雷达和机载气象雷达,如文献[5-6]对机载雷达的气象杂波建模进行了研究,但是由于球载雷达自身慢动的特性使得其杂波特性与机载雷达存在较大区别。文献[7-8]对地基雷达的气象杂波进行了仿真与研究,但是球载雷达升空工作,相对于地基雷达面临的气象杂波更强。因此本文在空间建模的基础上着重研究了球载雷达平台慢动情况下气象杂波建模与仿真问题,得到了较为准确的雷达杂波信号,为研究相应的杂波抑制技术提供了支撑。
1 球载雷达气象杂波模型
1.1 气象杂波空间模型
为了建模方便,假设云层等气象环境均匀分布于空间中,雷达与云层的空间坐标关系如图1所示。

图1 气象杂波空间模型示意图
图1中α为杂波分辨单元的方位角,φ为杂波分辨单元的俯仰角,假设球载雷达气球只作水平匀速运动,速度为V,云层相对于雷达以速度v作匀速运动,Hc表示云层的高度,Hr表示雷达的高度。
中重频模式下,由于存在距离模糊,雷达实际接收到的杂波信号是由多个距离环杂波采样叠加而成的。由于同一距离环中杂波分辨单元有相同的高低角,假设云层是平坦的,则这些杂波距离环就是一簇同心圆环,如图1中的等距离圆弧所示,每个杂波距离环的距离宽度取决于距离门宽度及该距离环对应的高低角。距离模糊环数的计算公式如式(1)所示:
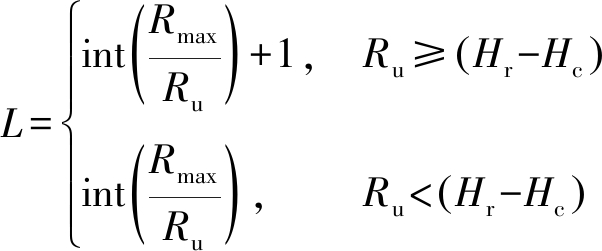
(1)
式中,int()为取整函数,![]() 为最大不模糊距离,fr为脉冲重复频率,Rmax为雷达最大作用距离。
为最大不模糊距离,fr为脉冲重复频率,Rmax为雷达最大作用距离。
图中Rl是第l个距离环上杂波分辨单元到雷达的距离,各相邻距离环与雷达斜距Rl之差为Ru,计算公式为
Rl=(Hr-Hc)+l·Ru
(2)
根据图1中几何关系,杂波分辨单元在坐标系中的坐标如式(3)所示:
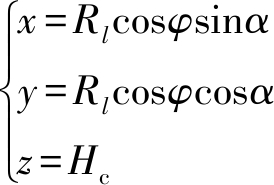
(3)
杂波相对于雷达的径向速度为
vr=vcosφcosα
(4)
因此,第l个距离环上杂波分辨单元相对于雷达的距离变化模型可以表示为
R(tm)=Rl-vrtmcosφcosθ
(5)
式中, tm=mTr,m表示第m个回波,Tr为脉冲重复周期。
由于球载雷达工作于中重频时,存在距离模糊,此时雷达观测到的视在距离应当为实际距离减去模糊数乘以最大不模糊距离,因此第l个距离环上杂波分辨单元到雷达的视在距离修正为
R=R(tm)-kRu
(6)
式中,k=1,2,3,…,N表示模糊数。
设雷达发射的LFM信号为
(7)
式中, 为调频斜率,B为带宽,Tp为脉冲宽度,
为调频斜率,B为带宽,Tp为脉冲宽度,![]() 为快时间,tm为慢时间,t为总时间,且有
为快时间,tm为慢时间,t为总时间,且有![]() 为载频。
为载频。
则目标的回波为
![]()
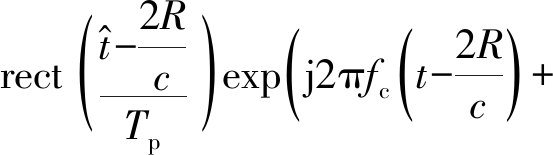
(8)
1.2 气象杂波数学模型
球载雷达在中重频模式下工作,同时存在距离模糊和多普勒模糊。由于距离模糊落入同一距离门的杂波回波由多个距离圆环的回波叠加组成,因此模拟气象杂波时将一定范围内的云层划分为网格状,一个网格表示一个杂波分辨单元。先计算一个网格即一个分辨体积单元中的杂波回波,再将同一个距离环上的所有网格的杂波信号相加,得到一个距离环的杂波回波,求得各个距离环上的杂波回波后,将各个距离环上的杂波回波相加即可得到落入一个距离门的杂波。根据杂波距离环宽度计算在球载雷达最大不模糊距离内距离门的个数,将落入每个距离门的杂波信号叠加起来,即可得到整个观测范围内的球载雷达气象杂波。
第l个距离环第i个分辨单元的杂波功率,由雷达方程得
(9)
式中,Pt为雷达发射功率,G为雷达天线增益,λ为发射波长,σc为杂波截面积,Rl为第l个距离环上杂波分辨单元到雷达的距离。
则第l个距离环第i个分辨单元的杂波信号为
Cil(k)=PilAilexp[j2πfd(k-1)Tr]
(10)
式中,Ail为杂波的幅度起伏值,k为相干脉冲处理长度,![]() 为脉冲重复周期。
为脉冲重复周期。
对第l个距离环上所有方位向的分辨单元杂波信号进行叠加后,得到第l个距离环的杂波信号为
(11)
式中,n为距离环内分辨单元个数。
某个距离门的杂波信号为
(12)
式中,L为根据式(2)计算出的杂波距离环个数。
由于气象杂波多普勒频率较小,而球载雷达工作频率为几千兆赫兹,所以一般不存在多普勒模糊,因此本文建模只考虑了距离模糊。
2 气象杂波的影响因素
雷达接收到的云、雨和雪的散射回波称为气象杂波。气象杂波是一种体杂波,其强度与天线波束照射的体积、信号的距离分辨率以及散射体的性质有关[9]。
气象上云滴、雨滴等粒子一般可以近似地看作是圆球形和椭球形。这些气象粒子的直径远远小于雷达工作波长λ,因此这些粒子的截面积σk处在瑞利区。计算公式如下:
(13)
式中:D为粒子直径;|K|2为复折射指数,对于云一般为0.9,对于雪一般为0.2;ε为水的介电常数。下面主要从气象杂波分辨单元特性和统计特性两个方面阐述。
2.1 气象杂波分辨单元特性
设杂波距离分辨单元体积为Vc,则杂波截面积为
σc=ηVc
(14)
式中,η为后向散射系数,Vc为分辨单元体积,且
(15)
式中,R为雷达到杂波分辨单元的距离,τ为脉压后的脉冲宽度,θB为雷达天线方位向波束宽度,φB为俯仰向波束宽度。
后向散射系数η计算公式如下:
(16)
式中,N为杂波分辨单元体积内气象粒子的个数。
通常用反射率因子Z来定义η,在瑞利散射条件下,
(17)
Z与降雨率有关:
Z=aγb
(18)
式中:Z是反射率因子,单位为mm6/m3;γ是降雨率,单位为mm/h。根据文献[10],a的经验值为200,b为1.6,降雨率的典型值如表1所示。
表1 几种情况下降雨率γ的典型值
细雨小雨中雨大雨暴雨0.251.04.016.0>40.0
2.2 气象杂波的统计特性
气象杂波是大量离散的气象粒子散射形成的,而且这些粒子之间的视在距离又可能会因为它们的实际移动或是由于球载雷达平台及天线的移动而改变,因此气象杂波幅度会随时间而起伏变化。起伏可用幅度统计值和起伏率或频谱来表示。幅度的统计特性可给出反射回波具有一定范围数值的时间百分数的信息,而频谱则给出这些数值改变快慢的信息。人们已经对杂波幅度的统计特性作过多年的研究,对于大量大小差不多且相位又均匀分布的散射体已发现其杂波的幅度值为瑞利分布。由此可以得出气象杂波的幅度值为瑞利分布[11]。
气象杂波的功率谱一般被看作高斯谱,频谱宽度受风速等的影响,表达式为
(19)
式中,σf为杂波谱的标准差,代表频谱展宽的程度,它与杂波速度起伏展宽值σv的关系为
(20)
考虑到气象杂波单元有一定的运动速度v,多普勒频率为
(21)
杂波功率谱修正为
(22)
式中,fd为中心频率,为杂波的平均多普勒频移,或者说是杂波的平均速度。
根据文献[12],气象杂波标准差如表2所示。
表2 杂波标准差

杂波种类风速标准差σv雨—1.8~4.0云雨—2.0
3 仿真结果与分析
为验证模型的有效性,设置仿真实验,仿真参数设置如下:
雷达高度Hr=3 000 m;脉冲重复频率PRF=5 000 Hz; 雷达最大天线增益Gt=35.6 dB; 发射功率Pt=20 kW;天线俯仰波束宽度θB=10°;天线水平波束宽度φB=1.8°;载频f0=1.5 GHz;LFM信号带宽B=1 MHz;波长λ=c/f0=0.2 m;脉冲宽度τ=20 μs;最小探测距离Rmin=30 km;最大探测距离Rmax=280 km;云层高度Hc=2 km,相对于雷达运动速度v=20 m/s,云层长度L=300 km;相干处理脉冲长度K=32;杂波分辨单元初始方位角α=30°;杂波分辨单元初始俯仰角φ=arcsin[(Hr-Hc)/R]=1.84°,杂波起伏模型为瑞利分布。
球载雷达接收到的回波如图2所示。
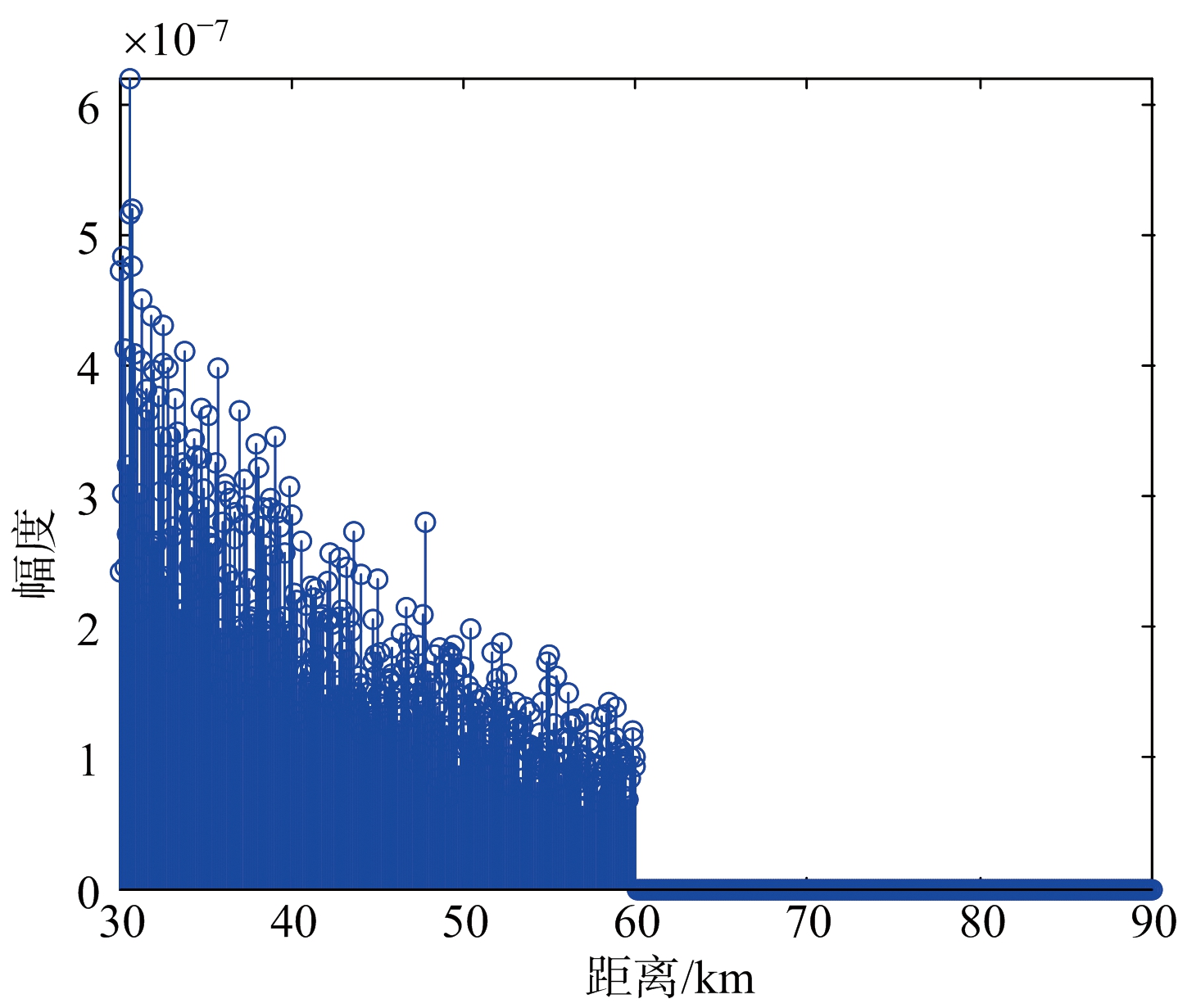
图2 雷达接收到的回波
根据给出的脉冲重复频率5 000 Hz,得出最大不模糊距离为30 km。从图2可以看出由于存在距离模糊,本应分布在整个接收距离的杂波都只在30 km内混叠,且越靠近雷达杂波幅度越强。
图3给出了落入一个距离门内的气象杂波的幅度起伏和功率谱。

(a) 杂波幅度
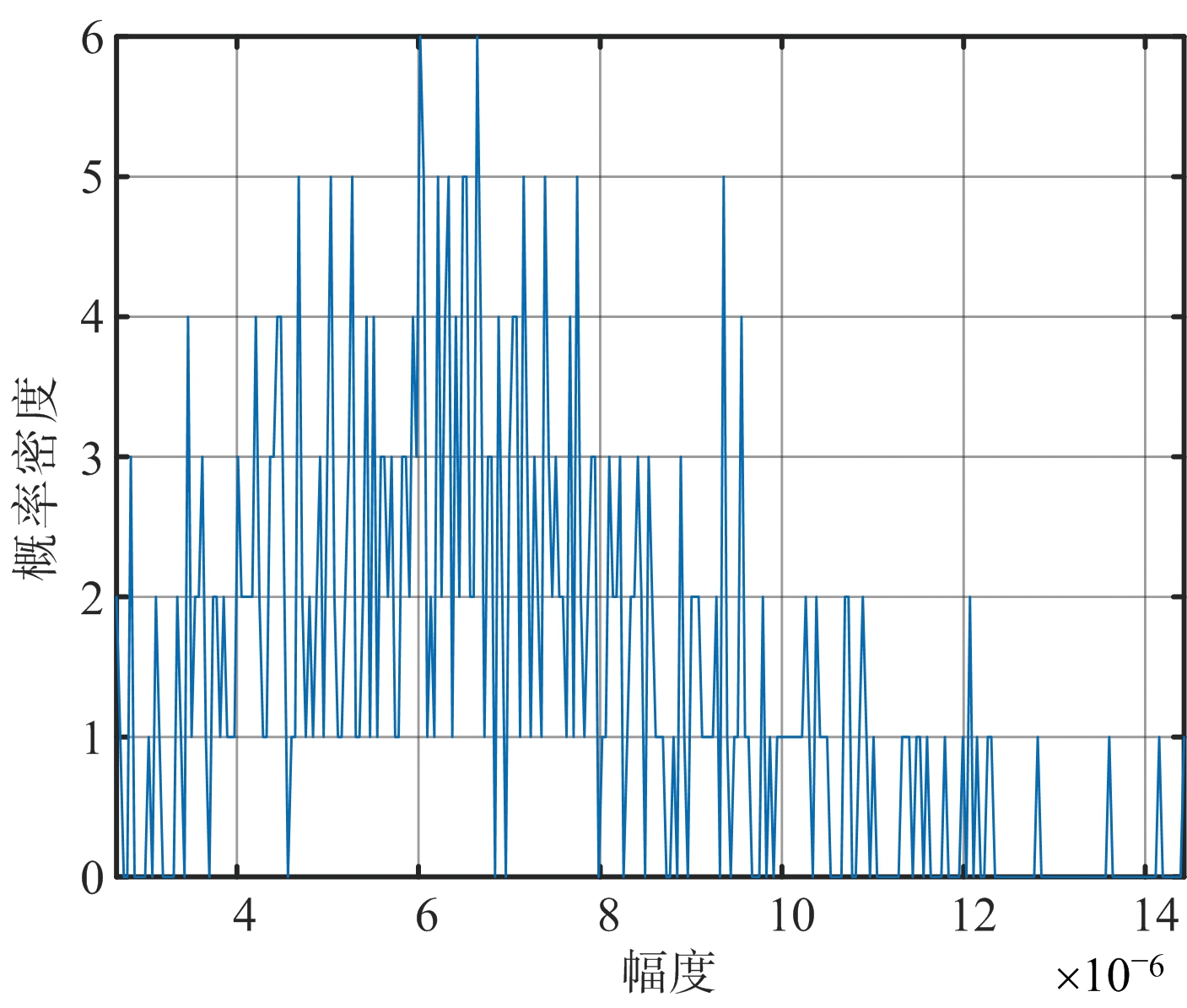
(b) 杂波幅度概率密度函数直方图
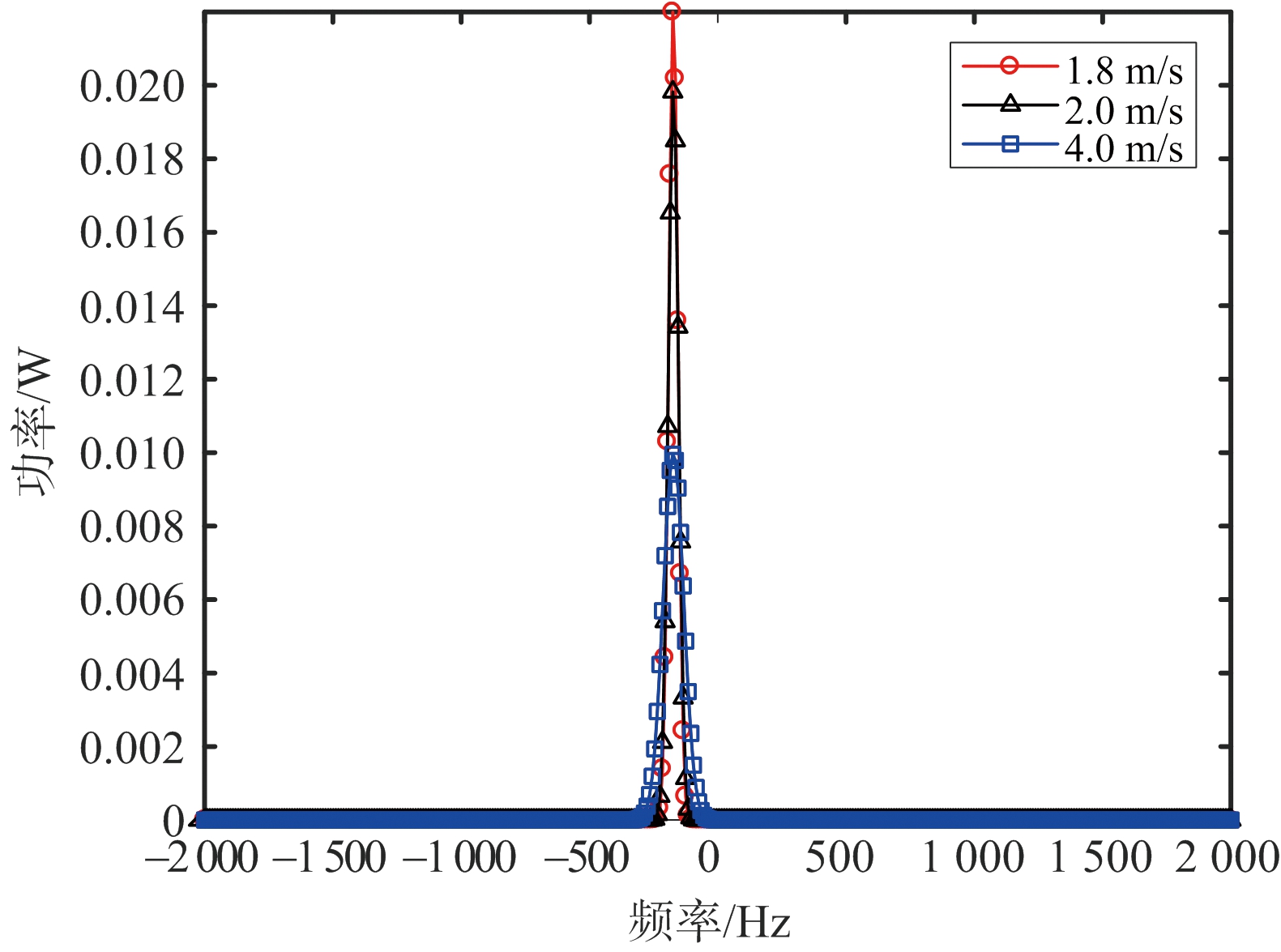
(c) 杂波功率谱
图3 杂波统计特性分析
从图3(a)可以看出杂波的功率幅度是随机的,且杂波功率幅度随着降雨概率的增大而增大;图3(b)为γ=40 mm/h时杂波幅度概率密度函数直方图,从图3(b)可以看出杂波幅度的分布是瑞利分布的;从图3(c)可以看出杂波功率谱为高斯型,气象杂波多普勒速度为中心频率,并且由于平台的运动,杂波功率谱有展宽,风速起伏变化越大,杂波谱展宽越多,能量越分散,这意味着球载雷达对地模式检测目标时要考虑使用AMTI来抑制气象杂波,改善目标信杂比。
对同一个距离单元上的回波对K个脉冲作FFT,得到此距离单元的回波多普勒谱,对所有距离单元作FFT,则得到球载雷达接收到的回波距离-多普勒谱,也就是作一个简单的MTD。图4给出了有杂波时球载雷达接收到的回波距离-多普勒谱。
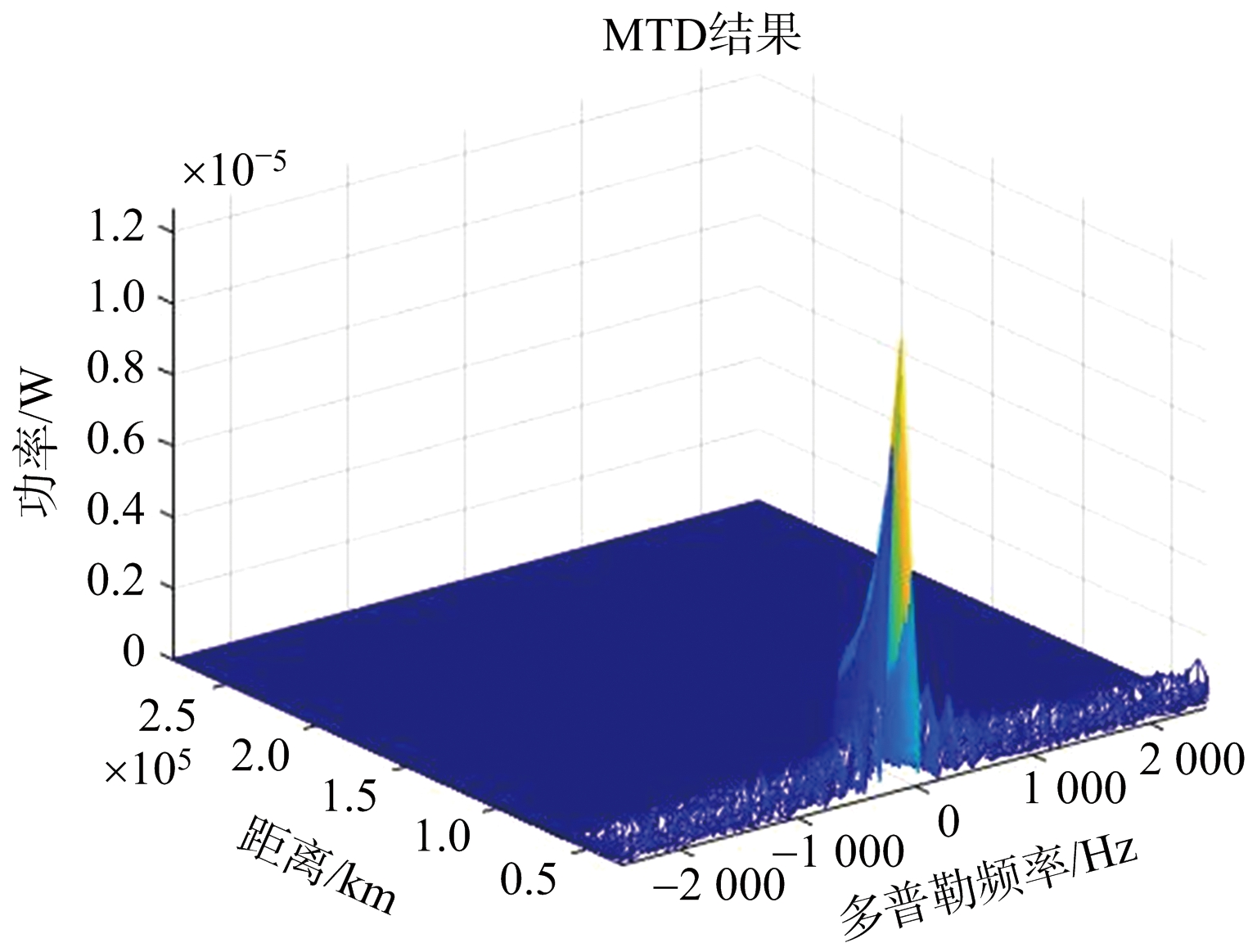
图4 杂波多普勒特性分析
由图4可知,由于气象环境自身的运动,杂波已经偏离了零频,由于平台的运动,杂波频谱有一定展宽。球载雷达使用的是低副瓣天线,因此副瓣接收到的杂波回波不强,所以抑制气象杂波应重点考虑抑制主瓣杂波,以此来改善目标信杂比。
4 结束语
本文提出了球载雷达气象杂波的建模方法,并根据这种方法得到了相应的仿真结果。通过分析,对球载雷达的气象杂波特性和气象杂波的影响因素有了更深入的认识,有利于以后解决目标落入气象杂波区雷达难以检测的问题,同时为后续的气象杂波抑制方法提供了仿真数据。
[1] 陈昌胜,赵攀峰.系留气球载雷达系统分析[J].雷达科学与技术,2007,5(6):410-414.
CHENG Changsheng,ZHAO Panfeng. Analysis of Tethered Aerostat Borne Radar System[J]. Radar Science and Technology, 2007,5(6):410-414.(in Chinese)
[2] 杨大伟.球载雷达探测低空小目标的性能分析[J].舰船电子对抗,2012,35(2):38-43.
[3] 战立晓,汤子跃,朱振波,等.气球载雷达云雨杂波建模与仿真[J].雷达科学与技术,2010,8(1):15-19.
ZHAN Lixiao,TANG Ziyue,ZHU Zhenbo,et al. Modeling and Simulation of Rain Clutter for Tethered Aerostat Borne Radar[J]. Radar Science and Technology, 2010,8(1):15-19. (in Chinese)
[4] 邓赛强,金林,梁浩.海杂波背景下的雷达性能评估研究[J].雷达科学与技术,2017,15(5):525-530.
DENG Saiqiang,JIN Lin,LIANG Hao. Study on Radar Performance Evaluation in Sea Clutter[J]. Radar Science and Technology, 2017,15(5):525-530. (in Chinese)
[5] 于莹洁,李勇.机载气象雷达的三维湍流模型和探测仿真方法[J].系统工程与电子技术, 2016,38(2):293-297.
[6] 王磊,于超鹏,刘平.机载相控阵天气雷达回波仿真与分析[J].系统仿真学报,2016,28(8):1869-1877.
[7] 王旭,蔡兴雨,朱思桥,等.基于点迹特征的气象杂波抑制技术[J].火控雷达技术, 2017,46(2):6-14.
[8] THOMSON A D, RISEBOROUGH E S. Evaluation of a Weather Clutter Simulation[J]. IEE Proceedings: Radar, Sonar and Navigation,2001,148(3):119-129.
[9] 黄向清,林新党.雷达海杂波与气象杂波模拟方法研究[J].雷达与对抗,2017,37(3):5-9.
[10] SKOLNIK M I.雷达手册[M].2版.北京:电子工业出版社,1999:940-941.
[11] 杨尚军.雷达模拟器气象杂波的建模与仿真[D].长沙:国防科学技术大学,2006.
[12] 刘霞飞.雷达杂波分类与抑制技术研究[D].西安:西安电子科技大学,2015.
