0 引言
随着信息技术的迅速发展,现代战争中雷达所处的电磁环境变得越来越复杂,有效地对抗高强度、多样式的电磁干扰已经成为提高雷达作战水平和生存能力的重要体现。针对旁瓣干扰问题,传统的自适应旁瓣相消技术、干扰零陷技术等[1-3]都可以有效地进行抑制。但是干扰可能从主瓣方向进入,当存在主瓣干扰时,常规的自适应波束形成便暴露出两个严重的问题[4-5]:一是旁瓣水平明显升高,这将导致虚警概率的急剧上升;二是主瓣严重变形且峰值偏移,从而影响了测角的精度。不仅如此,由于雷达阵列的阵元数目较多,在不影响目标所在区域有效检测的前提下,如何对接收数据进行预处理,以达到为后续信号处理减少计算量的目的,也是现代雷达需要考虑的一个问题。近些年来,国内关于主瓣抗干扰的研究也非常多[6-8],但是由于实际雷达系统阵元数量巨大,阵元域的抗干扰方法有一定的局限性,如何减小阵元域数据的计算量非常重要。研究表明通过在信号所在的区域形成一组覆盖这个空间的波束,这样可以在不影响感兴趣区域信号性能的前提下大大降低信号的维度,从而大大减小信号的计算量,使多阵元阵列的后续信号处理成为可能。
本文给出了一种基于谱估计预处理的波束域[7]主瓣抗干扰方法。主要针对上述两个问题:一是在不影响目标所在区域有效检测的前提下,对数据进行适当预处理,有效地减少后续信号处理的工作量;二是在保证正确估计目标位置的前提下,有效地抑制主瓣和旁瓣干扰。具体的做法是:首先将原始接收信号从阵元域转化到波束域,得到维数大大降低的波束域信号,能够为后续的信号处理工作减少计算量;其次通过空间谱估计的方法对波束域数据进行分析,准确地估计出信号、主瓣干扰和旁瓣干扰的方向,由此可以准确地得出干扰子空间(包含主瓣干扰和旁瓣干扰)和信号子空间,然后将包含主瓣干扰和旁瓣干扰的干扰子空间斜投影到信号子空间上,从而抑制掉所有的干扰信号。在文献[7]中虽然也运用了斜投影滤波的方法去除主瓣干扰。但是文献分析的都是阵元域数据,并且假设期望信号方向已知,然后对只包含干扰和噪声的协方差矩阵进行特征分解,通过分析干扰方向向量和期望方向向量的相关性,从而准确地估计出主瓣干扰和旁瓣干扰,这种做法虽然有效,但是实际情况下期望方向向量是未知的,而且很难得到只包含干扰和噪声的协方差矩阵,所以对信号进行斜投影滤波之前,需要准确地分析出信号子空间和干扰子空间。本文在分析时,首先通过空间谱估计的方法对波束域数据进行处理,从而准确地估计出信号、主瓣干扰和旁瓣干扰的方向,由此可以准确地得出干扰子空间(包含主瓣干扰和旁瓣干扰)和信号子空间,之后再利用斜投影滤波的方法进行处理,比较符合实际情况。
1 理论模型
1.1 阵元域空间谱估计
对于一个由M个阵元组成的均匀线阵,阵元间距为d。假设空间中存在1个目标、P个主瓣干扰和Q个旁瓣干扰,P+Q+1<M。其中目标信号为s0(t),入射角度为θ0;第p个主瓣干扰的信号为sp(t),入射角度为θp;第q个旁瓣干扰的信号为sq(t),入射角度为θq,假设接收数据的快拍数为N。并且假设所有的干扰之间都是独立不相关的,则阵列接收到的信号可以表示为
x(t)=A(θ)S(t)+n(t)=
(1)
式中:A=[a(θ0),a(θ1),…,a(θP+Q)]为信号的阵列的导向矢量,a(θ)=[1,exp(j2πdsin(θ)/λ),…,exp(j2π(M-1)dsin(θ)/λ)]T为阵列的流形向量;S(t)=[s(θ0),s(θ1),…,s(θP+Q)]为信号矢量;n(t)为噪声,并且假设各通道的噪声为相互独立的高斯白噪声,方差为![]() 且与信号和干扰不相关。则阵列输出信号的协方差矩阵为
且与信号和干扰不相关。则阵列输出信号的协方差矩阵为![]() 为接收信号的快拍数。对于主瓣干扰,干扰机和目标虽然同处于主波束内,但是在空间上仍会相差一定的角度,本文中干扰角度与信号角度之间的间隔小于半功率波束宽度时的干扰定义为主瓣干扰。其中,半功率波束宽度定义为
为接收信号的快拍数。对于主瓣干扰,干扰机和目标虽然同处于主波束内,但是在空间上仍会相差一定的角度,本文中干扰角度与信号角度之间的间隔小于半功率波束宽度时的干扰定义为主瓣干扰。其中,半功率波束宽度定义为
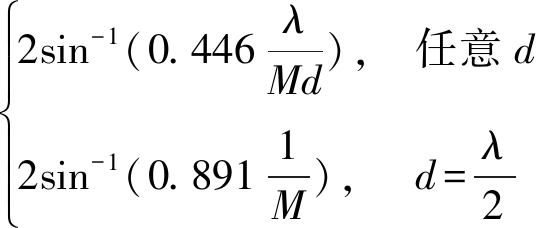
(2)
阵元域中,对包含1个信号、P个主瓣干扰、Q个旁瓣干扰和噪声的波束域接收信号x(t)进行特征分解:
![]()
(3)
式中:E=[ESJ,EN],ESJ=[e1,e2,…,eP+Q+1]为信号和干扰子空间,EN=[eP+Q+2,eP+Q+3,…,eM]为噪声子空间;![]() 由于信号和干扰之间都是不相干的,所以矩阵R是满秩矩阵。由矩阵理论可知:ESJ的列张成了一个由A(θ)的列张成的空间,并且和噪声子空间正交即
由于信号和干扰之间都是不相干的,所以矩阵R是满秩矩阵。由矩阵理论可知:ESJ的列张成了一个由A(θ)的列张成的空间,并且和噪声子空间正交即
(4)
式中,Span{·}表示张成的空间,符号⊥表示正交。由于阵列流型向量与噪声子空间的所有向量正交,所以扫描向量a(θ)扫描到信号方向时,到噪声子空间的欧几里德距离的平方为零,即![]()
(5)
由上分析,定义式(6)的方位谱估计,扫描得到的峰值位置即为信号和干扰的方位。
(6)
1.2 波束域信号分析
由相关文献[7]表明,波束空间预处理相当于阵元空间到波束空间的变换,假设对某一确定区域[θleft,θright]处理时需要平均形成的波束有K个,一般情况下,K≪M,则间隔Δθ=(θright-θleft)/(K-1),则定义如下一个矩阵:
C=[a(θleft),a(θleft+Δθ),…,a(θright)]
(7)
由于波束形成矩阵需要满足正交矩阵,而矩阵C不是正交矩阵,需要对矩阵进行正交化处理得
T=C(CHC)-1/2
(8)
当然波束形成矩阵的方法有很多种,使用时可以通过不同的需求使用不同的波束形成矩阵。在得到需要的波束形成矩阵后,可以得到波束空间的数据为
y(t)=THx(t)
(9)
式中,x(t)的维数为M×N,T的维数为M×K,则y(t)的维数为K×N。由于K≪M,所以波束域数据y(t)的维数大大降低,为后续的处理带来极大的方便。对于阵元域数据而言,基于空间谱估计算法的计算复杂度为O(M3),而对于变换后的波束域数据而言,基于空间谱估计算法的计算复杂度为O(K3)。一般来说,对于雷达数据经常会是大阵列、小信号源数目的情况,波束域处理就能够有效地减少算法的计算量,并且通过减少数据的接收通道数,能够大大降低系统的复杂性。
1.3 斜投影滤波(OPF)
式(3)~式(6)给出了阵元域空间谱估计信号和干扰方位的具体过程,由于本文处理的数据是波束域数据y(t),则波束空间数据的协方差矩阵可以写为
Ryy=THRxxT=TH(ARSAH+σ2I)T=
THARSAHT+σ2I=
DRSDH+σ2I
(10)
式中,D=THA=[THa(θ1),THa(θ2),…,TH a(θP+Q+1)]=[d(θ1),d(θ2),…,d(θP+Q+1)]为波束空间的阵列流型,则波束空间的谱估计公式可以表示为
P(θ)=![]()
(11)
式中,EdN为波束域数据协方差矩阵Ryy的噪声子空间。通过空间谱估计的方法可以准确地得到信号方位θ0、主瓣干扰方位θp1,θp2,…,θpp和旁瓣干扰方位θq1,θq2,…,θqq,判断时可以通过信号和干扰的能量大小排序判断。然后可以直接写出只包含信号的子空间为ES=a(θ0),包含主瓣干扰和旁瓣干扰的子空间EJ=[EP,EQ],EP=[a(θp1), a(θp2),…,a(θpp)],EQ=[a(θq1),a(θq2),…, a(θqq)]。
紧接着,通过将包含主瓣干扰和旁瓣干扰的子空间EJ投影到只包含信号的子空间ES上,然后计算出斜投影矩阵为
(12)
式中,![]() 为干扰子空间EJ的正交补空间。由于斜投影矩阵具有如式(13)所示的性质,所以波束域数据斜投影后对信号子空间没有影响,但是可以完全滤除掉干扰子空间。
为干扰子空间EJ的正交补空间。由于斜投影矩阵具有如式(13)所示的性质,所以波束域数据斜投影后对信号子空间没有影响,但是可以完全滤除掉干扰子空间。
BES=Es
BEJ=B[EPEQ]=0
(13)
得到斜投影矩阵后,对波束域接收信号通过斜投影矩阵进行滤波处理,得到波束域斜投影滤波输出信号为
z(t)=By(t)=BTHx(t)
(14)
滤波输出的信号即为将主瓣干扰和旁瓣干扰都消除掉后的只包含信号和噪声的信号,可以用于后续相关的信号处理工作。图1给出了本文方法的具体流程图。并通过仿真分析了本文方法的影响因素。
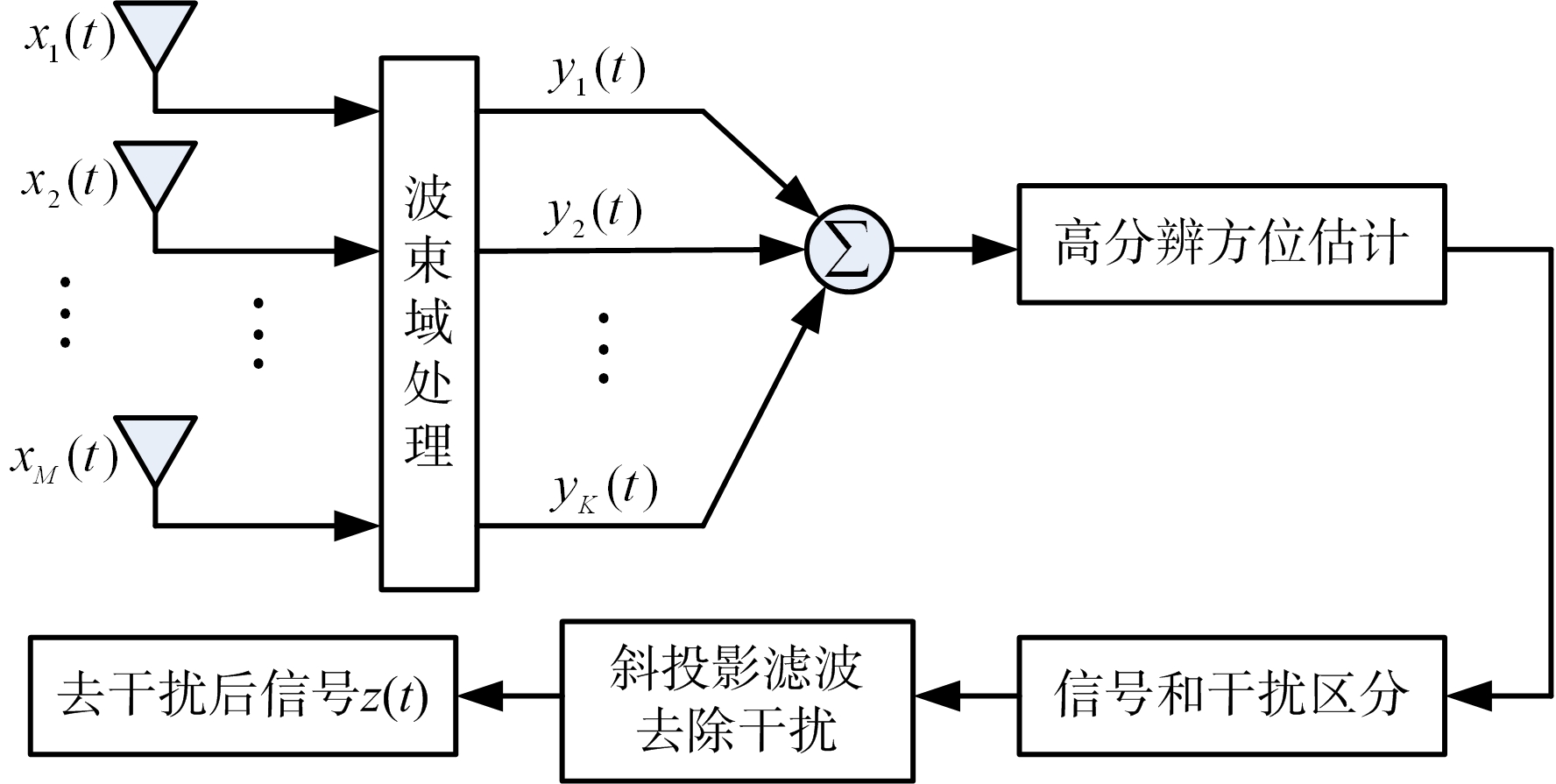
图1 本文方法流程图
1.4 性能评估
对于提出的新算法,需要论证算法的有效性和适用性。在后文的仿真中通过将提出的斜投影滤波抗干扰算法与常用的自适应旁瓣对消抗干扰算法进行对比,来说明算法的有效性。而在分析算法的适用性时,则需要准确分析出算法的影响因素,在算法研究过程中,分析发现数据的快拍数、信号和主瓣干扰的方位间隔、信噪比和主瓣干噪比的间隔这3个因素对本文的方法影响较大。所以在后文的仿真实验中,分别分析了这3个影响因素变化时斜投影滤波抗干扰算法在检测目标信号时的检测概率曲线,根据检测概率曲线可以准确地给出3个影响因素的设置范围,只有在正确的设置范围内,斜投影滤波抗干扰算法在检测目标时检测概率会很大,满足实际需求。
2 仿真实验
仿真时,假设接收阵列为20元均匀线阵,阵元间距为半波长,期望信号方位为10°,信噪比为25 dB。半功率波束宽度为5.106 7°,空间中存在一个主瓣干扰和一个旁瓣干扰:主瓣干扰角度为11.276 7°,与信号间隔为1/4波束宽度,干扰比为35 dB;旁瓣干扰角度为17°,干扰比为20 dB。噪声为零均值的高斯白噪声。
数据处理时,首先将原始阵元域接收信号变换到波束域,需要确定扫描所需要的波束扇。由于目标方位为10°,波束域处理时,感兴趣的区域限定为[8°,18°](实际情况下,会有一定的先验知识,感兴趣的区域一般不会太大),每隔2°形成一个波束,共形成6个波束,图2给出了扫描所需要的波束方向图。通过波束扇对阵元域接收信号进行扫描,得到波束域数据y(t)。
在得到波束域数据后,通过式(11)画出波束域数据的归一化方位谱图,图3给出了波束域数据的归一化方位谱图。由于算法研究的是主瓣抗干扰算法,所以主瓣干扰和信号之间间距较小,并且一般假设干扰强度大于目标强度,在以上假设下根据图3可以准确地判断出角度1对应目标信号,角度2对应主瓣干扰信号,角度3对应旁瓣干扰信号。然后可以直接写出信号子空间ES=a(θ0)和干扰子空间EJ=[EP,EQ],之后可以通过式(12)计算出斜投影变换矩阵,最后通过式(14)得到斜投影滤波后的波束域数据z(t)。
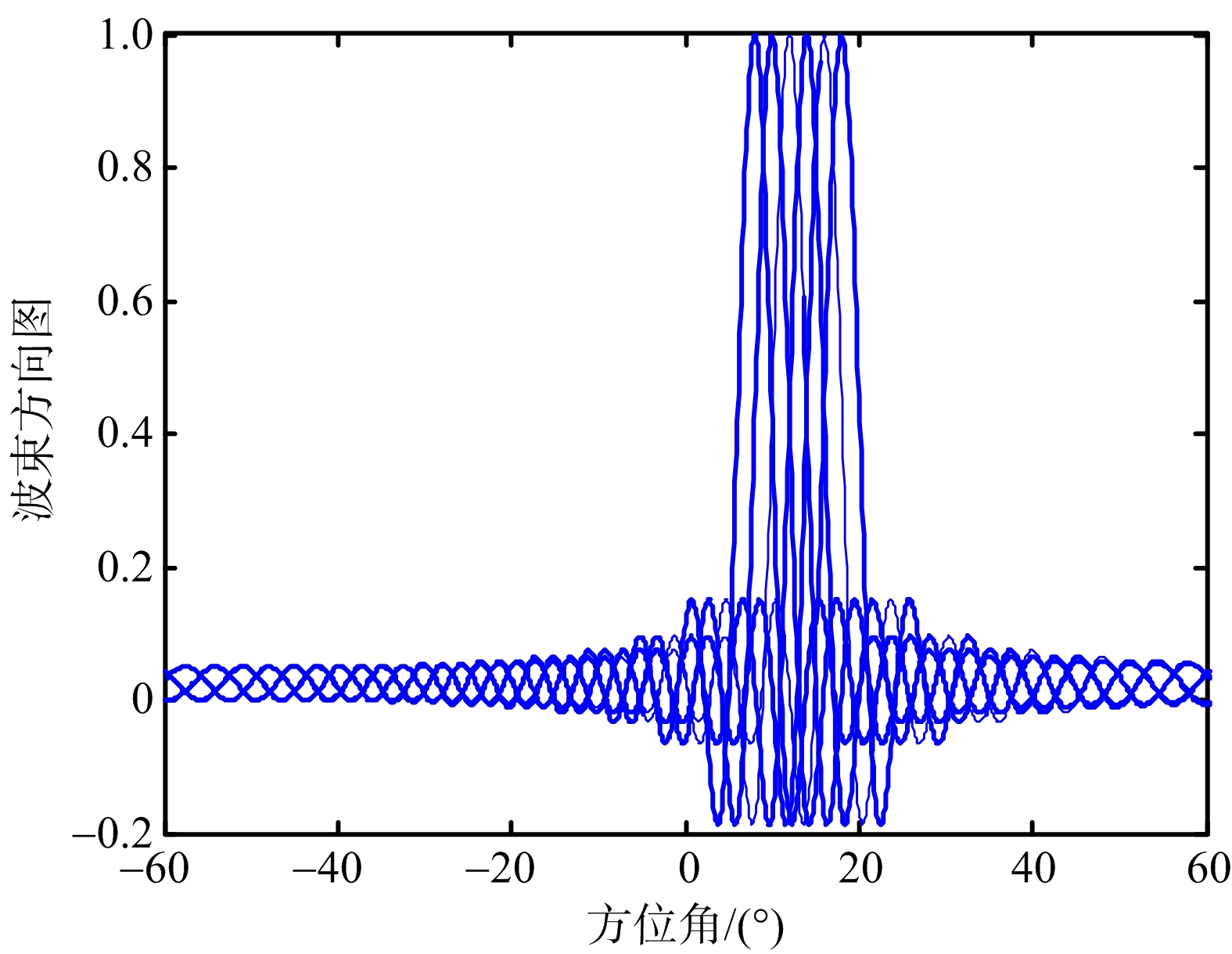
图2 扫描区域波束方向图
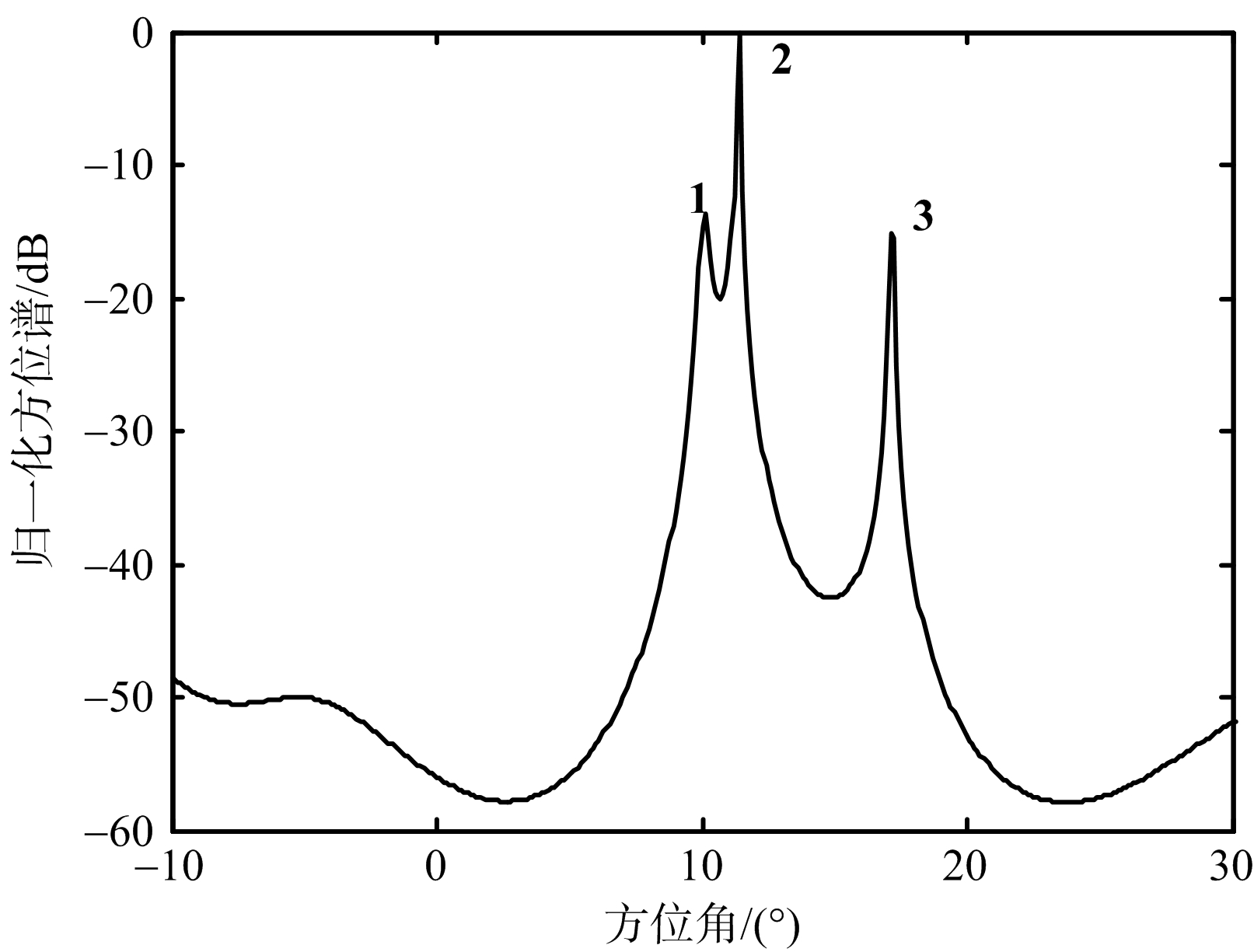
图3 波束域数据的归一化方位谱图
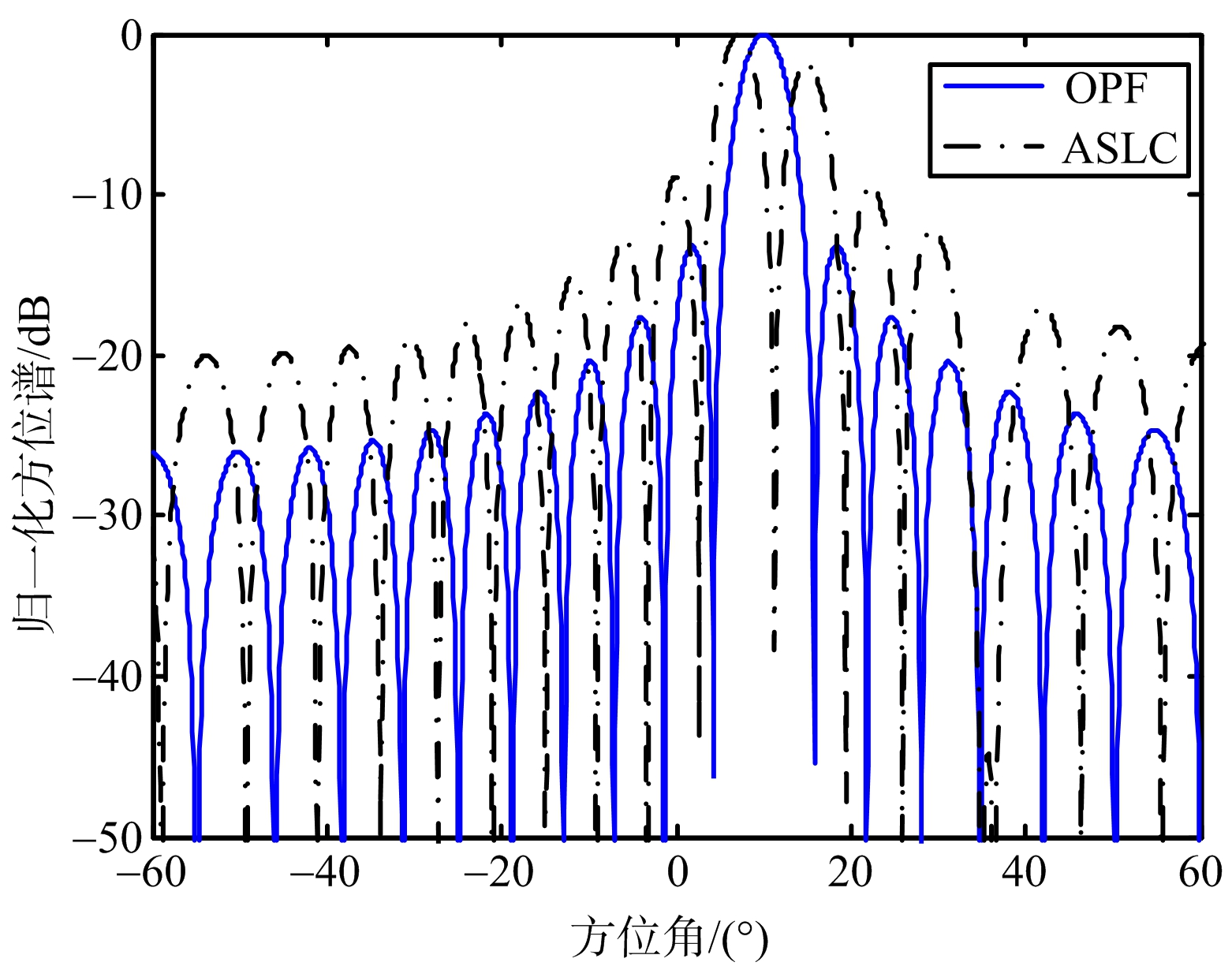
图4 斜投影滤波抗干扰波束与自适应旁瓣对消抗干扰波束的对比
图4给出了利用斜投影滤波后波束域数据z(t)进行波束形成,图中同时给出了雷达普遍应用的自适应旁瓣对消(Adaptive Sidelobe Cancellation,ASLC)抗干扰的波束图。由图可知:斜投影滤波后数据的波束图不但完全抑制掉了主瓣干扰和旁瓣干扰,并且波束图不畸变地指向了信号的正确方位10°;而基于自适应旁瓣对消的波束方向图虽然在主瓣和旁瓣干扰位置对消掉了干扰,抑制掉了主瓣和旁瓣干扰,但是在抑制干扰的同时引起了主波束的变形,波束指向为7.5°,引起了主瓣大幅度的偏移,并且旁瓣电平明显高于斜投影滤波的方法。所以将斜投影滤波后的波束域数据用于后续相关的信号处理工作比较可行。
在仿真过程中,分析发现数据的快拍数、信号和主瓣干扰的方位间隔、信噪比和主瓣干噪比的间隔这3个因素对本文的方法影响较大。在分析方法的影响因素时,本文通过变换各个影响因素得到的波束域数据在检测目标的检测概率曲线来说明。图5给出了检测概率与快拍数之间的关系曲线。由图5可知:当接收数据的快拍数大于2倍阵元数目M时,通过本文给出的方法得到的波束域数据,估计目标方位不会出现误差,目标的检测概率很大;当接收数据的快拍数小于2倍阵元数目时,目标方位估计会出现误差,目标的检测概率随快拍数的减少而减小。图6给出了检测概率与信号和主瓣干扰方位间隔之间的关系曲线,图中,θ0表示信号方位,θm表示主瓣干扰方位,|·|表示取绝对值因子,BW表示由式(2)求出的半功率波束宽度。
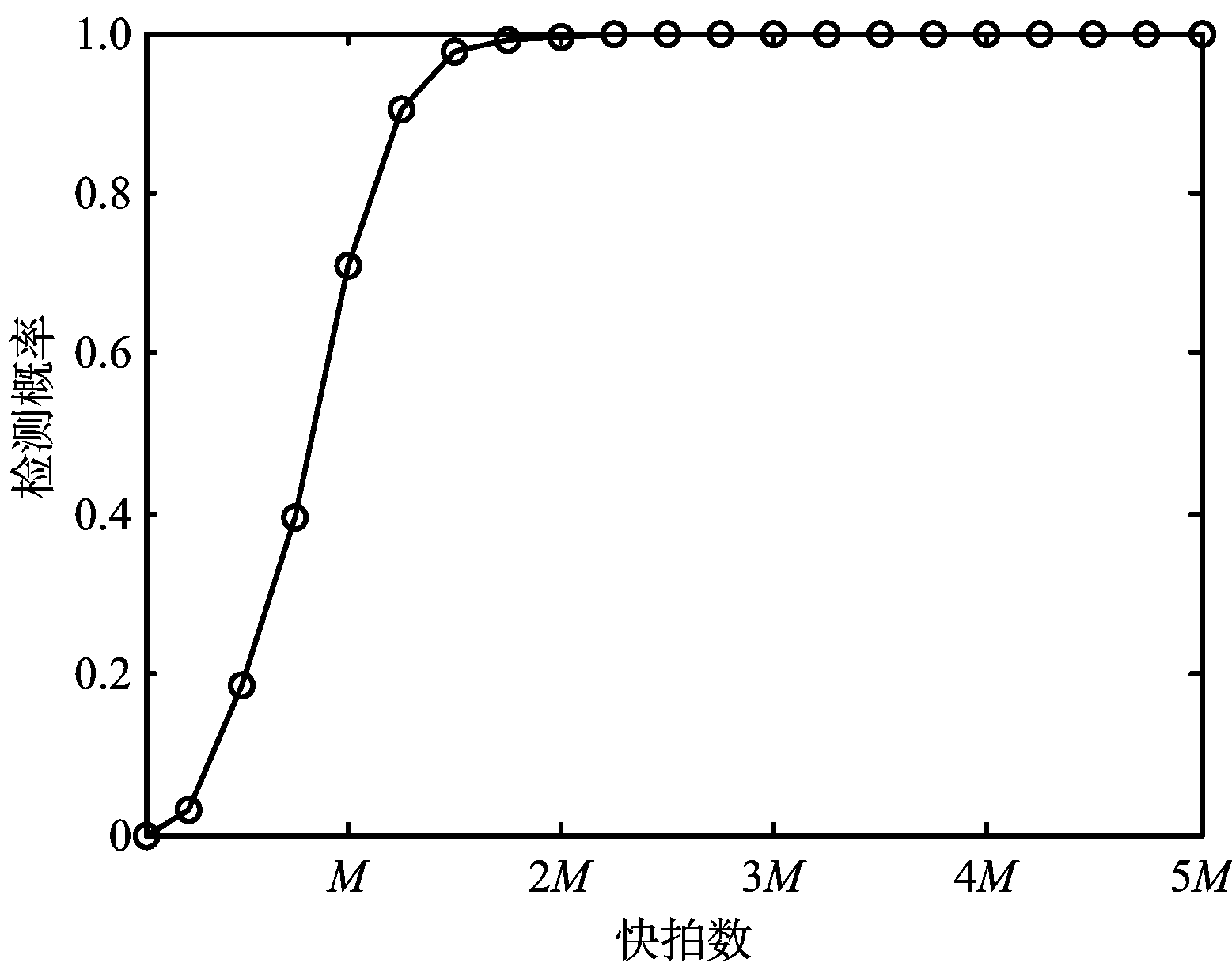
图5 检测概率与快拍数之间的关系曲线
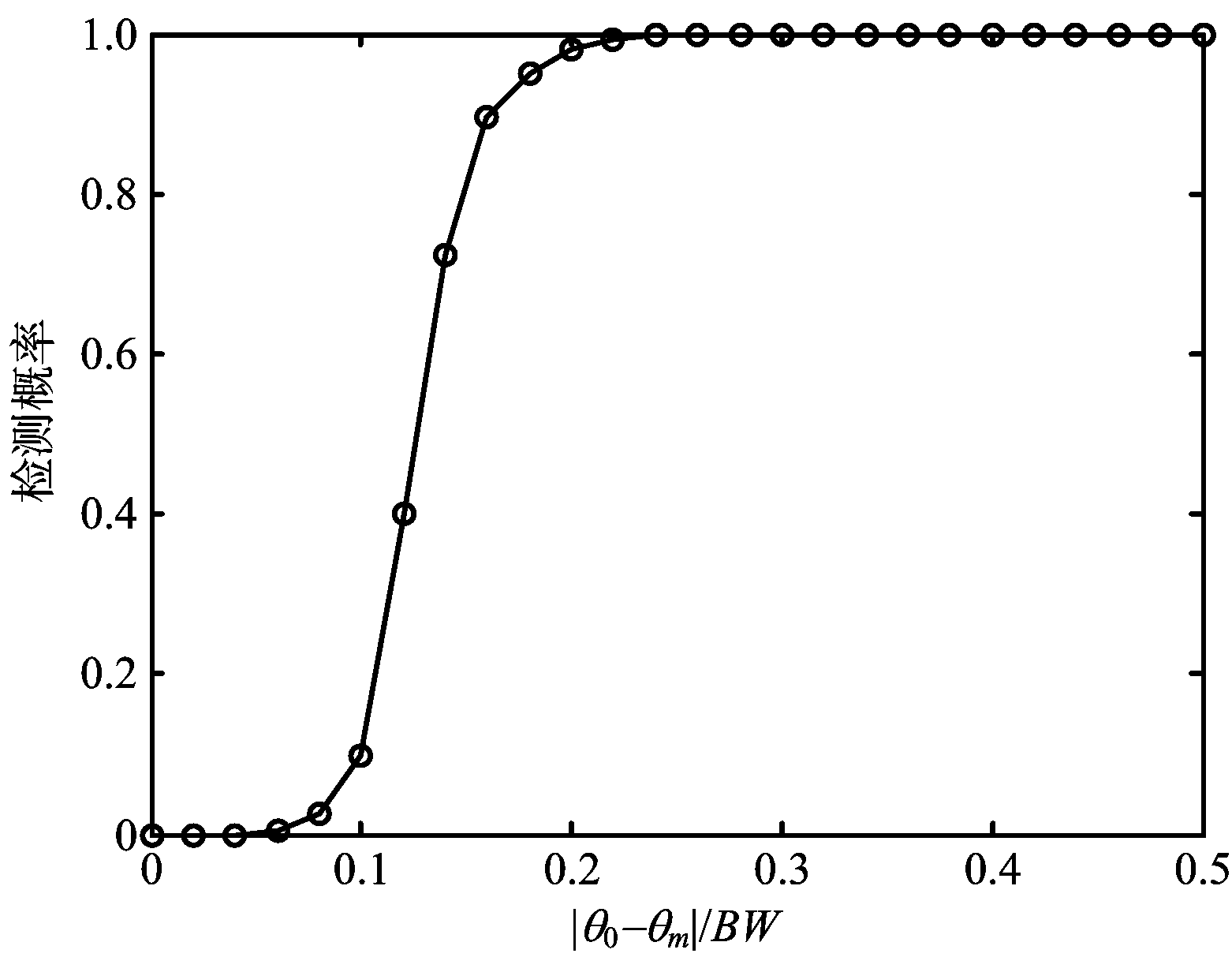
图6 检测概率与信号和主瓣干扰方位间隔之间的关系曲线
由图6可知:在仿真条件下,当信号与主瓣干扰方位间隔大约大于1/4波束宽度时,由斜投影滤波后的波束域数据估计信号方位时不会出现估计误差。当信号与主瓣干扰方位间隔小于1/4波束宽度时,波束域数据估计信号方位时会出现误差,目标信号的检测概率随信号与主瓣干扰方位间隔的减小而迅速减小。这主要是因为,当信号与主瓣干扰方位间隔太近时,在信号子空间和干扰子空间划分时出现了误差。图7给出了检测概率与信噪比(SNR)和主瓣干噪比(INR)间隔之间的关系曲线。由图7可知,在仿真条件下,需要保证信噪比和主瓣干噪比的差异在20 dB以内,本文的方法得到的波束域数据在信号估计时不会出现误差,但是当信噪比和主瓣干噪比的差异大于20 dB时,波束域数据目标信号的检测概率随信噪比和主瓣干噪比的差异的减小而迅速减小;特别是当信噪比和主瓣干噪比的差异大于30 dB时,目标检测概率几乎为零。
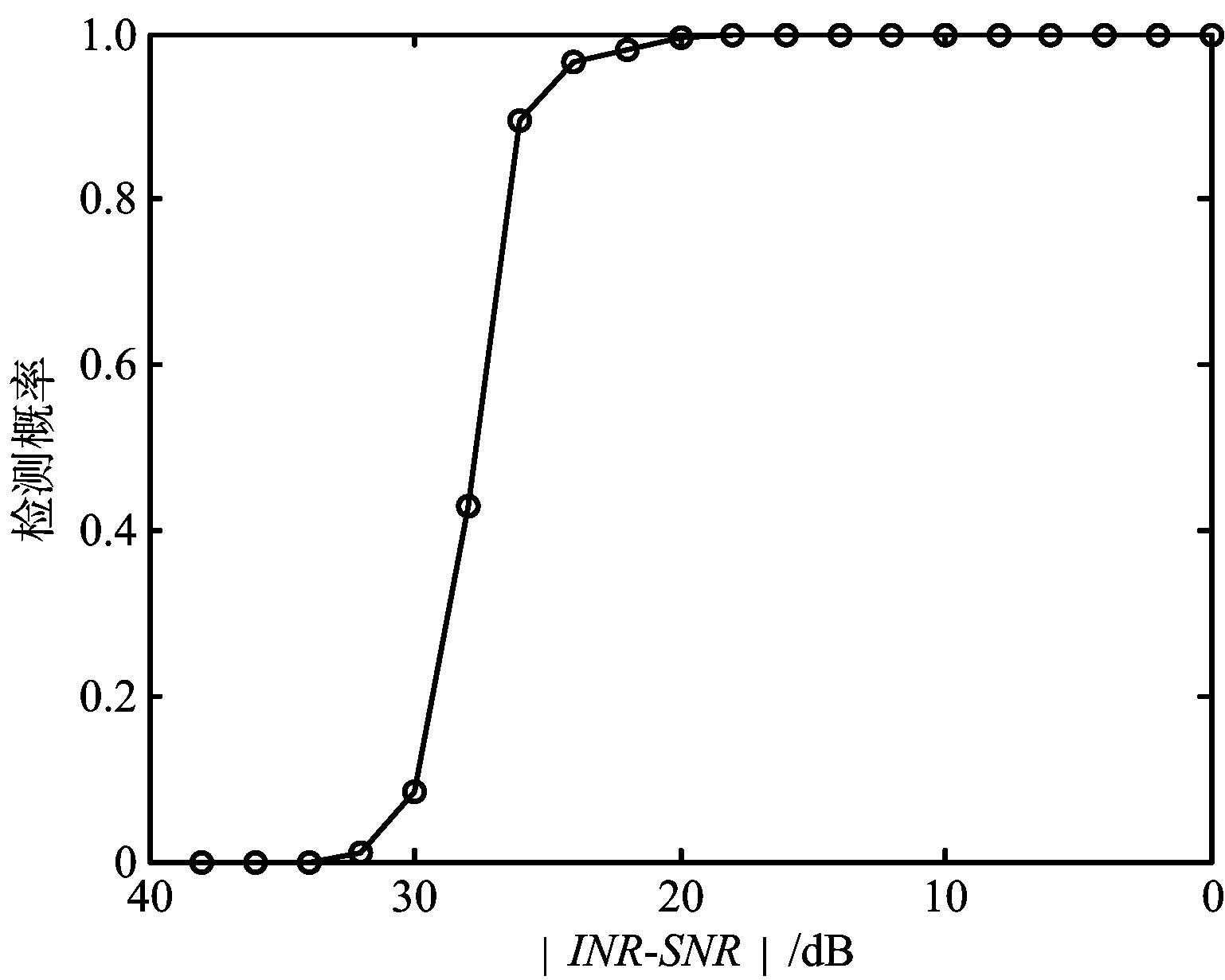
图7 检测概率与信噪比和主瓣干噪比间隔之间的关系曲线
3 结束语
本文提出了一种基于空间谱估计斜投影滤波的波束域主瓣抗干扰方法。首先通过将阵元域接收数据变换到波束域,然后对波束域数据进行斜投影滤波,能够同时消除掉所有的主瓣干扰和旁瓣干扰,得到的波束域数据能够在保证感兴趣区域内性能不变的情况下大大降低计算量,满足现代雷达的发展需求。并且分析表明:只有保证接收数据的快拍数大于2倍的阵元数目,信号与主瓣干扰方位间隔大于1/4波束宽度,并且信噪比和主瓣干噪比的差异在20 dB以内时,本文的方法得到的波束域数据在信号估计时才不会出现估计误差,保证能够正确地检测出目标。
[1] 邱炜,朱德智,范明意. 基于AA的多通道雷达自适应抗干扰方法[J]. 火控雷达技术,2016,45(2):21-25.
[2] VENDIK O G,KOZLOV D S. Phased Antenna Array with a Sidelobe Cancellation for Suppression of Jamming [J]. IEEE Antennas Wireless Propagation Letters,2012,11(12):648-650.
[3] LI J, STOICA P. Robust Adaptive Beamforming [M]. New York,USA:Wiley,2005:198.
[4] THEIL A. On Combining Adaptive Nullsteering with High Resolution Angle Estimation Under Main Lobe Interference Conditions [C]∥IEEE International Conference on Radar,Arlington,VA:IEEE,1990:295-297.
[5] 宁立跃,杨小鹏.多基地极化雷达主瓣干扰抑制算法[J]. 信号处理,2017,33(12):1571-1577.
[6] 戴幻尧,李永祯,刘勇,等.主瓣干扰极化抑制的新方法[J].中国科学:信息科学,2012,42(4):460-468.
[7] 陈伯孝,项喆,王睿智,等.基于斜投影预处理的自适应波束形成方法[J].制导与引信,2017,38(2):18-24.
[8] 陈辉,王永良.波束空间DoA算法性能综合分析[J].系统工程与电子技术,2004,26(10):1353-1356.
