0 引言
在空间阵列信号处理中，常规算法通过最优准则计算得出的阵列权矢量对输入信号进行加权处理，这样可以零陷干扰，但副瓣电平一般较高。实际工程应用中，阵列权矢量的计算需要一定的时间才能使空间阵列权矢量调整到新的最优状态。在新的权量形成之前，干扰环境变化很快时，新出现的干扰方向不能形成有效的零陷，从而影响接收性能。解决的方法是将对方向图进行低副瓣控制，这样就降低了突变干扰对空间阵列输出方向图的性能影响，这就是方向图控制(Pattern Control, PC)。另一方面，一些算法在采样数较少即小样本条件下性能急剧下降，出现主峰可能偏移、整体旁瓣上升和波束波动较大的情况，这时低副瓣的控制方法也将失效，所以解决阵列输出方向图副瓣较高问题的同时进行小样本量处理是非常有意义的。控制副瓣电平的方法有二阶锥规划(Second-Order Cone Program, SOCP)、旁瓣搜索及加窗等。文献[1-3]将多约束的优化问题转化为二阶锥规划求解以降低副瓣电平，但求解条件多，比较复杂。文献[4]通过采用对子阵级噪声归一化的方法改善了面阵非均匀划分结构的旁瓣电平，但没有对低采样下的算法进行分析。另一种方法是加窗，即幅度加权，如Chebyshev和Taylor加权，详细的推导可见文献[5]。这些降低副瓣电平的算法在小样本下会失效，输出方向图副瓣电平会很高。基于对角加载的波束形成算法[6]通过对相关矩阵特征值加载一个值来解决低采样下的方向图畸变问题，但具体加载量不好确定。文献[7]对常规算法的协方差矩阵进行修正，在低快拍情况下得到了稳健的波束形成方向图。特征干扰相消器(Eigencanceler, EC)最早由文献[8]提出，通过直接约束在干扰特征向量方向产生零陷，使得零陷深度独立于干扰噪声比，从而使干扰抑制能力加强[9-10]。EC不仅可以增强干扰抑制能力，还能使阵列权矢量位于噪声子空间，这样波束形成器输出方向图在小样本下也很稳定。上述几种降低样本量的方法得到的方向图副瓣电平都比较高。
本文基于MVDR算法，提出一种小样本下的方向图副瓣控制算法。该算法将常规算法输出方向图低副瓣控制和小样本处理方法相结合，得到的输出方向图在小样本情况下，期望信号方向增益最大，在干扰方向形成较深零陷的同时具有设定的低副瓣电平，下面将给出详细公式推导过程，并进行仿真实验验证。
1 信号模型及新的波束形成器
1.1 算法流程图
如图1所示，本文先将MVDR算法分别进行低副瓣和小样本量处理，然后将两者结合得到新的具有低副瓣、低采样特性的MVDR算法，即DREC-PC。具体详细推导过程和理论分析见1.2节和1.3节，并对MVDR和DREC-PC算法进行了小样本和低干噪比下的仿真，结果表明DREC-PC算法在小样本下也具有良好的波束形成性能。
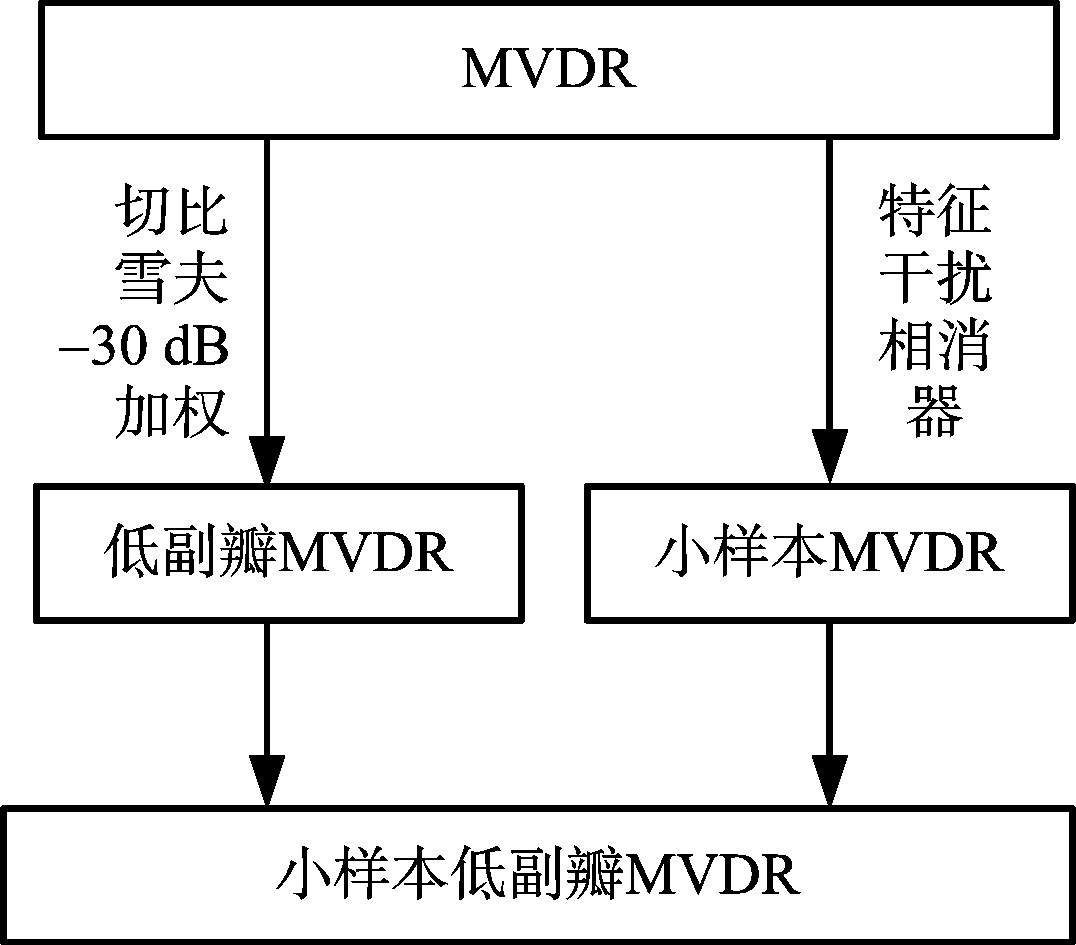
图1 算法流程图
1.2 低副瓣MVDR波束形成器(MVDR-PC)
考虑阵列为N元等距直线阵，阵元间距d，波长λ，假设阵元均为各向同性阵元。1个目标信号和M个干扰从远场以平面波入射到阵列上，目标信号方向为θ0，则阵列接收数据矢量X(k)可表示为
X(k)=AS(k)+N(k)
(1)
式中，A为阵列流形矩阵，A=[a(θ0),a(θ1),…, a(θM)]，a(θj)=[1,ejβj,…,ej(N-1)βj]T，j=0,1,…,M，为j个方向信号的导向矢量，且
(2)
S0(k)为目标信号向量，S(k)=[s0(k), s1(k),…,sM(k)]，N(k)为线阵阵元噪声向量，阵列协方差矩阵RX=E[X(k)XH(k)]。空间阵列处理的直接形式如图2所示，图中y(k)为空间阵列输出。
图2 空间阵列处理的直接形式
MVDR波束形成器在期望信号方向接收最大，单位约束增益为1，且干扰和噪声输出功率最小。MVDR波束形成器的准则为
(3)
可由拉格朗日法求解式(1)，经整理得到
(4)
MVDR波束形成器输出方向图副瓣电平的降低可以通过加窗方法实现。随着使空间阵列单元的幅值成锥形减弱，旁瓣电平也会进一步减少，现在使用锥化截取矢量W0，W0采用Dolph-Chebyshev加权加窗，加窗后的期望信号方向矢量为
aT(θ0)=W0⊙a(θ0)
(5)
式中，⊙表示两个矢量的元素与元素之间相乘。用式(5)中的aT(θ0)代替式(4)中的a(θ0)，将加窗方法应用到空间阵列中，得到低旁瓣MVDR波束形成器的权值
(6)
1.3 小样本下的方向图副瓣控制算法(DREC-PC)
虽然已经对MVDR波束形成器进行了低副瓣处理，但在小样本情况下，输出方向图会出现畸变，旁瓣电平偏高，下面通过特征干扰相消器解决这一问题。
特征干扰相消器直接在干扰特征向量方向建立零陷约束，这样空间阵列权矢量只位于噪声子空间，可以在一个波束宽度内产生多个零陷(即所谓“超对消”)，优点是减小噪声的不稳定对方向图形成的影响的同时，零陷深度独立于干扰噪声比，从而使干扰抑制能力在小样本数下得到加强。对应MVDR算法，特征干扰相消器可称为无失真响应特征干扰相消器(DREC)。
DREC的准则为
(7)
式中，Us的列展成干扰子空间，阵列协方差矩阵
为噪声子空间，Us为干扰子空间，Λs,Λn均为对角阵，对角元素为Us,Un中各特征向量对应的特征值。对于一个N元空间阵列，有N个自由度可以利用。其中一部分用来满足特定的约束(如单位增益约束及其他线性约束)，剩下的自由度用来抑制干扰和噪声。抑制干扰及噪声的自由度越多，算法的计算量越大，对应所需样本量越大；反之，能在较少的样本下得到良好的效果。
将式(3)与式(7)相比较，可以看出式(3)中抑制干扰的自由度转化为式(7)中的约束自由度，剩余的自由度使空间阵列权矢量的模最小，即高斯白噪声增益最小。
由拉格朗日法求得式(7)的解为
(8)
由
则式(8)等效为
(9)
本文将上述处理方法应用到低副瓣MVDR波束形成器中，通过将式(5)中的aT(θ0)代替式(9)中的a(θ0)，得到一种小样本下的方向图副瓣控制算法，权值为
(10)
在小样本下，干扰子空间的大特征值及特征向量很稳定，而小特征值及其特征向量(对应噪声子空间)发生抖动，求得的协方差矩阵RX误差很大，式(4)和式(6)求解过程中都需要利用到RX，所以常规的MVDR和加上副瓣控制的MVDR算法在小样本下性能下降很大。在式(10)中，DREC-PC完全消除了噪声子空间抖动的影响，尽管小特征向量(噪声特征向量)发生抖动，但
却相对稳定，小样本下算法也很稳定；DREC-PC的权矢量被完全投影到噪声子空间，说明了DREC-PC可以使权矢量位于噪声子空间，能直接在干扰方向产生零陷，使得干扰抑制独立于干噪比，干噪比的降低对小样本下的波束形成方向图影响不是很大。
1.4 算法计算量分析
表1列出了各个算法的权值求解运算量情况。因为常规的MVDR和低副瓣加权的MVDR算法权值需要求阵列相关矩阵的可逆，所以相对文中提出的DREC-PC算法运算量较多，DREC-PC算法有相对较少的运算量。
表1 各算法运算量对比
算法运算量实数加实数乘MVDRN3-1N3+N2+2NMVDR-PCN3-1N3+N2+3NDREC-PCN3-2N2-1N3-N2+3N
2 仿真实验分析
取N=16元等距线阵，阵元间距为半波长，目标信号方向为30°，干扰方向角度为-40°和50°，干扰间互不相关，W0采用-30 dB的Chebyshev低副瓣加权，干噪比为3 dB。
2.1 低副瓣MVDR波束形成器输出方向图
实验1 方向图采用副瓣为-30 dB的Chebyshev加权。样本数取为3 000N时，图3(a)比较了常规MVDR和MVDR-PC方法的波束形成器输出方向图。从图3(a)可以看出，常规MVDR虽然在干扰方向产生零陷，但方向图的副瓣较高。而MVDR-PC方法在形成所要求零陷干扰的同时，较好地拟合了-30 dB的Chebyshev低副瓣特性，满足设计需要。
相同条件下样本数1.5N时两种算法的波束形成器输出方向图如图3(b)所示。MVDR和MVDR-PC波束形成器的输出方向图在干扰方向形成零陷，但整体副瓣起伏很大，电平较高，可见较少的采样次数对其输出方向图影响很大，这些原因是低采样数下式(2)和式(4)协方差矩阵中噪声子空间对应的特征值发生抖动，造成协方差阵的估计值与实际有偏差。
(a) 样本数3 000N
(b) 样本数1.5N
图3 MVDR和MVDR-PC波束形成方向图
2.2 基于MVDR小样本下的方向图副瓣控制算法
为了解决MVDR算法在小样本条件下，输出方向图出现的畸变、旁瓣电平过高和主瓣方向可能出现的偏移问题，本文提出基于最小方差无失真响应(MVDR)将低副瓣加权和EC相结合的方法，即一种小样本下的方向图副瓣控制算法(DREC-PC)，条件与上面相同，用-30 dB的Chebyshev低副瓣加权和特征干扰相消器的小样本处理方法来处理期望信号方向为30°，干扰角度为-40°和50°，干噪比为3 dB。
实验2 图4(a)和图4(b)分别给出了大样本和小样本时MVDR-PC和DREC-PC的波束形成输出方向图。
(a) 样本数3 000N
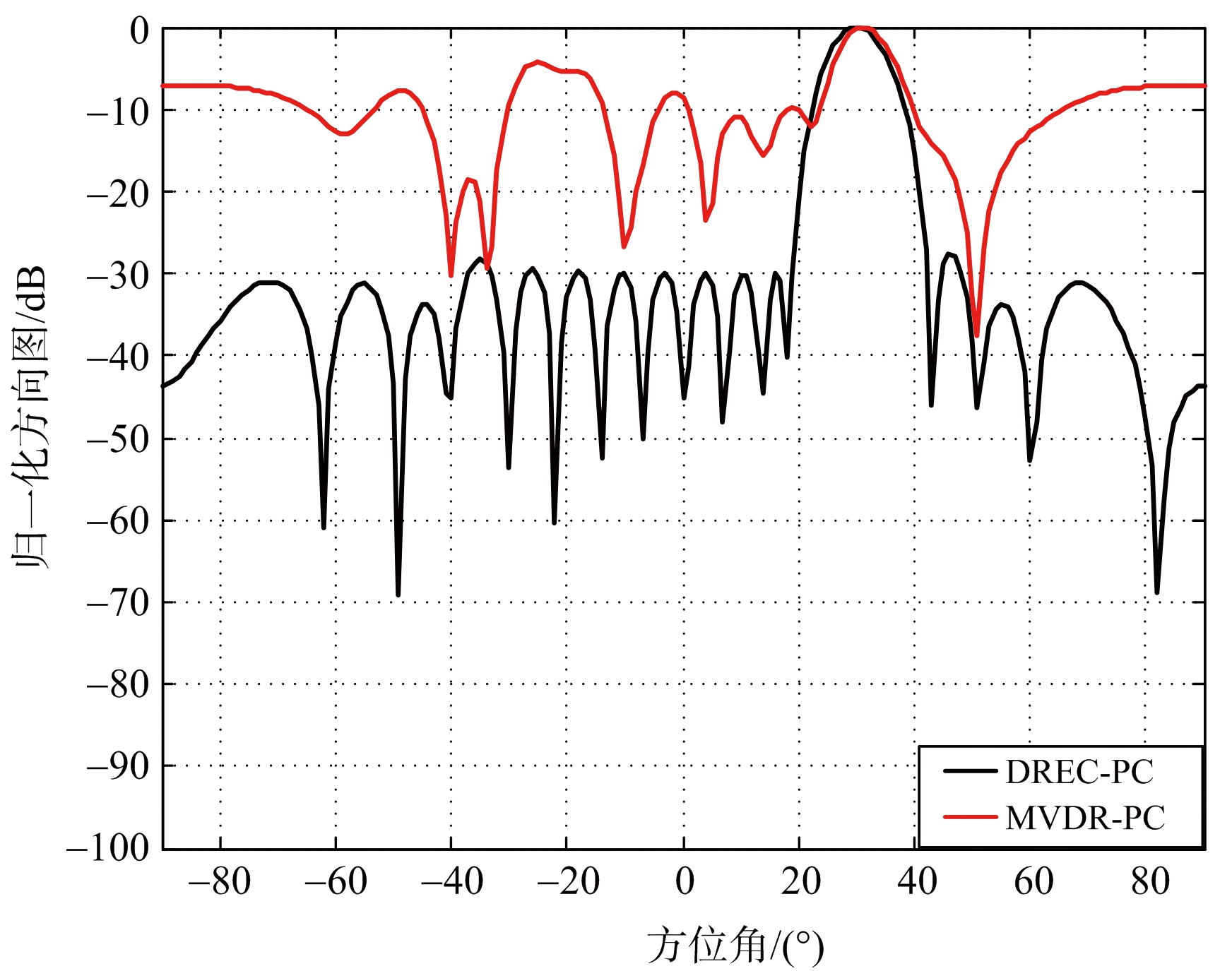
(b) 样本数1.5N
图4 MVDR-PC和DREC-PC波束形成方向图
图4(a)和图4(b)分别给出了高低采样数时MVDR-PC和DREC-PC算法的输出方向图，从 图4(a)可以看出，采样数为3 000N时，DREC-PC和MVDR-PC波束形成方向图较吻合，都有在-35°和40°干扰处形成零陷和-30 dB的低副瓣特征，这也初步验证了低副瓣加权和EC相结合的方法的正确性。从图4(b)可以看出，采样数为1.5N时，MVDR-PC方向图虽然在两个干扰处形成零陷，但副瓣区出现不同程度的起伏，副瓣电平偏高，主波束形成方向也发生了偏移，两种方法相结合的DREC-PC方向图在小样本量下，副瓣电平较拟合设定的 -30 dB，整个副瓣区电平值很稳定，主波束形成方向没有发生偏移，由于干扰置零的作用，在-35°和40°附近出现个别电平值大于-30 dB的现象，但这不想影响整体的效果，在可接受范围内。
在相同的小样本量下，图5为在干扰-40°方向时MVDR-PC和DREC-PC算法的干扰零陷深度绝对值随干噪比的变化曲线。从图中可以看出，本文提出的DREC-PC算法对干扰的零陷深度在干噪比0 dB到10 dB都比MVDR-PC算法高，而且方向图如图4(b)所示很稳定，干噪比10 dB以后两种零陷深度将非常接近。
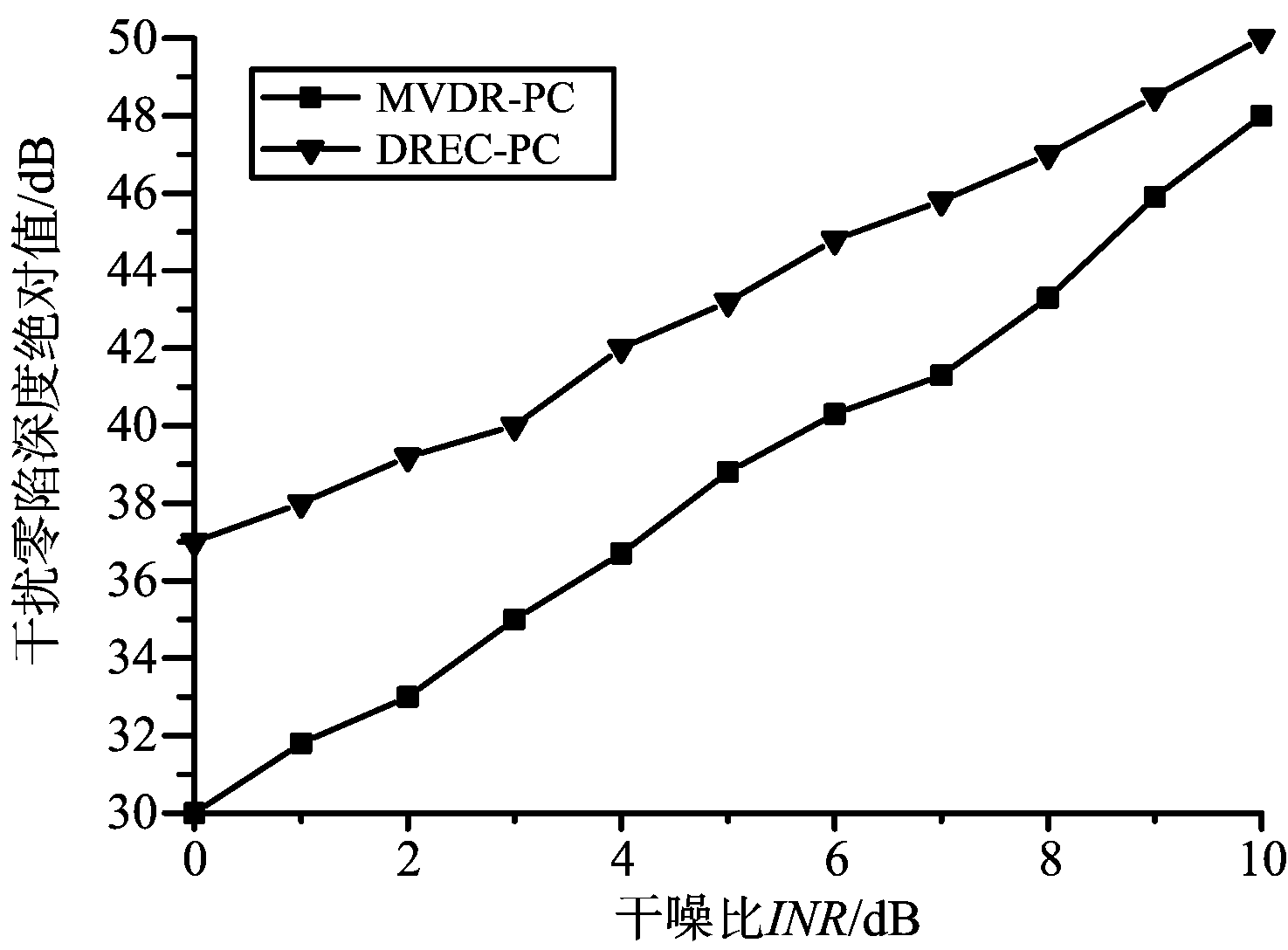
图5 零陷深度随干噪比的变化曲线
小样本量的处理可能会带来改进后的算法输出信干噪比的下降，特别是在常规算法的波束形成需要的样本量很大的情况下；因为对MVDR算法进行了低副瓣处理，所以波束宽度也有一定展宽。
3 结束语
本文提出一种小样本下的方向图副瓣控制算法(DREC-PC)。基于MVDR波束形成器，采用的低副瓣加权方法可以在大样本量下实现低的副瓣，但样本较多；在MVDR波束形成器加入特征干扰相消器可以解决小样本下方向图电平值的不稳定问题，但副瓣电平偏高。本文的算法将MVDR波束形成器的低副瓣加权方法和小样本解决方法相结合，在小样本条件下，所得到的方向图可以有效抑制干扰和保持方向图稳定，具有预先设置低副瓣电平。
[1] 黄聪,孙大军,张殿伦,等. 强相干干扰下基于二阶锥规划的圆弧阵宽带二维成像[J]. 电子与信息学报, 2014, 36(11):2633-2639.
[2] JIANG A, KWAN H K, ZHU Y, et al. Peak-Error-Constrained Sparse FIR Filter Design Using Iterative L1 Optimization[C]∥ 24th European Signal Processing Conference, Budapest, Hungary: IEEE, 2016:180-184.
[3] YANG Yixin, YANG Long, ZHU Jiannan. Sidelobe Suppression for Time-Domain Adaptive Broadband Beamforming with Sparse Constraint[C]∥ OCEANS 2016 MTS/IEEE Monterey, Monterey, CA: IEEE, 2016:1-4.
[4] 邓金花,谢菊兰. 一种接收相干信号的盲多波束形成方法[J]. 雷达科学与技术, 2015,13(6):567-571.
[5] 王永良,丁前军,李荣锋. 自适应阵列处理[M]. 北京: 清华大学出版社, 2009:104-106.
[6] YANG Jian, LIU Ruiqi, XI Xuqi. An Adaptive Beamforming Design in Low Sample Number Conditions Based on Diagonal Loading Algorithm[C]∥ IEEE International Conference on Signal and Image Processing, Beijing: IEEE, 2016:755-758.
[7] 朱玉堂,赵永波,水鹏朗,等. 一种低快拍情况下的稳健自适应波束形成算法[J]. 西安电子科技大学学报(自然科学版), 2015, 42(6):37-42.
[8] HAIMOVICH A. The Eigencanceler: Adaptive Radar by Eigenanalysis Methods[J]. IEEE Trans on Aerospace and Electronic Systems, 1996, 32(2):532-542.
[9] CHANG A, CHIANG C, CHEN Y. An Eigenanalysis Interference Canceler with Robust Capabilities[J]. Microwave and Optical Technology Letters, 2000, 25(2):100-103.
[10] DING Wenbing, YU Kai, FAN Zhenhong, et al. LCEC Beamforming Applied to a Time-Modulated Array[C]∥ International Applied Computational Electromagnetics Society Symposium, Suzhou: IEEE, 2017:1-2.
