0 引言
在许多相控阵雷达中,特别是大型相控阵雷达中,一方面这些雷达的使用可用度要求很高,如某大型相控阵雷达要求大于99%;另一方面,由于阵面庞大,T/R组件数量达到几千乃至几万。由于雷达设备量很大,单个组件可靠性有限,使得雷达整机的基本可靠性很低,为了同时满足高可用度和高可靠性要求,雷达中的许多分系统,如相控阵雷达的阵面分系统、大功率开关电源分系统等,越来越多地采用冗余设计(即使用k/N系统)。通过采用冗余设计,提高雷达的任务可靠性。然而,任务可靠性高不等于使用可用度就高,任务可靠性一定的情况下,使用可用度的高低取决于平均修复时间(MTTR)的长短,而维修方式、初始备件量、维修人员配置等因素对MTTR有显著影响。也就是说在任务可靠性一定的情况下,使用可用度很大程度上取决于维修方式、初始备件量、维修人员配置等因素。为此本文将通过建模和仿真的方法研究这些因素对雷达使用可用度的影响,最终给出提高雷达使用可用度的途径。
文献[1]用定时截尾寿命试验理论来处理k/N系统的故障时间数据和维修时间数据,分析了维修组数与系统停止工作时部件故障数相同情况下的使用可用度,但未考虑备件对系统使用可用度的影响;文献[2]通过建立多态串并联可控系统可用度的精确求解模型,研究了基于状态维修模式下,通信指挥装备的可用度评估问题,但对冗余系统考虑不足;文献[3]针对现有备件冗余度建模中无限呼叫总体假设不合理、供应可用度计算困难的问题,提出一种k/N(G)结构系统初始备件配置方法,文章仅考虑了备件对使用可用度的影响;文献[4]提出了当系统可用度较低,采用串件策略提高系统可用度的方法;文献[5]给出了以备件购置费用为优化目标、装备可用度为约束条件,构建了有限维修能力下的备件库存优化模型,没有考虑系统冗余设计;文献[6]建立了m视情维修策略下k/N热贮备系统的使用可用度模型,m维修策略是指当N个部件中失效数量达到m(0<m≤N-k+1)个,系统停止工作进行维修,直至系统可工作单元恢复到N个;文献[7]放宽了文献[6]的条件,将系统恢复工作时可工作单元数由N放宽到NG(N-m<NG≤N),给出了(m,NG)维修策略下k/N热贮备系统使用可用度模型,(m,NG)维修策略属于一种非完美维修策略;文献[8]模型考虑k/N系统不同的故障类型对备件配置的影响,以配置备件数目最小为目标函数,使用可用度模型和保障费用为约束条件考虑单件送修条件下备件配置问题。以上研究主要集中在部件故障后立刻送修策略和m维修策略两个方面,而针对定期成批维修策略考虑较少。定期成批维修策略是指k/N系统工作满一定时间L即停止工作,利用备件更换所有失效的部件并对拆卸下来的失效部件进行修复,在完成备件的安装之后系统重新开始工作。在实际维修活动中,某些应用k/N系统的复杂装备如大型相控阵雷达常采取定期成批维修策略。因此有必要研究定期成批维修策略下不同备件、人员配置时k/N系统的使用可用度,为该类系统的维修提供决策支持。
1 使用可用度模型
设k/N热贮备系统包含N个失效时间都服从参数为λ的指数分布且相互独立的部件,至少需k个部件正常工作,系统才能正常运行。系统开始工作时,N个部件都工作,系统工作满一段时间L后停止工作,开始拆卸和更换失效部件,停止工作时故障部件数为n,是一个随机变量。系统使用单位有C1个部件拆卸安装人员,C2个部件修理人员,S0个初始备件。每个拆卸安装人员一次只能拆卸安装一个故障件,拆卸、安装时间都服从参数为v的指数分布。每个部件修理人员一次只能修理一个故障件,修理时间服从参数为μ的指数分布,可以独立不间断地工作,修复好的故障件可作为备件使用。故障件全部拆卸后,在部件修理人员进行修复的同时检查备件数量,若此时的备件数量s大于故障件数量n,则进行安装;若备件数量s小于故障件数量n,则等待维修人员修复安装所需的剩余n-s个故障件。安装完毕后,系统恢复正常工作,开始下一个工作周期。系统的运行过程如图1所示。

图1 系统运行过程图
设L时间内系统平均工作时间为E(UL)(L时间内系统至少有k个部件正常工作的时间),平均拆卸时间为E(R),平均等待的备件时间为E(D),平均安装时间为E(I),则系统的使用可用度可表示为
(1)
由于L已知,所以计算A0的关键是求解E(UL)、E(R)、E(D)及E(I)。
2 雷达使用可用度模型求解
2.1 计算E(UL)
由于t(0≤t≤L)时间内单个部件可靠性函数为e-λt,所以k/N系统的可靠性函数为
(2)
式中,![]()
进而得到L时间内系统平均工作时间E(UL)为
(3)
2.2 计算E(D)
平均等待备件时间E(D)取决于以下3个因素:L时刻系统部件失效数n、失效部件全部拆卸时可用备件数s和修理剩余n-s个故障件的时间,可由式(4)表示:
E(D)=![]()
PL(n)·π(s)
(4)
式中,E[RC2(n-s,S0-s+n)]为C2个部件修理人员修复总的S0-s+n个待维修故障件中n-s个的平均时间;π(s)为失效部件全部拆卸完毕时系统有s个可用备件的稳态概率;PL(n)为L时刻系统部件失效数为n的概率,服从参数为N和1-e-λt的二项分布,可由式(5)表示:
(5)
下面,求解E[RC2(n-s,S0-s+n)]。
令x=n-s,y=S0-s+n,x≤y,则E[RC2(x,y)]为C2个部件修理人员将总的y个待维修故障件中修复x个的平均时间。采用递推法进行求解。递推公式如下:
E[RC2(x,y)]=![]() +
+
E[RC2(x-1,y-1)]
(6)
当x≤0,可以得出:
E[RC2(x,y)]=0
(7)
对于x>0,分为y≤C2,y>C2且x≤y-C2,y>C2且y-C2<x≤y三种情况讨论。
当x>0且y≤C2时,表示所有待修部件数量y小于等于部件修理人员数量,可以得到:
(8)
当x>0,y>C2且x≤y-C2时,表示修复前x个故障件时剩余等待修复故障件数都大于部件修理人员数C2,由递推公式可以得到:
(9)
当x>0,y>C2且y-C2<x≤y时,表示修复前y-C2个故障件时剩余等待修复的故障件数都大于部件修理人员数量C2,而修复x个故障件数中剩余x-(y-C2)个时剩余等待修复的故障件数都小于部件修理人员数C2,由递推公式可以得到:
E[RC2(x,y)]=![]()
(10)
下面,求解π(s)。
设第f次全部拆卸完成时系统可用备件数量为s(f),0≤sf≤S0,由于部件失效时间、拆卸时间、修复时间、安装时间都服从指数分布,则第f+1次全部拆卸完成时系统可用备件数量s(f+1)仅与s(f)有关,所以,{s(f),f=1,2,…}形成一个马尔可夫链。
用pij表示从第f次全部拆卸完成时系统可用备件数量s(f)为i的状态转移到第f+1次s(f+1)为j的状态的转移概率,即
pij=P{s(f+1)=j|s(f)=i}
(11)
根据马尔可夫链理论,可以得到π(s)与pij的关系式如下:
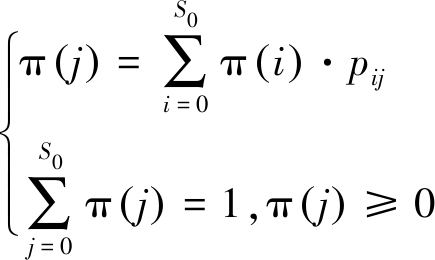
(12)
由式(12)可知,求解π(s)的关键是得出状态转移概率pij。
定义Pr(a,b,C2,t)为时间t内,C2个部件修理人员通过维修将总故障部件数量从a减少到b的概率。由文献[7]可知:
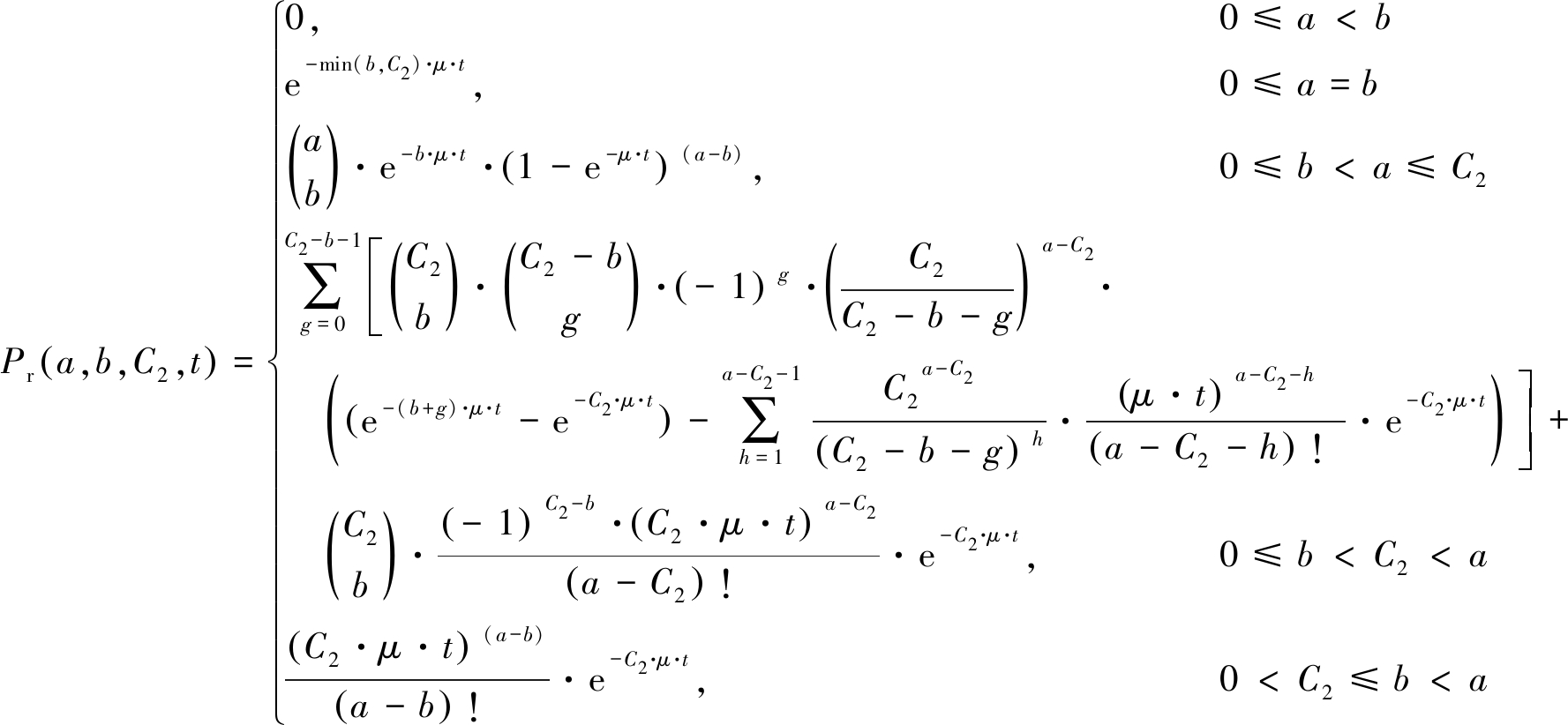
(13)
在失效部件拆卸数量为n且拆卸全部完成时可用备件为i时,所有等待修复的失效部件总数为S0-i+n。若i<n,需要等待可用备件数增加到n时,才能开始安装工作,安装开始时所有等待修复的失效部件总数将下降到S0。若i≥n,可立即开始安装工作,安装开始时所有等待修复的失效部件总数为S0-i+n。因此,安装开始时所有等待修复的失效部件总数为min{S0,S0-i+n}。在已知下一次全部拆卸完成时系统可用备件数量为j时,上述失效部件总数min{S0,S0-i+n}将在系统经历安装、定期工作L、拆卸三个阶段后下降到S0-j。
因此,状态转移概率pij可表示为
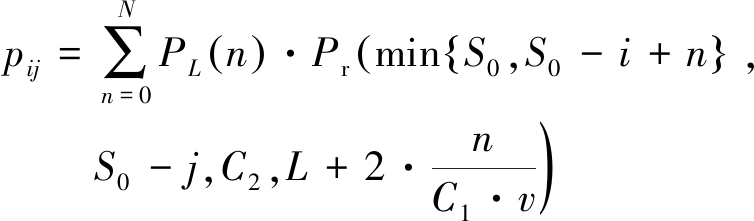
(14)
将式(14)代入式(12)可求出π(s),在此基础上,联合式(4)可求解出平均等待备件时间E(D)。
2.3 计算E(R)和E(I)
部件的拆卸是安装的反方向,在拆卸、安装部件数量相同且拆卸、安装人员数量相同时,拆卸时间可近似等于安装时间。当单个部件拆卸(安装)时间服从参数为v的指数分布且拆卸(安装)人员为C1时,平均拆卸时间E(R)或安装时间E(I)可由式(15)表示:
(15)
3 雷达阵面使用可用度实例分析
某相控阵雷达阵面模块为116/128热贮备系统(本文方法适用于更大阵面的情况,为仿真计算方便以较小的雷达阵面为例进行分析),模块中各部件的失效时间服从λ=0.000 08 h-1指数分布,拆卸和安装时间服从参数为v=2 h-1指数分布,修复时间服从参数为μ=0.006 h-1指数分布。下面讨论系统停机前工作时间L、初始备件数量S0、部件修理人员数C2对使用可用度的影响。
实验1:假设部件拆卸安装人员数C1=1,系统停机前工作时间L=100 h,部件修理人员数C2的取值范围为[1,4],初始备件数量S0的取值范围为[1,10]。得出C2与S0对使用可用度A0的综合影响如图2所示。
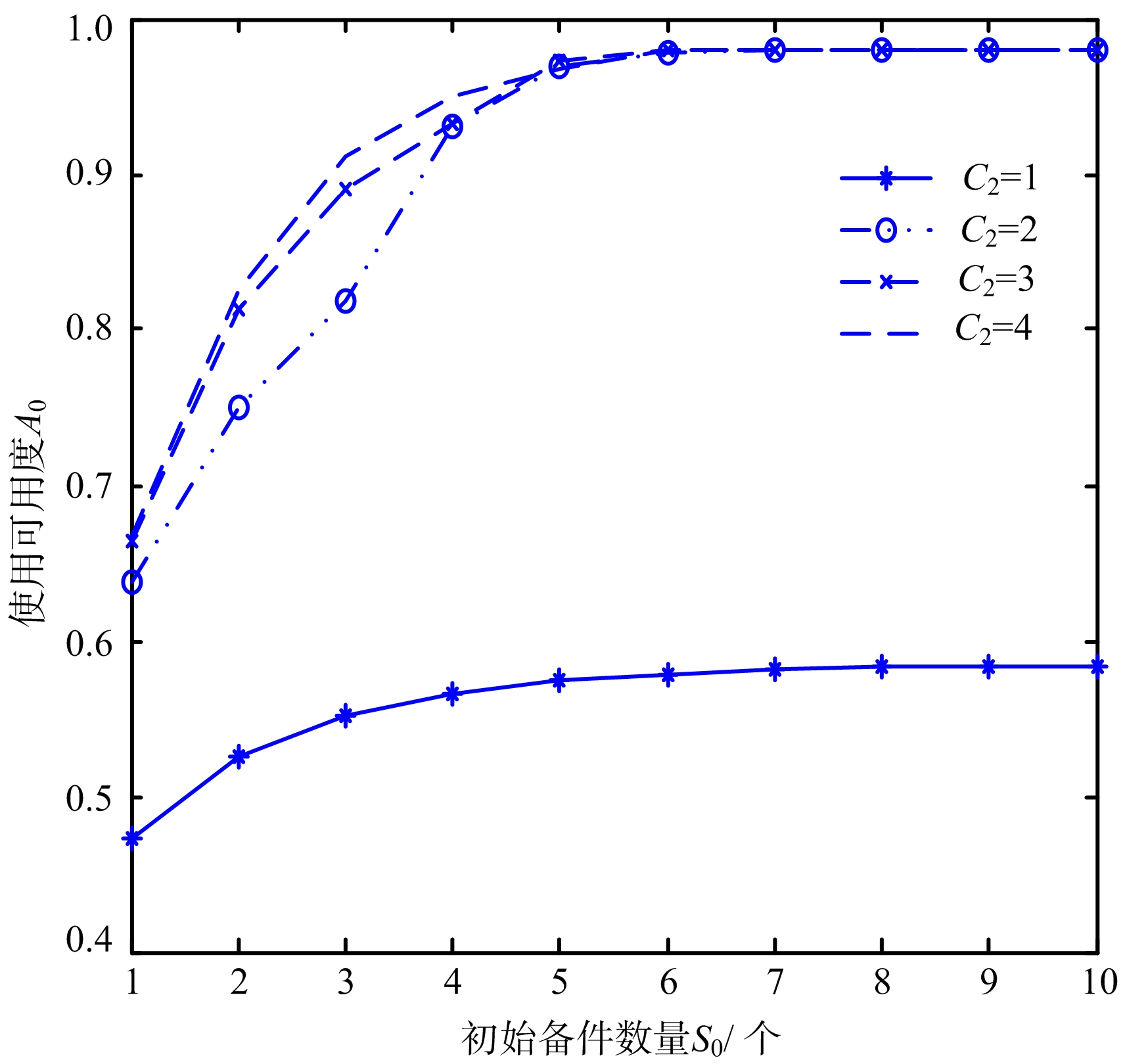
图2 C2与S0对A0的综合影响
由图2可知,在部件拆卸安装人员数C1和工作时间L保持固定时,当部件修理人员数C2的取值较小时(C2=1),增大S0只能有限增加使用可用度值,要大幅度增加使用可用度需增大C2值;而当C2的取值大于2时,增加C2对使用可用度值的提升作用较小,而增大S0(S0≤5时)可大幅提升使用可用度值。
下面,选取大于2的C2值,分析在部件维修能力足够强时,初始备件数量S0、停机前工作时间L对使用可用度A0的综合影响。
实验2:假设部件拆卸安装人员数C1=1,部件修理人员数C2=3,系统停机前工作时间L以步长24 h在24 h到240 h区间内变化,初始备件数量S0的取值范围为[1,4]。得出S0与L对使用可用度A0的综合影响如图3所示。

图3 S0与L对A0的综合影响
由图3可知:在部件维修能力足够大条件下(C2>2),当停机前工作时间L固定时,使用可用度值随着初始备件数量S0的增大而增加,但增加的幅度趋于缓和;当初始备件数量S0固定时,使用可用度值并不随时间L单调变化,而是先增大再减小,存在一个最佳L值使使用可用度值最大。
综合实验1和2,可以得到以下结论:
1)在部件维修能力不足的条件下(C2≤2),使用可用度值将停留在一个较低的水平,且此时初始备件数量S0、停机前工作时间L对提高使用可用度值帮助不大。
2)在部件维修能力足够大的条件下(C2>2),若想保持较高的使用可用度值,初始备件数量S0也不应太小,应配置一定数量的备件。
3)在备件数量S0、部件修理人员数C2都充足的情况下,应合理选取时间L值以保证使用可用度值最大,因为使用可用度值并不随时间L单调变化。
4 结束语
本文给出了定期成批维修策略下k/N系统使用可用度模型,通过实例分析了停机前工作时间L、初始备件数量、部件修理人员数量等因素对系统使用可用度的影响。该模型可以为k/N系统保障方案的制定、保障资源的规划提供决策支持。
[1] 贾秀芹,刘瑞元. k/n系统在(n, L, r, r)维修策略下的可用度[J].西南大学学报(自然科学版),2011, 33(9):17-21.
[2] 刘欢庆,罗长远,庞松超,等.状态维修下通指装备可用度评估[J].火力与指挥控制,2017, 42(5):90-94.
[3] 卢雷,杨江平. k/N(G)结构系统初始备件配置方法[J].航空学报,2014, 35(3):773-779.
[4] 周亮,李庆民,彭英武,等.串件拼修对策下k/N(G)结构系统可用度评估建模[J].航空学报,2017, 38(4):123-132.
[5] 李华,周亮,李庆民,等.有限维修能力下作战单元装备可用度评估及备件配置优化[J].海军工程大学学报,2017,29(1):69-73.
[6] DE SMIDT-DESTOMBES K S, VAN DER HEIJDEN M C, HARTEN A V. On the Availability of a k-out-of-N System Given Limited Spare and Repair Capacity Under a Condition Based Maintenance Strategy[J]. Reliability Engineering and System Safety,2004,83(3):287-300.
[7] 张涛,张建军,郭波.基于使用可用度的k/N系统(m, NG)维修策略分析[J].宇航学报,2009, 30(1): 395-401.
[8] 付冰,刘福胜,闫旭.装备k/N系统保障备件配置优化模型[J].现代防御技术,2017,45(5):155-161.

