0 引 言
消极干扰中使用最早和最广的是箔条干扰。箔条干扰源于二战时期，是对抗雷达探测的软杀伤技术手段[1-6]。箔条干扰就是利用箔条的物理特性干扰破坏地面雷达、制导雷达的跟踪系统，使其无法跟踪真实目标。
由于收发分置，双基地雷达具有与单基地雷达的不同之处，在抗干扰方面有一定优势[7-10]。双基地雷达T, R的位置关系不同、突防航线不同、雷达频段不同，以及箔条厚度不同，使其抗无源箔条干扰的效果也不同。本文分析计算了几种特定干扰情况下的双基地雷达抗无源箔条干扰的性能，仿真得出雷达在箔条干扰下的干扰暴露区。
1 双基地雷达目标探测判决式
1.1 无干扰情况
根据双基地雷达方程，在雷达未受到外界的有源与无源干扰的情况下，设雷达最小可检测回波功率为Smin，则判断双基地雷达是否能够发现目标的充要条件为[11-12]
(1)
式(1)即为双基地雷达探测目标的判决式。式中：r1, r2分别为目标与双基地雷达发射站、接收站的距离；σT(β)为目标在无干扰下的双基地雷达散射截面积；Gt, Gr分别为发射机与接收机的天线增益；λ为雷达的工作波长。计算σ(β)大小的经验公式为
σT(β)=σ{1+exp[m|β|-(2.4m+1)]}
(2)
式中，σ为目标的单基地雷达截面积，m一般为 7～10，β为雷达的双基地角。具体β的计算公式为
(3)
1.2 无源箔条干扰情况
本文研究的箔条干扰属于压制箔条干扰，它是通过在一定空域中大量投撒，形成干扰走廊，从而达到掩盖真正目标回波的目的。在推导干扰下的目标判决式之前，首先要计算双站箔条云的有效干扰面积。
1.2.1 双站箔条云的有效干扰面积
对于箔条云中的每根箔条而言，
其中
为单个箔条的双基地雷达截面积的全方向平均值，L为箔条的长度，λ为雷达的工作波长，Tu，Rv分别指发射机与接收机天线的极化方式，β为双基地角。单根箔条的散射集合关系如图1所示。
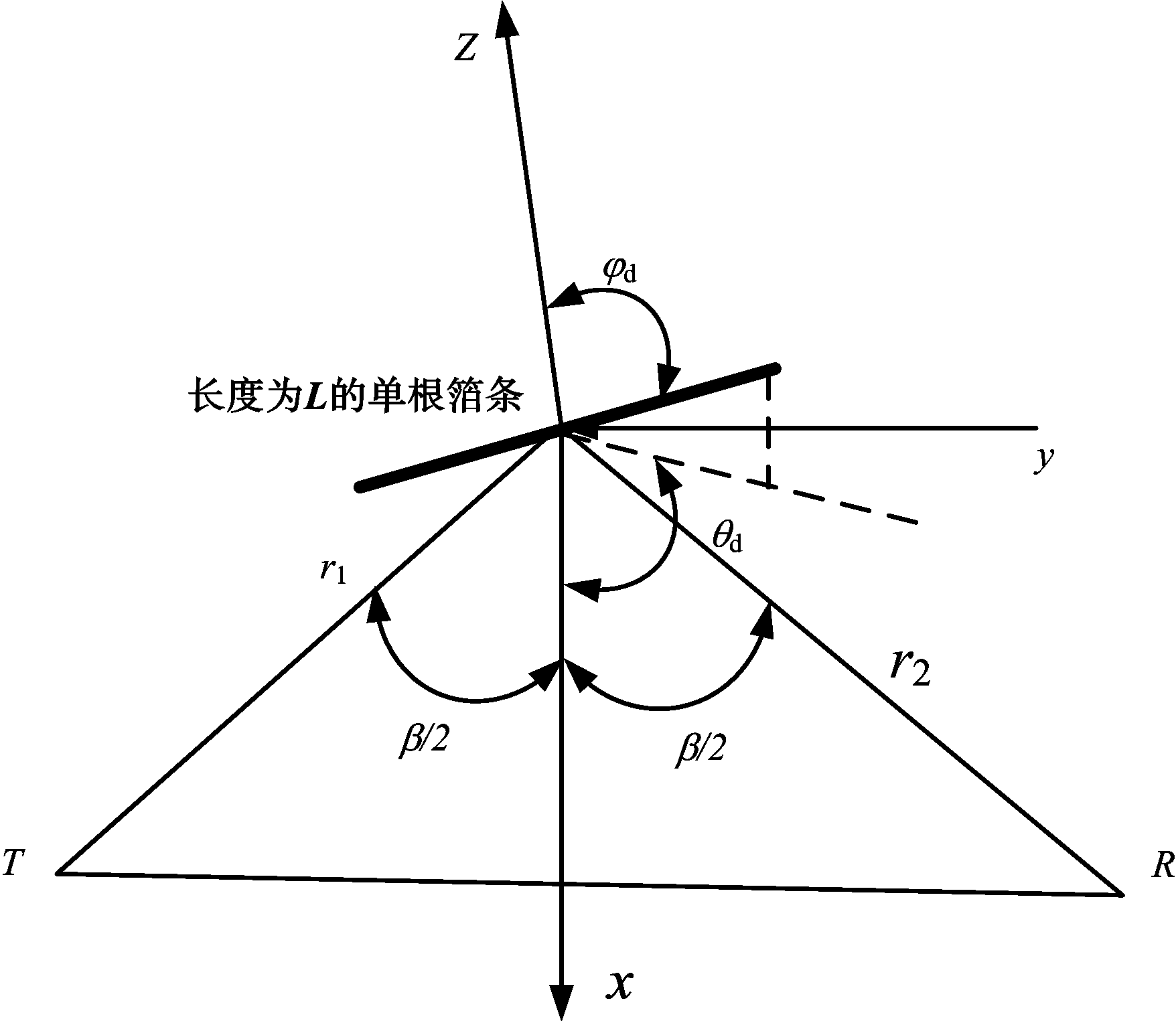
图1 长度为L的单根箔条的散射几何关系
下面就几组常用的收发极化方式，给出的计算表达式。
1) 当收发均采用垂直极化方式：
A2(π/2,-β/2)cos4φd]
(4)
2) 当收发有一个采用水平极化，另一个采用垂直极化方式：
(5)
3) 当收发均采用水平极化方式：
(6)
式中，
A(θ,φ)=
·
(7)
(8)
(9)
利用式(4)、式(5)、式(6)，可以求得不同情况下单根箔条的双基地全向平均截面积，由于箔条云中不同箔条的双基地全向平均截面积相同，则双站箔条云的有效干扰面积为
σC=
(10)
式中，N为既能被发射基地照射又能被接收基地观测到的箔条数目，η为云中有效箔条的比例系数，ρ为单位体积内的箔条数目，ΔV为双基地雷达的体积分辨单元，τ为脉冲宽度，Δθt，Δθr分别为发射与接收波束在方位平面上的波束宽度，Δφt，Δφr分别为发射与接收波束在仰角平面上的波束宽度。
1.2.2 无源箔条干扰下的目标判决式
为了有效评估压制效果，在此引入箔条干扰压制系数。其定义[1]为：在给定虚警概率的条件下，使在箔条散射体背景中正确检测目标的概率小于某一数值(0.1～0.5)所需的最小干扰信号比。压制系数一般要大于1.5～2.0。其表达式具体如下：
(11)
利用压制系数推导出双基地无源箔条有效压制干扰方程为
≥kj
(12)
整理上式得，双基地无源箔条压制干扰的干扰暴露区必须满足
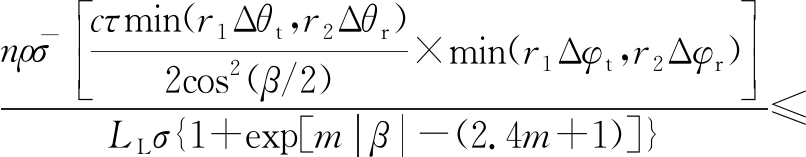kj
(13)
进一步讨论式(6)，存在以下4种情况：
1) 若r1Δθt≤r2Δθr且r1Δφt≤r2Δφr：
(r1r2)2≤
(14)
2) 若r1Δθt≤r2Δθr且r1Δφt≥r2Δφr：
r1r23≤
(15)
3) 若r1Δθt≥r2Δθr且r1Δφt≤r2Δφr：
r1r23≤
(16)
4) 若r1Δθt≥r2Δθr且r1Δφt≥r2Δφr：
r24≤
(17)
2 双基地雷达区域网格搜索算法
在复杂电磁环境下，双基地雷达的探测区域呈现不规则性，不便于直接仿真计算。在此利用区域网格搜索算法来实现探测区的仿真。具体算法如下：1)设定双基地雷达的警戒区域Xmin≤x≤Xmax，Ymin≤y≤Ymax；2)用矩形网格对警戒区域进行剖析；3)设定x，y轴的搜索步长分别为Δx，Δy；4)在每一个网格点检测是否存在目标，具体由式(1)判定；5)利用Matlab仿真出所有划定的网格点，近似计算探测区面积。警戒区网格剖析简图如图2所示。
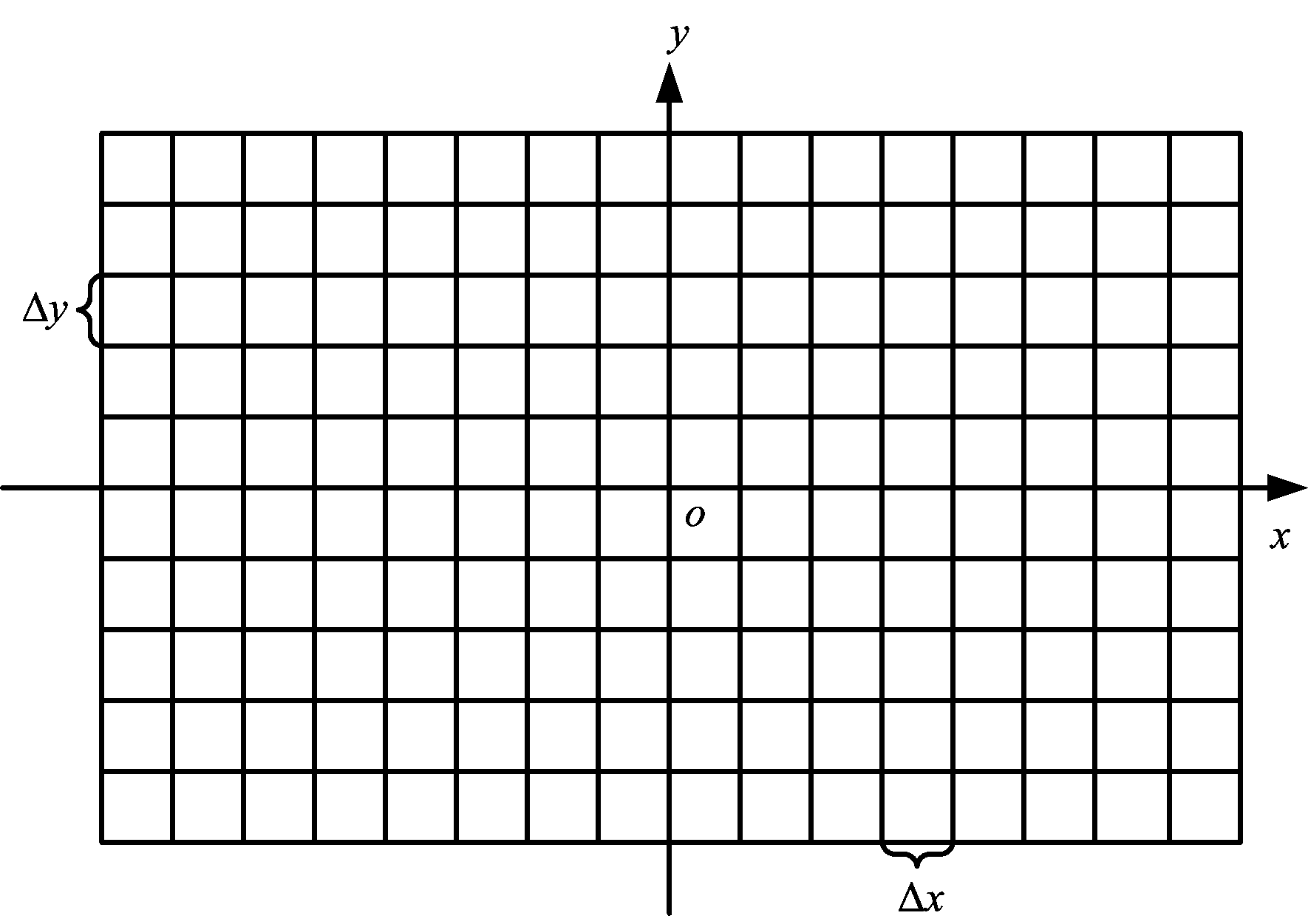
图2 警戒区网格剖析简图
在警戒区网格平面内，统计每个网格节点的探测情况，根据以下原则计算探测区面积：
1) 当某个网格的4个顶点处均能被探测到目标，便认定该网格及其相邻顶点的网格部分存在于探测面积中，对应探测面积为
2) 当某个网格只有两个相邻顶点处能被探测到目标，便认定相邻的两个网格部分存在于探测面积中，对应探测面积为
若两个顶点不相邻，则探测面积为ΔS≈ΔxΔy。
3) 当某个网格中有3个顶点处能被探测到目标，便认定分别以其中两个点为顶点的3个网格均有部分存在于探测面积中，对应探测面积为
即
4) 当某个网格中仅有一个顶点或没有顶点能被探测到目标，该网格不存在于探测面积内，对应探测面积为ΔS≈0。
基于以上4点的考虑，最终探测区域总面积为S=∑ΔS。
3 无源箔条干扰下探测区仿真分析
3.1 参数设定
假设双基地雷达的参数为：Pt=200 kW，Gt=Gr=32 dB，雷达的最小可检测功率为Smin=-60 dBmW，λ=0.1 m，τ=1 μs，雷达系统损耗LL=3 dB，发射机俯仰与方位平面3 dB波束宽度主瓣波束宽度为θ0.5=3°，接收机波束宽度与发射机相同；目标的参数为：目标的飞行高度为7 km，单基地雷达的目标截面积σ=5 m2；设定警戒区范围为：-180 km≤x≤180 km，-180 km≤y≤180 km；区域网格仿真步长为Δx=Δy=3 km；箔条云参数为：平均密度n=4根/米3，有效箔条比例系数ρ=0.4，箔条长度为λ/2。
3.2 仿真分析
基线长为160 km，双基地雷达在有无箔条干扰下，发射机与接收机分别采用不同极化方式时，雷达的探测区域与干扰暴露区。仿真结果如图3、图4和图5所示。
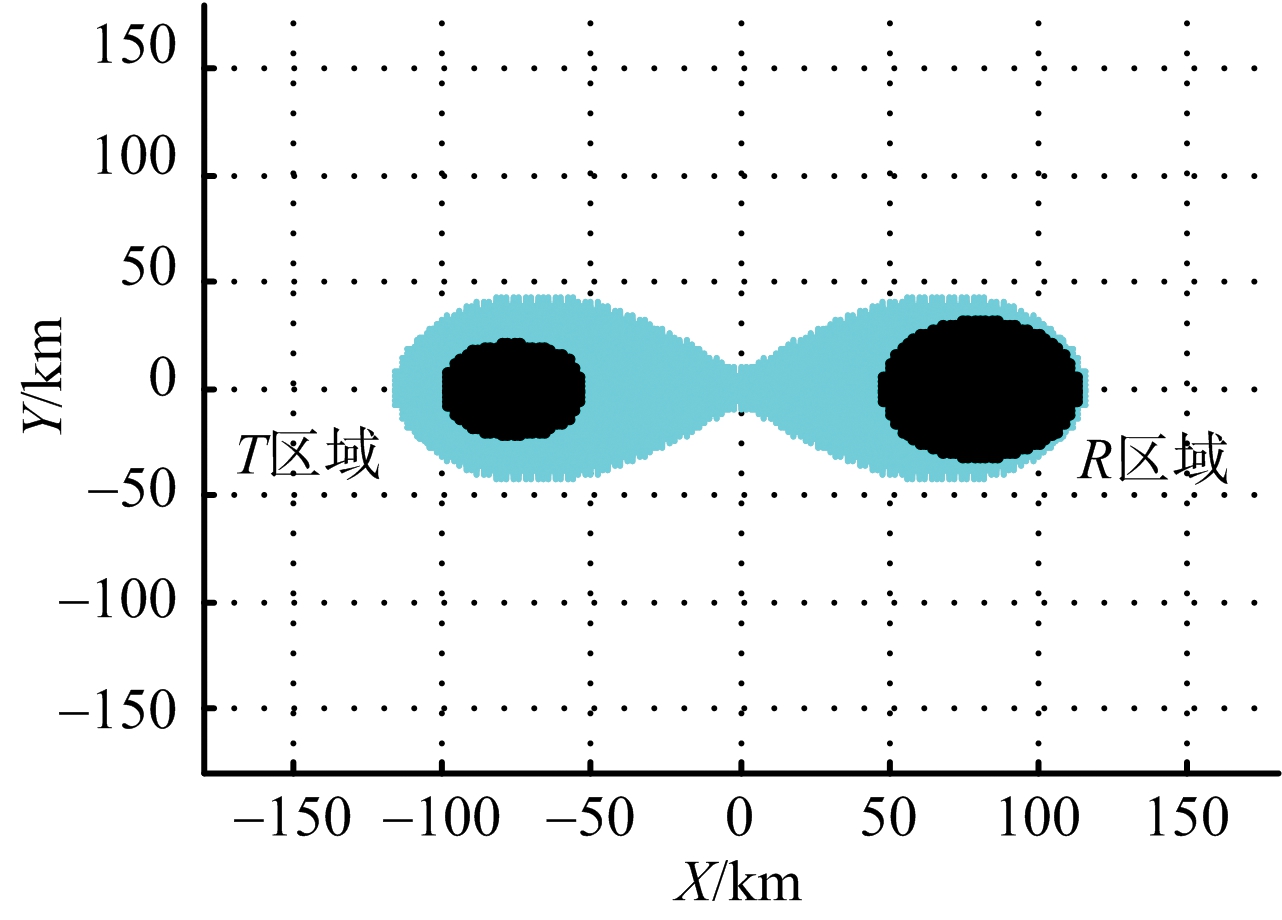
图3 收发一个采用水平极化、一个采用垂直极化的探测区域与干扰暴露区
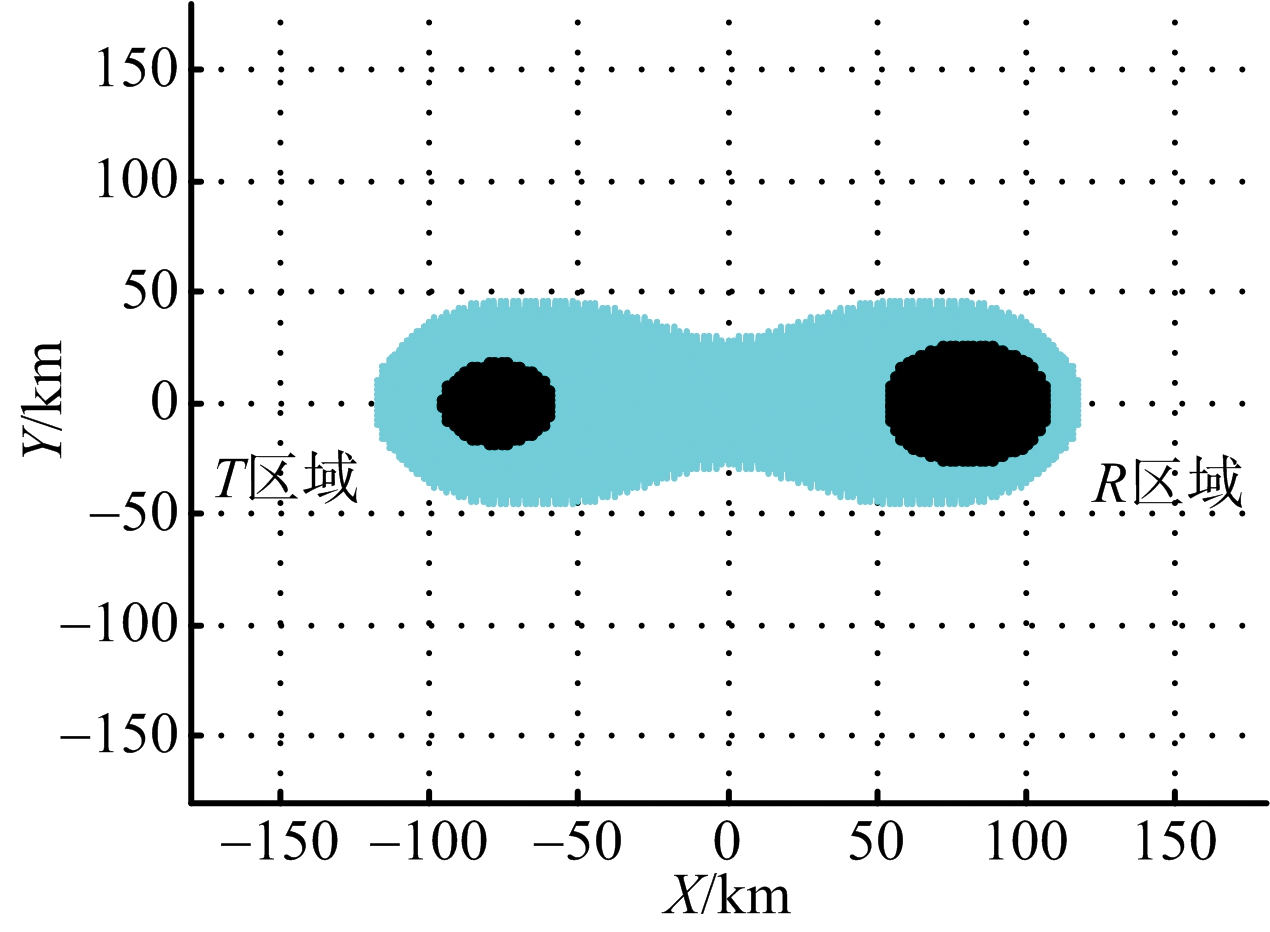
图4 收发均采用水平极化的探测区域与干扰暴露区
基线长为50 km，双基地雷达在有无箔条干扰下，收发分别采用不同极化方式时，雷达的探测区域与干扰暴露区。仿真结果如图6、图7和图8所示。
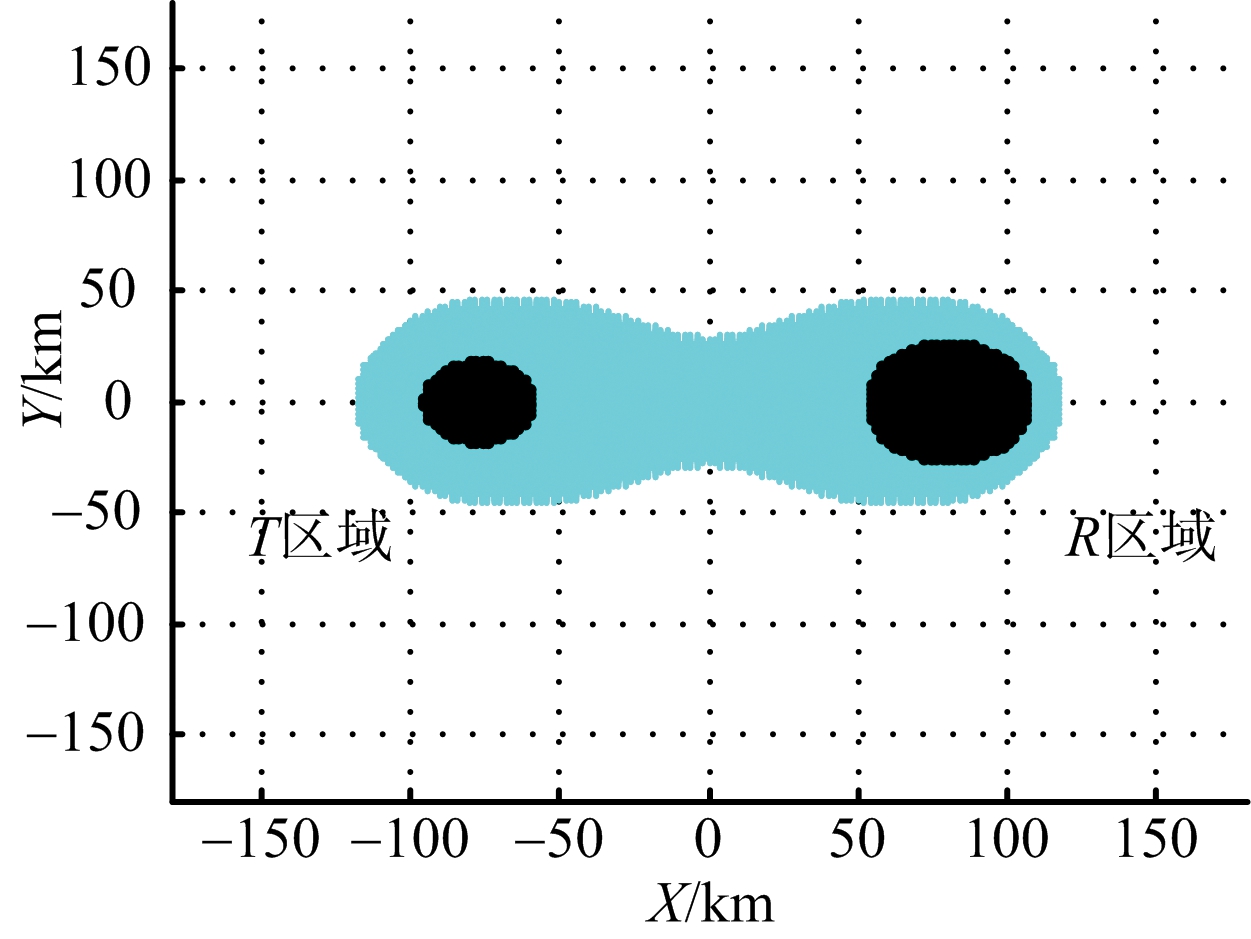
图5 收发均采用垂直极化的探测区域与干扰暴露区
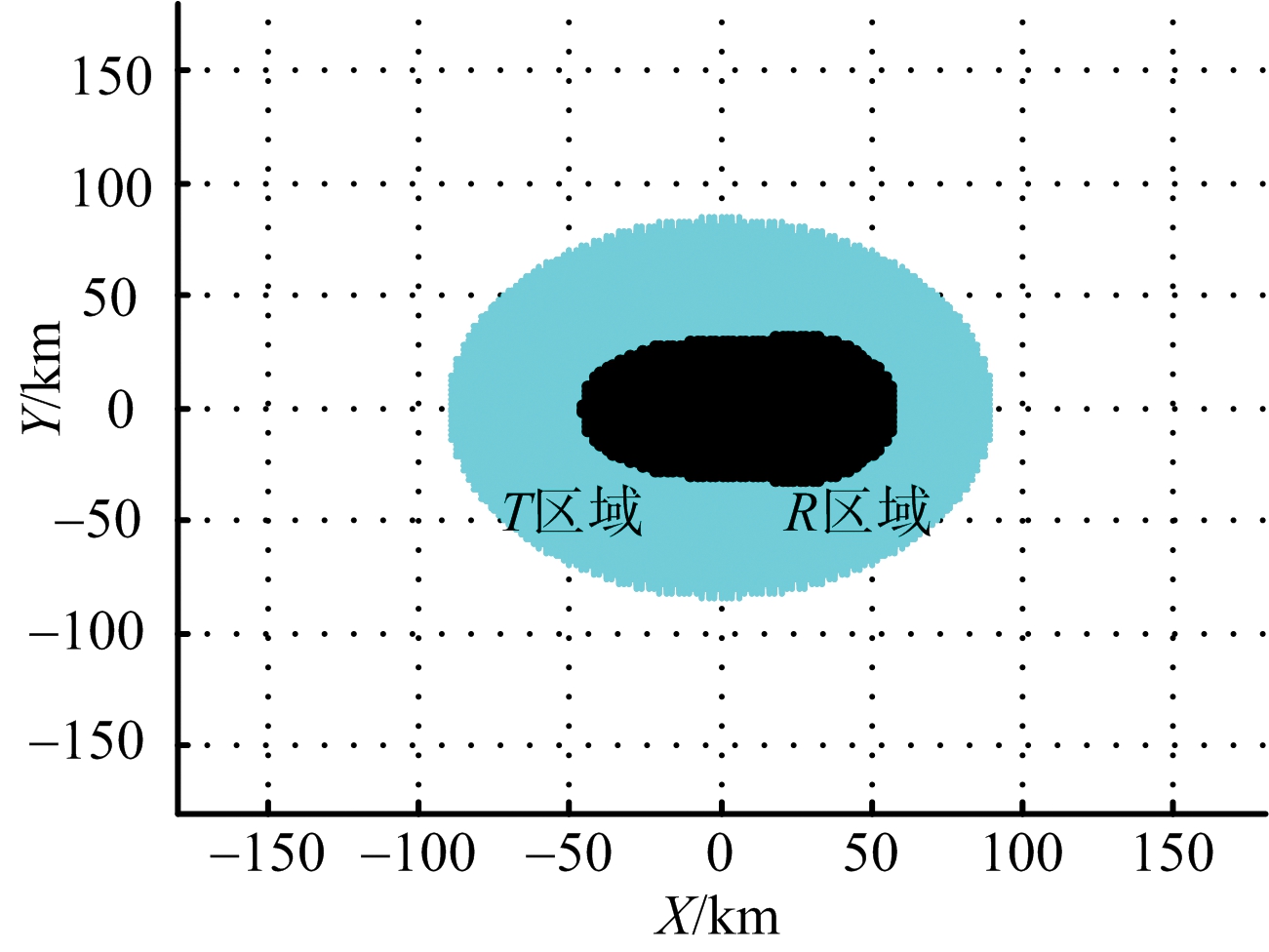
图6 收发一个采用水平极化、一个采用垂直极化的探测区域与干扰暴露区
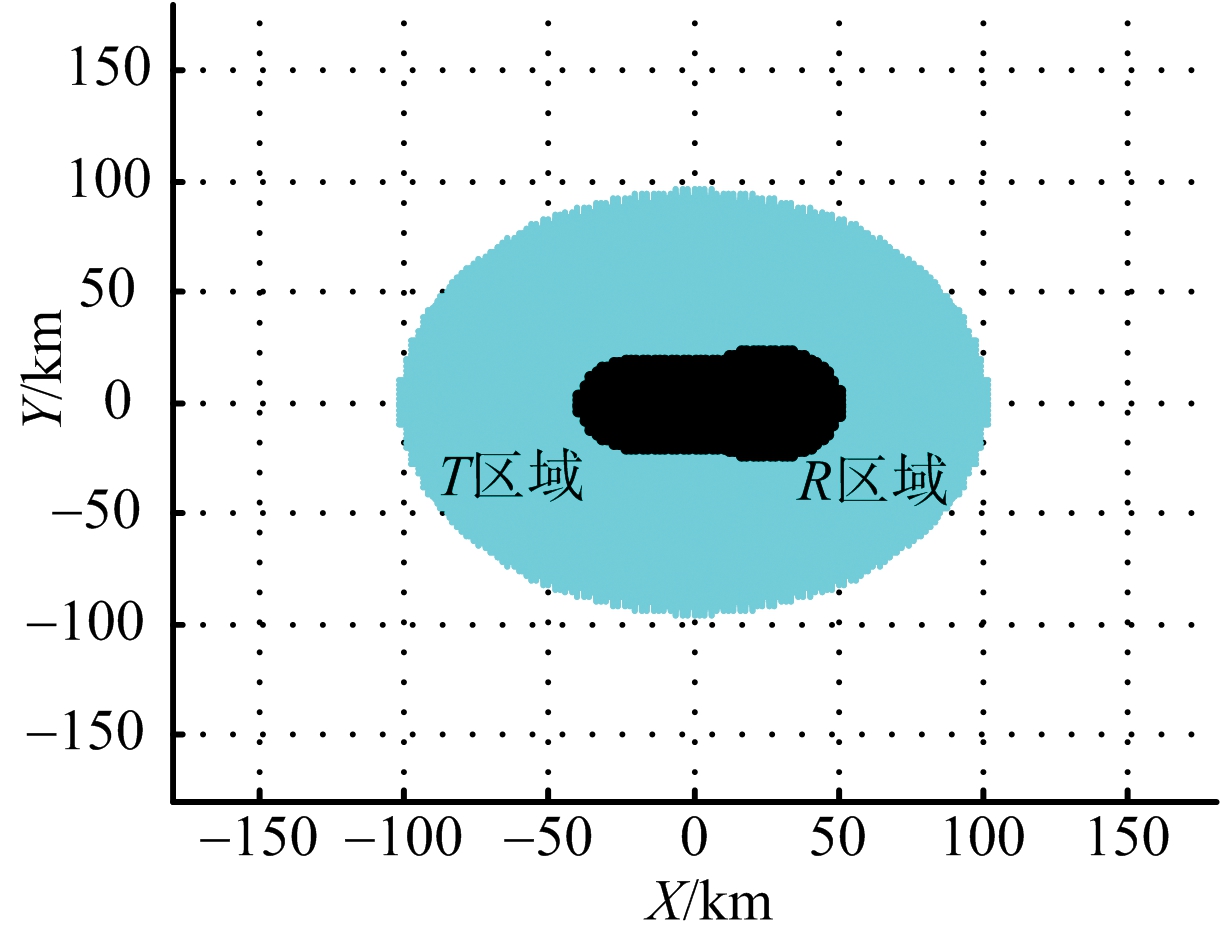
图7 收发均采用水平极化的探测区域与干扰暴露区
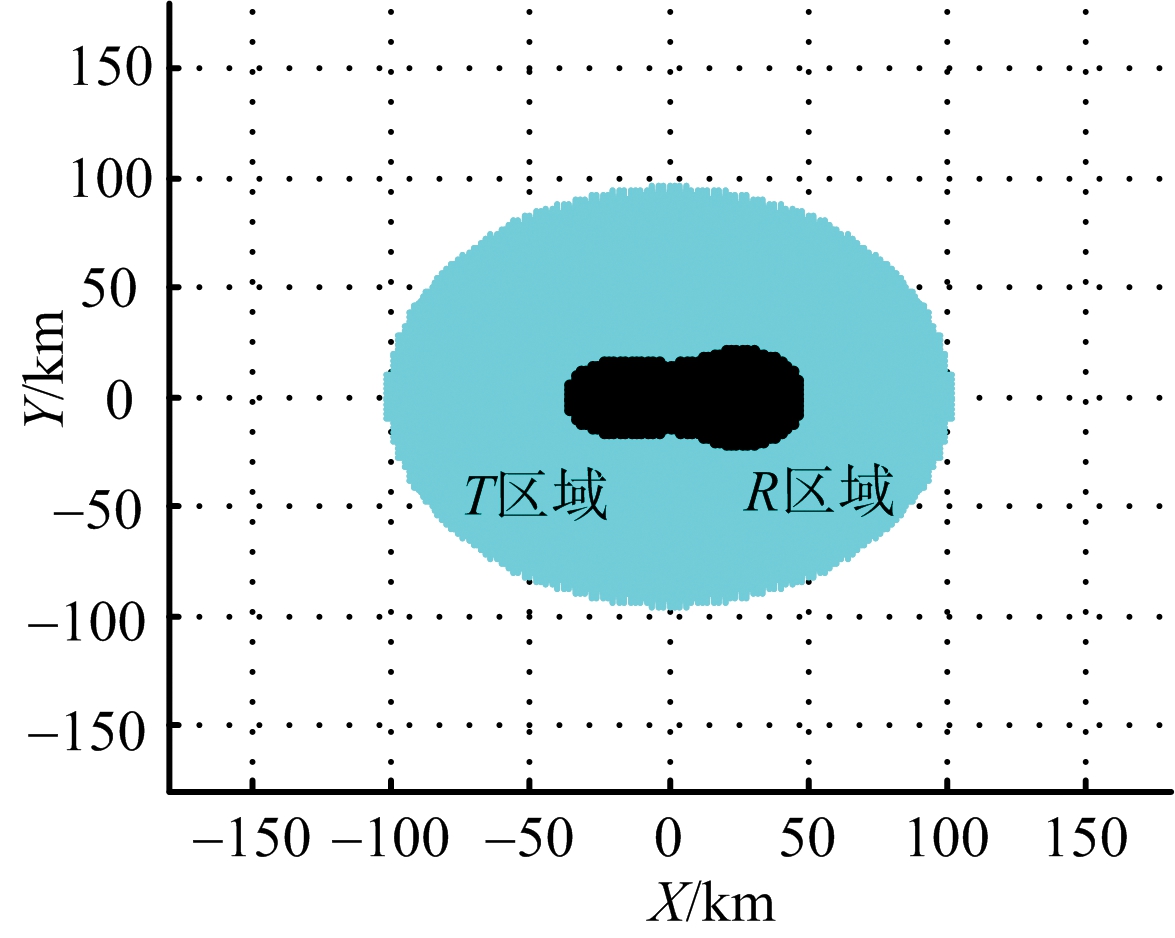
图8 收发均采用垂直极化的探测区域与干扰暴露区
将以上6张图的探测区面积与干扰暴露区面积统计汇总，如表1、表2所示。
表1 基线长度为160 km的探测区面积与干扰暴露区面积
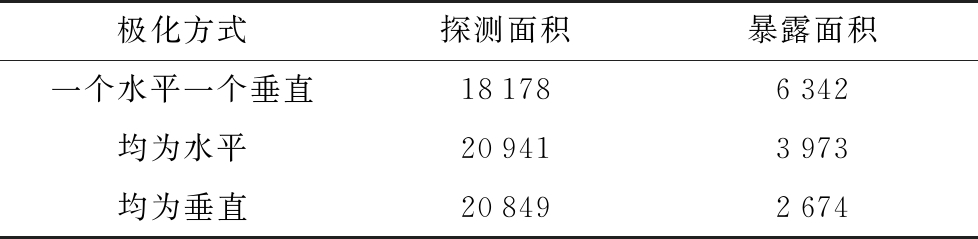
极化方式探测面积暴露面积一个水平一个垂直181786342均为水平209413973均为垂直208492674
表2 基线长度为50 km的探测区面积与干扰暴露区面积
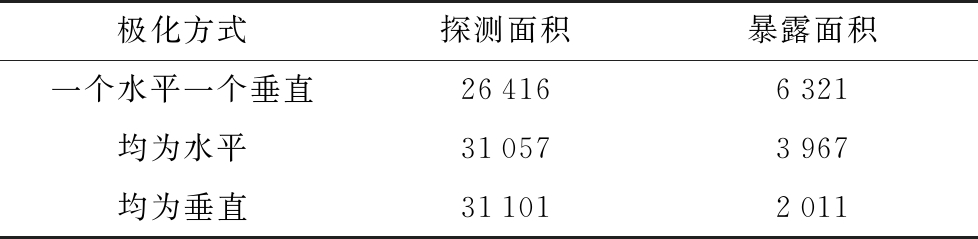
极化方式探测面积暴露面积一个水平一个垂直264166321均为水平310573967均为垂直311012011
当箔条长度采用λ/2时，结合表1和表2的数据比较可得如下结论：1)在基线长度一定时，采用收发一个水平极化、一个垂直极化方式，可得较大的干扰暴露区；2)同种极化方式下，基线长度越长，探测面积越小；3)垂直极化下，随着基线长度的减小，雷达的干扰暴露区面积变小，其他两种极化方式，干扰暴露区面积几乎不变；4)干扰暴露区域由以发射机为中心的区域和以接收机为中心的区域组成，且后者的区域面积大于前者的区域面积。
4 结束语
本文定量分析了双基地雷达在有无箔条干扰下的探测能力，推导了收发天线不同极化方式下箔条截面积的精确表达式，在区域网格剖分搜索算法的基础上定义了探测区面积的计算方法，当箔条长度采用λ/2时，极化方式与基线长度将很大程度影响双基地雷达抗无源箔条干扰的能力。这为双基地雷达布站及天线的采用提供了有利的参考和依据。
[1] 李本朋. 国外机载箔条干扰技术的发展[J]. 机械管理开发, 2018, 33(2):56-58.
[2] 白爽,姜宁. 舰艇箔条幕干扰使用与布放研究[J]. 舰船电子对抗, 2017, 40(5):18-23.
[3] 刘艳平. 箔条在电子战中的战术运用研究[J]. 舰船电子对抗, 2017, 40(2):28-31.
[4] XU Jin, BAI Bowen, DONG Chunxi, et al. A Novel Passive Jamming Method Against ISAR Based on Resonance Absorption Effect of Metamaterials[J]. IEEE Access, 2018(6):18142-18148.
[5] LI Yingtian, CHEN Yonghua, YANG Yang, et al. Passive Particle Jamming and Its Stiffening of Soft Robotic Grippers[J]. IEEE Trans on Robotics, 2017, 33(2):446-455.
[6] WANG Ruijia, WANG Xing, CHENG Siyi, et al. Plasma Passive Jamming for SAR Based on the Resonant Absorption Effect[J]. IEEE Trans on Plasma Science, 2018, 46(4):928-933.
[7] 王庚,袁俊泉,王力宝,等. 天空双基地预警雷达空间同步技术研究[J]. 雷达科学与技术, 2017, 15(4):449-456.
WANG Geng, YUAN Junquan, WANG Libao, et al. Research on Spatial Synchronization Technique of Space-Air Based Bistatic Early Warning Radar[J]. Radar Science and Technology, 2017, 15(4):449-456. (in Chinese)
[8] ZHAO Yongsheng, ZHAO Yongjun, ZHAO Chuang. Joint Delay-Doppler Estimation for Passive Bistatic Radar with Direct-Path Interference Using MCMC Method[J]. IET Radar, Sonar & Navigation, 2018, 12(1):130-136.
[9] BEAUDOIN C, HORGAN T, DEMARTINIS G, et al. Fully Polarimetric Bistatic Radar Calibration with Modified Dihedral Objects[J]. IEEE Trans on Antennas and Propagation, 2018, 66(2):937-950.
[10] COMITE D, PIERDICCA N. Bistatic Radar Systems at Large Baselines for Ocean Observation[J]. IEEE Trans on Geoscience and Remote Sensing, 2018, 56(3):1816-1828.
[11] 杨振起,张永顺,骆永军. 双(多)基地雷达系统[M]. 北京: 国防工业出版社, 1998.
[12] 张正言,张剑云. 双基地 MIMO 雷达多目标高精度跟踪算法[J]. 系统工程与电子技术, 2018, 40(6):1241-1248.
