0 引 言
随着科技的发展进步，战争的形势也在不断地发生变化。早期的雷达主要用于检测发现目标并提供目标的位置，随着战争的高科技化和信息化，需要雷达提供更加精确、更加详细的目标信息，比如目标的形状、类别，甚至是型号，雷达目标识别的工作就随之展开。雷达发射电磁波，当电磁波遇到目标就会发生后向散射，由于目标的自身的几何结构、材料属性等各方面的不同，会对电磁波产生不同的调制。雷达目标识别技术就是利用雷达接收机接收到的目标的后向电磁散射回波信号来对目标的属性进行识别分类。高分辨一维距离像(High Resolution Range Profile, HRRP)是实现宽带雷达目标识别的一种形式，目标的高分辨一维距离像是目标的雷达回波沿距离维的分布，可以反映出目标的结构信息，包含丰富的目标特征信息可以对目标进行有效的识别[1]，基于一维距离像的雷达目标识别技术得到了很好的应用。
在接收目标回波的同时，无法避免地会将非目标回波一起接收，产生含噪回波信号，实际过程中常常会遇到低信噪比的情况，容易导致一维距离像的质量降低，影响目标识别的结果，所以需要对低信噪比的回波进行降噪处理。小波阈值去噪方法是由Donoho提出[2]，分为软阈值法和硬阈值法，小波变换在雷达信号处理中得到不少的应用[3-5]，本文针对雷达目标一维距离像回波低信噪比的情况，提出了利用小波降噪方法，设计了一种改进的阈值函数，对低信噪比的回波信号进行预处理再成像作识别研究，提高了信噪比和识别率。
1 基于改进阈值的小波降噪预处理
通常来说，雷达回波中的噪声主要是由外界事物的噪声以及接收机内部的热噪声组成的，可以看作是加性高斯白噪声。因此可以设雷达回波信号为
s(t)=x(t)+n(t)
(1)
式中，s(t)为雷达接收到的回波，x(t)为目标的信号回波，n(t)为噪声。先对雷达回波信号进行离散采样，而后再进行小波变换，则可以得到小波系数dj,k。
Donoho提出了软硬阈值函数法。将软阈值函数定义成
(2)
当小波系数小于给定的阈值(门限)T时，则将小波系数设为0；当其大于等于T时，减小了小波系数进行收缩处理，将其设为式(2)中的值。
将硬阈值函数定义成
(3)
当小波系数小于给定的阈值(门限)T时，则将小波系数设为0；当其大于等于T时，则直接保留。式(2)和式(3)中，dj,k为小波变换系数，
为经过阈值处理得到的小波系数估计值，j为分解尺度，且j=1,2,…,J。
如图1所示，当门限T为1时，画出软硬阈值函数示意图。
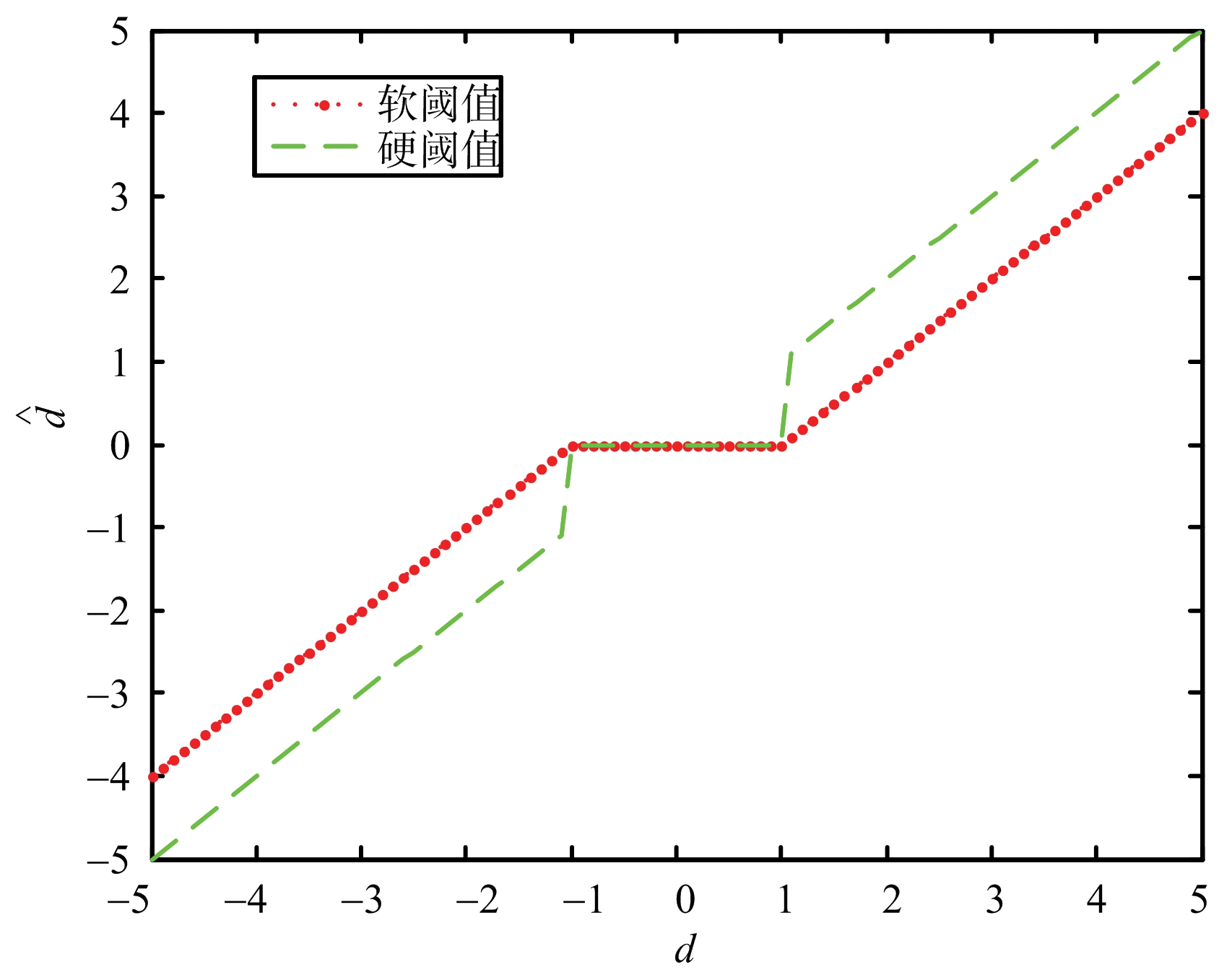
图1 软硬阈值函数示意图
根据Donoho提出的思想：当dj,k小于设定的阈值(门限)时，认为dj,k主要是由噪声引起的，则舍去；当dj,k大于等于设定的阈值(门限)时，认为dj,k主要是由信号引起的，则保留。在对小波系数进行处理后，再小波重构，即可得到高信噪比的回波信号。
软硬阈值方法能够较好地降低信号中的噪声从而提高信噪比，但是其本身也存在一定的问题。软阈值方法在|dj,k|≥T时，由式(2)得到新的小波系数与原先dj,k存在偏差，当小波重构时影响真实度。而硬阈值方法虽然直接保留了原先的小波系数，但从图1中能够看出硬阈值是不连续函数，不方便处理并且容易产生震荡。因而在雷达回波降噪预处理时单独使用软阈值或硬阈值进行降噪处理都达不到很理想的效果。
为了克服上述提及的问题，结合大量的仿真实验研究，本文提出了一种改进的阈值函数，能够有效地弥补上述提及的软硬阈值存在的不足之处。改进的阈值函数表达式为
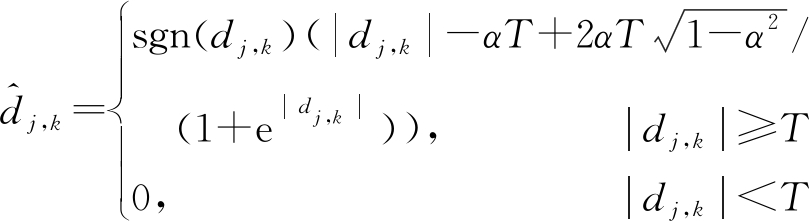
(4)
式中，将α定义为可变因子，且α∈[0,1]。
分析式(4)可得：当α=0时，改进的函数将变为硬阈值函数；当α=1时，改进的阈值函数变为软阈值函数。图2为3种阈值函数的示意图，由图可知，新阈值函数是介于软硬阈值函数之间的，在0<α<1时，所得的值的大小介于软硬阈值方法所得的值之间，可以通过选择不同的α来灵活选择阈值函数。当dj,k→
时，考察
发现，趋于-αT，相较于软阈值函数，大大缩小了两者之间的恒定偏差，提升了去噪效果。
因而，从理论分析上来说，新的阈值函数在一定程度上克服了原始阈值函数的一些缺点，有助于提高降噪效果。
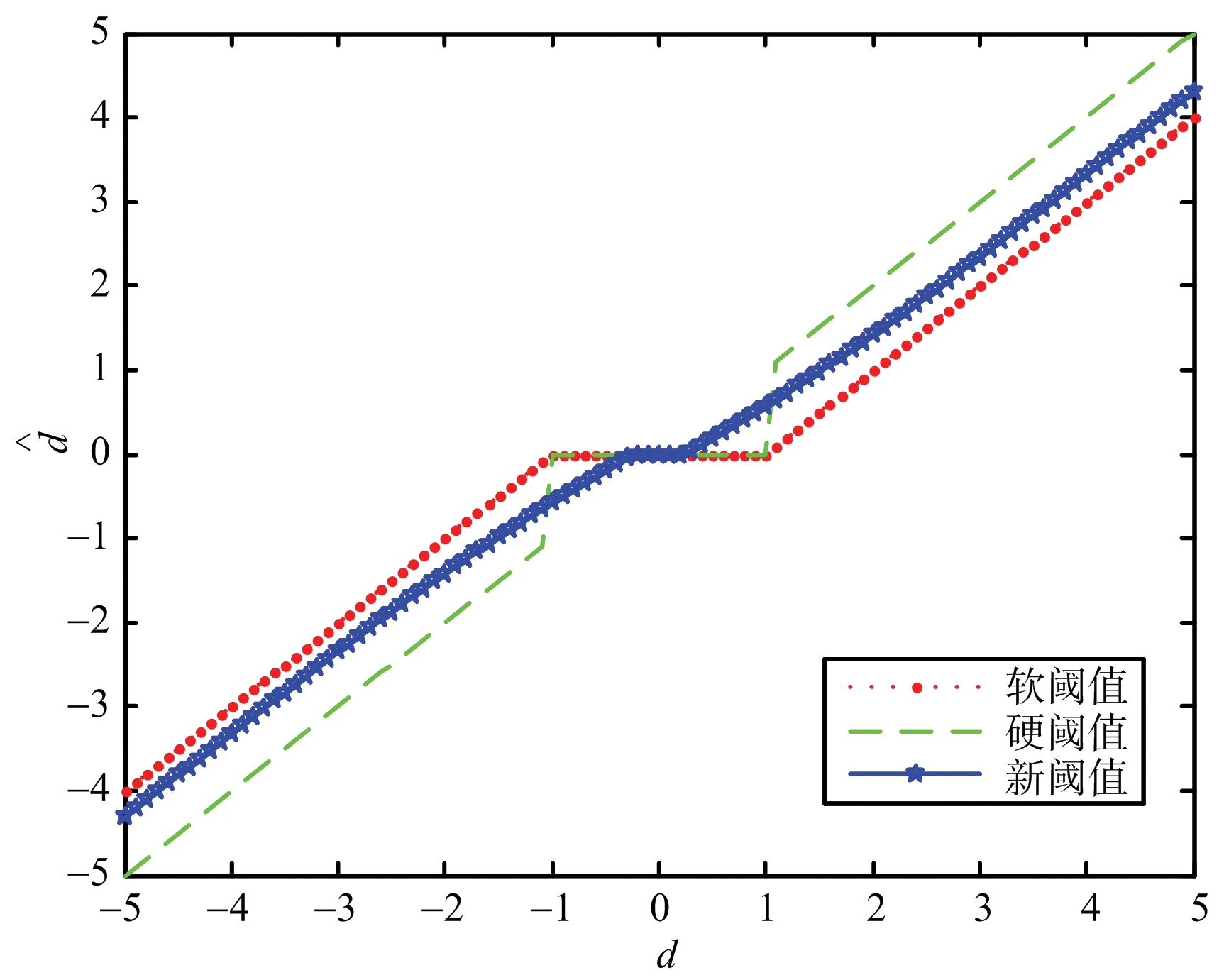
图2 3种阈值函数示意图
2 雷达目标一维距离像识别
在利用小波阈值降噪方法的基础上，提出了基于阈值降噪的一维距离像识别的方法，图3为基于阈值降噪的一维距离像识别流程图，主要分为降噪预处理、一维成像和距离像敏感性预处理，以及分类识别三部分。
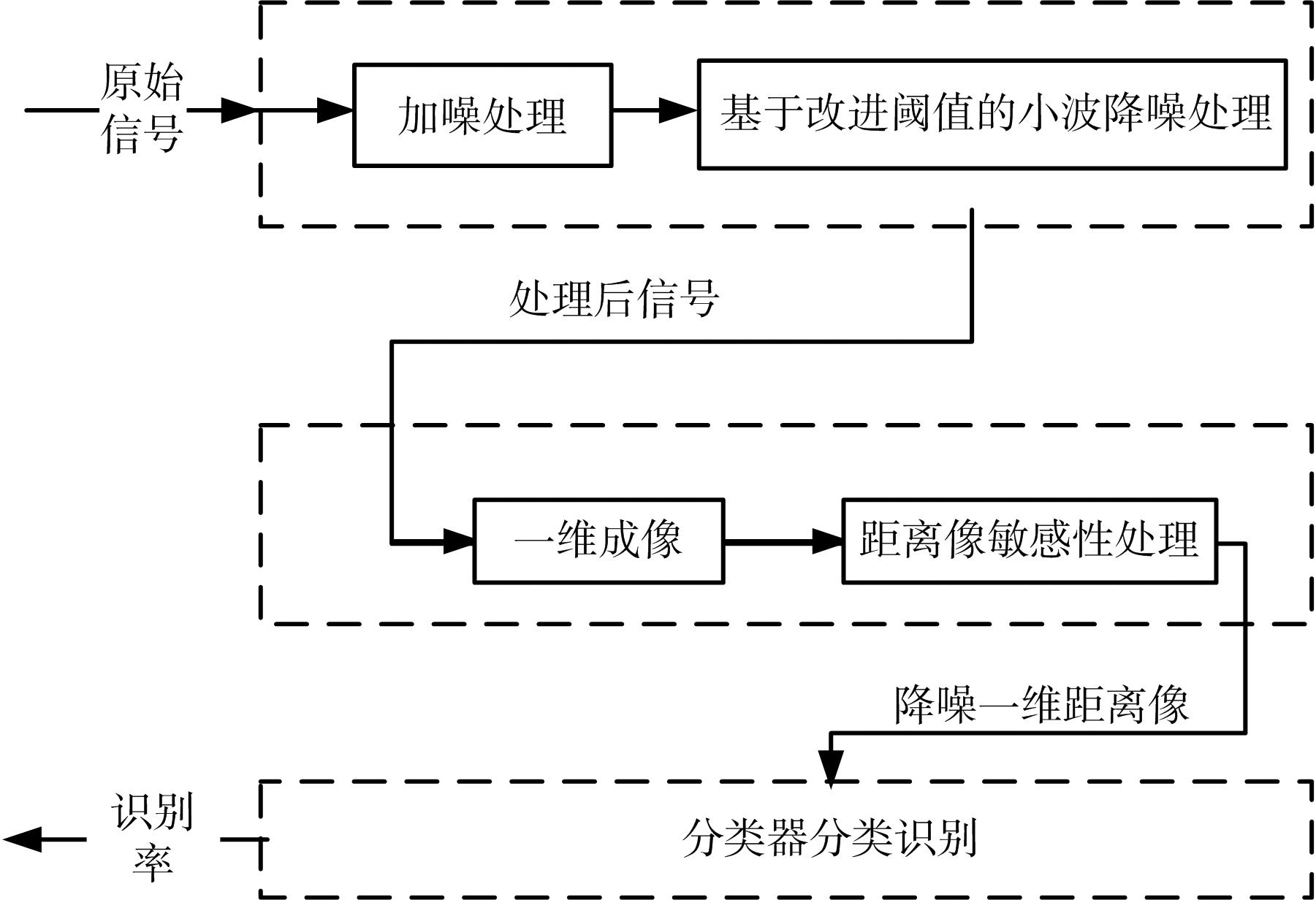
图3 基于阈值降噪的一维距离像识别流程图
2.1 成像及敏感性预处理
通常来说，目标回波可以看作是多个散射点的回波向量和，式(5)为散射中心模型[6]：
(5)
式中，αk表示第k个单独散射中心点的散射特性，τk表示第k个散射点的波到达的时间。进行离散采样，而后采样序列进行逆傅里叶变换得到目标的复距离像，对复距离像取模值得到实距离像[7]。
雷达目标的一维距离像是其各个距离单元内的所有散射点的回波和，因此任意一个散射点回波的变化都会使一维距离像发生变化。为了达到有效识别目标提高雷达目标一维距离像可用性的目的，必须考虑到一维距离像本身的特性，需要对目标的一维距离像进行幅度归一化、提取平移不变特征等数据预处理工作。目标的距离像的幅度是会发生变化的，与雷达的硬件系统、目标的位置以及雷达目标所处的环境有着复杂的关系，在实际的应用过程更加复杂，单纯地利用原始的幅度信息很难达到需要的效果。对距离像幅度作归一化处理，能很好地解决这个问题。本文采用2-范数作为幅度归一化因子：
(6)
(7)
式中，x为单个距离像样本，
为进行归一化处理之后的单个距离像样本。
通常获取雷达目标一维距离像是通过距离窗的方法。目标在空间中的位置事先是没法预知的，当使用距离窗方法的时候，距离像出现在窗中的位置也是没法估计的。目标在距离窗中的位置发生变化的时候，距离像的位置也会发生变化，造成距离像的平移敏感性。傅里叶变换(FFT)[8]法在频域具有平移不变性，对目标的一维距离像作傅里叶变换，在时域里的平移对频域没有产生影响，这样就能克服雷达目标一维距离像的平移敏感性。
2.2 LVQ神经网络识别器
识别分类器就是确定一定的准则关系，将提取出的目标特征与事先训练好建立的目标模板库进行匹配，寻找出最佳的匹配模板以此来确定该目标的属性类别。分类识别器的选择关系到识别的效果和精度，通常分类器要求有好的识别性能，同时算法的复杂度不高以减小计算量。学习向量量化(LVQ)神经网络[9]是一种自适应学习能力强、识别性能稳定的分类器，常用于模式识别中。该网络为3层网络，第一层为输入层，设每个距离像为向量Xi，输入层的每个输入模式均为一个距离像；第二层为竞争层竞争获胜的神经元表示一个子类，输入层和竞争层之间采用全连接的方式，其连接权值在进行网络训练的时候会发生改变，网络训练就是竞争层对输入的向量依据距离最近准则进行学习分类；第三层为线性输出层，每个输出神经元表示一个类别。
3 实验及分析
3.1 实验条件
仿真实验所采用的数据是利用计算机仿真[10-11]所得的3类目标的一维距离像。距离像仿真利用的是简单的散射点模型，存在噪声的时候，频域采样的方式为
S(n)=
noise(n)
(8)
式中，ai和R(i)分别为第i个散射中心的强度和位置，f(n)为频域的第n个采样点，noise(n)为噪声。
仿真实验中的一些参数设置如下：雷达工作的中心频率f0=5.5 GHz，步进频率间隔为Δf=2 MHz，采样点N=256，则径向距离分辨率可计算得到ΔR=c/(2NΔf)=0.586 m。目标俯仰角为0°，方位角变化范围为0°～30°，采样间隔为0.2°，仿真得到每个目标各151个样本。
实验采用的小波为db7小波，设定α的取值为0.5，小波的分解尺度J取值为6，对每组原始测量数据添加高斯白噪声n，小波阈值门限T采用文献[12]中提出的阈值门限：
其中σ为噪声的方差，N为信号长度。在实际的数据降噪处理过程中，无法知道噪声的方差，因此，通常采用中值估计器来获取噪声方差，即σ=median(dj,k)/0.674 5。实验采用的小波为db7小波，设定α的取值为0.5，小波的分解尺度J取值为6，利用信号的信噪比(SNR)和均方根误差(MSE)作为去噪的效果和性能的量化评判指标：
(9)
(10)
式中，s(n)为含噪信号，
为经过小波阈值降噪处理之后得到的估计信号。
在降噪及一维成像后，对一维距离像进行如下敏感性预处理：
第一步：归一化，将每一幅图像用其总能量归一化；
第二步：距离对准，利用Fourier变换的平移不变性，将一维距离像作Fourier变换即可对齐。
每种目标选取100个样本组成训练集，剩余51个样本组成测试集，利用LVQ神经网络进行分类识别，隐含层神经元数设为20。
3.2 结果分析
实验分别验证分析了小波阈值降噪方法应用于雷达目标一维距离像降噪识别的可行性，新旧阈值算法的对比分析，以及不同信噪比下小波阈值降噪方法对雷达目标一维距离像目标识别率的影响。
图4为降噪前后的目标一维距离像对比分析图。从图中能明显看出，经过降噪的距离像比含噪的距离像更加平滑，在整体上降噪后的距离像也更加接近原始的距离像，明显地减低了噪声含量，相对提高了一维距离像的质量。也由此说明，小波阈值降噪的方法对雷达目标一维距离像回波进行降噪处理取得了很好的效果。
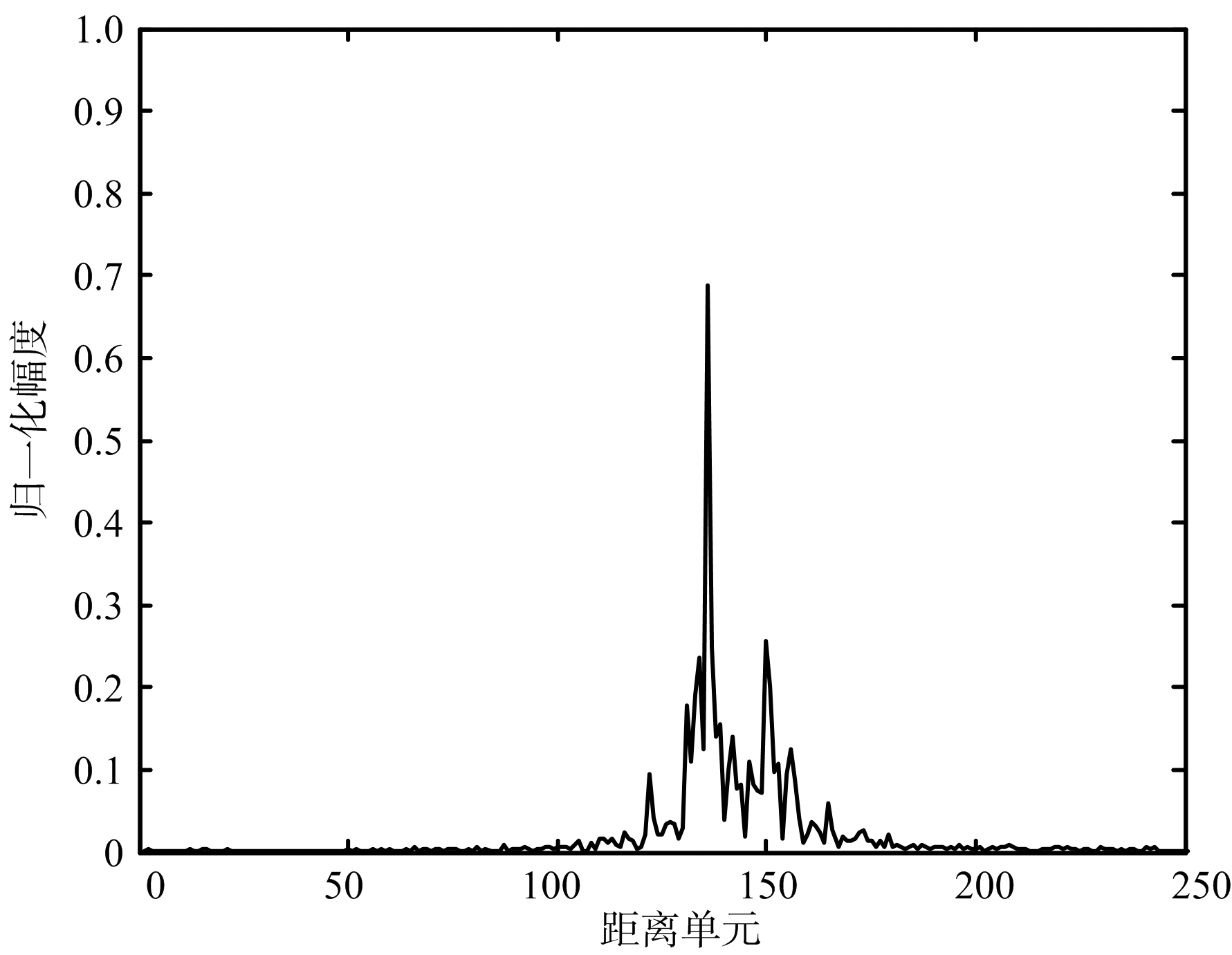
(a) 原始距离像
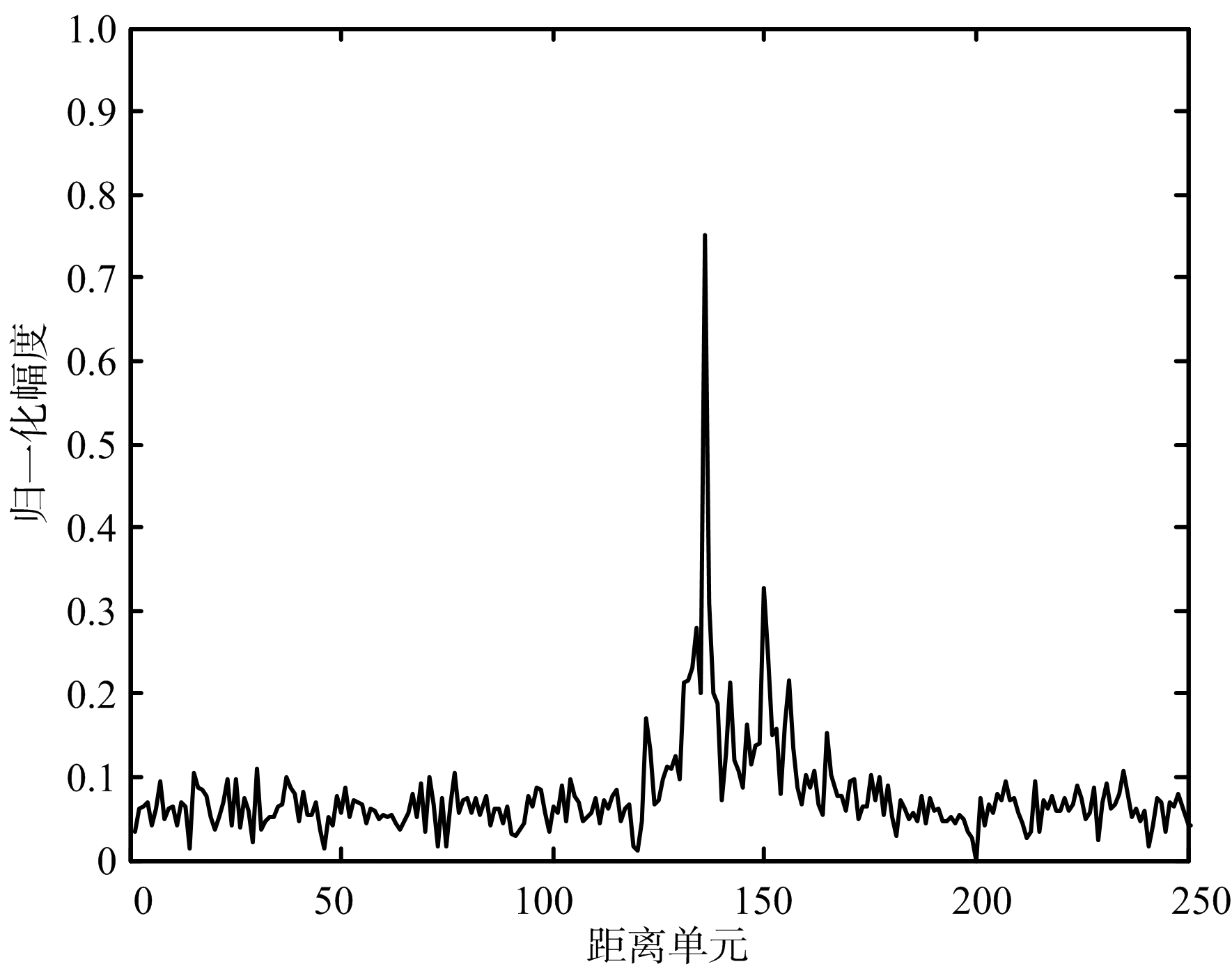
(b) 含噪距离像
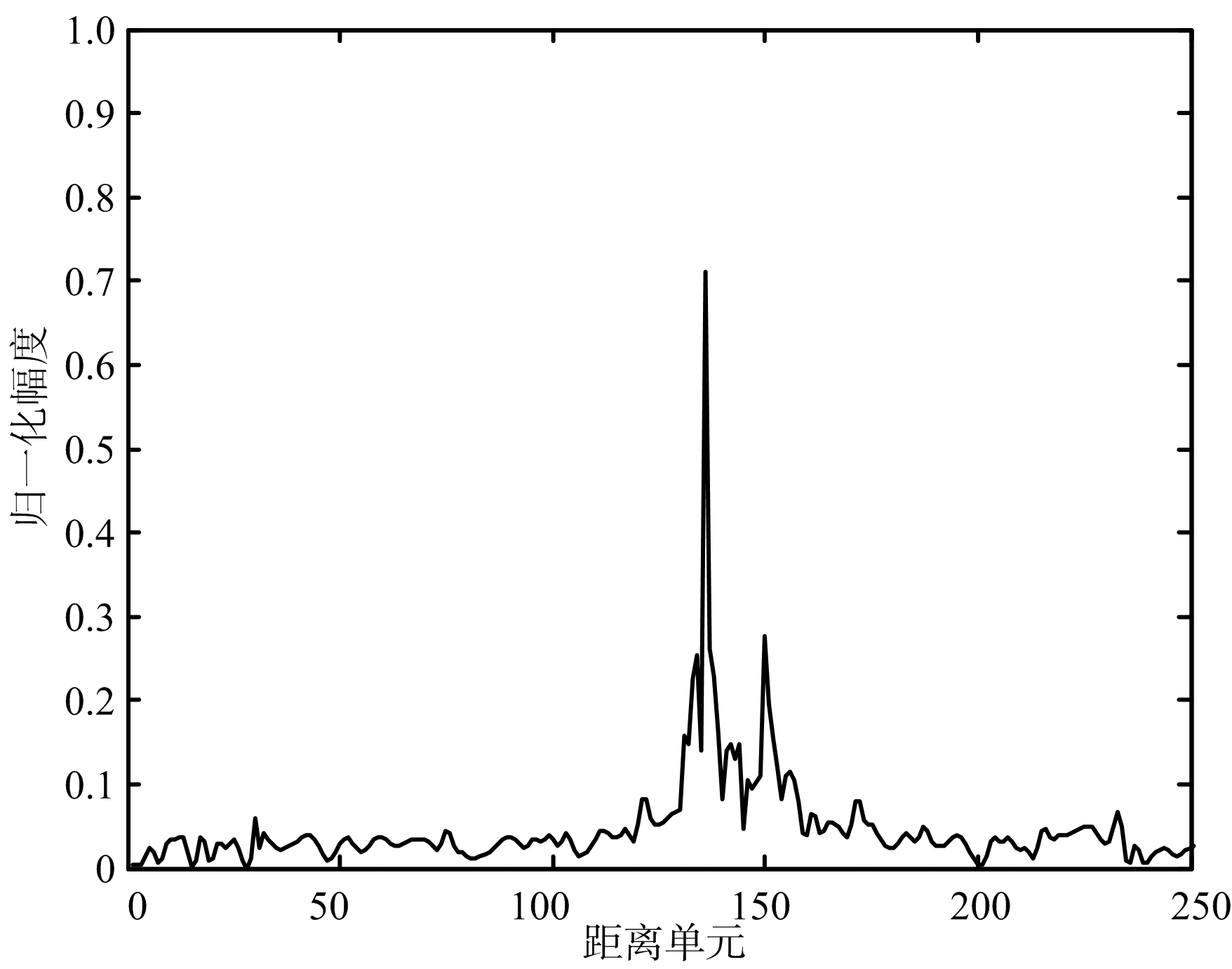
(c) 降噪距离像
图4 降噪前后各距离像对比
表1给出了进行20次蒙特卡洛仿真实验，在不同信噪比情况下分别用原阈值降噪方法和新阈值降噪方法进行降噪处理的效果。在不同信噪比的情况下，比较新阈值方法和原阈值方法降噪后的信噪比，前者的效果相较于后者好很多，进一步验证了小波阈值降噪方法能有效地降低雷达回波中的噪声，并提高一维距离像的质量，同时也验证了本文提出的新阈值降噪方法比原阈值方法要好。随着信噪比的逐渐增大，采用小波阈值降噪处理的效果增幅开始下降，新阈值方法和原阈值方法降噪效果的差别开始缩小靠近。
表1 新阈值去噪和原阈值去噪效果比较
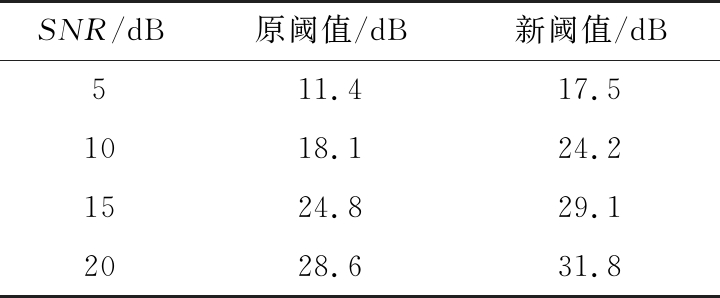
SNR/dB原阈值/dB新阈值/dB511.417.51018.124.21524.829.12028.631.8
图5为不同的信噪比之下在利用小波阈值降噪和没有进行阈值降噪处理前后所得到的分类识别率的变化图。经过小波降噪处理之后能很好地提高一维距离像的质量，进而提高目标识别率，新阈值降噪方法相较于原来的阈值函数降噪方法有更好的识别率。在当随着信噪比的提高，识别率的增幅开始下降，说明降噪处理随着信噪比的增大对识别率的影响开始减弱，没有在低信噪比时效果显著。
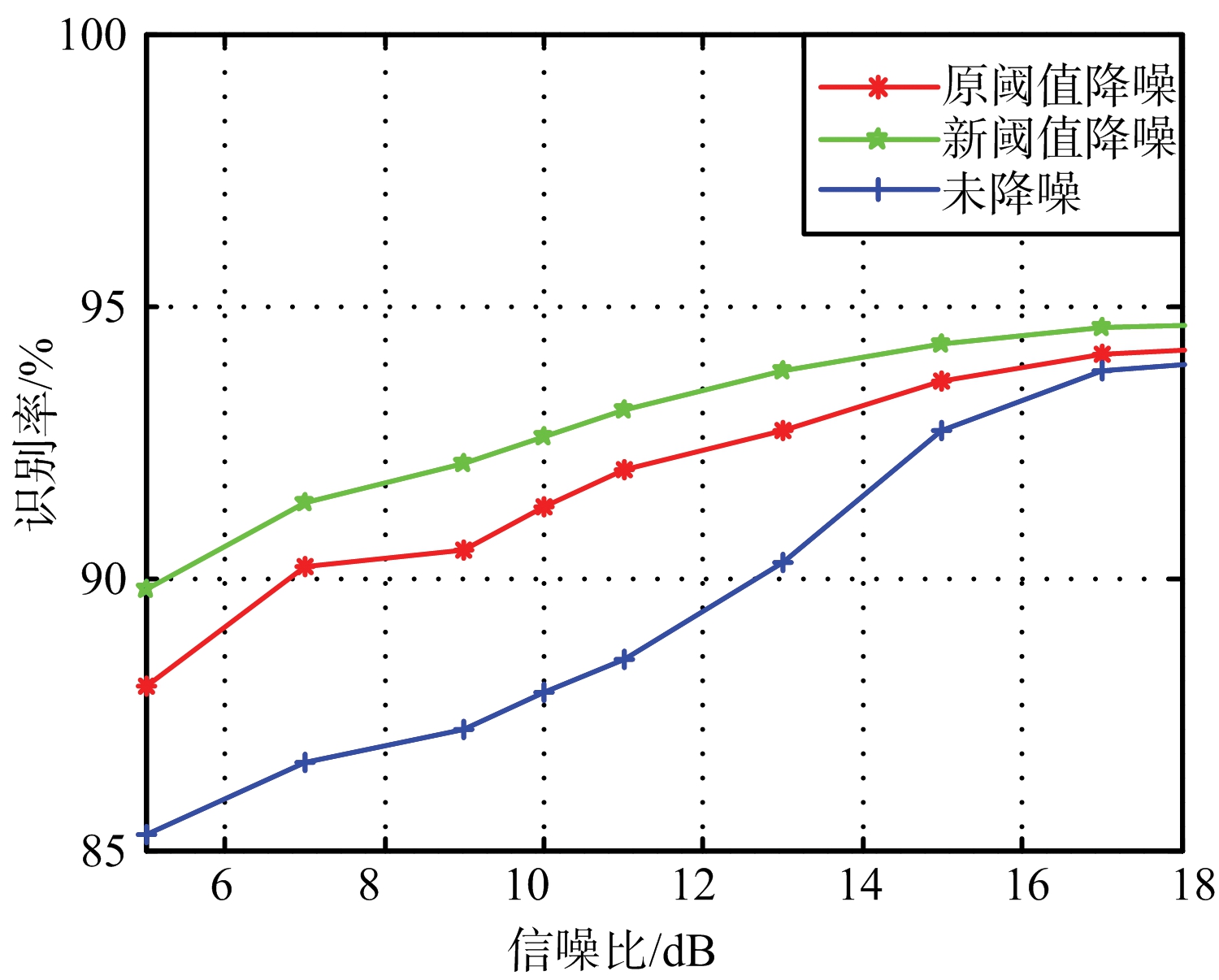
图5 不同信噪比下小波阈值降噪前后平均识别率对比
4 结束语
分析了小波阈值降噪的原理和方法，提出了利用小波阈值降噪处理来进行一维距离像，同时，针对原阈值函数存在的问题和缺点对其进行改进提出了一种新的阈值函数，取得了更好的效果。通过实验比较分析，结果表明小波阈值降噪的方法能够有效地降低噪声从而提高一维距离像的质量，并且本文所提出的新的阈值函数在低信噪比时降低噪声的效果较原阈值方法得到了大大的提高。又通过实验分析不同信噪比条件下降噪前后对分类识别率的影响，降噪处理相较于未降噪识别率得到了显著提升，且这种提升效果随着信噪比的增加开始减弱。
[1] HE Songhua, ZHANG Wei, GUO Guirong. Target Discrimination and Recognition Using High Resolution Range Features[C]∥ IEEE 1992 National Aerospace and Electronics Conference, Dayton, OH: IEEE, 1992:280-283.
[2] DONOHO D L. De-Noising by Soft-Thresholding[J]. IEEE Trans on Information Theory, 1995, 41(3):613-627.
[3] 章琴,刘以安. 基于改进的Morlet小波变换的雷达信号特征提取[J]. 微型机与应用, 2015, 34(10):70-73.
[4] 李文鹏. 小波理论在探地雷达信号处理中的应用[J]. 城市建设理论研究(电子版), 2015(30):1352-1353.
[5] 陈文会,刘芹,刘小民,等. 小波阈值去噪在FMCW雷达信号处理中的应用[J]. 计算机工程与应用, 2015, 51(8):195-199.
[6] LI H, WANG Y, WANG L. Matching Score Properties Between Range Profiles of High-Resolution Radar Targets[J]. IEEE Trans on Antennas and Propagation, 1996, 44(4):444-452.
[7] 蒋跃. 雷达目标RCS建模与识别技术研究[D]. 南京: 南京理工大学, 2017.
[8] 袁莉,刘宏伟,保铮. 基于中心矩特征的雷达HRRP自动目标识别[J]. 电子学报, 2004, 32(12):2078-2081.
[9] CHEN Z, FENG T J, HOUKES Z. Texture Segmentation Based on Wavelet and Kohonen Network for Remotely Sensed Images[C]∥ IEEE International Conference on Systems, Man, and Cybernetics, Tokyo, Japan: IEEE, 1999:816-821.
[10] 黄德双. 高分辨雷达智能信号处理技术[M]. 北京: 机械工业出版社, 2001.
[11] 姜义成. 高距离分辨雷达目标识别方法的研究[D]. 哈尔滨: 哈尔滨工业大学, 1997.
[12] 彭洪江,陈盛双,曾延安. 基于改进阈值函数的小波降噪算法与仿真分析[J]. 计算机应用与软件, 2015, 32(10):188-191.
