0 引 言
目标微动特征往往蕴含着对SAR图像解译极为有利的稳定信息，是目标识别的重要依据[1-6]。微多普勒效应是目标微动对雷达回波产生的频率调制现象，由于目标的微多普勒特征具有“唯一性”，所以被认为是最重要的目标识别特征之一[7-10]。考虑到微多普勒是雷达照射时间函数，常用时频分析的方法提取微多普勒特征[7-9]。但在实际应用中，时频分析法对回波信噪比要求较高，这极大限制了它的应用[10-13]。为克服这个不足，本文提出一种基于DPCA和逆Radon变换的微多普勒特征提取方法。针对机载SAR系统，研究了其对微动目标检测与参数估计的有效方法。针对检测环境变化比较剧烈或者载机飞行不稳造成较大噪声的问题，提出了基于DPCA信号时频分析和逆Radon变换的微动目标检测与参数估计方法。
利用DPCA技术，对双通道信号进行复图像插值、配准及时间配准之后进行共轭相乘，得到干涉相位。由进一步得到SAR系统参数与运动目标参数之间的关系，最终导出微动目标参数。所提方法首先对振动目标回波信号作DPCA处理；接着对其进行时频分析，提取微动目标的微多普勒特征；最后对时频分析后的信号进行逆Radon变换，DPCA处理对运动目标信号进行了平方，因而提高了信噪比。干涉信号的微多普勒频率表现为正弦函数的形式，逆Radon变换对正弦信号聚焦但对噪声不聚焦，所以整个系统所需回波信噪比较单纯使用时频分析时低得多，即使在环境变化比较剧烈或者载机飞行不稳的情况下也能取得良好的检测效果。
1 DPCA基本原理
DPCA算法首先对通道1与通道2的回波信号分别进行距离向与方位向压缩，改善多普勒中心频率点的偏差。其次为了去除平台运动导致的多普勒线性调频，需要对脉冲压缩后的双通道信号进行相位补偿与时间校准。随之对两路信号进行快速傅里叶变换，变换到频域之后将两路回波信号作干涉处理即回波信号进行共轭相乘，获得两幅SAR图像的干涉相位。需要指出的是基线长度会影响到干涉SAR系统的检测性能。基线长度与两幅图像的相干性呈复相关特性，即当基线长度达到临界基线长度时，图像会完全不相干。只有基线长度小于临界基线长度，才能确保干涉系统的检测性能。下面通过对回波信号的处理来分析工作原理。假设载机以va的速度水平飞行，将双天线沿着航迹方向放置，双天线的中心间隔为2B，采用单发双收的工作模式。考虑到地面上存在某点目标，该点目标的径向运动速度为vr，且目标的方位向速度对双通道信号的影响相同，此处可以忽略。初始时刻t=0目标方位向位置为x0，目标到载机的距离表示为Rc。双通道接收到的信号经过合成孔径雷达成像处理后的复图像分别为S01(t)，S02(t)。若基线长度B、载机速度va与SAR脉冲重复频率PRF三者满足：B=m·va/PRF(m为非零整数)，此时不需要对S01(t)和S02(t)进行插值与配准。将S01(t)时移τa=m/PRF后与S02(t)的共轭相乘得
I(t)=
(1)
式中：λ是波长；常数k与运动目标后向散射系数相关；Ts是雷达的合成孔径时间；T02=(x0-B/2)/va。由式(1)可以看出，如果径向速度为0，则乘积的干涉相位也为零；相反，对运动目标而言vr≠0，对应的干涉相位为4πBvr/λva。由此可以通过干涉相位判断目标是否是运动的，并获得运动目标的相关信息。
2 SAR微动目标检测与参数估计
2.1 DPCA干涉回波信号
DPCA技术是对双通道回波信号作干涉处理，以达到在静止背景中抑制杂波的目的。假设雷达发射线性调频信号的波长为λ、带宽为B，则前置天线通道与后置天线通道的基带信号，经过相干检波与距离压缩之后分别为
(2)
(3)
式中，C0是与目标的后向散射系数以及天线的双程方向图相关的常数。在满足d=mvaT的条件下，对双通道回波信号作DPCA处理，即
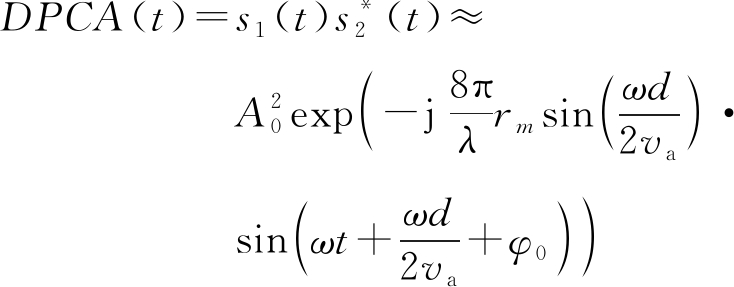
(4)
由上式可知，对于静止目标，R1(t)=R2reg(t)，DPCA信号的干涉相位为0；对于微动目标而言，R1(t)≠R2reg(t)，干涉信号的相位不为0。提取干涉信号的虚部即可检测到杂波背景下的微动目标。在提高信噪比之后，对干涉信号作时频分析可以进一步获取振动目标的微多普勒特性。
2.2 DPCA信号的微多普勒
当存在微动目标时，双通道干涉信号的瞬时微多普勒频率为
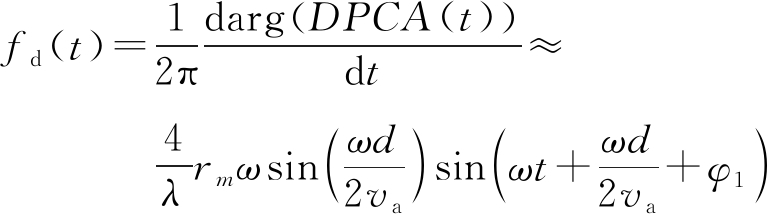
(5)
式中，φ1=φ0+π/2。上式表明DPCA信号的微多普勒调制可近似表示为正弦函数的形式，且参数A与目标的微动幅度和微动角频率有关，目标的微动角频率ω和相位φ记录了目标的微动初相信息。
2.3 通过逆Radon变换检测微动目标
假设f(t,ω)为平面(t,ω)上的二维函数，将原始坐标系旋转φ得到新的直角坐标系(u,v)，以不同的u值平行于v轴积分，所得结果即为Radon变换。将f(t,ω)的Radon变换记为Pf(u,φ)，计算如下：
Pf(u,φ)=
δ(u-tcosφ-ωsinφ)dtdω
(6)
可见，Radon变换本质上就是将(t,ω)平面上直线u=tcosφ+ωsinφ，映射到(u,φ)平面上的点。考虑平面(x,y)上过(x0,y0)的直线u=x0cosθ+y0sinθ。经过三角变换后得到
u=Bsin(θ+φ0)
(7)
式中，
随θ的变化在平面(u,θ)上作正弦变换。所以，(u,θ)平面上的正弦曲线对应着(x,y)平面上的定点(x0,y0)。逆Radon变换可以通过正弦曲线与参数空间上的点之间的映射关系来求出该点的坐标。由式(5)可知，DPCA处理后的微动目标回波信号在经过时频变换后，得到其微多普勒为
fm=Csin(θ+φm)
(8)
式中，C=4ωrmsin(ωd/2va)/λ，θ=ωt，φm=ωd/2va+φ1。微动目标的时频项可写为
R(fm,θ)=δ(fm-Csin(θ+φm))
(9)
由中心切片定理，图像经过逆Radon变换之后可以表示为
IR(x,y)=
ej2πkxx+j2πkyydfmdkxdky=
δ(x-Csinφm)δ(y-Ccosφm)
(10)
式中，kx=vcosθ，ky=vsinθ。可见，时频平面上的正弦曲线fm=Csin(θ+φm)在逆Radon变换之后被映射到了参数空间上的点(Csinφm,Ccosφm)。在逆Radon变换域，提取图像的特显点，根据特显点的坐标估计微动目标参数：
(11)
(12)
将上式代入C=4ωrmsin(ωd/2va)/λ，并结合微动频率，就可估计微动目标的振幅rm。图1为本文提出的基于DPCA和逆Radon变换的微动目标检测算法流程。
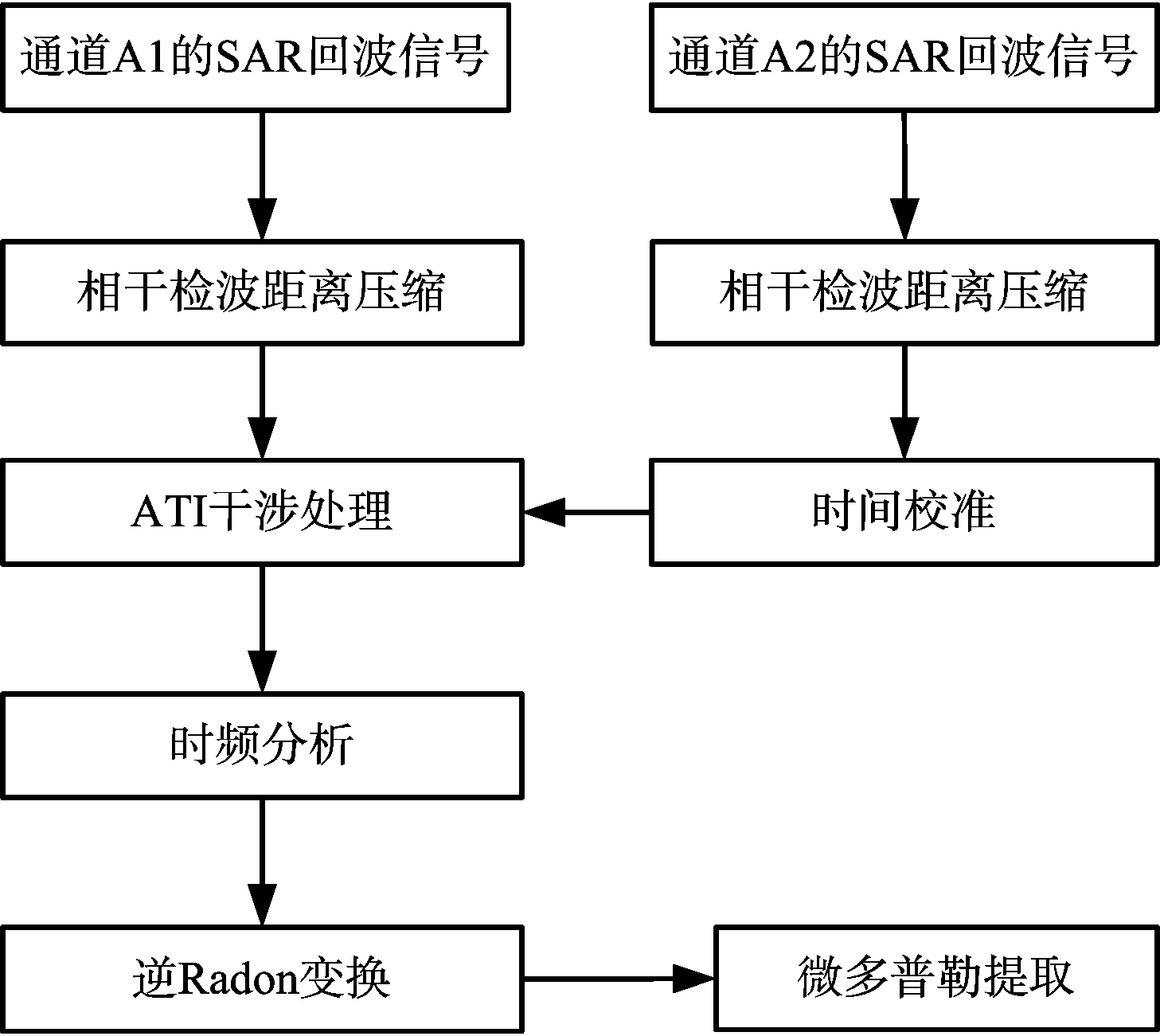
图1 基于DPCA和逆Radon变换的微动目标检测算法流程
3 仿真实验及结果
3.1 静止背景下DPCA处理
为了验证DPCA对动目标的检测性能，本节首先采用DPCA方法对一个振动目标和两个静止目标进行检测，振动目标的初相为π/2。DPCA仿真参数如表1所示，微动目标参数如表2所示。在不考虑系统噪声的情况下，双通道SAR微动目标3D成像图如图2所示。图3为双通道DPCA干涉信号的虚部，由图可以看出，在不考虑噪声的情况下，通过DPCA处理并取干涉信号的虚部后，静止杂波被抑制，仅保留微动目标。
表1 DPCA仿真参数
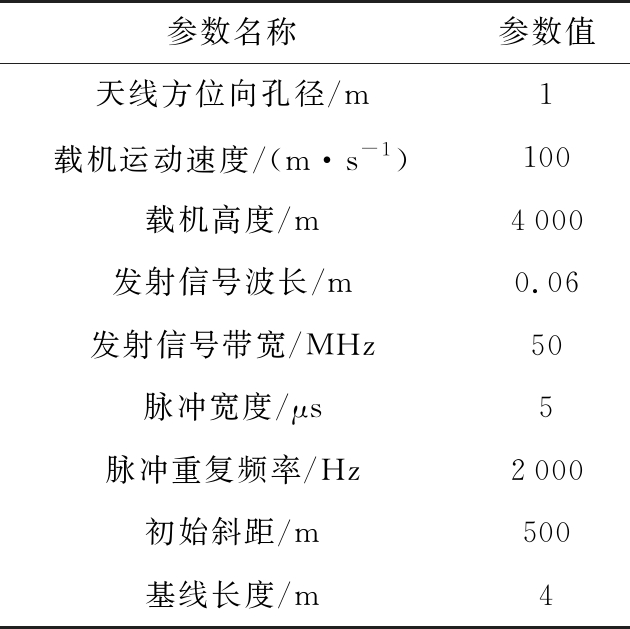
参数名称参数值天线方位向孔径/m1载机运动速度/(m·s-1)100载机高度/m4000发射信号波长/m0.06发射信号带宽/MHz50脉冲宽度/μs5脉冲重复频率/Hz2000初始斜距/m500基线长度/m4
表2 微动目标参数
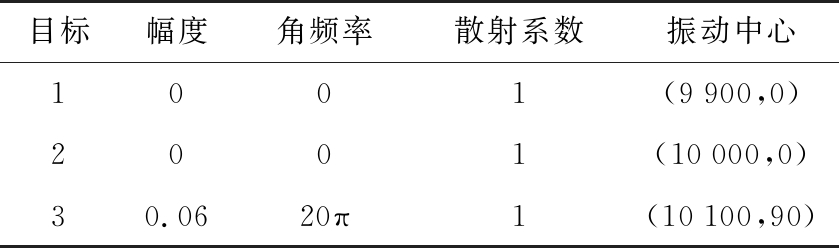
目标幅度角频率散射系数振动中心1001(9900,0)2001(10000,0)30.0620π1(10100,90)
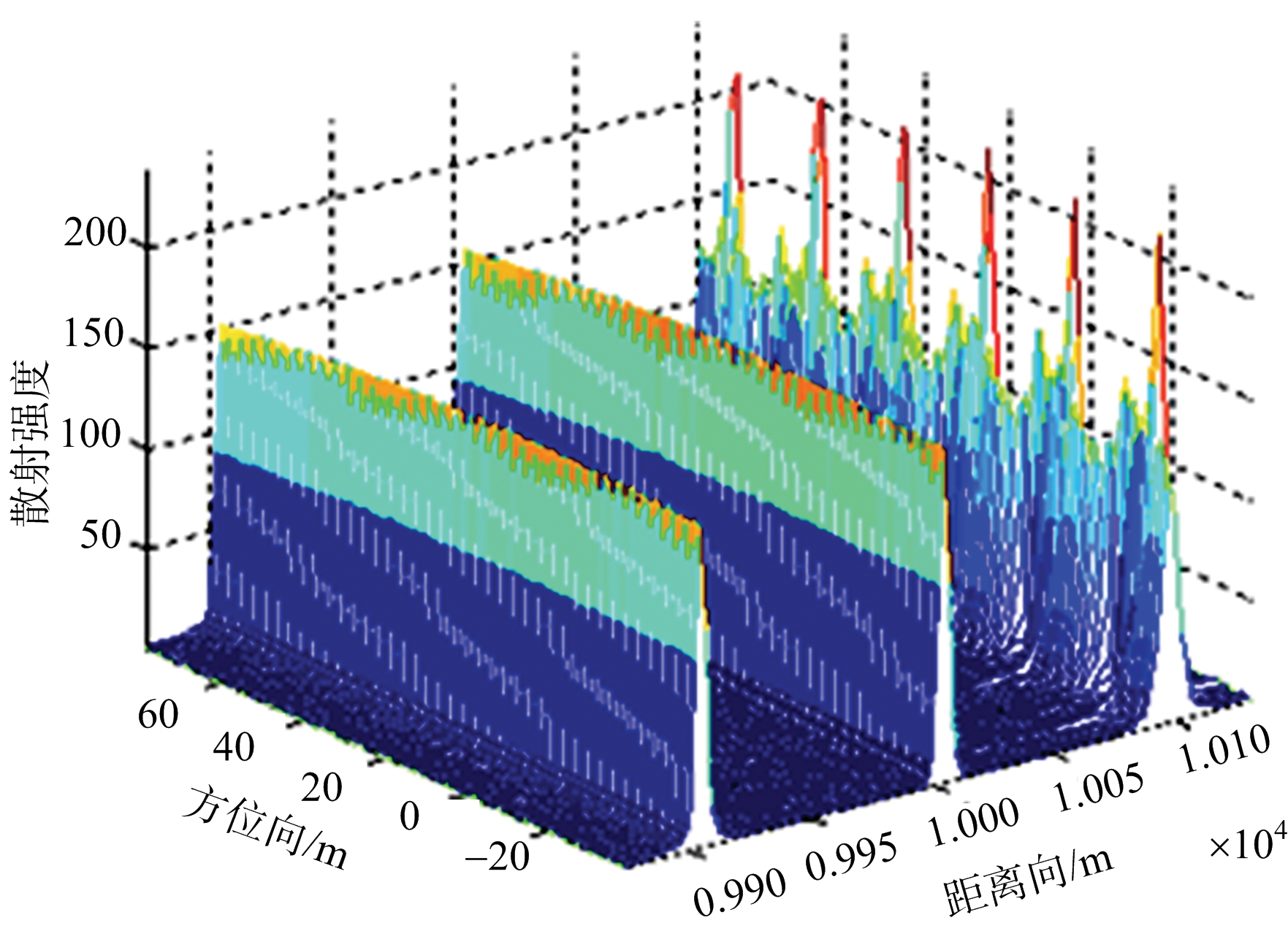
图2 双通道SAR微动目标3D图像
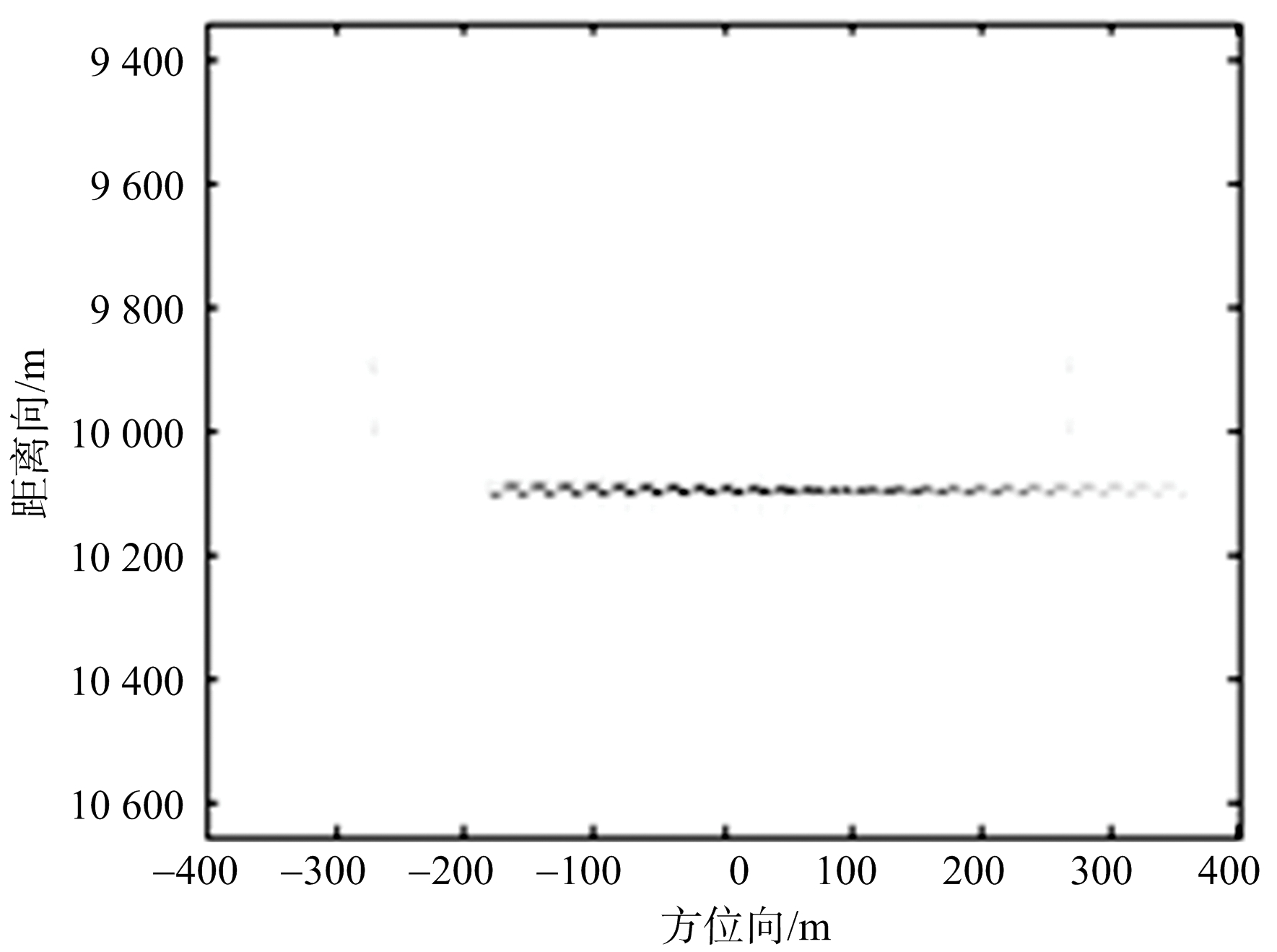
图3 双通道DPCA干涉信号的虚部
振动目标引起的微多普勒可以通过对DPCA处理后的信号作时频分析获得。图4为经DPCA处理后回波信号的STFT信号，图5为按照式(12)计算得到的振动目标的微多普勒谱图。由图4和图5对比可知，经过双通道DPCA干涉后的回波信号微多普勒频率实验仿真结果与理论计算一致。由图4可知，微多普勒频率的变换周期为 0.1 s，所以微动目标的振动频率约为10 Hz。
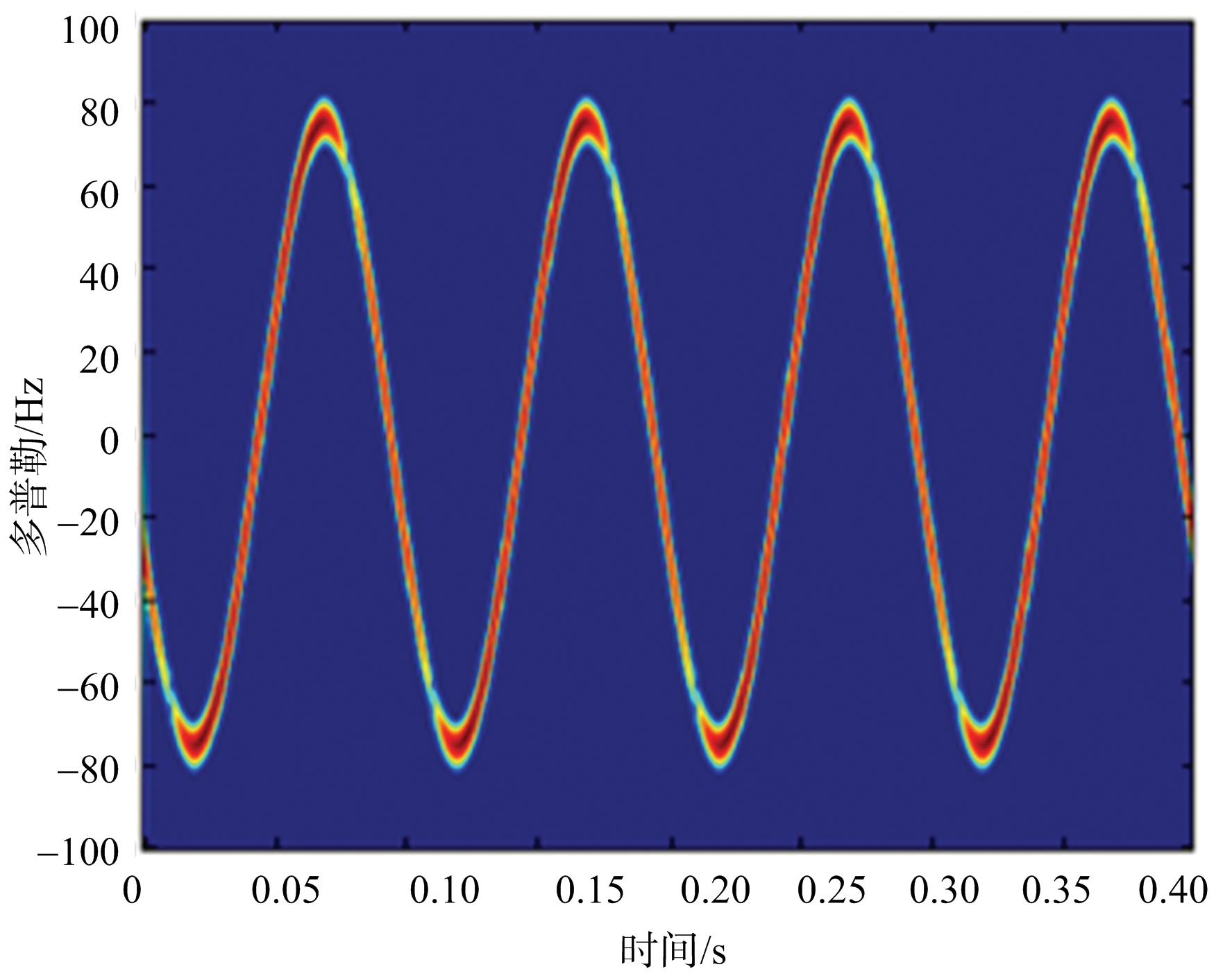
图4 振动目标的微多普勒频谱图
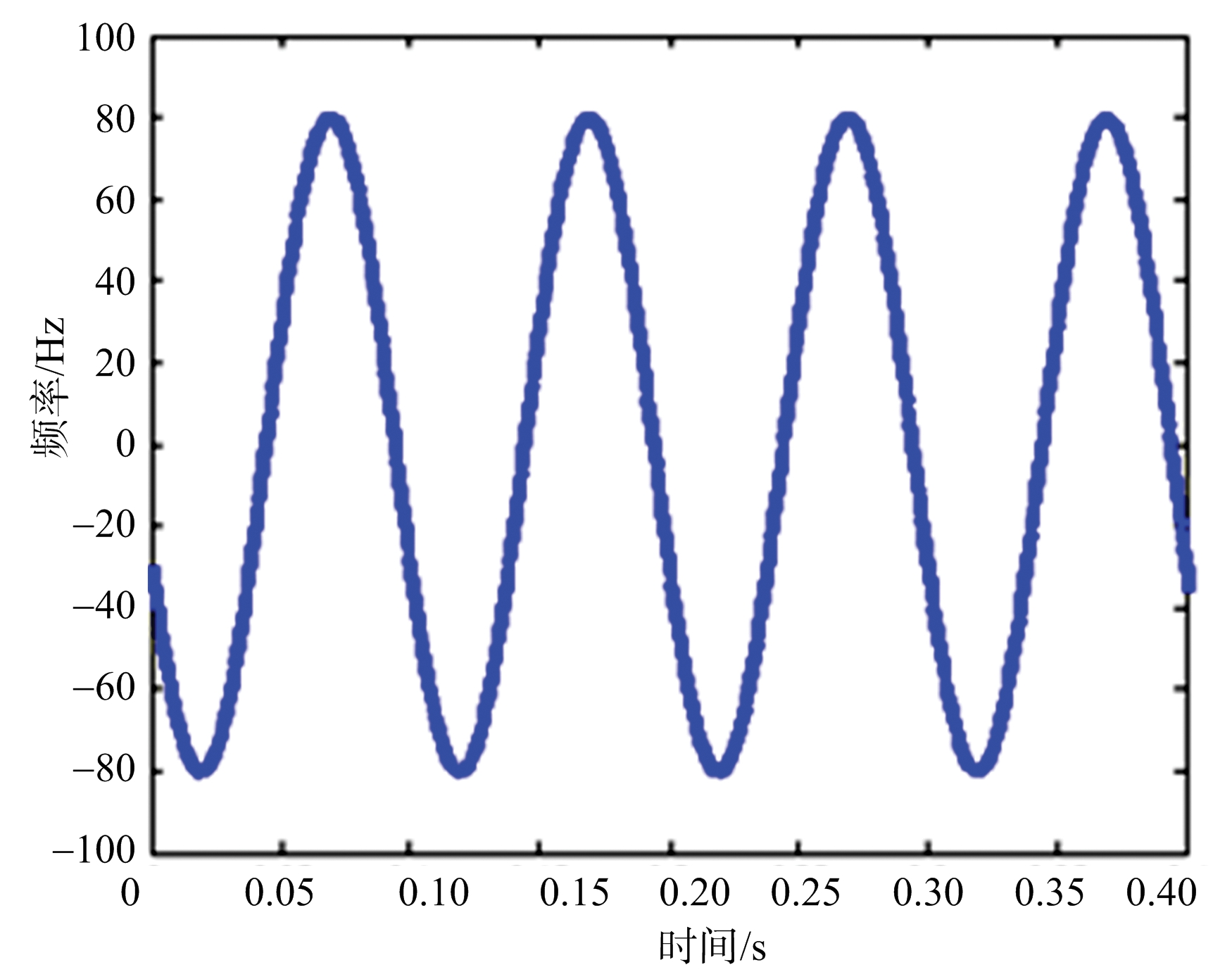
图5 振动目标微多普勒谱理论示意图
3.2 杂波背景下的DPCA和逆Radon微动目标检测与参数估计
图6为杂波背景下微动目标的3D图像。由图可知，振动目标淹没在杂波中，难以直观地辨别出运动目标。图7为微动目标信号经DPCA干涉处理后的实验结果。由于噪声的引入，使得DPCA信号的虚部静止杂波分量仍然存在，难以判断振动目标所在的距离单元，如果想要获得振动目标的微动信息，就需要对DPCA干涉结果进行二次处理。
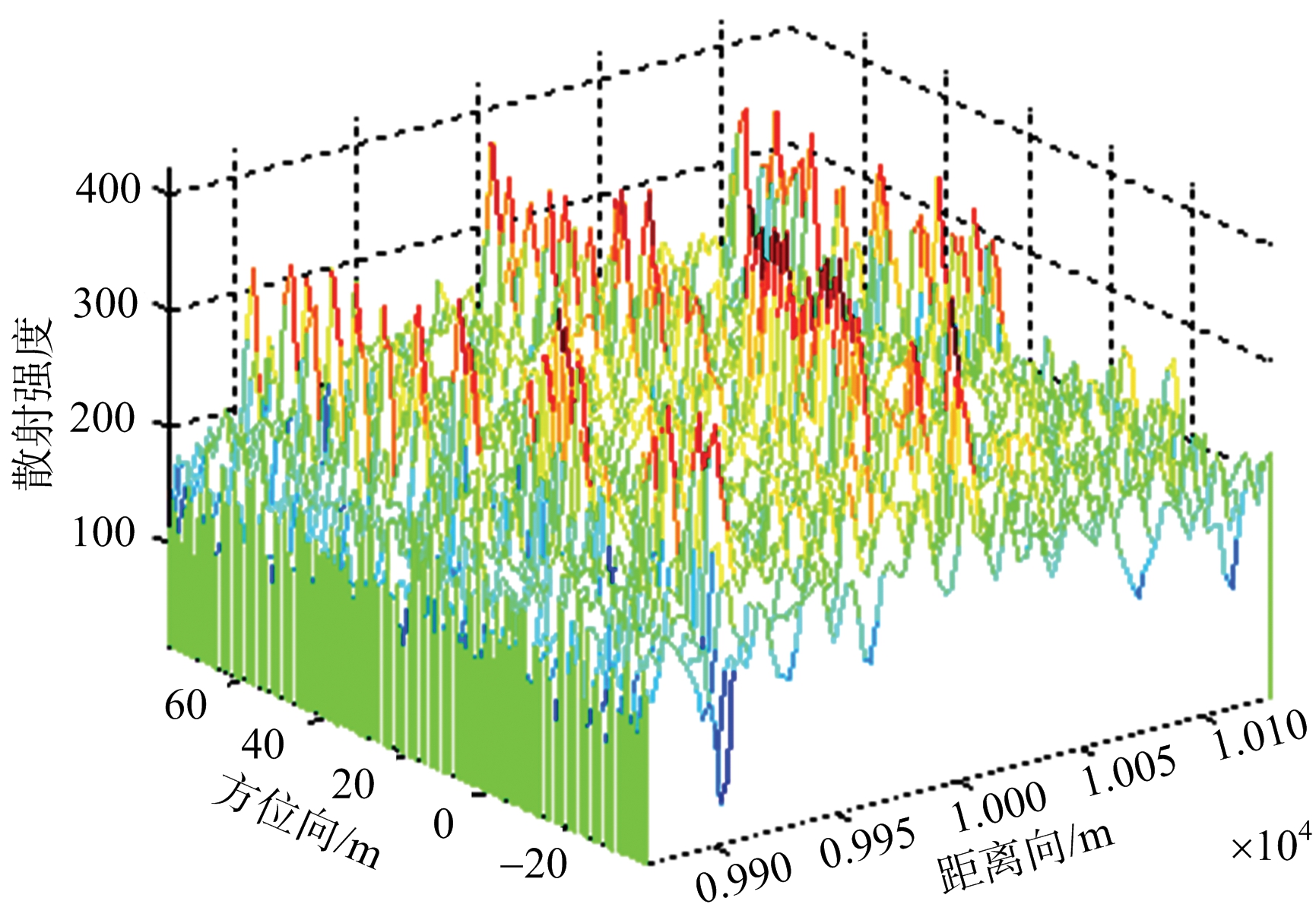
图6 杂波背景下微动目标3D图像
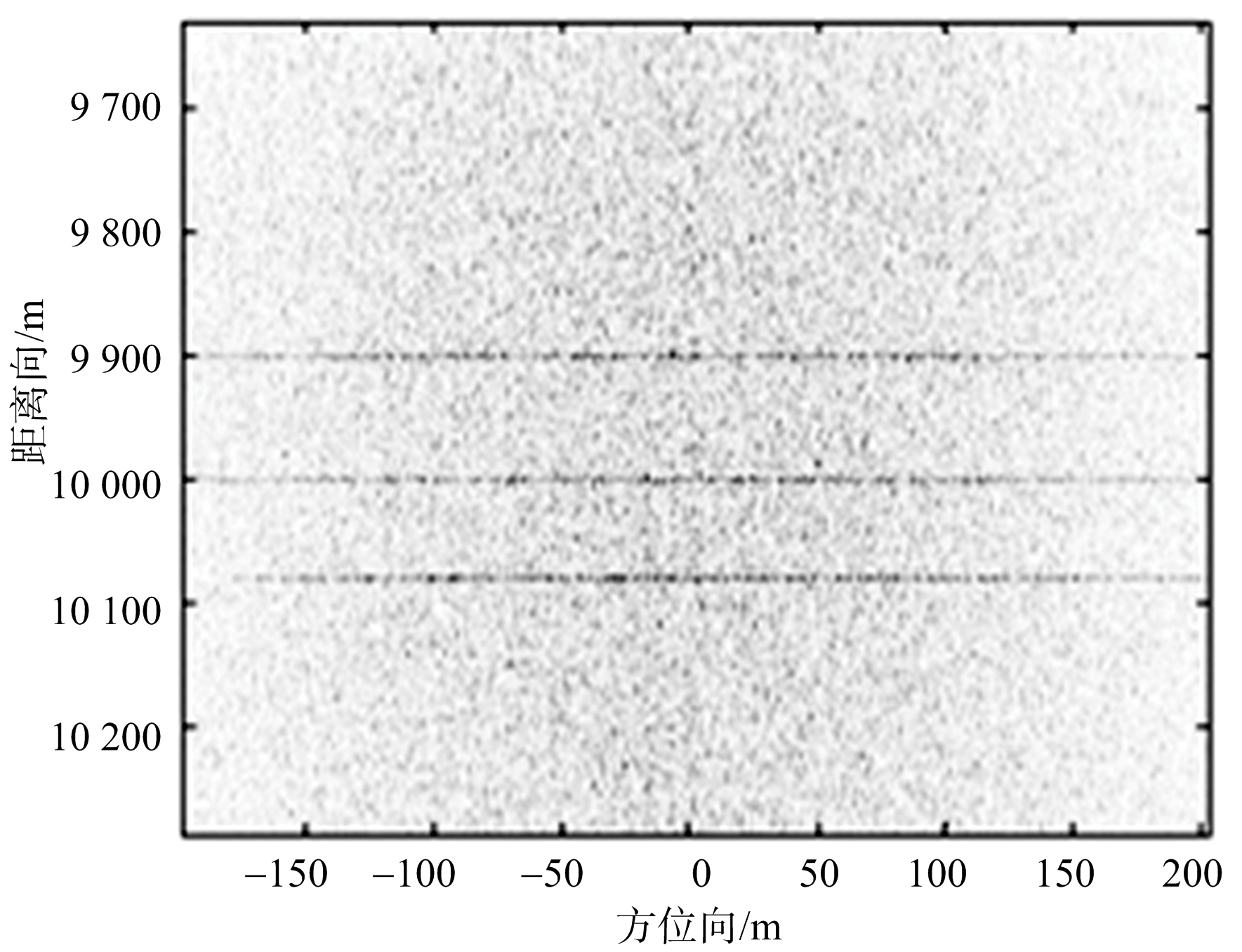
图7 噪声环境下双通道DPCA干涉信号的虚部
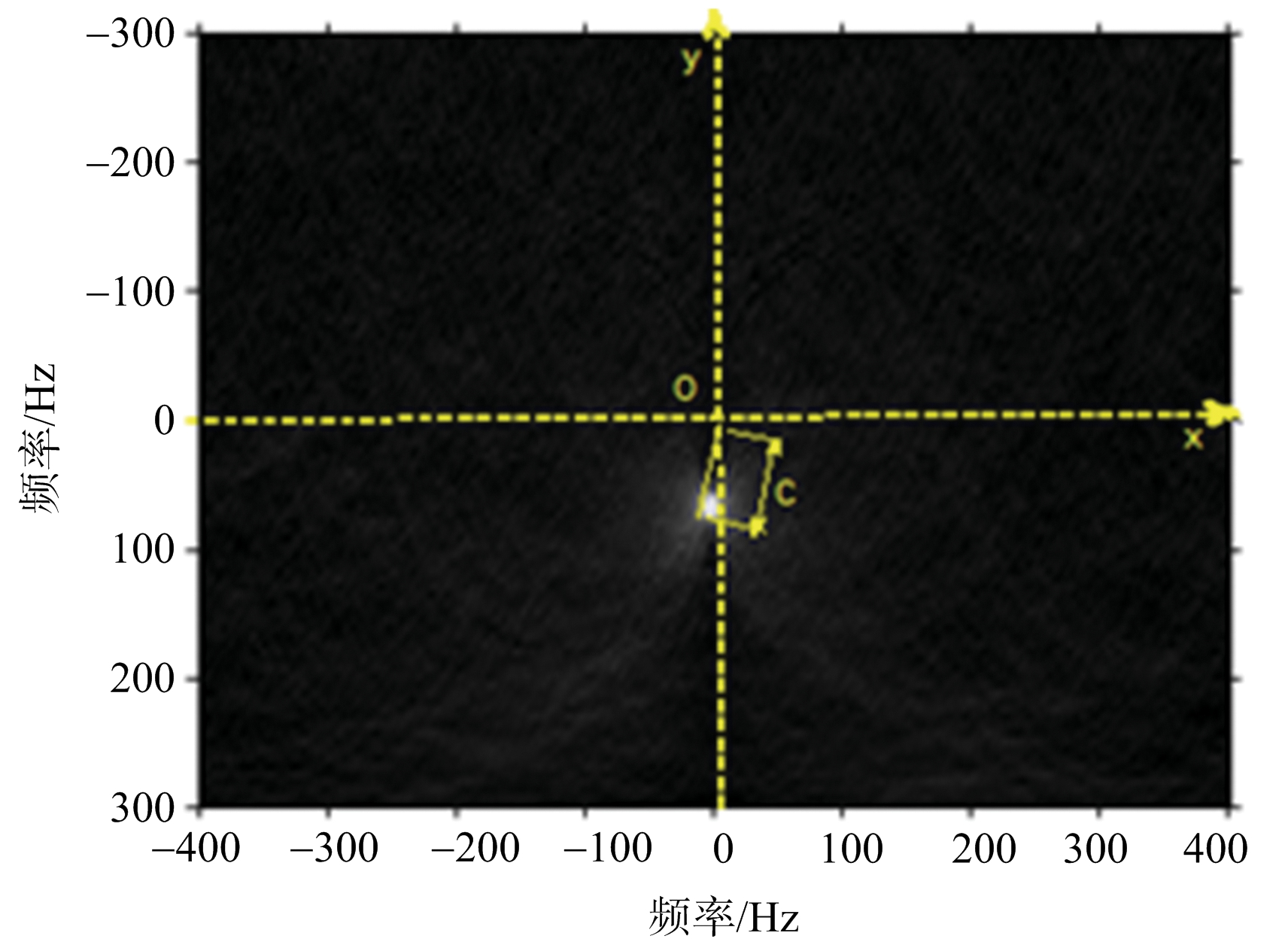
图8 噪声下微多普勒谱图的逆Radon变换图
按照前文基于DPCA信号时频分析和逆Radon变换的方法，对DPCA处理后的干涉信号作时频分析得到微多普勒谱图，如图4所示。利用逆Radon变换对正弦信号的聚焦性，DPCA信号时频分析的结果经过逆Radon变换后得到一个特显点。如图8所示，经过逆Radon变换振动目标的微多普勒谱图在参数空间中聚焦为一个特显点，以逆Radon变换结果图的几何中心为原点建立直角坐标系，则特显点到原点的距离表示最大的微多普勒值。最大微多普勒频率约为80.156 Hz，根据关系式C=4rmω/λsin(ωd/(2va))，且由图5测得目标的微动周期为0.1 s，据此推算得到振动目标的振幅为0.061 7 m与预设的0.06 m相对误差为2%，所以利用本节所提方法能够有效实现振动目标的检测。
3.3 基于DPCA和逆Radon变换算法的性能分析
为了分析DPCA和逆Radon变换的检测性能，在不同的信噪比下执行10 000次Monte Carlo仿真，得到的检测性能曲线如图9所示，该曲线表明基于DPCA和逆Radon变换算法可在SNR≥-9 dB时，达到80%以上的检测率。
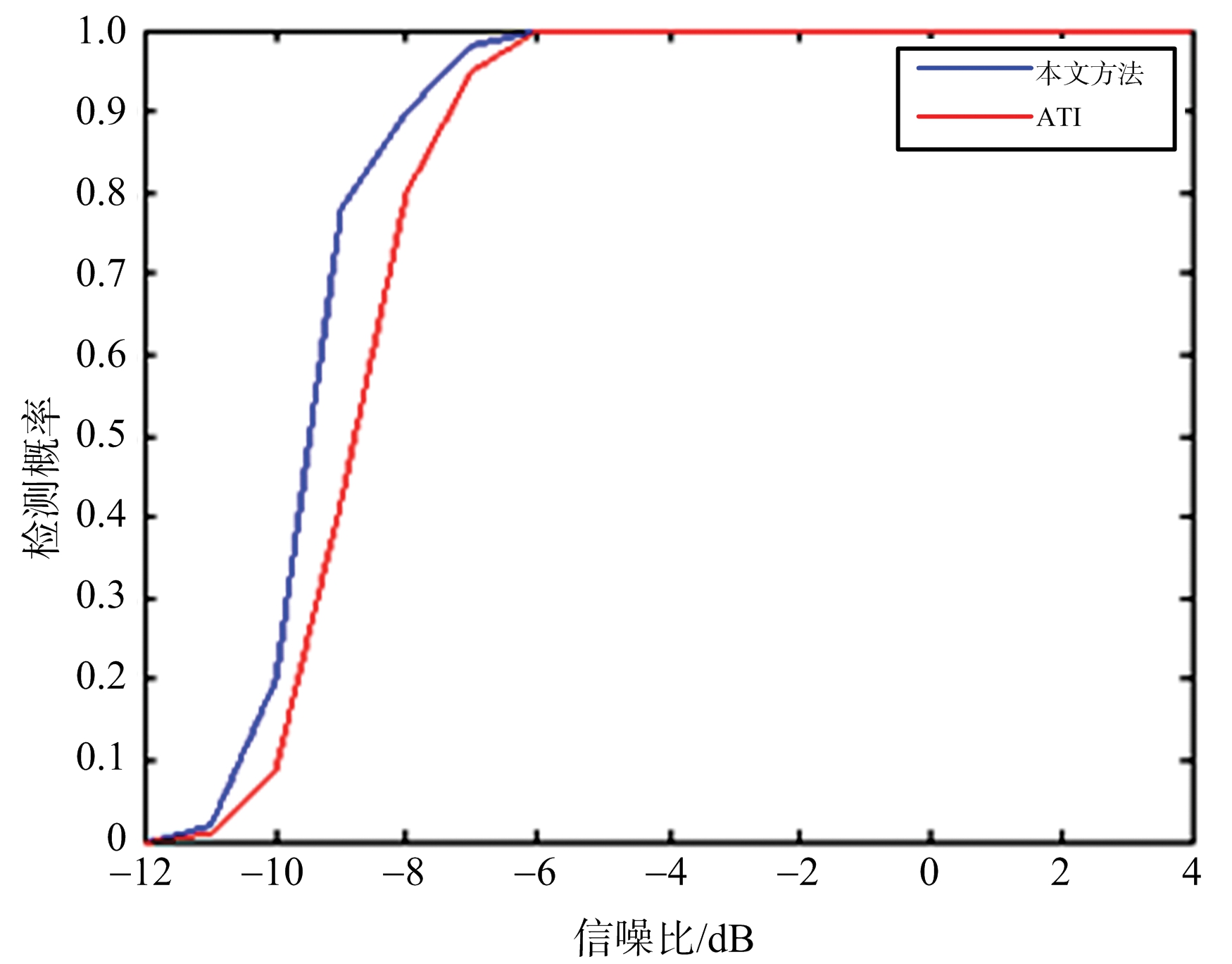
图9 微动目标检测性能曲线图
4 结束语
本文提出一种基于DPCA和逆Radon变换的微多普勒特征提取方法。所提方法首先对振动目标回波信号作DPCA处理；接着对其进行时频分析，提取微动目标的微多普勒特征；最后对时频分析后的信号进行逆Radon变换。DPCA处理对运动目标信号进行了平方，因而提高了信噪比。干涉信号的微多普勒频率表现为正弦函数的形式，逆Radon变换对正弦信号具有良好的积累增益，所以整个系统所需回波信噪比较单纯使用时频分析时低得多，即使在环境变化比较剧烈或者载机飞行不稳的情况下也能取得良好的检测效果。实验验证了算法的有效性。
[1] 陈沁根,张兴敢. 基于时频分析-随机Hough变换的微动目标参数快速提取[J]. 南京大学学报(自然科学), 2017, 53(6):1178-1186.
[2] 陈春晖,张群,罗迎,等. 一种空间微动目标宽带雷达干涉三维成像方法[J]. 电子与信息学报, 2016, 38(12):3144-3151.
[3] 董玲. 合成孔径雷达微多普勒特征研究[D]. 成都: 电子科技大学, 2009.
[4] 张伟,童明创,张群,等. 基于DPCA杂波抑制的地面振动目标微多普勒提取[J]. 系统工程与电子技术, 2011, 33(4):738-741.
[5] 吕蒙. 雷达信号中的微多普勒信息提取方法与应用研究[D]. 杭州: 浙江大学, 2014.
[6] LIU Junliang, LI Yanfang, CHEN Shangfeng, et al. Micro-Motion Dynamics Analysis of Ballistic Targets Based on Infrared Detection[J]. Journal of Systems Engineering and Electronics, 2017, 28(3):472-480.
[7] FLANDRIN P, AMIN M, MCLAUGHLIN S, et al. Time-Frequency Analysis and Applications[J]. IEEE Signal Processing Magazine, 2013, 30(6):19-150.
[8] 张伟,童创明,张群,等. 基于时频分析的双通道SAR自旋目标检测[J]. 航空学报, 2011, 32(10):1914-1923.
[9] 陈小龙,关键,董云龙,等. 稀疏域海杂波抑制与微动目标检测方法[J]. 电子学报, 2016, 44(4):860-867.
[10] 陈小龙,刘宁波,王国庆,等. 基于高斯短时分数阶Fourier变换的海面微动目标检测方法[J]. 电子学报, 2014, 42(5):971-977.
[11] 王童,童创明,李西敏,等. 扩展性微动目标回波模拟与特征参数提取研究[J]. 物理学报, 2015, 64(21): 210301.
[12] 黄小红,贺夏,辛玉林,等. 基于时频特征的低分辨雷达微动多目标分辨方法[J]. 电子与信息学报, 2010, 32(10):2342-2347.
[13] ZHANG Wenpeng, FU Yaowen, NIE Lei, et al. Parameter Estimation of Micro-Motion Targets for High-Range-Resolution Radar Using High-Order Difference Sequence[J]. IET Signal Processing, 2018, 12(1):1-11.
[14] 周辉,赵凤军,禹卫. SAR运动目标微动信号模型及微多普勒效应研究[J]. 电子测量技术, 2015, 38(11):135-142.
