0 引 言
超宽带穿墙雷达能够为墙后目标检测提供良好的手段，因而在灾后救援、反恐巷战等领域得到了广泛应用[1-3]，经典的成像算法如后向投影(Back Projection，BP)算法、延时求和算法等需要大量的空间与时间数据采样，耗时且无法避免成像结果中的杂波干扰。为了减少成像数据量并提高成像分辨率，基于压缩感知的成像技术被引入到穿墙成像中，通过在成像模型中引入稀疏的正则化约束，可将目标的重构问题转化为1范数优化问题，采用包括贪婪法[4-5]、贝叶斯方法[6-7]、正则化方法[8]等来恢复稀疏信号。文献[4]和文献[5]都是根据目标特性构建相应稀疏特性成像字典矩阵，然后通过正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法完成目标成像，这类算法最重要的一步是从成像场景的最小二乘估计结果中选取支撑集，显然这一步是最为耗时，且OMP算法极易受到信号输入信噪比影响。相比于OMP方法，贝叶斯方法能够在低信噪比情况下取得较好成像，文献[6]在BCS的基础上结合扩展目标像素间的结构性信息，然后利用吉布斯采样方法得到高分辨的成像结果，但该方法加大了成像模型的复杂度致使算法运算时间较长。而文献[7]通过构建点目标与扩展目标的组合字典，并利用一阶泰勒级数展开解决目标网格点偏移问题，算法成像结果具有较高分辨率，然而构建两个成像字典势必带来更多的成像时间。文献[8]提出一种基于迭代的拉格朗日乘子的穿墙扩展目标成像方法，通过稀疏增强、区域增强以及图像域优化三步，获得了高分辨的扩展目标结果，同时拉格朗日乘子项也避开了对先验信息的获取，然而该方法同样存在算法耗时过高的问题。显然，上述所列的稀疏成像方法均在一定程度上改善了成像结果的分辨率，但他们都不可避免地提高了成像时间，因此，如何保证成像分辨率较高的前提下缩短成像时间对于穿墙应用十分重要。
有鉴于此，本文提出一种基于交替迭代框架的墙后目标成像快速算法，首先利用贝叶斯框架建构起穿墙信号的稀疏表示模型，并利用最大后验估计准则得到包含参数与目标散射矢量的目标函数，然后在优化最小化(Majorization-Minimization，MM)框架下构造此时目标函数对应的稳健优化函数，最后对联合概率密度函数的目标散射系数、噪声功率以超参数依次进行交替迭代优化。与现有的成像方法对比，本文方法在信噪比较低时能实现墙后目标清晰成像的同时，也大幅提升了成像速度。
1 信号模型
使用收发天线共置的雷达系统沿着平行于前墙的方向对墙后目标进行J点的合成孔径探测，同时将感兴趣场景(SOI)在距离向和方位向上划分为N=Nx×Nz个像素网格，定义xn表示第n像素点的目标反射系数，n=1,2,…,N，则第j个探测位置接收到的目标回波信号表示为
sj(t)=
j=1,2,…,J
(1)
式中：p(t)表示系统发射的窄脉冲信号，τjn为发射脉冲从第j个探测位置到第n个像素网格点的双程传播时延，对均匀墙体的时延计算参考文献[9]，对非均匀墙体参考文献[10]；αjn表示发射信号从发射天线出发到第n个像素然后再回到接收天线距离衰减系数，其值可以表示为
这里的djn表示电磁波从发射天线到像素网格实际走过的距离；ej(t)表示测量过程中的加性噪声。
对式(1)的sj(t)进行K点采样，采样后的数据可以表示成
rj(k)=
ej(kTs)，k=1,2,…,K
(2)
式中，Ts表示采样周期。将式(2)写成矢量形式表示为
rj=PjDjx+ej
(3)
式中，rj=[rj(0),rj(1),…,rj(K-1)]T表示第j个测量位置处的回波信号矢量，x=[x1,x2,…,xN]T表示散射系数矢量的值，Dj是由距离衰减系数组成的对角矩阵，表示为Dj=diag(αj1,αj2,…,αjN)，Pj为一个K×N的矩阵，其中元素表示为脉冲信号相应平移，具体为
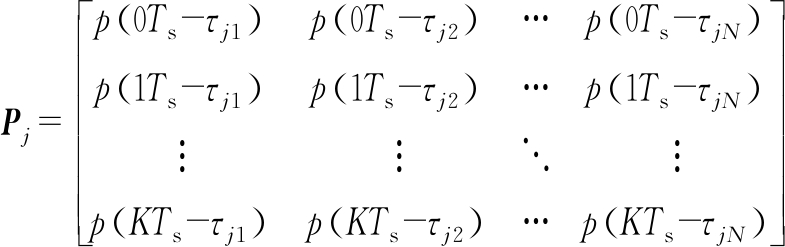
(4)
考虑到所有J个孔径接收到的回波数据，可以得到以下线性关系:
r=Ψx+e
(5)
式中：r表示所有的回波数据矢量，维度是JK×1，其值为
是一个维度为JK×N的矩阵，表示为Ψ=[(PjDj)T,(PjDj)T,…,(PjDj)T]T；e是维度JK×1的噪声矢量，表示为
考虑到这样构建采用的数据量过大，可以采用文献[11]中的测量矩阵Φ，对式(5)进行降采样处理，得到稀疏表示模型为
y=Φ(Ψx+e)=Αx+n
(6)
式中，Φ表示一个维度是M×JK的测量矩阵，矩阵Α=ΦΨ表示从Ψ中随机抽取行和列构成新的字典。
2 优化最小化框架的递归迭代成像算法
2.1 算法描述
假设穿墙回波信号y满足贝叶斯模型
p(y|x,η)=N(Ax,ηI)
(7)
式中，η为高斯白噪声的方差，且该数值即为噪声的功率，其取值范围η∈[0,+
)，因而可以合理假设其先验概率密度函数为
p(η)∝1
(8)
另外，假设目标散射系数x中的元素为独立同分布，并服从未知参数为λ的拉普拉斯分布，所以散射系数矢量的概率密度函数表示为
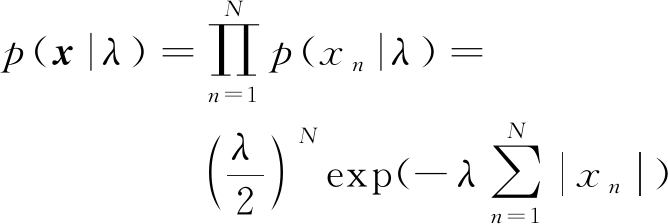
(9)
本文利用最大后验估计(MAP)准则来重构目标散射系数矢量，先给出目标散射系数的联合后验概率分布函数p(x|y,λ,η)：
p(x|y,λ,η)∝p(y|x,η)p(x|λ)p(η)=
(10)
根据MAP准则，需要通过最大化联合后验概率密度函数p(x|y,λ,η)，进行实现对多变量目标函数的优化求解。为方便描述，将式(10)取对数后表示为
(11)
通过最大化目标函数ln(p(x|y,λ,η))，同时忽略ln(p(x|y,λ,η))中的常数项，可以求解未知的散射系数矢量x、噪声功率η以及超参数λ的MAP估计值，即
(12)
式中，
表示MAP估计的目标函数。这里的x，η以及λ的最优估计是彼此联系，如果已知噪声方差η，式(12)的稀疏贝叶斯估计问题就转化为组合l1-l2范数最小化求解问题，此时超参数λ为对应的正则化参数；而已知稀疏矢量x与η和λ中任意一个，直接可以用封闭解的形式得到相应的估计值。从这个角度出发，采用一种交替迭代最小化[12]的方法依次求解(x,λ,η)，具体步骤如下：
第1步：固定噪声方差η以及超参数λ去估计散射系数矢量x，即
η(l))；
第2步：固定散射系数矢量x和超参数λ去估计噪声方差η，即
第3步：固定噪声方差η和散射系数矢量x去估计超参数λ，即
在第1步中，直接利用封闭解形式求解x的最优估计，就会涉及到矩阵求逆运算，求解过程耗时以及||x||1在某些点的不可导，通过观察步骤1中目标函数G(x,λ(l),η(l))可以看出，当噪声方差η和超参数λ固定后，对x的最优估计就转化成为一个l1正则化最小二乘估计问题，即
为了提高算法效率，采用优化最小化[10]去迭代估计x。
在寻找散射系数矢量x最优解过程中，随着迭代次数增加，目标函数G(x,λ,η)是一个递减的趋势[13]，第l+1次迭代得到的x(l+1)均比前一次的x(l)要小，因此，目标函数G(x,λ,η)存在以下不等式成立：
(13)
由优化最小化原理可知，对散射系数矢量的估计就转变成最小化
的过程，即
(14)
式中，
表示目标函数
在当前
下的最优函数，令G(x,λ,η)中的
由于
与q1(x)，q2(x)密切相关，因此只要找出当前
下q1(x)，q2(x)的最优化函数即可。接下来分别求出q1(x)，q2(x)的最优化函数Q1(x,x(l))和Q2(x,x(l))。
将
拆分开并表示成：
这里的ym和
分别表示观测值矢量y和Ax中的第m个元素，而Amn是矩阵A中的第m行第n列的元素。根据DePierro理论[14]，可以利用均方函数的凸性来构造([Ax]m)2的最优函数，进而构造出的q1(x)的最优函数。将[Ax]m重新表示为
[Ax]m=
(15)
式中，cmn定义为
这里的rm表示矩阵A中第m行非零元素个数。很明显，cmn中的n遍历所有列时，其值为1，即
因此，由均方函数的凸性可以得到以下不等式：
([Ax]m)2≤qk(x,x(l))
(16)
式中,
显然，qk(x,x)=([Ax]k)2，所以qk(x,x(l))可以作为([Ax]m)2的最优化函数，此时的q1(x)可以表示为
根据文献[15]，任意一个绝对值函数|θ|，都满足
且z(θ,θ)=|θ|，所以q2(x)=||x||1的最优化函数表示为
(18)
结合式(17)和式(18)，G(x(l),λ(l),η(l))在当前散射系数估计x(l)下的最优函数可表示为
(19)
且Q(x,λ(l),η(l)；x(l))满足
G(x,λ(l),η(l))≤Q(x,λ(l),η(l);x(l))
l=1,2,…,L
(20)
根据优化最小化原理可知，通过
迭代优化x就转变成
为求解第l+1次x(l+1)，将Q(x,λ(l),η(l)；x(l))对x(l)求偏导，并令其值为0，可得x(l+1)的迭代公式：
n=1,2,…,N
(21)
式中，
且x(l)，η(l)，λ(l)分别为第l次迭代后得到的目标散射系数矢量、噪声方差和超参数。
在第2步中，固定散射系数矢量x和超参数λ，对噪声方差η进行优化，此时的目标函数表示为
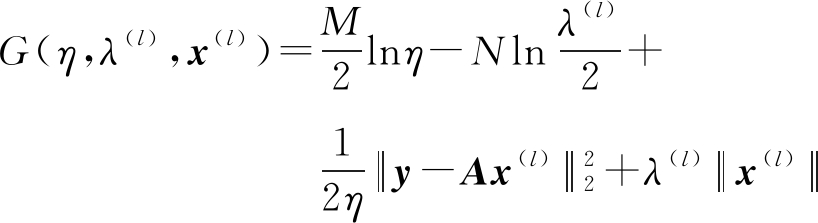
(22)
将G(η,λ(l),x(l))对η求偏导，并令其为0，可得
(23)
最后，固定噪声方差η和散射系数矢量x去估计超参数λ，此时的目标函数G(λ,x(l),η(l))表示为
G(λ,x(l),η(l))
(24)
计算G(λ,x(l),η(l))对λ的偏导数，并令其为0，可得
(25)
考虑到l1范数在零点处不可导，此处可以对向量范数进行平滑近似[12]，
(26)
此时的λ(l+1)可以改写为
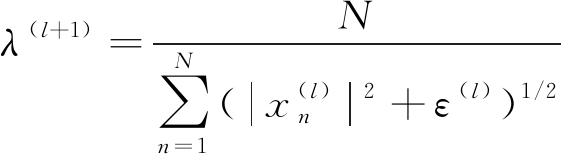
(27)
式中，ε表示平滑因子，其值采用逐渐递减参数的方法，即ε(l)=ε(l-1)/10，直到满足迭代终止条件为止。
由于本文算法的目标函数与文献[13]的代价函数类似，可知目标函数
随着迭代次数n增加而收敛，因此可以得到G(x(l+1),λ(l),η(l))<G(x(l),λ(l),η(l))，又因为η(l+1)和λ(l+1)分别是G(x(l+1),λ(l),η)和G(x(l+1),λ,η(l+1))最小化得到，则满足G(x(l+1),λ(l),η(l+1))<G(x(l+1),λ(l),η(l))和G(x(l+1),λ(l+1),η(l+1))<G(x(l+1),λ(l),η(l+1))，于是可以得到G(x(l+1),λ(l+1),η(l+1))<G(x(l),λ(l),η(l))，因此，代价函数G(x(l),λ(l),η(l))也是随着迭代次数n增加而收敛。
2.2 算法实现
本文算法在估计散射系数矢量x的步骤中，利用优化最小化框架避免了直接利用封闭形式求解带来的求逆运算，有效提高了算法运算效率。算法流程如表1所示。在构建字典矩阵、测量矩阵、测量值向量和初始参数后，进入式(21)、式(23)和式(27)的循环迭代过程，直到满足条件后退出循环。
表1 算法流程
算法名称:交替迭代最小化稀疏穿墙成像快速算法输入: 1.构造字典矩阵Ψ和测量矩阵Φ,生成感知矩阵A与测量值y; 2.初始化:x(0)=Ay,λ(0)=10-2,η(0)=1My-Ax(0)22,ε(0)=10-3设置收敛条件δ=10-6,迭代次数l=0;循环迭代: 1.根据式(21),利用噪声方差η(l)和超参数λ(l)更新估计散射系数矢量x(l+1); 2.根据式(23),利用散射系数矢量x(l+1)和超参数λ(l)更新估计噪声方差η(l+1); 3.根据式(27),利用散射系数矢量x(l+1)和噪声方差η(l+1)更新估计超参数λ(l+1); 4.如果x(l)-x(l-1)22x(l)22<δ,跳转到步骤5,否则返回步骤1,令l=l+1; 5.输出最大后验估计x^MAP,λ^MAP,η^MAP;输出:散射系数矢量x^MAP
3 仿真与实验结果与分析
3.1 仿真结果分析
利用电磁仿真软件GprMax仿真墙后目标成像得到仿真数据。前墙体长为3 m，墙体的厚度为0.2 m，相对介电常数为6.4，电导率为0.01 S/m。由31个收发共置的天线单元构成线性阵列均匀分布在横轴0.9～2.1 m、纵轴0.5 m处，阵元间隔0.04 m，线阵距离墙体0.5 m。发射脉冲宽度为1 ns高斯脉冲信号，GprMax的网格单元为0.01 m，时间步长为23 ps，采样时间窗为25 ns，仿真中成像区域的方位向与距离向网格大小均设置为0.05 m，为模拟真实情况，仿真中引入高斯白噪声。
图1给出了GprMax仿真模型，为模拟不同形态的墙后目标成像场景，设置混合目标并存的仿真场景，图1(a)为两个目标仿真示意图，图中扩展目标长宽分别为0.3 m和0.2 m，且两个目标彼此之间以及与前墙体的距离分别为0.6 m和1.3 m，图1(b)为点目标与扩展目标混合仿真示意图，扩展目标尺寸和距离与图1(a)一致，点目标分别位于(1.05,2)和(1.35,2.25)处。
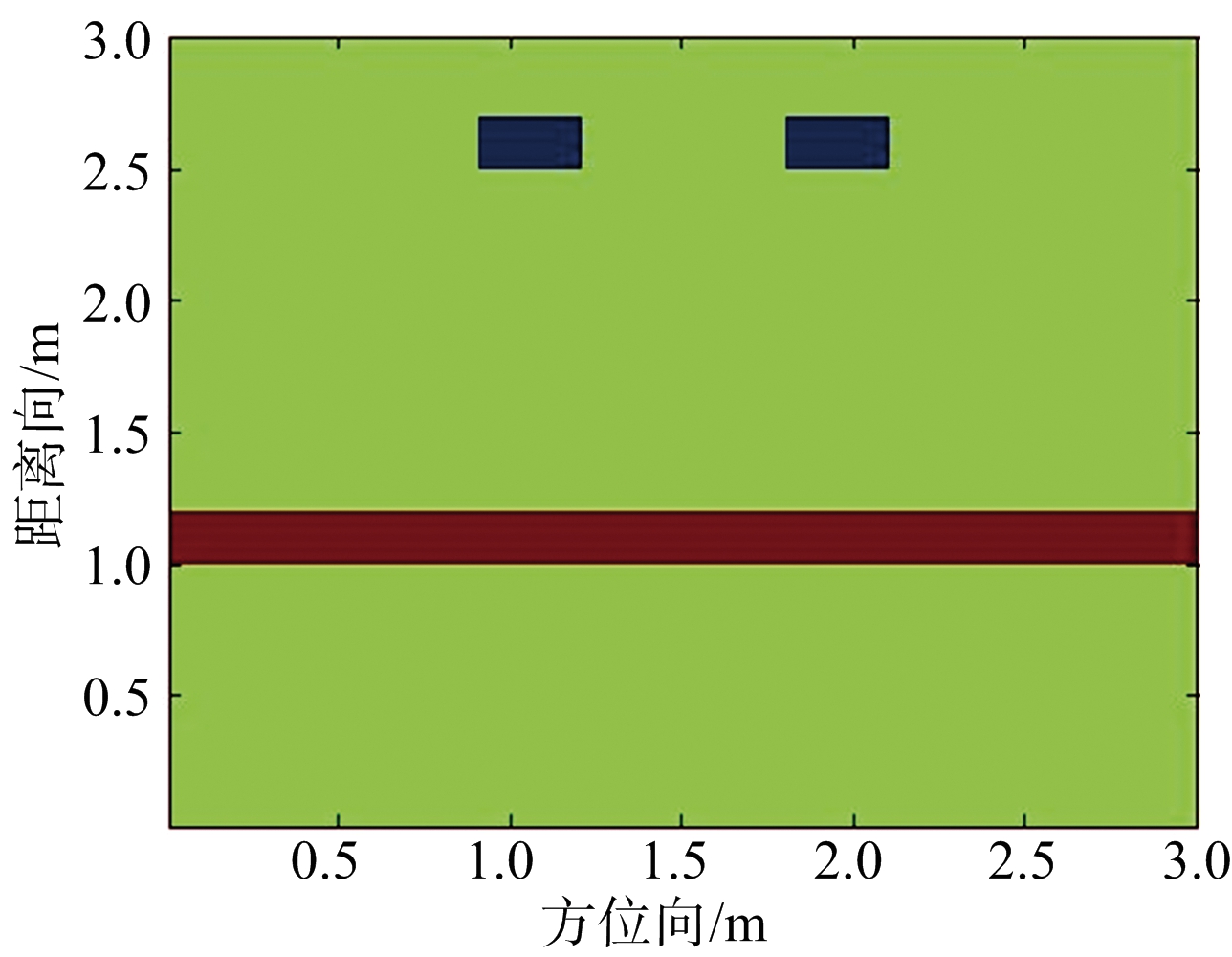
(a) 两目标
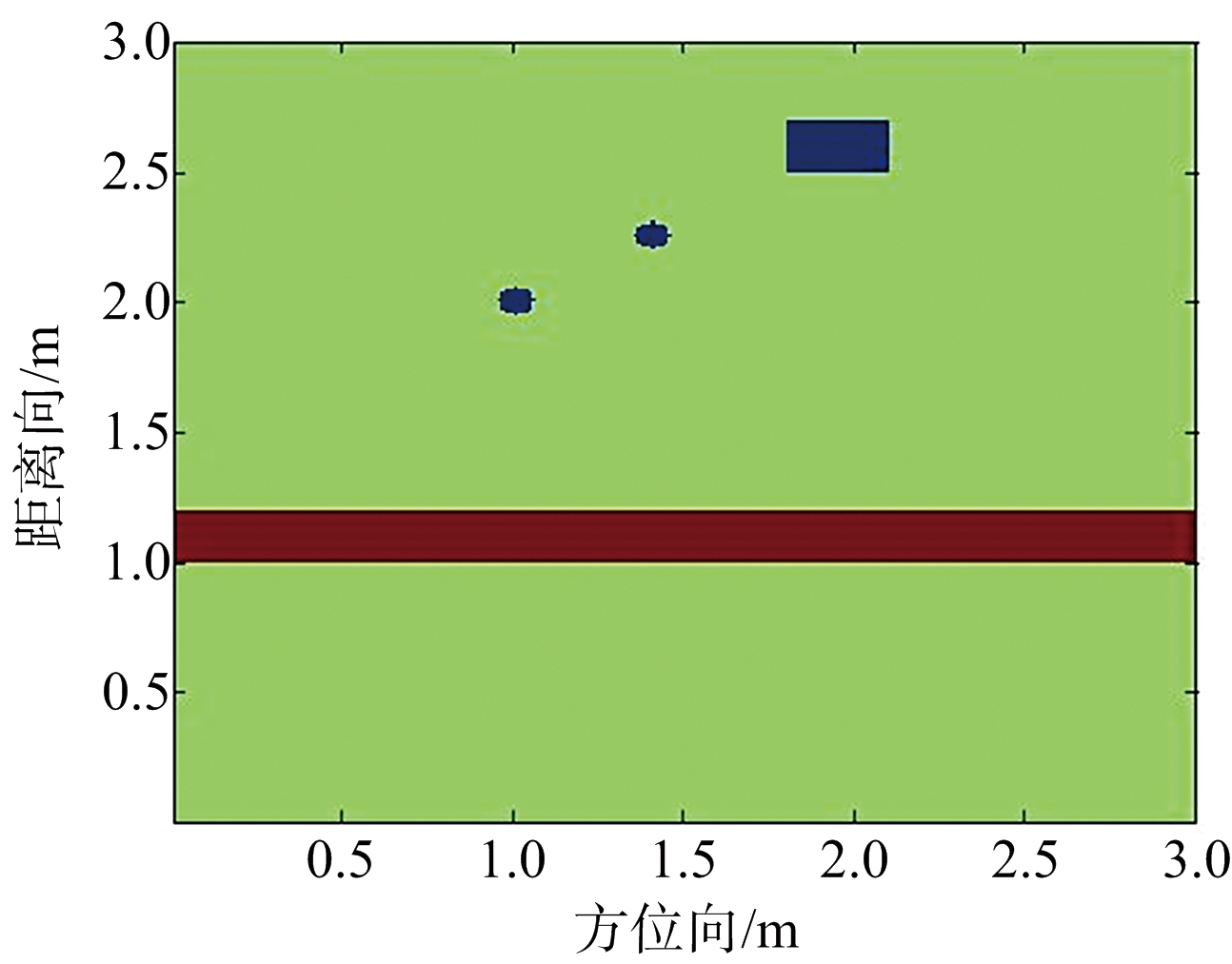
(b) 混合目标
图1 GprMax仿真模型
由于采用稀疏成像，本文选择全部31个天线单元，每个接收天线的数据随机选择200个采样点。图2和图3分别给出了两目标体和混合目标体的成像结果，图中的虚线框表示目标真实位置。图2(a)和图3(a)的BP成像方法，可以看出BP算法得到的旁瓣杂波较多，目标之间杂波干扰导致分辨率急剧下降，并且在目标真实位置的后面产生了严重的虚假像，难以识别出目标位置；图2(b)和图3(b)采用文献[4]的成像方法，成像结果相对BP算法分辨率提高，但仍然无法消除目标之间旁瓣影响，目标体之间轮廓特性不明显；而图2(c)和图3(c)是采用本文方法成像结果，相比较前两种成像结果，本文方法得到的扩展目标轮廓连贯，点目标成像聚焦性较高，而且目标与目标之间的旁瓣影响被抑制，图像较为清晰，同时本文的优化方法提高了计算速度。
(a) BP成像
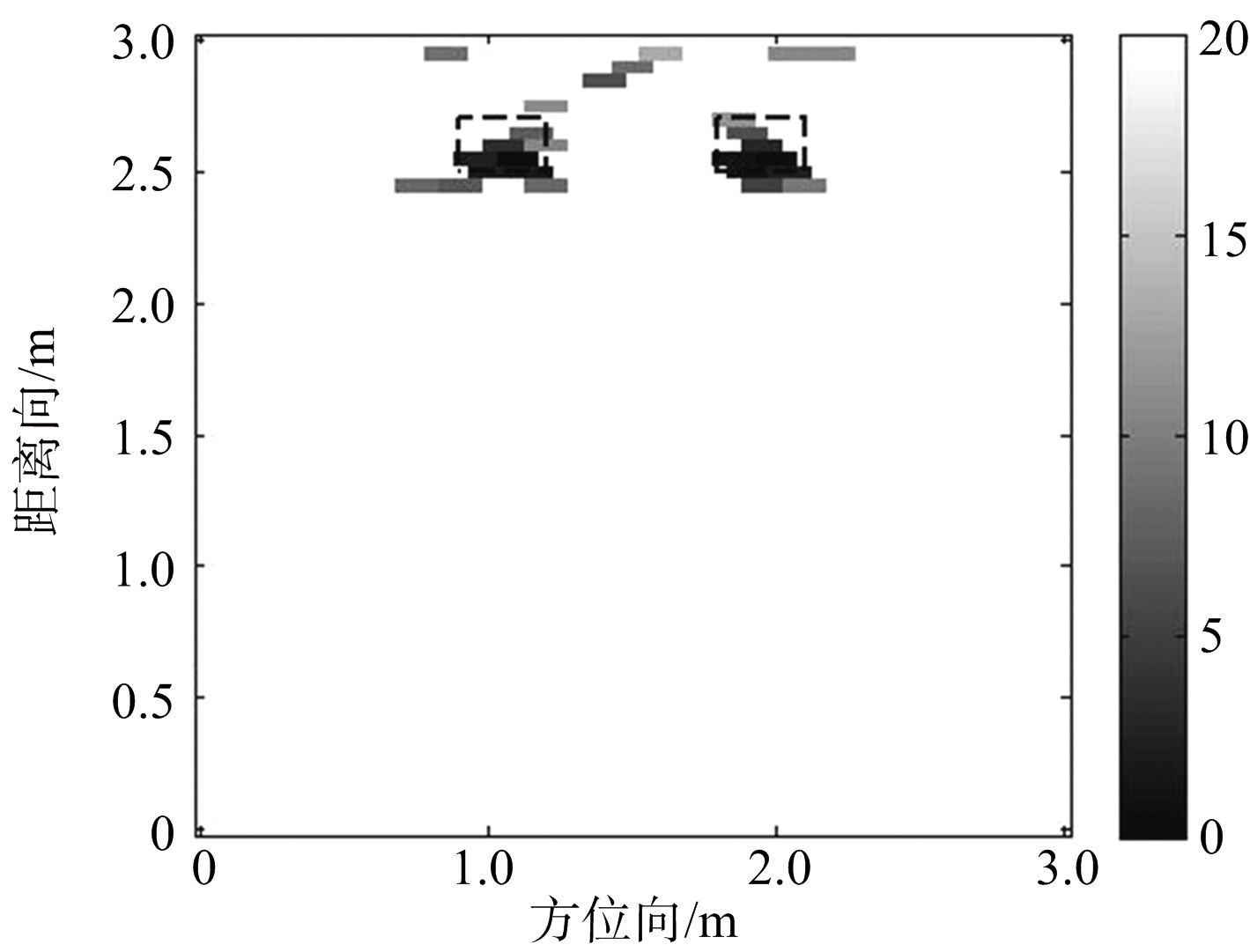
(b) 文献[4]方法
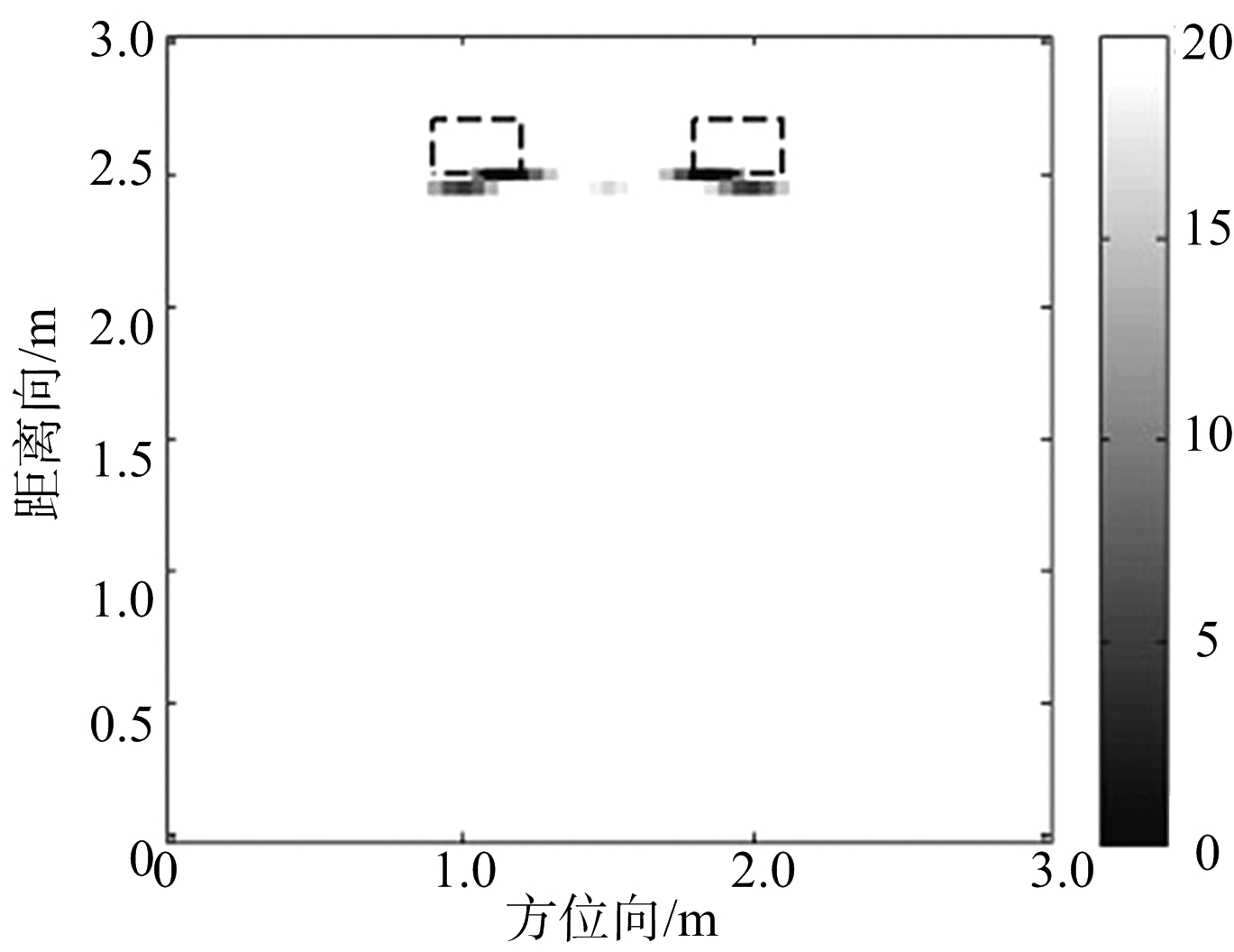
(c) 本文方法
图2 两目标成像结果
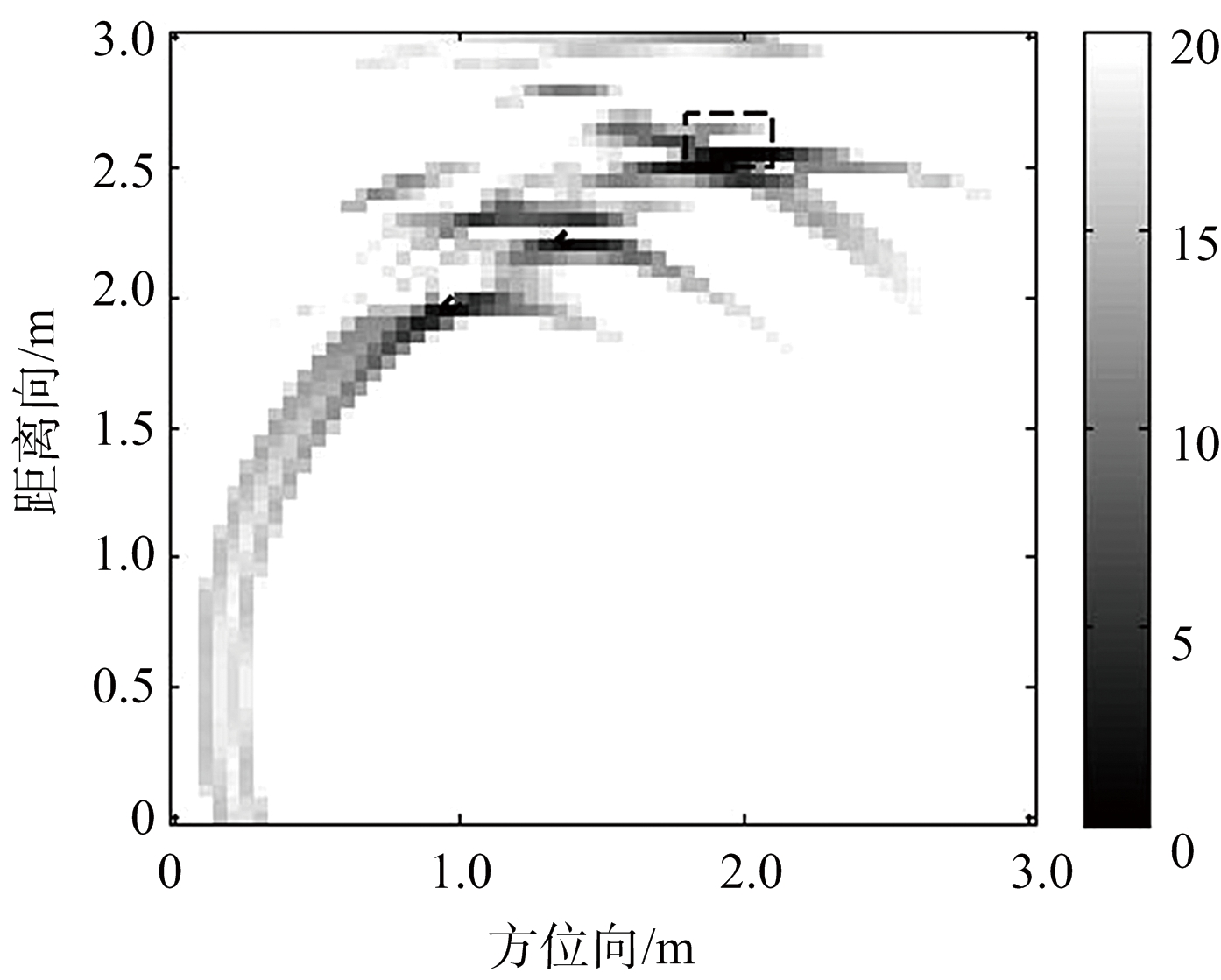
(a) BP成像
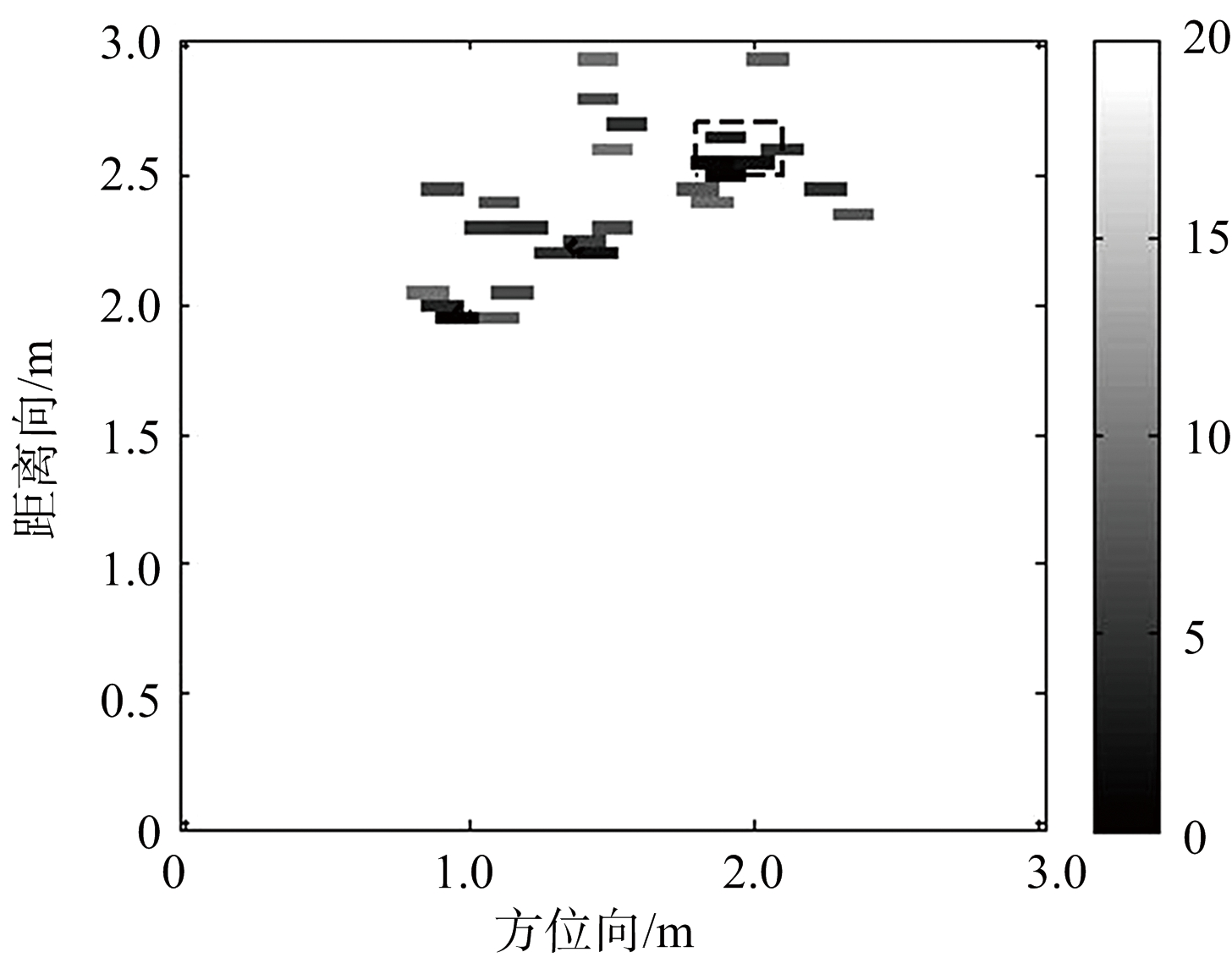
(b) 文献[4]方法
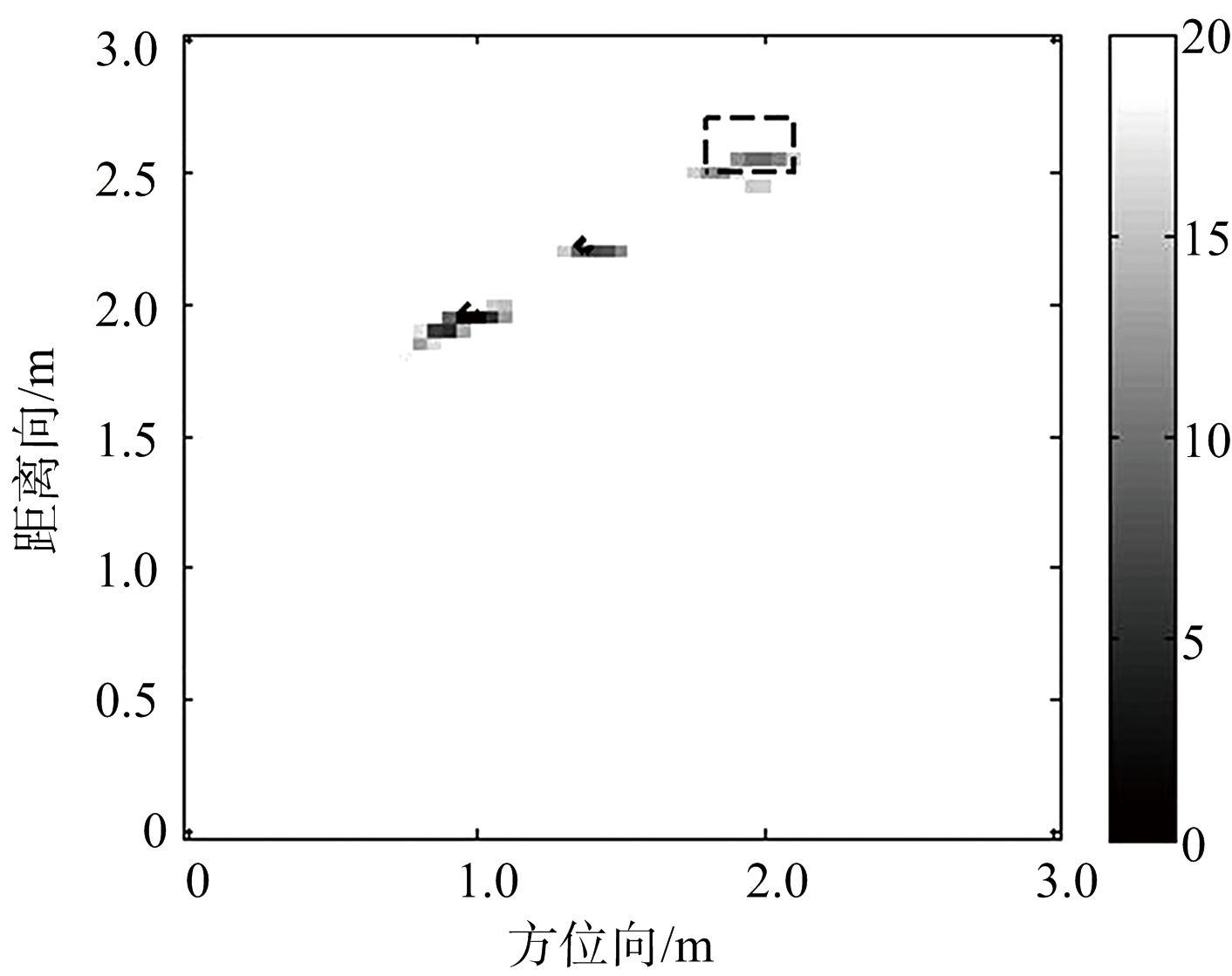
(c) 本文方法
图3 混合目标成像结果
为了对比算法的成像性能，图4给出了两种成像场景下目标杂波比(Target-to-Clutter Ratio, TCR)与信噪比之间的关系图，从图4(a)可以看出，随着信噪比提升TCR数值也呈现上升趋势，且在相同信噪比下，本文算法的TCR值都高于文献[4]算法和BP算法，说明本文得到的目标像聚焦性能优于这两种算法；考虑到图4(b)中成像场景是点目标与扩展目标共存，成像环境较为复杂，因而成像结果杂波较多，TCR数值相较于纯扩展目标场景要小，但本文算法的目标杂波比值仍略高于两种对比算法成像结果，进一步说明本文方法在复杂环境中也能得到较好的聚焦性能。
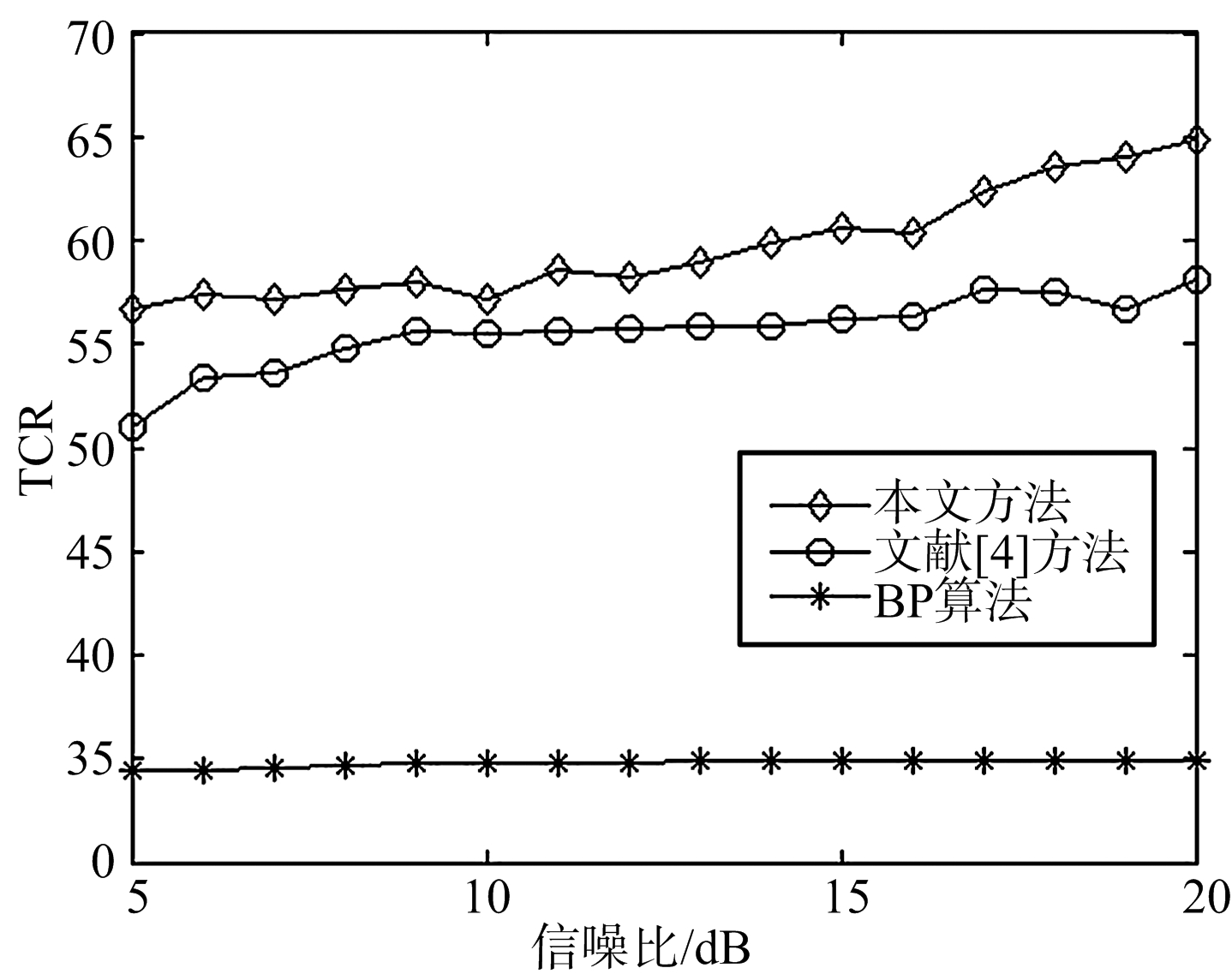
(a) 两目标成像
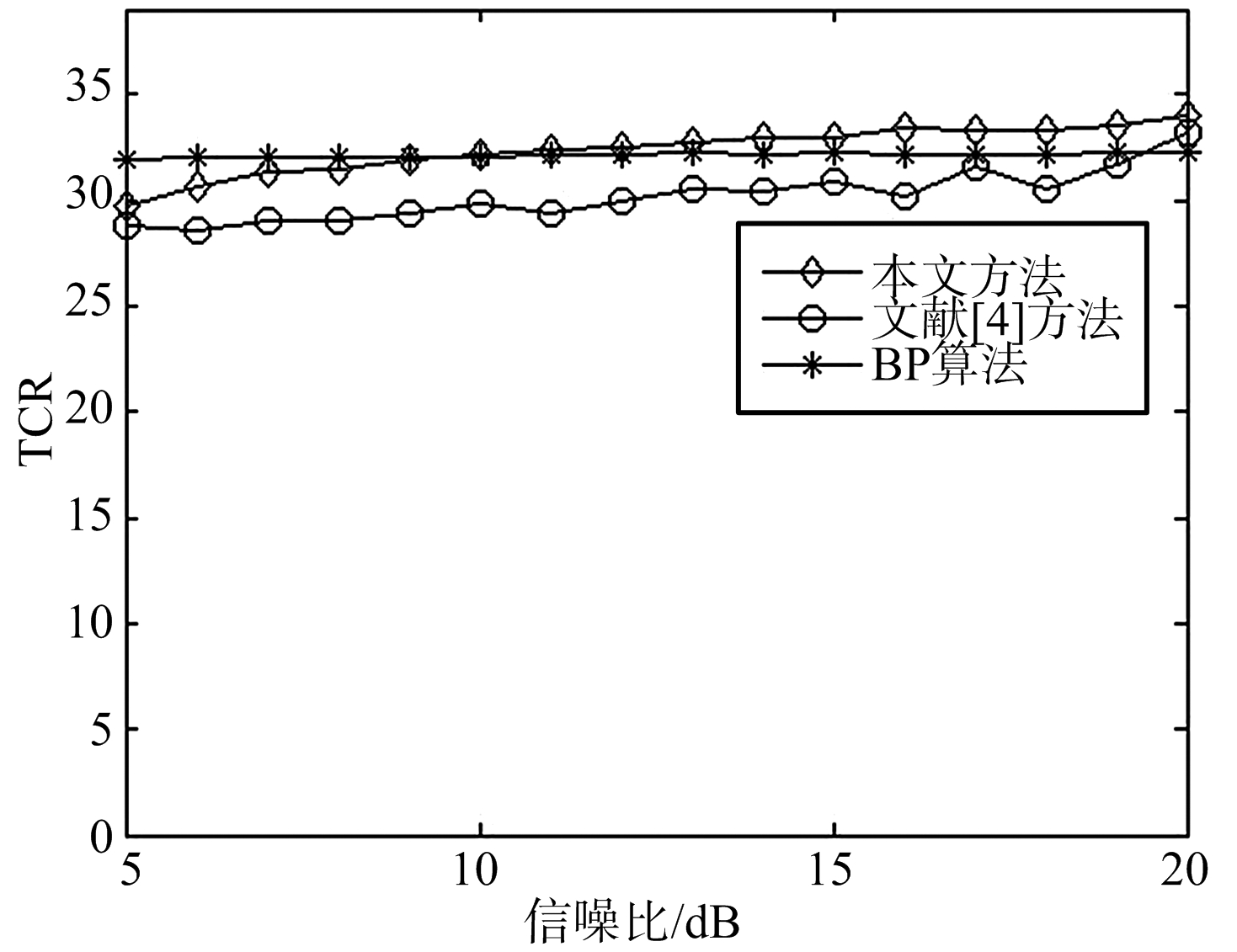
(b) 混合目标成像
图4 不同成像场景性能对比
为了看出本文算法在成像效率上的改进，将本文算法与对比算法进行对比，需要说明的是，由于本文算法进行的是稀疏信号恢复进而成像，所以这里仅是对比稀疏算法之间的效率问题，因此，可以根据稀疏成像所需数据量来对比程序运行时间，利用程序运行时间(Program Running Time, PRT)来对表征各算法效率，其值越小效率越高。表2分别给出了两种成像场景下的数据量与PRT之间的关系，从表中可以看出，在数据量比例相同时，本文方法回复信号所需时间远远小于文献[4]的成像结果，说明本文算法有效改进了成像效率。
表2 两种成像场景下的数据量与PRT之间的关系
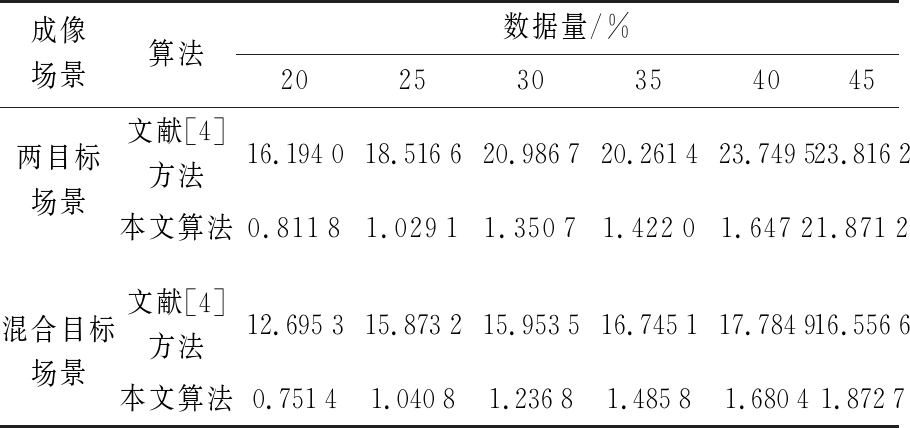
成像场景算法数据量/%202530354045两目标场景文献[4]方法16.194018.516620.986720.261423.749523.8162本文算法0.81181.02911.35071.42201.64721.8712混合目标场景文献[4]方法12.695315.873215.953516.745117.784916.5566本文算法0.75141.04081.23681.48581.68041.8727
3.2 实验结果分析
使用美国GSSI公司的探地雷达SIR-20搭建实验场景，实验墙体为实心砖墙，厚度为0.2 m，相对介电常数为6.4，天线距离墙体0.2 m，选用1 GHz的喇叭天线架高1.2 m，从-0.6 m到0.6 m以间距0.04 m水平移动扫描距前墙体1.8 m处的柜子，柜子长宽分别是0.9 m和0.3 m，共计测量31道，每道采样点数为1 024。将SIR-20系统收集的回波数据经取平均、去噪、杂波相消和自动增益控制等信号处理得到墙体回波，使用全部31个天线单元位置，每个接收天线随机选择200个采样点进行成像。
图5给出了实验场景的示意图，图6给出了BP算法、文献[4]方法以及本文方法的实验场景数据的成像结果，虚线框表示扩展目标的真实位置。可以看出，实验数据处理中BP方法成像图像旁瓣杂波较多，目标边缘轮廓无法识别，整体图像分辨率较低，聚焦性较差；由于实测数据的信噪比不高，文献[4]算法方法对此较为敏感，直接导致目标成像结果散焦严重，几乎无法分辨目标像。相比之下，本文方法由于在稀疏信号贝叶斯建模时充分利用分层模型的特点，使信号进一步稀疏，因此目标图像的边缘轮廓较为明显，图像旁瓣得到有效抑制，图像分辨率较高，同时该算法还结合MM优化框架，以较快速度形成成像结果。
(a) 实验设备
(b) 实验场景
图5 成像场景
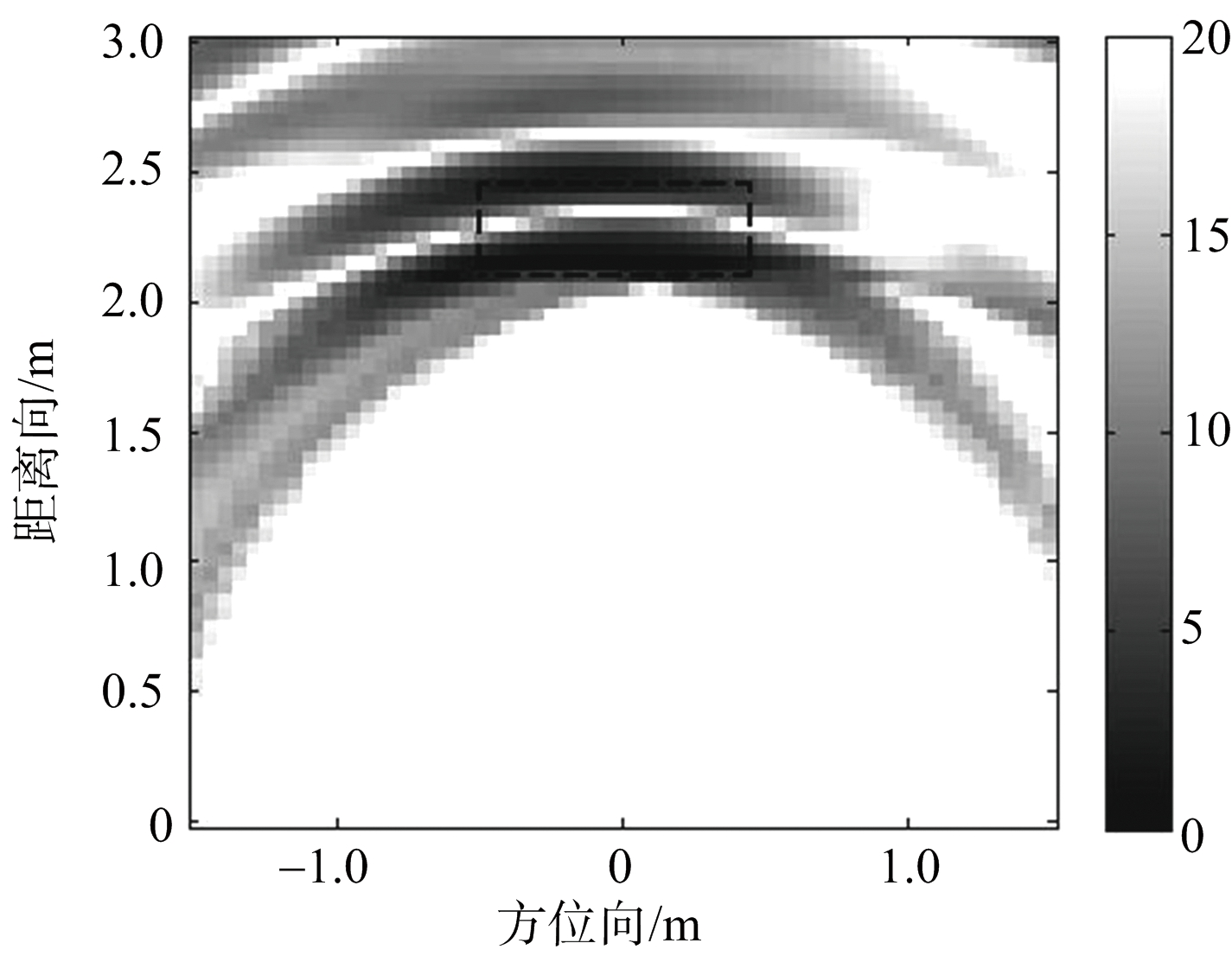
(a) BP成像
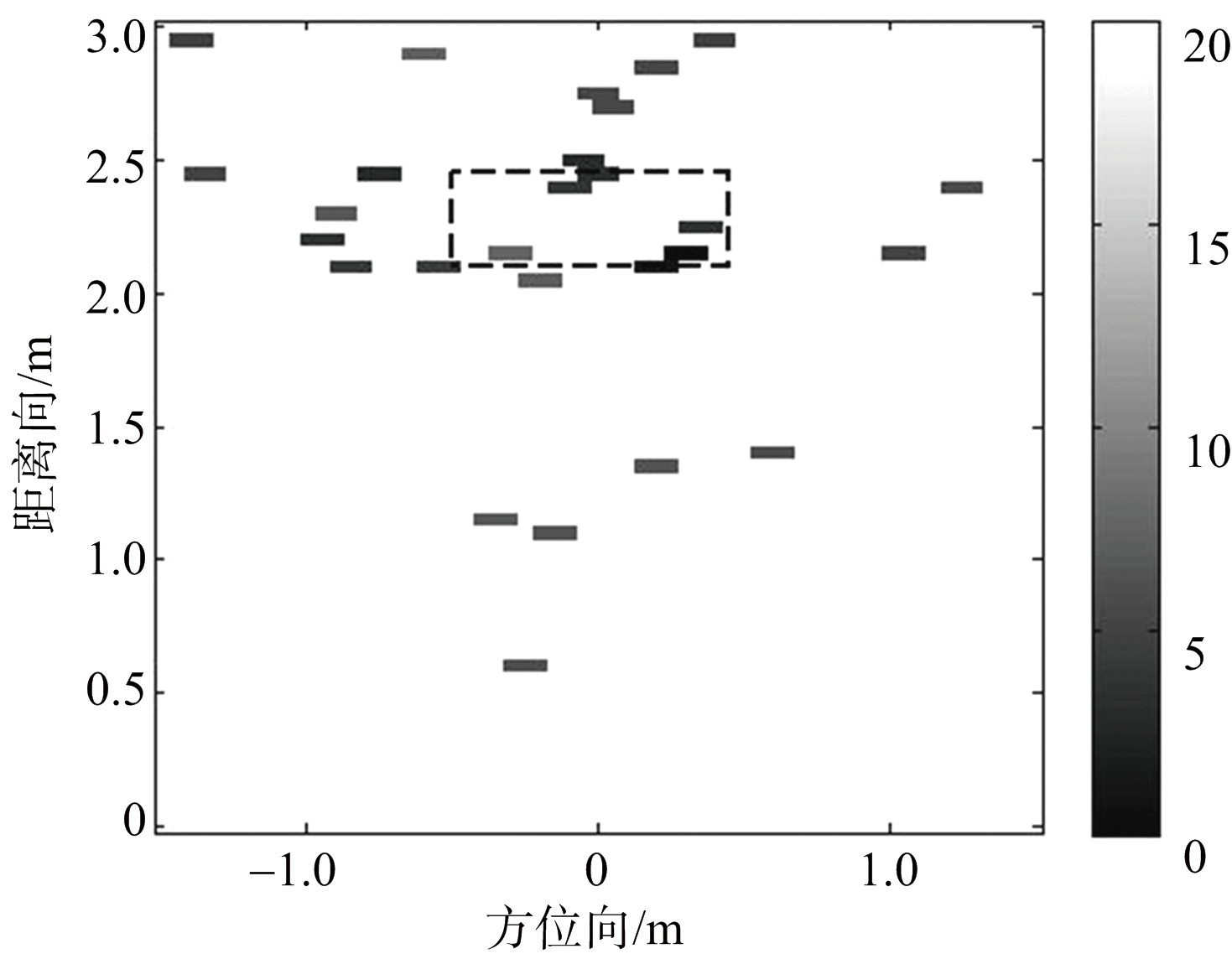
(b) 文献[4]方法
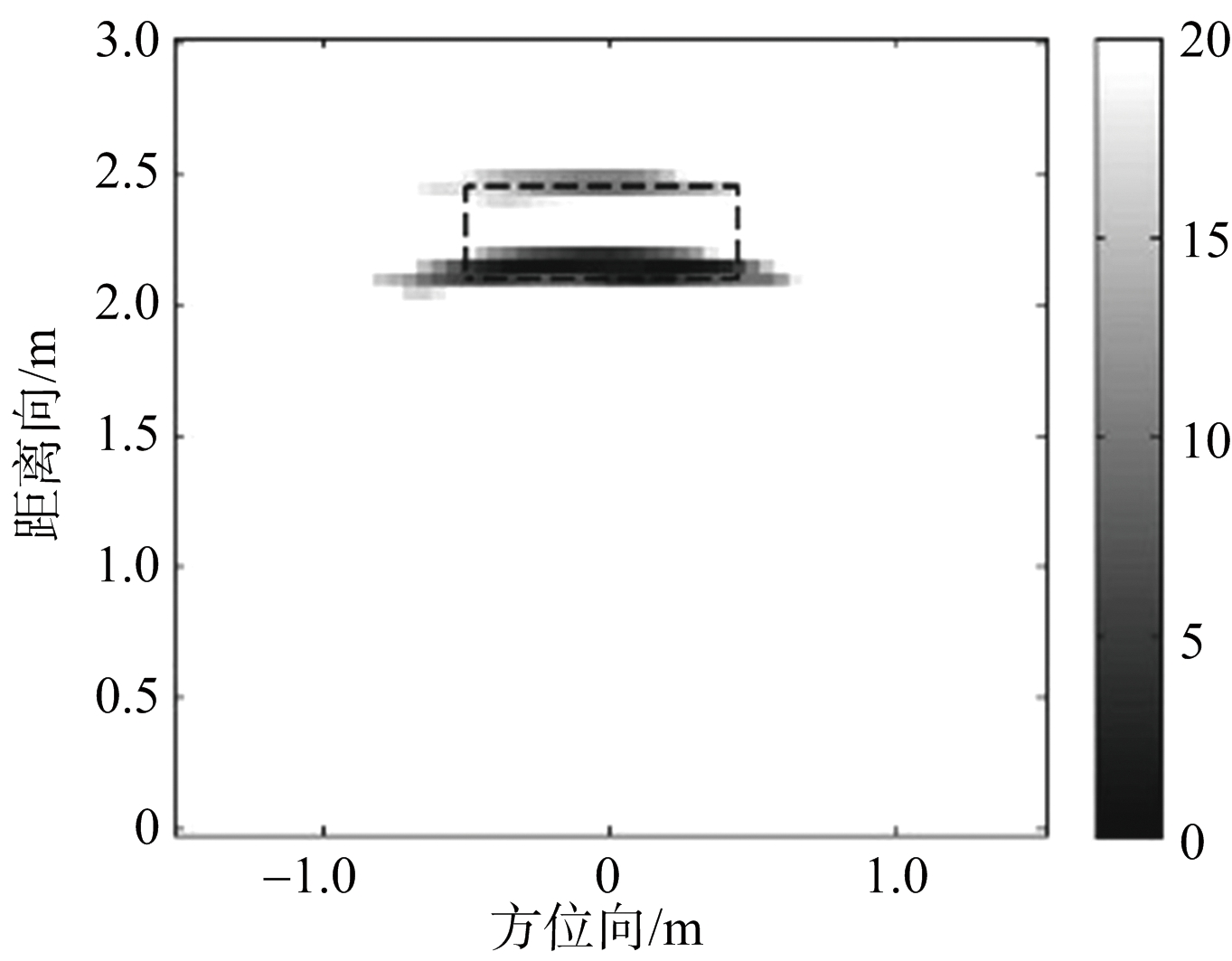
(c) 本文方法
图6 实测数据成像结果
4 结束语
本文提出一种基于交替迭代框架的墙后目标成像算法，利用稀疏信号贝叶斯模型的最大后验估计准则得到包含参数与目标散射矢量的目标函数，然后在优化最小化(MM)框架下利用目标函数对应的优化函数对目标散射系数、噪声功率和超参数进行交替迭代求解，贝叶斯分层模型保证了成像结果的分辨率，而基于优化最小化准则的交替迭代方式有效改善了该方法的成像效率。仿真数据和实验数据的处理结果表明，扩展目标轮廓边缘清晰，点目标成像聚焦度明显，同时成像速度得以较大提高。在下一步的工作中，将继续对该方法进行完善使其能应用到更复杂的场景中。
[1] ZHANG Peng, FEI Peng,WEN Xin, et al. A Novel Through-the-Wall Imaging Algorithm C Combined with Phase Shift Migration and NUFFT[J].Chinese Journal of Electronics,2017,26(5):1096-1100.
[2] MENG Q Y,ZHU A J,QI X K, et al. Two-Dimensional Through-Wall Imaging Based on Nonlinear Inversion Algorithms[C]∥International Applied Computational Electromagnetics Society Symposium (ACES),Suzhou: ACES, 2017:1-6.
[3] TANG V H, BOUZERDO A,PHUNG S L.Multipolarization Through-Wall Radar Imaging Using Low-Rank and Jointly-Sparse Representations[J].IEEE Trans on Image Processing,2018, 27(4):1763-1776.
[4] AMIN M G,AHMAD F.Compressive Sensing for Through-the-Wall Radar Imaging[J]. Journal of Electronic Imaging,2013,22(3):901-922.
[5] LAGUNAS E,AMIN M G,AHMAD F, et al.Determining Building Interior Structures Using Compressive Sensing[J].Journal of Electronic Imaging, 2013, 22(2):1-15.
[6] WU Q S,ZHANG Y D,AHMAD F,et al.Compressive-Sensing-Based High-Resolution Polarimetric Through-the-Wall Radar Imaging Exploiting Target Characteristics [J].IEEE Antennas and Wireless Propagation Letters,2014,14(1):1043-1047.
[7] 晋良念,申文婷,钱玉彬,等.组合字典下超宽带穿墙雷达自适应稀疏成像方法[J].电子与信息学报, 2016, 38(5):1047-1054.
[8] BROWNE K E,BURKHOLDER R J,VOLAKIS J L,et al. Fast Optimization of Through-Wall Radar Images via the Method of Lagrange Multipliers[J].IEEE Trans on Antennas and Propagation, 2013,61(1):320-328.
[9] GUO Shisheng, CUI Guolong, KONG Lingjiang, et al. An Imaging Dictionary Based Multipath Suppression Algorithm for Through-Wall Radar Imaging[J]. IEEE Trans on Aerospace and Electronic Systems, 2018, 54(1): 269-283.
[10] 张燕,晋良念.结合TV约束的穿墙雷达扩展目标成像方法[J].雷达科学与技术,2017,15(3):229-235.
ZHANG Yan,JIN Liangnian.Through-the-Wall Radar Extended Target Imaging with TV Constraints[J].Radar Science and Technology,2017,15(3):229-235.(in Chinese)
[11] CHEN Yijun, ZHANG Qun, LUO Ying, et al. Measurement Matrix Optimization for ISAR Sparse Imaging Based on Genetic Algorithm[J].IEEE Geoscience and Remote Sensing Letters, 2016, 13(12):1875-1879.
[12] 冯俊杰,张弓.参数迭代最小化稀疏信号重构ISAR成像算法[J].计算机工程,2017,44(10):228-234.
[13] OGWORONJO H C,ANDERSON J M M,NGUYEN L H.An Iterative Parameter-Free MAP Algorithm with an Application to Forward Looking GPR Imaging[J].IEEE Trans on Geoscience and Remote Sensing, 2017,55(3):1573-1586.
[14] NDOYE M, ANDERSON J M M,GREENE D J.An MM-Based Algorithm for l1-Regularized Least-Squares Estimation with an Application to Ground Penetrating Radar Image Reconstruction[J].IEEE Trans on Image Processing,2016,25(5):2206-2221.
[15] LEEUW J D, LANGE K.Sharp Quadratic Majorization in One Dimension[J].Computational Statistics and Data Analysis, 2009,53(7):2471-2484.
