0 引 言
先敌发现是对敌实施攻守行动的首要环节，也是信息化战争的关键阶段之一。雷达作为战场感知的主传感器，实现雷达的快速搜索是先敌发现的必要条件之一；在现代中远程空战中，预警机的引导与指挥发挥着至关重要的作用，在预警机提供的先验信息下，战斗机能够实现快速准确的发现目标和打击目标；现代战机所装备的有源相控阵雷达具有波束捷变的特点，在空域快速搜索方面潜力巨大。因此，如何有效利用预警机的先验信息来实现相控阵雷达的最优搜索是一个值得研究的方向。
关于相控阵雷达搜索问题，学术界已有较多的研究成果。文献[1]对搜跟一体化情况下的搜索参数进行研究；文献[2]对搜索驻留时间和帧周期进行研究；文献[3-5]对搜索数据率进行了优化；文献[6-9]各自针对不同的搜索工作参数，研究了优化算法。
现有的最优搜索模型主要考虑雷达时间资源的约束，较少从实际作战需求的角度进行约束条件的分析。对于雷达探测威力区内已有目标存在的情况，空域的初始搜索顺序优化要比搜索数据率的优化更为重要，然而，现有搜索模型较少考虑这方面问题；对于最优搜索过程中提出的多目标优化问题，现有文献大都采用遗传算法、粒子群算法等智能算法来进行模型的求解，虽然，这些算法能够获得有效解，但是，搜索速度较慢，相比于在实际作战过程中需要实时在线优化搜索参数的问题来说，上述算法更适用于离线优化问题，工程应用价值不高。
本文在现有研究的基础上，从预警机引导战斗机雷达搜索的角度出发，建立了一种更为全面、更符合实际作战需求的雷达最优搜索模型，并提出了一种适用于实际工程应用的实时求解算法。
1 基于预警机引导信息的雷达搜索问题描述
在实际作战过程中，预警机引导战斗机到达作战空域，为了不提前暴露，战斗机会在预警机的指引下确认敌机进入己方探测威力区后再打开雷达进行小范围搜索，在打开雷达后，也有可能会有新的目标进入雷达的探测威力区，此时，预警机同样可以为战斗机雷达提供新目标的大概方位以及数量。
在不考虑射频隐身性能的前提下，根据雷达搜索任务需求[6]，本文采用以下搜索优化准则：1)目标累积发现概率最大准则；2)目标平均发现时间最小准则。
针对预警机引导战斗机雷达搜索过程，雷达的搜索目标可以分为以下两类：1)打开雷达时，探测威力区内已存在的目标(现有目标)；2)后续进入雷达探测威力区内的目标(后续目标)，本文假设后续目标均从雷达扇形搜索区域的最大探测距离边界进入。
2 最优搜索模型的建立
2.1 模型描述
根据预警机的引导信息将搜索的扇形空域划分成如图1所示的M×N个子空域，即M行、N列，其中，行以距离为单位进行划分，列以角度(这里的角度具体指方位角)为单位进行划分。图1中空域Λij表示第j行、第i列子空域。
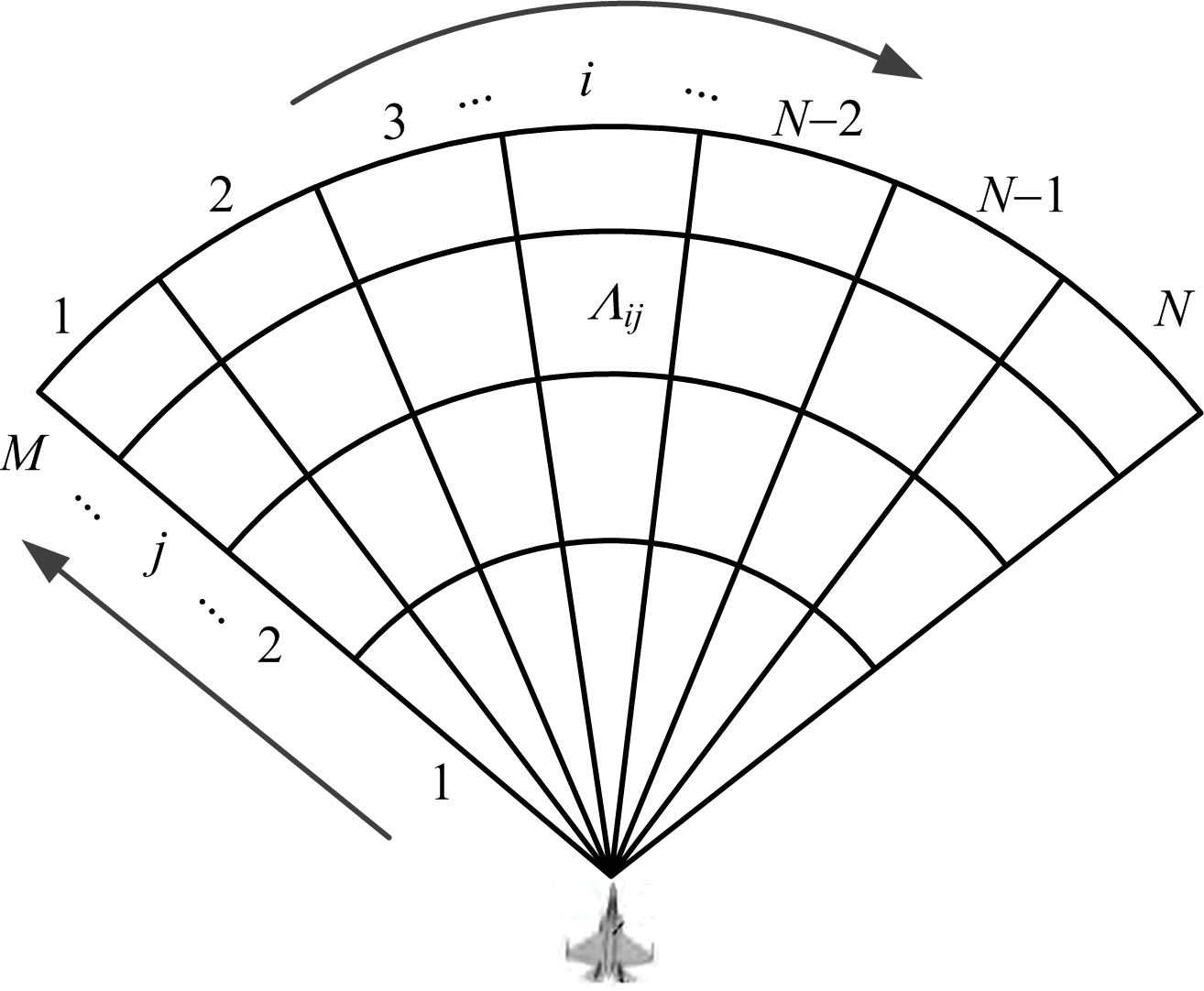
图1 子空域划分示意图
2.2 优化目标分析
根据本文采用的两个优化准则分别建立两个性能评价函数，即目标累积发现概率和目标平均发现时间。
1) 目标累积发现概率
由文献[5]可知，目标累积发现概率为
(1)
式中，pij为雷达在子空域Λij的平均探测概率，nij为更新时间Tg内子空域Λij的照射次数，ωij为各子空域的权重。
2) 目标平均发现时间
由文献[5]可知，目标被发现的平均时间为
tij=
t0i+Tsi·(1/pij-1)
(2)
式中，Tsi为第i列子空域的搜索间隔，t0i为第i列子空域中目标从出现到紧接一帧搜索时刻的平均时间，k为目标被发现前的等待周期。
考虑到各子空域的权重ωij后，整个空域内目标被发现的平均时间为
T
(3)
对于现有目标，第i列子空域中目标从出现到紧接一帧搜索时刻的平均时间为t0i即为该子空域的初始搜索时间，与子空域的初始搜索顺序有关，假设第i列子空域的初始搜索顺序为μi，则t0i的计算方法如下：
(4)
式中，Tk为搜索第k列子空域的时间。
对于后续目标，t0i则与目标出现的随机过程有关，假设进入子空域的目标流服从泊松流，则t0i的计算方法如下[5]：
(5)
2.3 约束条件分析
1) 雷达搜索时间约束分析
约束条件为搜索时间占雷达总时间资源的比例per(0≤per≤1)，因此，建立约束条件如下：
(6)
式中，Λ为所有列向子空域的集合，Λ=[1,2,…,N]，Ti为搜索第i列子空域的时间，ni为更新时间Tg内第i列子空域的照射次数，ni=Tg/Tsi。
2) 照射次数ni约束分析
显而易见，每个子空域在更新时间Tg内的照射次数ni需满足以下约束条件：
0<ni<Tg/Ti,i∈Λ
(7)
3) 目标最晚发现时间约束分析
在某些情况下，雷达在对目标进行搜索时对重点区域的目标会提出最晚发现时间的要求，因此，建立约束条件如下：
(8)
式中，ΛNimp为重点子空域的集合，Nimp为重点子空域的个数，即ΛNimp的元素个数；
为第i列子空域目标的最晚发现时间；
为第i列子空域可容忍目标最晚发现时间的时长。
第i列子空域现有目标的最晚发现时间为t0i。
为了建立第i列子空域后续目标最晚发现时间的数学模型，可以假设当目标累积发现概率超过一定阈值P0后一定会被检测到。本文假设后续目标均从雷达扇形搜索区域的最大探测距离边界进入，并且在搜索更新时间Tg内目标还未进入其他子空域，因此，第i列子空域后续目标在等待k个周期后被发现的概率为
Pki=piM·(1-piM)k
(9)
式中，piM为第M行、第i列子空域的平均探测概率。
根据假设：Pki≥P0时目标一定会被检测到，可计算出目标最晚在等待Ki个周期后一定会被发现，因此，第i列子空域后续目标最晚发现时间为
(10)
将式(10)代入式(8)可得
(11)
为了后文表达方便，将约束式表示成
的形式，其中
和
满足以下条件：
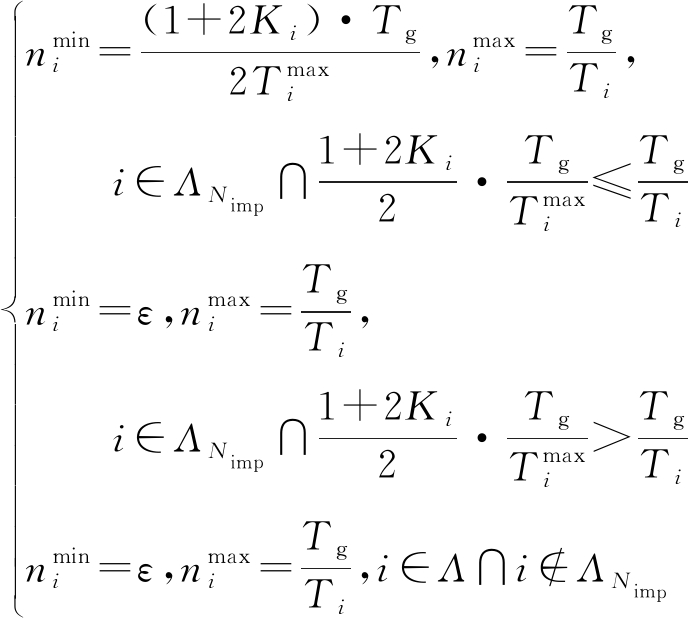
(12)
式中，ε∈R+，且ε→0，即ε为趋于0的正实数。
2.4 通用多目标优化模型建立
根据2.2节和2.3节建立通用优化模型：
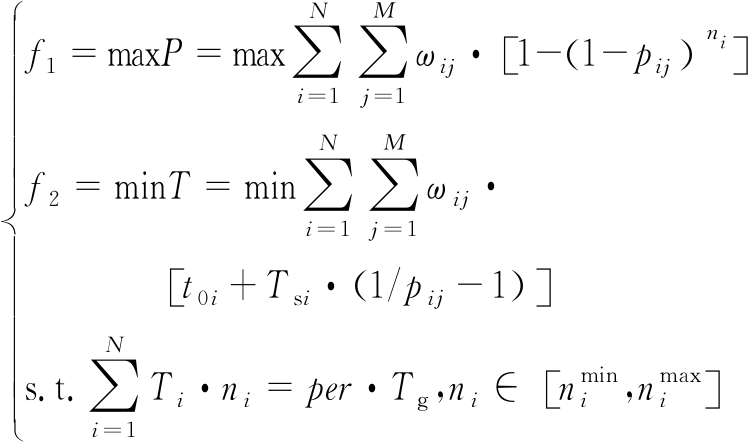
(13)
2.5 两步优化模型建立
对于现有目标来说，上述建立的通用优化模型的优化参数包括子空域的初始搜索时间T0以及子空域的搜索数据率Tsi；对于后续目标来说，优化参数只包括子空域的搜索数据率Tsi。对于两类目标即对应的两个搜索阶段无法同时进行参数的优化。为了解决上述问题，本文采用一种两步优化的方法。
1) 一步优化
在搜索的初始阶段，对于雷达探测威力区内现有目标的发现时间，子空域的初始搜索时间远比搜索数据率重要。一般在预警机的指引之下，雷达会在比较有把握的区域开机，即此时的探测概率较高。从数学角度分析，此时优化模型式(13)中的优化目标f1意义不大；另一方面，探测概率较高时，假设雷达可以一次探测到目标，此时，可以不用考虑数据率的影响。因此，可以将优化模型式(13)简化为
(14)
由于上述优化目标只对子空域的初始搜索顺序进行优化，因此，不存在约束条件。
2) 二步优化
在搜索的后续阶段，基于目标流服从泊松流、后续目标均从雷达扇形搜索区域的最大探测距离边界进入、在搜索更新时间Tg内目标还未进入其他子空域的假设，将式(5)代入式(13)后可得优化模型如下：
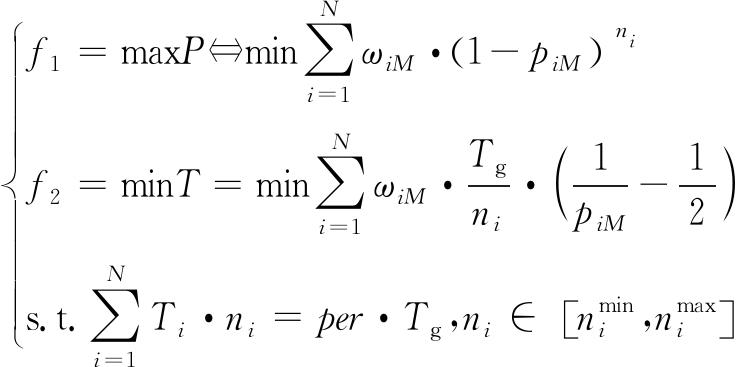
(15)
式中，ωiM为第M行、第i列子空域的权重。
3 优化问题求解
本文主要对二步优化的求解方法进行研究。
为了使得分析过程更加简洁，将优化模型式(15)进行如下变形：
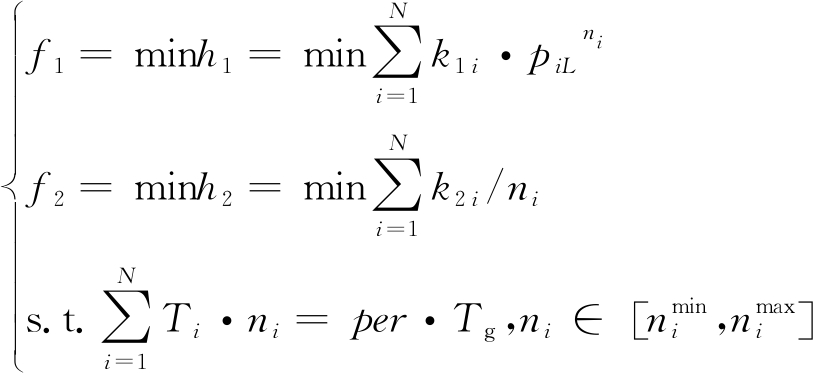
(16)
式中，k1i=ωiM，k2i=ωiM·(1/piM-0.5)·Tg，piL=1-piM。
式(16)属于多目标优化问题，本文通过归一化加权的方式将多目标优化问题转换成定义域为
并且带有1个等式约束条件的单目标凸优化问题：
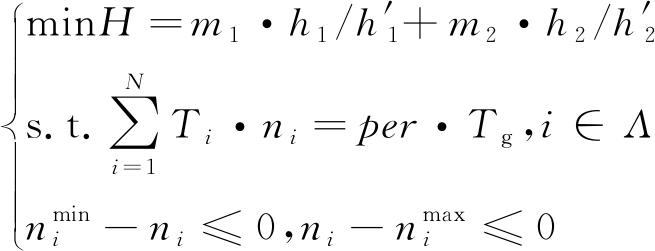
(17)
式中：h′1和h′2分别为优化函数h1和h2的归一化参数；m1和m2分别为两个优化目标的权值系数，m1+m2=1，可以通过调节m1和m2的大小来分配优化目标的重要程度。
3.1 严格凸函数证明
为了说明采用凸优化手段解决如式(17)所示优化模型的合理性，首先需要证明优化函数在定义域
是严格凸函数。
优化函数H在定义域是严格凸函数的证明方法如下：
当优化函数h1和h2在解空间上二阶连续可微时，h1和h2为严格凸函数的充要条件是在每一点处的Hessian矩阵都是正定的[10]，即
0,i∈[1,2]。
1) 优化函数h1和h2在解空间上二阶连续可微证明如下：
因为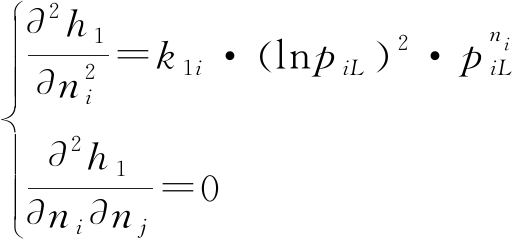
所以h1在解空间上二阶连续可微。又因为
所以h2在解空间上二阶连续可微。
2) 优化函数h1和h2在定义域上每一点的Hessian矩阵都是正定的证明如下：
优化函数h1的Hessian矩阵如下：
(18)
式中，β1i=k1i·(lnp2i)2。
因此，
的第k阶顺序主子式为
(19)
式中，piL∈(0,1]，β1i>0。
由式(19)可知，的各阶顺序主子式均大于0，由此可证，h1在每一点处的Hessian矩阵都是正定的。
同理，优化函数h2的Hessian矩阵如下：
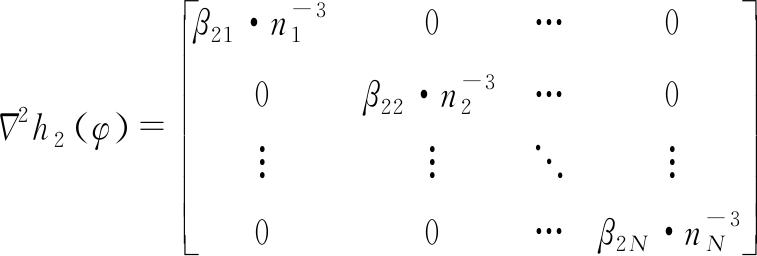
(20)
式中，β2i=2k2i。
的第k阶顺序主子式为
(21)
式中，
由式(21)可知，的各阶顺序主子式在其定义域上均大于0，由此可证，h2在定义域上的每一点处的
都是正定的。
由上述证明可知，在定义域上优化函数h1和h2是严格凸函数，优化目标H是h1和h2线性组合，由凸函数的性质可知优化函数H同样为严格凸函数，因此，在定义域上采用凸优化的手段进行求解是合理的。
3.2 拉格朗日结合障碍法求解
由于优化函数H在上为严格凸函数，所以，函数在定义域上的极小值点是唯一的，存在唯一的最优解，本文采用拉格朗日结合障碍法进行优化函数的求解。
拉格朗日结合障碍法求解的基本思路是：1)采用经典的拉格朗日乘数法对优化问题求解，如果求出的解n*在定义域
上，则n*是式(17)的唯一最优解；2)如果求出的解n*不满足定义域的约束，则采用障碍法进行带不等式约束的凸优化问题的求解。
本文没有直接采用障碍法求解是因为这种方法无法得到优化函数的最优解，只能得到与最优解相差不大于2N/t的次优解[11]，其中t>0是确定近似精度的参数，而拉格朗日乘数法可以获得优化函数的全局最小值或局部最小值，由于优化函数H在上为严格凸函数，因此，如果采用拉格朗日乘数法求出的解满足定义域的约束，则这个解一定是优化函数H在约束条件下的最优解；从另一方面考虑，采用拉格朗日可以实现优化函数解的快速计算，即使解不满足定义域的约束，也可以采用障碍法重新进行次优解的计算。因此，本文采用拉格朗日结合障碍法进行优化函数的求解。
下面对具体的求解过程进行分析。
3.2.1 拉格朗日乘数法求最优解
1) 拉格朗日函数
如式(22)所示的优化问题的拉格朗日函数为
L(φ,λ)=H+λ·G
(22)
式中，
为优化函数的解，
为等式约束G=0所对应的拉格朗日乘子。
通过求解如式(23)所示的由N+1个方程构成的非线性方程组在定义域上的解即可得到等式约束条件下优化函数H的最优解。
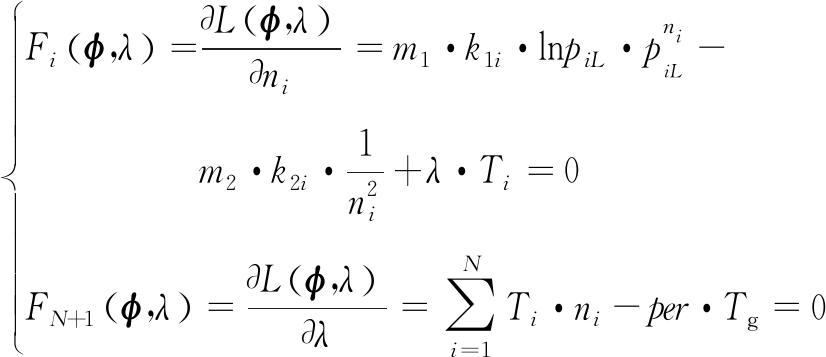
(23)
2) 牛顿迭代求解
由于式(23)所示的非线性方程组比较复杂，无法直接求出解析解，因此，需要采用牛顿迭代法进行求解。迭代方程如式(24)所示：
(24)
式中,
F(φk,λk)=
[F1(φk,λk)F2(φk,λk)…FN(φk,λk)]T
只有当式(23)所示的非线性方程组的雅克比矩阵是非奇异的，该方程组才可以用牛顿迭代法进行正常求解。方程组的雅克比矩阵如式(25)所示：
(25)
式中，
经过计算可得F′(φ,λ)的行列式：
|F′(φ,λ)|=
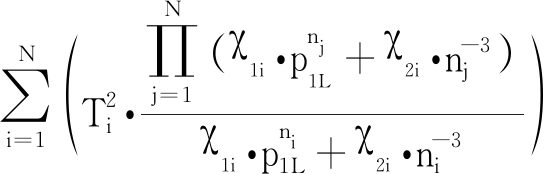
(26)
如果不对ni进行约束，|F′(φ,λ)|有可能等于0，此时，逆矩阵
不存在，无法进行式(25)的迭代更新，因此，在进行牛顿迭代的过程中需要对ni进行约束，即：当ni<0时，令ni=ζ，ζ∈R+，且ζ→0。在约束的情况下|F′(φ,λ)|≠0始终成立，雅克比矩阵F′(φ,λ)非奇异，逆矩阵始终存在，牛顿迭代可以正常计算。
在对ni进行约束的情况下，牛顿迭代有两种结果：
1) 正常收敛，获得迭代结果n*，判断n*是否满足定义域约束条件，如果满足，则n*为式(17)的最优解，如果不满足，则需进行障碍法计算。
2) 无法收敛，采用障碍法进行次优解的计算。
3.2.2 障碍法求次优解
1) 障碍法
采用障碍法求解，可以将式(17)所示的带有2N个不等式约束的优化问题近似成如式(27)所示的等式约束问题[11]。
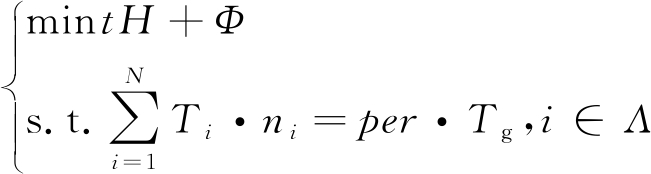
(27)
式中，Φ为对数障碍函数，t>0为确定近似精度的参数，在本文中Φ的具体表达式如式(28)所示：
Φ=
(28)
式(28)所示的优化问题与式(17)所示优化问题的最优解相差不超过2N/t，近似精度随参数t的增加而不断改进，然而，当参数t很大时，很难用牛顿迭代法极小化函数tH+Φ，这是因为Hessian矩阵在靠近可行集边界时会剧烈变动，因此，可以通过求解一系列形如问题(27)的优化问题来规避上述困难，在这一系列问题中的参数t将逐渐增加，对于每个问题应用牛顿方法求解时可以用上个t对应问题的最优解作为初始点开始迭代，具体方法可参考文献[11]。本文主要对确定某一个t值后式(27)的求解方法进行描述。
对数障碍函数Φ的Hessian矩阵如式(29)所示：
(29)
式中，
由式(29)可知
的第k阶顺序主子式为
(30)
由式(30)可知，的各阶顺序主子式均大于0，由此可证，Φ在每一点处的
都是正定的。因此，式(27)的优化函数tH+Φ在定义域
上为严格凸函数，因此，在定义域上存在唯一最优解。
在障碍函数Φ的影响之下，优化函数tH+Φ的最优解始终满足的约束，因此，对于式(27)的优化问题可以直接采用3.2.1节中的拉格朗日乘数法进行求解。
2) 拉格朗日函数
针对式(27)建立的拉格朗日函数如下：
L(φ,λ)=(tH+Φ)+λ·G
(31)
对应的最优解需满足如下方程：
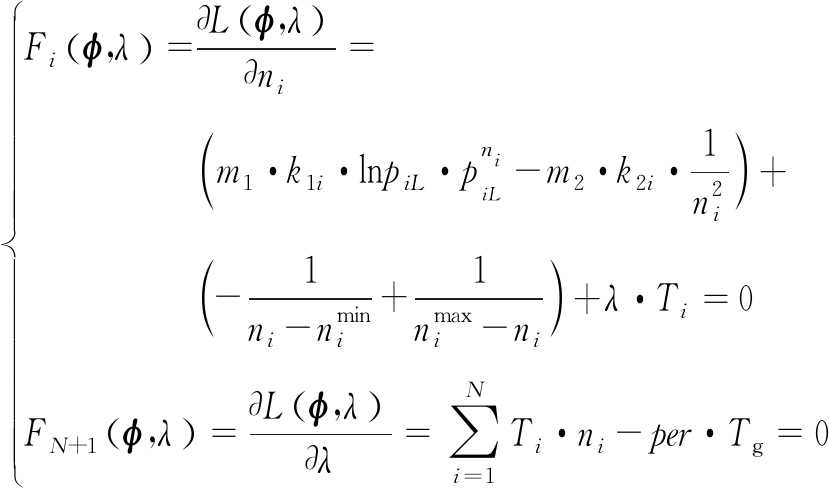
(32)
3) 牛顿迭代求解
为了求解上述非线性方程组，同样需要采用牛顿迭代法，此时，式(32)所对应的雅克比矩阵为
(33)
式中，
Ψi=
对应的行列式为
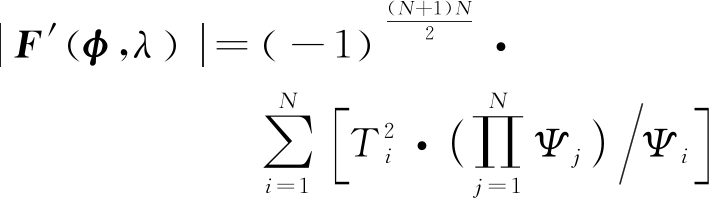
(34)
如果选取的牛顿迭代初值满足所有的约束条件，迭代的过程中由于障碍函数Φ的影响，通过式(24)每一次更新的解都满足
的约束，在这种情况下，每一步的雅克比矩阵对应的行列式|F′(φ,λ)|>0都成立，因此，采用牛顿迭代进行式(32)的求解是合理的。
3.2.3 牛顿迭代初值的选取
由于牛顿迭代初值的选取对迭代算法的收敛性能有很大影响，本文分别采用以下3种方法确定迭代初值。
方法1：在解的范围内任意选取一组数值作为初值；
方法2： 选取优化函数h1的最优解作为初值；
方法3： 选取优化函数h2的最优解作为初值。
4 仿真分析
4.1 仿真场景设置
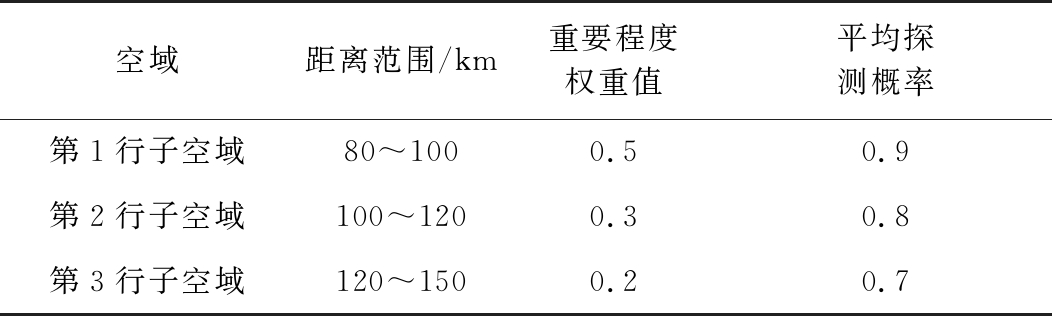
仿真场景设置如下：雷达方位角扫描范围为[-60°,60°]，俯仰角扫描范围为[-4.5°,4.5°]，最大探测距离为150 km，本文只考虑80～150 km范围内的空域；把搜索子空域按方位角和距离不同分为3×7个子空域，各子空域的重要程度和平均探测概率按目标离雷达的距离进行设置，具体参数如表1所示；各子空域的搜索时间和目标流强度按方位角进行设置，具体参数如表2所示；仿真时间为180 s。
表1 各行子空域参数表
空域距离范围/km重要程度权重值平均探测概率第1行子空域80～1000.50.9第2行子空域100～1200.30.8第3行子空域120～1500.20.7
表2 各列子空域参数表
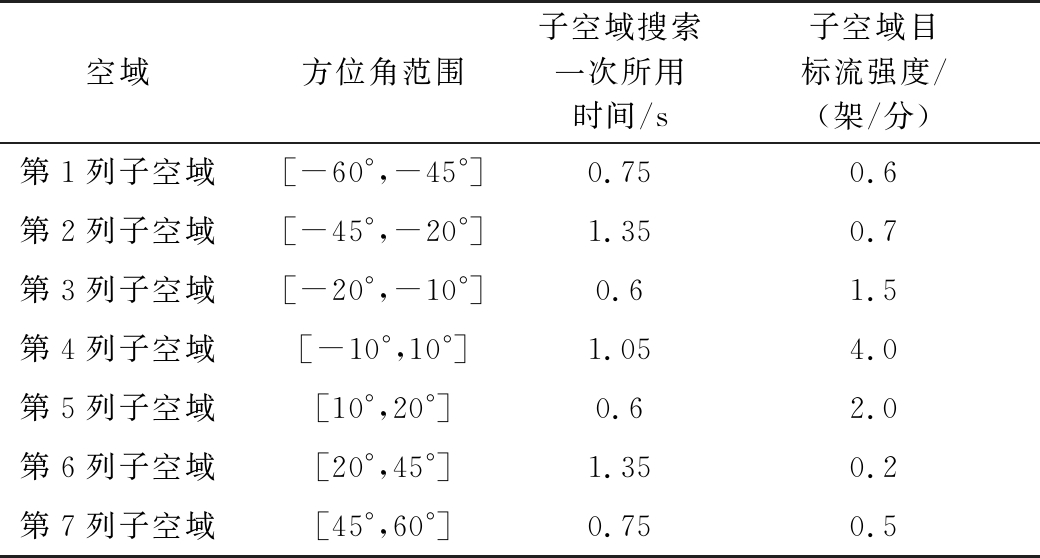
空域方位角范围子空域搜索一次所用时间/s子空域目标流强度/(架/分)第1列子空域[-60°,-45°]0.750.6第2列子空域[-45°,-20°]1.350.7第3列子空域[-20°,-10°]0.61.5第4列子空域[-10°,10°]1.054.0第5列子空域[10°,20°]0.62.0第6列子空域[20°,45°]1.350.2第7列子空域[45°,60°]0.750.5
4.2 拉格朗日结合障碍法求解性能分析
4.2.1 不同牛顿迭代初值收敛速度对比分析
1) 拉格朗日法求最优解
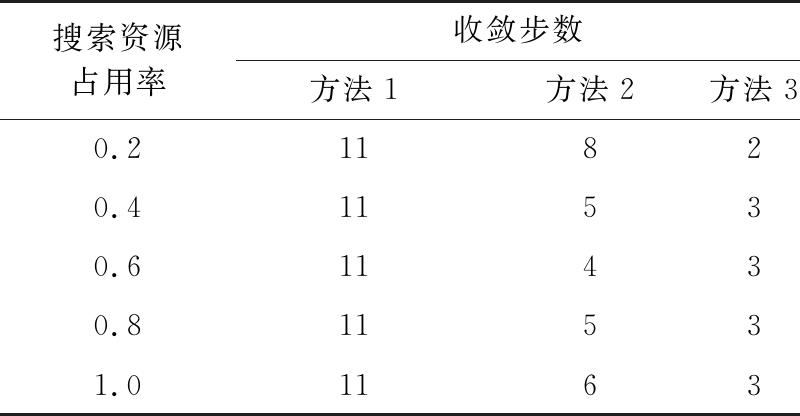
在进行牛顿迭代收敛性能仿真时将残差设置为10-6，不考虑目标最晚发现时间约束时，拉格朗日法求取的最优解大致都在定义域范围内，此时，3种牛顿迭代初值选取方法的收敛速度仿真结果如表3所示。
表3 3种初值选取方法的收敛性能对比
搜索资源占用率收敛步数方法1方法2方法30.211820.411530.611430.811531.01163
表3给出了m1=0.5时3种初值选取方式下牛顿迭代收敛步数的对比结果，从表中可以看出，无论选取何种初值都能快速收敛，最大收敛步数不过11步，3种方法相比之下，选取优化函数h2的最优解作为初值时收敛速度最快，最大收敛步数不超过3步。
2) 障碍法求次优解
加入目标最晚发现时间约束时，部分情况下需要用到障碍法求取次优解。这里设置次优解与最优解的相差的精度不超过10-4，即2N/t<10-4，内迭代的残差为10-6，假设第4列子空域为重点空域，式(11)右边的式子满足以下条件：
(35)
此时，3种牛顿迭代初值选取方法的收敛速度仿真结果如表4所示，从表中可以看出在使用障碍法求解时，3种初值的选取方式迭代步数相差不大。
表4 3种初值选取方法的收敛性能对比
搜索资源占用率收敛步数方法1方法2方法30.21641641630.48688880.69698980.88789891.0768079
3) 初值选取
从上述分析可知，采用拉格朗日求解时，优化函数h2的最优解作为初值时收敛速度最快，采用障碍法求解时，3种初值条件的收敛速度相当，因此，选取优化函数h2的最优解作为拉格朗日结合障碍法的初值是最为合理的。
4.2.2 拉格朗日结合障碍法与遗传算法求解性能对比分析
本文采用遗传算法中的NSGA-Ⅱ算法与拉格朗日结合障碍法的求解性能进行对比研究。
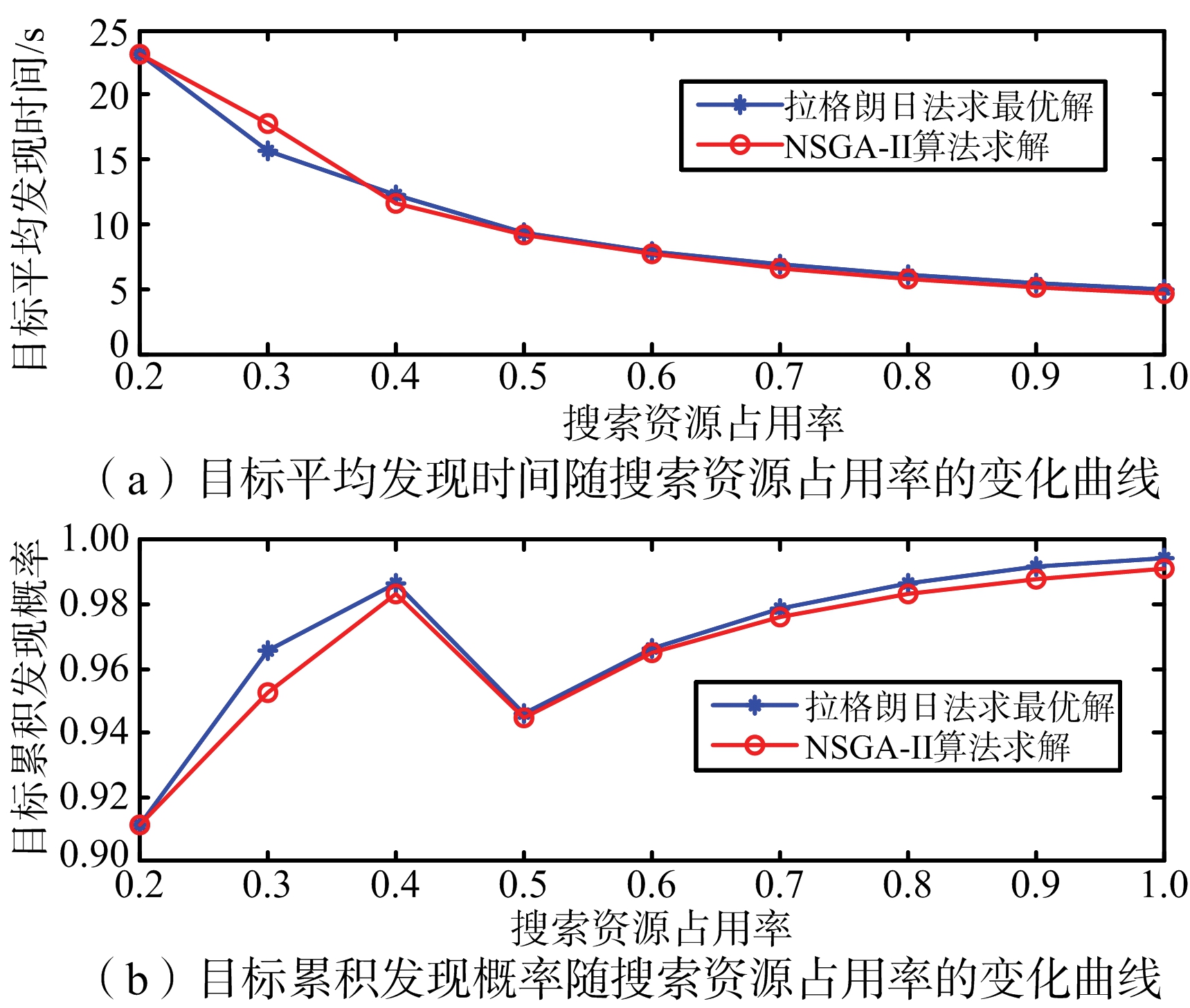
图2 拉格朗日法与NSGA-Ⅱ优化结果的对比
从优化性能分析：图2给出了m1=0.7时拉格朗日法和NSGA-Ⅱ算法的优化结果，从图中可以看出两种方法计算的目标平均发现时间相差不大，拉格朗日法略微好一点，但是拉格朗日法的目标累积发现概率优化结果明显比NSGA-Ⅱ算法好，从理论上讲拉格朗日法可以获得最优解，而NSGA-Ⅱ算法未必可以获得最优解，因此，拉格朗日法的优化结果肯定不会比NSGA-Ⅱ算法差，但实际在计算过程中由于无法获得拉格朗日函数的解析解，而是采用牛顿迭代进行计算，因此，采用拉格朗日获得解也是近似最优解的一个次优解。图3给出了m1=0.7时障碍法和NSGA-Ⅱ算法的优化结果对比图，从图中可以看出两种方法的优化结果相当。基于上述分析，拉格朗日结合障碍法的优化结果要优于NSGA-Ⅱ算法。
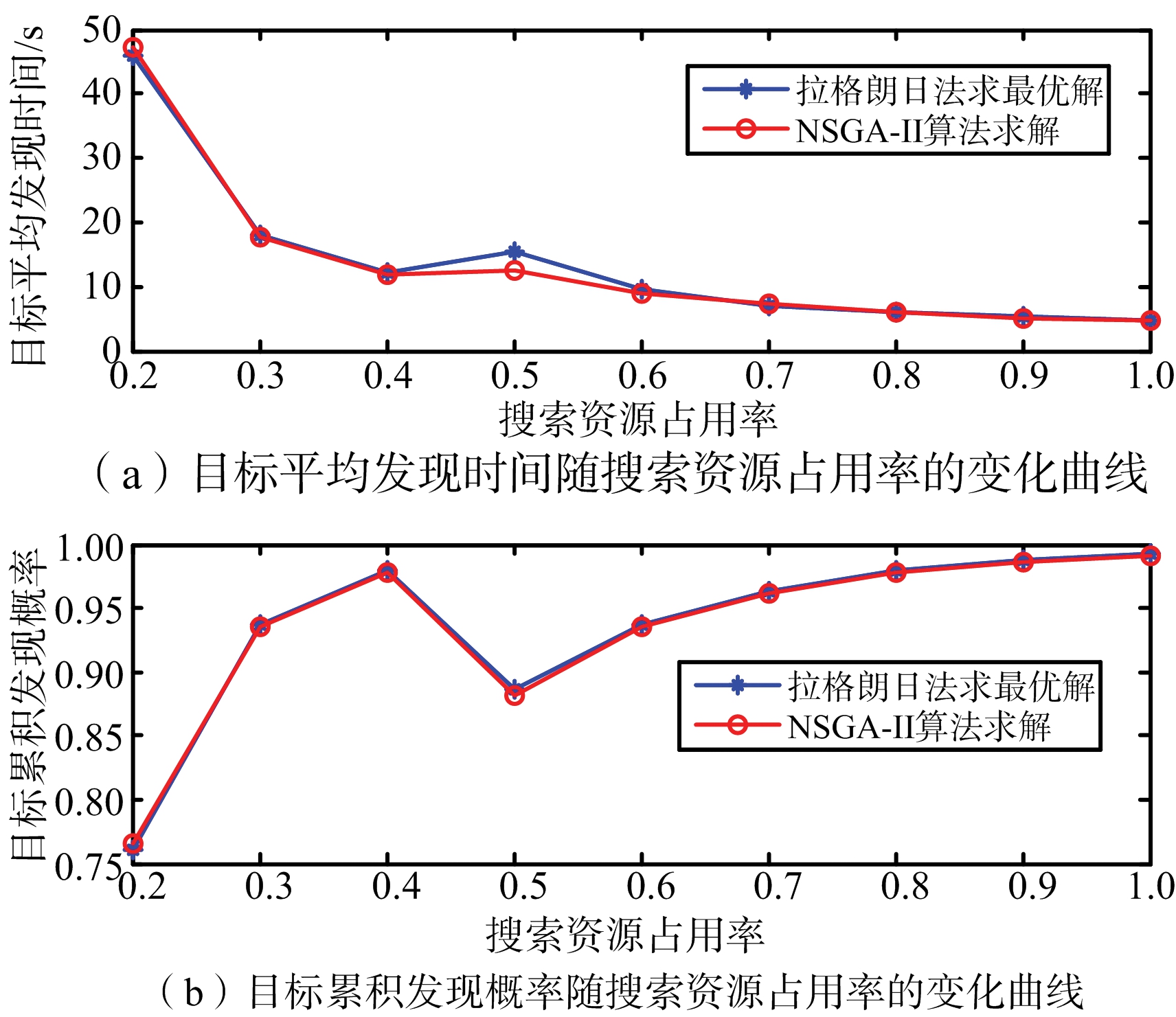
图3 障碍法与NSGA-Ⅱ优化结果的对比
从计算时间分析：本文采用MATLAB统计仿真时长，NSGA-Ⅱ算法平均一次计算时间约为53.8 s，拉格朗日结合障碍法平均一次计算时间约为3 ms。因此，采用拉格朗日结合障碍法的计算速度要远远小于NSGA-Ⅱ算法，满足实时性的要求。
从上述分析可知，拉格朗日结合障碍法即凸优化的方法明显比NSGA-Ⅱ算法有优势，在实际工程中也具有更高的应用价值。
4.3 最优搜索算法性能分析
仿真场景如4.1节所述，为了与顺序搜索进行对比分析，暂不考虑目标最晚发现时间的约束。按照上述仿真场景采用遗传算法计算子空域初始搜索顺序，采用拉格朗日结合障碍法计算各子空域的最优搜索数据率，并采用蒙特卡洛仿真对最优搜索算法的有效性进行验证，在蒙特卡洛仿真过程中，现有目标根据各子空域的目标存在概率随机生成，后续目标根据各子空域的目标流强度随机产生。
图4～图7给出了不同搜索资源占用率下的蒙特卡洛仿真结果。图4～图6分别为现有目标、后续目标以及所有目标按照子空域重要程度进行加权的平均发现时间，从图中可以看出，无论对于何种目标最优搜索的平均发现时间都要小于顺序搜索。图7给出了不同搜索资源占用率条件下，仿真时长内所有目标的发现概率对比图，从图中可以看出，最优搜索的发现概率要优于顺序搜索，特别是在搜索资源占用率较小的时候，最优搜索的发现概率明显优于顺序搜索，当搜索资源占用率较大时，发现概率接近于饱和，二者差别并不明显。
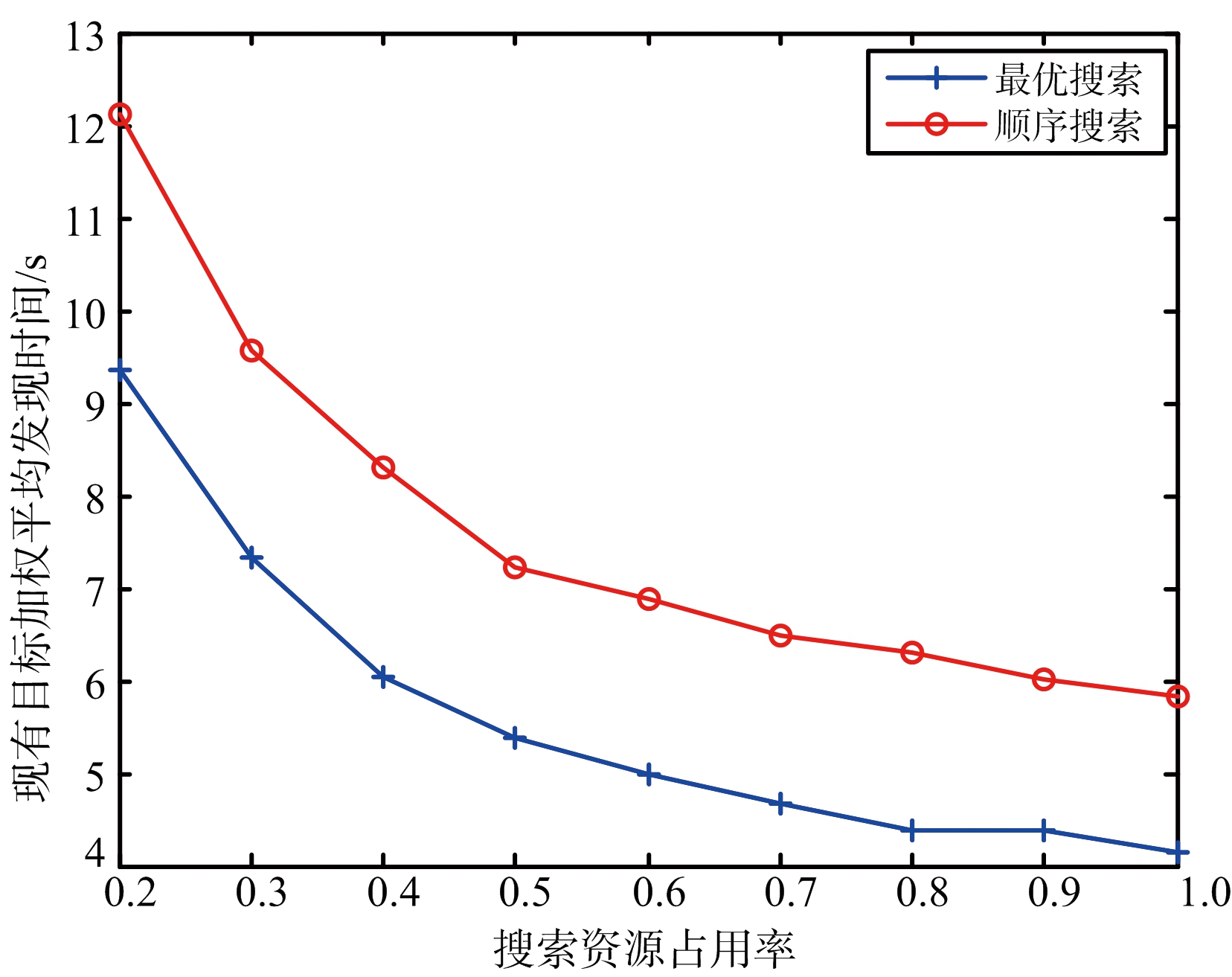
图4 两种搜索方式的现有目标加权平均发现时间对比
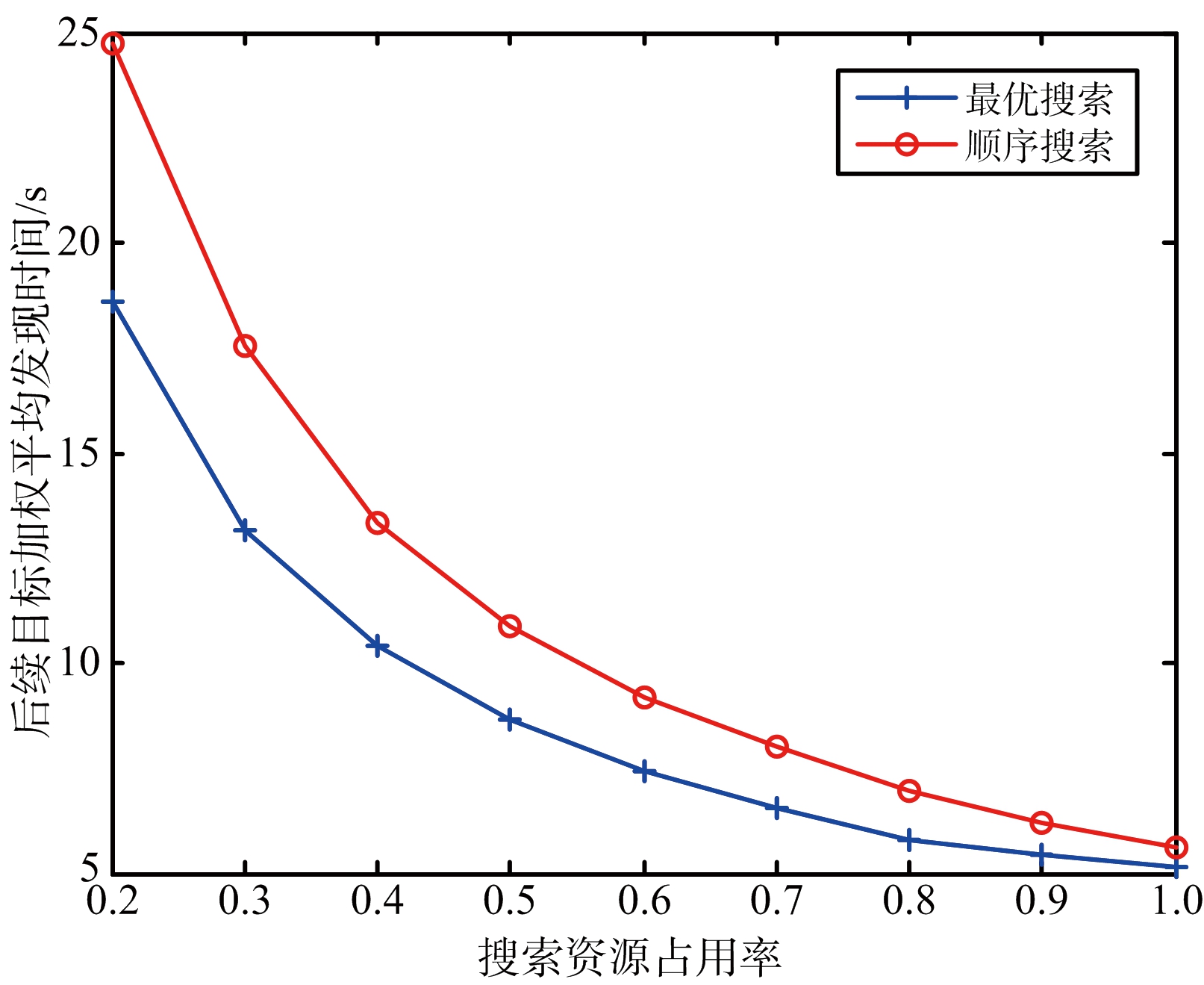
图5 两种搜索方式的后续目标加权平均发现时间对比
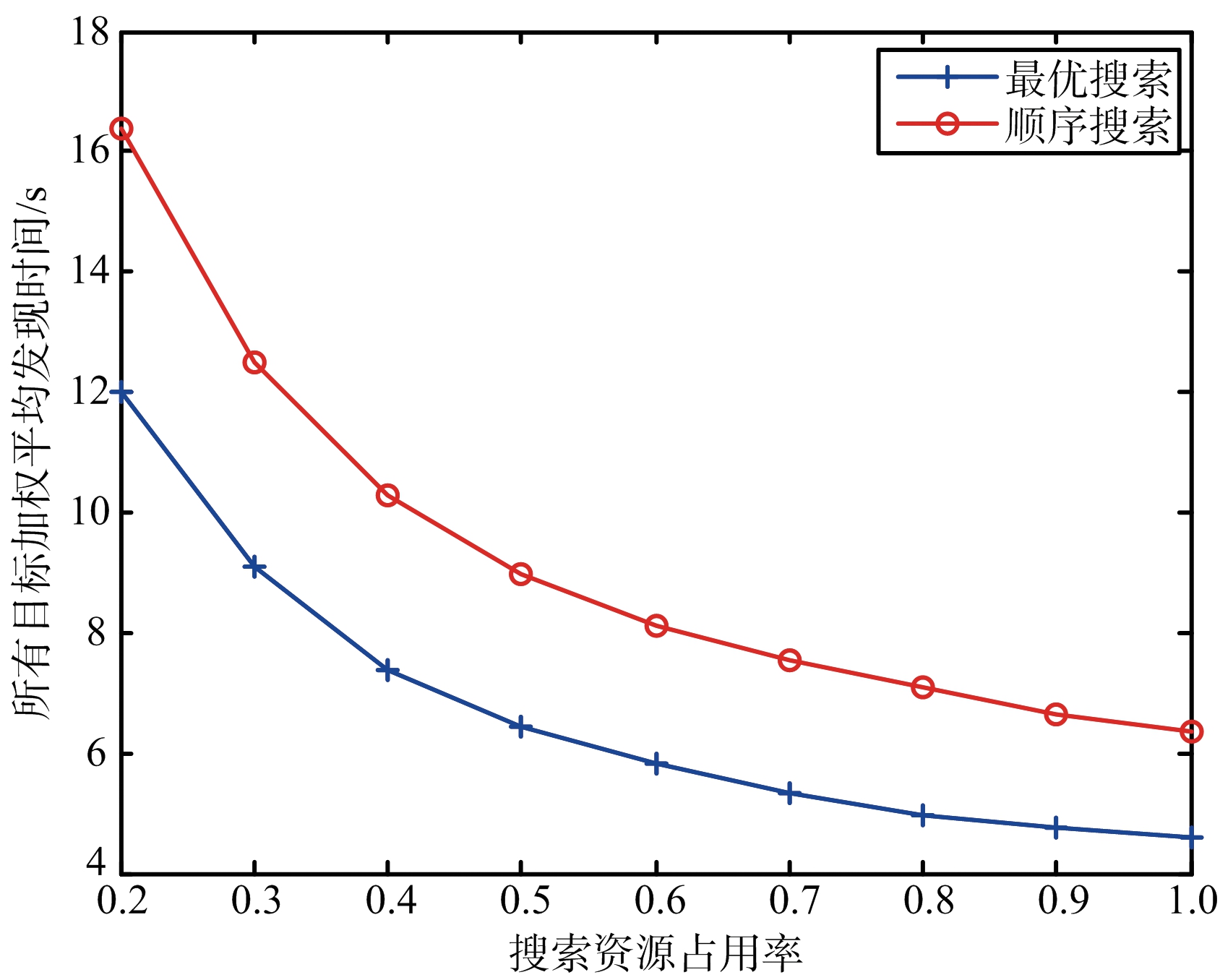
图6 两种搜索方式的所有目标加权平均发现时间对比
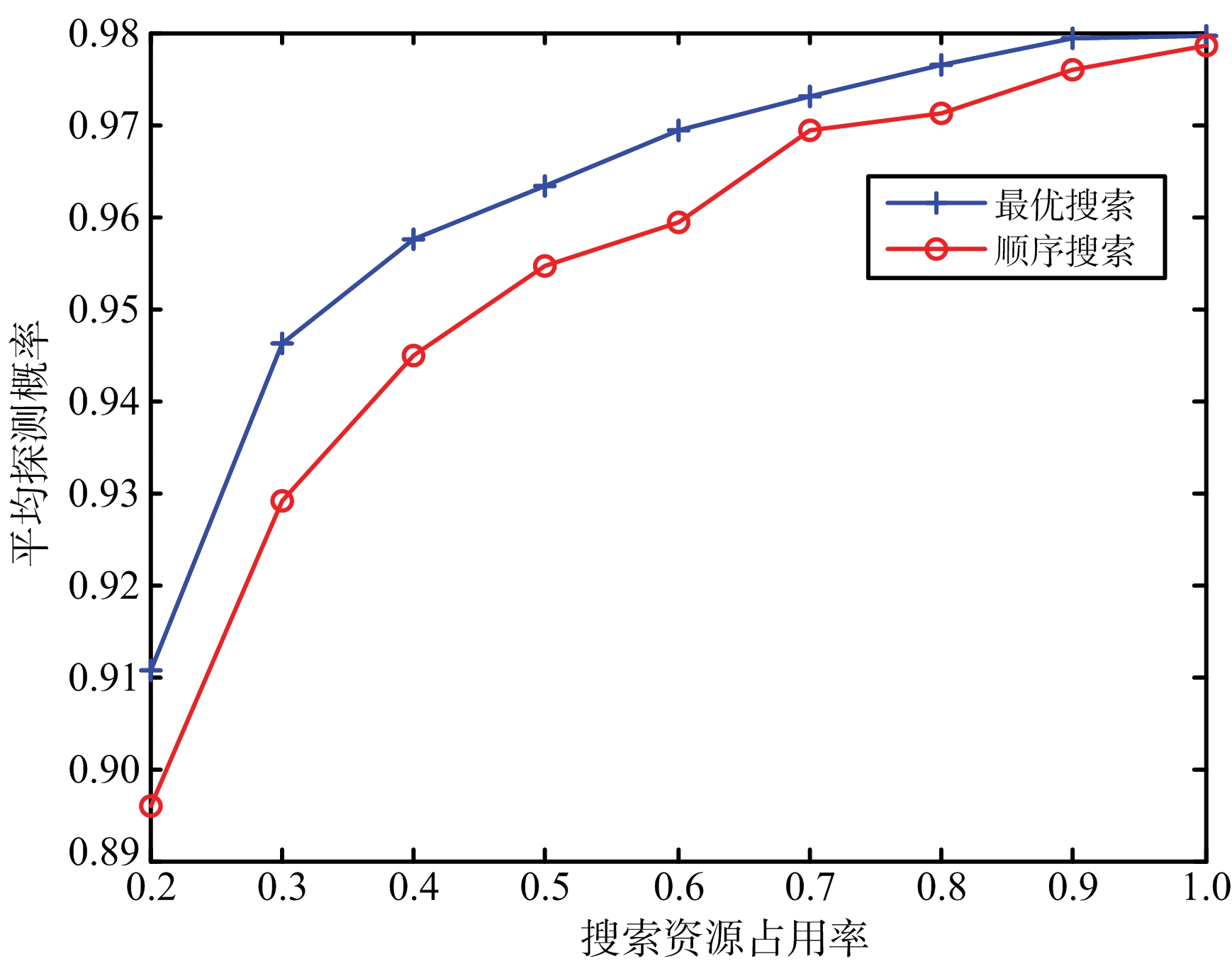
图7 两种搜索方式的发现概率对比
从上述分析可知，最优搜索的搜索性能要优于顺序搜索，特别是在搜索资源占用率较小的情况下，最优搜索的优势更为明显。
5 结束语
本文主要针对基于预警机引导信息的雷达搜索问题进行分析，将雷达的搜索目标分为现有目标和后续目标两类，并提出了通用的最优搜索模型，针对现有目标和后续目标的特点和差异，提出了两步优化的策略；针对遗传算法、粒子群算法等智能算法搜索速度慢，不适用于实际作战的问题，将最优搜索多目标优化模型转换成单目标凸优化问题，并提出拉格朗日结合障碍法实现搜索数据率的快速优化。通过数学推导验证了该方法的合理性，并对牛顿迭代初值的选取方法进行研究。最后对本文提出的最优搜索模型和求解方法的合理性进行仿真验证。
通过仿真结果可以看出：1)从优化性能和计算速度两个方面来说，拉格朗日结合障碍法都优于遗传算法；2)最优搜索算法的搜索性能优于顺序搜索，尤其在搜索资源占用率较小的情况下，最优搜索的优势更为明显。
[1] BYRNE M, WHITE K, WILLIAMS J. Scheduling Multifunction Radar for Search and Tracking[C]∥18th International Conference on Information Fusion, Washington:IEEE, 2015:945-952.
[2] 武俊青.阵列雷达资源管理算法与实现研究[D].成都:电子科技大学,2016.
[3] BRIHECHE Y, BARBARESCO F,BENNIS F, et al. Update Rates Constraints in Fixed-Panel Radar Search Pattern Optimization with Limited Time Budget[C]∥The 18th International Radar Symposium(IRS), 2017:1-10.
[4] SEVERSON T A, PALEY D A. Distributed Multitarget Search and Track Assignment with Consensus-Based Coordination[J]. IEEE Sensors Journal, 2015,15(2):864-875.
[5] 吴其华,刘进,赵峰,等. 基于最小平均发现时间的相控阵雷达最优搜索[J].航天电子对抗,2015,31(6):28-31.
[6] 李寰宇,查宇飞,李浩,等. 联合截获威胁下的雷达射频隐身目标搜索算法[J].航空学报,2015,36(6):1953-1963.
[7] 廖俊,胡凡俊,沈卫中,等. 相控阵雷达LPI搜索方法研究[J].火力与指挥控制,2016,41(10):113-121.
[8] YU Chenlong, TAN Xiansi, LI Fan. Study on Search Performance of Long Range Early-Warning Phased Array Radar[C]∥CIE International Conference on Radar, Guangzhou：IEEE，2016:1-5.
[9] ABDELAZIZ F B, MIR H. An Optimization Model and Tabu Search Heuristic for Scheduling of Tasks on a Radar Sensor[J]. IEEE Sensors Journal, 2016,16(17):6694-6702.
[10] 程鹏.基于凸优化理论的无线网络跨层资源分配研究[D].杭州:浙江大学,2008.
[11] BOYD S, VANDENBERGHE L. Convex Optimization [M]. London: Cambridge University Press, 2004.
[12] 刘松林.基于博弈论和凸优化的异构网络资源分配方法研究[D].哈尔滨:哈尔滨工业大学,2016.
