0 引 言
极化合成孔径雷达(Polarimetric Synthetic Aperture Radar, PolSAR)通过不同极化的收发通道组合能够获取相对于单极化SAR更为丰富的目标散射信息，在覆盖地物分类以及目标的检测识别等方面具有广泛的应用[1-2]。但是，由于观测维度的增加及系统复杂性的提高，其获取的极化散射信息会受到天线串扰、极化通道幅相不平衡等系统误差的影响而产生失真，从而影响后续的应用处理[3-4]，因此对极化数据的精确校准至关重要[5]。
极化定标方法可分为基于点目标和基于分布式目标两类。前者的定标精度高度依赖于定标体的指向精度[6-7]，且由于误差参数的空域依赖特性需在测绘带布置大量定标体，实用性不足。目前比较成熟的定标算法多为点目标和分布式目标结合的定标算法，包括Klein算法[8](K算法)、Quegan算法[9](Q算法)和Ainsworth算法[10](A算法)。其中，Q算法和A算法已分别被应用于PALSAR2[12]和UAVSAR[13]极化数据的校准。然而，由分析可知，K算法不收敛概率较高，Q算法准确度较低，A算法存在严重缺陷[14]，在反射对称性假设条件下的A算法(Az算法[15])精确度较高，但是在串扰值较大时会出现较大的误差。因此，随着极化终端应用对极化数据精确度要求的提高，在分布式目标反射对称性假设的大框架下需寻找更为精确以及稳定的定标算法。
本文将极化定标算法对极化误差参数的求解问题转化为对分布式目标二阶极化散射特征的优化问题，采用的是粒子群优化算法(Particle Swarm Optimization, PSO)。PSO是由Kennedy和Eberhart提出的一种随机的、基于群体的优化方法[16]，同传统的优化方法相比，PSO具有更强的全局优化能力，也能较快地收敛于可接受解。仿真实验证明了PSO算法用于极化定标的有效性，其相比于传统算法有着更准确的参数估计，且在串扰值较高时仍能保持较高的精确度。
1 极化定标模型
测量的极化散射矩阵(Polarimetric Scattering Matrix，PSM)即O和实际的PSM即S的关系如式(1)所示：
O=RST+N
(1)
式中，T和R是发射和接收通道的误差矩阵，N是系统噪声。O,R,S,T,N的统一形式为
其中，矩阵元素下标即代表各个极化通道。O,S,N的向量形式可表示为
如式(2)所示：
o=YMAs+n
(2)
式中，Y=rvvtvv，A=diag(α,1,α,1)，K=diag(k2,k,k,1)，
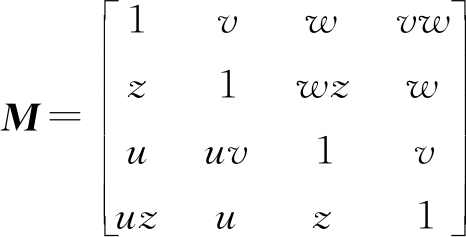
(3)
式中，u=rvh/rhh，v=tvh/tvv，z=thv/thh，w=rhv/rvv，k=rhh/rvv，α=thh/tvvk。o,s,n的协方差矩阵模型Cx=〈xxH〉之间的关系为
Co-Cn=|Y|2MAKCsKHAHMH
(4)
假设目标满足散射互易性，即shv=svh，分布式目标的协方差矩阵的形式为
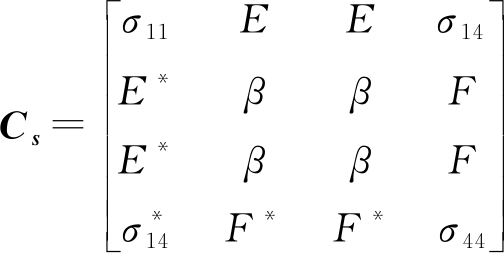
(5)
注意到KCsKH和Cs的形式完全一致，所以仅利用分布式目标无法求解k的值，需结合点目标定标技术进行估计。本文仅对分布式目标的定标部分进行分析，因此在下面的理论及仿真分析中设定k=1，K为单位阵，同理误差参数的绝对幅相Y也无法求解，设定Y=1。
除了目标散射互易性的假设，K算法、Q算法和Az算法假定自然地物目标具有反射对称性，即共极化通道与交叉极化通道数据不相关：
(6)
2 基于PSO的极化定标算法
2.1 经典极化定标算法
文献[15]对K算法、Q算法、A算法和Az算法的定标效果进行了仿真对比分析，分析结果表明，Az算法的估计准确度很高，K算法次之，A算法和Q算法定标效果一般。但是，文献[15]的分析结果是在串扰参数低于-20 dB的基础上获得的。由下面的分析可知，当串扰设定范围扩大时，K算法收敛概率大大降低，Az算法会出现较大的失误，K算法和Az算法都不是稳健的定标算法。
2.2 PSO算法
PSO算法的思想最初来源于对鸟类与鱼类觅食过程的模拟。在PSO中，每个解决方案都是搜索空间中的“鸟”，称之为“粒子”。这些粒子在搜索空间中不断移动以找到最佳位置。每个粒子在问题空间中都具有位置yi=[yi1,yi2,…,yiN]和速度vi=[vi1,vi2,…,viN]，其中i表示第i个粒子，N表示未知量的数量。PSO首先初始化一群随机粒子，粒子总数为pop_size，然后通过更新迭代来搜索最优解。在每次迭代过程中，每个粒子都会根据两个“最佳”值更新自己的位置矢量，第一个是这个粒子到目前为止所取得的最优解的位置矢量，即pBest，另一个是这个群体的所有粒子到目前为止所取得的最优解的位置矢量，即gBest。找到两个最优解后，粒子从第n代更新到n+1的方式如式(7)、式(8)所示：
(7)
(8)
式中：b是惯性权重系数；c1是粒子自身加速度权重系数，c2是全局加速度权重系数；r1，r2是两个相互独立的、在[0,1]范围内均匀分布的随机数。
2.3 将PSO算法用于极化定标
基于PSO算法的极化定标假定分布式目标具有反射对称性，在此假设前提下，定义矩阵D：
(9)
通道不平衡度α可由D求得：
(10)
串扰值u,v,z,w和矩阵D由PSO算法求得，优化过程以D(1,2)=0，D(1,3)=0，D(2,4)=0，D(3,4)=0为约束条件。粒子的位置矢量设定为y=[u,v,z,w]，将粒子位置矢量的元素值代入式(4)，忽略噪声，可求得粒子位置矢量y对应的
(11)
将f作为适应度值来判断粒子所处的位置优劣，f越小，表明当前的粒子更接近最优解：
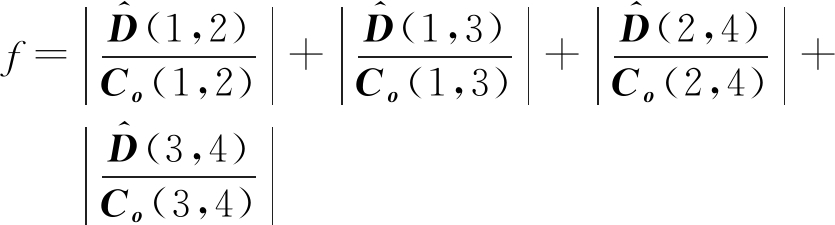
(12)
PSO算法具体步骤如下：
Step 0 初始化一组粒子，包括位置矢量yi0、速度矢量vi0；
Step 1 由式(11)、式(12)计算每个粒子的适应度值
Step 2 对于每个粒子，将其适应度值
与其目前最好位置pBesti对应的适应度值 f(pBesti)进行比较，若较小，则将
作为当前的pBesti；
Step 3 对于每个粒子，将其适应度值与整个群体目前最好位置f(gBest)对应的适应度值进行比较，若较小，则将作为当前的gBest；
Step 4 利用式(7)、式(8)更新
Step 5 若f(gBest)满足条件或达到最大循环次数nmax，则循环结束并返回gBest，否则转Step 1。
3 仿真分析
3.1 PSO参数设定
PSO算法根据经验一般设定c1=c2=2，粒子在根据速度不断调整自己的位置时，还要受到最大速度vmax的限制，通常令vmax=mymax，0.1≤ m≤0.2，这样可以防止粒子远离搜索空间[17]，本文令m=0.1。为了在尽量避免陷入局部最优解的同时兼顾收敛速度，可令惯性权重系数b随迭代次数线性下降，Shi等证明了b取值范围在0～1.4更有利于提高算法的性能[18]，本文令bmax=1.4，bmin=0。群体数量pop_size越大，相互协同搜索的粒子就越多，更能发挥PSO的搜索能力，然而pop_size过大，需要计算的时间大幅增加[19]，经过反复测试对比分析，本文选择pop_size=200，最大循环次数取nmax=1 000。为了达到好的定标效果，将f(gBest)<10-10设置为优化过程结束条件。经后续仿真分析，以上PSO参数的设定收敛性较好，在优化精度和效率之间达到了较好的平衡。
本文方法可以看作在经典算法初始值基础上的优化问题，优化过程中，各个粒子的初始位置将影响迭代和收敛的速度，良好的初始值将大大减少迭代次数并确保收敛。在对经典算法的分析中可以看出，Q算法的定标准确度不高但是较稳定，而Az算法仅在串扰值较小时可以达到很高的准确度。因此，将Q算法的串扰估计值作为初始值是较合适的选择。当经典算法对串扰的估计值均低于-20 dB时，将Az算法初始值会得到更为精确的解。
表1 典型协方差矩阵参数
目标类型σ11σ14σ44β植被10.0110.25
3.2 定标算法的对比分析
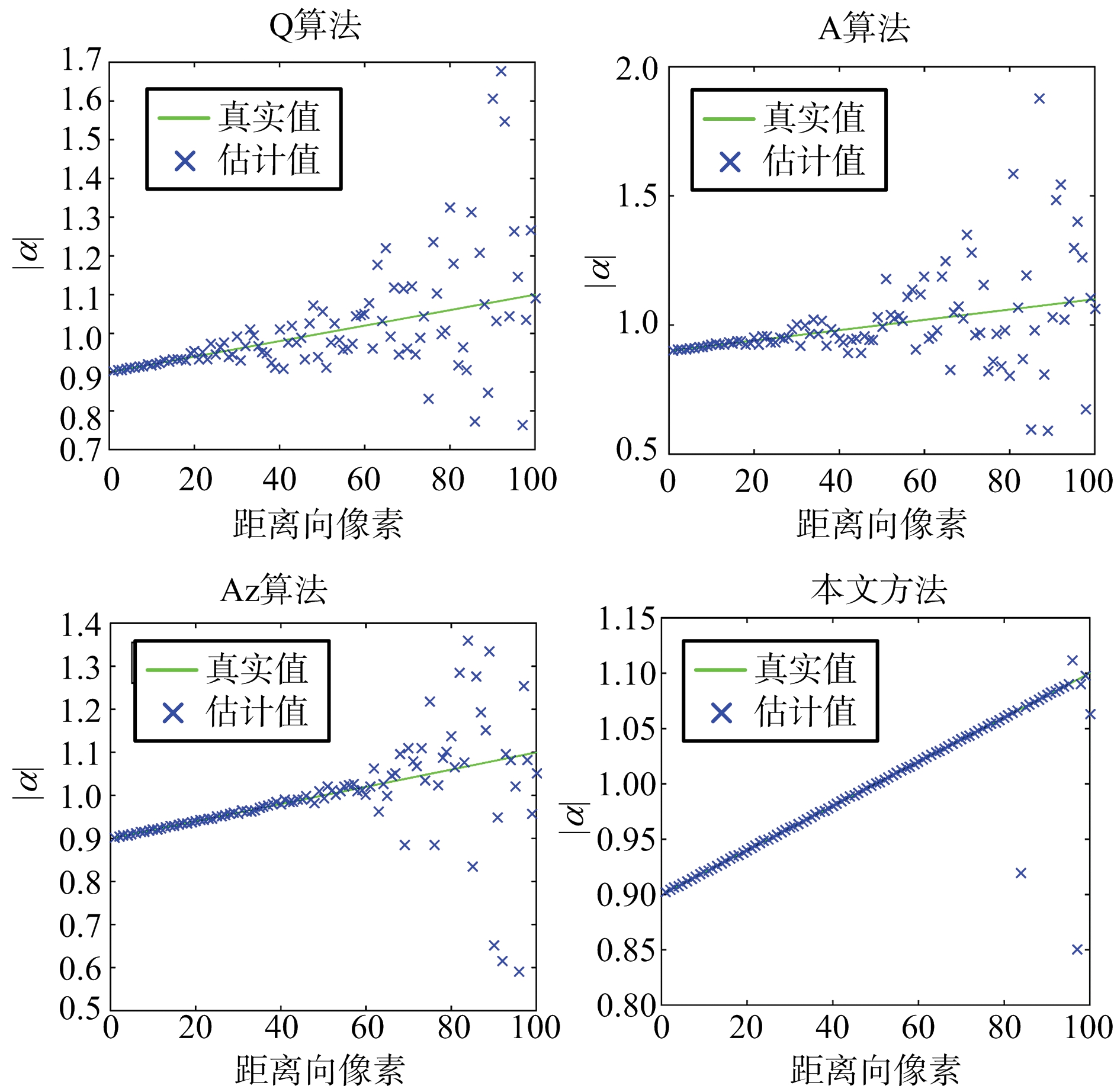
(a) 4种算法通道不平衡值估计
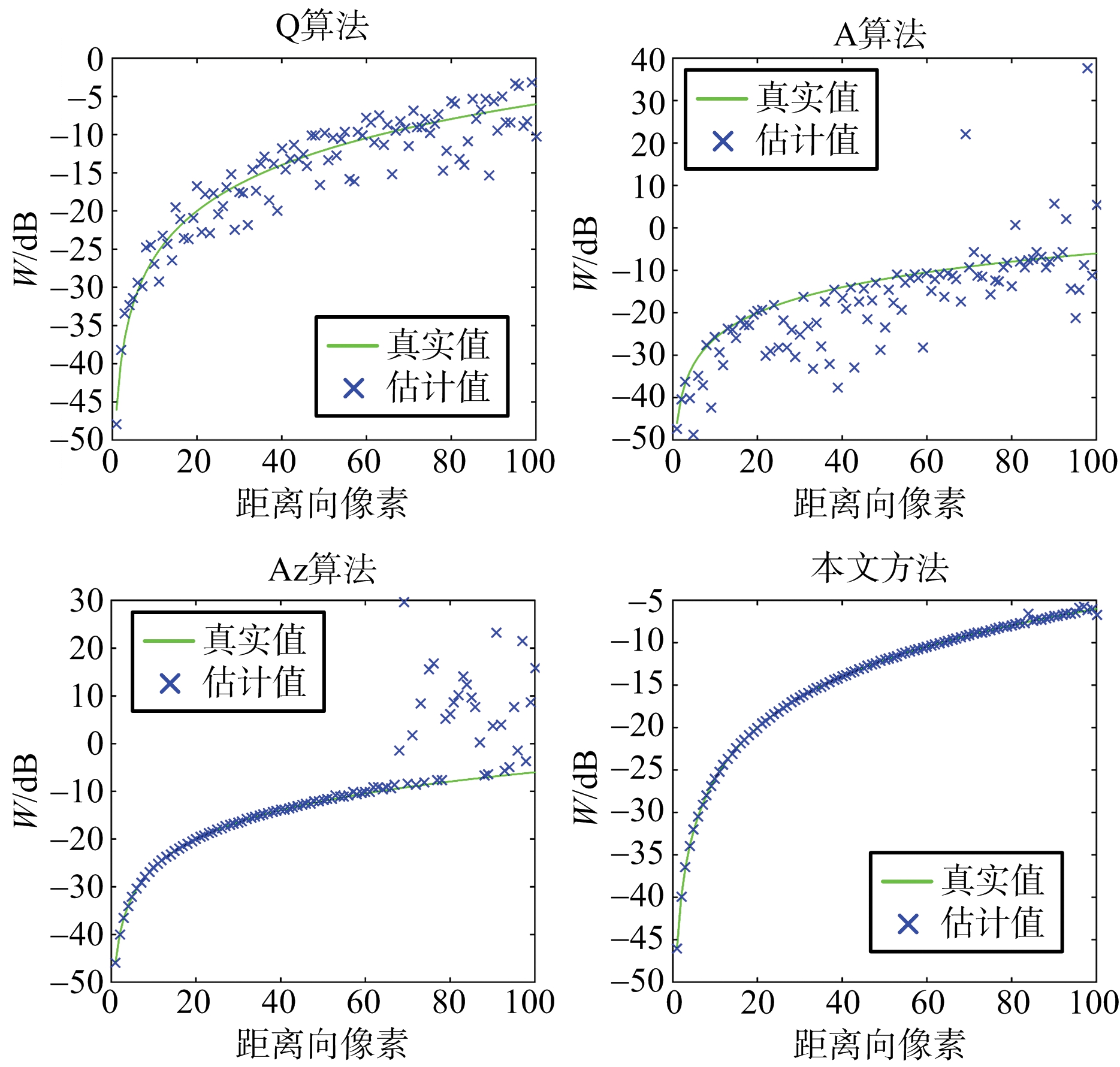
(b) 4种算法串扰估计
图1 串扰值随距离向均匀增加时定标算法对比
首先基于仿真的分布式目标进行分析，目标的协方差矩阵参数如表1所示。对表1所示理论的协方差矩阵额外附加误差矩阵形成失真的协方差矩阵，并对失真矩阵进行校准，其中串扰幅值随距离向从0均匀增加至0.5，而不平衡度幅值随距离向从0.9均匀增加至1.1。基于PSO优化的方法以Q算法的估计值为初始值，由于K算法不收敛次数较多，仅对Q算法、A算法、Az算法进行分析比较，图1是不同算法对误差参数的估计结果。从图1可以看出，Q算法和A算法定标效果较差，Az算法仅在串扰值较小时有着较准确的估计，而本文方法在整个距离向均有着准确的估计。另外，即使串扰值低于-20 dB时，本文方法仍可以得到较Az算法更高的准确度，由于图1无法直观进行对比，以
即估计参数的相对误差幅值对不同方法进行评估，串扰幅值为0～0.1的随机数，不平衡度幅值为0.9～1.1的随机数。基于PSO优化的方法以Az算法的估计值为初始值，图2是不同算法的校准结果。从图2可以看出，即使对于串扰值较小的失真极化数据，本文方法相比于Az仍有着更高的精确度。
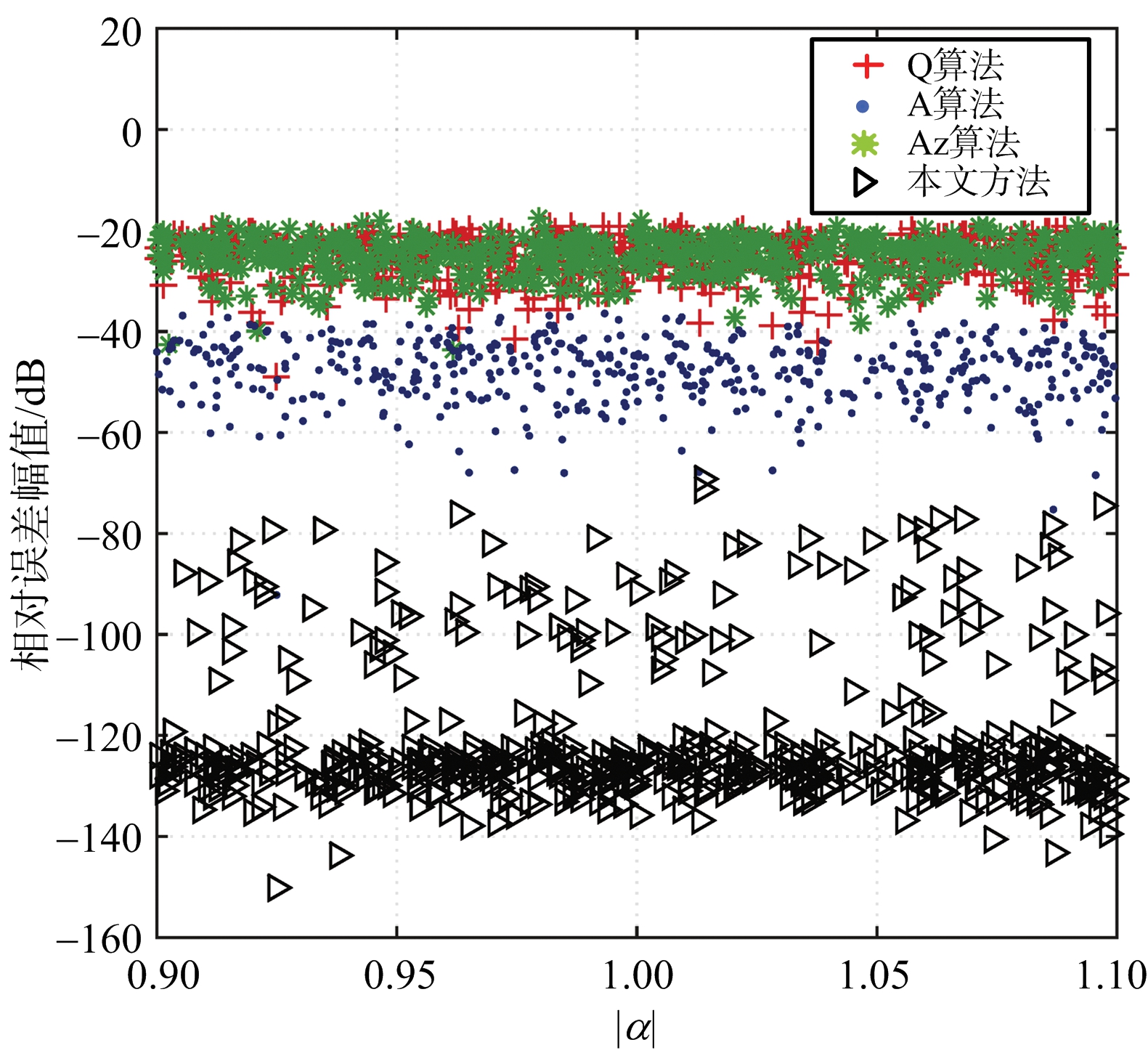
(a) 通道不平衡值估计
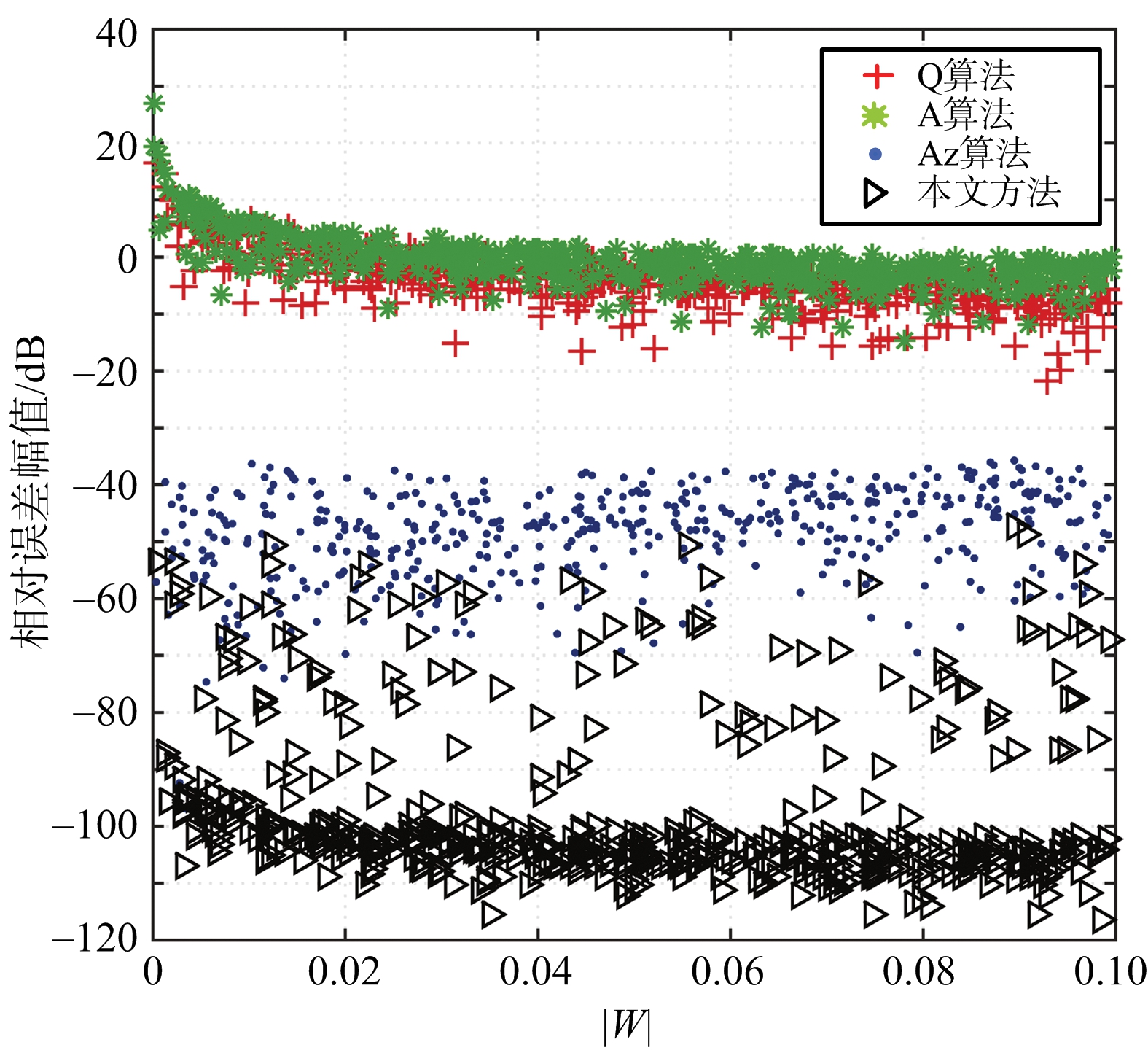
(b) 串扰值估计
图2 串扰值低于-20 dB时定标算法对比
实际上，在极化信息的测量过程中噪声不可避免，因此，E, F不可能完全为0。图3(a)、图3(b)给出了|E|=|F|=10-6, 10-4, 10-2时串扰参数w的校准结果，参数设置分别和图1、图2相同。由图3(a)可以看出，本文提出的方法在串扰值范围较大时仍是最优的算法。由图3(b)可以看出，在串扰值低于-20 dB的情况下，当E, F足够小时，Az算法仍有优化的空间，用PSO算法进行优化可以得到更精确的解。限于篇幅，图1、图2和图3仅给出了串扰值w的估计结果，串扰值u，v，z有着相同的结论。
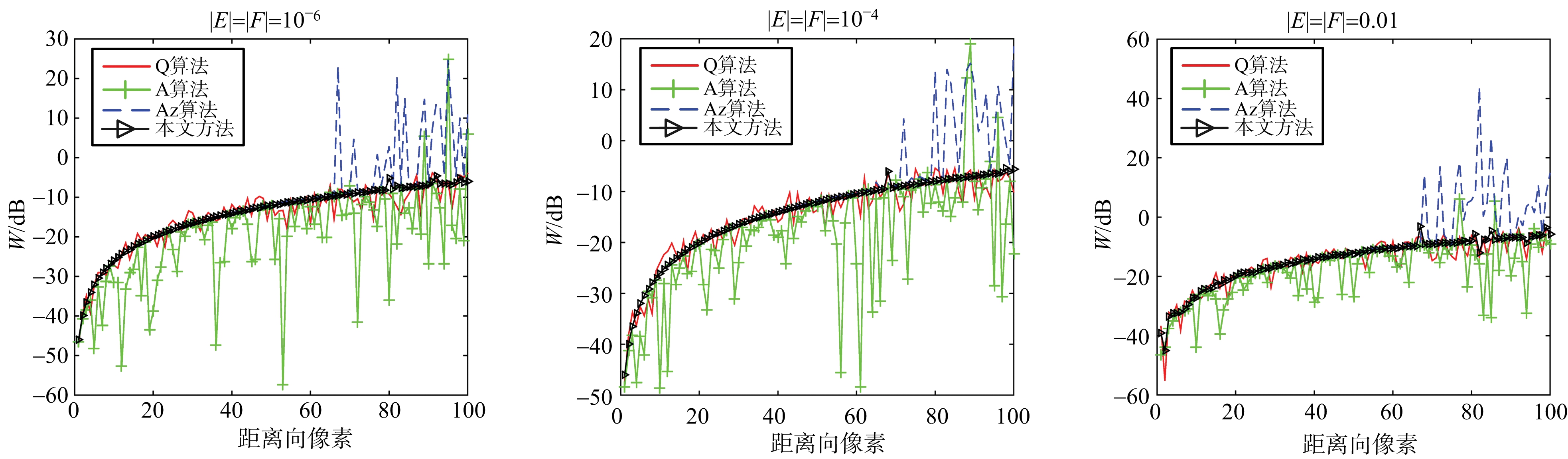
(a) 串扰值随距离向均匀增加
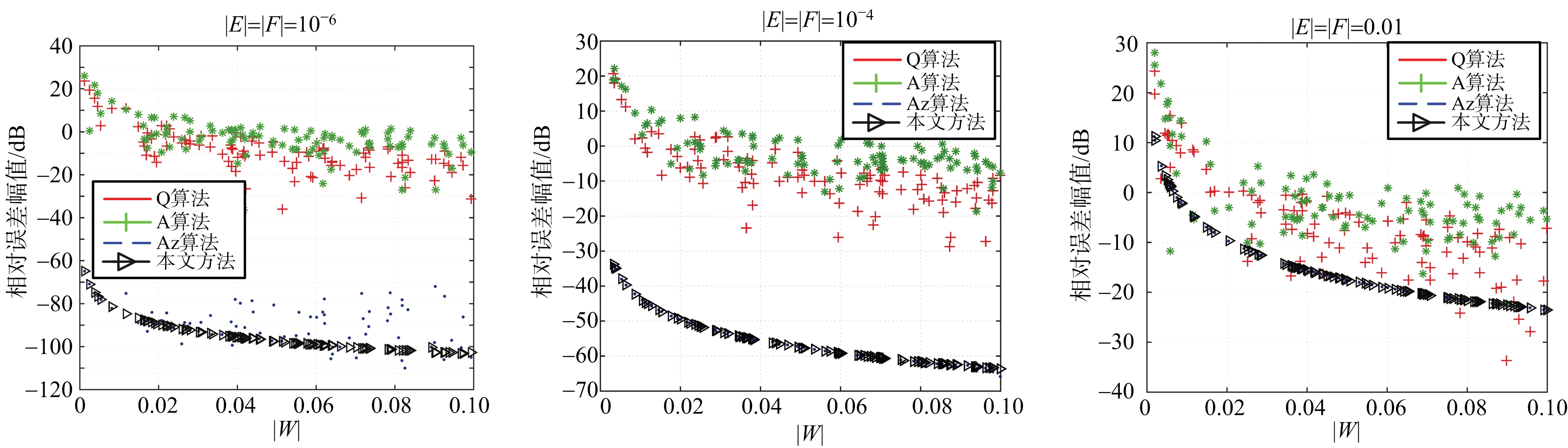
(b) 串扰值低于-20 dB
图3 |E|≠0, |F|≠0时定标算法对比
此外，本文使用NASA/JPL AIRSAR系统在荷兰Flevoland地区获得的L波段全极化SAR数据进行极化定标的分析。该数据获取时间为1991年6月15日，数据方位向分辨率为12.1 m，距离向分辨率为6.6 m，所用区域大小为1 279×500(方位×距离)像素点。图4(a)为原始数据Pauli RGB图，图中，上下方向为距离向，自下而上对应成像斜距由近到远。成像区域多为农作物等自然地物目标，基本满足反射对称性假设。对原始数据进行校准，串扰幅值均低于-20 dB，证明该数据经过了良好的极化定标，图4(b)为定标后数据Pauli RGB图。对原数据额外增加串扰及通道不平衡值模拟失真数据，其中，串扰幅值随距离向从0均匀增加至0.5，而不平衡度幅值随距离向从0.9均匀增加至1.1，图4(c)是模拟失真数据的Pauli RGB图。
用4种算法对模拟的失真数据分别进行校准，图5给出了4种算法对误差参数的估计结果。从图5可以看出，Q算法在整个距离向的估计结果较稳定但是准确度不高，A算法串扰的估计值比真实值小很多，在串扰值仅比-20 dB略高时，Az算法的估计值开始出现较大误差，而本文方法在整个距离向均有着准确的估计。
(a) 原始数据
(b) 定标后
(c) 模拟的失真数据
图4 AIRSAR全极化数据Pauli RGB图
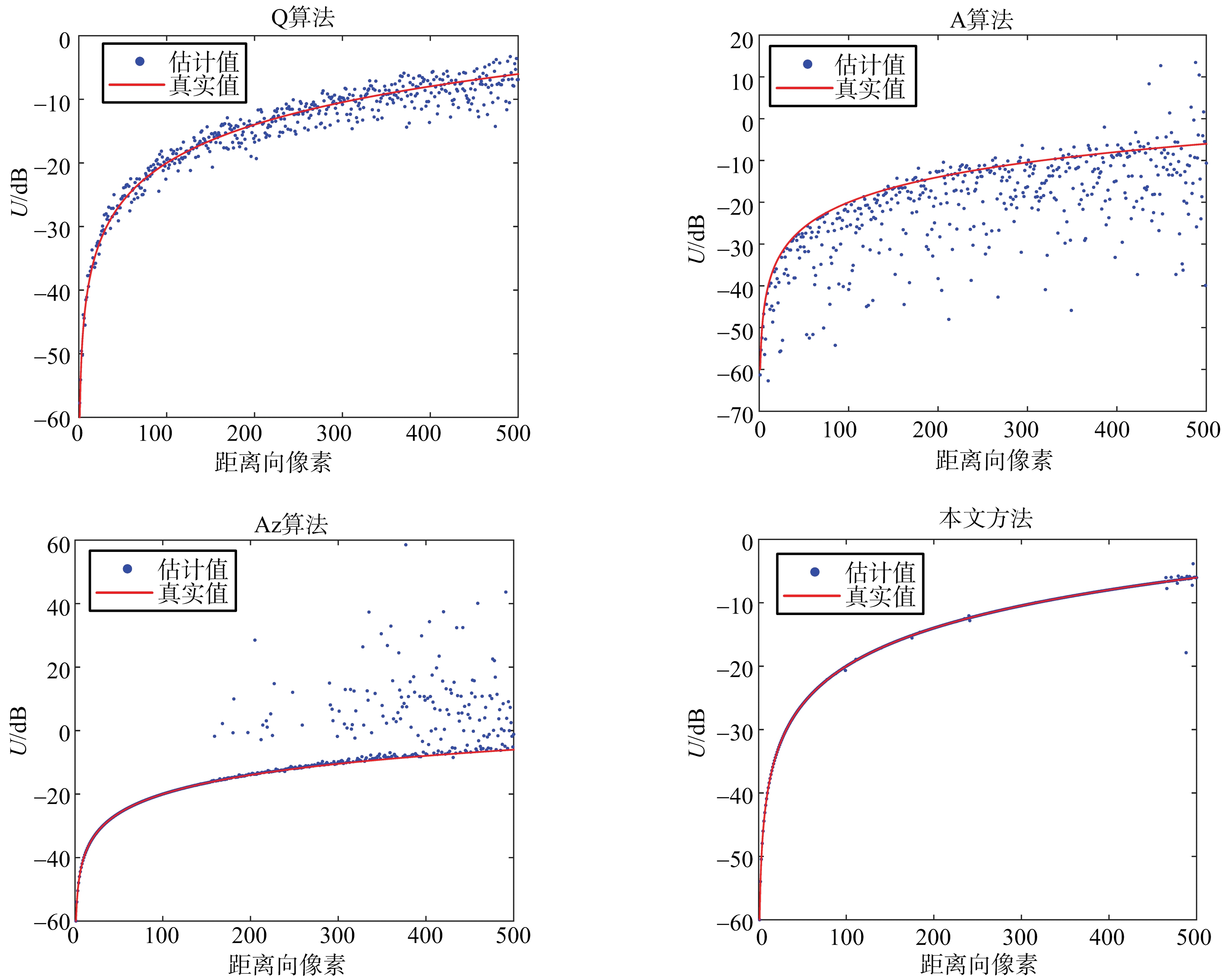
(a) 串扰值估计
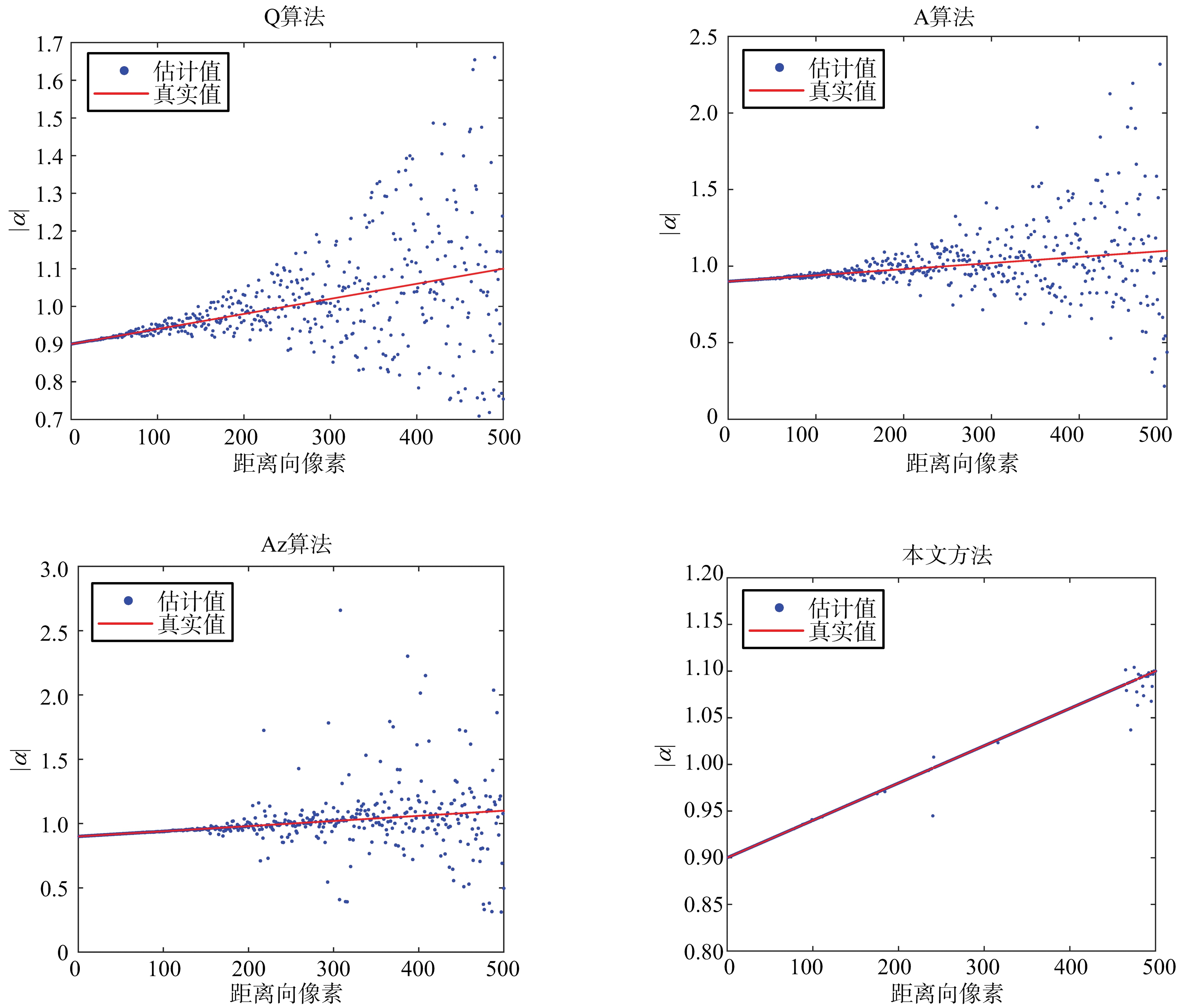
(b) 通道不平衡度估计
图5 4种算法对串扰和通道不平衡度的参数估计
图6给出了4种算法校准后数据的Pauli RGB图像。从图6可以看出，Az算法的校准结果出现了较大的错误，A算法在近距离处有着不错的定标效果，然而随着远距离串扰值的增大，校准后颜色与原图像不对应，Q算法在远距离仍有未准确定标的区域，而本文的方法能够准确地还原图像。
(a) Q算法
(b) A算法
(c) Az算法
(d) 本文方法
图6 4种算法校准后的Pauli RGB图
4 结束语
理论分析和实验结果表明，经典的极化定标算法无法兼顾稳定性和精确性。本文提出了一种基于PSO的极化定标算法，文章详细地阐述了PSO算法的应用过程，并基于仿真的极化失真数据进行极化定标试验，实验证明了PSO算法用于极化定标的有效性，对极化误差参数相比经典算法有着更加稳定精确的估计。
[1] 王雪松. 雷达极化技术研究现状与展望[J]. 雷达学报, 2016, 5(2):119-131.
[2] 代大海,廖斌,肖顺平,等. 雷达极化信息获取与处理的研究进展[J]. 雷达学报, 2016, 5(2):143-155.
[3] 胡丁晟,仇晓兰,雷斌,等. 极化串扰对基于Cloude分解的地物散射机制特征量影响分析[J]. 雷达学报, 2017, 6(2):221-228.
[4] XU Feng, WANG Haipeng, JIN Yaqiu, et al. Impact of Cross-Polarization Isolation on Polarimetric Target Decomposition and Target Detection[J]. Radio Science, 2015, 50(4):327-338.
[5] 陶利,曲圣杰,陈曦. 简述极化SAR定标处理技术研究进展[J]. 遥感技术与应用, 2016, 31(3):459-467.
[6] HU Dingsheng, QIU Xiaolan, HU Donghui, et al. Improved Airborne PolSAR Calibration Algorithm Based on Time-Variant Attitude Compensation[J]. International Journal of Remote Sensing, 2015, 36(12):3184-3195.
[7] 刘云龙,梁兴东,李焱磊,等. 一种补偿时变姿态的Whitt极化定标改进算法[J]. 电子与信息学报, 2017, 39(10):2354-2359.
[8] KLEIN J D. Calibration of Complex Polarimetric SAR Imagery Using Backscatter Correlations[J]. IEEE Trans on Aerospace and Electronic Systems, 1992, 28(1):183-194.
[9] QUEGAN S. A Unified Algorithm for Phase and Cross-Talk Calibration of Polarimetric Data-Theory and Observations[J]. IEEE Trans on Geoscience and Remote Sensing, 1994, 32(1):89-99.
[10] AINSWORTH T L, FERRO-FAMIL L, LEE J S. Orientation Angle Preserving A Posteriori Polarimetric SAR Calibration[J]. IEEE Trans on Geoscience and Remote Sensing, 2006, 44(4):994-1003.
[11] 张海瀛,李真芳,李锦伟,等. 一种考虑通道噪声的极化SAR定标改进算法[J]. 西安电子科技大学学报(自然科学版), 2016, 43(6):45-50.
[12] MORIYAMA T. Polarimetric Calibration of PALSAR2[C]∥ IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy: IEEE, 2015:1284-1287.
[13] FORE A G, CHAPMAN B D, HAWKINS B P, et al. UAVSAR Polarimetric Calibration[J]. IEEE Trans on Geoscience and Remote Sensing, 2015, 53(6):3481-3491.
[14] XING Shiqi, DAI Dahai, LIU Jin, et al. Comment on “Orientation Angle Preserving A Posteriori Polarimetric SAR Calibration”[J]. IEEE Trans on Geoscience and Remote Sensing, 2012, 50(6):2417-2419.
[15] GOH A S, PREISS M, GRAY D A, et al. Comparison of Parameter Estimation Accuracy of Distributed-Target Polarimetric Calibration Techniques[C]∥ IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain: IEEE, 2007:4175-4178.
[16] KENNEDY J, EBERHART R. Particle Swarm Optimization[C]∥ International Conference on Neural Networks, Perth, WA, Australia: IEEE, 1995:1942-1948.
[17] EBERHART R, SHI Y. Particle Swarm Optimization: Developments, Applications and Resources [C]∥ Congress on Evolutionary Computation, Seoul, South Korea: IEEE, 2001:81-86.
[18] SHI Yuhui, EBERHART R C. Parameter Selection in Particle Swarm Optimization[C]∥ 7th International Conference on Evolutionary Programming VII, London: Springer-Verlag, 1998:591-600.
[19] 刘建华. 粒子群算法的基本理论及其改进研究[D]. 长沙: 中南大学, 2009.
