0 引 言
雷达干扰[1]是指一切破坏和扰乱雷达及相关设备正常工作的战术和技术措施的统称，按照干扰信号的作用机理可分为压制性干扰和欺骗性干扰。其中，压制性噪声干扰是当前雷达干扰系统内一种重要干扰方式，主要以大功率的噪声淹没目标回波，大幅度降低雷达的工作性能，甚至使其无法正常工作。
认知雷达[2]通过自适应优化波形可以提高输出信干噪比，提升雷达在干扰环境中的性能。对压制干扰的抑制性可理解为发射信号与干扰协方差矩阵的二次型最小化，特征目标匹配波形设计问题可以归结为二次约束下的二次型规划(Quadratic Constrained Quadratic Programming，QCQP)问题。文献[3]根据压制干扰模型下的波形优化设计问题，提出了白化滤波器结构下基于干扰相关矩阵的波形设计方法。由于该方法获得的优化波形往往具有很高的峰均比，不利于固态发射机发射功率的利用，且自相关性能较差。考虑到上述问题，文献[4]将设计波形与典型波形间的相似度引入目标函数，提出了一种干扰环境下SWORD波形设计方法，能够同时优化峰均比和自相关性能，提高干扰抑制能力。文献[5]利用二次型规划的迭代算法，设计了一种能够同时设计恒模序列和干扰抑制滤波器的方法。文献[6]以最小化不同距离单元的散射系数的均方误差(Mean Square Error，MSE)为目标函数，在干扰谱方差矩阵内的子空间内，采用交替迭代法对目标函数进行优化求解，提高系统的信干噪比，达到抗干扰的效果。
但上述抑制压制性干扰波形设计方法都是针对一维调制优化，即快时间维，并没有充分利用雷达系统发射端的自由度。而二维调制优化能够发挥雷达系统的自由度，提高接收端目标检测性能。二维调制的维度一般可分为快时间域(又称距离维、脉内调制)、慢时间域(又称多普勒维、脉间调制)这两个维度，由于通常调幅方式会降低发射机效率，因此调制维度一般限制在相位域。
本文针对压制性干扰环境中认知雷达捷变波形设计，研究发射端二维调制优化准则和数学模型，并且提出降维策略，设计低复杂度的优化算法，在脉间采用动目标检测处理，最终提出完整的捷变波形二维调制优化流程和方法，并仿真验证该算法的可行性。
1 认知雷达二维自适应抗干扰捷变波形设计算法模型
认知雷达捷变波形波形设计中，二维调制模型如图1所示。在一个相干处理间隔(Coherent Processing Interval，CPI)内，发射端发射N个脉冲，每个脉冲利用M个子脉冲编码进行调制，且各个脉冲的调制都不相同。
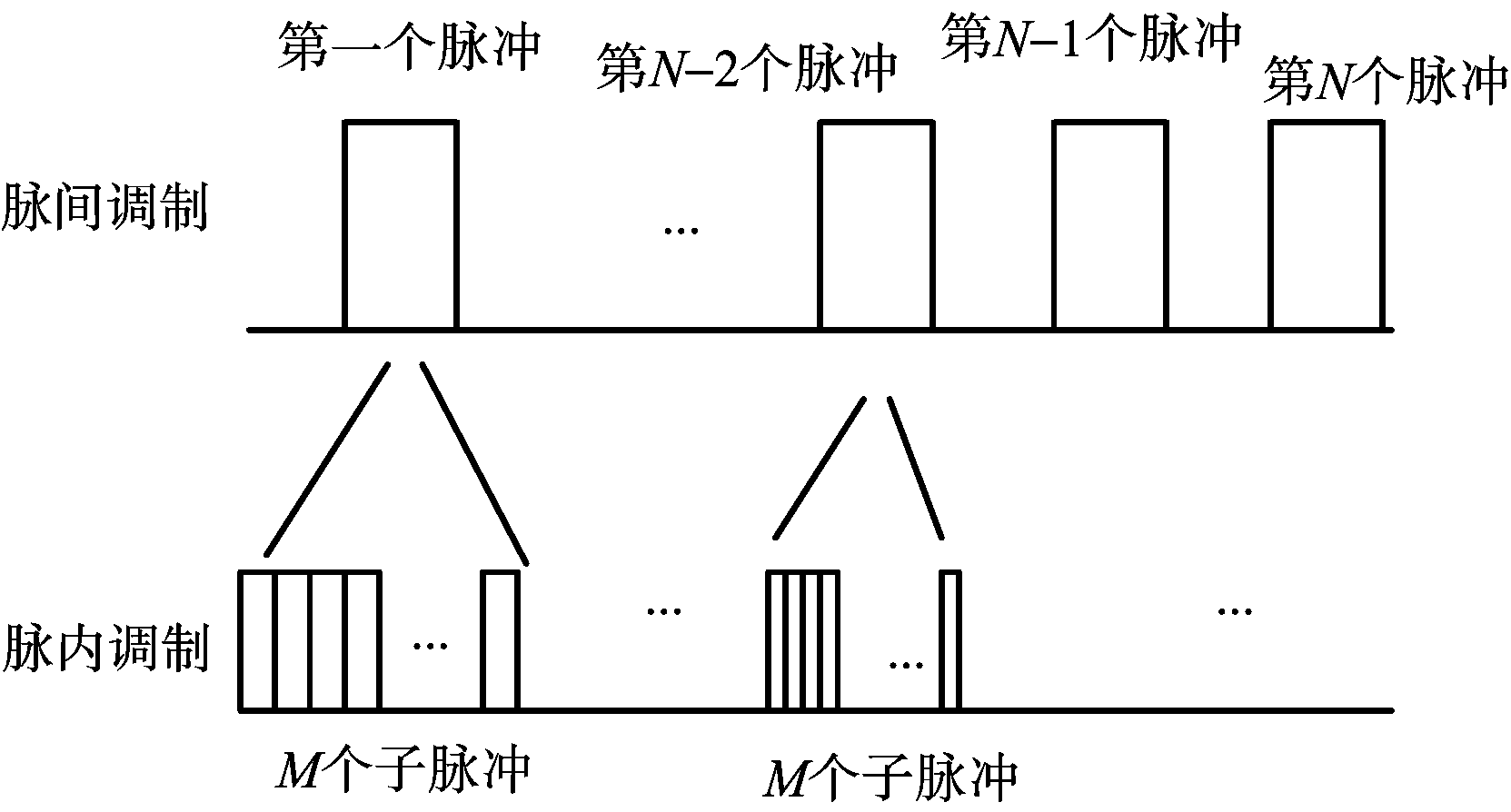
图1 二维调制模型
设一个发射雷达系统发射N个连续脉冲序列，表示如下：
(1)
式中，sn(t)为第n个发射脉冲的复包络，Tr为脉冲重复周期(Pulse Repetition Interval, PRI)。假设脉冲sn(t)的持续时间T=Mtp，其中tp表示子脉冲持续时间，M表示sn(t)的子脉冲码长。
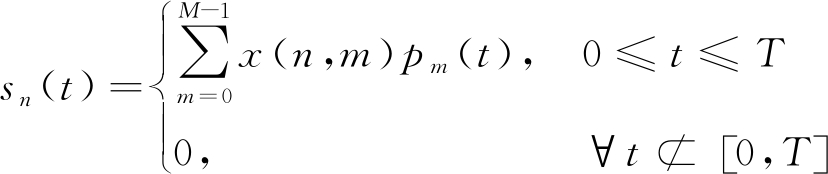
(2)
式中，x(n,m),n=0,1,…,N-1,m=0,1,…, M-1是需设计的调制编码序列。
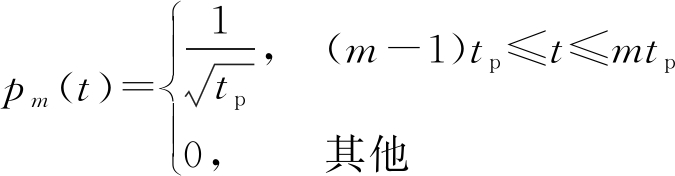
(3)
式中，pm(t)是时间长度为tp的理想矩形脉冲。每个脉冲序列x(n,m)的能量约束为M，即
那么发射的单位模序列为 x(n,m)=ejφn,m，其中，{φn,m}为单位模序列为 x(n,m)的相角。在典型的脉冲多普勒雷达体制中，在一个相干处理时间间隔内，连续发射相同的调制脉冲，即sn(t)=s0(t),∀n。
脉冲sn(t)的脉冲能量为
en=
|sn(t)|2dt=M
(4)
假设雷达环境中干扰信号为j(t)，J为干扰协方差矩阵，接收端的信号为
yn(t)=sn(t-τ)ej2πf(t-nTr)+j(t)
(5)
脉冲多普勒信号处理的第一步是对接收端的回波进行滤波处理，对于点目标的第n个脉冲，设接收端的滤波器为
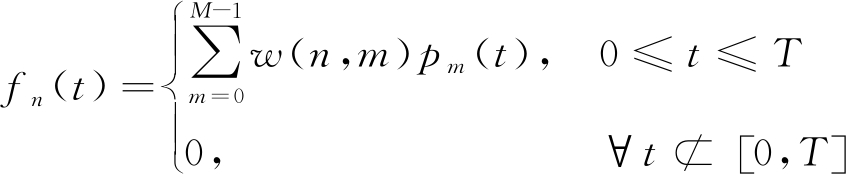
(6)
那么滤波器的输出为
χn(τ,f)=
fn(t)sn(t-τ)ej2πf(t-nTr)dt+
fn(t)j(t)dt=
fn(t)j(t)dt
(7)
式中，τ和f分别为目标时间延迟和多普勒频移。若所有多普勒移频满足-1/2Tr≤f≤1/2Tr ，对于任意第n个脉冲，其持续时间足够小，满足|2πfT|<π/5，即T≤Tr/5，因此由动目标多普勒频率引起的回波相位变化，可以忽略不计。并且，设时间点τ=ptp，p=-M,…,1,…,M，为子脉冲时间长度tp的整数倍。在τ=ptp时间处，由于Tr≫tp，χn(τ,f)为
χn(ptp,f)=
fn(t)j(t)dt≈
fn(t)j(t)dt
(8)
在脉冲多普勒雷达处理流程中，第二步是基于离散傅里叶变换处理相干脉冲序列。为了对一个特定延迟脉冲组进行相干处理，就必须在特定延迟处对前N个脉冲进行采样。因此，匹配滤波结果可用一个2(M-1)×N的二维矩阵 ξ(p,v)来构造，第一维表示时间延迟，第二维表示脉冲数目。对于一个特定的延迟，对匹配滤波结果的每一行进行N点逆离散傅里叶变换。并且频率间隔v=q/NTr，其中q=0,1,…,N-1，为表示方便，化简如下：
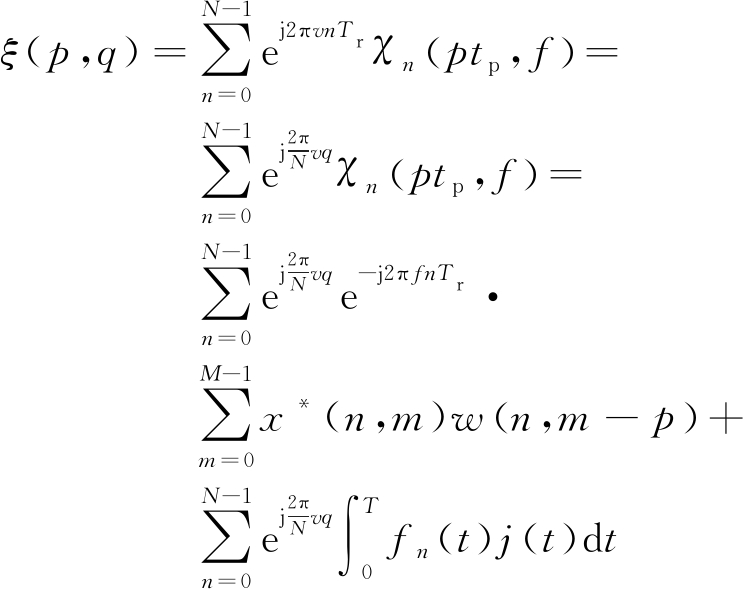
(9)
显然，理想的模糊函数在原点处具有高的窄峰，在其他地方旁瓣和干扰信号为零。由于目标多普勒频率f仅影响多普勒频率轴上的高峰值位置，并且旁瓣能量及干扰信号被限制在所有相关的f，因此可以设置f=0并且定义脉冲串的距 离-多普勒模糊函数。
ξ(p,q)=
(10)
式中，
第n个脉冲编码及其滤波器的互相关系数。
假设IΩ是距离-多普勒范围内除零延时位置处(p=0)，包含(p,q)位置的子集，为抑制旁瓣和干扰信号，则需在IΩ范围内最小化ξ(p,q)，可表示为
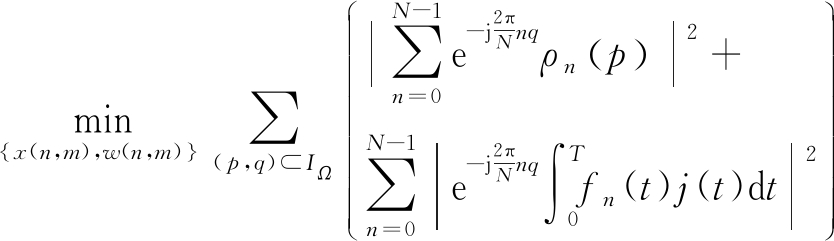
s.t. x(n,m)Hw(n,m)=1
(11)
|x(n,m)|=1
n=0,1,…,N-1,m=0,1,…,M-1
优化过程中，N个发射波形及其接收滤波器{x(n,m)，w(n,m)}，n=0,1,…,N-1，m=0,1,…,M-1均需优化，但同时优化N个脉冲较困难。因而可通过交替迭代法，在其他发射波形固定时，优化第n个发射波形的调制编码
及滤波器
因此式(11)中的优化问题可转化为N个优化问题，且第n个问题可表示为
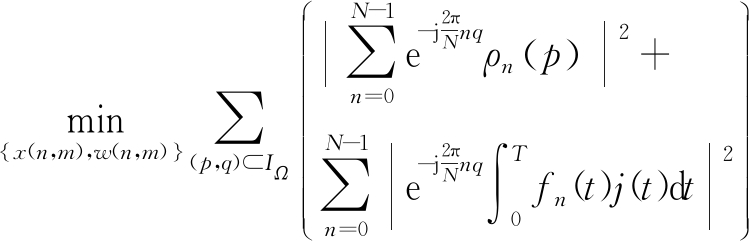
s.t. x(n,m)Hw(n,m)=1
(12)
|x(n,m)|=1
m=0,1,…,M-1
显然式(12)最小化目标函数的物理意义为在理想状态下，在p=0位置处，滤波器的输出χn(ptp,f)有一个尖峰，其他位置在IΩ区域内，滤波器的输出χn(ptp,f)接近于零，能够达到抑制旁瓣及干扰的作用。
设
设Jp为转移矩阵，定义为
Qs为发射信号与滤波器的互相关矩阵，⊙为哈达玛积。
(13)
那么调制信号的旁瓣经过滤波器时，目标函数中
可表示为
干扰j(t)的协方差矩阵为J，那么
可表示为
则优化模型转化为
2 模型求解方法
针对模型
需优化用xn，wn，可通过交替迭代，即分为两步：1)假设xn已知时，用
模型优化wn，其中Qx为发射信号xn的旁瓣协方差矩阵；2)假设wn已知时，用
模型优化xn，其中Qw为滤波器wn的旁瓣协方差矩阵。
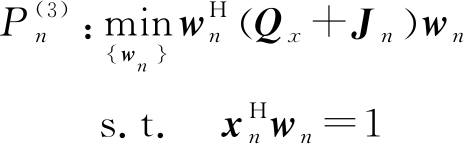
(15)
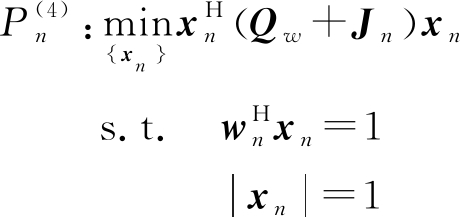
(16)
针对模型
目标函数的Lagrange函数[7]为
L(wn,a)=
(17)
式中，a是Lagrange乘子，不为0的常数。
利用数学上的对偶原理，求式(17)L(wn,a)的最小值：
当式(18)成立时，L(wn,a)取得最小值。
(18)
则目标函数转化为
(19)
利用线搜索法求得a，将a，xn的表达式代入式(18)，可求得滤波器wn。接着，求解模型
针对模型
目标函数的Lagrange函数为
L(xn,b)=
(20)
式中，b是Lagrange乘子，不为0的常数。
利用数学上的对偶原理，求式(20)L(xn,b)的最小值：
当式(21)成立时，L(xn,b)取得最小值。
(21)
则目标函数转化为
(22)
利用线搜索法求得b，将b，wn的表达式代入式(21)可求得发射信号xn。认知雷达二维自适应抗干扰捷变波形设计模型算法求解过程如下：
Step 1：设参数脉冲个数为N，码长为M，初始发射信号为随机相位编码信号，模恒为1，设定干扰信号为j(t)=[U0+Un(t)]exp[j2πf0t+φ0]，计算其协方差矩阵为J；
for n=0∶N-1
Step 2：针对模型
计算发射信号wn的旁瓣协方差矩阵Qw：
1) 令
求解b，使得g(b)达到最小值；
2) 求解
3) 对xn进行恒模处理，xn=ej(arg(xn))；
Step 3：重复Step 1和Step 2，直到
和
达到最小值。
end
3 仿真实验和性能分析
选取参数：发射信号s码长N为200，旁瓣信号用平均旁瓣电平来表征旁瓣性能，在数学形式上表征为2范数平方的均值。接收端滤波器为w，干扰信号为Uj，其协方差为Rn。输入信干比定义为在雷达发射端，发射信号与干扰信号平均功率之比，SIRin=10lg(E(s2)/E(Uj2))；输出信干比定义为在雷达接收端，目标信号回波和干扰信号平均功率之比，SIRout=10lg((s*w)2/wHRnw)。干扰信号为压制性噪声调幅干扰信号，信号表达式为Uj=[U0+Un(t)]exp[j2πf0t+φ0]，射频信号的幅度U0为0，中心频率f0为35 MHz，初始相位φ0为0，调幅噪声Un(t)是一个均值为0，方差为1，分布区间为[-U0,+∞]的广义平稳随机过程，φ0服从[0,2π]均匀分布。
图2为噪声调幅干扰信号功率谱分析。其中图2(a)为调幅噪声Un(t)功率谱，图2(b)为已调波噪声功率谱。从仿真结果可见噪声调幅干扰功率集中在中心频率f0=35 MHz，幅度为20 dB左右。
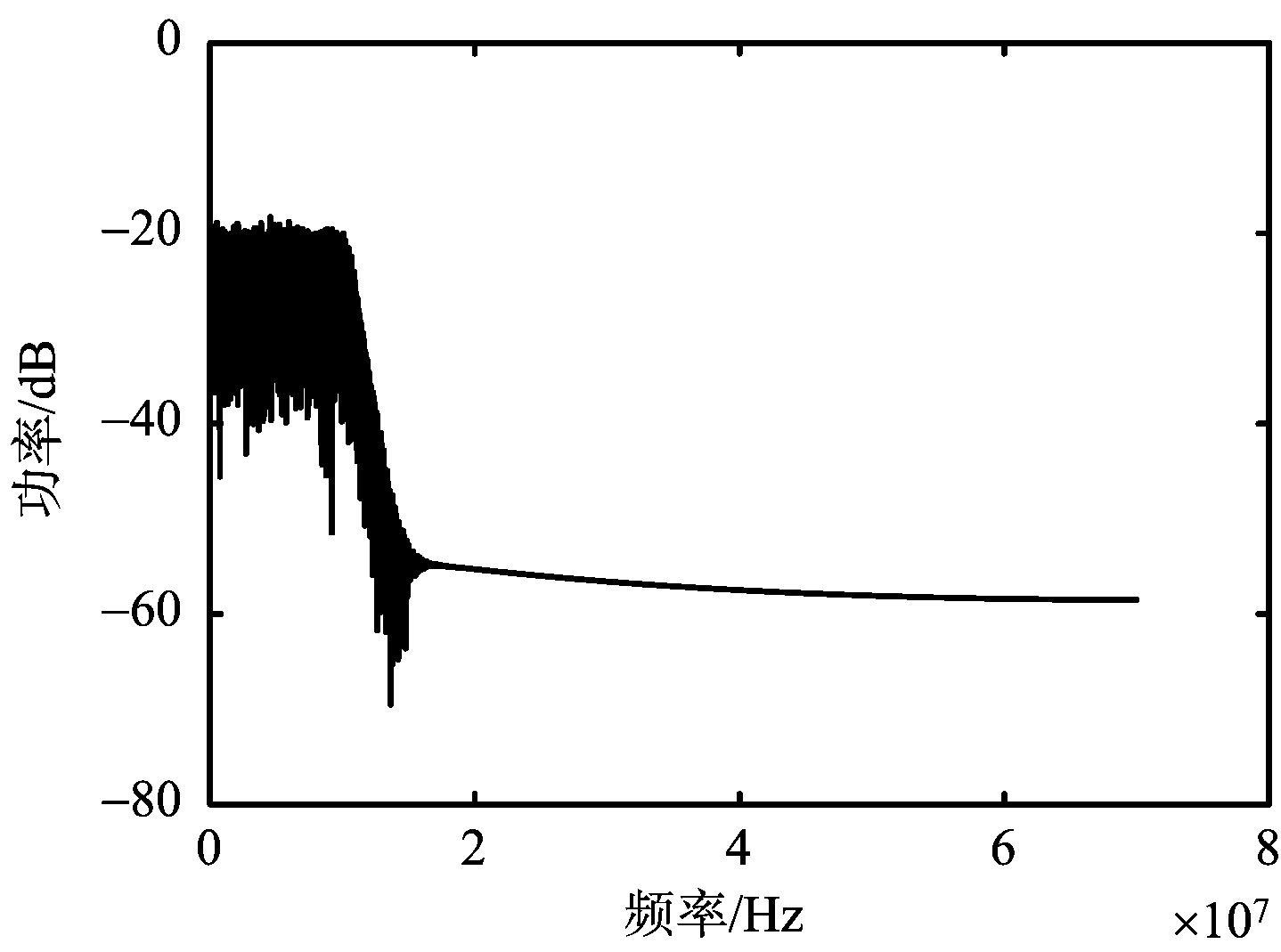
(a) 调制噪声功率谱
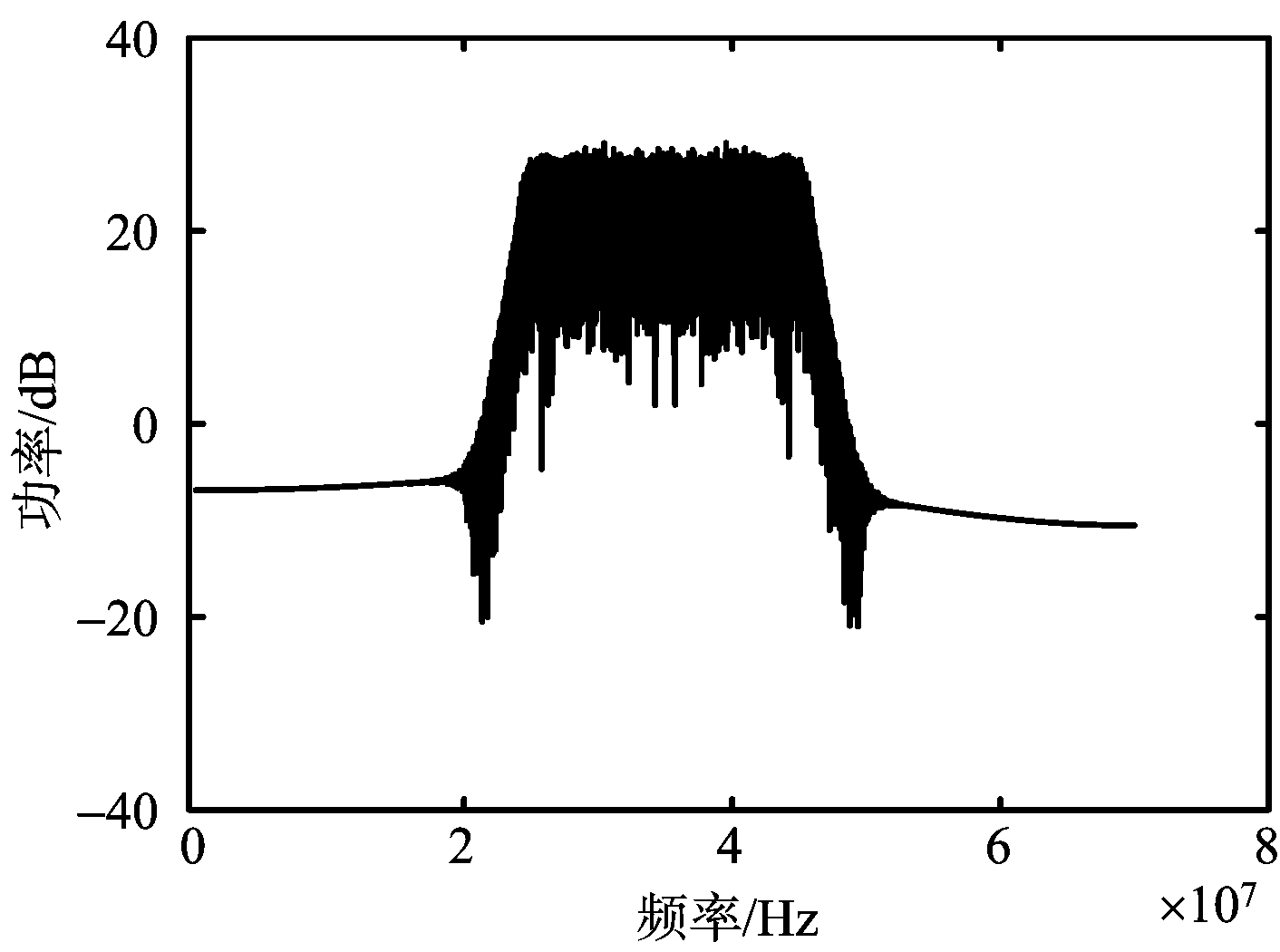
(b) 噪声调幅干扰功率谱
图2 噪声调幅干扰信号功率谱分析
图3为针对模型的干扰抑制性能分析。由图3(a)可知，优化前发射信号及接收滤波器为随机相位编码信号，对干扰没有抑制效果，在接收端滤波器的输出，干扰的输出为0 dB，且信号的旁瓣较高，目标检测性能较低。由图3(b)可知，优化后发射信号及接收滤波器对干扰和旁瓣均有抑制效果，在接收端滤波器的输出中，干扰被抑制到 -45 dB。验证了该算法的可行性。
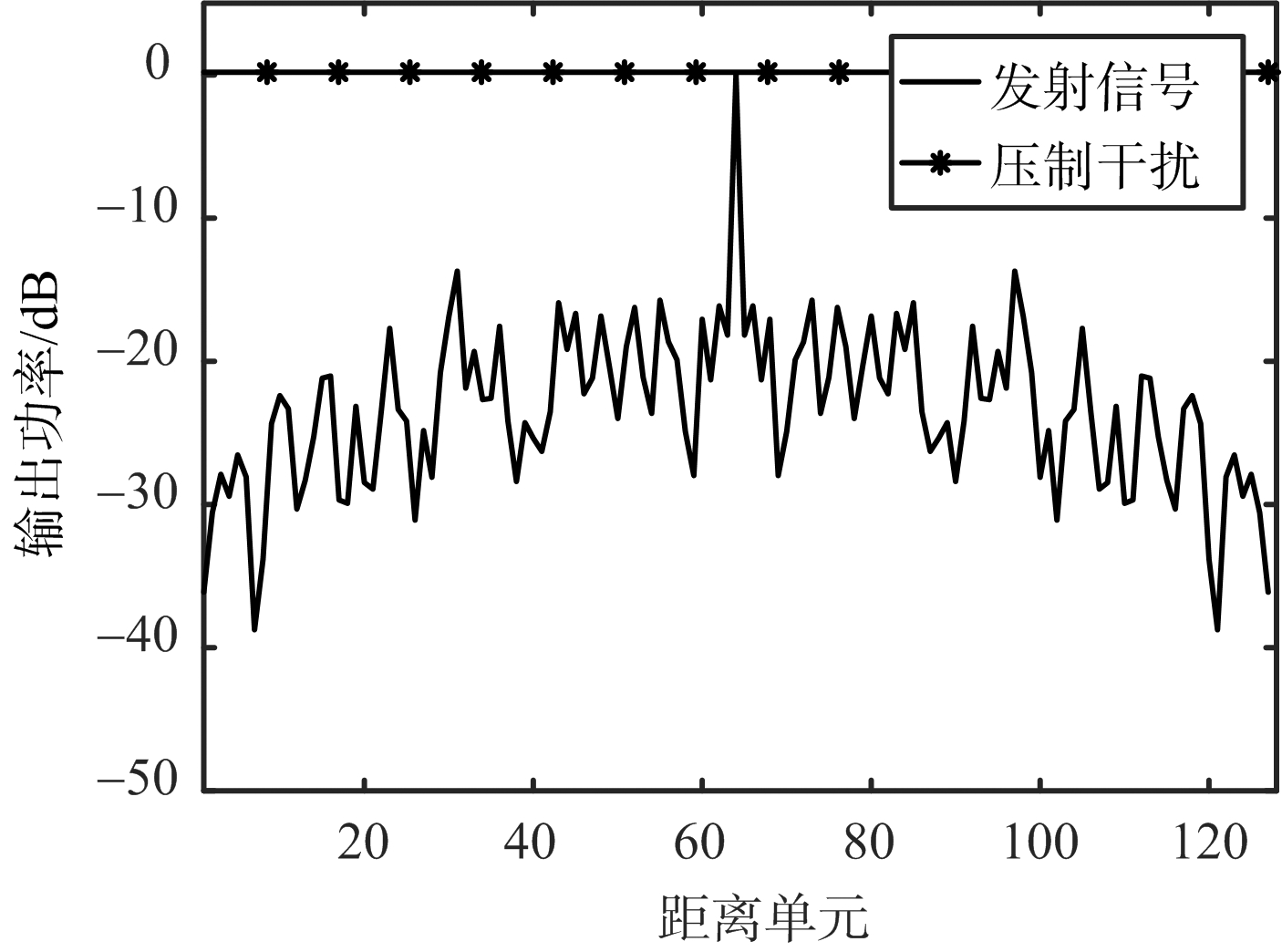
(a) 优化前
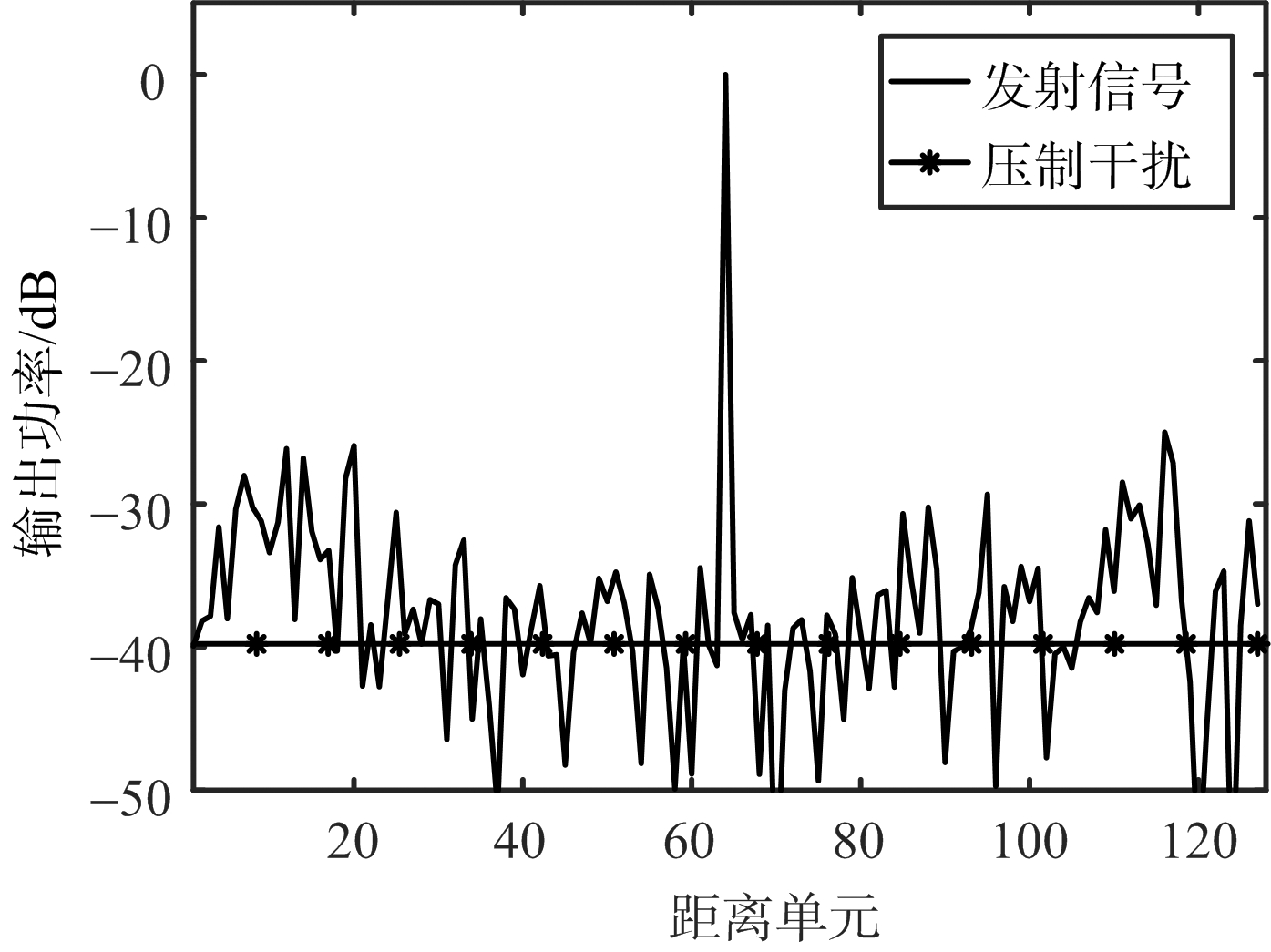
(b) 优化后
图3 单脉冲干扰抑制的优化前后对比图
图4为二维自适应抗干扰优化模型的模糊函数图。其中颜色条表示信号强度，单位为dB。由图4可知，当输入信干比较大时，目标信号被淹没在压制干扰中，无法被检测出。通过优化设计二维发射信号及接收端滤波器，能有效抑制干扰信号，提高目标检测性能。
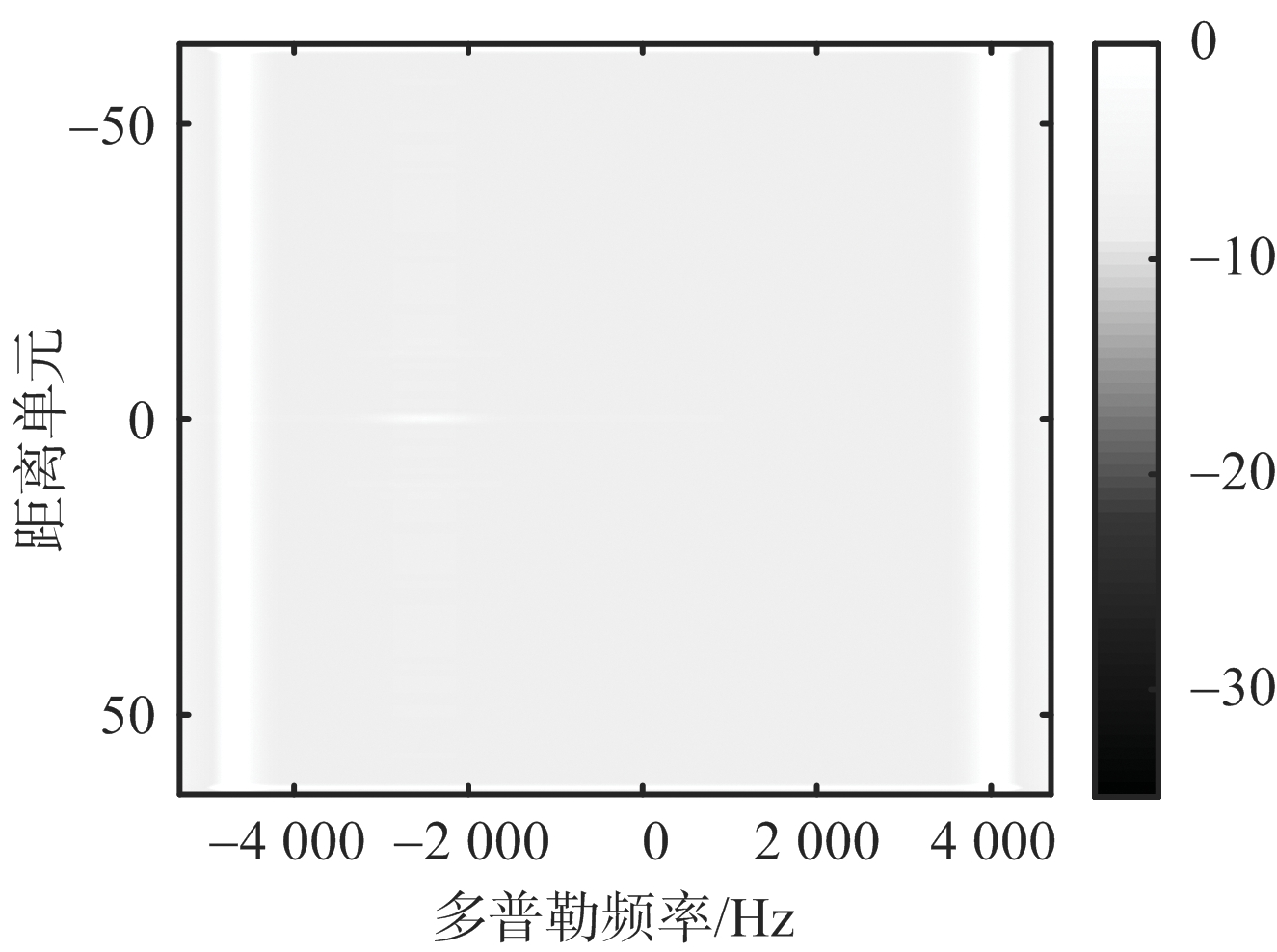
(a) 优化前
(b) 优化后
图4 二维自适应抗干扰优化模型的模糊函数图
在一维(脉内编码)波形设计中，相位编码的码长为M。在二维(脉内编码与脉间编码)波形设计中，脉冲个数为N，每个脉冲码长为M。表1为一维(脉内编码)波形优化和二维(脉内编码与脉间编码)波形优化的自由度对比。由表1可见，二维波形优化能够提高雷达系统的自由度。
表1 一维与二维波形优化自由度对比
编码维度自由度一维(脉内编码)M二维(脉内编码与脉间编码) M·N
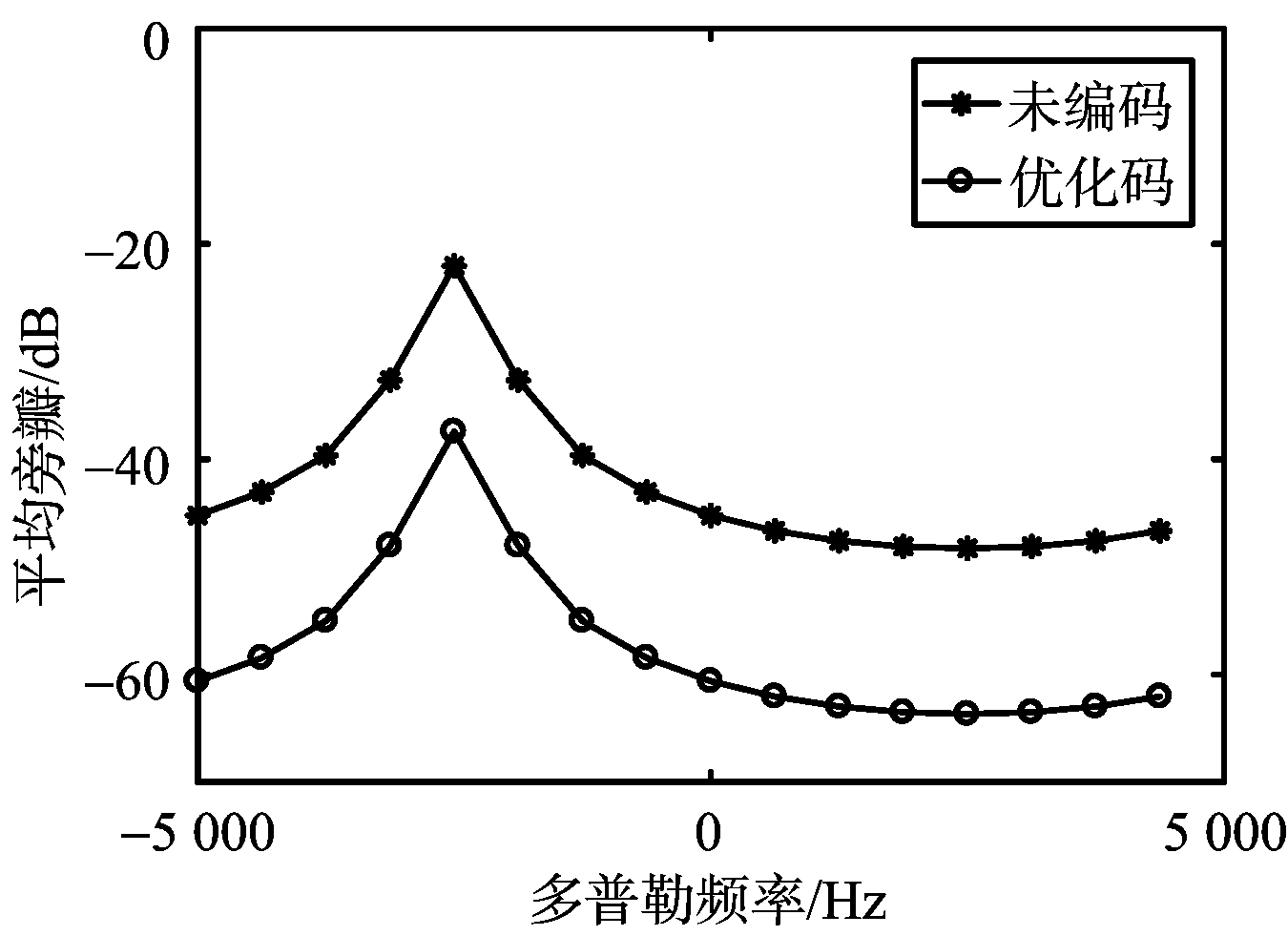
(a) 优化前后平均旁瓣电平
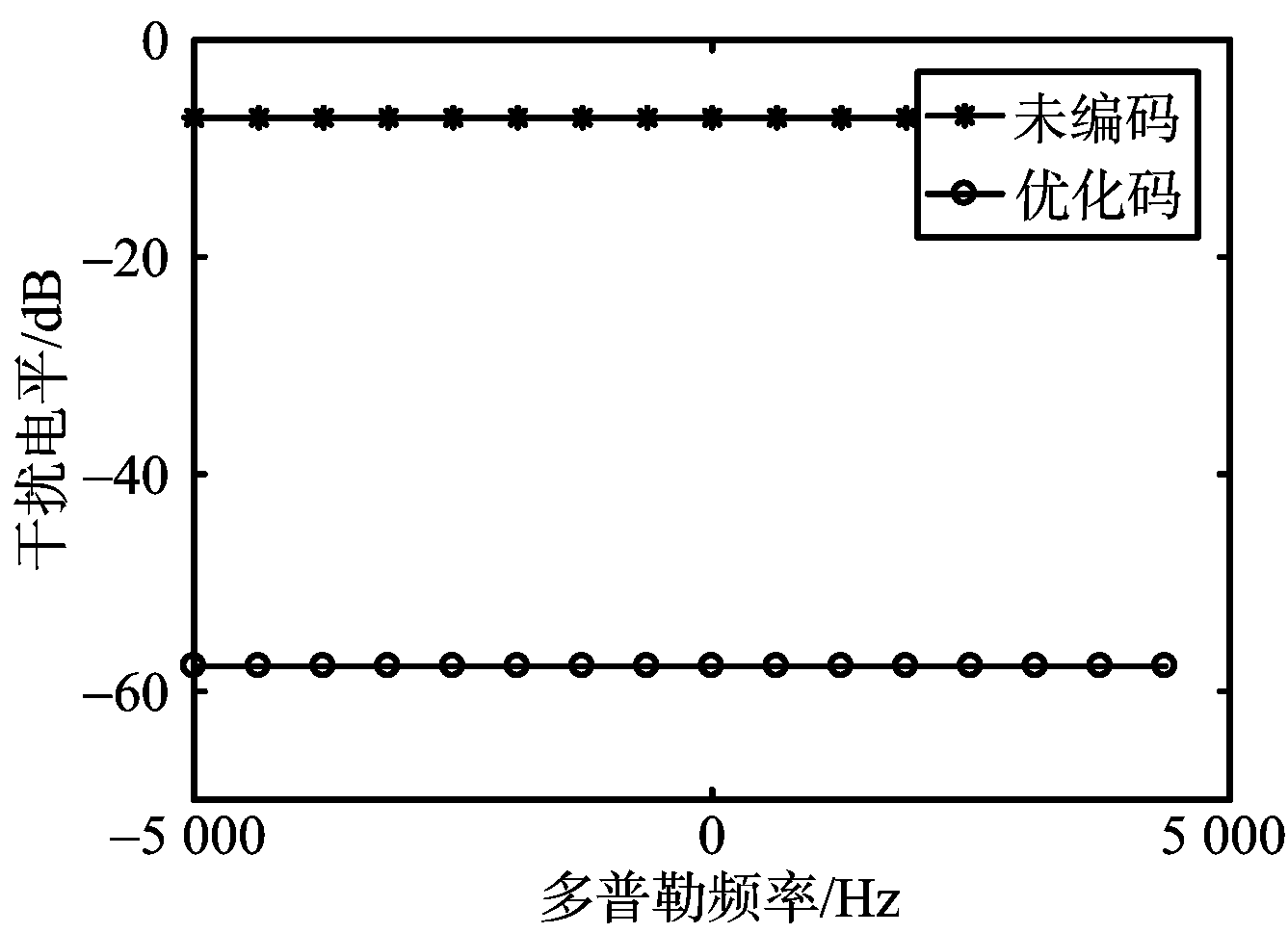
(b) 优化前后干扰电平
图5 优化前后积分旁瓣与干扰电平对比分析
图5为优化前后输出端平均旁瓣与干扰信号电平的对比分析。由图5(a)可知，随机相位编码(即未编码)的平均旁瓣较高。优化后，各通道的旁瓣被抑制，抑制程度在15 dB左右。由图5(b)可知，未编码信号对干扰的抑制程度较低，优化信号波形后，输出端干扰电平下降到-58 dB，干扰抑制程度较高，验证了算法的可行性。
图6为不同输入干信比下输出端的信干比曲线图。从优化码和随机相位编码(即未编码)的对比分析可知，随着输入端干信比的增大，未编码信号的输出信干比呈下降趋势，而优化码的输出信干比在39 dB左右。
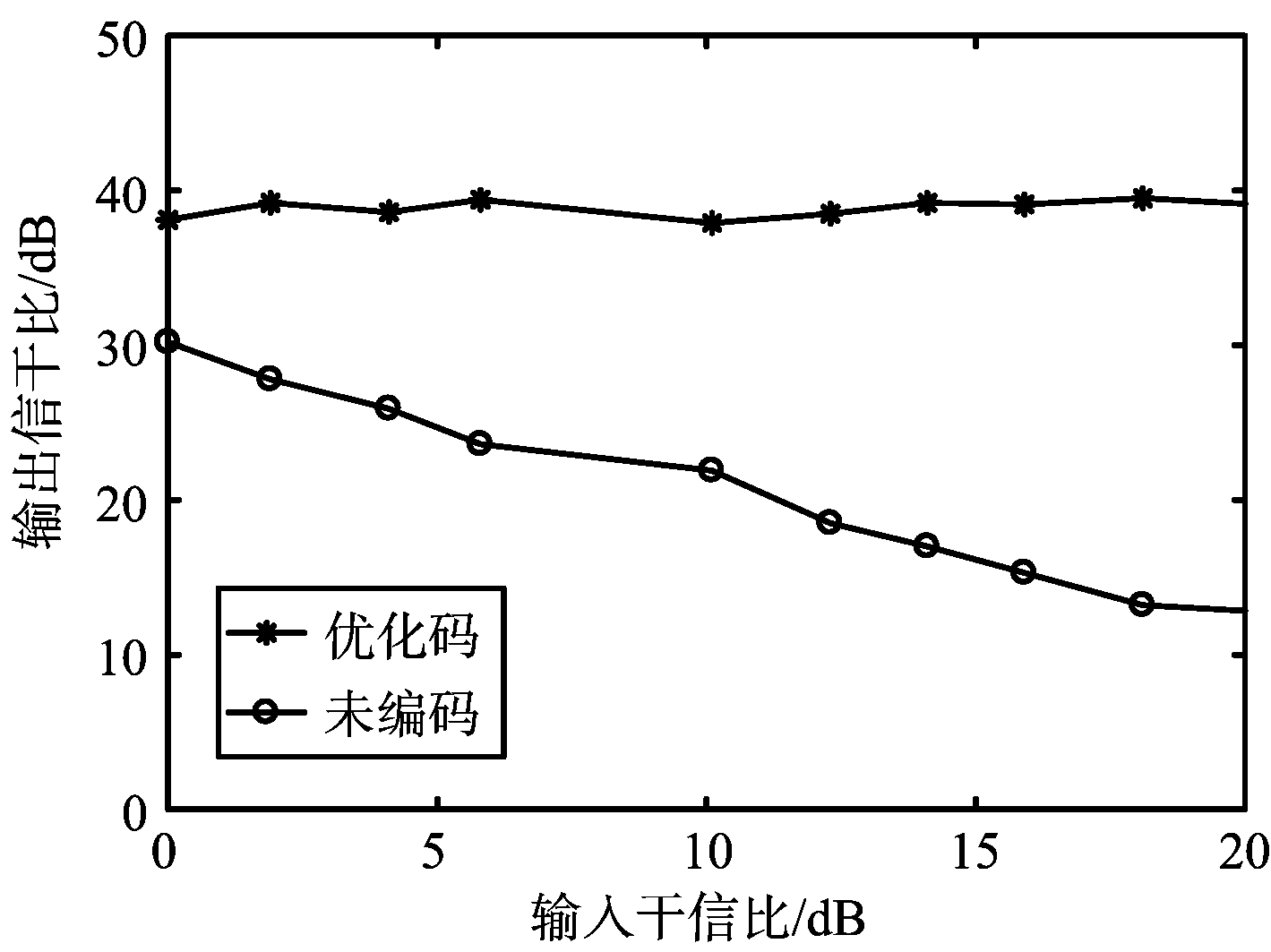
图6 输入输出对比分析
4 结束语
认知雷达采用有效的反馈机制，把接收处理系统“感知”到的目标、场景特征信息反馈到发射端，指导天线系统采用与之“匹配”的发射方式。本文研究认知雷达二维抗干扰波形设计方法，提高了发射端的自由度。首先研究基于模糊函数的发射端二维抗干扰捷变波形调制优化准则和数学模型；其次设计降维策略，将复杂的高维优化问题拆解为多个低维度子优化问题。接着，简化模型并采用Lagrange乘子法及交替迭代法对模型进行求解，形成完整的二维自适应抗干扰捷变波形调制优化流程和方法。相比较于传统的单一维度优化波形，该算法的创新点在于二维抗干扰捷变波形能够从发射端提高雷达系统的自由度。最后通过仿真验证算法的可行性。
[1] 姜智卓. 极化认知雷达抗干扰波形设计研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.
[2] HAYKIN S. New Generation of Radar Systems Enabled with Cognition[C]∥ IEEE Radar Conference, Washington, DC: IEEE, 2010:1.
[3] 石荣，刘江.干扰资源分配问题的智能优化应用研究综述[J].电光与控制，2019，26(6)：1-11.
[4] LI J, GUERCI J R, XU L. Signal Waveform’s Optimal-Under-Restriction Design for Active Sensing[J]. IEEE Signal Processing Letters, 2006,13(9):565-568.
[5] SOLTANALIAN M, TANG B, LI J, et al. Joint Design of the Receive Filter and Transmit Sequence for Active Sensing[J]. IEEE Signal Processing Letters, 2013, 20(5):423-426.
[6] LESHEM A, NAPARSTEK O, NEHORAI A. Information Theoretic Adaptive Radar Waveform Design for Multiple Extended Targets[J]. IEEE Journal of Selected Topics in Signal Processing, 2017,1(1):42-55.
[7] 韦增欣,陆莎. 非线性优化算法[M]. 北京: 科学出版社, 2015:6.
