0 引 言
空时自适应处理(STAP)是一种有效的杂波与干扰抑制技术[1-2]。然而，在实际工程中，全维STAP方法面临运算量大、样本需求大的问题。为解决这些问题，降维STAP方法受到广泛关注[2-4]。
目前，降维STAP方法主要分为两类：第一类是基于自适应结构的降维STAP方法，该类方法直接对全空时数据进行分级分解，如基于相关相减结构的多级维纳滤波[5]，以及基于数据分级的快速全维自适应算法(FFA)[6]，然而，对高维数据的直接处理使此类方法的运算量较大；第二类是基于固定结构的降维STAP方法，该类方法选择固定的辅助通道实现降维，如扩展因子化方法(EFA)[7]、局域联合处理方法(JDL)[8-9]。
在上述方法中，第二类基于固定结构的降维STAP方法受到广泛关注。该类方法通过选择固定的辅助通道作为局域，实现降维的自适应处理。文献[7]提出一种在时域实现局域化处理的EFA算法，该方法联合多个邻近的多普勒通道与所有的空域通道进行空时自适应处理。但是，随着系统中的天线阵元数增大，该方法的计算量也增大。针对这一问题，文献[8-9]提出了一种在空域和时域都进行局域化处理的JDL方法，该方法联合多个邻近的多普勒通道与多个邻近的空域通道进行空时自适应处理。然而，该类方法中辅助通道的选择往往是固定的，从而使该类方法的性能受限。
针对上述问题，本文考虑到天波雷达的海杂波信号具有低秩的特点，利用该特点，提出一种基于稀疏降维的STAP方法。该方法首先选择与待检测角度-多普勒通道邻近的多个通道作为辅助通道，得到初步的降维矩阵。然后，结合天波雷达的海杂波信号具有低秩的特点，进一步用稀疏方法选择通道和降维。所提方法基于稀疏正则化的原理，寻找稀疏的滤波权向量，从而可以自适应地选择性能更好的辅助通道，进一步提高了海杂波抑制性能。对天波雷达实测数据的处理结果表明，与文献[8-9]中的JDL方法相比，所提方法的杂波抑制性能提高了6.17 dB。
1 问题描述
考虑一个由N个阵元构成的阵列，一个相干处理间隔发射M个脉冲。匹配滤波后，第l0个距离单元的回波信号x(l0)∈CMN×1表示为
x(l0)=η(l0)s(ω,θ)+c(l0)
(1)
式中，η(l0)是目标的散射系数，c(l0)是杂波和干扰，s(ω,θ)是目标的空时导向矢量，其表示为
s(ω,θ)=st(ω)⊗ss(θ)
(2)
式中，⊗表示Kronecker积，st(ω)=[1;ei2πω;…;ej(M-1)2πω]T是目标时域导向矢量，ss(θ)=[1;ei2πθ;…;ej(N-1)2πθ]T是目标空域导向矢量，ω是归一化多普勒频率，θ是空间频率。
在文献[8-9]中的JDL降维方法中，将与待检测的角度-多普勒通道邻近的p×p个通道(包括1个待检测通道和p2-1个邻近通道)选为局部处理域，利用这些局部处理域构造降维矩阵T∈CMN×p2。此时，假设目标在第l个距离单元(CUT)，该距离单元的最优滤波权向量w(l)满足：
(3)
求解上述优化问题，得到CUT的最优滤波权向量w(ω,θ)(l)为
(4)
式中，上标H表示共轭转置，
表示降维后的空时导向矢量，R(l)表示CUT单元的杂波协方差矩阵，需要选取L个样本距离单元 x(li), i=1,…,L对其进行估计，估计结果为
2 所提稀疏降维的STAP方法
本文注意到在天波雷达的海杂波信号具有低秩特性，因此，只需利用少量的辅助通道就能实现海杂波的有效抑制。根据这个特性，本文将传统的JDL方法与稀疏正则化理论结合，提出了一种基于稀疏滤波的降维STAP方法，更有效地抑制海杂波。
2.1 基于JDL算法构建降维矩阵
在稀疏滤波之前，本文所提方法根据JDL方法获得初步的降维矩阵T。假设CUT距离单元中待检测角度-多普勒通道的空时导向矢量为 s(ωm,θn)，选择与其邻近的p×p个通道作为局部处理域，得到的降维矩阵Τ为
T=[s(ωm,θn) s(ωm-⎣p/2」,θn-⎣p/2」) …
s(ωm+⎣p/2」,θn+⎣p/2」)]
(5)
式中，⎣p/2」表示向下取整。
求出R(l)以及待检测通道降维后的空时导向矢量
结合式(4)求出待检测通道的滤波权向量w(ωm,θn)(l)。
2.2 稀疏滤波
考虑到天波雷达中海杂波信号具有低秩特性。在滤波时，结合稀疏正则化理论进一步选择性能更好的辅助通道，从而更有效地抑制海杂波。此时，式(3)中的优化问题写为
(6)
式中，
是一个正则化约束项，wopt(l)是一个稀疏向量。
求解式(6)中的最优化问题，利用拉格朗日乘子法构造代价函数J(w)：
J(w)=w(l)HR(l)w(l)+k‖w(l)‖1+
(7)
为保证式(7)的导数均存在，将正则化约束项近似为k‖w(l)‖1≈kw(l)HΛw(l)，其中Λ是一个对角矩阵，表示为
Λ=
(8)
式中，w(ωm,θn),i(l), i=1,2,…,p2表示权向量w(ωm,θn)(l)的第i个元素值，ε避免Λ中对角元的分母为0。此时，式(7)中的代价函数近似为
J(w)≈w(l)HR(l)w(l)+kw(l)HΛw(l)+
(9)
对式(9)中代价函数关于w(l)求梯度，并令其为0，则
J(w)=2R(l)w(l)+2Λw(l)-
(10)
即
此时，式(6)中的最优解为
wopt(l)=
(11)
对于同一个待检测通道的最优权向量，与式(4)中传统的JDL算法的结果相比，式(11)中由正则化约束项产生了kΛ，使得式(11)的滤波权向量具有稀疏特性。
上述算法在进一步对参考数据降维的过程，实际上就是进一步选取性能更好的参考通道的过程，因此所提方法进一步提高了STAP性能。
3 仿真分析
天波雷达实测数据的仿真结果表明，与文献[8-9]相比，本文所提方法可以将海杂波的抑制性能提升6.17 dB。
天波雷达工作参数为：阵元的数目N=192，脉冲重复间隔T=12 ms，脉冲数M=512，雷达工作频率fc=18.3 MHz。
为评估杂波抑制性能，本节定义输出SCNR为
(12)
式中，Et表示目标的能量，
表示所有杂波的平均能量。
3.1 杂波抑制结果
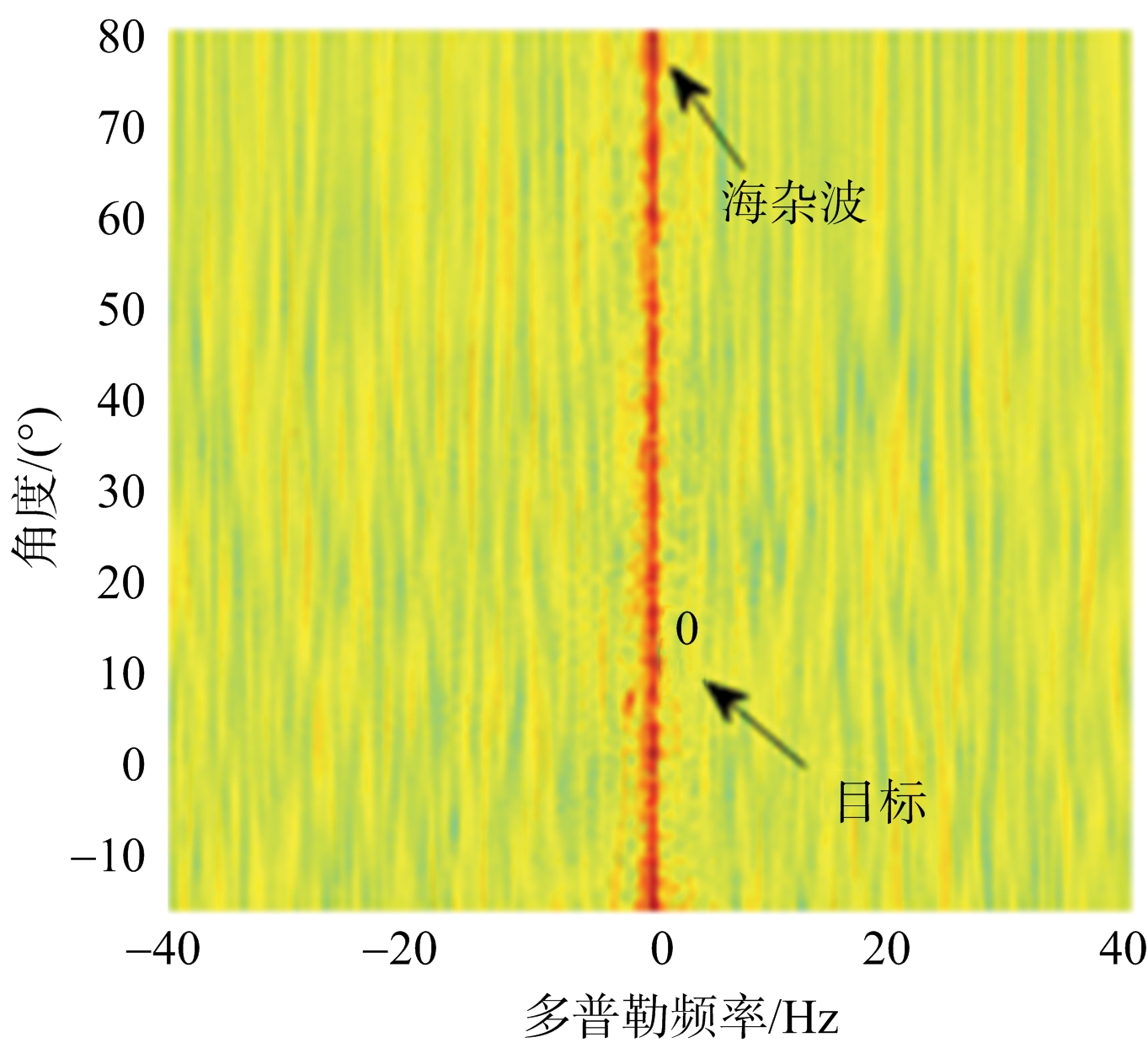
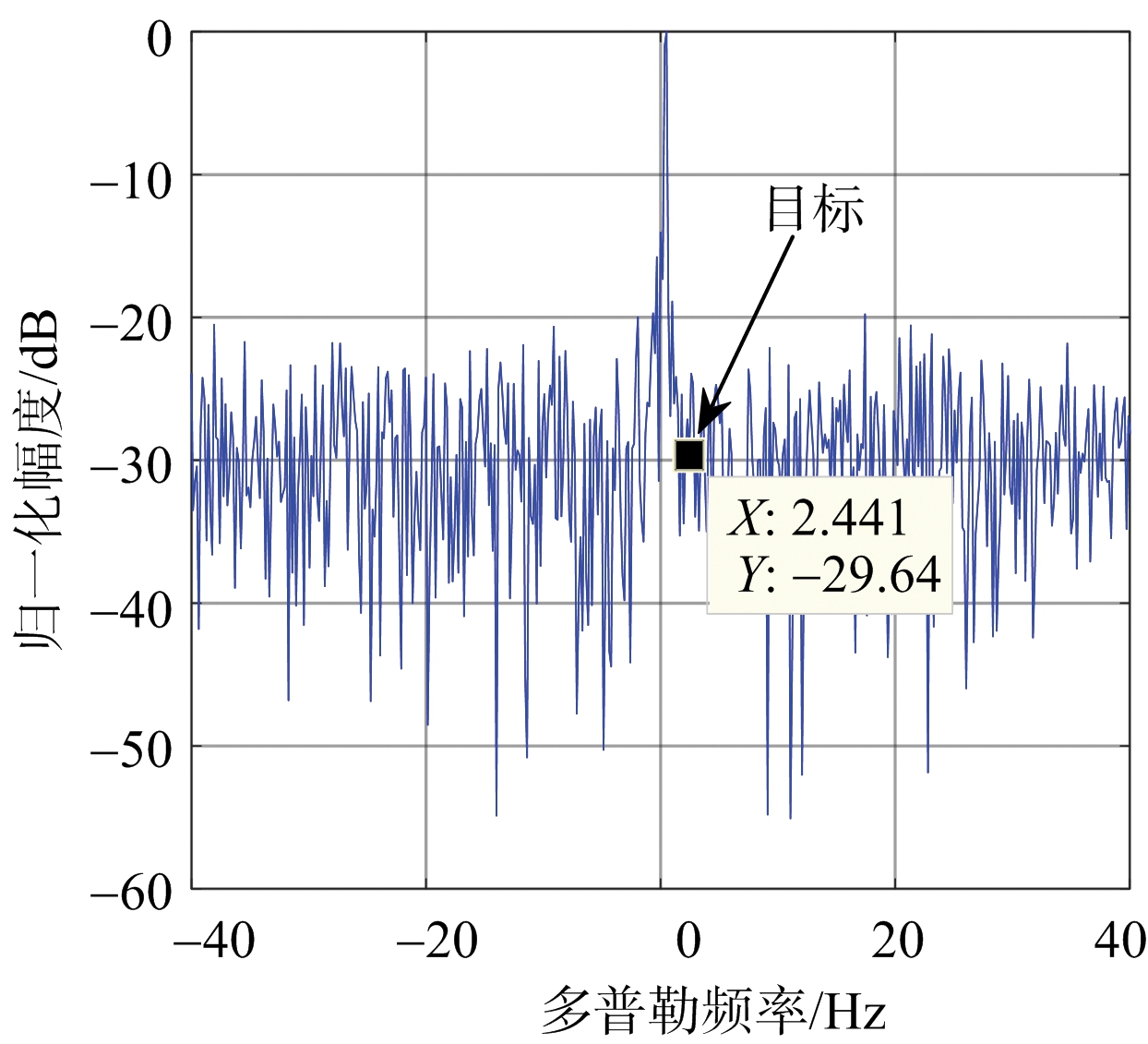
本组仿真实验中，第144个距离单元为待检测距离单元，目标多普勒频率为2.441 4 Hz，目标空间角度为11.516 5°。图1(a)是待检测距离单元的角度-多普勒谱，图1(b)是图1(a)固定在第26个角度的多普勒频谱。
(a) 角度-多普勒谱
(b) 图1(a)固定在第26个角度的多普勒频谱
图1 待检测距离单元的谱
从图1可以看出，目标信号被淹没在强海杂波中，难以检测。
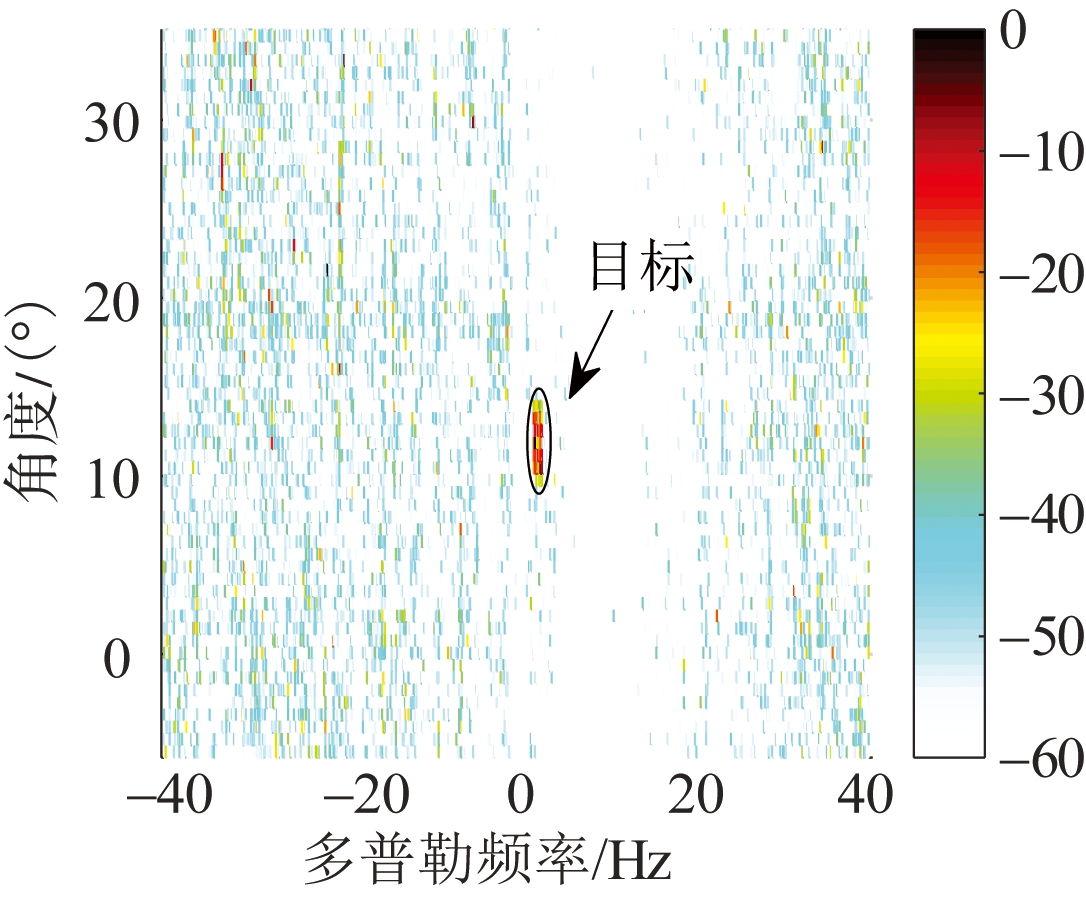
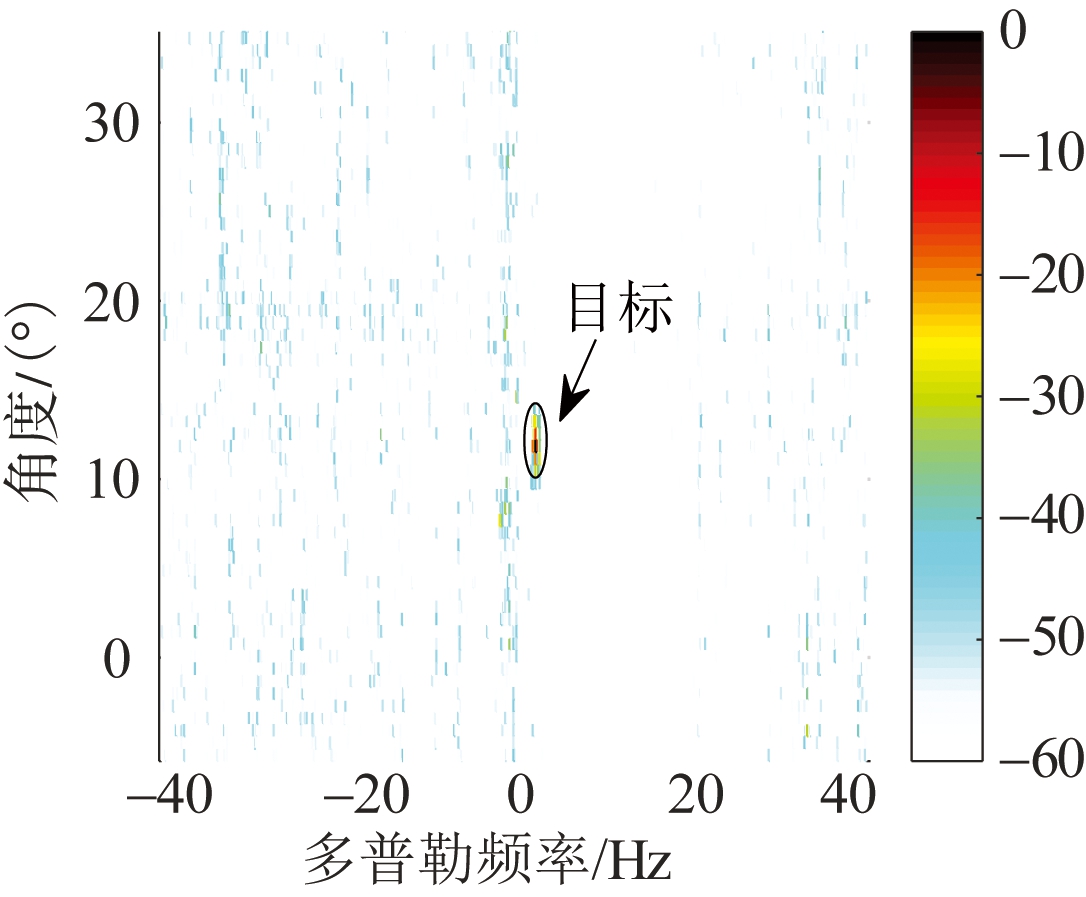
图2是待检测单元的杂波抑制结果。图2(a)是文献[8-9]中的JDL方法的结果，图2(b)是本文所提方法的结果。
(a) 文献[8-9]中的JDL方法
(b) 本文所提方法
图2 实测数据在待检测单元的杂波抑制结果
从图2(a)可以看出，回波信号经过文献[8-9]中的JDL方法处理后，仍有较强的残留杂波；图2(b)表明，利用本文所提方法对回波信号处理后，残留杂波明显减弱。
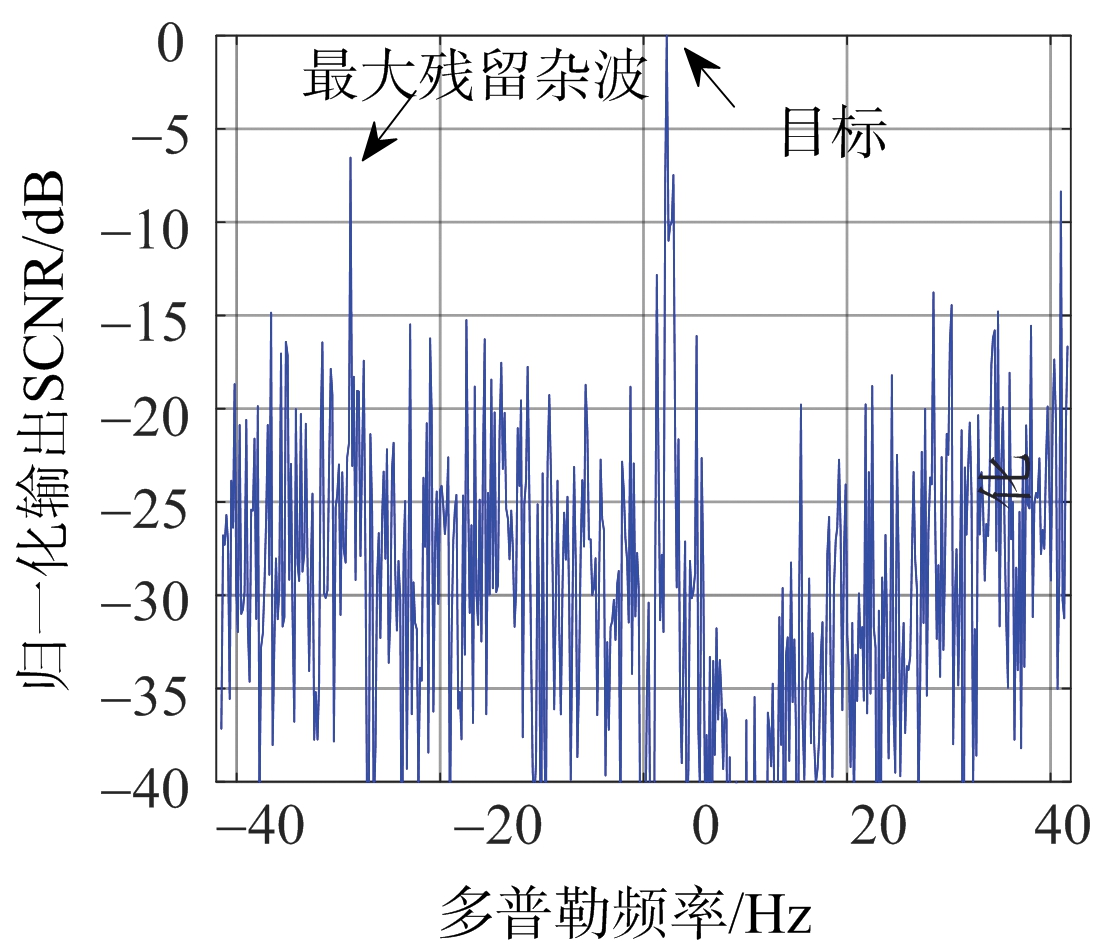
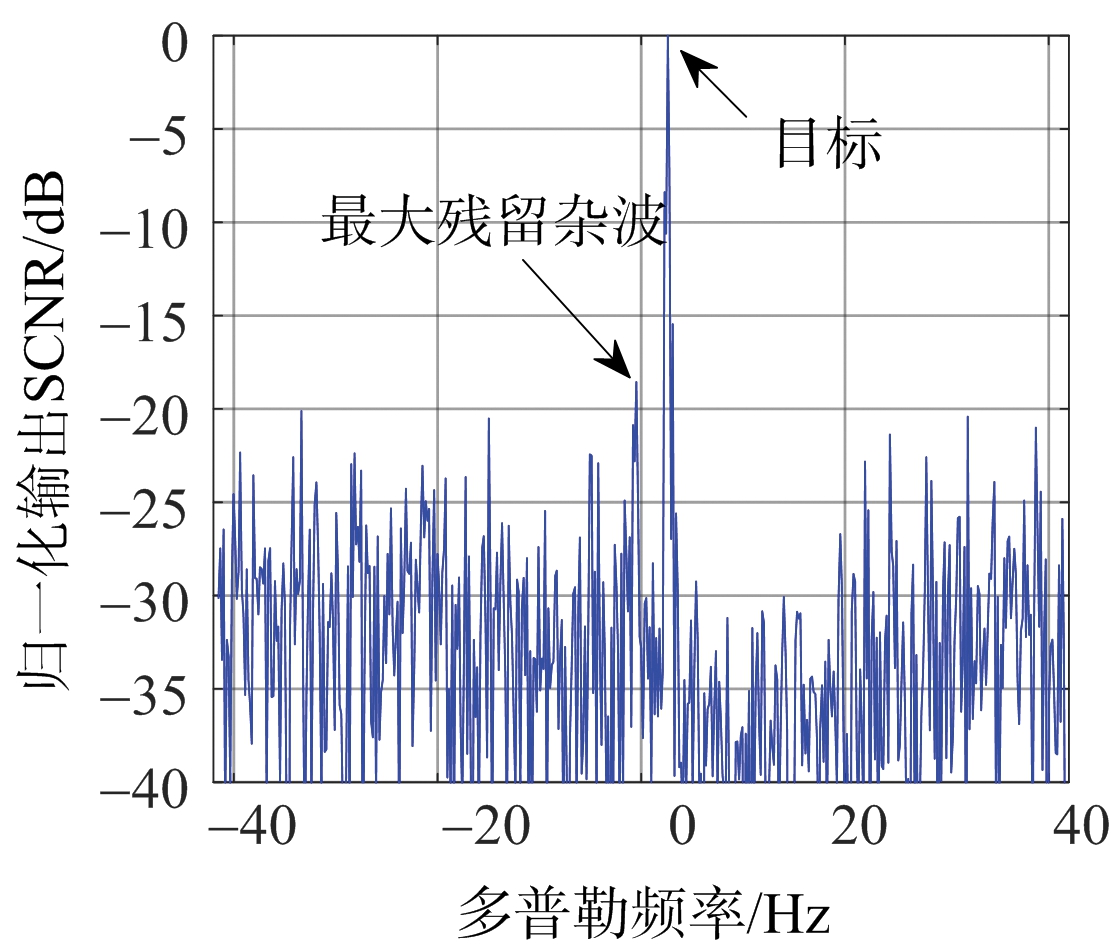
为更清晰地观察图2中两种方法的杂波抑制结果，本文将图2中的结果固定在第26个角度，观察多普勒频谱如图3所示。图3(a)是文献[8-9]中的JDL方法处理后的结果，图3(b)是本文所提方法的处理结果。
在图3(a)中，最大残留杂波的输出SCNR是-6.531 dB，杂波信号的平均输出SCNR为 -23.83 dB；在图3(b)中，最大残留杂波的输出SCNR为-18.55 dB,杂波信号的平均输出SCNR为 -30 dB。
(a) 文献[8-9]中的JDL方法
(b) 本文所提方法
图3 图2固定在第26个角度的多普勒频谱
图3结果表明，与图3(a)相比，图3(b)可以将杂波抑制性能提高了6.17 dB。因此，本文所提方法的杂波抑制性能明显优于文献[8-9]中的JDL方法。
3.2 性能对比分析
本节验证不同输入SCNR时，本文所提方法与文献[8-9]中的JDL方法的杂波抑制性能。其中，目标多普勒频率为2.441 4 Hz，目标空间角度为11.516 5°，输入SCNR从-100 dB到-70 dB变化。两种方法的杂波抑制性能如图4所示。
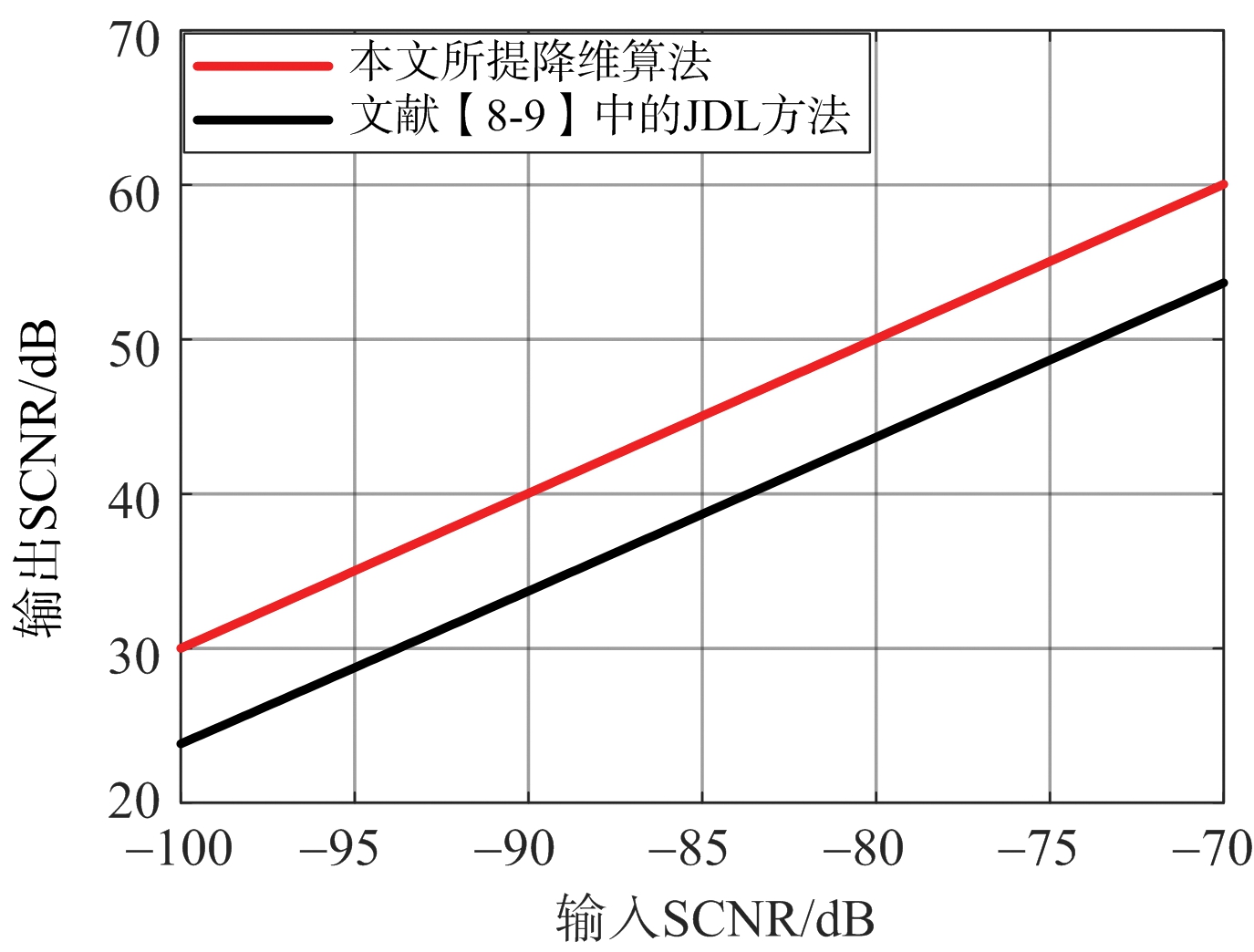
图4 杂波抑制性能
图4表明，与文献[8-9]中的JDL方法相比，本文所提方法可以将输出SCNR平均提高6.353 dB。因此，本文所提方法的杂波抑制性能明显优于文献[8-9]中JDL方法的杂波抑制性能。
4 结束语
针对目前自适应结构降维STAP方法运算量大，以及固定结构降维STAP方法的辅助通道选择方式固定的问题，本文注意到天波雷达的海杂波信号具有低秩特点，提出了一种基于稀疏滤波的降维STAP方法。天波雷达的实测数据的仿真结果表明,与文献[8-9]中的JDL方法的杂波抑制性能相比，所提方法将杂波抑制性能提高了6.17 dB。
[1] 李明. 一种机载前视SAR动目标检测方法[J]. 雷达科学与技术, 2017, 15(3):266-270.
LI Ming. A Ground Moving Target Detection Method for Airborne Forward-Looking SAR[J]. Radar Science and Technology, 2017, 15(3):266-270. (in Chinese)
[2] 周成家,鲍庆龙,沈锐超,等. 一种基于互谱思想的STAP 降维方法[J]. 雷达科学与技术, 2011, 9(4):330-334.
ZHOU Chengjia, BAO Qinglong, SHEN Ruichao, et al. An Rank-Reduced STAP Method Based on Cross Spectrum[J]. Radar Science and Technology, 2011, 9(4):330-334. (in Chinese)
[3] 刘洋,张永顺,刘汉伟,等. 改进的机载MIMO雷达局域联合自适应处理方法[J]. 空军工程大学学报(自然科学版), 2017, 18(4):24-27.
[4] 魏民,李小波,黄中瑞,等. 改进的最佳子集降维STAP方法[J]. 信号处理, 2016, 32(12):1406-1410.
[5] 李晓明,冯大政. 一种机载雷达两级降维空时二维自适应处理方法[J]. 航空学报, 2008, 29(1):170-175.
[6] SALEH O, RAVAN M, RIDDOLLS R, et al. Fast Fully Adaptive Processing: A Multistage STAP Approach[J]. IEEE Trans on Aerospace and Electronic Systems, 2016, 52(5):2168-2183.
[7] TONG Yalong, WANG Tong, WU Jianxin. Improving EFA-STAP Performance Using Persymmetric Covariance Matrix Estimation[J]. IEEE Trans on Aerospace and Electronic Systems, 2015, 51(2):924-935.
[8] ZHANG Xin, YANG Qiang, DENG Weibo. Weak Target Detection Within the Nonhomogeneous Ionospheric Clutter Background of HFSWR Based on STAP[J]. International Journal of Antennas and Propagation, 2013, 2013:382516.
[9] 张兰英,陈祝明,江朝抒,等. 一种新的JDL-STAP算法的研究[J]. 信号处理, 2009, 25(10):1612-1615.
