0 引 言
外辐射源雷达是一种双/多站构型的雷达系统，本身并不发射电磁波，通过被动接收第三方发射的电磁信号，对目标进行定位、跟踪。相对于传统雷达，外辐射源雷达具有优良的“四抗”性能[1-3]。
然而传统外辐射源信号采用多频网模式(各辐射站频率不同)，频率利用率低、功耗大，容易对其他网络产生干扰并且覆盖盲区大。而随着数字信号和正交频分复用技术的发展，单频网模式应运而生。单频网由多个处于同步状态的无线电发射塔组成，这些发射塔采用相同的频率，在同一时刻发射相同的电磁波，以完成对特定服务区的可靠覆盖[4]。
单频网外辐射源雷达是指辐射源采用单频网辐射源的外辐射源雷达，属于多基地雷达(多发射单/多接收雷达)的一种。其不仅兼有单频网和传统外辐射源雷达的优势，而且相比于多频网外辐射源雷达具有以下优点[5]：1)系统多采用多发单收模式并且各回波信号同时处理，相对于多频网采用多发单收(分时处理)或单发多收的模式具有系统性能高、硬件成本低的优点；2)只有一个发射站，设备集中，系统维护简单便捷；3)接收的数据集中于一个节点，处理集中，软件成本低；4)各节点之间通信少，安全性更高(抗反辐射导弹能力强)，而多频网数据分散于各个节点，联合处理各节点之间需要频繁通信，安全性能低。近年来，数字广播电视信号逐步取代模拟信号，单频网技术因具有频率节约、频谱利用率高等诸多优势，更是得到广泛应用。基于单频网数字广播电视信号的外辐射源探测也相应成为近年来的研究热点。
然而，由于单频网中所有发射站发射信号完全相同，在接收端能够接收到所有发射站信号的回波，但是无法对每个发射站的回波进行区分，从而导致测量-发射站模糊[6-9]。即恒虚警检测后能够获得距离-多普勒点迹，但是这些点迹来自哪一个发射站是未知的。如果不解决该模糊问题，直接进行目标关联会出现海量虚警，后续的目标跟踪无法实现。本文首先对测量-发射站关联问题进行了建模，然后从目标定位算法选择的角度出发，分析了不同定位方法的定位精度以及对测量-发射站关联问题的影响，并通过三发单收的外辐射源定位模型进行了仿真分析。
1 测量-发射站关联
测量-发射站的关联是单频网外辐射源雷达的一个关键问题，主要是由同频发射站对同一目标的照射引起的，如图1所示。
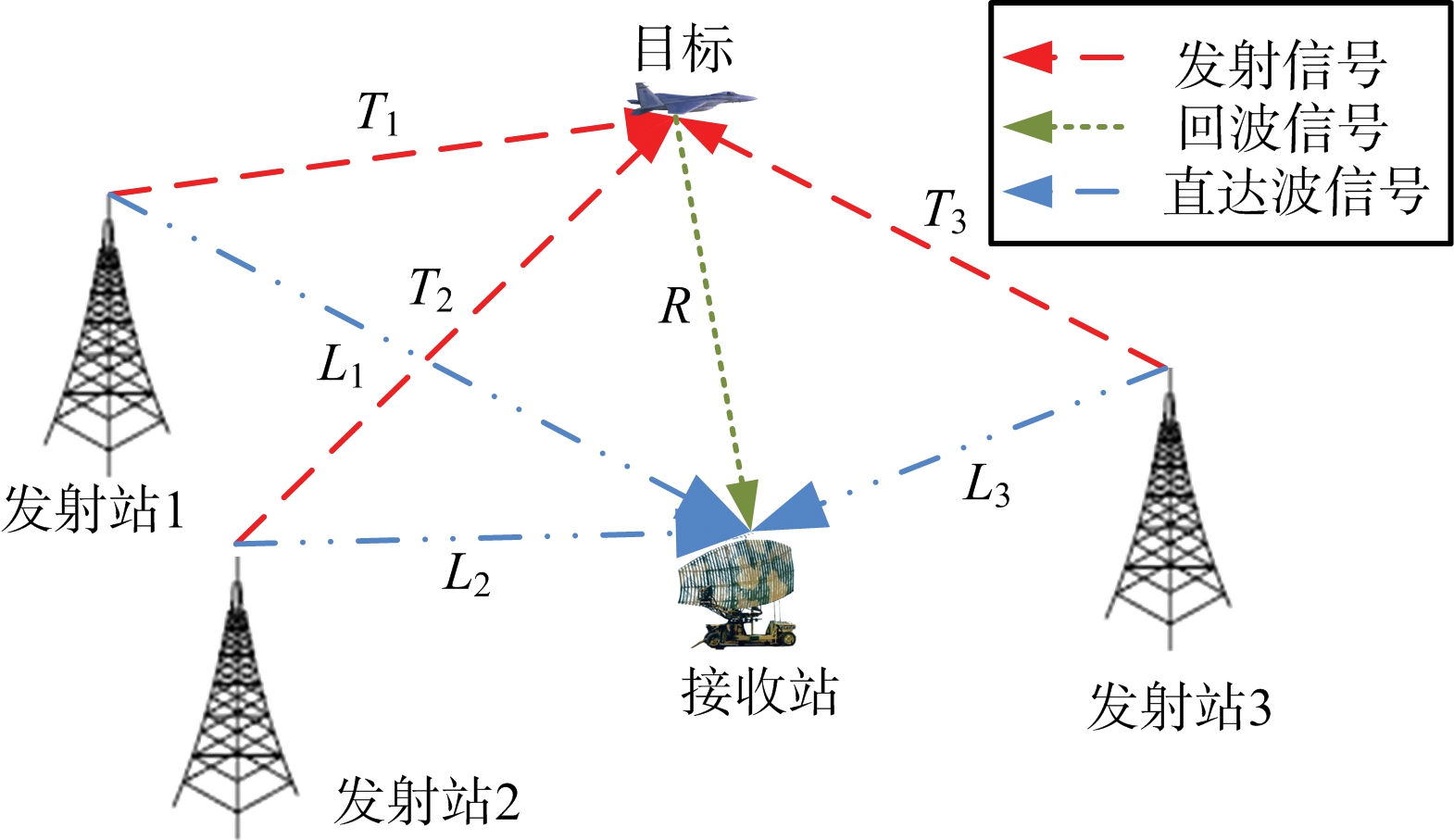
图1 单频网外辐射源雷达探测系统
假设发射站位置为TXs，接收站位置为RX，目标位置xt，目标速度为vt，则目标的距离和多普勒频率为
(1)
考虑噪声的影响，假设噪声是高斯加性白噪声nr～N(0,σr),nf～N(0,σf)，则
(2)
式中，c表示电磁波在空气中的传播速度。如果目标状态已知，则测量的条件概率可表示为
(3)
(4)
在实际场景中，并不是所有的发射站都能够探测到目标，则S维测量的似然概率可表示为
Λ(Wi1…is|xt)=
[Pdp(ωs,is|xt)]u(is)
(5)
式中，u(is)是一个指示函数，表征第is个测量是否属于目标，其定义如下：
(6)
当所有测量均为虚警时，似然概率可表示为
(7)
式中，Ψs表示第s个发射站观测区域的体积。这样，S维测量-发射站关联的代价函数可表示为
(8)
但是，目标xt的状态是未知的，其可以用下式的似然估计代替：
(9)
假设一个测量最多与一个目标关联，一个测量最多与一个发射站关联，同一个目标同一发射站最多有一个测量，则目标的测量-发射站的正确关联可通过下式获得：
(10)
式中，
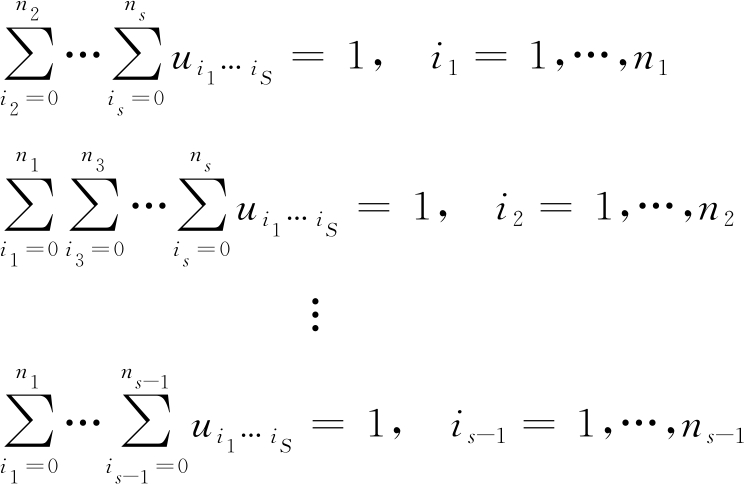
(11)
因为每个测量值的发射站来源是未知的，其可能来自于S个发射站中的任何一个，因而在利用这些测量时必须假设每个测量来自于所有的发射站。这样测量的数目变为了原来的S倍。假设有M个测量，则每个发射站对应的测量会有M+1个(需要考虑某发射站漏检的情况)，如图2所示。
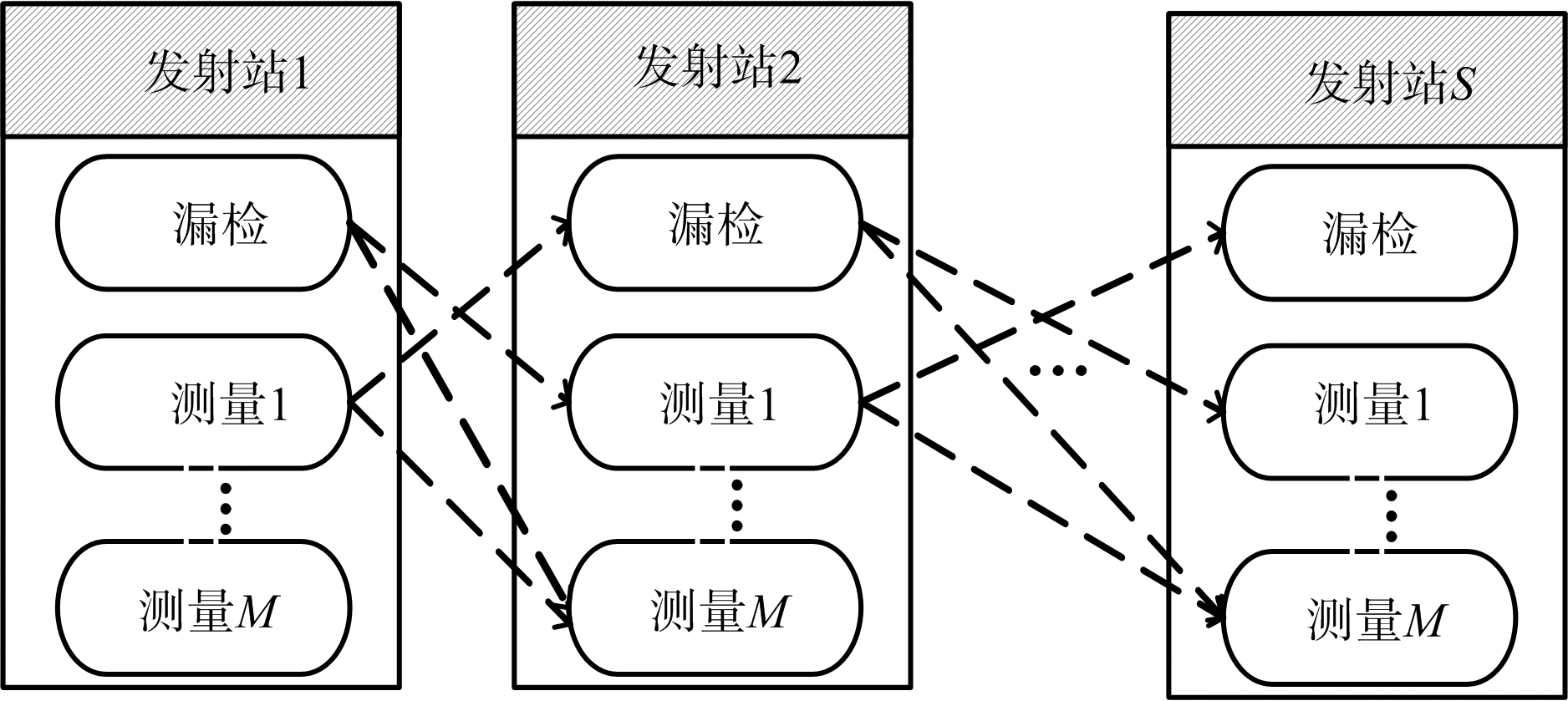
图2 测量-发射站关联示意图
利用TOA测量信息进行定位时，每两个测量可以确定一个椭圆交点。则对于有S个发射站、1个接收站、M个测量、1个目标的场景，通过TOA定位获得的疑似目标数目为
如图3所示。
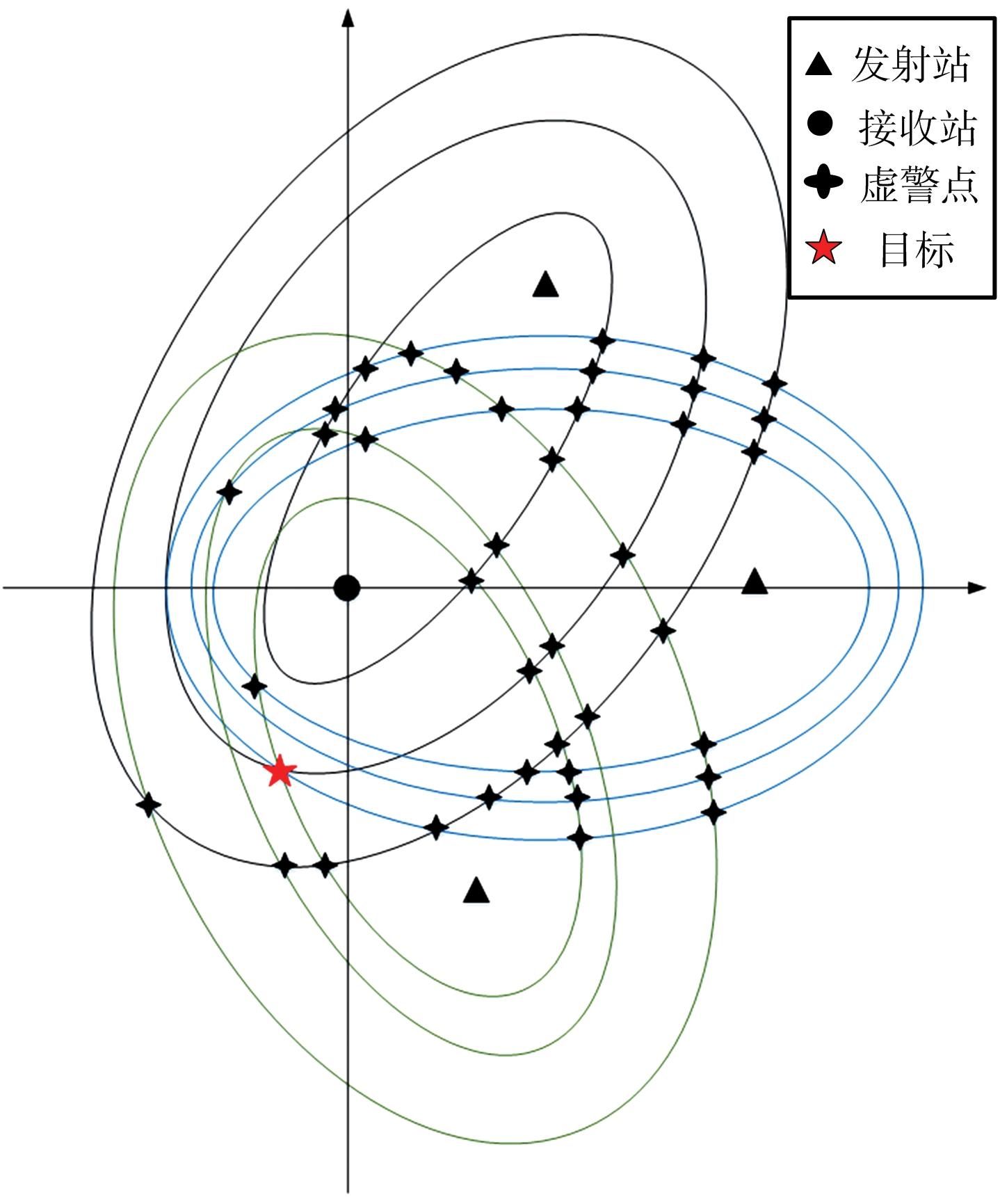
图3 关联问题示意图
假设有S个发射站、1个接收站、N个目标和M个测量，则需要关联的事件的数目为
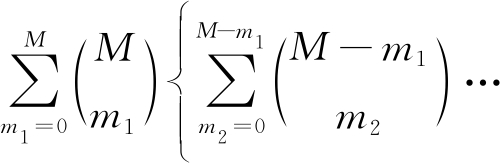
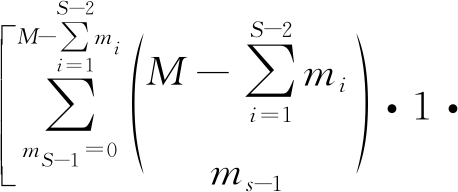
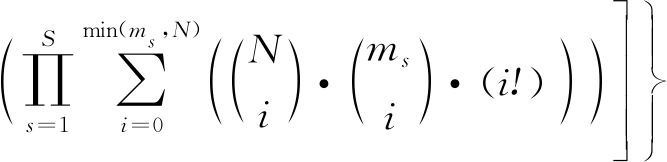
(12)
式中，ms表示与发射站s关联的测量数目。假设有3个目标、5个发射站、12个测量，则需要考虑的关联的数目高达353 767 425。已经被证明[10]，当发现概率小于1、发射站数目S≥3时，该关联问题是一个NP的问题。
2 基于TOA的定位方法原理
2.1 三维TOA定位方法
TOA定位采用同一目标的多个时延测量τs构造多个空间曲面求交点即可得到目标的位置[11]。
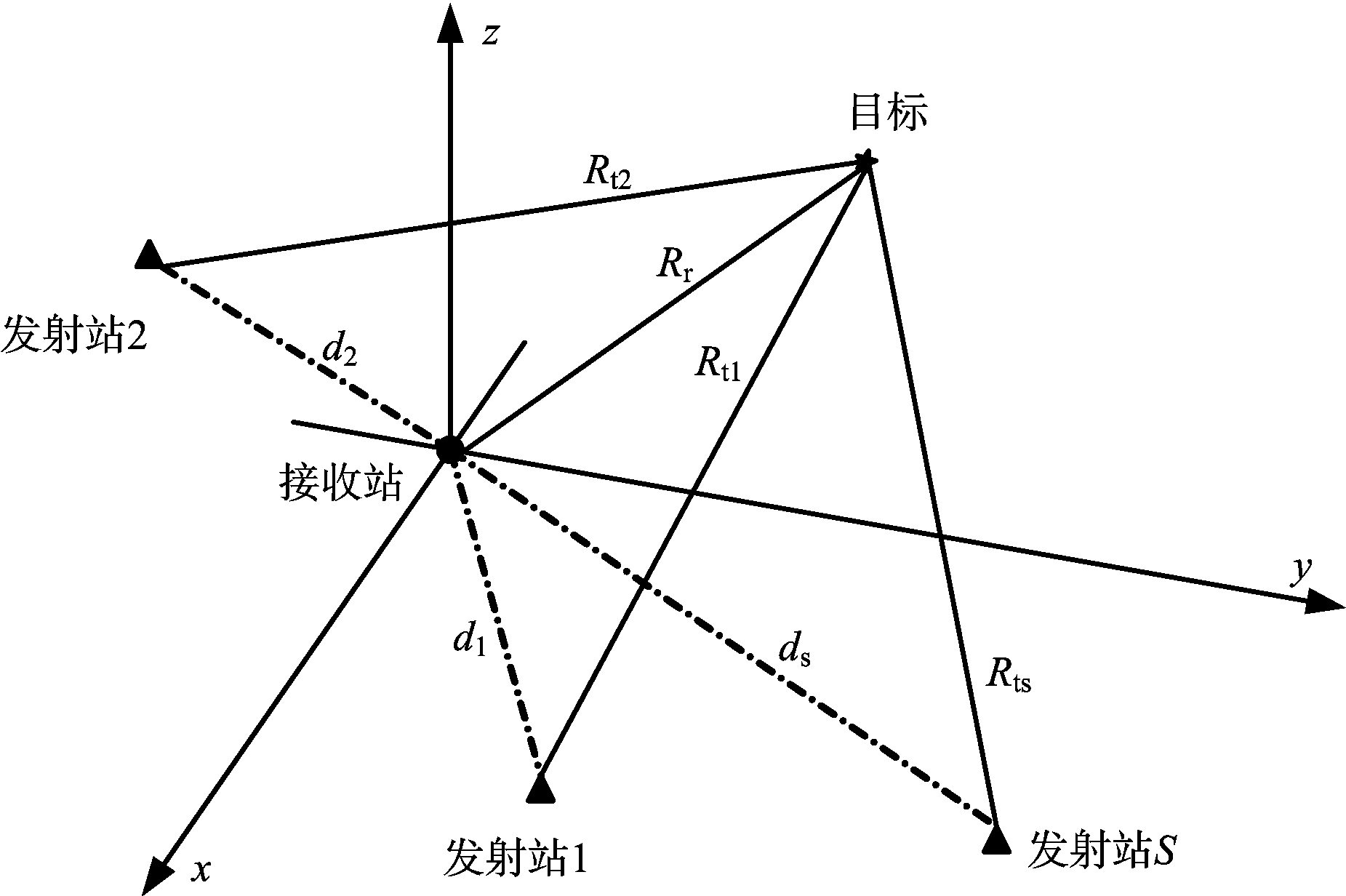
图4 TOA定位示意图
如图4所示，为不失一般性，假设接收站位置为坐标原点RX(0,0,0)T，第s个发射站位置TXs(xts,yts,zts)T，目标位置xt(x,y,z)T。目标与接收站的距离Rr可表示为
(13)
目标与发射站之间的距离可表示为
(14)
同样，第s个发射站与接收站之间基线的距离可表示为
(15)
通过时延信息可以获得目标与发射站和接收站的距离和信息：
Rs=
(16)
则上式变形可得
(17)
两边平方可得
(18)
令
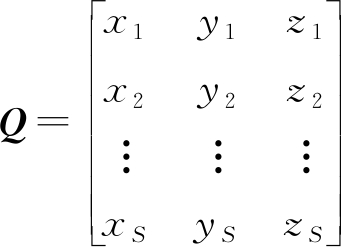
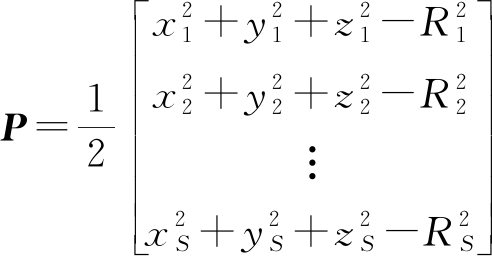
(19)
则
Qxt=P+rRr
(20)
式中，r表示S个发射站-接收站的距离和信息向量，r=[R1,R2,…,RS]T。如果Rr已知，目标的最小均方误差解可表示为
(21)
假设
(22)
则有
(23)
因为
可知
(24)
方程的解为
(25)
2.2 估计目标高度的二维TOA定位方法
假设目标位置为xt(x,y,H)，其中H表示根据目标的飞行高度范围估计的目标高度，则目标与接收站的距离为
(26)
目标与发射站之间的距离可表示为
(27)
通过时延信息可以获得目标与发射站和接收站的距离和信息：
(28)
则可得
(29)
两边平方可得
(30)
令
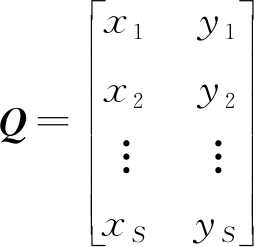
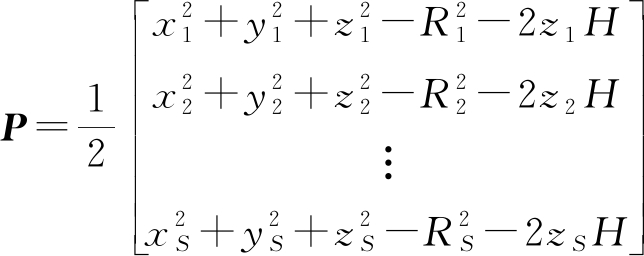
(31)
则
Qxt=P+rRr
(32)
如果Rr已知，目标的最小均方误差解可表示为
x′t=[x,y]T=(QTQ)-1QTP+(QTQ)-1QTrRr
(33)
假设
(34)
则有
x′t=a+bRr
(35)
因为
可知
(36)
方程的解为
(37)
2.3 定位精度分析
同一目标经过不同发射站照射可以得到多个距离和测量，根据多个距离和测量信息对应的发射站-目标-接收站空间关系可以得到目标的空间位置。距离和测量公式两边求微分可得
dRi=(ci1+cr1)dx+(ci2+cr2)dy+kzi+
kti+kr,i=1,2,…,S
(38)
式中：
kti=-(ci1+cr1)dxti-(ci2+cr2)dyti-
(ci3+cr3)dzti
kr=-(ci1+cr1)dxr-(ci2+cr2)dyr-
(ci3+cr3)dzr
kzi=(ci3+cr3)dH
令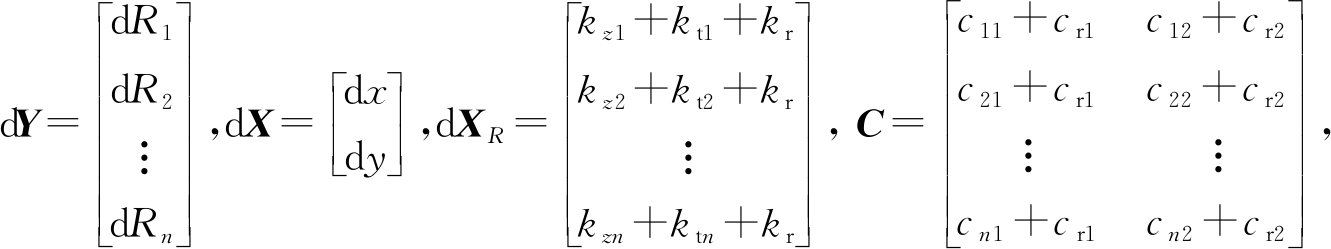
则写成矩阵形式可得
dY=CdX+dXR
(39)
目标位置误差矢量为
dX=(CTC)-1CT(dY-dXR)
(40)
假设不同发射站得到距离和的测量误差不相关，站址误差不变，则定位误差协方差为
P=E[dXdXT]=
(41)
式中，
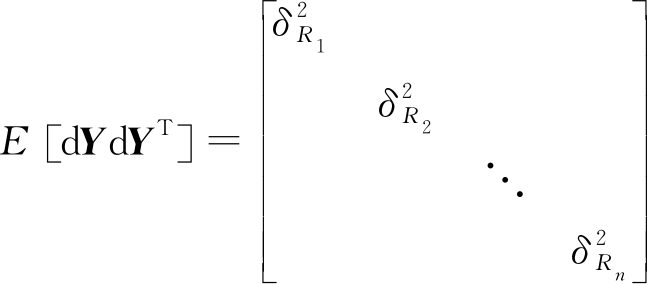
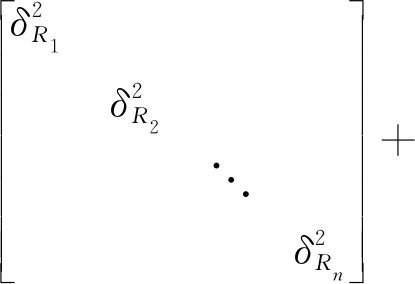
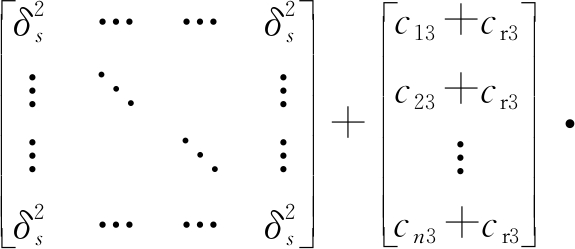
(42)
(43)
式中，δRi表示第i个发射站与接收站的距离和的标准差，δs表示站址误差，δH表示目标估计高度与真实高度偏差的标准差。则基于TOA信息的定位精度表示为
(44)
3 仿真实验分析
仿真条件：接收站坐标(30,40,0.1)km，发射站1坐标(-40,30,0.1)km，发射站2坐标(0,0,0.2)km，发射站3坐标(50,0,0.1)km，距离和测量误差30 m，站址误差10 m，目标位置在如图5所示轨迹上，飞行高度7～11 km随机选取。
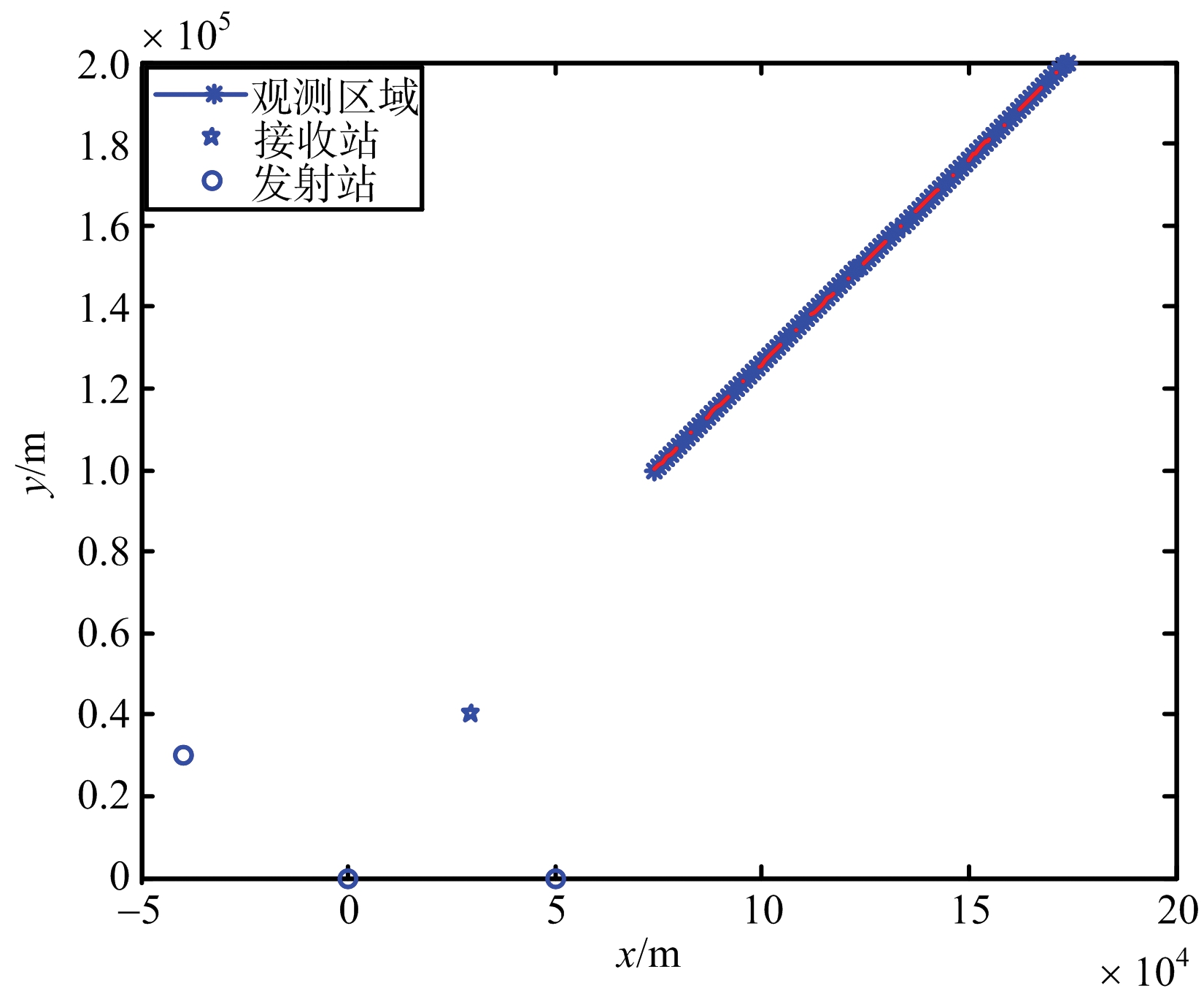
图5 仿真场景
仿真从二维定位误差和目标估计的距离和误差对两种定位方法性能进行分析，其中二维定位误差是通过定位方法获得的目标估计值与真实值的差即为
而距离和误差是估计的距离和与目标距离和测量值的差值，即为
其中
表示定位后通过估计的目标位置解算的目标距离和信息。距离和误差表征单频网外辐射源雷达的测量-发射站关联性能，误差越小性能越好[12]。图6为两种定位方法的定位误差仿真结果。
如图6(a)和图6(b)所示，在双基距离较小时，三维定位算法在二维平面的定位精度要高于二维定位方法的定位精度，当双基距离较大时二维定位算法的定位精度较高。在图6(c)和图6(d)中可以发现，三维定位算法在高度方向的定位精度随双基距离增加衰减较为严重，当双基距离超过350 km时，高度方向的定位误差甚至大于10 km，而根据目标的实际情况估计的目标高度误差较为稳定。综合图6可知，当目标距离较近时，三维定位方法的定位精度较高；当目标距离较远时，三维定位方法的高度定位误差很大，导致目标的定位精度降低。而单频网外辐射源雷达属于预警探测雷达的一种，主要针对远距离目标的探测和监视，因而二维定位方法相对三维定位方法更加适用。
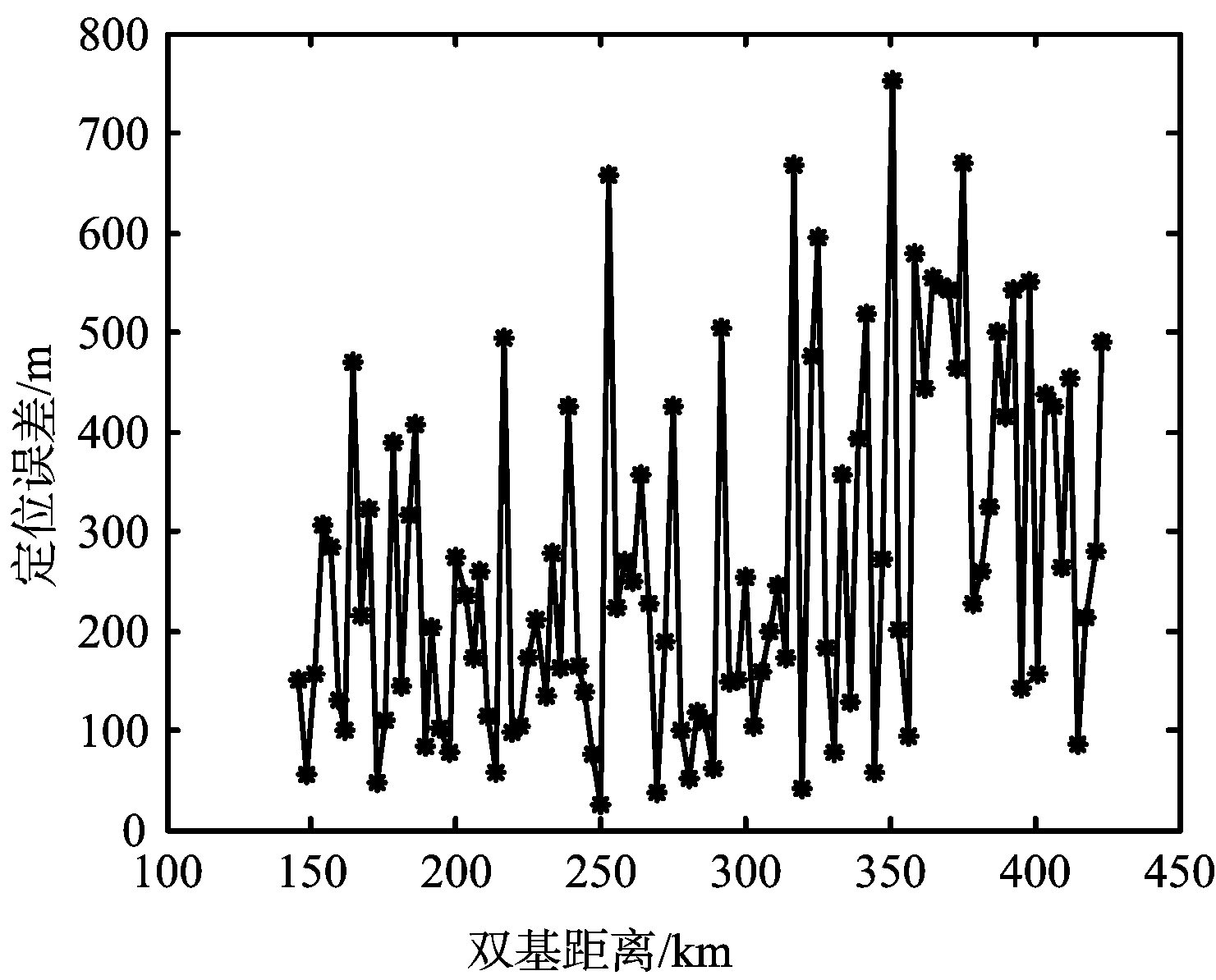
(a) 三维定位方法二维定位误差
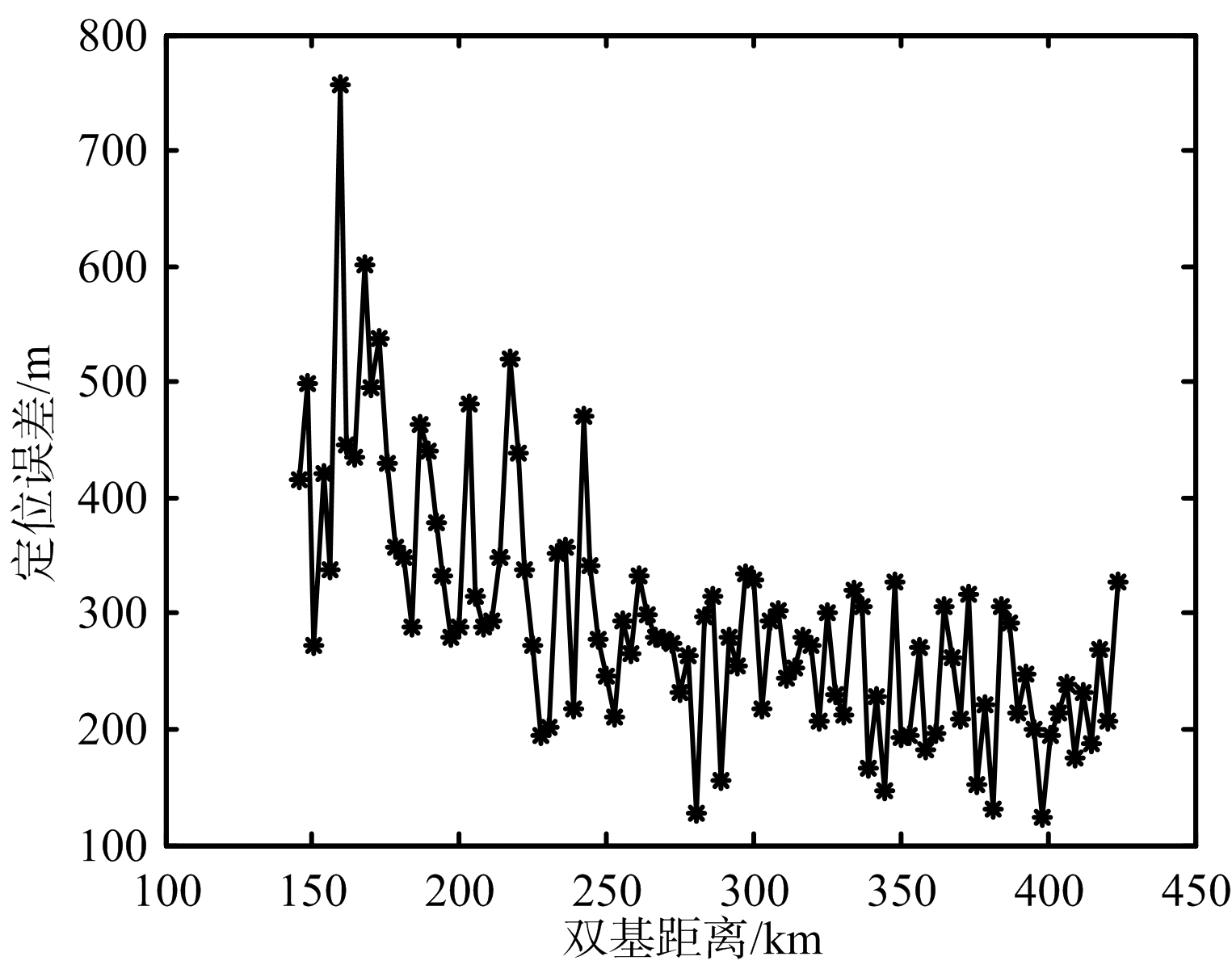
(b) 二维定位方法二维定位误差
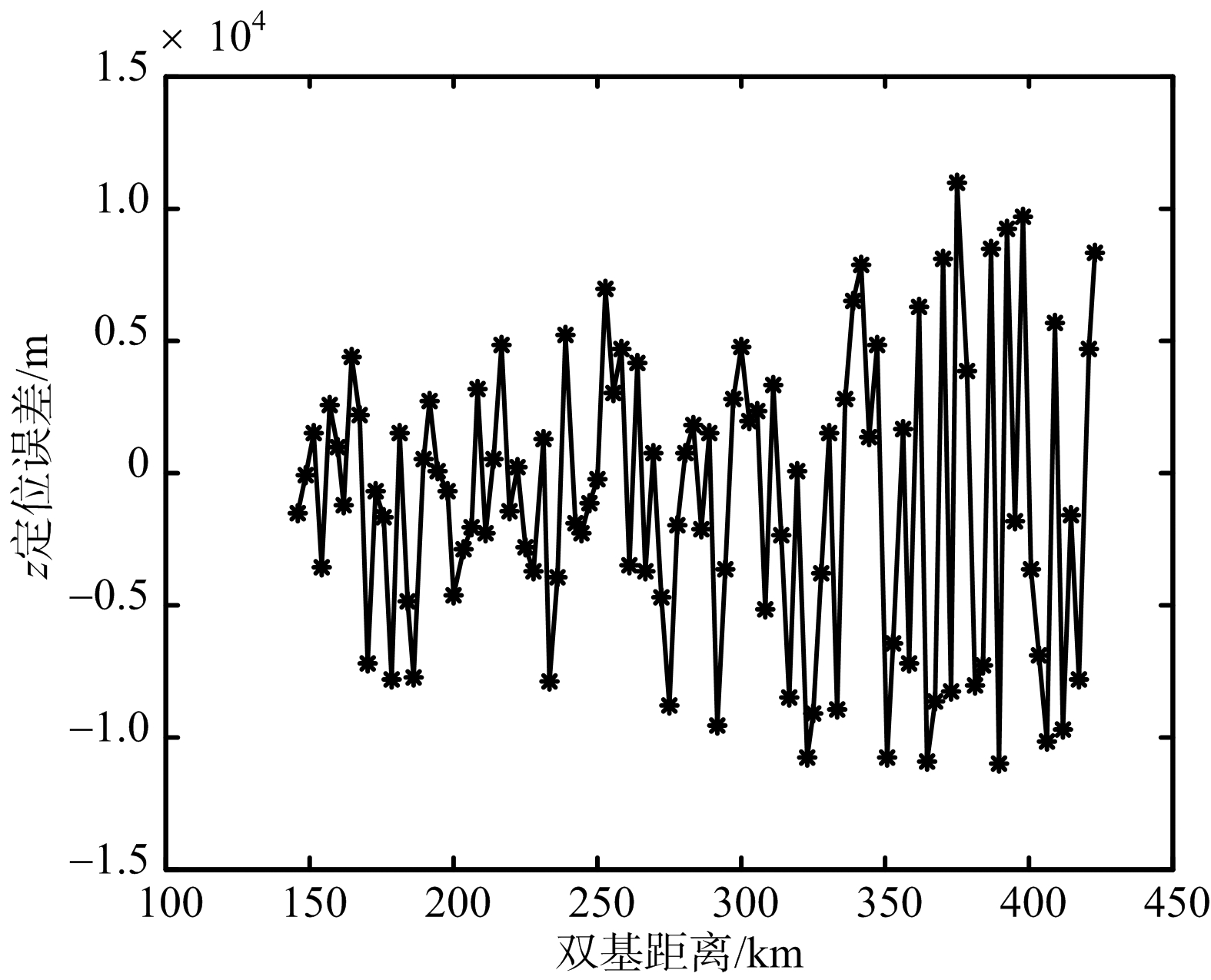
(c) 三维定位方法高度定位误差
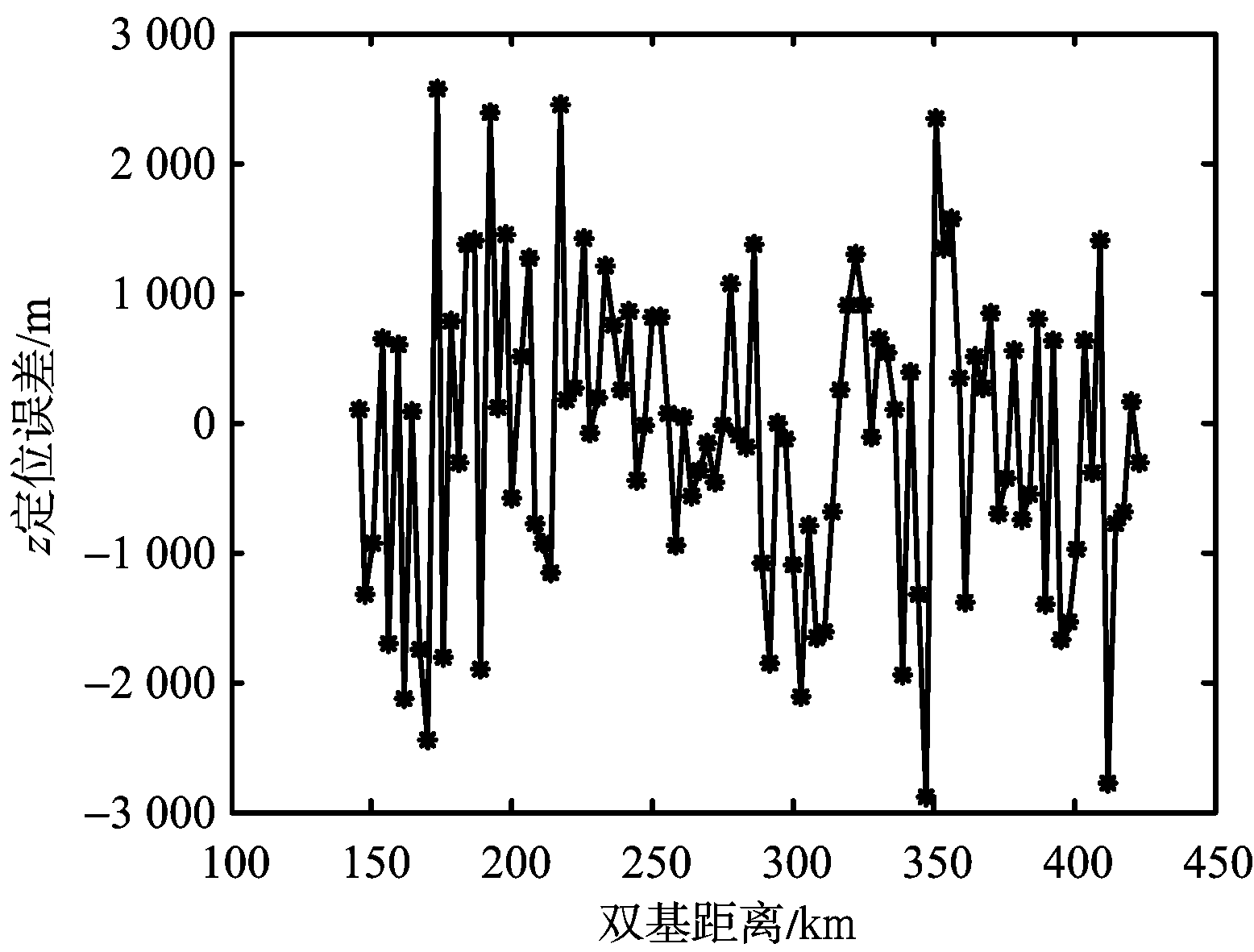
(d) 目标高度估计误差
图6 定位误差分析
而由之前的工作[13]可知，估计目标的距离和误差越大，正确关联的概率越小，在单频网外辐射源雷达定位方法选择时必须确保估计目标的估计误差尽量的小以保证较高的关联概率。图7表示目标估计的距离和误差。
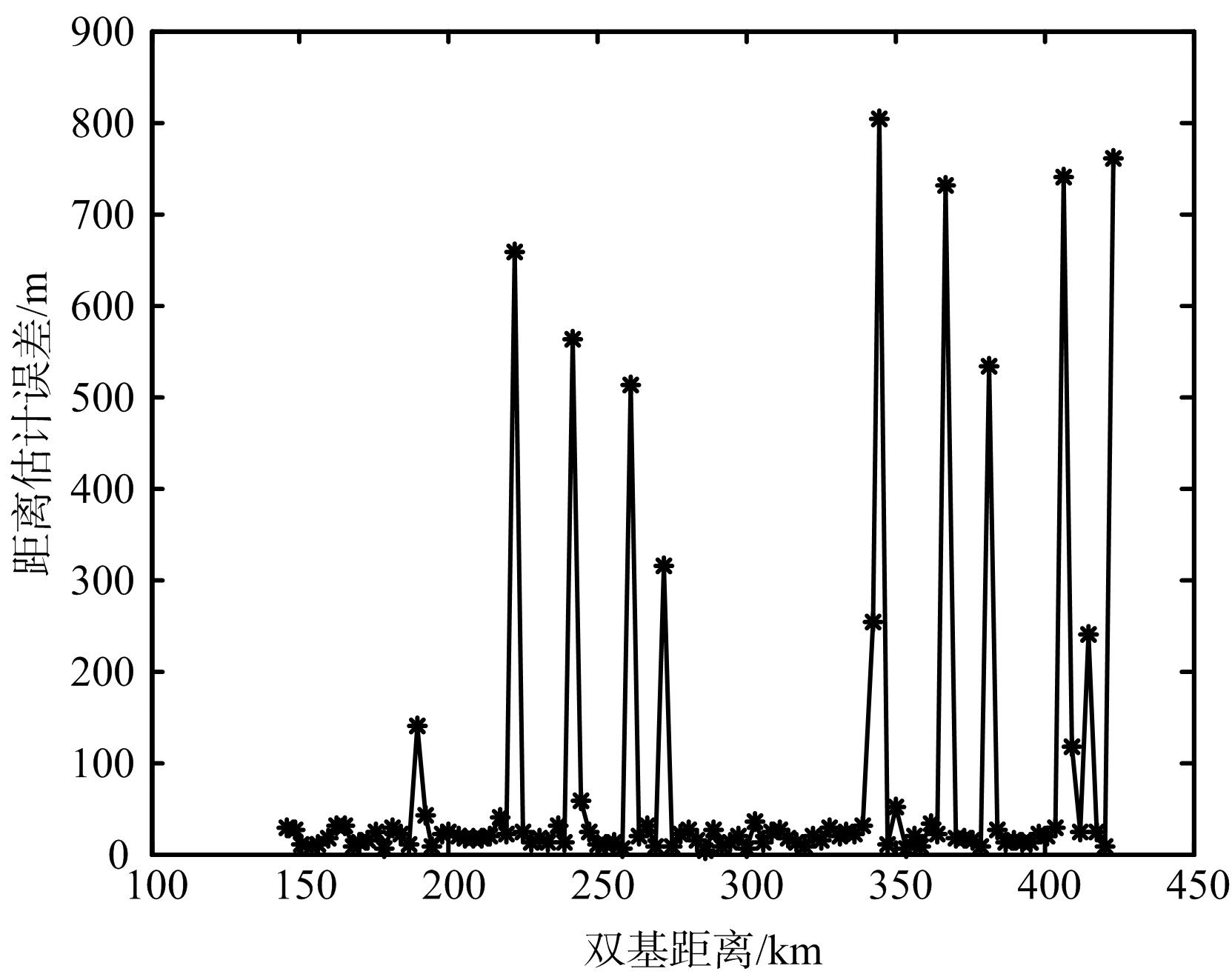
(a) 三维定位方法目标距离和误差
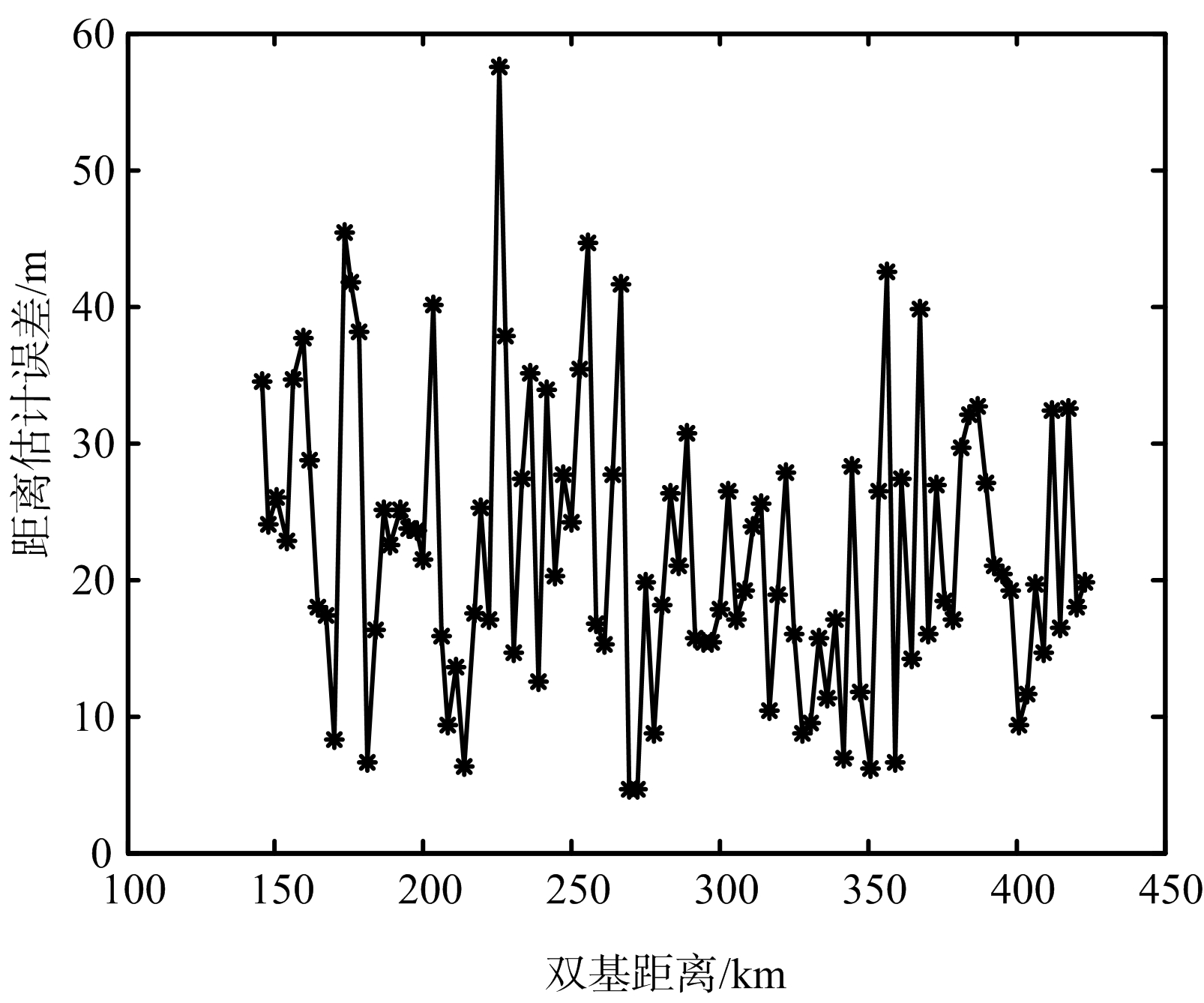
(b) 二维定位方法目标距离和误差
图7 距离和误差分析
目标距离和误差的测量值一般小于一个距离单元的距离(对于10 MHz采样率的数字电视信号，一个距离单元双基30 m)，因而可以将距离和的测量值作为目标距离和的真值。当目标距离和的估计值与测量值相差较小时，可以完成正确关联。由图7(a)和图7(b)可知，三维定位方法获得的目标距离和误差存在很多奇点会导致关联概率降低，错误关联数目上升，而估计目标高度的二维定位方法获得的距离和误差较小较稳定，能够更好地保证测量-发射站关联质量。
4 结束语
本文建立了单频网外辐射源雷达测量-发射站关联模型，分析了测量-发射站关联问题对后续数据处理的影响。然后从目标定位算法选择的角度出发，分析了不同定位方法的定位精度以及对测量-发射站关联问题的影响，并通过一个三发单收的单频网外辐射源雷达定位模型进行了仿真验证。综合目标的二维定位精度和目标距离和估计误差可以发现，估计目标高度的二维定位方法更适合单频网外辐射源雷达的定位和测量-发射站解模糊。
[1] GRIFFITHS H D, LONG N R W. Television-Based Bistatic Radar[J]. IEE Proceedings F: Communications, Radar and Signal Processing, 1986:649-657.
[2] PALMER J E, HARMS H A, SEARLE S J, et al. DVB-T Passive Radar Signal Processing[J]. IEEE Trans on Signal Processing, 2013, 61(8):2116-2126.
[3] 张丹,吕晓德,杨鹏程,等. 外辐射源雷达多普勒徙动补偿新方法[J]. 雷达科学与技术, 2017, 15(4):375-380.
ZHANG Dan, LU Xiaode, YANG Pengcheng, et al. A New Doppler Migration Compensation Method for Passive Radar[J]. Radar Science and Technology, 2017, 15(4):375-380. (in Chinese)
[4] IACOB M I, DEMCIUC Y I, AVRAAM I A. Comparative Evaluation of Received Signal Parameters in SFN DVB -T2 Service Area[C]∥ 2018 Systems of Signal Synchronization, Generating and Processing in Telecommunications, Minsk, Belarus: IEEE, 2018:1-6.
[5] 万显荣. 基于低频段数字广播电视信号的外辐射源雷达发展现状与趋势[J]. 雷达学报, 2012, 1(2):109-123.
[6] FANG Liang, WAN Xianrong, FANG Gao, et al. Passive Detection Using Orthogonal Frequency Division Multiplex Signals of Opportunity Without Multipath Clutter Cancellation[J]. IET Radar, Sonar & Navigation, 2016, 10(3):516-524.
[7] SUBEDI S, ZHANG Y D, AMIN M G, et al. Group Sparsity Based Multi-Target in Passive Multi-Static Radar Systems Using Doppler-Only Measurement[J]. IEEE Trans on Signal Processing, 2016, 64(14):3369-3634.
[8] BOK D, GALDA D, SIART U. A Multistatic Passive Coherent Location System with Receiver Location Constraints[C]∥ 2017 18th International Radar Symposium, Prague, Czech Republic: IEEE, 2017:1406-1410.
[9] RADMARD M, KARBASI S M, NAYEBI M M. Data Fusion in MIMO DVB -T-Based Passive Coherent Location[J]. IEEE Trans on Aerospace and Electronic Systems, 2013, 49(3):1725-1736.
[10] CHOI S, CROUSE D F, WILLETT P, et al. Approaches to Cartesian Data Association Passive Radar Tracking in a DAB/DVB Network[J]. IEEE Trans on Aerospace and Electronic Systems, 2014, 50(1):649-663.
[11] LIU Yuqi, WAN Xianrong, TANG Hui, et al. Digital Television Based Passive Bistatic Radar System for Drone Detection[C]∥ IEEE Radar Conference, Seattle, WA: IEEE, 2017:1493-1497.
[12] RADMARD M, KARBASI S M, KHALAJ B H, et al. Data Association in Multi-Input Single-Output Passive Coherent Location Schemes[J]. IET Radar, Sonar & Navigation, 2012, 6(3):149-156.
[13] LI Xiaobo, GUAN Xin, ZHONG Lihua, et al. Promoted Clustering Method for the Measurement-Transmitter Association in SFN Based Passive Radar Systems[J]. IET Radar, Sonar & Navigation, 2017, 10(7):1295-1302.
