0 引 言
在雷达目标识别、反隐身及雷达系统设计等应用场合中,分析目标宽带电磁散射特性有着十分重要的意义。计算导体目标雷达散射截面(Radar Cross Section,RCS),通常建立表面积分方程(Surface Integral Equation,SIE),采用矩量法(Method of Moments,MoM)来进行求解。在传统的MoM中,选用定义在三角面片上的RWG(Rao-Wilton-Glisson)函数[1]可把SIE离散成矩阵方程。当入射电磁波为单一频率时,RCS可通过求解矩阵方程得到的感应电流来计算。此时若需要获得一个感兴趣频段内的RCS频率响应特性,传统的MoM就需要在不同的频率点重复求解矩阵方程,由于MoM中的阻抗矩阵为稠密矩阵,故重复求解将花费大量的时间。
为了解决这个问题,渐近波形估计(Asymptotic Waveform Evaluation,AWE)技术[2]通过插值矩阵方程的解,以节约在不同频率点重新构建阻抗矩阵及求解矩阵方程的时间;阻抗矩阵插值方法则通过插值阻抗矩阵,以避免重复构建不同频率点的阻抗矩阵。然而这些方法都不能降低MoM中稠密矩阵的阶数。
特征基函数法[3](Characteristic Basis Function Method,CBFM)是快速求解MoM矩阵方程的一种有效方法,其基于区域分解概念提取的特征基函数(Characteristic Basis Function,CBF)能有效降低传统矩量法生成的全局矩阵阶数,从而可以直接求解矩阵方程,避免迭代求解可能带来的迭代缓慢或不收敛问题。虽然采用CBFM可以有效提高单个频率点的求解速度,但在计算宽带RCS频率响应时,由于CBF与频率有关,不同频率点的CBF是需要重新计算的,故不能有效减少频率扫描时的计算时间。文献[4]基于CBFM提出了超宽带特征基函数法(Ultra-Wide Band Characteristic Basis Function Method,UCBFM)。该方法利用较高频率点提取的CBF能够反映较低频率点感应电流特征的特性,在待分析的频段最高点,提取定义为超宽带特征基函数(UCBF)后,用以代替该频段其他频率点的CBF,由此减少逐个频点重复计算CBF的时间,达到快速频率扫描的目的。近年来,学者对该方法开展研究,并将该方法、改进算法或结合其他快速算法成功地应用于散射等电磁问题求解中,并且已有文献大多针对单个导体目标算例,验证了该方法的准确性和有效性[5-8]。
本文在阐述UCBFM的快速频率扫描原理后,将其应用于由单个导体目标扩展而得的多导体目标宽带电磁散射问题,通过数值仿真验证该方法在这类问题求解中的准确性、有效性。
1 超宽带特征基函数法
采用传统的矩量法分析导体目标散射问题时,利用RWG基函数离散电场积分方程后,得到如下形式的矩阵方程:
Z(f)I(f)=V(f)
(1)
式中,Z为N×N维阻抗矩阵,V为N×1维激励矩阵,I为未知的N×1维感应电流系数矩阵,其中,N为待求解的未知数个数,f为频率。
采用传统的CBFM求解式(1)时,包括3个基本步骤:1)将求解区域划分为M块子域,从每块(子域)提取特征基函数;2)运用Galerkin方法构建降阶矩阵;3)求解矩阵方程。
计算宽带RCS时,上述传统的CBFM方法需要在频段的各个频率点重复计算CBF,相比传统的CBFM方法,UCBFM包含3个关键步骤:1)在最高频率点提取生成UCBF;2)在各个低频率点重复应用UCBF;3)用UCBF构建每个频率点的降阶矩阵并求解。由此避免重复计算,以实现快速频率扫描。
1.1 提取超宽带特征基函数
在最高频率点处,运用平面波法产生超宽带特征基函数(UCBF)。平面波从不同方向激励每个独立的子域i后,求解下式可以得初始UCBF:
(2)
式中,Zii为Ni×Ni维第i块子域的阻抗矩阵,ViMPW为Ni×NMPW维第i块子域的激励矩阵,![]() 为Ni×NMPW维未知的从第i块子域提取出的初始UCBF矩阵,其中,Ni为待求解的第i块未知数个数,NMPW为平面入射波的个数,这里取110,fH为待分析频段的最高频率点。
为Ni×NMPW维未知的从第i块子域提取出的初始UCBF矩阵,其中,Ni为待求解的第i块未知数个数,NMPW为平面入射波的个数,这里取110,fH为待分析频段的最高频率点。
对于第i块子域,由于JiUCBF为平面波多方向激励后产生的,直接用作UCBF会包含冗余信息,故随后,采用奇异值分解算法(SVD)分解![]() 并定义一个门限,这里取10-3,只有大于门限的奇异值所对应的列可以保留下来,组成该子域的UCBF。假设SVD后,有Ki个奇异值大于门限,则可从Ni×NMPW维
并定义一个门限,这里取10-3,只有大于门限的奇异值所对应的列可以保留下来,组成该子域的UCBF。假设SVD后,有Ki个奇异值大于门限,则可从Ni×NMPW维![]() 中对应提取Ki列,组成Ni×Ki维的第i块子域的UCBF,用Ki表示第i块子域的UCBF个数。
中对应提取Ki列,组成Ni×Ki维的第i块子域的UCBF,用Ki表示第i块子域的UCBF个数。
从各个子域提取出UCBF后,可生成整个求解区域的UCBF:

(3)
式中,Uii为Ni×Ki维从第i块子域中提取的UCBF,U为N×K维整个求解区域的UCBF,其中,K为整个求解区域的UCBF个数,是各子域的UCBF个数之和。频率扫描时,该U被用在各个低频率点,而不需要在低频率点再重复提取相应的CBF。
1.2 产生降阶矩阵方程并求解
此时,式(1)的解可用UCBF表示为如下形式:

(4)
式中,αi为第i块子域上待求解的Ki×1维UCBF系数矩阵。
为构建低频率点的降阶矩阵,将式(4)代入式(1),可得
ZCα=VC
(5)
式中,ZC=UTZU,VC =UTV,α=[α1,α2,…,αM]为K×1维待求解的对应于频率点f的UCBF系数矩阵。从式(1)和式(3)可见,UCBF确定后,从原来需要求解I的N个未知数转化成只需求解α的K个未知数,通常K要小于未知数个数N。
最后,求解式(5)得系数矩阵α后,代入式(4)可求出导体目标在频率点f时的感应电流系数I,继而可利用场方程求解相关电磁散射问题,如计算目标在该频率点的RCS等。
2 数值算例与结果
对由单个导体目标扩展而得的多导体目标,为验证采用UCBFM分析其宽带电磁散射特性的有效性,分别以2×2导体球和3×1立方导体为例,计算其宽带RCS频率响应。仿真均在Intel Core i7-3520M CPU,2.90 GHz,8 GB RAM的PC机上完成。仿真时,入射波为θ极化方向的平面波且从θ=75°,φ=0°入射,采用三角形面片剖分扩展导体目标,计算时考虑VV极化情况。
算例一 半径为0.6 cm的2×2导体球,两两中心间距为3 cm,放置于xoy平面。采用UCBFM,分别计算频率为9,6,3 GHz时的双站RCS,计算结果如图1所示。其中,提取UCBF的频率点选择为10 GHz,奇异值分解(SVD)后,每个导体球提取的UCBF个数为308。
作为对比,采用传统CBFM和MoM(商业FEKO软件)计算的结果也如图1所示。其中,传统CBFM分别在9, 6, 3 GHz频率点处提取CBF,SVD后,每个导体球上提取的CBF个数分别为236, 126, 48。
图1显示了3种结果的一致性很好,这也进一步表明,将最高频点处提取的UCBF用于低频点的计算过程中,不会带来精度损失。
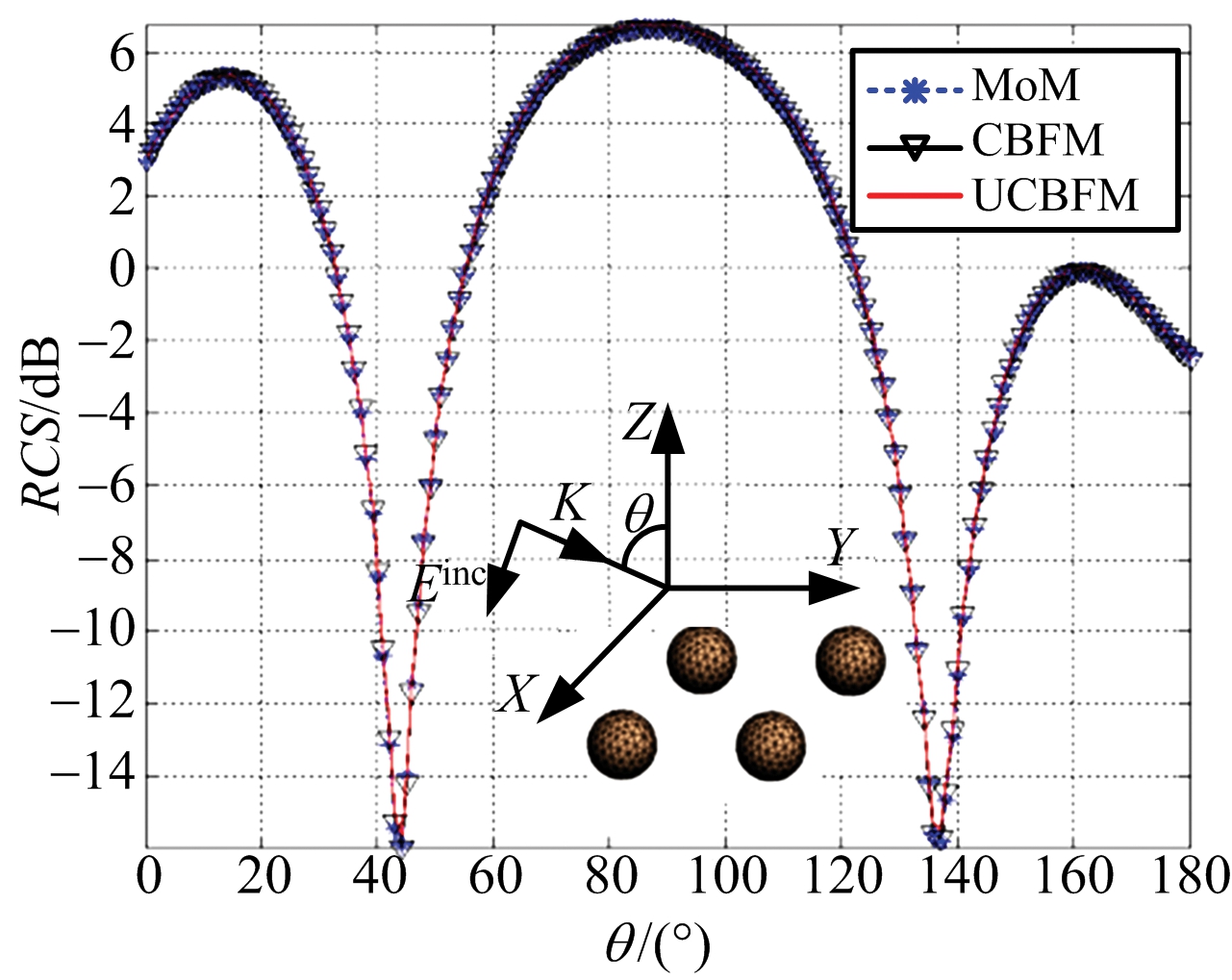
(a) f=9 GHz
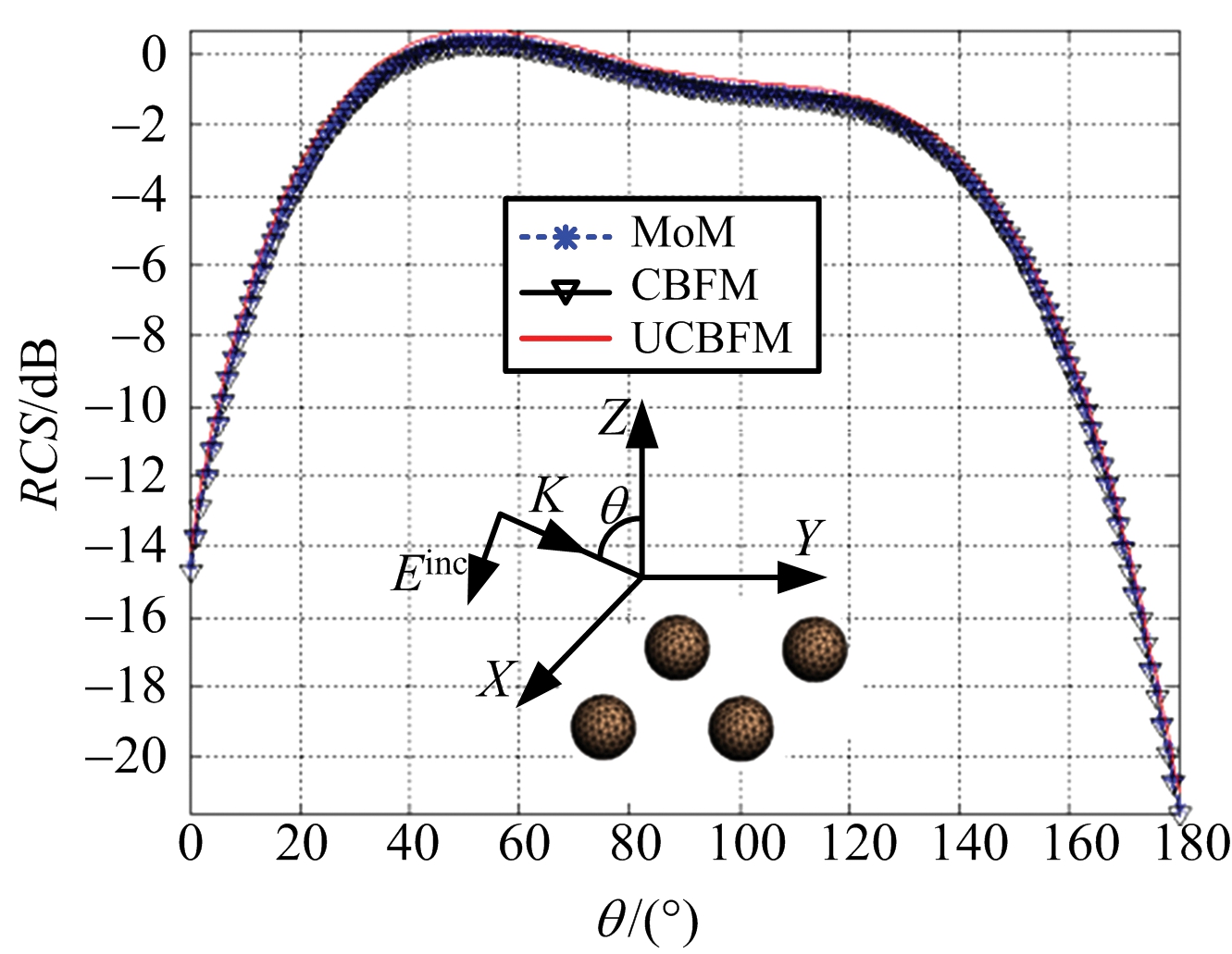
(b) f=6 GHz
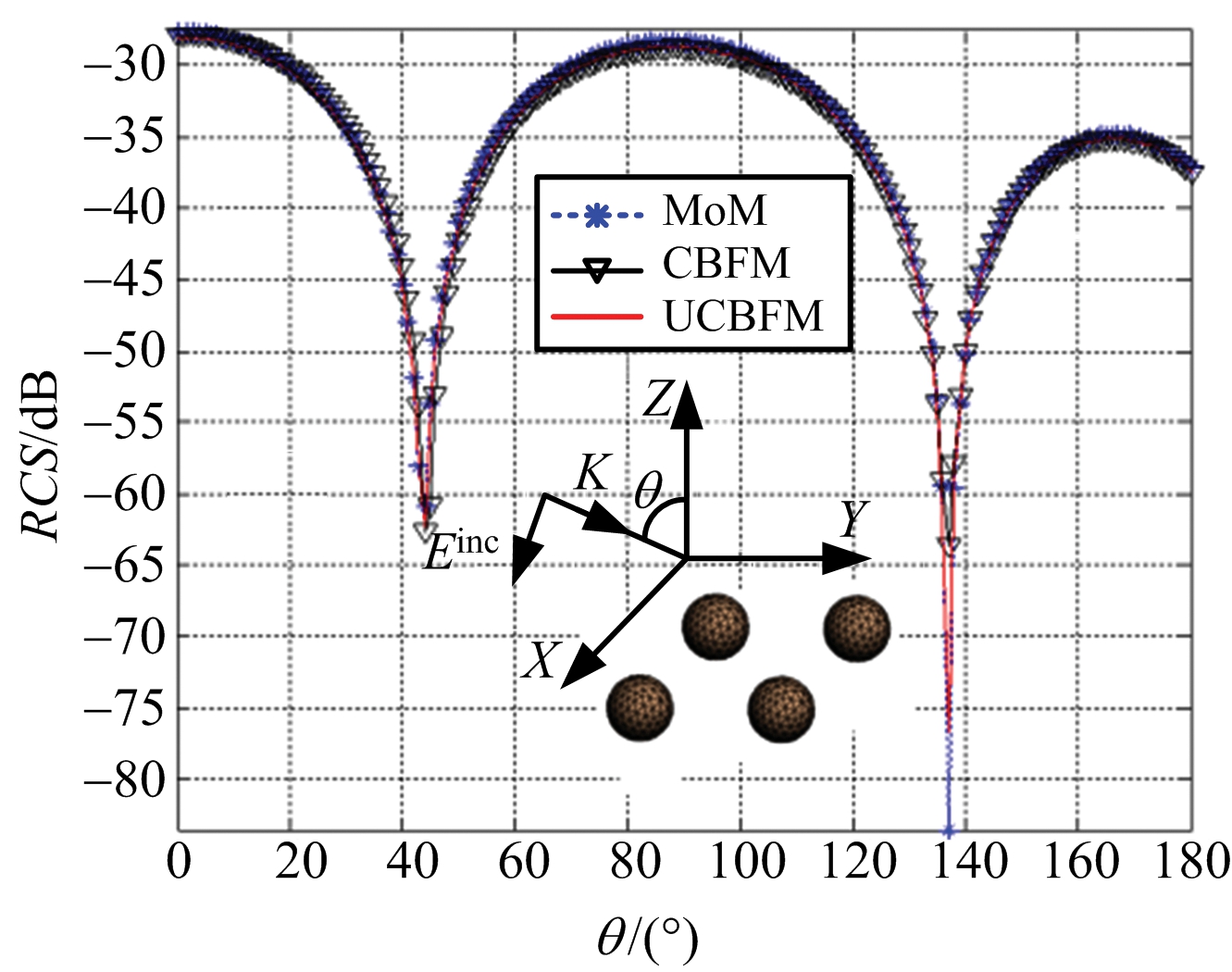
(c) f=3 GHz
图1 2×2导体球双站RCS(f=9, 6, 3 GHz,VV极化)
算例二 计算上述2×2导体球的宽带单站RCS。频率带宽为8~10 GHz,计算时选择50个频率点。作为比较,采用两种频率扫描的方法:一种是UCBFM,在最高频率点提取UCBF后,在每个频率点重复运用;另一种是传统的CBFM,在每个频率点重复提取CBF。
两种方法的计算结果如图2所示。其中,UCBF在最高频率点10 GHz提取,SVD分解后,单个导体球提取的UCBF个数为308,该方法的CPU计算时间为1 170.470 s;CBF分别在50个频率点提取,相应的CPU计算时间为4 418.552 s。图2的结果表明两者的一致性很好,且采用UCBFM进行频率扫描,可节约73.51%的计算时间。
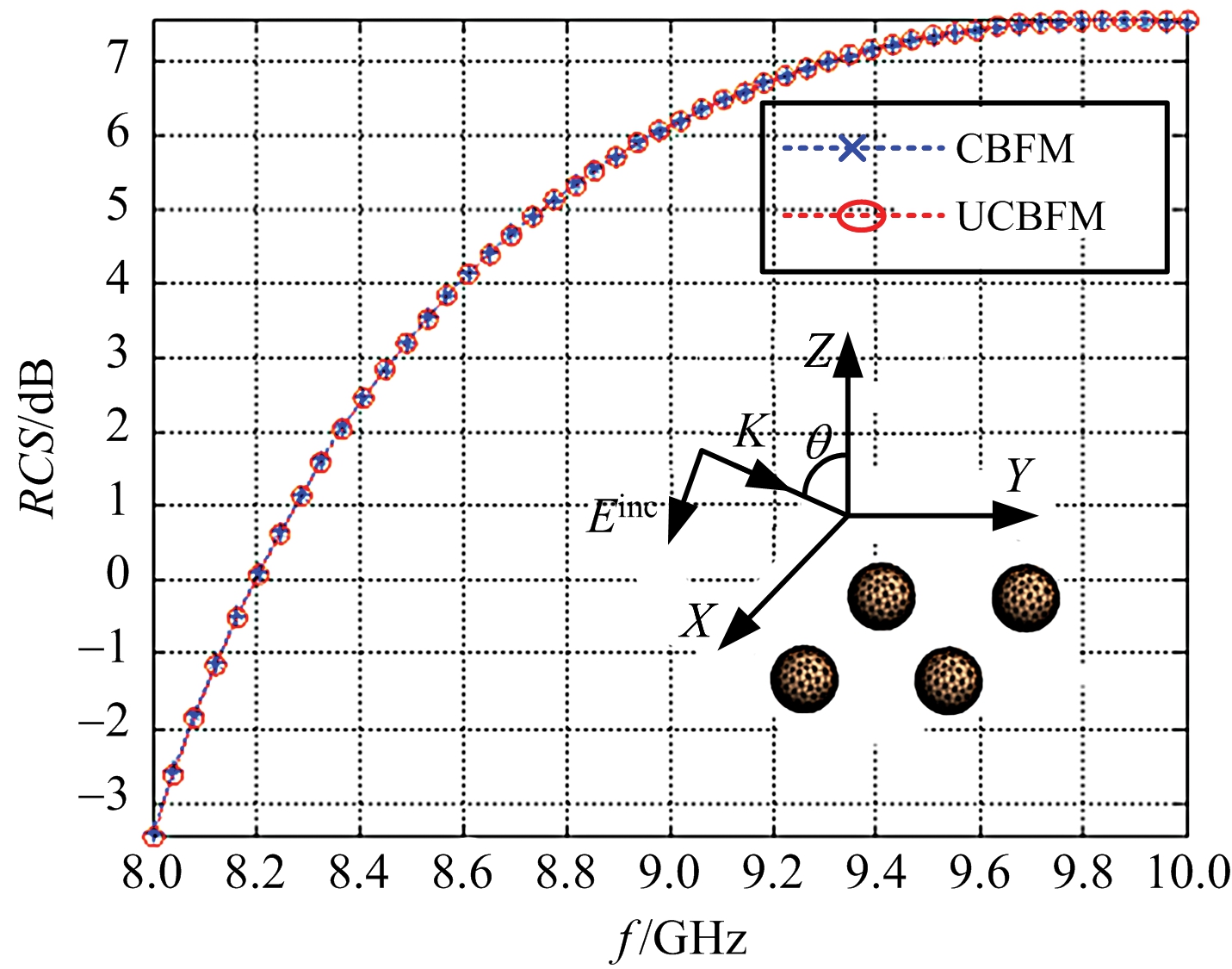
图2 2×2导体球单站RCS(f=8~10 GHz,VV极化)
算例三 3×1立方导体,边长为0.9 cm,两两中心间距为3 cm,沿X轴放置。计算其在8~10 GHz的单站RCS,计算时选择50个频率点。计算结果如图3所示,其中,UCBF在最高频率点10 GHz提取,SVD分解后每个立方体提取的UCBF个数为426;当重复利用UCBF进行频率扫描时,CPU计算时间为2 083.752 s;相应地,重复计算CBF进行频率扫描时,为5 435.187 s。
图3的结果表明两者的一致性很好,且采用UCBFM可节约61.66%的计算时间。
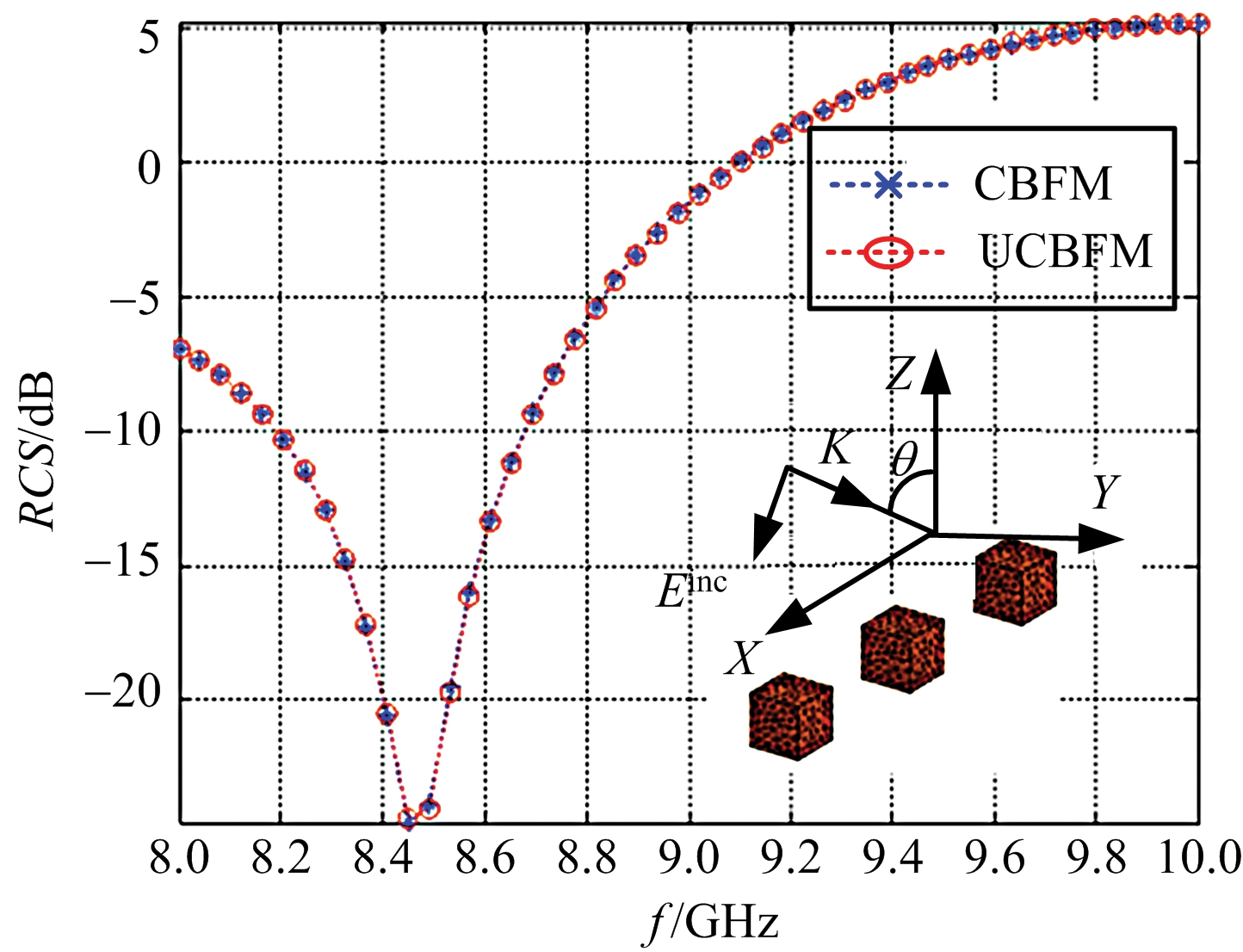
图3 3×1立方导体单站RCS(f=8~10 GHz,VV极化)
3 结束语
重复利用在最高频率点处提取的UCBF实现快速频率扫描的方法,即UCBFM,被用于计算扩展导体目标的宽带RCS频率响应。该方法在计算单个频点的RCS时,保留了传统CBFM中对MoM矩阵方程加速求解的优势;在计算宽带RCS频率响应时,相比传统CBFM,因不需要在每个频率点重复计算CBF,减少了计算时间。数值仿真验证了此频率扫描方法的有效性,可用于扩展目标的宽带RCS快速频率扫描中。数值结果验证,该方法为快速分析扩展导体目标宽带电磁散射特性提供了一种可能的解决途径。如果进一步研究宽带特征基函数快速提取,并结合其他快速算法求解矩阵方程,将进一步减少计算时间上的花费,拓展UCBFM在目标散射问题上的应用空间。此外,将UCBFM用于扩展目标时,其适用的频率扫描范围相对单目标会更加严格,其与目标个数、结构形状等的关系有待下一步深入研究。
[1] RAO S, WILTON D, GLISSON A. Electromagnetic Scattering by Surface of Arbitrary Shape[J]. IEEE Trans on Antennas and Propagation, 1982, 30(3):409-418.
[2] REDDY C J, DESHPANDE M D, COCKRELL C R, et al. Fast RCS Computation over a Frequency Band Using Method of Moments in Conjunction with Asymptotic Evaluation Technique[J]. IEEE Trans on Antennas and Propagation, 1998, 46(8):1229-1233.
[3] PRAKASH V V S, MITTRA R. Characteristic Basis Function Method: A New Technique for Efficient Solution of Method of Moments Matrix Equations[J]. Microwave and Optical Technology Letters, 2003, 36(2):95-100.
[4] DE GREGORIO M, TIBERI G, MONORCHIO A, et al. Solution of Wide Band Scattering Problems Using the Characteristic Basis Function Method[J]. IET Microwave Antenna & Propagation, 2012, 6(1):60-66.
[5] 王仲根,孙玉发,王国华,等. 应用通用特征基函数求解目标宽带雷达散射截面[J]. 电波科学学报, 2015, 30(1):91-96.
[6] 李琛璐. 特征基函数法及其改进技术在电磁散射中的应用[D]. 合肥: 安徽大学, 2017.
[7] 王仲根,王宵,李敏,等. 基于最小二乘拟合和特征基函数法的目标宽带RCS快速计算[J]. 安徽师范大学学报(自然科学版), 2017, 40(1):38-42.
[8] 朱金玉,孙玉发,方红雨,等. 一种基于SVD-CBFM和RACA的单站RCS快速求解方法[J]. 中国科学技术大学学报, 2017, 47(10):843-847.
