0 引 言
近年来,小目标飞行器的快速发展对目标探测雷达提出了新的挑战。小目标飞行器的雷达散射截面积小,难以被有效探测,因此需要积累雷达回波以提高信噪比,提升检测效果。但由于目标相对雷达的运动导致目标回波包络无法对齐,距离向和方位向存在耦合,积累后会导致主瓣展宽、峰值下降[1]。
针对积累过程中出现的距离单元走动,文献[2]提出的Keystone变换方法可在保持回波相位的同时,补偿跨距离单元的走动。然后方位向对多个回波信号进行相参积累,提高信噪比。文献[3-4]使用Keystone变换有效校正了距离走动,但是引入了sinc插值,增加了运算负担,因此,工程实现难度较大。另外,在雷达系统中,为了提高空域覆盖范围,需要使用数字波束形成(DBF)技术合成多个波位。此时,需要对多个波束数据进行并行实时处理,提高了对FPGA的处理能力,在资源非常有限的FPGA中无法得到实现。文献[5-6]提出非均匀快速傅里叶变换,并对其原理进行了说明。
本文将非均匀快速傅里叶变换方法应用于多波束距离走动校正和相参积累中,并提出一种新的硬件方案来进行工程实现。该方法通过方位向的NUFFT来代替插值操作,明显降低了运算复杂度。在FPGA实现方案中,通过改写旋转因子来编写可输入旋转因子的FFT运算模块,利用两级NUFFT,按照FFT流程来进行计算,既可以提高运算速度,又可以节约存储旋转因子的内存空间。
1 非均匀快速傅里叶变换实现原理
目标相对雷达的运动导致相参积累时需要考虑距离走动。Keystone变换通过时间轴的缩放有效消除距离向和方位向之间的耦合,校正在距离方向上的越单元走动[7]。
在雷达处理过程中,传统做法是使用插值来对距离走动进行校正,常用的插值方法有sinc插值、stolt插值和拉格朗日插值。
若使用插值来完成Keystone变换,对一个 Na×Nr大小的矩阵进行计算。计算每个离散点时都需要进行若干点的插值函数实时计算,资源消耗较大,而且速度也较慢。而在进行距离走动校正之后,还需要对每个距离门进行方位向上的傅里叶变化以实现相参积累。因此,无法满足雷达系统的实时性要求。非均匀FFT正是针对这一问题的解决方案。
1.1 非均匀FFT方法
对一个回波积累后距离向和方位向均为时域的大小为Na×Nr的矩阵进行非均匀FFT,处理完成之后,可将目标在长时间相参积累过程中导致的距离走动进行校正并在方位向上进行相参积累,得到距离向为时域、方位向为多普勒域的大小为Na×Nr的二维矩阵。
Ykt[la,mr]=![]()
(1)
式(1)即为对二维矩阵Y[ma,la]在方位维进行非均匀FFT操作。其中,la和ma分别为方位向坐标和距离向坐标,fc为载频,fs为AD采样率,K为调频率有关的一个常数,因此![]() 为一个常数,记为η。由于硬件资源的限制,使用非均匀快速傅里叶变换来实现多波束距离走动校正和相参积累,不需要使用插值函数实时计算,只需要提前计算并将系数进行存储。
为一个常数,记为η。由于硬件资源的限制,使用非均匀快速傅里叶变换来实现多波束距离走动校正和相参积累,不需要使用插值函数实时计算,只需要提前计算并将系数进行存储。
该矩阵的标准FFT形式为
YFFT[la,mr]=
![]()
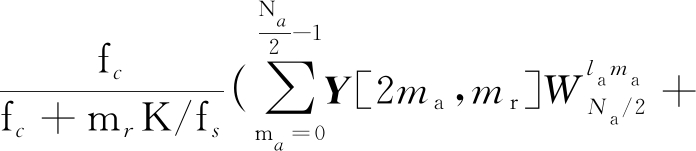
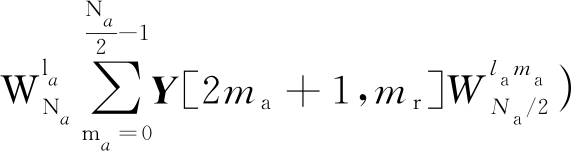
(2)
将式(1)按照式(2)形式进行变化得到
Ykt[la,mr]=
![]()
(3)
式(3)对应的旋转因子为
![]()
(4)
由式(4)可知,在进行一次Na点的NUFFT时,前半部分旋转因子与标准FFT相同,而后半部分旋转因子的指数为一个常数。因此,可以根据这个特点,重新改写FFT旋转因子,依然可以使用标准FFT计算流程。
基于此思路,编写可变旋转因子FFT模块来进行NUFFT的实现,计算量得到很大程度的降低,提高了运算速度,而且极大程度地节省了系数存储所需的存储空间。
1.2 运算资源评估
常规NUFFT通过复乘来实现,需要提前将系数进行计算和存储,计算每个点所需要的系数都是不同的,因此,存储容量需求较大。而改进的NUFFT实现方案使用旋转因子来进行计算,因此,存储容量需求很少。而且,由于使用了FFT计算流程,需要的复数乘法和复数加法次数都明显减少,运算速度也得到明显提升。表1列出了两种方式所需要的复数乘法、复数加法以及存储系数所需要的存储空间大小。
表1 运算资源分析

方法复数乘法复数加法存储系数常规NUFFT实现方案Na×Na×NrNa×(Na-1)×NrNa×Na×Nr改进NUFFT实现方案Na/2×Nr×log2NaNa×Nrlog2NaNa×Nr
由此可以看出,相比于常规实现方式,改进NUFFT实现方式明显减少运算量和系数存储所需空间。当需要对多波束数据进行并行处理的时候,该方法可以极大降低在资源非常有限的FPGA中对NUFFT进行工程实现的难度。
2 算法的工程实现流程
2.1 系统参数
该设计方案基于某目标探测雷达系统,系统使用Xilinx第七代Virtex-7系列FPGA和TMS320C6678协调工作来进行目标探测,NUFFT在FPGA中实现。系统使用多个接收天线,接收信号经过DBF合成左右各6个波束来覆盖更大的空域范围。因此,需要对12个通道数据进行并行操作。每个通道经过AD转换、脉冲压缩、杂波抑制之后截取8 192点,积累128个PRT的回波以提高信噪比。12通道处理前后结果数据量较大,以16 bit整形存储在SDRAM中。而旋转因子固化在Flash中,以16bit整形存储,共需要4 MB空间。
2.2 FPGA实现方式
FPGA实现方案包括4个功能部分:NUFFT旋转因子生成、128点可变旋转因子FFT运算模块、软核架构设计、SDRAM缓存设计。
2.2.1 NUFFT旋转因子计算
NUFFT旋转因子的计算循环较多,不适合由FPGA在线生成,选择由上位机生成数据文件后,写入FPGA外挂的Flash中,上电后由FPGA读取到Microblaze软核外挂的SDRAM缓存中使用。由于雷达系统集成了DSP,也可选择用DSP来生成旋转因子,通过EMIF写入SDRAM。NUFFT旋转因子生成方式如图1所示。
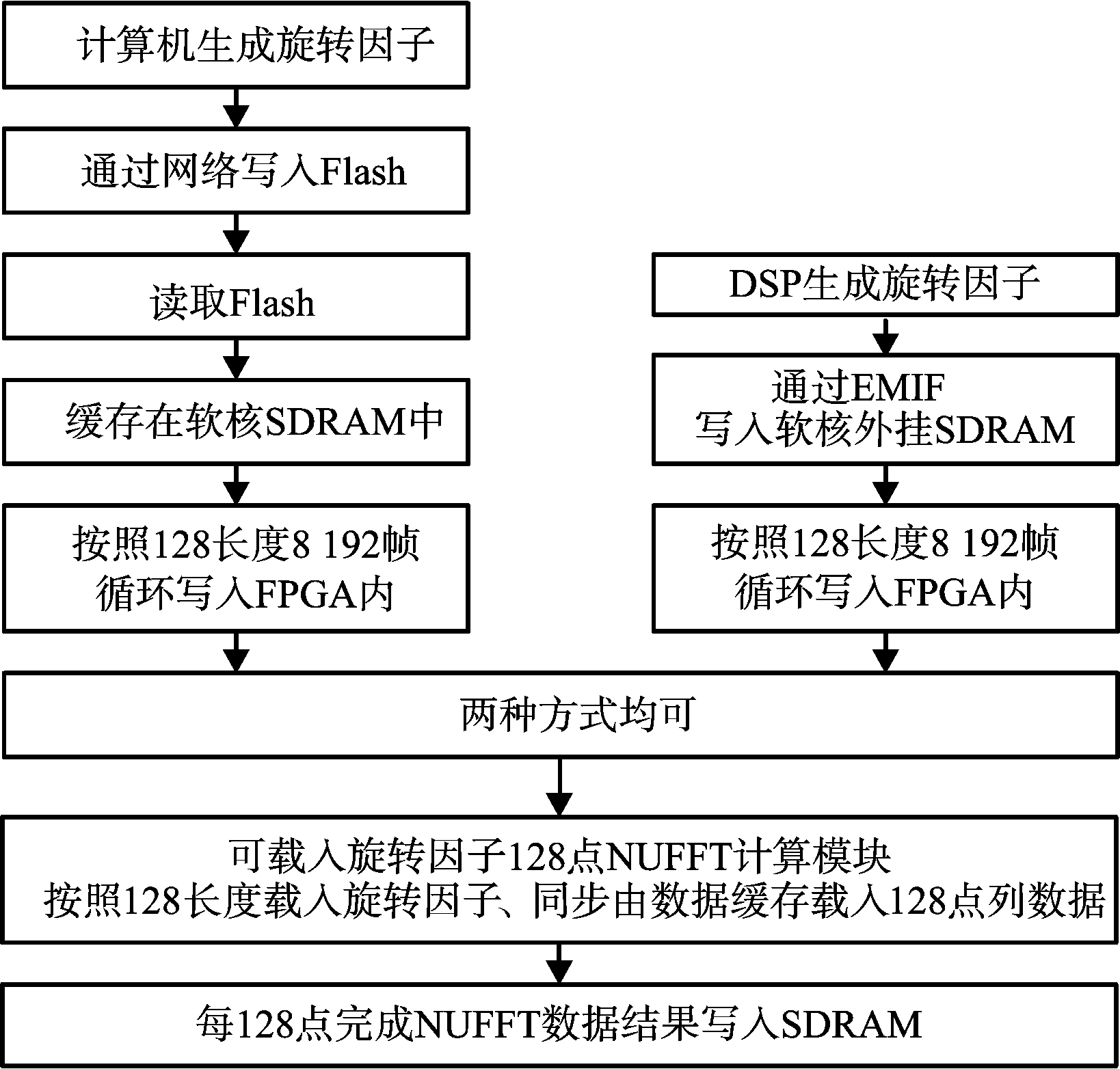
图1 NUFFT旋转因子生成方式
2.2.2 可变旋转因子FFT模块
由于旋转因子与标准FFT不同,因此,需要设计可自定义旋转因子的NUFFT计算模块。基于这个设计思路,设计两级NUFFT实现方案,不仅简便易行,而且具有比较高的吞吐量。
(5)
将式(5)计算过程进行分解:
Y(k)=Y(16r+s)=
r=0~15,s=0~7
(6)
由式(6)看出,将128点FFT分解为两级FFT来进行设计,先按照一定顺序分成16组,进行8点FFT,然后,再重组序列分成8组,进行16点FFT。
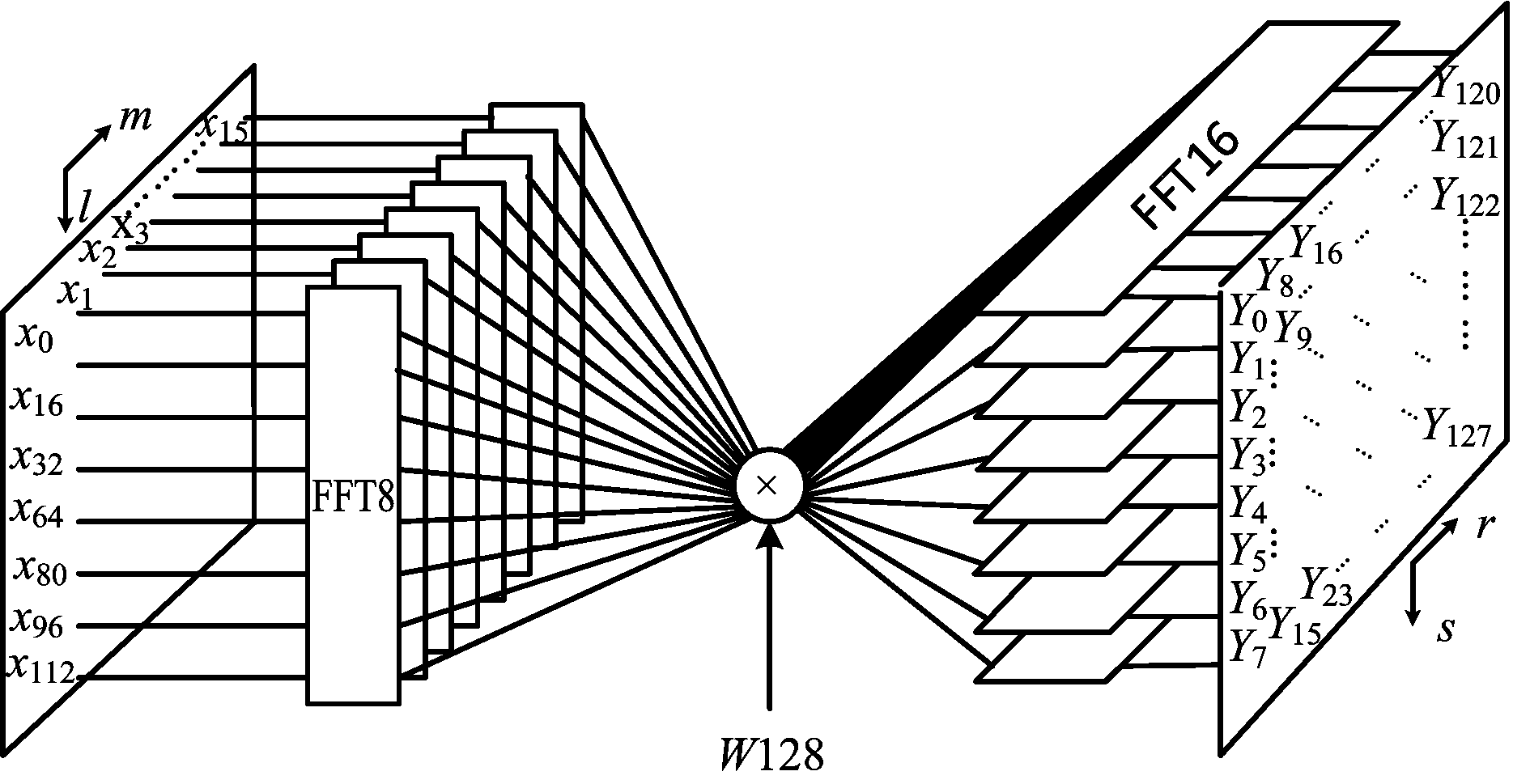
图2 可变旋转因子FFT设计
如图2所示,FFT模块均为自定义可输入旋转因子FFT模块,计算过程依旧和标准FFT计算过程相同,使用蝶形单元进行计算,不同的是提供接口由用户输入旋转因子。在使用该模块时,旋转因子将持续按照128帧结构8 192组方式写入FPGA内部提供给该计算模块。由于算法流程与标准快速傅里叶变换计算流程相同,因此,算法的复乘和复加的次数明显减少,该模块的实现使得NUFFT的计算方便而高效。
2.2.3 软核架构设计
在设计及仿真过程中,采用Virtex7芯片,设计软核子系统实现方案,以Microblaze为核心,外挂多种子模块,以实现NUFFT相关控制功能和数据传输功能。
如图3所示,Microblaze负责旋转因子的写入及各个模块的调度。128点可变旋转因子FFT运算模块被封装成IP以供Microblaze设计调用。在Microblaze循环中不断将旋转因子写入FPGA内置缓存FIFO中,并按照FPGA时序逻辑将采样数据按照数据帧节拍载入该模块中进行计算。
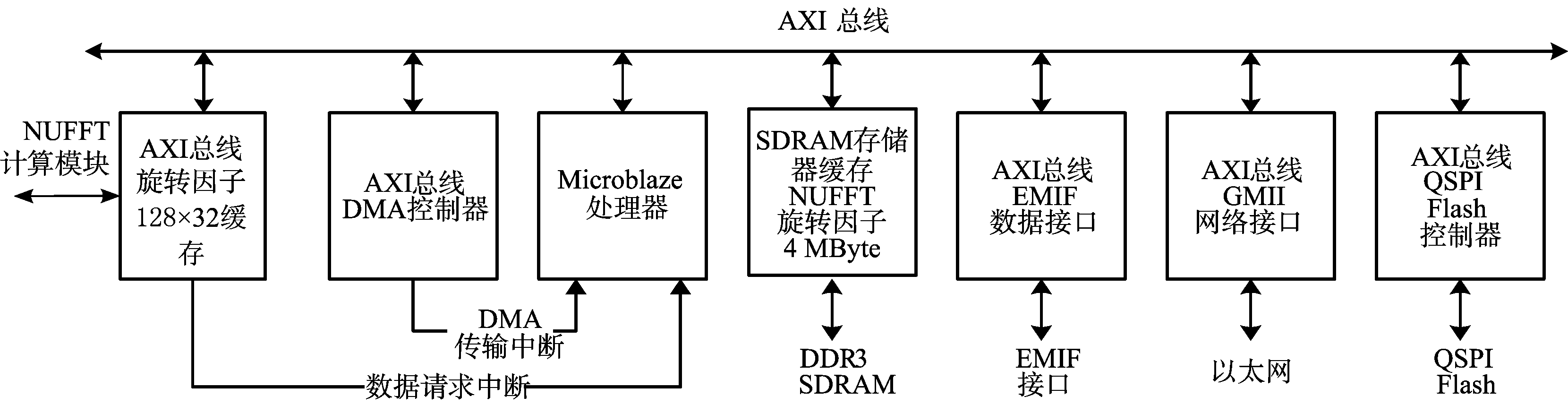
图3 软核系统架构
为了减少Microblaze处理器的CPU负载,使用AXI DMA控制器进行offload,AXI DMA控制每次负责搬运24组128点旋转因子数据到AXI 总线旋转因子缓存。AXI总线旋转缓存被设计为内部只要有大于17组数据,不输出中断,当缓存的旋转因子小于17组时向Microblaze发出中断请求。
此时CPU还有最少125 μs(二维数据矩阵更新时间为64 ms,16帧最多允许的时间为64 ms/ 8 192×16=125 μs)来完成下16组参数的传输工作配置。而由于每次传输24组数据,每秒钟共需要传输最多5 334次24帧数据,也就是CPU每秒响应5 334次数据请求中断。根据实际项目测试,Microblaze运行在100 MHz情况下,中断响应能力为20 000次以上,因此设计冗余较大,不会出现时序混乱的情况。
AXI总线的DMA控制器带宽为800 MB/s左右,因此,24组数据所需要的传输时间为15.36 μs,传输延迟与实际使用数据速率比不到10%,数据传输与使用的冗余较大。
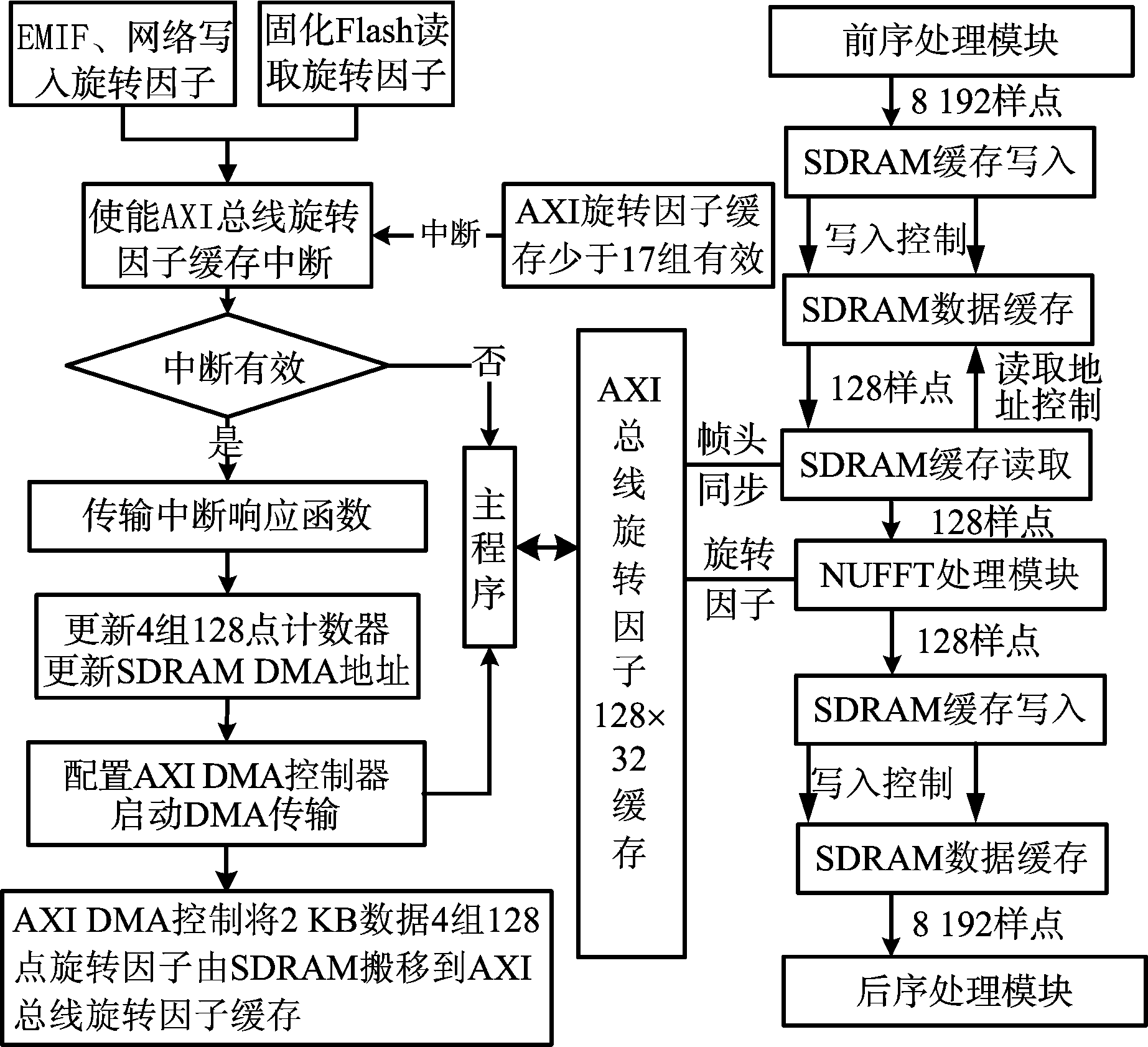
图4 NUFFT处理流程
如图4所示是NUFFT处理流程,为了保证结果的正确性,必须要避免旋转因子和待处理数据出现错帧的情况,两者要严格对应。为此,设计同步信号来保障数据与旋转因子的一致性,每8 192帧数据之前需要填充一个帧头数据作为指示信号,同步FPGA内部NUFFT处理模块进行SDRAM采样点数据读取的同步校准,触发相应模块将数据缓存SDRAM读写地址同步到第一列。这种方式保证Microblaze写入的旋转因子与待处理数据严格对应。而且,即便是FPGA内部计数器出现故障,也可以被同步信号进行复位,错误不会累计持续存在,最多存在于一组128帧数据中。
2.2.4 SDRAM缓存
在NUFFT处理前后,采样数据需要按照128×8 192在SDRAM进行阵列缓存。对于12通道数据,其数据存储容量需求为:12×128×8 192× 4 B=48 MB,数据读取带宽为:48 MB/64 ms=750 MB/s,数据写入带宽是数据读取带宽的两倍,因此,读写带宽为2.25 GB/s。SDRAM控制器性能为1 600 MS/s×32 bit=6.4 GB/s,因此,不会出现带宽瓶颈。
为了便于旋转因子与采样点数据的严格对应与异常处理归零,采用跳动写入而使读取连续的方式。另外,为了满足系统的实时性处理要求,对数据进行乒乓读写。
如图5所示,设定每帧8 192点数据序号为Y,128帧的帧序号为X,那么每个数据缓存阵列应当为12×8 192,但是为了保证数据读取的连续,将数据的写入进行跳动,每次写入12个通道样点Y之后,将Y+1样点偏移128地址单元进行写入,当这样排列完成后,后续NUFFT运算读取数据的时候,可以顺序读取到所有12个波束128帧数据的Y样点,直接便可以进行NUFFT运算。另外,当第一组128×8 192×12波束数据写入完成后,写入模块直接在SDRAM上另一个64 MB再次进行写入,实现地址空间的乒乓,使得数据处理更加高效。乒乓写入模块必须将数据写入状态告诉数据读取模块,以便读取模块控制开始从AXI总线读取旋转因子并对齐旋转因子与读取数据。旋转因子从Microblaze的读取被设计为阻塞式的,也就是NUFFT模块没有查看到足够的帧数据写入的时候,是不会读取数据进行旋转因子载入与样点数据读取的。
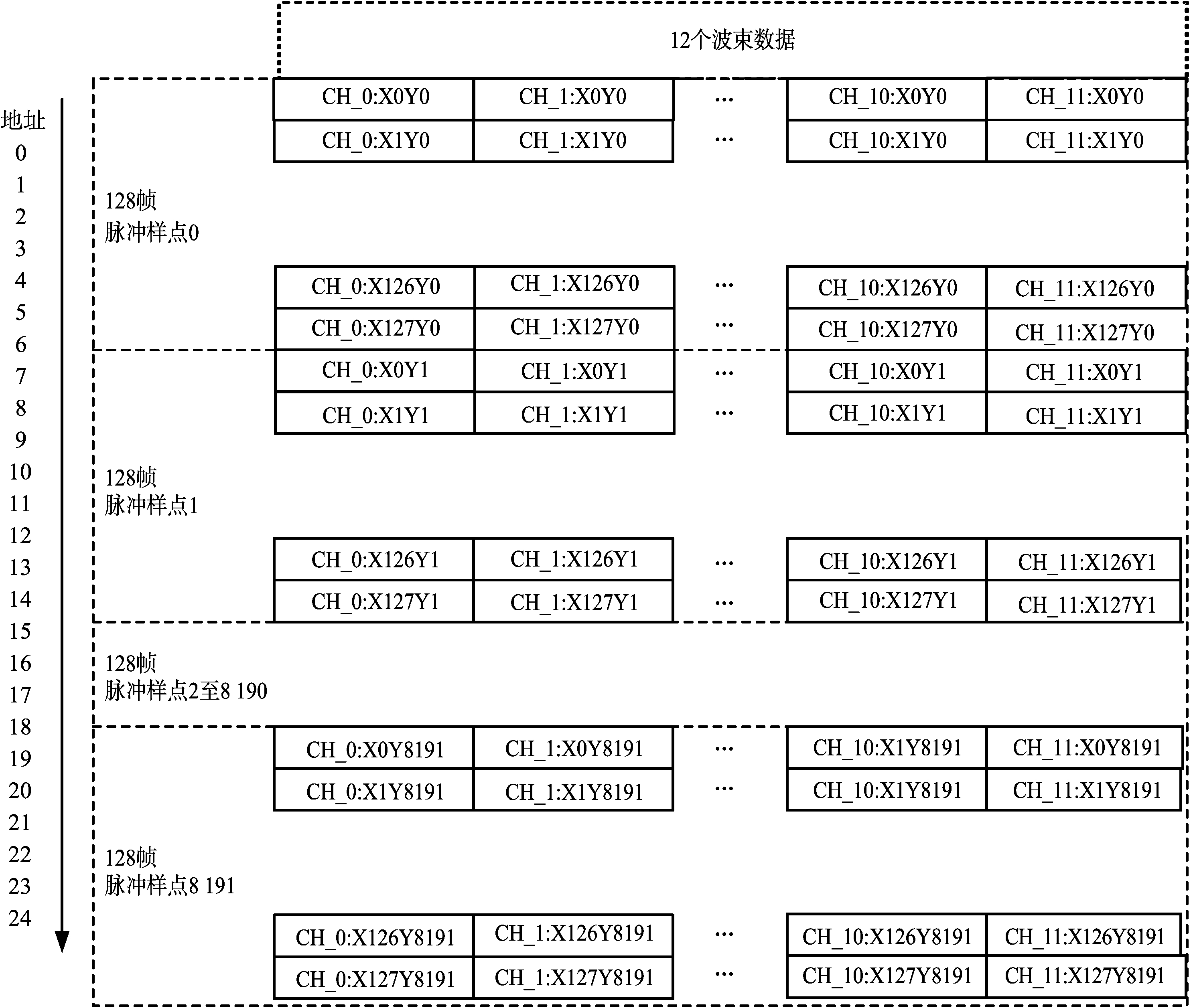
图5 SDRAM存储设计
SDRAM控制器的突发模式为256 B,而12波束样点为48 B,根据突发模式,使用3组突发写入数据一次性写入16组采样点数据,那么在连续读取时,将得到16组×128样点数据,此时只需要16×12×4×128 B= 98 304 B数据缓存,相当于24个36 Kbit的BlockRAM,而XC7VX690T FPGA内置了1 470个36 Kbit BlockRAM,经实际仿真,验证了其可行性。
3 实现结果
经过硬件实现之后,多波束硬件资源使用情况如表2所示。
表2 FPGA资源使用情况
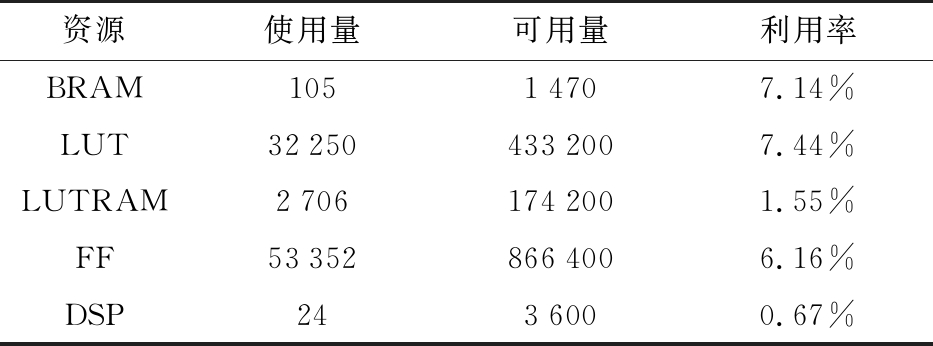
资源使用量可用量利用率BRAM10514707.14%LUT322504332007.44%LUTRAM27061742001.55%FF533528664006.16%DSP2436000.67%
为了验证算法有效性和硬件实现方案的正确性,对采集到的雷达回波数据分别作方位向的快速傅里叶变换和非均匀快速傅里叶变换,比较校正前后相参积累效果。为了效果更加直观,将其中一个波束FPGA处理结果数据通过光纤传输到现有雷达数据记录回放系统,该系统可以实现雷达数据的高速传输并将数据进行存储。将存储的文件导出,由Matlab读取计算结果并画出相参积累效果图,如图6所示。
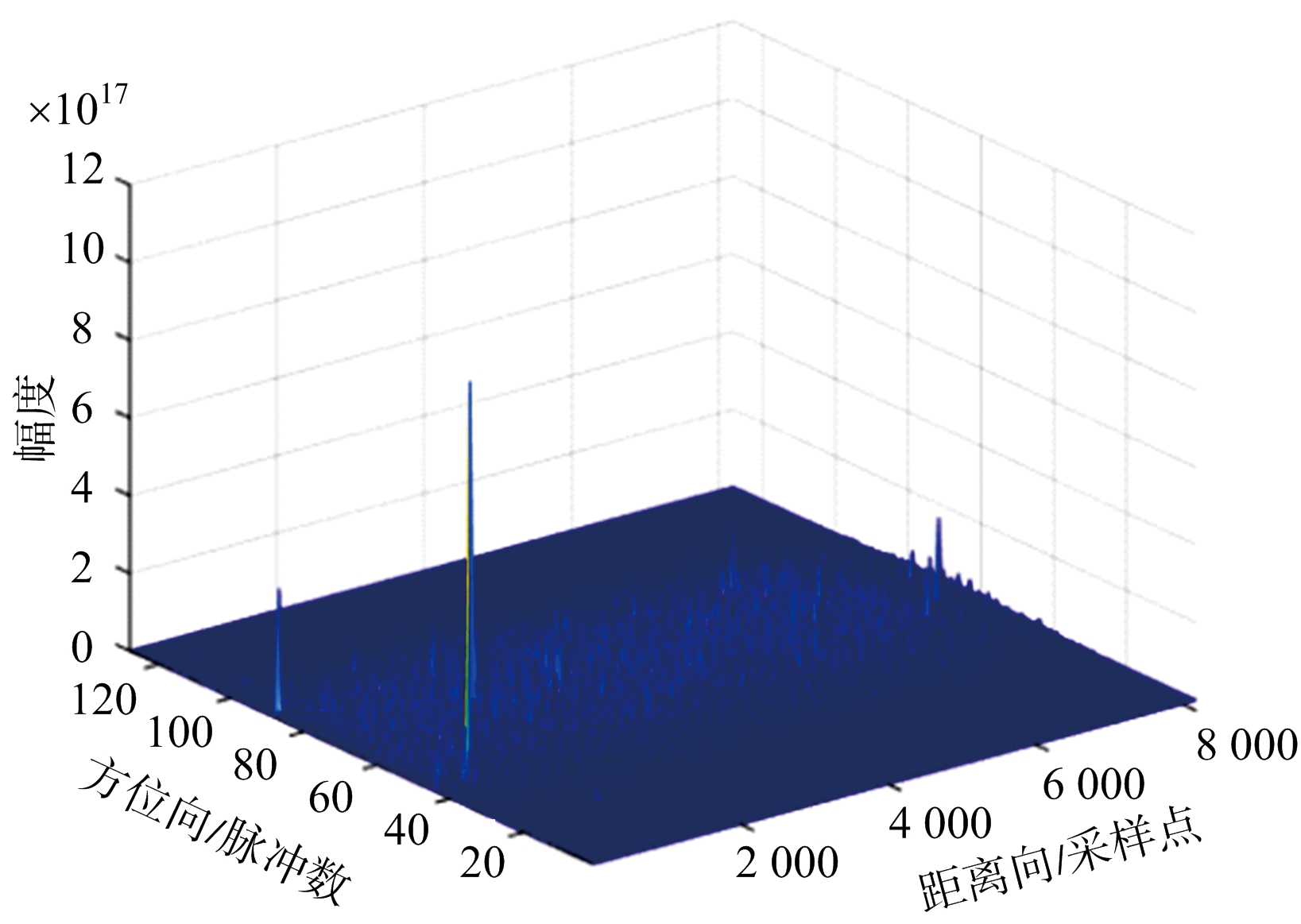
(a) 校正前效果

(b) 校正后效果
图6 校正前后效果
由图6可以看出,经过NUFFT之后,可以明显提升相参积累效果,提高弱小目标的检测能力。经计算,信噪比较未作处理的结果提升了3 dB左右,达到了预期效果,为目标检测奠定了基础。
4 结束语
本文针对相参积累过程中出现的距离走动,采用NUFFT来进行校正,有效解决了距离走动问题,提升了相参积累效果,提高了对弱小目标的探测能力。同时,使用多波束并行处理来扩大空域覆盖范围。针对多波束距离走动校正传统实现过程中出现的资源不足的问题,提出了一种新的NUFFT硬件实现方案,并验证了算法和硬件实现方式的正确性。该实现方式显著减少了运算量和存储量,使得即使在资源非常有限的FPGA中,也能实现多波束的并行运算,非常适合工程实现。
[1] 张都川,文才,刘辉. 高速弹载雷达目标相参积累技术研究[J]. 电子科技, 2017, 30(3):174-177.
[2] 李春林,吴琳拥. 基于Keystone变换的长时间相参积累研究[J]. 电子科技, 2013, 26(6):148-152.
[3] 高玉祥,张兴敢,柏业超. 基于Keystone变换的高速运动目标检测方法研究[J]. 南京大学学报(自然科学版), 2014, 50(1):30-34.
[4] 王万田,袁俊泉,王力宝,等. 天空双基地预警雷达长时间相参积累算法研究[J]. 雷达科学与技术,2017, 15(4):397-402.
WANG Wantian, YUAN Junquan, WANG Libao, et al. Long-Time Coherent Integration Algorithm for Space-Air Based Bistatic Early Warning Radar[J]. 2017, 15(4):397-402. (in Chinese)
[5] SUBIZA B, GIMENO-NIEVES E, LOPEZ-SANCHEZ J M, et al. An Approach to SAR Imaging by Means of Non-Uniform FFTs[C]// IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France: IEEE, 2003:4089-4091.
[6] 李银斌. 非均匀快速傅里叶变换及其在SAR成像中的应用[D]. 南京: 南京航空航天大学, 2016.
[7] SUN Zhi, LI Xiaolong, YI Wei, et al. Detection of Weak Maneuvering Target Based on Keystone Transform and Matched Filtering Process[J]. Signal Processing, 2017, 140:127-138.


