0 引 言
在雷达对抗中交叉眼干扰是一种针对单脉冲跟踪雷达实施角度欺骗的经典而重要的干扰手段[1-3],在各种关于雷达对抗原理的教科书[4-6]与公开文献[7-8]中对交叉眼干扰的技术原理都有较为详细的分析。但上述这些原理性讲述大都是从数学的角度进行繁杂的公式推导之后才得出最终的干扰效果表达式,而且该表达式的物理意义不明显,甚至还有奇异值的出现,从而限制了该理论方法在雷达干扰与抗干扰工程实践中的指导性应用。
实际上早在1873年英国物理学家麦克斯韦创建描述电磁波特性的著名麦克斯韦方程组时就指出光波也是一种电磁波。既然光波与微波都同属于电磁波这个大家族,那么光学研究中所得到的部分物理原理同样也可以借鉴到微波领域而加以应用。正是在这一思想的指引下,回想到了1801年英国物理学家托马斯·杨完成的相干光双缝干涉实验[9-10],并将此实验结果类比借鉴过来解释交叉眼干扰对单脉冲雷达的作用效果。所以本文在对杨氏双缝干涉实验现象与原理简要介绍之后,将光学成像接收屏类比成单脉冲雷达接收天线面;将两条双缝类比成空间中的两个干扰信号发射源。在此基础上,利用杨氏双缝干涉实验中的干涉条纹来解释交叉眼干扰对单脉冲雷达测量目标信号来波方向的误差引入作用,从而生动形象地揭示了交叉眼干扰对单脉冲雷达测向所产生的影响。从这一全新的视角来解释交叉眼干扰的技术原理,不仅物理意义清晰,而且还可以对干扰效果进行定量分析,从而为其广泛的理论指导应用奠定基础。
1 杨氏双缝干涉实验
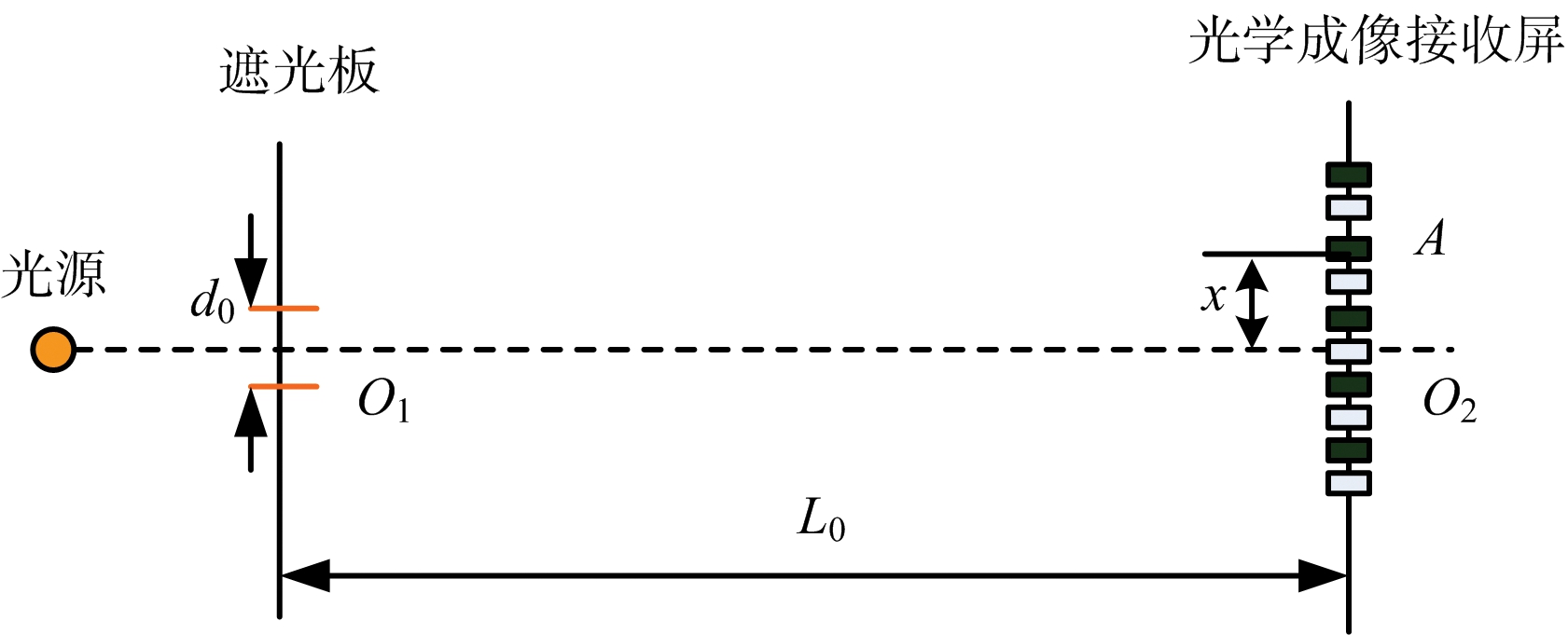
为了便于类比,在此将杨氏双缝干涉实验过程与结果进行简要回顾。杨氏双缝干涉实验是波动光学部分的重要内容之一[9-10],如图1所示。

(a) 三维立体图
(b) 俯视图
图1 杨氏双缝干涉实验场景
图1中光源到遮光板上双缝之间的距离相等,双缝的中点为O1,光学成像接收屏的中点为O2,遮光板与光学成像接收屏相互平行且距离为L0,双缝之间的距离为d0,且O1O2的连线与遮光板、光学成像接收屏垂直。光源发出的光波在经过遮光板上的双缝之后,将会在光学成像接收屏的中部产生明暗相间的干涉条纹。设光波长为λ0,在图1(b)的俯视图中光学接收屏上一点A与O1O2之间的距离相对坐标记为x。于是A点处与双缝之间的光程差D0(x)如下式所表达:
xd0/L0
(1)
式(1)的化简过程中利用了|x±d0/2|≪L0的特性,因为当y≪1时,有近似式![]() 成立。于是光学成像接收屏上点A处条纹的复振幅A0(x)由下式确定:
成立。于是光学成像接收屏上点A处条纹的复振幅A0(x)由下式确定:
(2)
式中,γ0为由光源发光强度所决定的系数,φ0为干涉相位,且满足如下关系式:
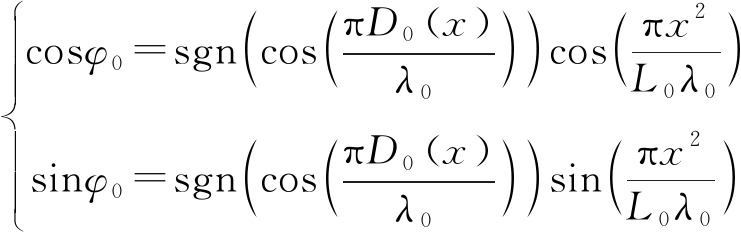
(3)
式中,sgn(·)表示符号函数。由式(2)可知:当光程差D0(x)为半波长的偶数倍时,复振幅的模值达到最大值γ0,即产生同向叠加的明条纹;而当光程差为半波长的奇数倍时,达到最小值0,即产生反向叠加的暗条纹。相邻两条明条纹或相邻两条暗条纹之间的距离Dz如下式所表达:
Dz=λ0L0/d0
(4)
上述有关杨氏双缝干涉实验中的现象与性质在此不再展开赘述。
2 对单脉冲雷达的交叉眼干扰
单脉冲雷达有比幅单脉冲测角与比相单脉冲测角两种方式,在工程中最常用的是比幅单脉冲测角,所以下面以此类目标为干扰对象,首先建立该类单脉冲雷达测角的数学模型。
1) 单脉冲雷达测角的数学模型
不失一般性,在一维测角条件下单脉冲雷达对天线口面的信号通过3种不同的分布式加权方式来形成和波束、左波束与右波束信号,如图2所示。在此维度上雷达天线口径尺寸为da,天线中心点为O3,和波束直接指向天线正前方,左/右波束与天线法线之间的夹角为θr,由左/右波束来形成差波束。
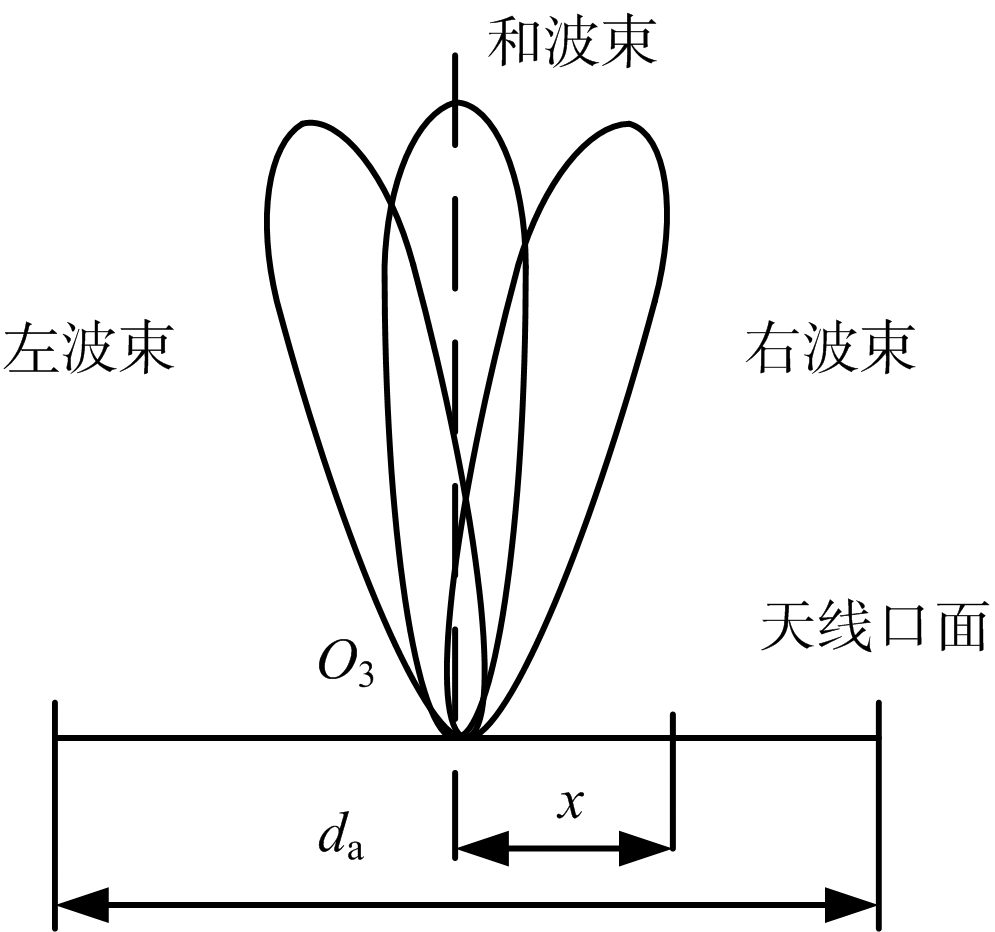
图2 比幅单脉冲测角中天线波束的形成
和波束、左波束和右波束信号Asum,Aleft,Aright实际上是对天线口面处复信号Ar(x)进行不同的加权积分处理,分别如下式所表达:
Asum=![]() Ar(x)dx
Ar(x)dx
(5)
Aleft=![]() Ar(x)sin(2πxsinθr/λr)dx
Ar(x)sin(2πxsinθr/λr)dx
(6)
Aright=![]() Ar(x)sin(-2πxsinθr/λr)dx
Ar(x)sin(-2πxsinθr/λr)dx
(7)
式中,λr为雷达信号的波长,θr为左/右波束与和波束之间的夹角,一般θr≈λr/(2da)。于是差信号Adiff,am输出为
Adiff,am=Aright-Aleft
(8)
2) 交叉眼干扰原理
针对单脉冲雷达的交叉眼干扰又称为相干干扰,需要两个干扰源同时对雷达发射具有稳定相位关系的干扰信号。在工程上为了满足这一要求,通常在飞机两个机翼的翼尖处布置一对收发互补型天线,其连接关系如图3所示,其中接收天线R1与发射天线J2处于同一位置,接收天线R2与发射天线J1处于同一位置,并在其中一路插入相移值为π的移相器。工作时还需要保证两路射频通道的幅相一致性。
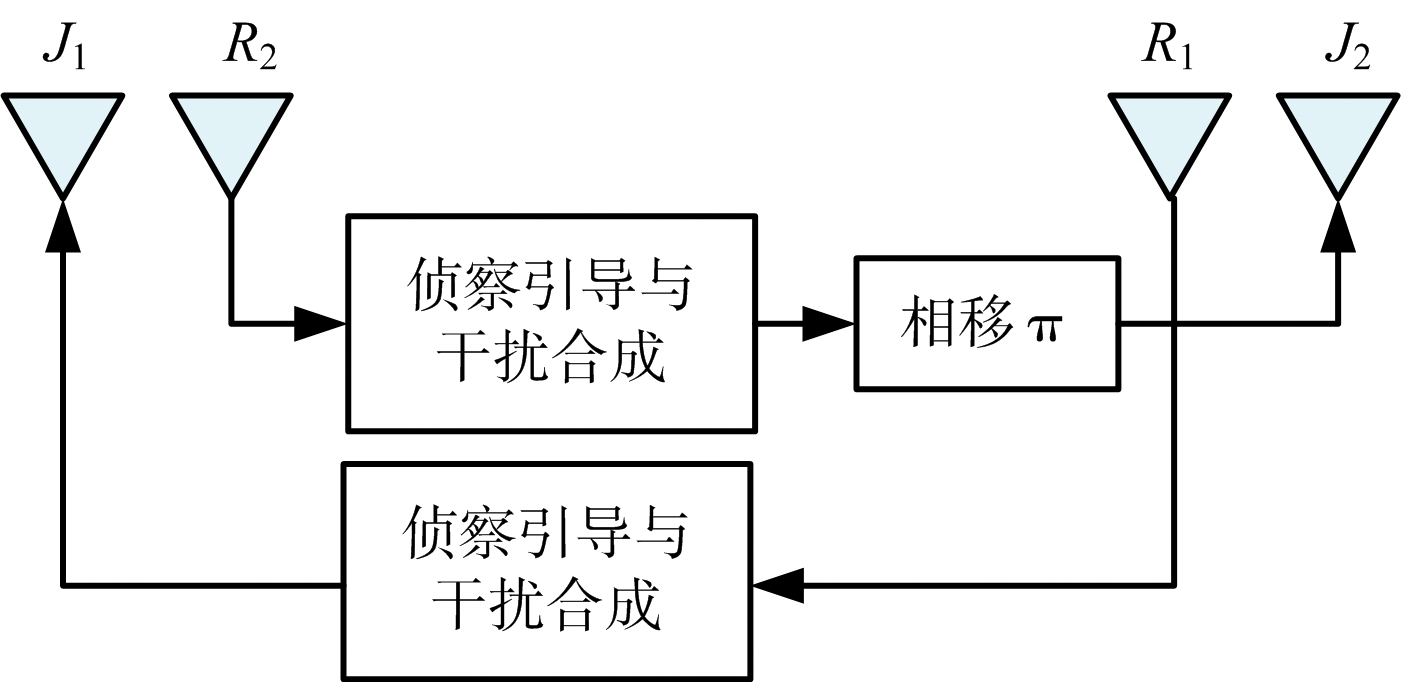
图3 交叉眼干扰中互补反相收发天线配置示意图
地面的高炮火控雷达、导弹目标指示雷达,以及导弹导引头上的制导雷达一般都采用单脉冲测角体制,对空中目标进行测角跟踪。而飞机上的干扰机在使用交叉眼方式对上述雷达实施干扰时就采用了如图3所示的天线配置形式,R1与J2位于飞机的右翼尖,而R2与J1位于飞机的左翼尖,左右之间的距离大约等于飞机的翼展尺寸,随飞机型号的不同而不同,一般在10~30 m量级。当两个接收天线截获到雷达脉冲信号后,按照图3所示的流程产生干扰信号,并控制其中一路干扰信号的相位相对于另一路信号保持具有π的恒定相位差;从而使得J1与J2两个发射天线所辐射的干扰信号在到达雷达天线口面的中心点O3处时,两路信号大小相等,相位刚好相反,从而使得雷达产生较大的测角误差。关于这一过程的复杂数学公式推导在有关雷达对抗的教科书上都有较详细的表述[4-6],在此不再赘述,而是从一个全新的视角来解释交叉眼干扰原理,这就要利用交叉眼干扰中一个关键点,即2个干扰天线所辐射的干扰信号是相干的,相干信号就意味着这两路信号除了相位上有差异之外,其他参数都相同,这一点与前面回顾的杨氏双缝实验中两个双缝相干光源是相似的,这也是启发从杨氏双缝干涉实验结果来解释交叉眼干扰原理的重要原因。
3 相干干扰信号形成空间干涉效应
对比图3与图1,将干扰发射天线J1和J2分别看成是两个相干点源,它们所发射的相干信号会在空间形成稳定的干涉条纹,将单脉冲雷达的天线面看成是杨氏双缝干涉实验中的成像接收屏,这样一来,干扰信号在雷达天线处所形成的干涉条纹就完全决定了干扰效果的好坏。在此以对导弹导引头上的单脉冲制导雷达进行交叉眼干扰为例说明。
1) 干涉条纹的间距
通过类比,交叉眼干扰信号在单脉冲雷达天线面处形成的干涉条纹中明暗条纹之间的间距仍然可由式(4)描述,只不过式(4)中的各个物理量需要从杨氏光学实验类比映射到微波干涉中来。即相邻两条干涉明条纹或相邻两条干涉暗条纹之间的距离DzJ如下式所表达:
DzJ=λJLJ/dJ
(9)
式中,λJ为干扰信号的波长,且λJ=λr,dJ为干扰发射天线J1和J2在弹目垂直方向上的投影距离,LJ为飞机与导弹导引头之间的距离。通常情况下,导弹导引头雷达工作于X至Ka频段,所以λJ在0.8~3 cm范围内,dJ一般在10~30 m量级。于是由式(9)可知,相邻两条干扰明条纹或相邻两条干扰暗条纹之间的距离DzJ一般在LJ/ 1 000的量级,即使在弹目距离为5 km时,DzJ也在5 m左右;如果弹目距离更大,DzJ也会更大。而导弹导引头雷达的天线孔径尺寸一般不超过0.5 m,由此可见,整个导引头的雷达天线面仅仅位于干扰信号所形成的干涉条纹中比较小的一部分空间。
2) 干涉条纹的位置变化
通过类比式(2)和式(3),并结合交叉眼干扰中π的相移可知,在整个雷达天线口面处的干扰所形成的干涉条纹的复振幅分布AJ(x)如下式所表达:
(10)
式中,AJ为与干扰源信号发射强度相关的一个系数,φJ为干涉相位,且满足如下关系式:
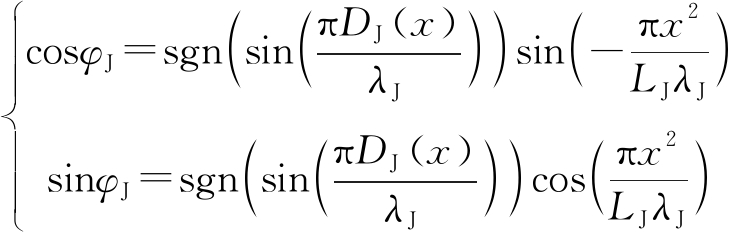
(11)
式中,DJ(x)为两路干扰信号的路程差,类比参照式(1)可得
DJ(x)≈xdJ/LJ
(12)
在图1中由于透过双缝的光信号完全相干,且成像接收屏的中心点处于等光程差位置,在此处所形成的是最亮的明条纹。而在图3所示的交叉眼干扰中,干扰发射天线J1和J2之间增加了一个π的恒定相移,这就相当于附加了半个波长的路程差,所以图3的条纹相对于图1的条纹刚好明暗相反。将DJ(0)=0代入式(10)之后可得:干涉条纹在此处的振幅AJ(0)=0,即这两路干扰信号在单脉冲雷达的中心位置处合成的干涉条纹为最暗的暗条纹。
3)干扰对和差信号形成的影响
由于只关心雷达天线口面处的干扰信号所形成的干涉条纹,所以式(12)中x的取值范围为[-da/2,da/2]。如前所述,实际应用中通常满足da≪λJLJ/dJ,且da与dJ相差不是太大,且一般da<dJ,于是有下式成立:
(13)
由式(12)和式(13)可得
(14)
由式(14)可见,干涉条纹的复振幅在雷达天线中心点两边的相位刚好相反,相差了180°。
由式(5)可知,干扰形成的干涉条纹对单脉冲雷达的和支路信号产生的影响如下式所表达:
Asum,J=![]() AJ(x)dx
AJ(x)dx
(15)
将式(14)和式(10)代入式(15)可得Asum,J≈0,这意味着交叉眼干扰所形成的干涉条纹对单脉冲雷达的和支路的影响非常小,几乎可以忽略不记。
由式(6)和式(7)可知,干扰形成的干涉条纹对单脉冲雷达的左波束和右波束信号Aleft,J,Aright,J产生的影响分别如下式所表达:
Aleft,J=![]() AJ(x)sin(2πxsinθr/λJ)dx
AJ(x)sin(2πxsinθr/λJ)dx
(16)
Aright,J=![]() AJ(x)sin(-2πxsinθr/λJ)dx=
AJ(x)sin(-2πxsinθr/λJ)dx=
-Aleft,J
(17)
于是干扰所形成的差信号Adiff,J输出为
Adiff,J=Aright-Aleft=2Aright
(18)
由上可见,交叉眼干扰所形成的干涉条纹造成单脉冲雷达的左波束信号与右波束信号的大小相等,而符号刚好相反,于是这对单脉冲雷达的差信号输出造成巨大影响,直接形成了新的差信号分量,正是这一干扰差分量的产生使得单脉冲雷达的角度误差剧烈增大,并出现角度跟踪失锁的现象,这即是交叉眼干扰起效的物理本质原因。
4 仿真验证
在此以一个典型的空中防御场景为例来对前面的理论分析结果进行仿真验证。空中飞行的一枚导弹已锁定了5 km距离外的一架飞机,导弹上的导引头雷达是一个典型的比幅单脉冲跟踪雷达,工作于15 GHz,发射脉宽为1 μs的脉冲信号对目标实施探测与跟踪,脉冲信号的峰值功率为2.2 kW,占空比为1/100,由此可计算出其平均功率为22 W,脉冲周期为100 μs。该导引头上单脉冲雷达的天线口径为0.3 m,天线效率为50%,由此可估算出天线增益约为30 dB。被此雷达锁定的飞机的雷达截面积RCS为6 m2,由雷达方程可计算出该飞机的雷达回波信号功率Po如下式所表达:
Po=![]() ≈
≈
5·10-12 W=-83 dBm
(19)
由此可计算出雷达天线口面处目标回波信号的功率密度PoM=7.07·10-11 W/m2,阻抗Ω按377 Ω计算,对应的场强![]()
该飞机被导弹导引头雷达锁定之后由雷达告警接收机发出导弹逼近告警信号,并同时启动双翼尖的干扰设备对该单脉冲雷达实施交叉眼干扰,每部干扰机的发射功率为50 W,干扰发射天线的增益为5 dB,其两天线之间的距离为18 m。按照干扰方程可计算出单部干扰机发射的干扰信号到达雷达天线处的干扰信号功率PJS如下式所表达:
(20)
由此可计算出雷达天线口面处干扰信号的功率密度PJSM=7.07·10-6 W/m2,对应的场强 EJS=51 627 μV/m。
虽然PJS≫Po,即EJS≫Eo,但是单个干扰机无法对导引头单脉冲雷达的角度跟踪环路形成有效干扰的,因为在此情况下由式(6)~式(8)可知,单个干扰机无法驱使单脉冲雷达的角度误差信号发生改变。所以需要飞机上的两部干扰机通过信号相干干涉方式来形成单脉冲雷达的角度误差信号,从而达到角度拉偏的目的。
交叉眼干扰正是采用飞机上两部干扰机所发射的相干干扰信号在单脉冲雷达天线处产生干涉,并形成稳定的干涉条纹,如图4所示(为了形象地展现应用场景,图中没有按照统一比例尺作图)。与图1对比可知,这一场景与杨氏双缝干涉实验场景十分类似。
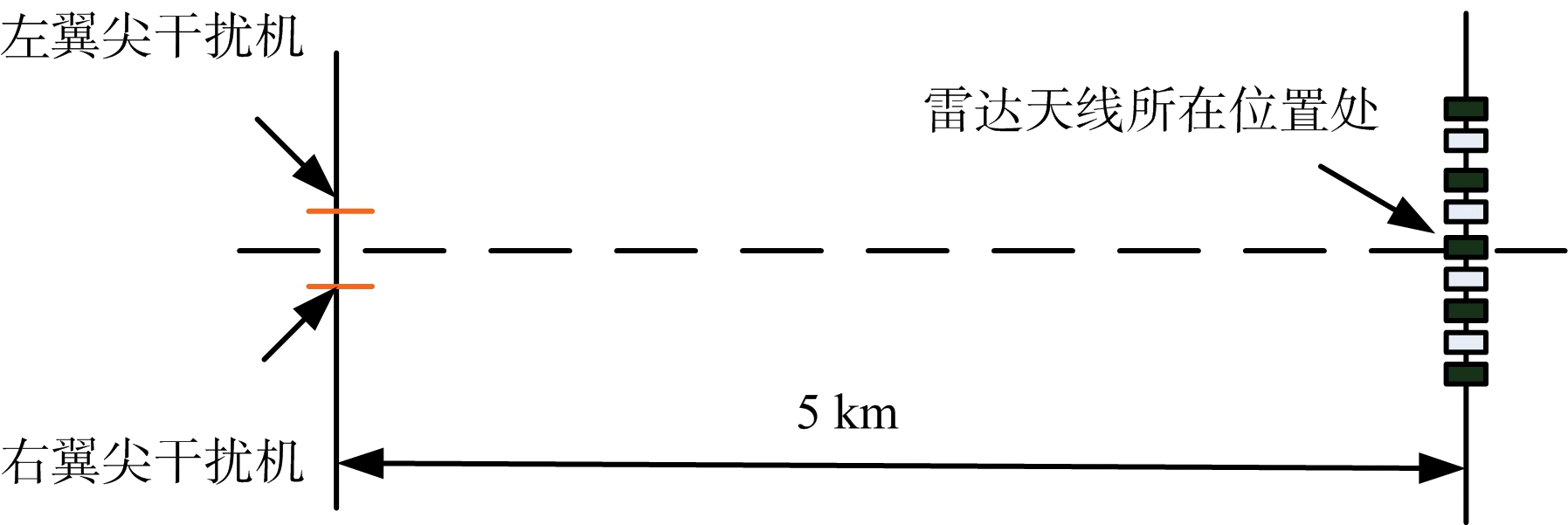
图4 对单脉冲导引头雷达实施交叉眼干扰示意图
由图4可见,雷达天线所在位置正好处于干涉条纹的暗条纹中心处,通过式(9)可计算出相邻两条暗条纹之间的间距为5.6 m,而导引头天线口径为0.3 m,由此可见,整个导引头天线几乎都处于干涉暗条纹的中心区域。为了更加形象地将单脉冲雷达天线位置处干扰信号所产生的干涉条纹展现出来,下面沿雷达天线口面以半个波长1 cm为空间采样间距,对天线口径范围内干扰形成的干涉条纹的复振幅进行采样,如图5所示。图中坐标原点位置处即是雷达天线口面的中心。
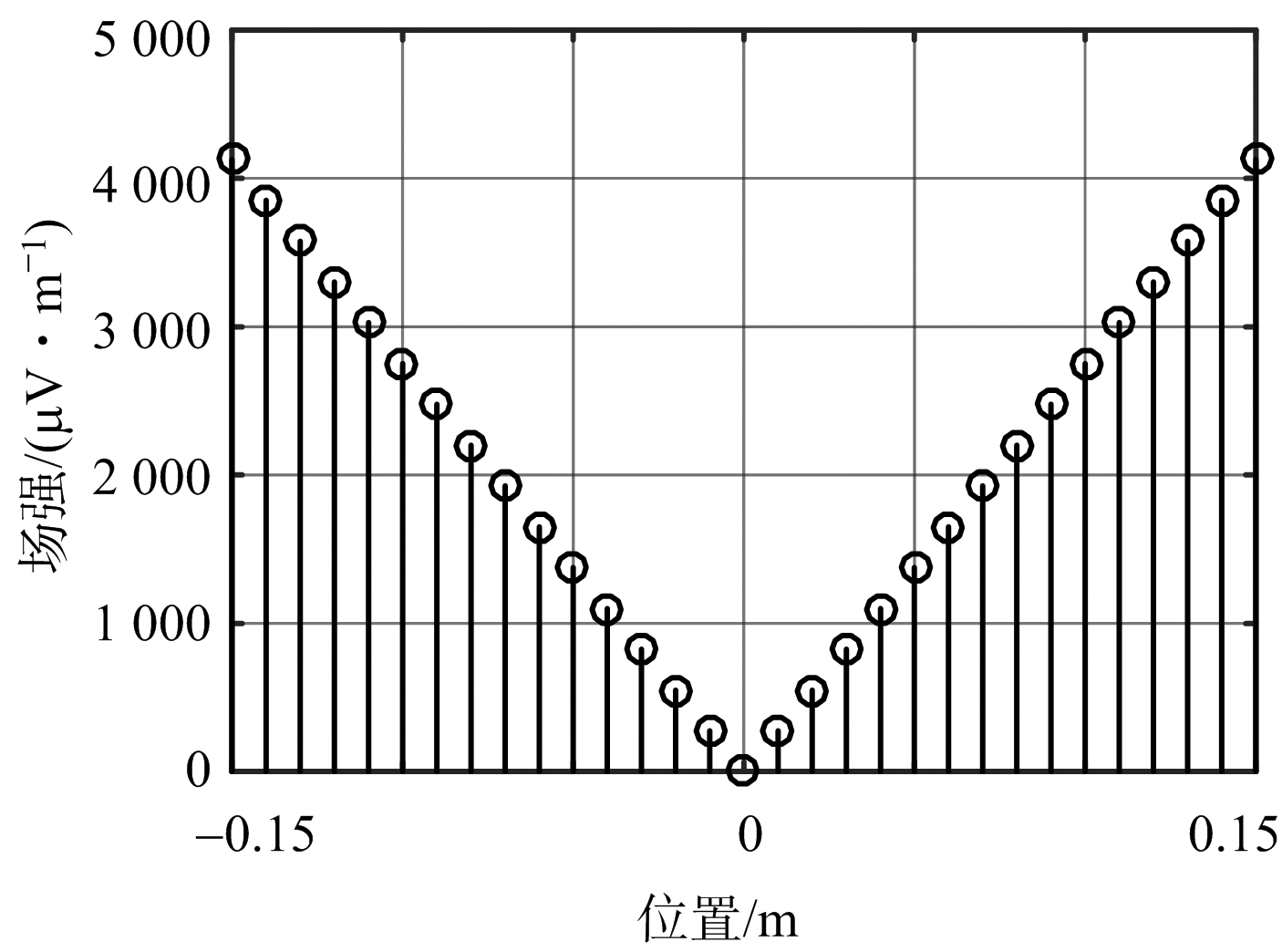
(a) 幅度值
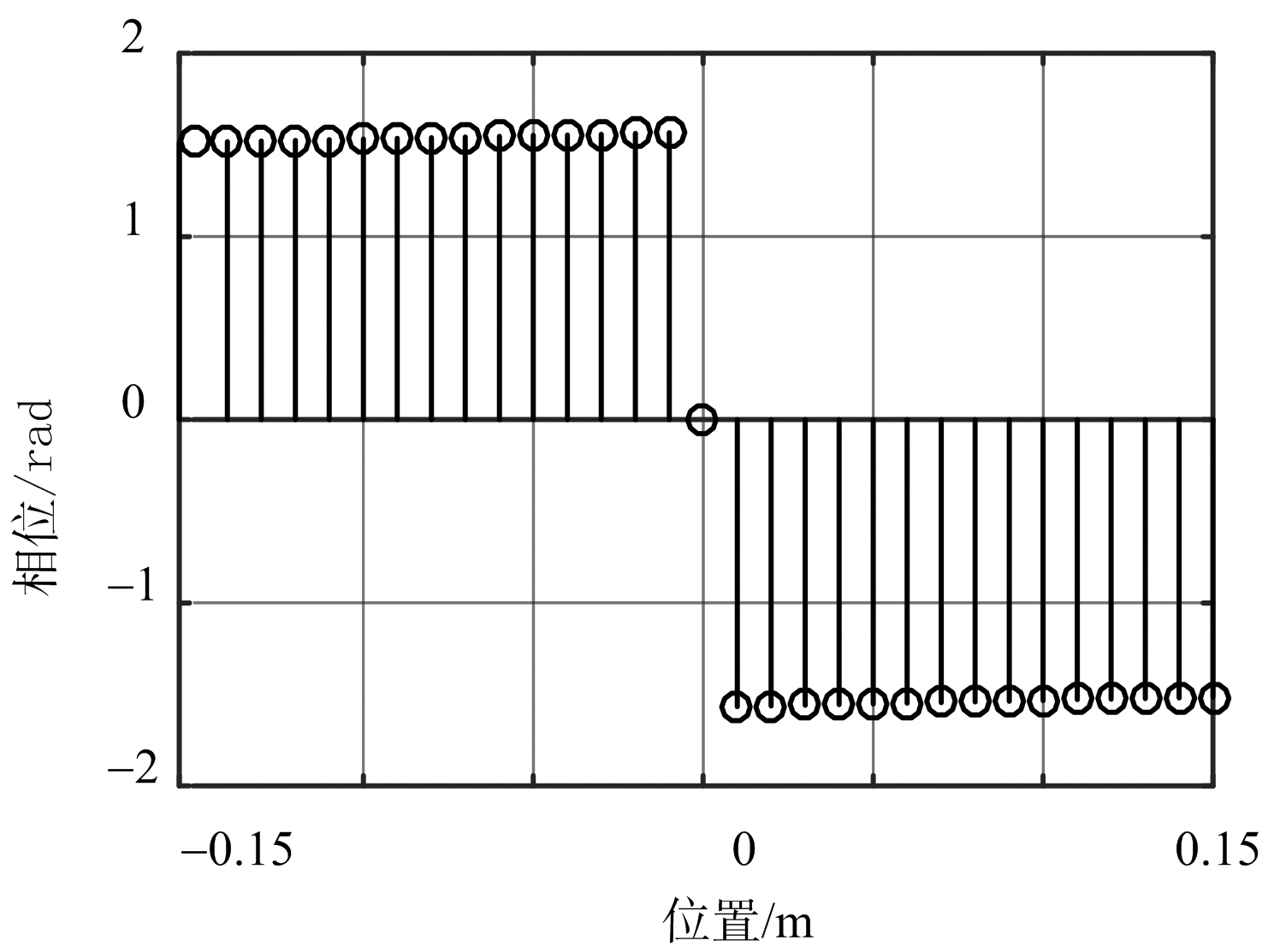
(b) 相位值
图5 干扰形成的干涉条纹的复振幅采样图像
由图5可见,图中左右两部分信号场强的幅度大小对称相等,而相位接近相反,所以由此可得干扰信号在比幅单脉冲雷达测角的和支路的输出几乎为0,这一仿真结果与前面的理论分析结果是完全一致的。在差信号的合成中,由于左右两部分信号场强的相位接近相反,所以差信号的绝对值实际上等于整个信号幅度的求和,这与前面的理论分析结果也是吻合的,这说明交叉眼干扰的作用几乎全集中在雷达的差信号支路中,而和信号支路趋近于无。虽然和信号支路中几乎没有干扰信号,但是和信号支路中的目标回波信号仍然是存在的,即交叉眼干扰信号并没有掩盖和支路中的目标回波信号。尽管如此,从图5中的干扰信号仿真结果与前面的目标回波信号计算结果对比可见,差支路中的干扰信号强度远大于和支路中的目标回波信号强度,按照比幅单脉冲雷达的角度误差计算式,在此情况下将产生一个巨大的角度拉偏条件,使得雷达主波束向单一方向偏转,从而将雷达天线的指向角拉出目标所在的角位置,从而达到角度欺骗的目的。
5 结束语
针对单脉冲雷达实施交叉眼干扰的传统理论分析中的不足,充分利用光学实验的光波与微波干扰实验中的微波都同属于电磁波这一共同点,本文通过历史上经典的杨氏双缝干涉实验来解释了雷达对抗中的交叉眼干扰原理。虽然光波的波长在μm量级,而微波的波长在cm量级,二者相差了近4个数量级,但是这两种实验都利用了两个具有相干特性的电磁波在空间中形成稳定干涉条纹的性质,来展现了二者在本质上的同一性。这样一来,通过杨氏双缝干涉实验解释雷达对抗中的交叉眼干扰原理,不仅直观形象,而且更能揭示出其中蕴含的本质物理意义,使大家更加深刻地认识到交叉眼干扰对单脉冲雷达测角环节中引入误差的因素与起效的过程,从而可以更加准确地分析干扰起效的原因与干扰有效的程度,为后续干扰样式优化和工程实现因素控制的进一步研究提供了新的方法与手段。这一新视角不仅具有理论意义,而且也具有工程应用价值。
[1] NERI F. Introduction to Electronic Defense Systems[M]. 2nd ed. New York: SciTech, 2006.
[2] DE MARTINO A. Introduction to Modern EW Sytems[M]. Boston, MA: Artech House, 2012.
[3] 崔炳福. 雷达对抗干扰有效性评估[M]. 北京:电子工业出版社,2017.
[4] 赵国庆. 雷达对抗原理[M]. 2版. 西安: 西安电子科技大学出版社, 2015.
[5] 周一宇,安玮,郭福成,等. 电子对抗原理与技术[M]. 北京: 电子工业出版社, 2014.
[6] 贺平. 雷达对抗原理[M]. 北京: 国防工业出版社, 2016.
[7] 刘庆云,马亮. “交叉眼”干扰在单脉冲雷达中表现特征分析[J]. 航天电子对抗, 2016, 32(1):59-61.
[8] 付孝龙,白渭雄,杨忠,等. 交叉眼分析及实施方法[J]. 现代防御技术, 2016, 44(3):121-126.
[9] 曲一线.高中知识清单:物理[M].3版.北京:首都师范大学出版社,2013.
[10] 周平,冯庆. 大学物理(下册)[M]. 3版. 北京: 科学出版社, 2016.
