0 引 言
天基预警雷达空中动目标指示在战略预警体系建设中具有重大意义,其目标检测算法是当今雷达信号处理领域的研究热点。天基预警雷达的优势在于卫星平台高度高、下视范围广,具有全天候、全天时的大范围监视能力[1]。由于星载雷达对目标的观测距离较远,目标回波的信噪比较低,在不增加雷达功率孔径积的情况下,长时间相参积累是提高雷达检测性能的一种有效手段[2-5]。但卫星平台和目标间的高速径向运动,导致目标回波产生距离徙动和多普勒走动,使得回波信号能量散焦,FFT相参积累增益将严重降低。
文献[2-3]利用Keystone变换校正了回波信号的距离徙动,补偿了径向速度对相参积累的影响,但长时间相干积累时,卫星平台和目标间的径向加速度不能忽略,加速度导致的多普勒走动没有得到补偿。文献[4]根据回波高阶相位项对包络补偿效果的影响程度,对数据进行分段处理,先通过Keystone变换补偿距离徙动,再利用分数阶傅里叶变换和最小二乘方法估计出目标的径向速度和加速度,最后根据运动参数估计值构造补偿因子,对回波信号进行运动补偿。但分数阶傅里叶变换需要对参数进行二维搜索,计算量较大,不利于星上信号的实时处理。文献[5]利用Keystone变换补偿回波信号距离徙动后,通过遍历搜索得到径向加速度的估计值,并构造二次相位补偿函数补偿多普勒走动。但遍历搜索不仅需要目标运动的先验信息,而且计算数据量大、速度慢,占用了大量时间和空间资源。
基于天基预警雷达星上信号处理计算量小、实时性高的需求,本文提出了一种天基预警雷达目标运动参数估计方法。首先建立了目标回波模型,并利用Keystone变换校正了回波信号的距离徙动;其次对多普勒模糊数进行广义最大似然估计,利用MTD估计得到目标径向速度;然后对校正后的回波信号在方位向上作延迟自相关处理,再基于FFT和Jacobson校正算法估计得到目标的径向加速度;最后通过仿真实验,验证了本文算法的有效性。
1 回波模型及距离徙动校正
1.1 回波模型
假设雷达发射线性调频脉冲信号,在一个相干处理间隔内,卫星平台和目标的径向距离可以表示为
![]()
(1)
式中:R0为径向初始距离;vr为径向速度;ar为径向加速度,方向以与雷达接近为正方向;tm为慢时间,且有tm=(m-1)Tr,m=1,…,M,Tr为脉冲重复周期,M为相参脉冲数。
回波信号经脉冲压缩后可表示为[6]
![]()
![]()
exp(-j4π/λ·R0+j2π·2vr/λ·tm+
(2)
式中,![]() 为快时间,B为信号带宽,D为信号时宽带宽积,c为光速,λ为波长。
为快时间,B为信号带宽,D为信号时宽带宽积,c为光速,λ为波长。
由式(2)可知,脉压后回波包络峰值存在距离徙动,vr和tm的一次耦合项导致包络峰值的距离徙动,ar和tm的二次耦合项导致包络峰值的距离弯曲。此外,在方位向上,回波信号的多普勒频率为fd=2vr/λ+2ar/λ·tm,fd是tm的一次函数,相干时间内的多普勒走动量为2ar/λ·(M-1)Tr。
1.2 Keystone变换校正距离徙动
对式(2)在距离时域作FFT,得到距离频域-方位时域回波信号:
sr(f,tm)=![]()
(3)
式中,f为距离频率,fc为载频,μ为调频率。由于式(3)距离频率f和慢时间tm存在耦合,因此回波信号逆傅里叶变换到距离时域时,包络峰值会随慢时间tm变化而产生走动。
Keystone变换本质上是时间轴的伸缩变换,变量代换式为tm=fc/(f+fc)·τn,其中τn为虚拟慢时间[7]。式(3)经Keystone变换后为
sr(f,τn)=![]()
exp[j2π(-2R0/λ+2vr/λ·τn+
(4)
式(4)表明,当存在径向加速度时,Keystone变换后距离频率f和慢时间τn仍然存在二次耦合项。实际上天基预警雷达发射窄带信号,信号带宽远远小于载波频率,即B≪fc,1/(f/fc+1)近似为1,因此式(4)可近似为
sr(f,τn)=![]()
exp[j2π(-2R0/λ+
(5)
将式(5)逆傅里叶变换到距离时域得
![]()
![]()
exp[j2π(-2R0/λ+
(6)
由式(6)可知,Keystone变换后回波包络峰值只与初始时刻卫星平台和目标的径向距离有关,和虚拟慢时间τn无关,相干时间内的所有回波脉冲都校正到初始距离单元内。
1.3 Keystone变换实现方法
天基预警雷达发射信号一般采用中脉冲重频,由于目标径向速度较大,回波信号存在严重的多普勒模糊[8]。在存在多普勒模糊情况下,Keystone变换辛格内插法的计算表达式为[9]
sr(f,n)=![]()
(7)
式中,sr(f,m)为信号变量替换前的离散形式,sr(f,n)为信号变量替换后的离散形式,![]() 为多普勒模糊数的广义最大似然估计。
为多普勒模糊数的广义最大似然估计。
2 目标运动参数估计算法
2.1 多普勒模糊数估计
接收回波信号的模糊多普勒频率和真实多普勒频率的关系为
fdact=fdamb+Ffr,|fdamb|<fr/2
(8)
式中,fdact为真实多普勒频率,fdamb为模糊多普勒频率,fr为脉冲重复频率。
在不知道目标速度先验信息的情况下,可以通过广义最大似然估计方法估计出多普勒模糊数F,其计算步骤如下:
(a)设定多普勒模糊数搜索区间[-Fmax,Fmax],其中Fmax=round(2vr max/λfr),vr max为目标径向速度可能的最大取值,round(·)表示向下取整数。
(b) 在区间内对多普勒模糊数进行一维搜索,并对回波信号进行Keystone变换和FFT相参积累,得到距离多普勒信号RD(Ramb,fdamb,F),其中Ramb为模糊距离,fdamb为模糊多普勒频率,F为多普勒模糊数。
(c) 比较不同多普勒模糊数下距离多普勒信号的输出峰值,基于单元选大准则,输出峰值最大单元对应的多普勒模糊数即为多普勒模糊数的广义最大似然估计![]()
多普勒模糊数的广义最大似然估计表达式为
(9)
式中,KT(·)表示Keystone变换,FFT(·)表示快速傅里叶变换,sr表示回波信号。
2.2 目标径向速度估计
由式(9)得到多普勒模糊数F和模糊的多普勒频率fdamb后,根据式(8)得到目标的真实多普勒频率fdact,进而得到目标径向速度的估计表达式为
(10)
目标径向速度估计的算法流程如图1所示。
图1 目标径向速度估计算法流程
2.3 目标径向加速度估计
回波信号经Keystone变换后,所有脉冲包络都校正到初始距离单元。由式(6)可知,在方位向上,回波信号为线性调频信号,其离散表达式为
sr(n)=σexp(-j4πR0/λ+j2πfd0Trn+
(11)
式中:![]() 表示方位向信号的幅度;fd0=2vr/λ,表示起始多普勒频率;μd=2ar/λ,表示多普勒调频斜率;n为虚拟离散时刻,且n=0,1,…,M-1。
表示方位向信号的幅度;fd0=2vr/λ,表示起始多普勒频率;μd=2ar/λ,表示多普勒调频斜率;n为虚拟离散时刻,且n=0,1,…,M-1。
由式(11)可知,通过估计多普勒调频率可以得到目标径向加速度的估计,因此需要对回波方位向信号进行解线性调频。以线性调频信号的延迟信号作为参考信号,参考信号与原信号的自相关函数定义为
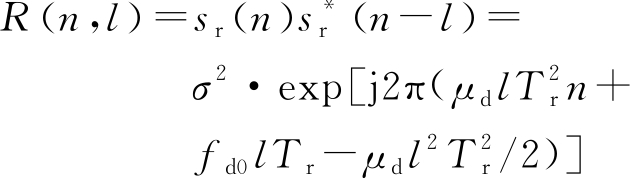
(12)
式中,l为延迟量。文献[10]研究了延迟量对频率估计精度的影响,提出了最佳延迟量为l=round(0.4M),其中M为相干脉冲数。
由式(12)可知,经延迟自相关后,线性调频信号变为复正弦信号,其中复正弦信号频率包含了多普勒调频率的信息。通过对复正弦信号频率进行估计,可以得到多普勒调频率的估计,进而得到目标径向加速度的估计。
基于FFT的正弦信号频率估计方法具有运算速度快、信噪比增益高、对参数不敏感等优点,但当信号真实频率落于主瓣内两根FFT 谱线之间时,频率的估计精度会下降。为了提高估计精度,可以采用插值的方法来估计信号真实频率与粗估计值之间的误差。
天基预警雷达回波信噪比一般较低,而且相干时间内的回波脉冲数有限,针对这一问题,文献[11]提出的Jacobsen算法在低信噪比和FFT点数较少的情况下对频率误差具有较好的估计效果。Jacobsen算法不需要进行傅里叶系数插值迭代,它只需利用FFT频谱最大的3根谱线即可对频率估计值进行校正。
对复正弦信号R(n,l)作FFT,得到其频谱 R(k),Jacobsen校正表达式为
(13)
式中,k0为最大谱线位置,![]() 为信号实际频率与最大谱线对应的频率的相对偏差,其变化范围为
为信号实际频率与最大谱线对应的频率的相对偏差,其变化范围为![]() 表示取实部。Jacobsen校正后的复正弦信号频率为
表示取实部。Jacobsen校正后的复正弦信号频率为
(14)
由式(12)~式(14)得到目标径向加速度的估计为
(15)
根据以上步骤,估计目标径向加速度的算法流程如图2所示。
图2 目标径向加速度估计算法流程
3 仿真实验
3.1 仿真参数及场景
设置卫星平台的轨道参数、目标运动参数如表1所示,雷达参数和波形参数如表2所示。
表1 轨道参数和目标参数
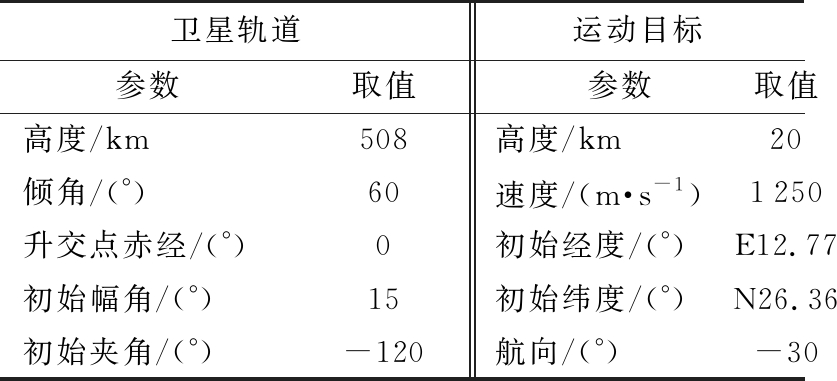
卫星轨道运动目标参数取值参数取值高度/km508高度/km20倾角/(°)60速度/(m·s-1)1250升交点赤经/(°)0初始经度/(°)E12.77初始幅角/(°)15初始纬度/(°)N26.36初始夹角/(°)-120航向/(°)-30
表2 雷达参数和波形参数
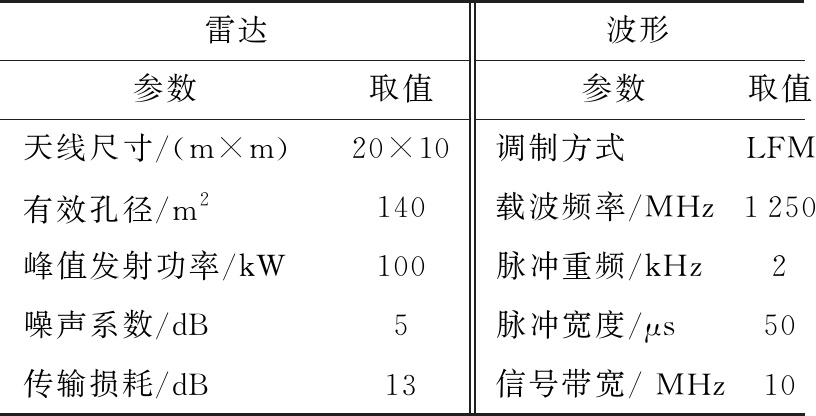
雷达波形参数取值参数取值天线尺寸/(m×m)20×10调制方式LFM有效孔径/m2140载波频率/MHz1250峰值发射功率/kW100脉冲重频/kHz2噪声系数/dB5脉冲宽度/μs50传输损耗/dB13信号带宽/ MHz10
图3是天基预警雷达系统的几何模型。图中P表示卫星平台,O表示地心,Oxyz表示转动地心坐标系,Ox′y′z′表示不转动地心坐标系,Ox″y″z″表示轨道平面坐标系,φ表示卫星平台的轨道幅角,i表示轨道倾角,Ω表示升交点赤经,γ表示x轴和x′轴间的夹角。
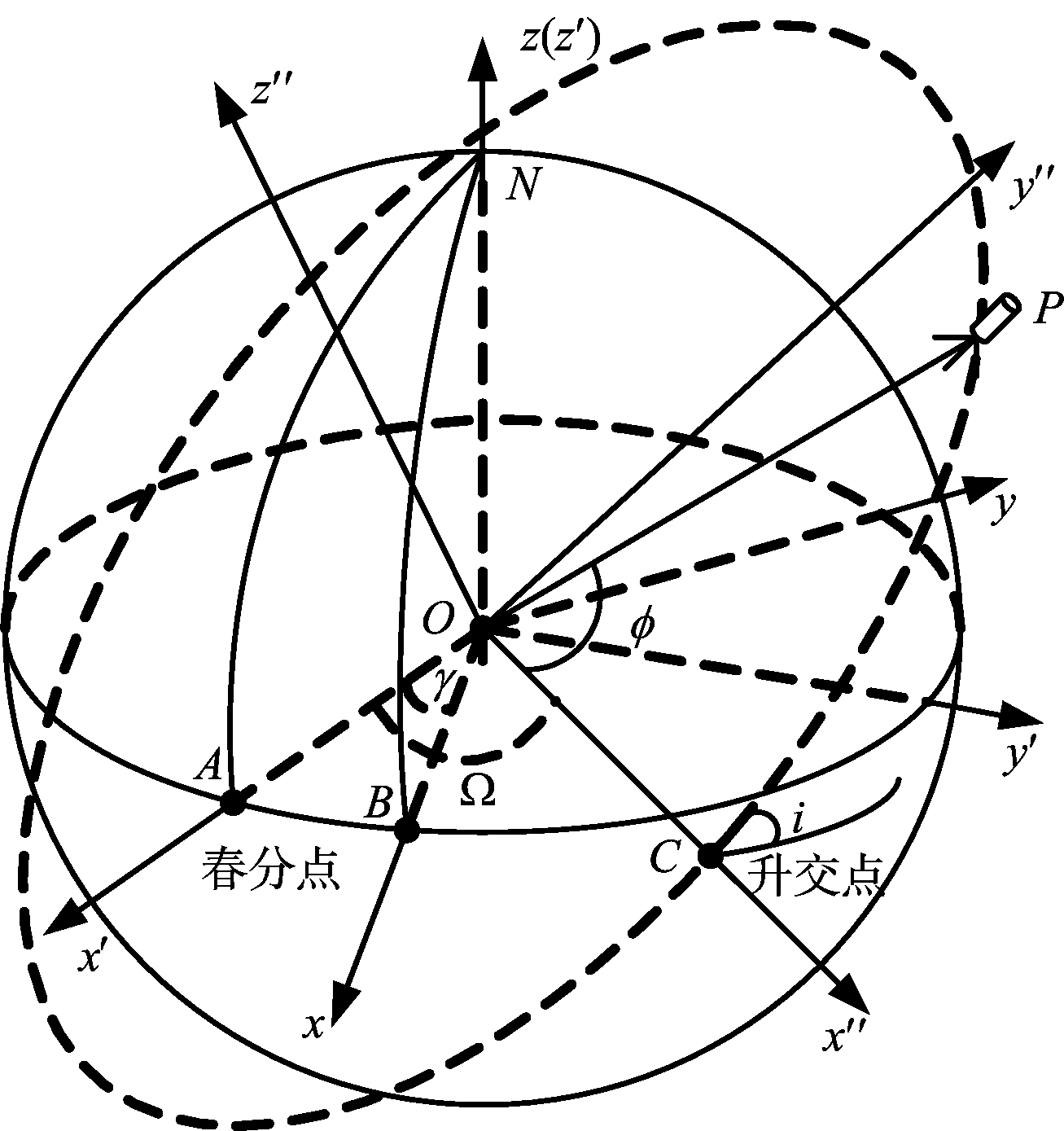
图3 天基预警雷达几何模型
仿真时间从0 s至第600 s,卫星平台和目标的投影点轨迹如图4所示,其中实线表示目标的投影点轨迹,点划线表示卫星平台的投影点估计。
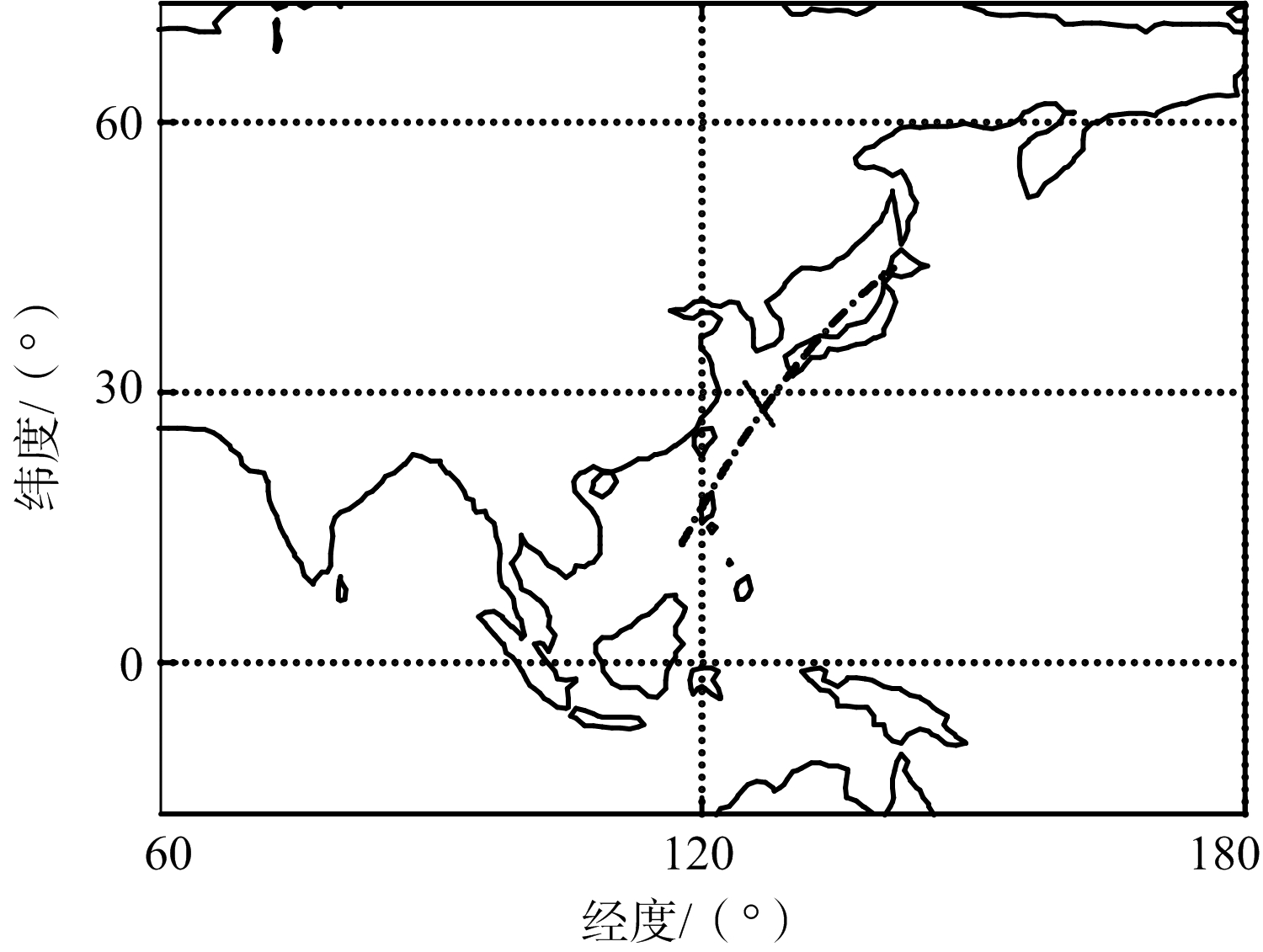
图4 投影点轨迹
观测时间内,径向距离、速度、加速度随时间的变化情况如图5所示。
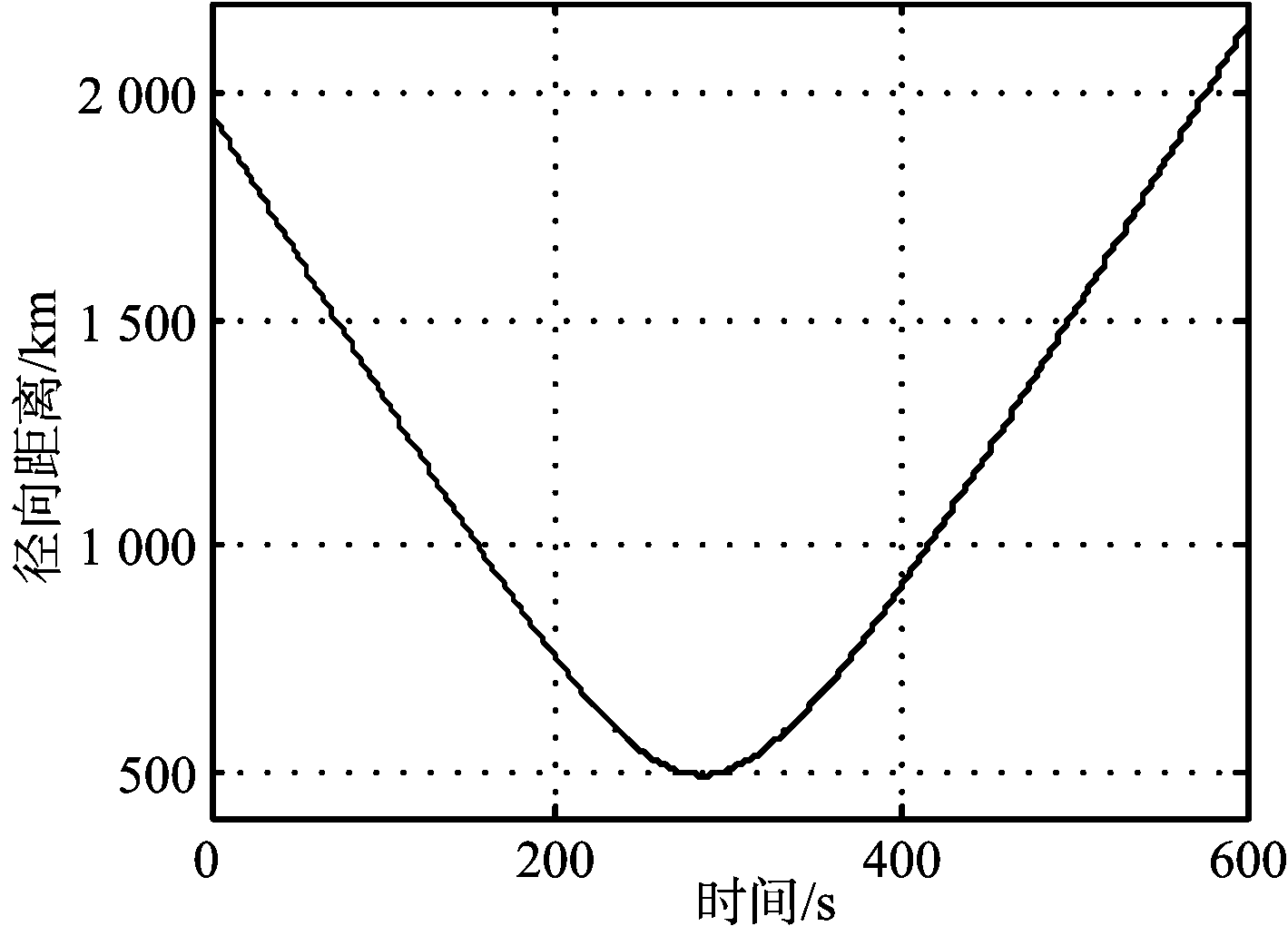
(a) 径向距离
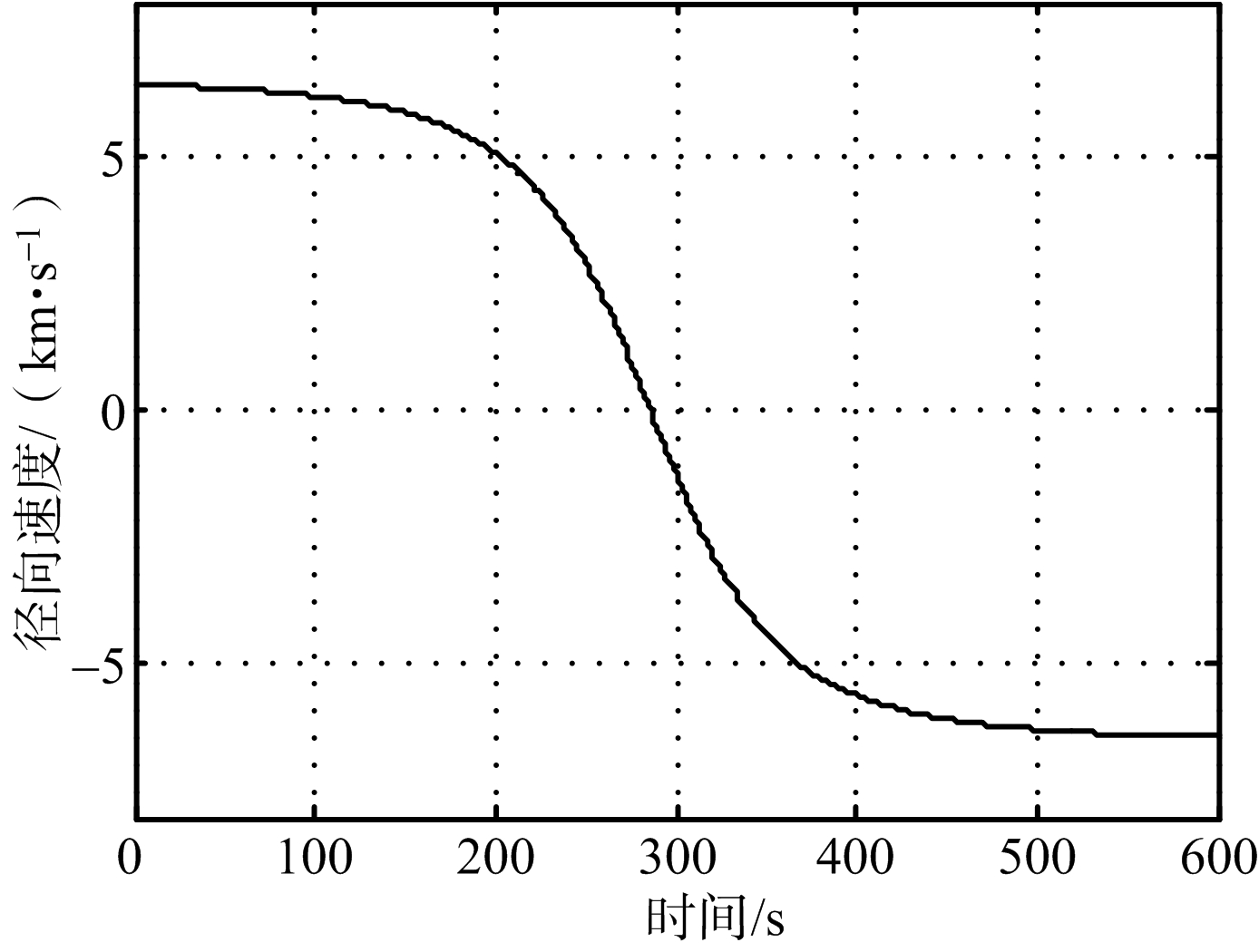
(b) 径向速度
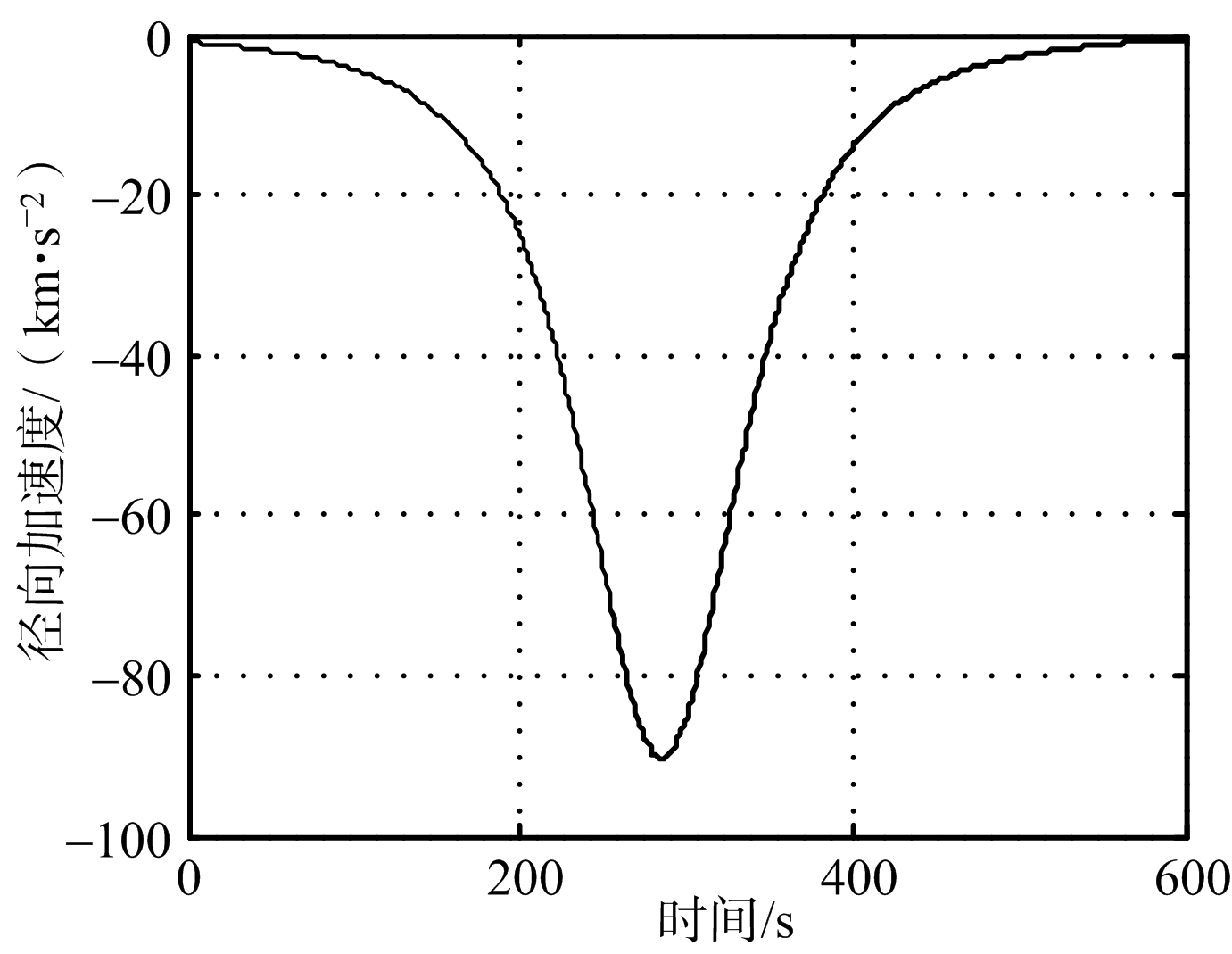
(c) 径向加速度
图5 卫星平台和目标间的径向距离、速度和加速度随时间变化情况
假设天基雷达的威力范围为800 km,由图5可知,雷达能够观测到目标的时间范围为190~380 s。在这一时间段内,目标径向速度的变化范围为-2.1~5.3 km/s,径向加速度的变化范围为-20~-90 m/s2。
3.2 多普勒模糊数估计及徙动校正
设一个相干处理间隔内的回波脉冲数M=512,不失一般性,以起始时间为240 s的相干周期为例,此时目标的相对径向速度vr=3.503 6 km/s,相对径向加速度ar=-56.071 3 m/s2。
在不同多普勒模糊数下,对信号作Keystone变换,MTD处理后得到距离-多普勒信号输出峰值如图6所示。
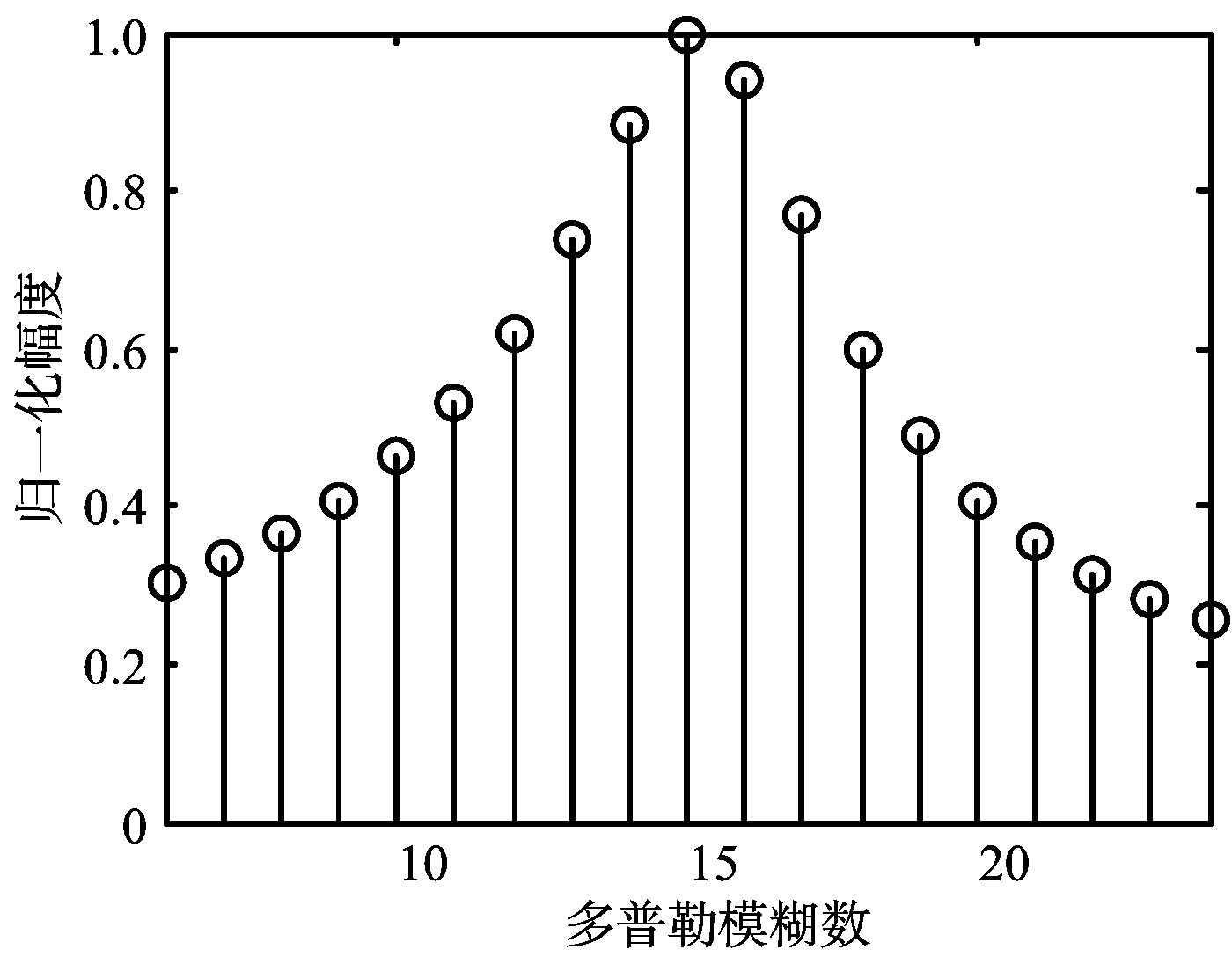
图6 不同多普勒模糊数MTD结果
由图6可知,多普勒模糊数为15时,距离-多普勒信号的输出峰值最大,因此得到多普勒模糊数的广义最大似然估计![]() 再由式(7)对回波信号作距离徙动校正,如图7所示。
再由式(7)对回波信号作距离徙动校正,如图7所示。
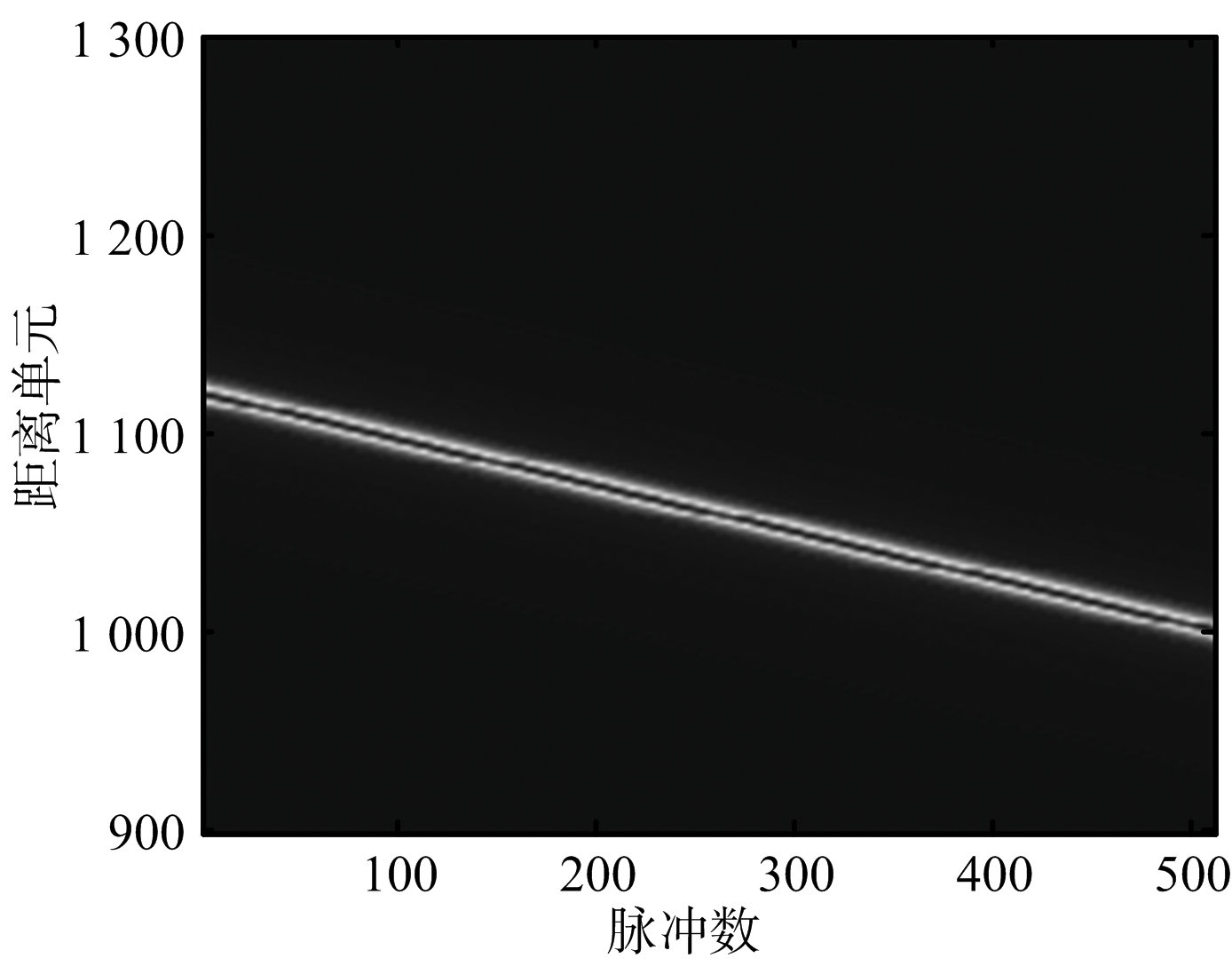
(a) Keystone处理前
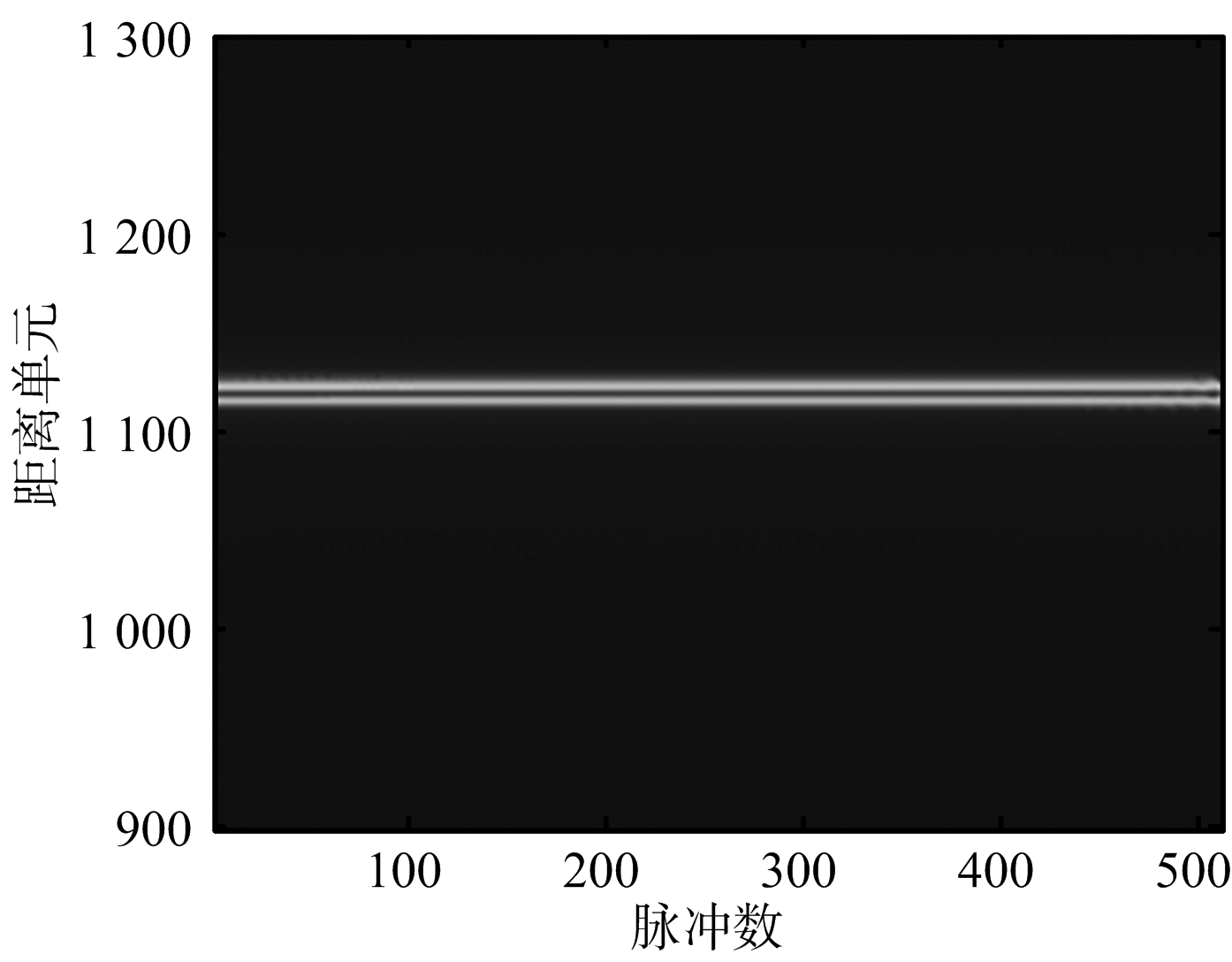
(b) Keystone处理后
图7 距离时域-方位时域回波信号
从图7可以看到,尽管卫星平台和目标间的径向加速度导致回波信号存在二阶相位项,但回波信号的距离弯曲并不明显,在窄带条件下,Keystone变换仍具有良好的距离徙动校正效果。
3.3 运动参数估计
表3是观测时间为240 s时,不同信噪比下径向速度的估计。信噪比指脉压前信噪比,蒙特卡洛仿真次数为100。
表3 径向速度估计
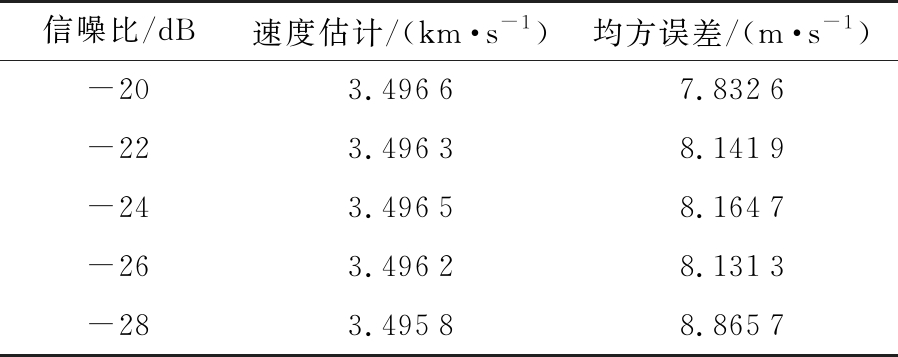
信噪比/dB速度估计/(km·s-1)均方误差/(m·s-1)-203.49667.8326-223.49638.1419-243.49658.1647-263.49628.1313-283.49588.8657
从表3可以看出,径向速度在km/s数量级时,估计的均方误差在10 m/s以内,这一误差范围相对于较大的径向速度是可以接受的。此外,信噪比在-16~-24 dB变化时,估计的均方误差变化不大,说明Keystone变换后利用MTD估计的方法对信噪比变化不敏感,具有良好的鲁棒性。
表4是同一时间径向加速度的估计。
表4 径向加速度估计
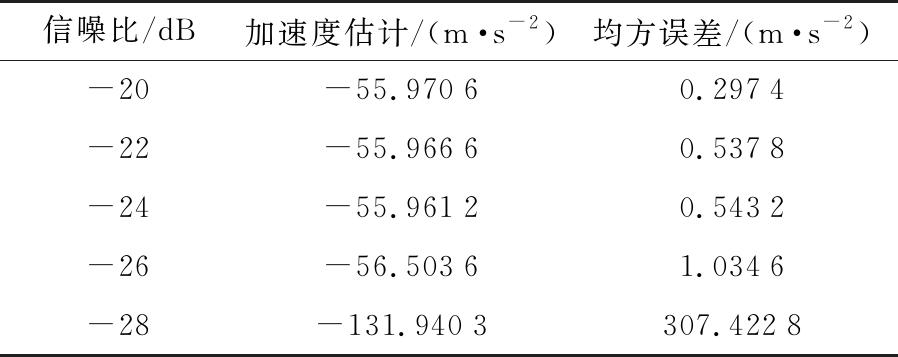
信噪比/dB加速度估计/(m·s-2)均方误差/(m·s-2)-20-55.97060.2974-22-55.96660.5378-24-55.96120.5432-26-56.50361.0346-28-131.9403307.4228
由表4可以看出,基于FFT和Jacobsen校正的径向加速度估计方法在回波信噪比大于-26 dB的条件时,估计均方误差在1 m/s2左右,具有良好的估计精度;但当信噪比降低到-28 dB时,估计均方误差达到300 m/s2,因此估计方法存在信噪比门限,当回波信噪比低于门限时,估计方法失效。
估计方法失效的原因是Jacobsen校正方法需要搜索复正弦信号FFT后的最大3根谱峰,当回波信噪比低于门限时,噪声完全淹没了信号,峰值最大的3根谱线位置发生了较大的偏移,如图8所示。
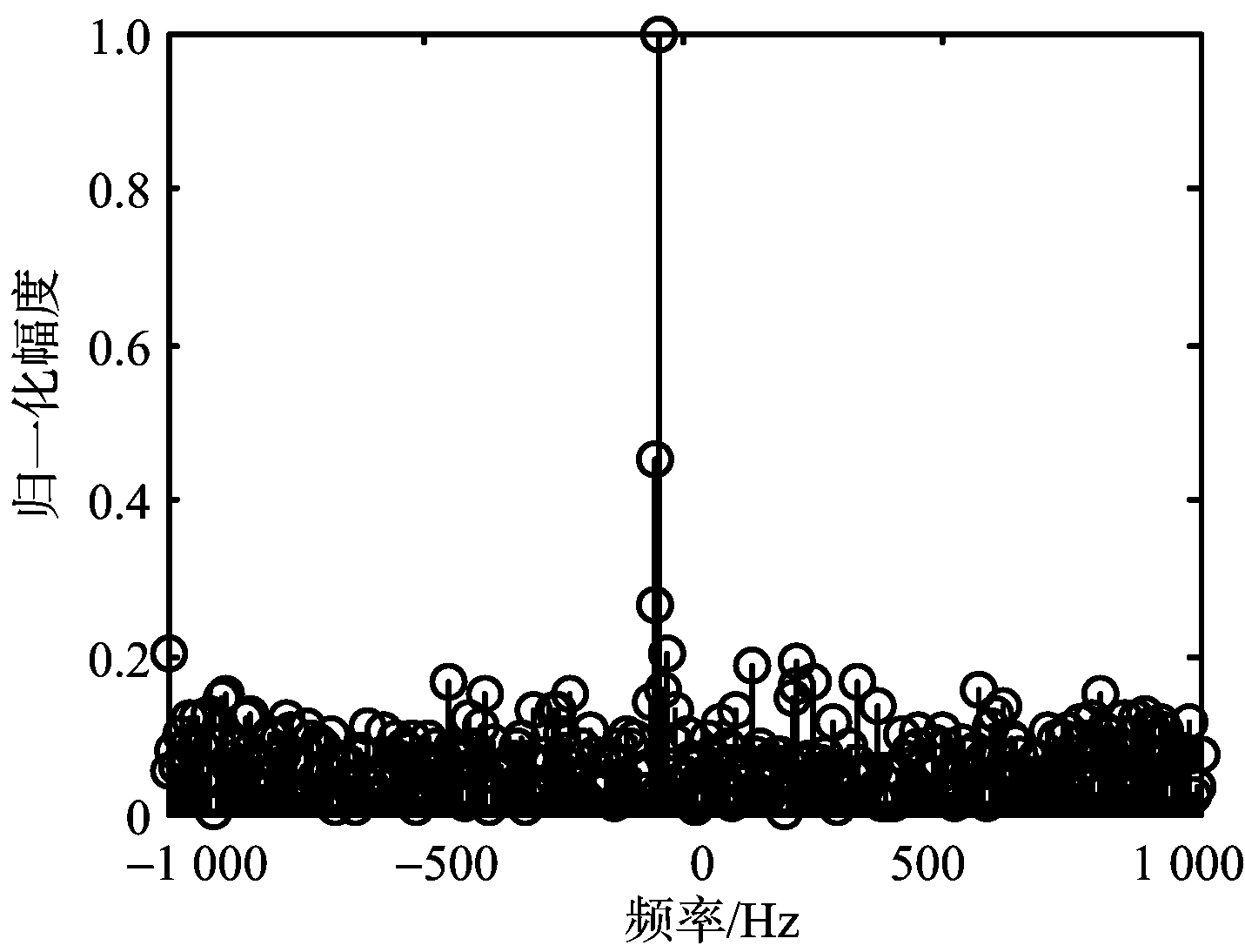
(a) SNR=-20 dB
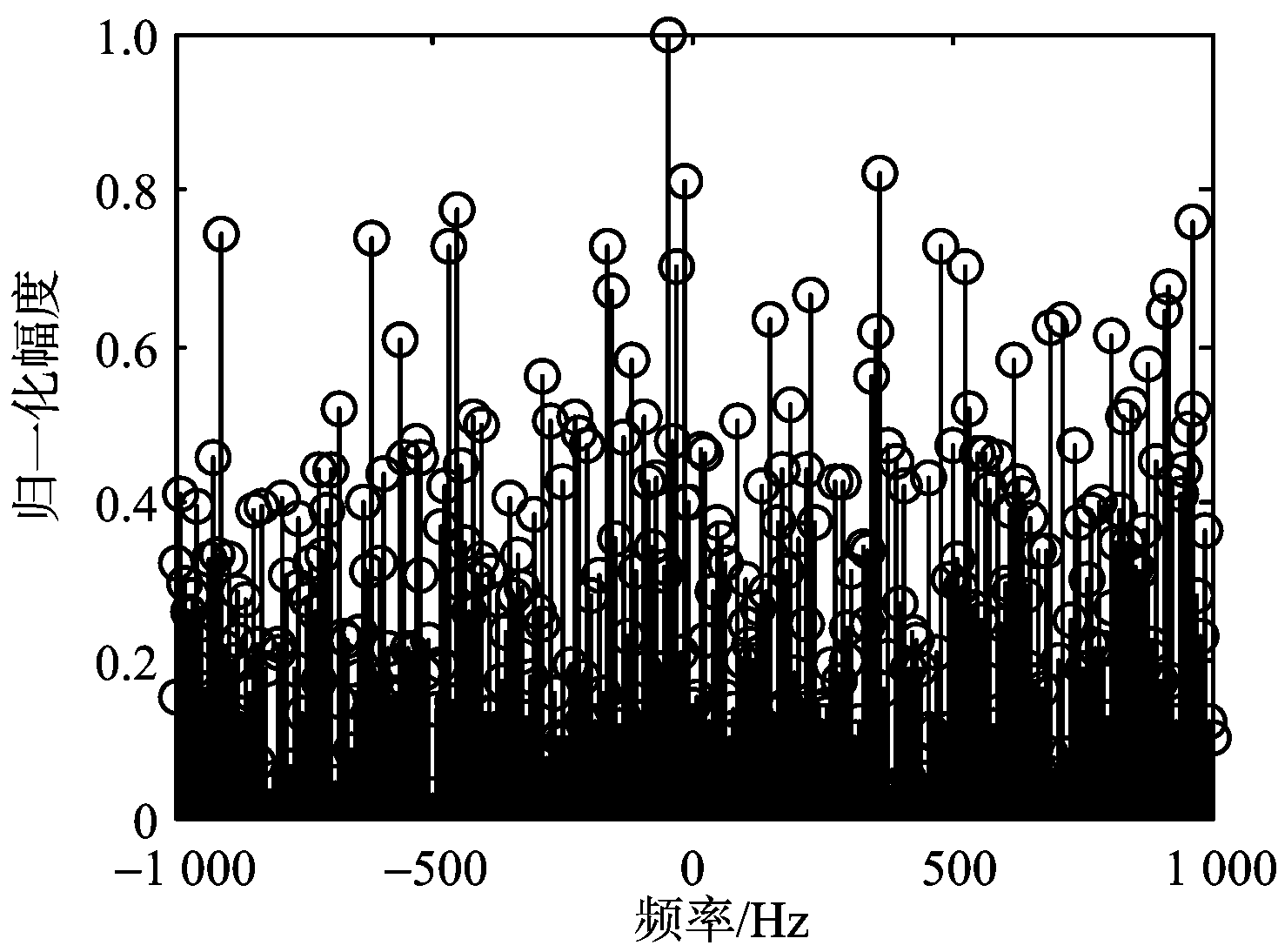
(b) SNR=-28 dB
图8 复正弦信号频谱图
4 结束语
天基预警雷达由于卫星平台和目标间的高速径向运动,在相干积累时间内存在距离徙动和多普勒走动等问题,传统的FFT相参积累检测性能下降。改善目标检测性能的一种方式是通过对目标运动参数进行估计,并构造补偿因子,对回波信号进行运动补偿。本文提出了一种天基预警雷达目标运动参数估计算法,首先由广义最大似然估计得到多普勒模糊数,利用Keystone变换校正回波信号的距离徙动,并对校正后的回波信号作MTD处理,得到径向速度的估计;然后对校正后的回波方位向信号作延迟自相关处理,再利用FFT和Jacobsen校正算法对自相关后的复正弦信号进行频率估计,最后由频率估计值得到径向加速度的估计;仿真结果验证了本文算法的有效性。
[1] 贲德,龙伟军.天基雷达关键技术[J].数据采集与处理,2013,28(4):391-396.
[2] 汤春林,汪学刚,陈祝明.基于距离走动校正的星载雷达空中动目标检测[J].电子测量与仪器学报,2011,25(10):829-834.
[3] 王万田,袁俊泉,王力宝,等. 天空双基地预警雷达长时间相参积累算法研究[J].雷达科学与技术,2017,15(4):397-402.
WANG Wantian,YUAN Junquan,WANG Libao,et al. Long-Time Coherent Integration Algorithm for Space-Air Based Bistatic Early Warning Radar[J].Radar Science and Technology, 2017,15(4):397-402.(in Chinese)
[4] 杨志伟,贺顺,吴孙勇.天基雷达高速微弱目标的积累检测[J].宇航学报,2011,32(1):109-114.
[5] 王万田,袁俊泉,王悦,等.一种天空双基地预警雷达高速机动目标检测算法[J].空军预警学院学报,2017,31(5):313-318.
[6] 周亮,袁俊泉,陈阿磊.天基预警雷达回波建模与分析[J].空军预警学院学报,2018,32(2):84-89.
[7] 张顺生,曾涛.基于keystone变换的微弱目标检测[J].电子学报,2005,33(9):1675-1678.
[8] 易锋,刘春静.基于斑马图的天基雷达PRF设计[J].雷达科学与技术,2015,13(6):667-670.
YI Feng,LIU Chunjing. PRF Design of Space-Based Radar Based on Coverage Diagram[J]. Radar Science and Technology, 2015,13(6):667-670. (in Chinese)
[9] 王娟,赵永波.Keystone变换实现方法研究[J].火控雷达技术,2011,40(1):45-51.
[10] 刘渝.快速解线性调频技术[J].数据采集与处理,1999,14(2):175-178.
[11] CANDAN C.A Method for Fine Resolution Frequency Estimation from Three DFT Samples[J].IEEE Signal Processing Letters,2011,18(6):351-354.
