0 引言
车载毫米波雷达的研究始于20世纪60年代,早期受到元器件的限制发展较慢,随着近年来集成电路的进步和无人驾驶研究的深入,车载毫米波雷达的研究变得活跃起来[1-4]。毫米波雷达探测范围适中,对目标的速度信息比较敏感。在常见的天气状况下,如雾、雨、雪等,毫米波雷达均能正常工作。即使在比较恶劣的环境下,毫米波雷达也能维持一定的性能水平[5]。基于以上原因,毫米波雷达相比于其他的无人驾驶传感器有着明显的优势和不可替代的作用。
车载毫米波雷达通常采用线性调频连续波体制(Frequency Modulation Continuous Wave,FMCW),这是由于线性调频连续波频率随着时间线性增长,信号产生和处理简单,能同时获得较高的距离分辨率和速度分辨率。在线性调频连续波体制雷达中,锯齿波调制方式检测精度高,不涉及多目标的匹配问题,能获得更低的虚警率和漏警率[6],因此被广泛研究和使用。车载毫米波雷达的实际应用场景中,目标的相对速度较大,又由于线性调频连续波慢时间采样频率较低的特点,在速度参数估计中需要解决速度模糊问题。不同于激光雷达角度分辨率较高的特点,车载毫米波雷达受到体积和成本的限制,其发射和接收天线阵列较小,导致角度分辨率较低。
针对车载毫米波雷达角度分辨率较低的问题,业内多参考MIMO雷达中的虚拟阵列算法以提高天线孔径。虚拟阵列算法通过编码分集、频率分集和时间分集的方式,利用发射和接收天线间的位置关系形成更大孔径的虚拟天线阵列。针对编码分集的方式,文献[7]提出一种基于空时分组码的脉冲雷达杂波抑制算法,但该算法不适用于调频连续波雷达。针对调频连续波雷达,文献[8]提出了一种基于频率分集的虚拟阵列算法,但在车载毫米波雷达实际应用中存在系统采样频率较小、模拟滤波器参数不够灵活等问题,导致其实现困难。目前车载毫米波雷达产品中能够实现的虚拟阵列算法多是采用时间分集的方式[9],该方式对硬件性能需求较低、实现简单,但未能利用多发射天线同时工作带来的功率增益,同时其运动相位校准算法无法适用于相干目标,系统性能较差。
本文提出了一种基于空时分组码的FMCW车载毫米波雷达信号处理算法,该算法实现简单,能充分利用多根发射天线带来的功率增益。同时,针对调频连续波雷达虚拟阵列算法中运动相位误差的问题,提出了一种低复杂度的、适用于相干目标的相位校准算法。
1 系统模型
1.1 阵列模型
图1为系统天线阵列示意图。系统采用如图1(a)所示的2×4的天线阵列,单根发射通道的最大发射功率受限。如图1(a)所示,两根发射天线间距为4d,接收天线间距为d,d=λ/2,λ为空气波长。
图1(b)为虚拟天线阵列,虚拟阵列的接收信号由实际天线阵列分别接收发射天线1和发射天线2的发射信号所对应的目标回波信号组成,形成1×8的虚拟天线阵列,以增大天线孔径。
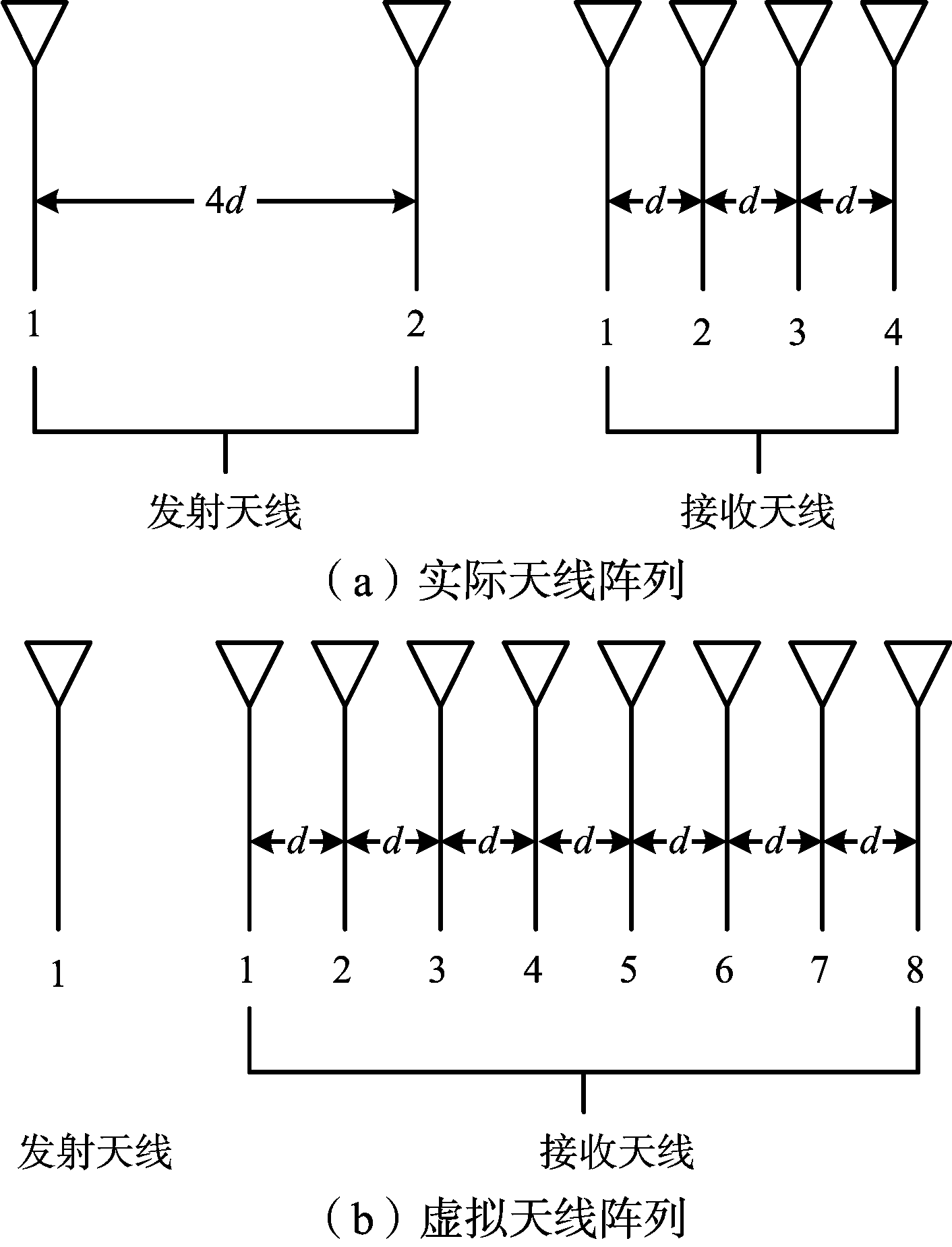
图1 天线阵列示意图
1.2 回波模型
图2为锯齿波雷达时频关系图,其横轴为信号时间,纵轴为信号频率。如图2所示,锯齿波调制方式的雷达发射信号波形幅度恒定,但频率随时间线性锯齿变化。第i(i=1,2,…,Nsa)个扫频周期发射信号可表示为
(1)
式中:![]() 为发射信号幅度;f0为载波中心频率;
为发射信号幅度;f0为载波中心频率;![]() 0为初始相位;μ=B/T为扫频斜率,B和T分别为扫频带宽与扫频周期,Nsa为一个相干处理周期内锯齿波的个数。
0为初始相位;μ=B/T为扫频斜率,B和T分别为扫频带宽与扫频周期,Nsa为一个相干处理周期内锯齿波的个数。
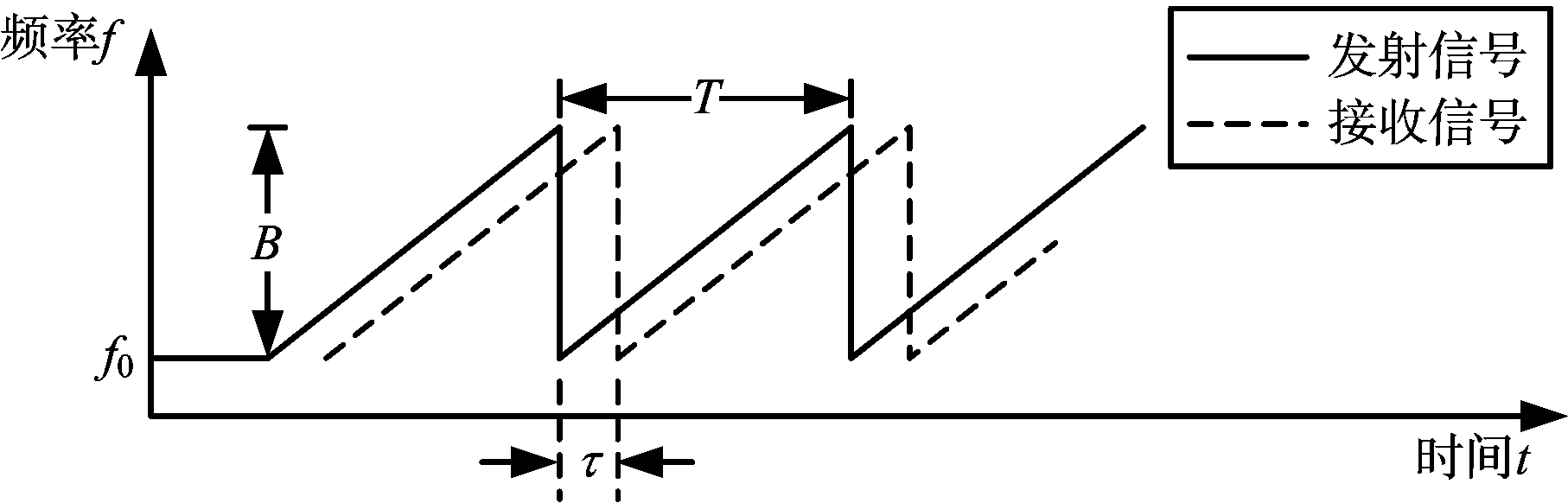
图2 锯齿波雷达时频关系图
考虑t=0时刻,雷达前方存在一个径向距离为r,速度为v(目标相对于雷达的径向速度,以靠近雷达方向为正)的目标,则接收信号(忽略噪声的表示,后续处理类似)为
(2)
式中,(i-1)T≤t≤iT,A0为接收信号幅度,τ=2(r-vt)/c为t时刻目标与雷达间距离引起的时延,c为电磁波在自由空间的传播速度。
将接收信号与发送信号进行混频和低通滤波,舍掉高次项和固定相位项后,得到中频信号
yi(t)=![]() cos(2π((2μr-
cos(2π((2μr-
(3)
式中,(i-1)T+τ≤t<iT。
对中频信号快时间维进行FFT,得到关于目标参数r和v的频率为
fr,v=2μr/c-2vf0/c0
(4)
对中频信号慢时间维进行FFT,得到关于目标参数v的频率为
fv=-2vf0/c
(5)
根据式(5)可以得到目标速度v,将v代入式(5)可以得到目标距离r。
2 基于时间分集的虚拟阵列算法
基于时间分集的虚拟阵列算法,两根发射天线轮流发射相同的调频连续波,相位调整(简称相调)矩阵为
(6)
Ψi,k表示第k个发射时隙时第i根发射天线的发射信号相移,Ψi,k=0则表示在第k个发射时隙时第i根发射天线不工作。假设t时刻,发射天线1发射信号为x(t),接收天线1接收信号为y(t),则阵列接收信号(忽略噪声)可表示为
Y=y(t)·H·Ψ⊙E
(7)
式中,
(8)
Hi,j代表第i根接收天线接收的第j根发射天线的信号相对于y(t)的相位变化,![]() =2πdsinθ0/λ,其中θ0为目标相对于发射天线和接收天线法线的夹角。
=2πdsinθ0/λ,其中θ0为目标相对于发射天线和接收天线法线的夹角。
(9)
E为运动相位误差矩阵。目标在发射间隔内的运动会引起相位变化,由于发射周期很短,可认为目标雷达散射截面积(Radar-Cross Section,RCS)不变,忽略幅度变化,其中φ表示第2个符号周期时目标运动引起的相位变化,
(10)
由式(6)、(7)、(8)、(9)可得,阵列接收信号为
(11)
在高信噪比条件下,基于时间分集的虚拟阵列算法在二维FFT处理后,采用差值相位校准法,利用虚拟接收天线4,5和6的相位信息对运动相位变化进行校准[9]。基于同一频谱位置内只存在一个目标的假设基础上,接收天线4和5之间的相位差![]() 4,5
4,5![]() +φ,而
+φ,而![]() 5,6
5,6![]() ,则需要补偿的相位差
,则需要补偿的相位差![]() =
=![]() 5,6-
5,6-![]() 4,5。
4,5。
基于时间分集的虚拟阵列算法同一时间只允许一根天线工作,损失了多根发射天线同时工作可以获得的功率增益。同时,差值相位校准法在同一频谱内出现多个目标(下面称作相干目标)时会有较大性能损失。
3 基于空时分组码的虚拟阵列算法
3.1 基于Alamouti码的虚拟阵列算法
以2发X收这种典型低成本车载毫米波雷达系统为例,本文提出了一种基于Alamouti码[10]的FMCW虚拟阵列算法。所提方案通过利用更高维度的空时分组码可以扩展到具有更多发射接收天线的车载毫米波雷达系统。
无线通信中的Alamouti码需要接收端获得完美的信道状态信息,利用信号的正交性,进行最大似然译码,以获得原始发送信息。而FMCW车载毫米波雷达信号处理中,调频连续波信号等价于无线通信中的导频,目的是获得信道状态信息,完成信道估计。由于车载毫米波雷达天线间距较小,多根天线信道幅度衰落基本相同,且较少涉及多径传输,因此FMCW车载毫米波雷达信号处理中,利用Alamouti码的解耦矩阵以及空间谱估计算法,完成目标的角度参数估计。为方便表示,本节的理论推导皆基于单目标场景,但理论推导的结果同样适用于多目标的场景。
两根发射天线同时发射一组相位基于Alamouti编码调制的线性调频连续波,相调矩阵如下:
(12)
由式(7)、(8)、(9)、(12)可得,基于Alamouti码的阵列接收信号为
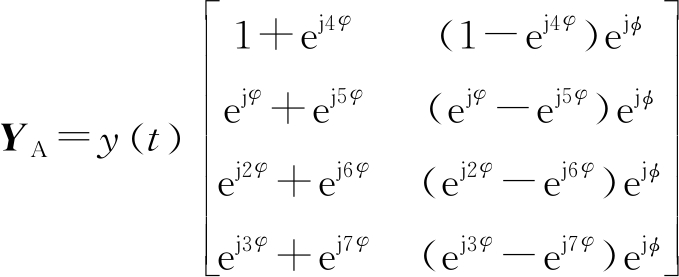
(13)
由式(13)可知,基于Alamouti码的阵列接收信号无法采用文献[9]中提出的差值运动相位校准算法,同时文献[9]中的相位校准算法不适用于相干目标,存在较大的局限性。因此,针对车载毫米波雷达低复杂度的需求,本文提出一种基于速度参数估计的虚拟阵列运动相位校准算法,适用于相干目标场景,且复杂度较低。
对锯齿波中频信号进行二维FFT处理后,不同的频谱单元分别对应不同的距离参数和速度参数,因此,针对任意频谱单元可将其对应的速度参数代入式(10),计算其运动相位变化估计,并对其相位信息进行校准。针对目标频谱位置m,其对应的速度参数为![]() 波束形成前目标频谱位置的频谱信息
波束形成前目标频谱位置的频谱信息![]() 为
为
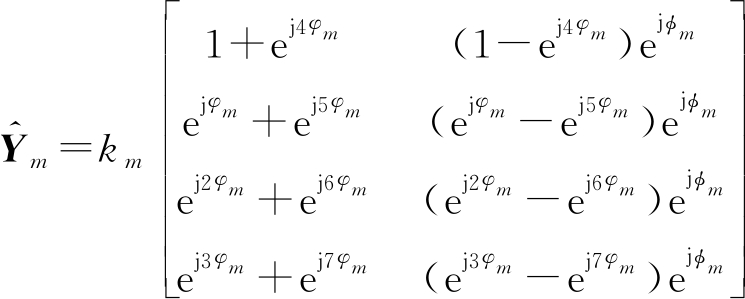
(14)
式中,km为目标频谱位置m处的幅值,![]() m=2πdsinθm/λ为目标频谱位置m处因天线间隔引起的相位变化,其中θm为目标m与发射天线和接收天线法线的夹角,φm为目标频谱位置m内的目标在发射间隔内的运动相位变化。可由式(10)及对应的速度参数
m=2πdsinθm/λ为目标频谱位置m处因天线间隔引起的相位变化,其中θm为目标m与发射天线和接收天线法线的夹角,φm为目标频谱位置m内的目标在发射间隔内的运动相位变化。可由式(10)及对应的速度参数![]() 计算其运动相位变化估计:
计算其运动相位变化估计:
(15)
针对目标频谱,利用计算得到的运动相位变化估计,对其进行运动相位校准并进行解耦处理,得到解耦后的目标阵列相位信息为
![]()
![]()
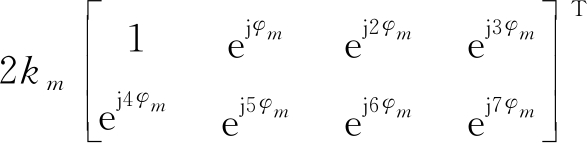
(16)
则基于Alamouti码的虚拟天线阵列相位信息为
(17)
对虚拟天线阵列相位信息进行相应的空间谱估计算法处理,即可得到目标的角度参数估计。
本文所提出的基于速度参数估计的运动相位校准算法同样适用于相干目标的场景下。这是由于相干目标处在同一频谱单元内,其径向速度、运动相位变化相同,所以该相位校准算法能够同时补偿。
3.2 算法分析
表1为算法复杂度分析,其中Nq为系统快时间维FFT点数,Ns为系统慢时间维FFT点数,系统天线阵列如图1所示。如表1所示,本文提出的基于空时码的虚拟阵列算法相比于基于时间分集的虚拟阵列算法,需要引入额外8×Nq×Ns次复乘和复加计算量。与此同时,本文提出的基于速度参数估计的运动相位校准算法,相比于差值运动校准算法,其复乘计算量相同,而且不需要进行复加运算,其复杂度较低。
相比于基于时间分集的虚拟阵列算法,基于空时分组码的方式能够充分利用多根发射天线带来的功率增益,在单根发射通道功率受限的情况下,提高系统整体性能,其增加的计算量代价对于一般的车载毫米波雷达而言是可以接受的。同时,相比于差值相位校准算法,基于速度参数估计的相位校准算法能够适用于相干目标场景,且复杂度更低。
表1 算法复杂度比较

算法名称复乘次数复加次数基于时间分集的虚拟阵列算法00差值运动校准算法4×Nq×Ns3×Nq×Ns基于空时码的虚拟阵列算法8×Nq×Ns8×Nq×Ns速度参数估计运动相位校准算法4×Nq×Ns0
注:Nq为系统快时间维FFT点数,Ns为系统慢时间维FFT点数,系统天线阵列如图1所示。
4 仿真结果与分析
本节将基于实际车载毫米波雷达的系统参数搭建仿真平台,对比仿真时间分集方案、空时分组码方案以及同时发射方案,共计3种方案的系统测角性能以及运动相位校准算法,天线阵列如图1(a)所示。同时发射方案即发射天线同时工作,接收端不作虚拟阵列处理,其相应的等效相调矩阵如下:
(18)
图3为上述3种方案基于常规波束形成(Conventional Beamforming,CBF)空间谱估计[11]的角度分辨率仿真图,其横轴为CBF角度值,纵轴为能量值,其中噪声功率归一化为1。如图3所示,两个仿真目标具有相同的径向距离、径向速度以及RCS,方位角度分别为0°和20°。其中空分组码和时间分集虚拟阵列算法,皆采用本文提出的基于速度参数估计的运动相位校准算法。如图3(a)、图3(b)所示,空时码方案能够通过对目标频谱信号进行运动相位校准并解耦形成虚拟阵列,获得和时间分集方案相同的角度分辨率。相比于图3(c)的同时发射方案,车载毫米波雷达通过虚拟阵列算法,显著提高了系统的角度分辨能力。
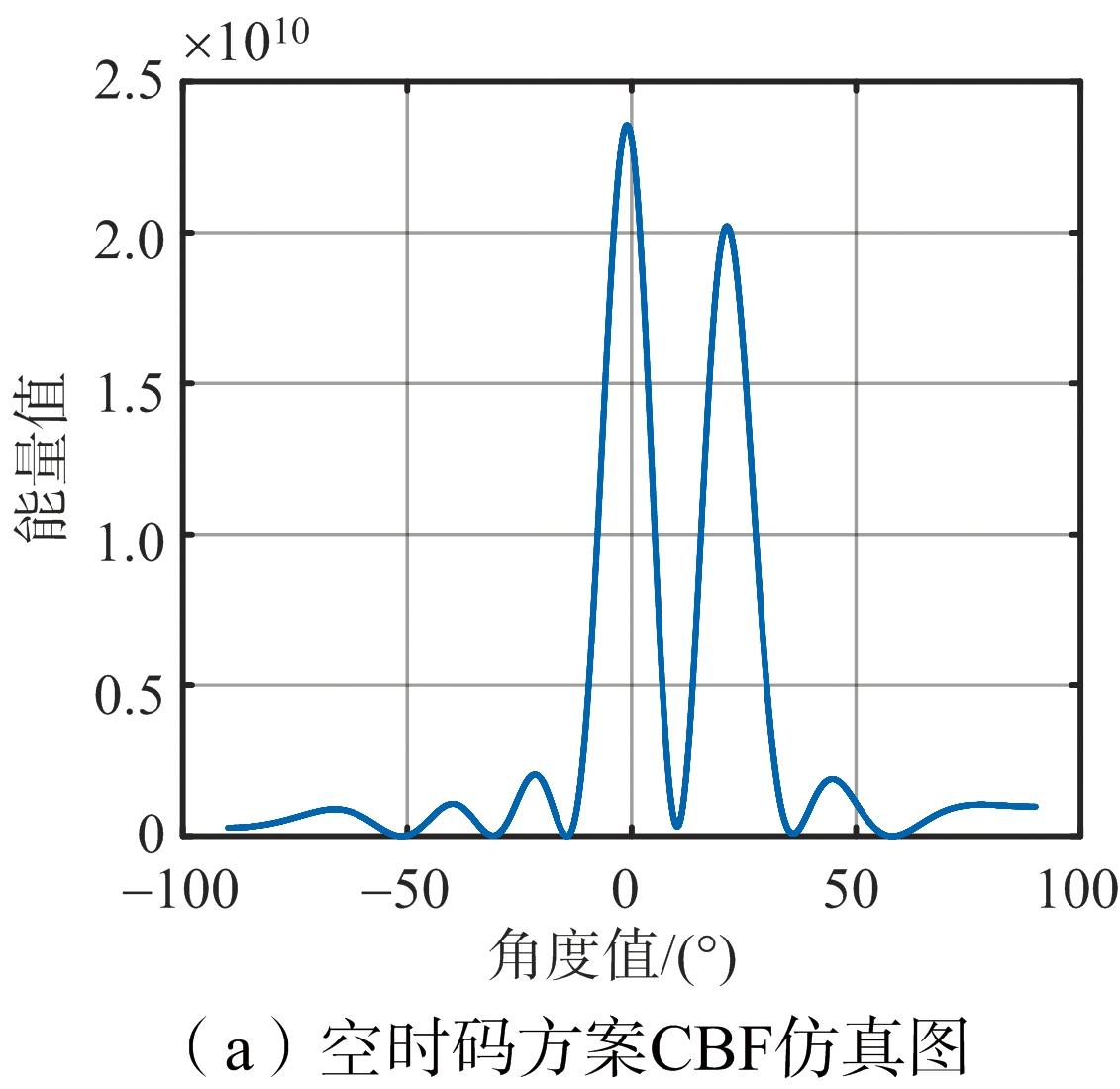
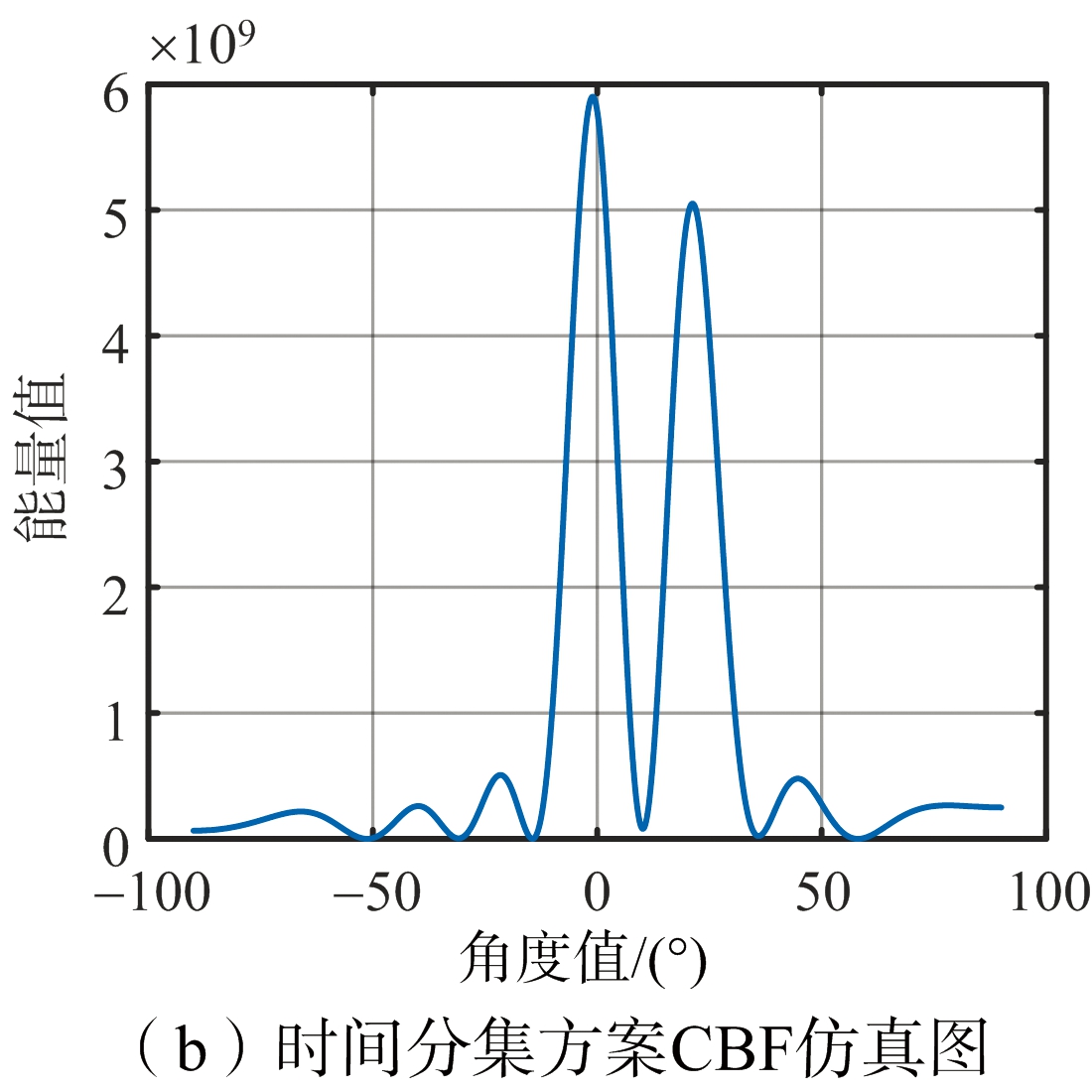
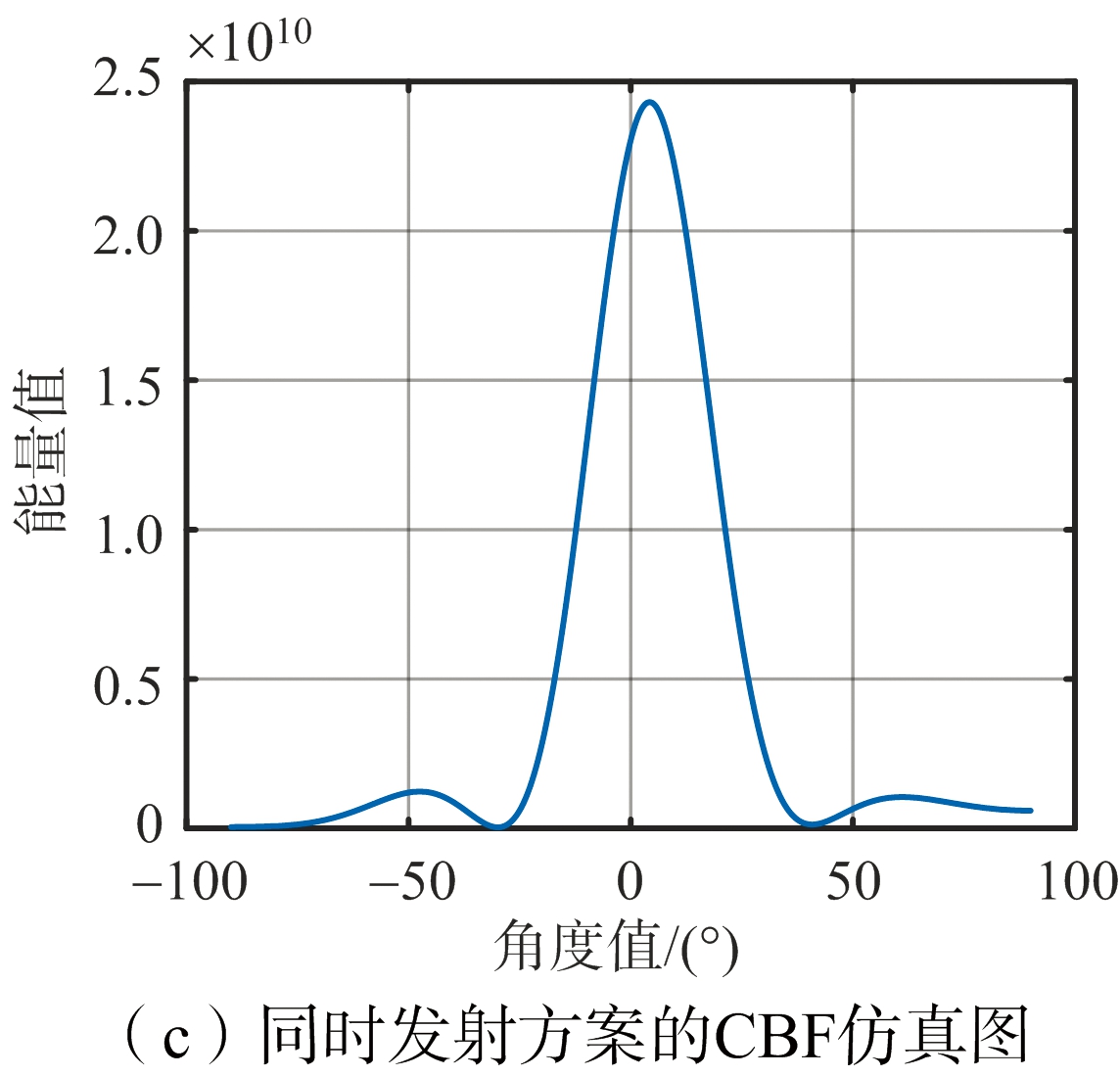
图3 系统分辨率仿真图

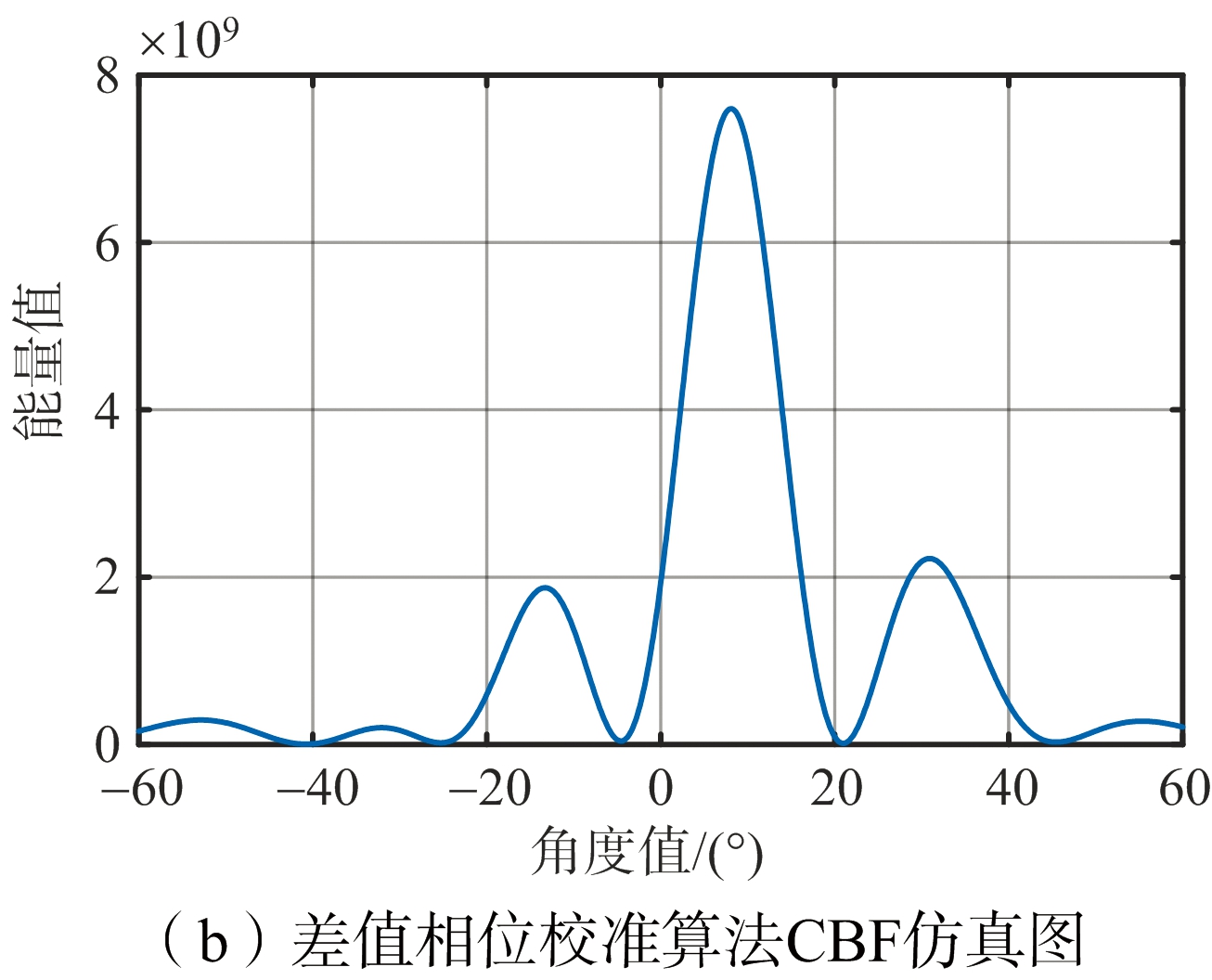
图4 基于不同相位校准算法的相干目标仿真图
图4为时间分集方案在相干目标场景下,基于不同相位校准算法的CBF仿真结果,其中噪声功率归一化为1。两个仿真目标具有相同的径向距离、径向速度以及RCS,方位角度分别为0°和20°。如图4(a)所示,本文提出的基于速度参数估计的相位校准算法能够明显分辨出两个相干目标。而如图4(b)所示,差值相位校准算法在相干目标的场景下并不适用,无法准确得到两个目标角度参数估计,甚至无法分辨相干信号源数。
图5、图6分别为时间分集方案和空时分组码方案的系统角度估计精度仿真及漏警率仿真,其中漏警率的定义为:未检测到的目标占总目标的数的比例。如图5、图6所示,基于空时分组码的系统角度参数估计性能及漏警率,在车载毫米波雷达有效探测距离范围内,均要优于时间分集毫米波雷达系统,尤其是在远距离信噪比较低的场景下,其性能提升更加明显。这是由于空时分组码相较于时间分集,能够在车载毫米波雷达单发射通道功率受限的系统特点下,获得多根发射天线同时工作带来的功率增益,从而在波束形成及角度估计时拥有更高的信噪比。
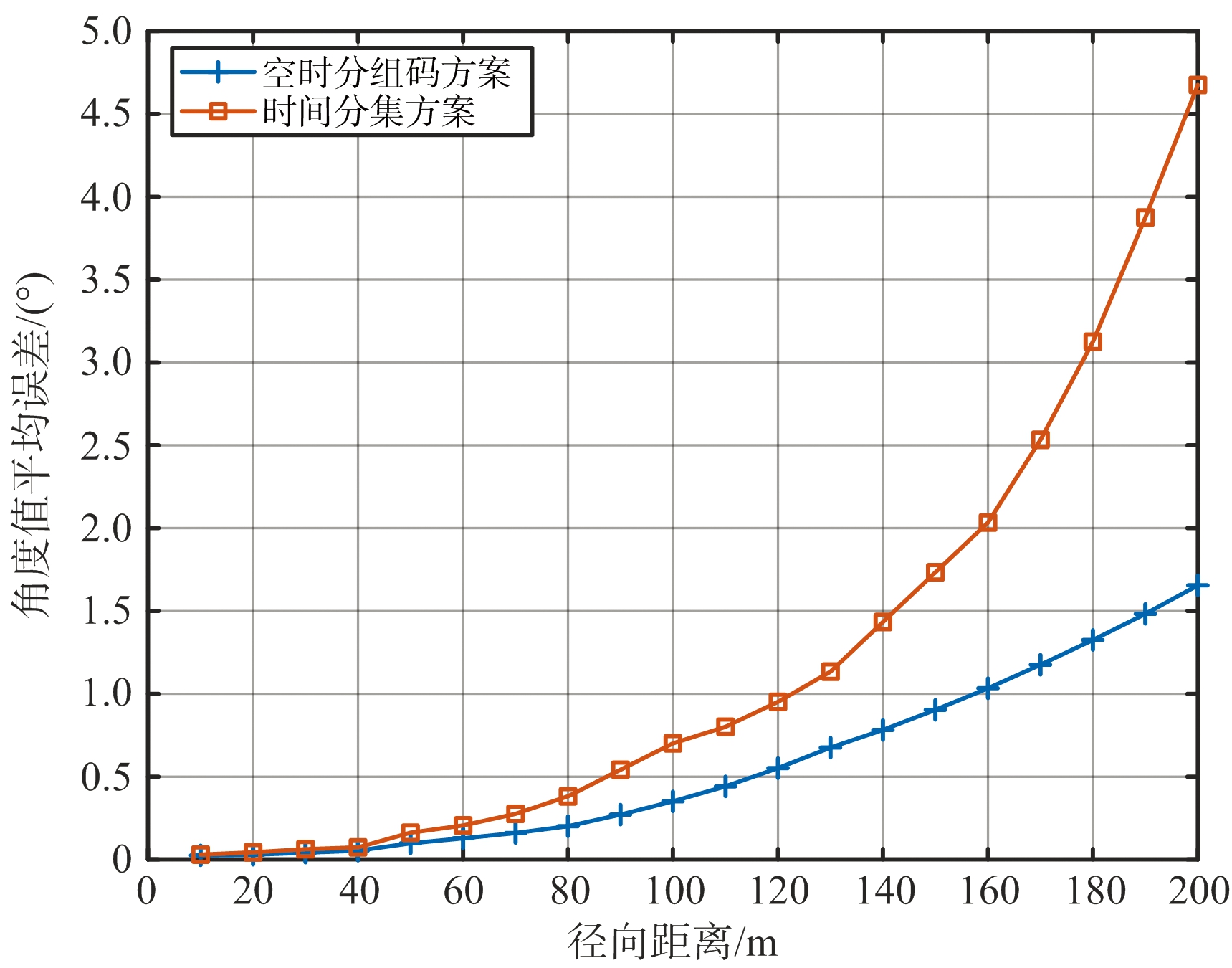
图5 系统角度估计精度仿真图
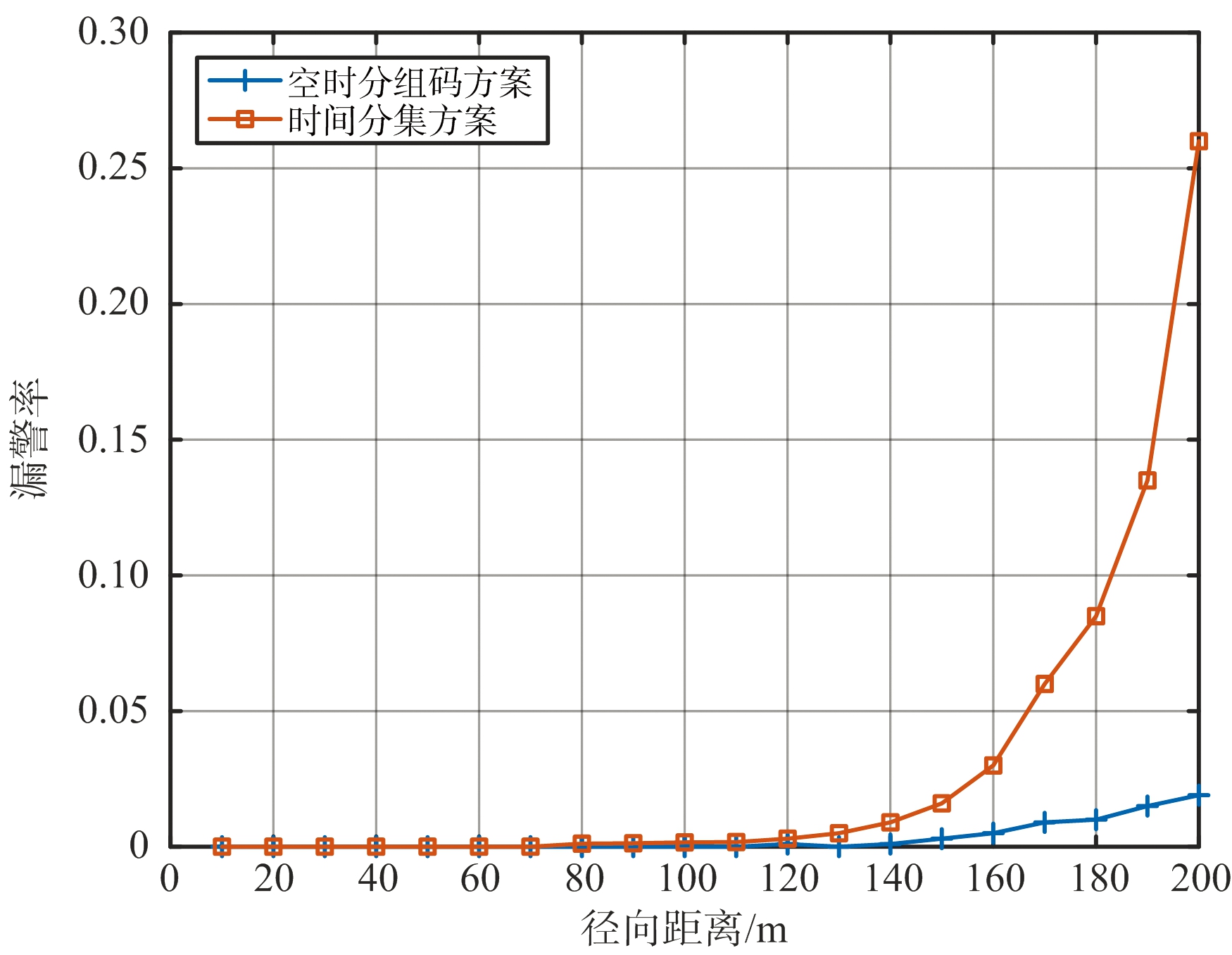
图6 系统漏警率仿真图
5 结束语
本文设计了一种基于空时分组码的FMCW车载毫米波雷达信号处理算法,相比于基于时间分集的虚拟阵列算法,能够在形成相同天线孔径虚拟阵列的同时,利用多根天线同时工作带来的功率增益,获得更高的系统性能。同时针对车载毫米波雷达系统低成本的需求,设计了一种低复杂度且适用于相干目标的虚拟阵列相位补偿算法。仿真结果验证了算法的有效性。
[1] ZHANG Zhili, ZHANG Renli, SHENG Weixing, et al. Feature Extraction and Classification of Human Motions with LFMCW Radar[C]∥ IEEE International Workshop on Electromagnetics: Applications and Student Innovation Competition,Nanjing:IEEE, 2016:1-3.
[2] LEE S, YOON Y J, LEE J E, et al. Human-Vehicle Classification Using Feature-Based SVM in 77-GHz Automotive FMCW Radar[J]. IET Radar, Sonar & Navigation, 2017, 11(10):1589-1596.
[3] STURM C, GANG L, HEINRICH G, et al. 79 GHz Wideband Fast Chirp Automotive Radar Sensor with Agile Bandwidth[C]∥ IEEE MTT-S International Conference on Microwaves for Intelligent Mobility, San Diego, CA:IEEE,2016.
[4] KIME H, KIMK H. Random Phase Code for Automotive MIMO Radars Using Combined Frequency Shift Keying-Linear FMCW Waveform[J]. IET Radar, Sonar & Navigation,2018,12(10):1090-1095.
[5] PATOLE S M, TORLAK M, WANG D, et al. Automotive Radars: A Review of Signal Processing Techniques[J]. IEEE Signal Processing Magazine, 2017, 34(2):22-35.
[6] DUAN Zhiyi, WU Yongle, LI Mingxing, et al. A Novel FMCW Waveform for Multi-Target Detection and the Corresponding Algorithm[C]∥ IEEE International Symposium on Electromagnetic Compatibility, Beijing:IEEE, 2017.
[7] ROSSUM W V, HUIZING A. Space-Time Block Coding Waveform for Suppression of Jamming in a MIMO Radar[C]∥ 16th International Radar Symposium,Dresden, Germany:IEEE, 2015:517-522.
[8] ZWANETSKI A, KRONAUGE M, ROHLING H. Waveform Design for FMCW MIMO Radar Based on Frequency Division[C]∥ 14th International Radar Symposium,Dresden, Germany:IEEE, 2013.
[9] 严鑫, 黄永明, 王海明, 等. LFMCW 车载防撞雷达信号处理模块研究[J]. 雷达科学与技术, 2016, 14(5):498-504.
[10] ALAMOUTI S M. Simple Transmit Diversity Technique for Wireless Communications[J].IEEE Journal on Selected Areas in Communications, 1998, 16(8):1451-1458.
[11] 王永良. 空间谱估计理论与算法[M]. 北京:清华大学出版社, 2004.




