0 引言
对雷达信号脉间、脉内两大类调制方式进行识别是电子情报分析(ELINT,Electronic Information Technology)的重要内容,有助于实现雷达辐射源有效识别[1]。随着近年来数字电子技术的迅速发展,雷达信号波形、调制方式更加复杂多变,加之外部所面临的电磁环境也越来越恶劣。在这样的军事需求牵引下,展开雷达辐射源信号调制方式识别技术研究,对电子侦察而言具有重要的理论意义与实用价值。
雷达信号脉间参数主要包括中心频率、脉宽、PRI等,其中尤以PRI的调制特征最为复杂,包括固定、抖动、参差、滑变、脉组捷变、周期变化(如正弦调制、三角调制)等,对PRI调制类型的正确识别可以帮助我们判断雷达辐射源的工作模式、用途以及威胁等级[2-3]。传统的PRI调制识别方法可以归类为直方图统计法、支持向量机算法等[4-8],前者主要通过统计各时间间隔段的脉冲个数,依据操作员的经验进行人工识别,当截获脉冲较少时识别效果较差,而且对PRI复杂调制识别的能力较弱;后者要求分类器设计要科学合理,而且需要足够的样本数据进行训练,但方法复杂程度比较高,目前仅停留在理论研究层面,尚未投入工程实践。
鉴于此,本文针对雷达脉冲常见的PRI调制方式,在融合去交错后PRI序列的时域、频域特性基础上,提取了零交叉密度等多个特征量,在充分考虑脉冲丢失与虚假脉冲处理、外部噪声等实际应用的基础上,设计了基于多特征量的综合识别处理算法流程,实现了对雷达常规PRI调制方式的识别输出。仿真结果表明,该方法具有较为稳健的识别性能,运算量较小,适用性较强。
1 雷达辐射源信号脉间PRI调制分析
1.1 典型PRI调制样式
在雷达信号特征参数中,PRI是其中工作样式最多、参数范围最大、变化最快的一个参数,即使是同一部雷达其也可能有几种甚至十几种。随着电子反侦察和雷达新技术的投入使用,雷达辐射源的体制也愈加复杂[6]。图1给出了6种常见的雷达脉间PRI复杂调制序列波形,固定PRI由于比较简单,在此不再赘述。
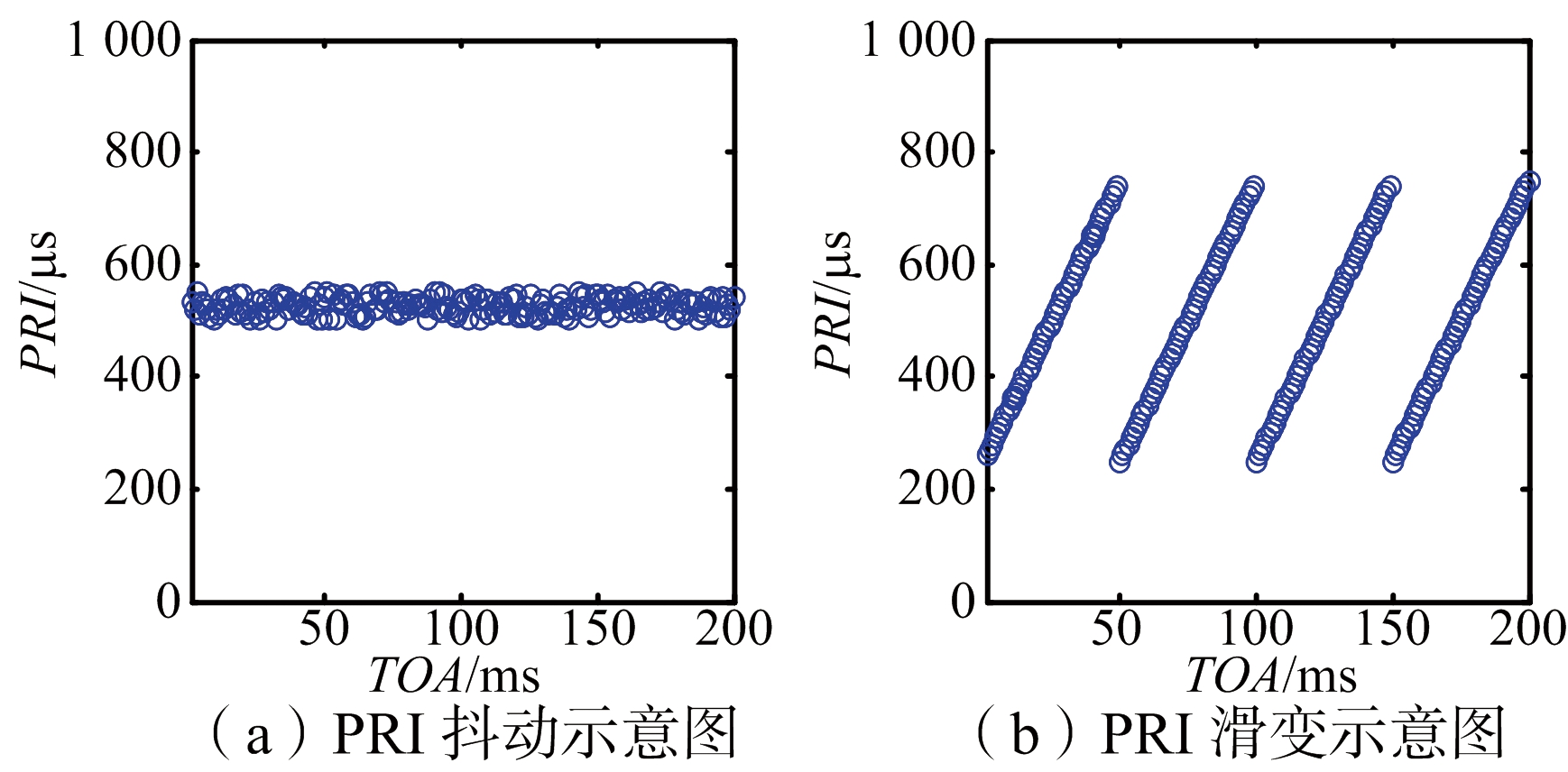
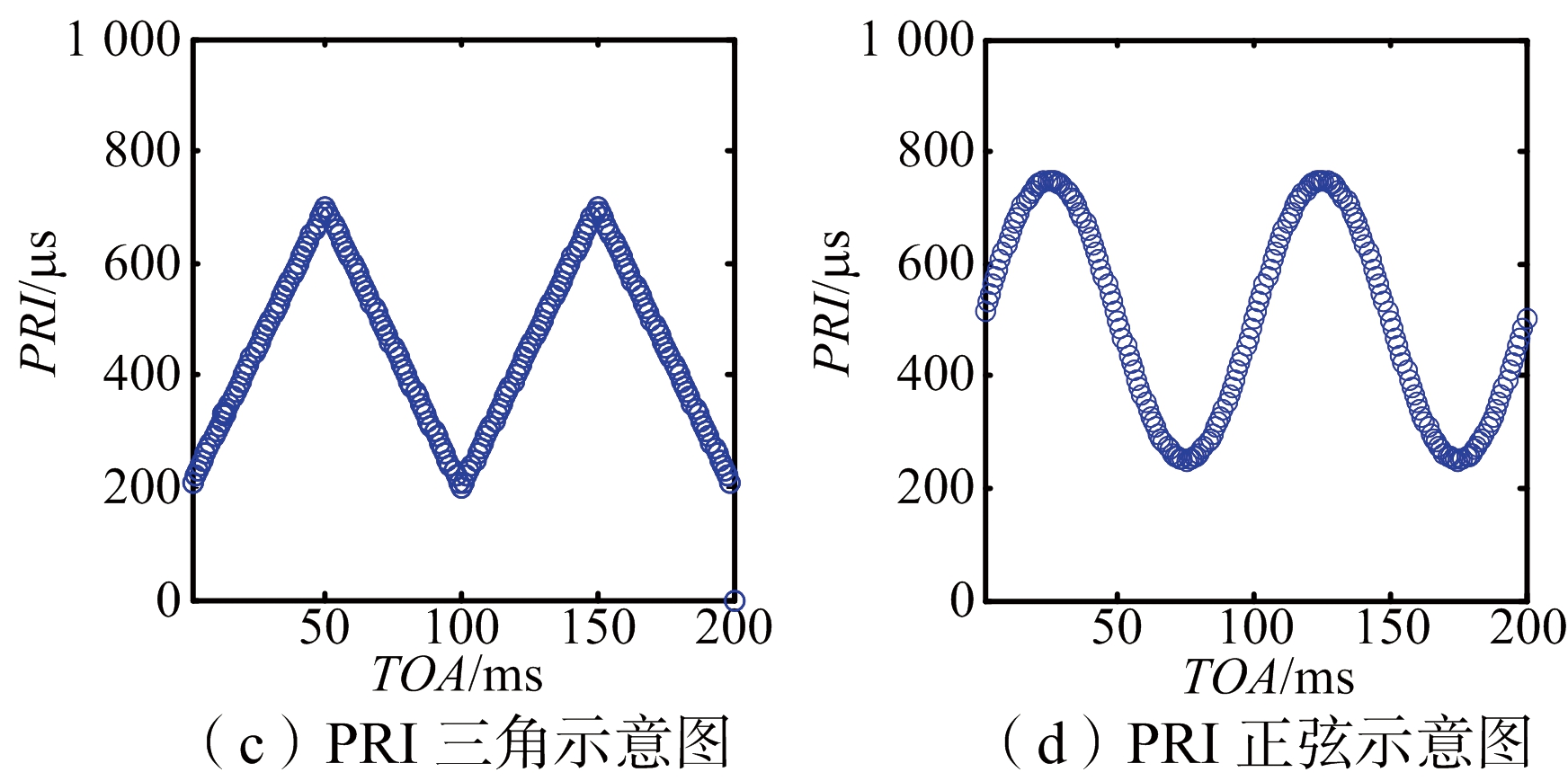
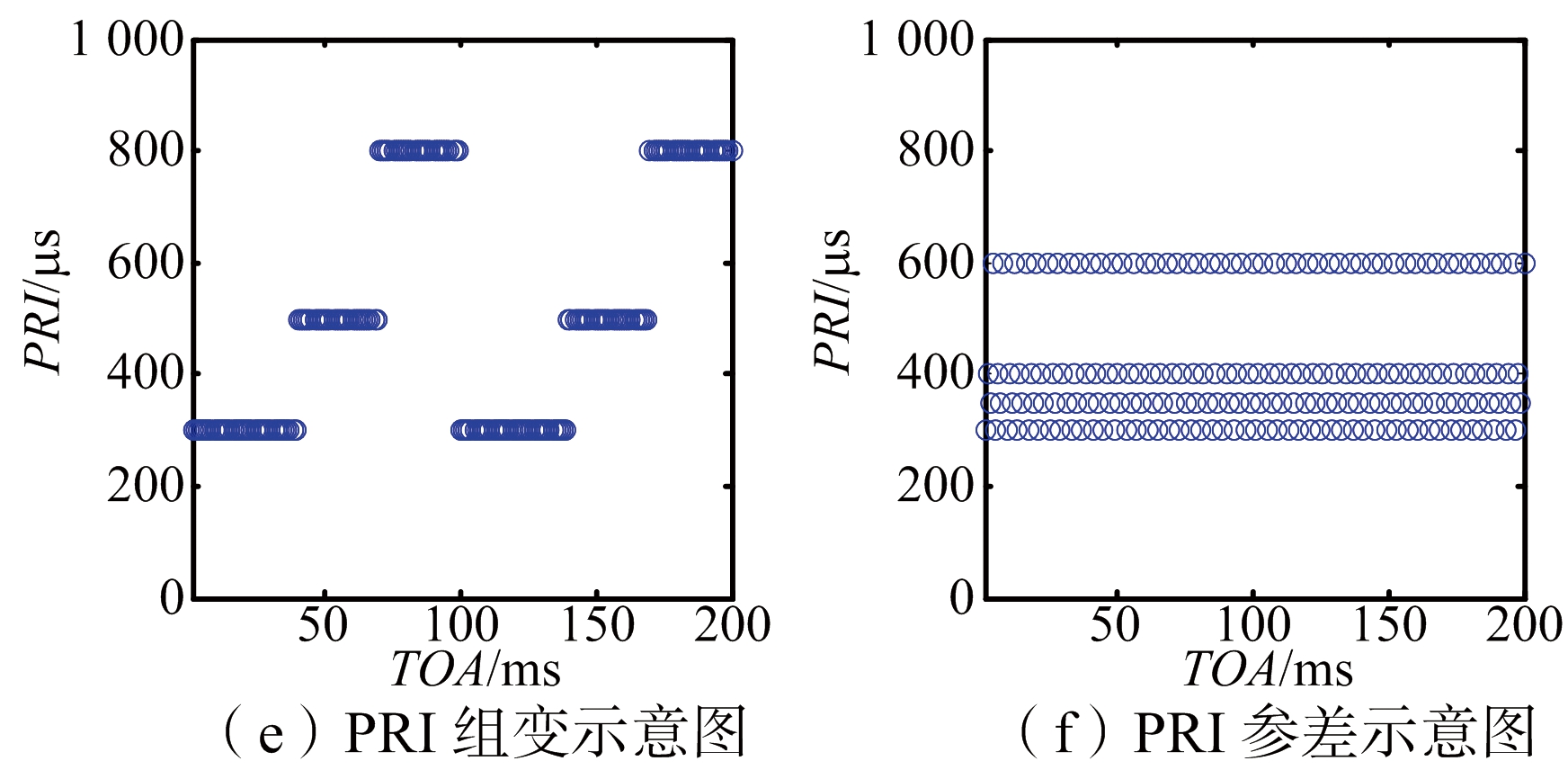
图1 6种常见的雷达脉间PRI复杂调制序列波形示意图
1.2 典型PRI脉冲数学模型
对于有N+1个脉冲的雷达信号序列,设定每个脉冲前沿到达时间t(n) ,做一次差分为
p(n)=t(n+1)-t(n), n=0,1,…,N-1
(1)
p(n)为PRI序列,它的变化反映了PRI调制方式的变换规律,下面对常见7种PRI调制的信号模型进行介绍。
1) 固定PRI调制序列
p(n)=Tm, n=0,1,…,N-1
(2)
式中,Tm为PRI的均值。
2) 抖动PRI调制序列
p(n)=Tm+w(n), n=0,1,…,N-1
(3)
式中,Tm为PRI的均值,w(n) 为抖动量,一般服从高斯或均匀分布。随机抖动量最大可到达PRI均值的30%。对抖动的量值和类型的判别有助于判定雷达辐射源的类别。
3) 滑变PRI调制序列
(4)
式中,A0为p(n)的最小值,B为p(n)的最大值与最小值之差,Tp为周期长度。对于滑变PRI调制,其PRI序列变化的规律为周期性单调增加或减少,当达到一个极值时迅速返回到另一极值,这种PRI调制可以用来消除遮盖(盲距)。
4) 三角PRI调制序列
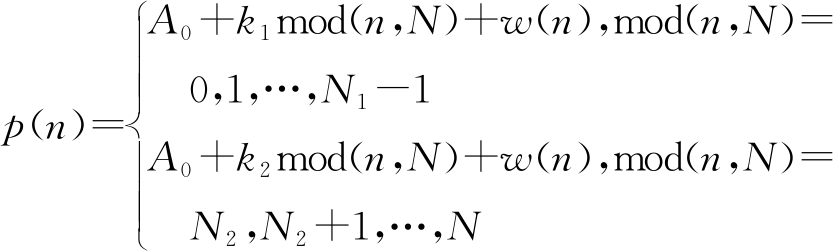
(5)
式中,A0为p(n)的最小值,N为三角PRI调制周期长度,k1和k2分别为p(n)的每个调制周期内前N1和后N2点对应的调制斜率,且N=N1+N2。
5) 正弦PRI调制序列
p(n)=![]()
n=0,1,…,N-1
(6)
式中,A0为p(n)的最小值,B为p(n)的真幅度,f0为基波频率。正弦PRI调制的p(n)振幅值一般为其平均值的5%左右。
6) 脉组捷变PRI调制,以常见的三重频PRI为例,在一个周期内有3次切换,其PRI序列为
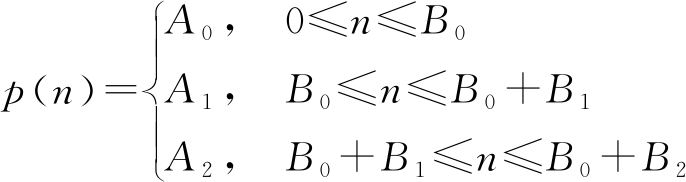
(7)
式中:A0,A1,A2分别表示切换的值;B0,B1,B2分别为其对应的驻留时间。此类型主要用在脉冲多普勒雷达中消除距离模糊、速度模糊问题,或者消除目标的遮盖(盲距)与盲速等。
7) 参差PRI调制序列
p(n)=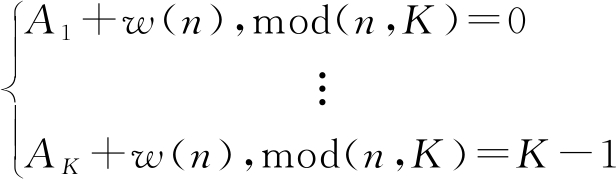
n=0,1,…,N-1
(8)
式中,![]() 表示K参差PRI集合。
表示K参差PRI集合。
1.3 典型PRI调制应用模式
PRI是雷达辐射源的固有特征参量,它决定了雷达的最大不模糊距离和径向速度,可能是固定的,也可能是时变的;同时PRI也是雷达信号分选最重要的参数,是雷达信号主分选过程中使用的唯一参数。根据雷达体制和功能的不同,脉冲序列PRI调制方式也不同[4-10]。表1给出了常见PRI变化规律及其应用模式映射关系。
表1 常见PRI变化规律及其应用模式映射关系

序号类型典型应用模式备注1固定常规的搜索和跟踪雷达,MTI和脉冲多普勒雷达变化小于PRI均值的1%2抖动用于对抗预测脉冲到达时间的干扰,降低特定干扰的效果PRI值线性增加或减小,大的变化,高到平均PRI的30%3组变解决速度(或距离)模糊问题,特别是对脉冲多普勒雷达一组脉冲具有稳定的PRI,然后切换到另一组4参差在MTI系统中消除盲速在脉间以周期的方式交替使用几个稳定的PRI5滑变在俯仰扫描中提供恒定的高度覆盖,或避免遮盖效应通常最大PRI(为最低高度使用)小于最小PRI(为最大高度使用)的6倍6正弦7三角导弹制导、避免遮盖、测距达到平均PRI的5%周期变化、速率为50Hz或更高
2 基于多特征量的综合识别方法
2.1 特征量提取
由于雷达信号PRI模式复杂多变,只采用单一特征参数很难将其全部识别[4]。针对前面提到的7种PRI调制方式,在分析去交错后PRI序列的时、频域特性的基础上,有针对性地提取了零交叉密度、谐波幅度比、PRI序列差分极性特征、PRI序列差分零点密度、PRI二级差分序列5个特征量,其中不同的分类特征量所表征的物理内涵也各不相同。
1) 零交叉密度(C1)
设PRI序列p(n)去直流后的交流分量为 w(n) 。令z(i)为
(9)
式中,i=0,…,L-1,L=N-2。定义一定数据长度下PRI序列中交流成分过零点的总次数为零交叉密度,其可表示为[4]
(10)
对于滑变、正弦调制及脉组捷变等几种周期性非随机抖动PRI调制方式,其PRI序列交流分量的过零点个数与周期有关,一般较小。由式(3)可知,对于抖动PRI调制而言,z(i)服从0-1分布,取1或0的概率。实质上,对抖动PRI而言,C1就是统计L次独立重复实验事件{z(i)=1}成功的次数。因此,随机变量C1服从参数为L,q的二项分布,即C1~b(L,q),于是有
(11)
式中,k为一门限值。
图2所示为PRI高斯抖动时,不同数据长度L下k的取值范围为0.2~0.3L时,Pr(C1>k)的变化曲线。由图可知,当数据长度为50左右时,Pr(C1>0.2L)、Pr(C1>0.25L)的值接近1,即在一定的数据长度下,抖动类型零交叉密度远大于其他3种PRI调制类型。因此,用零交叉密度区分抖动PRI调制的依据是合理的。
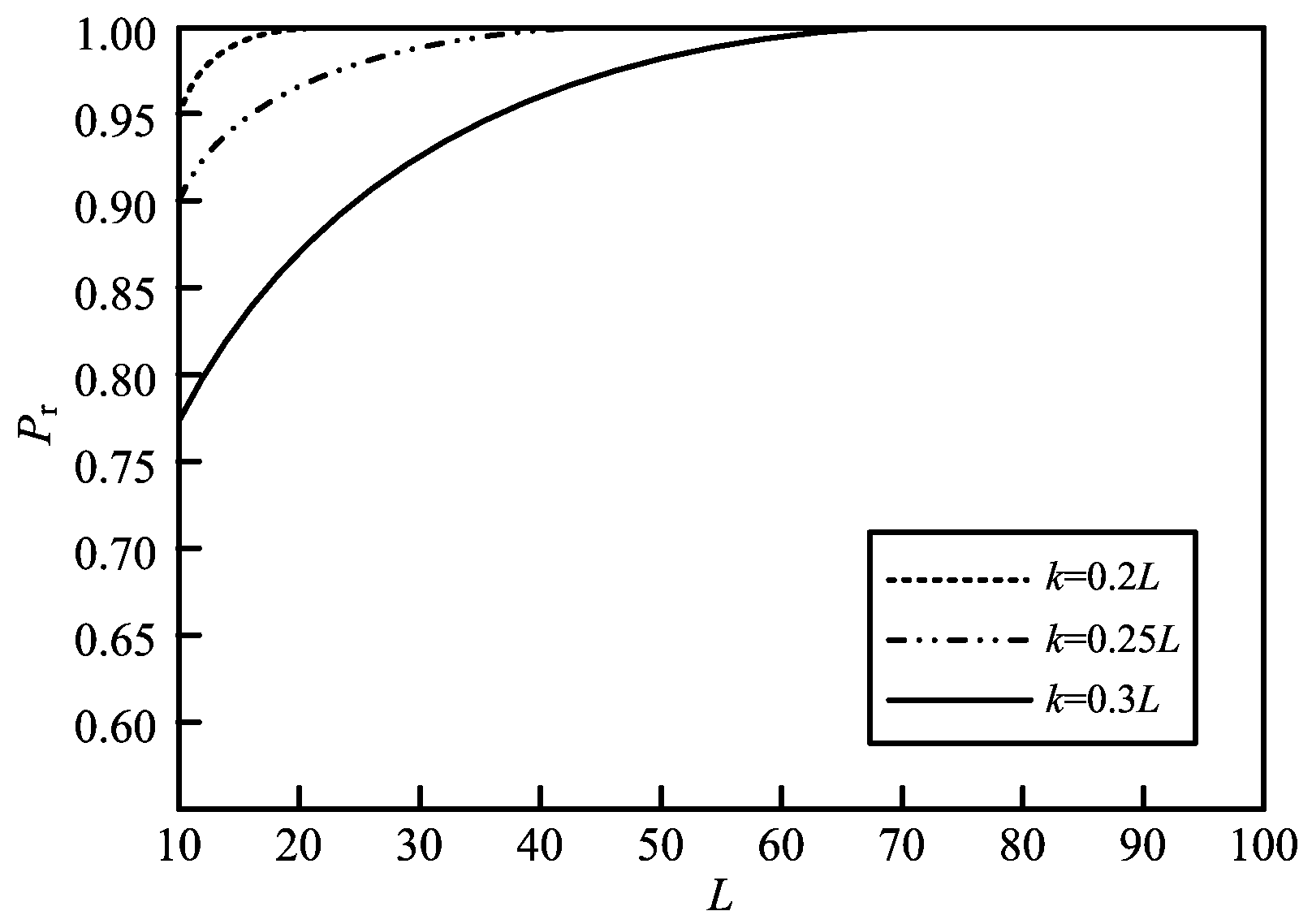
图2 PRI高斯抖动参数变化示意图
2) 谐波幅度比(C2)
为了分析方便,对非抖动PRI序列(正弦调制、滑变、脉组捷变)p(n),考虑其连续时间形式 p(t),可知p(t)具有周期性。现考虑其第一个周期0≤t≤Tp的情形。
对于正弦PRI调制,p(t)及频谱p(ω)可表示为
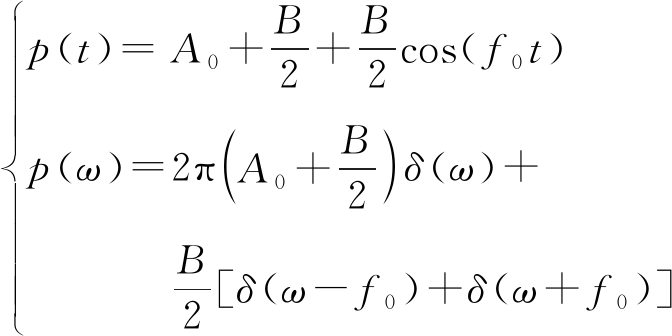
(12)
式中,A0为p(t)的最小值,B为p(t)的真幅度,f0为基波频率。可见正弦调制PRI序列的频谱中只有直流分量和一次谐波分量,无其他谐波分量。
对于滑变PRI调制,p(t)及其频谱p(ω)可表示为
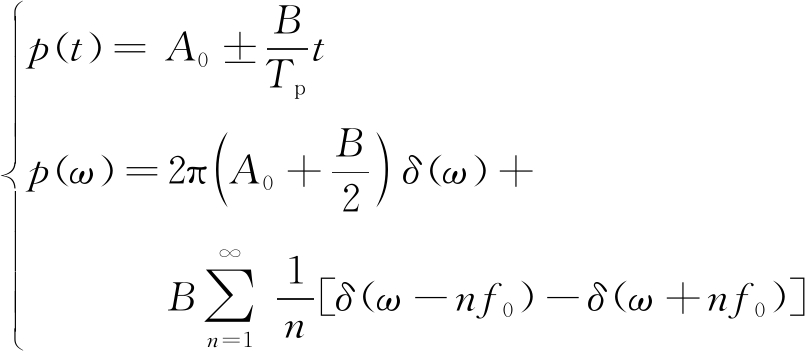
(13)
式中,A0为p(t)的最小值,B为p(t)的最大值与最小值之差。由式(13)可知,其频谱中包含直流及各次谐波分量,且一次谐波分量的大小分别是二次谐波的2倍,三次谐波的3倍,之后各次谐波的分量都以单调方式衰减。
对于脉组捷变类型,由式(7),其频谱为
p(ω)=![]()
(14)
式中,sinc(x)=sin(x)/x为辛克函数。由式(14)可知,其频谱分量中也包含了各次谐波分量及直流分量,但各谐波分量之间的大小以辛克函数方式衰减,具体的比例关系受参数集{A0,A1,A2}及{B0,B1,B2}的影响。上述规律可推广到多重频切换情形。
于是,定义谐波幅度比特征量为[4]
(15)
式中,P1为基波分量的幅度,P2为二次谐波分量的幅度。从上述分析可知,对于正弦调制,理论上其频谱中除基波分量外,其他各次谐波分量均无能量分布。考虑测量噪声较小时,P2≈0,所以C2较大。对于滑变、脉组捷变PRI调制方式,由于基波与二次谐波上均有能量分布,所以C2要远小于正弦调制PRI情况(特别地对于滑变类型,C2=2),这样利用特征量C2可将正弦PRI调制方式识别出来,且此特征只跟PRI调制形式有关,基本不受具体参数变化的影响。
此外,一般所截获雷达信号的PRI序列是整个周期序列中的一部分,其起点时刻具有随机性。由于傅里叶变换的模值具有时移不变性,所以被截获PRI序列的起点随机性对谐波幅度比特征量无影响。
3) PRI序列差分极性特征(C3)
对滑变、脉组捷变的PRI序列做差分,可得
Dp(n)=p(n+1)-p(n), n=0,1,…,N-2
(16)
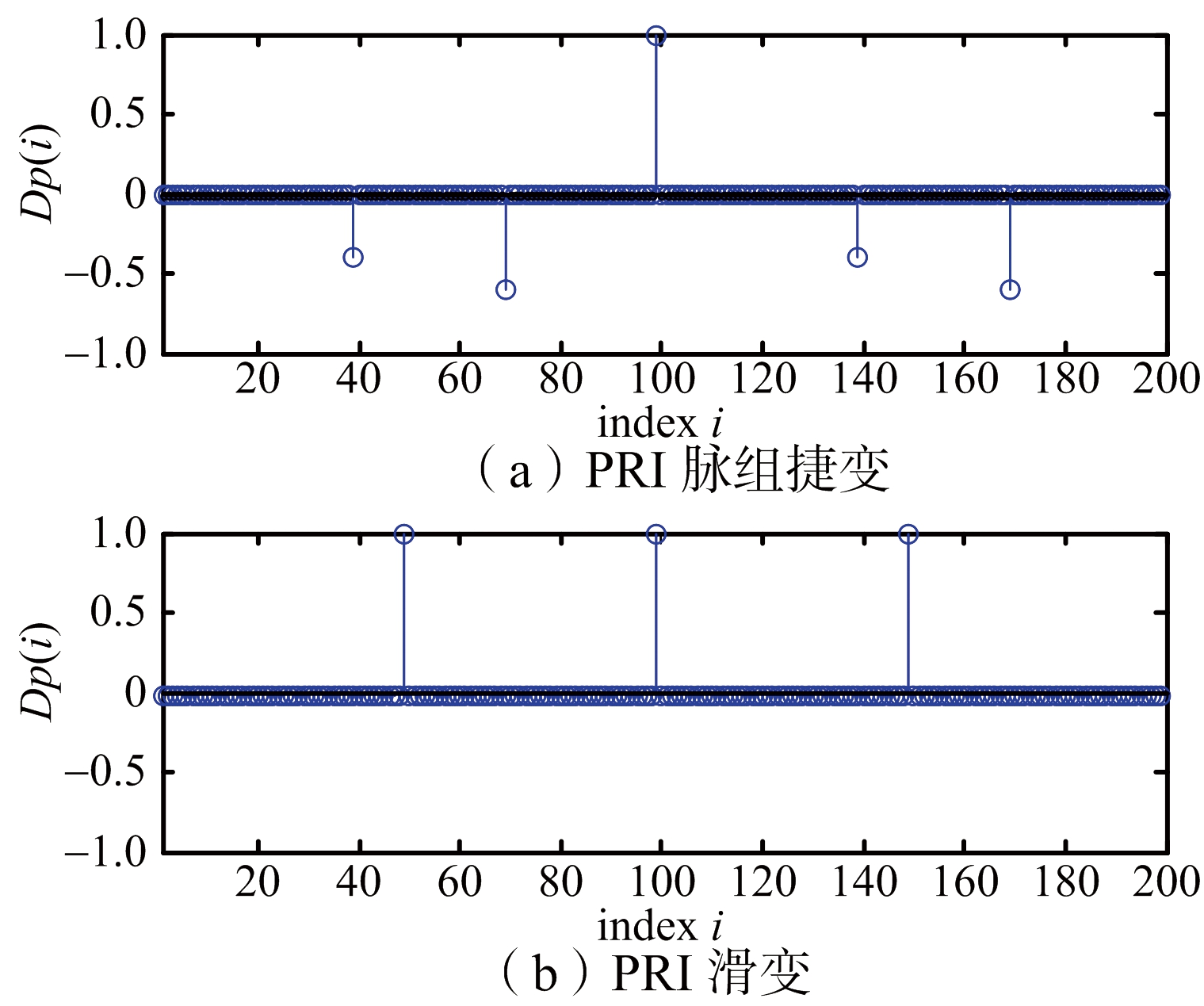
图3 脉组捷变与滑变PRI序列的二次差分波形
滑变、脉组捷变的PRI序列一次差分波形如图3所示。对于脉组捷变PRI类型,其PRI序列的差分波形中极值符号有正有负,而滑变类型PRI差分序列极值符号是一致的(全正或全负)。为此,先寻找Dp(n)的极值点li,(i=1,…,Q),再定义特征量。
(17)
式中,
(18)
其中,符号“—”表示逻辑非。符号函数sgn(x)的取值为逻辑型,C3也是逻辑型,其实质是统计PRI序列差分后极值符号的种类。当极值符号有正有负时,取值为1,可同步统计PRI序列差分零点密度(详见C4定义),从而判别是否为脉组捷变PRI类型;当极值符号全正或全负,并且在容差范围内PRI差分值递增/递减相对固定时,取值为0,可判别为滑变PRI类型。
4) PRI序列差分零点密度(C4)
由脉组捷变、参差、三角调制的PRI序列表达式可知,对于参差PRI类型和三角调制PRI类型,其PRI序列的差分波形中不存在零点,而脉组捷变PRI差分序列中有较多零点。
设PRI序列一阶差分Dp(n),令g(i)表示为
(19)
式中,i=0,1,…,L-1,L=N-2。定义一定数据长度下PRI一阶差分序列中零点的总次数与序列长度之比为零点密度,表达式为
(20)
显然,对于脉组捷变类型,其零点密度要远大于参差类型和三角调制类型。
5) PRI二阶差分序列(C5)
对三角、参差的PRI序列做二阶差分,可得
DDp(n)=Dp(n+1)-Dp(n)
n=0,1,…,N-2
(21)
由参差、三角调制的PRI序列表达式可知,对于参差PRI类型,其PRI序列的差分波形中极点数目很多(数目与PRI序列数几乎相等),而三角调制的PRI类型,其PRI序列的差分波形中极点数目在一个调制周期内最多只出现2次。即对于二阶差分序列图,在一个周期内三角调制最多出现2次非零值,而参差调制出现多次非零值,如图4所示。
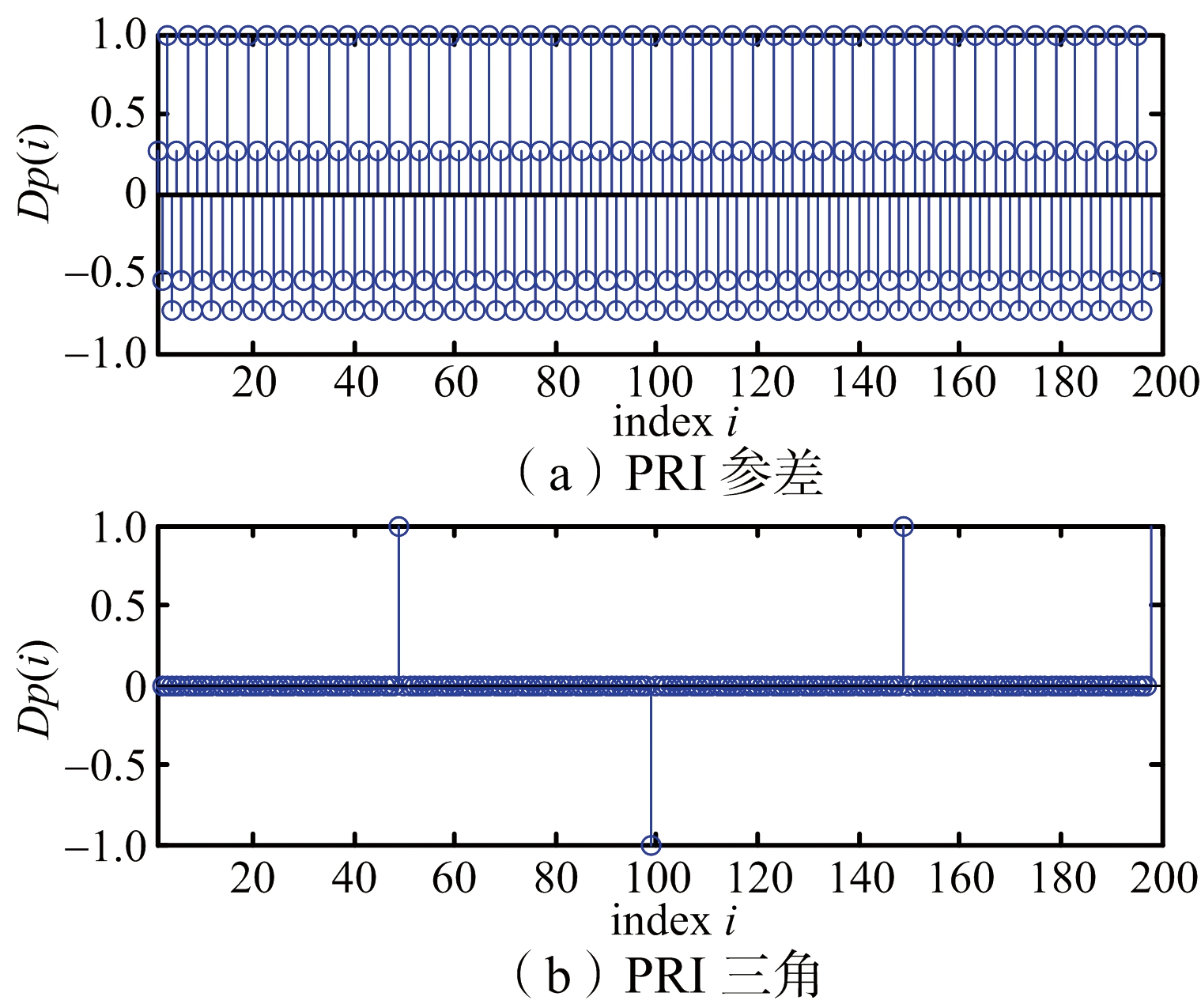
图4 参差与三角PRI序列的二次差分波形
一定数据长度下PRI二阶差分序列中非零点次数Q与周期内总点数L之比,可表示为
(22)
显然,对于参差类型,其极点密度要远大于三角调制类型。
2.2 多特征量综合识别
结合前面定义的多个特征量,设计了基于PRI序列特征分析的综合识别算法流程如图5所示。通过比较5个特征量C1,C2,C3,C4,C5与其对应门限d1,d2,d3,d4,d5之间的逻辑关系,可对7种常用体制PRI调制信号进行识别。其中,用于检测固定PRI的序列均方差值(假定为C0)门限用d0表示,d3为逻辑型变量(取值为0或1),本文设置为0,其他门限取值为工程经验值,具体取值结果详见仿真实验。
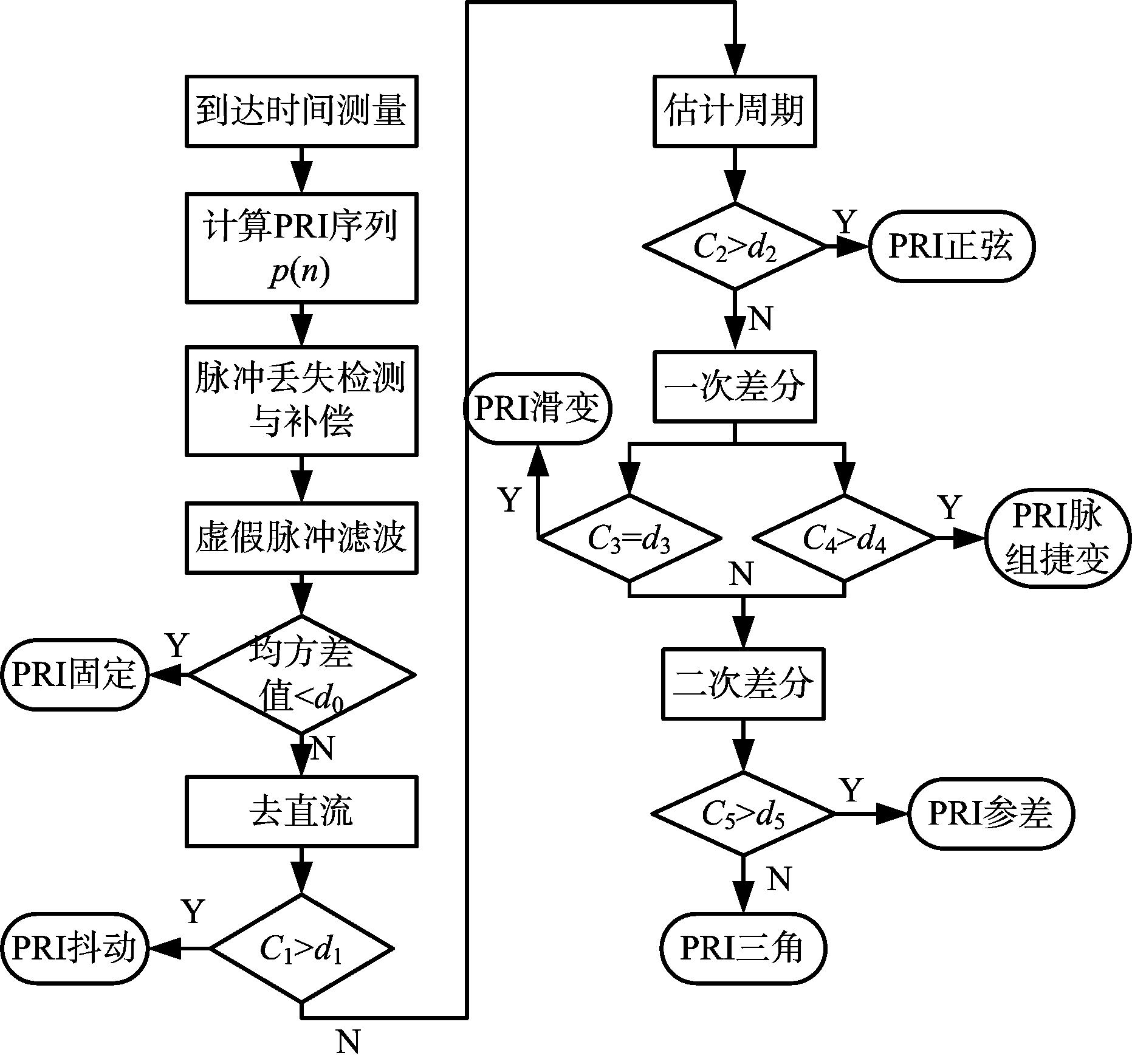
图5 PRI调制方式识别算法流程
为了更好地解读识别算法流程,下面对图5中涉及的三项关键技术进行说明。
1) 去直流的方法
工程上,先取PRI序列的平均值作为直流分量的估计,然后在PRI序列p(n)中将此PRI平均值减去,可得到去直流后的交流分量。
2) 关于脉冲丢失与虚假脉冲的处理方法
工程上,如果PRI序列中某个值大于1.5倍的PRI平均值,就认为有脉冲丢失,用其前一个PRI序列的值作为该值的修正值。对虚假脉冲则用中值滤波法,将3个PRI序列的中值作为修正值。
3) 谐波幅度比计算过程中DFT(离散傅里叶变换)点数的确定方法
特征量C2需要计算基波分量与二次谐波的幅度比。这个值在实际计算中需要通过对PRI序列做DFT后得到,且要求在做DFT后,基波分量及二次谐波分量对应的谱线尽量落在量化频率点上,这样才能保证谐波幅度比的计算有效性。一般来说,若DFT点数与序列的周期相等,可以保证基波分量及二次谐波分量对应谱线落在量化频率点。本算法对正弦、滑变及脉组捷变三类周期性PRI进行区分之前,事先没有其PRI序列周期的先验信息,很难保证DFT点数是PRI周期的整数倍。由于序列的周期信息事先不可知,所以在做DFT时需要对其进行估计,估计的具体方法如下。
去直流后,估计出基波频率![]() 取其倒数作为周期的估计值,即
取其倒数作为周期的估计值,即
(23)
进而由![]() 折算出p(n)序列周期估计点数
折算出p(n)序列周期估计点数![]() 然后以此作为对PRI序列做DFT的点数。
然后以此作为对PRI序列做DFT的点数。
2.3 仿真实验
为进一步验证算法的有效性,开展了典型雷达辐射源脉间PRI调制识别的仿真实验。其中,雷达信号通过计算机仿真生成,其脉间参数设置如下:载频(RF)在1 258 MHz和1 317 MHz频点间交替发射,脉冲到达时间相差(TOA)固定值25 μs,不同频点间发射信号脉宽(PW)设置不同,分别为25 μs和13 μs,PRI调制类型设置为“参差”,以24个脉冲为周期交替变化。脉内参数设置如下:调制类型设置为LFM,带宽设置为0.5 MHz。在数字信号生成基础上,通过叠加外部噪声,实现了信号空间合成的模拟,初始信噪比设置为10 dB。后端目标信号分布特性如图6所示。
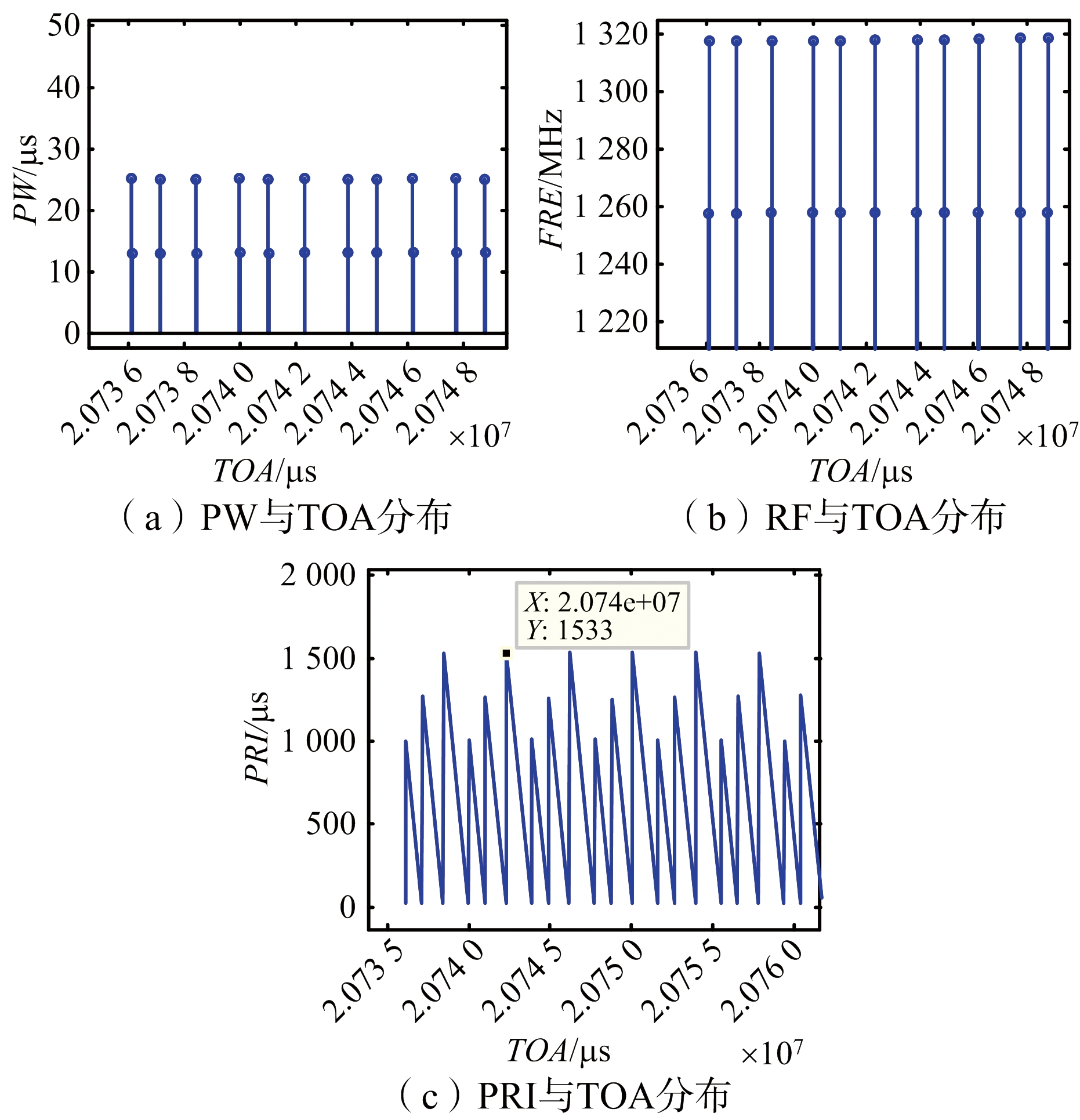
图6 雷达脉冲信号分布特性仿真结果图
按照前面特征量的定义,得到了典型特征量的计算结果及门限工程经验值(考虑测量噪声等容差),如表2所示。
表2 仿真实验结果
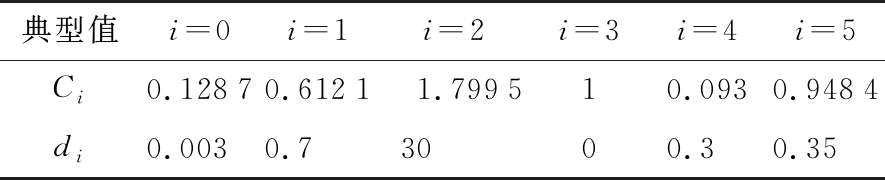
典型值i=0i=1i=2i=3i=4i=5Ci0.12870.6121 1.799510.0930.9484di0.0030.73000.30.35
按照多特征量综合识别算法流程,对比Ci与di之间的逻辑关系,得到该雷达辐射源的脉间PRI调制类型为“参差”,这与仿真初始设置条件相一致,进一步验证了算法的有效性及识别输出的稳健性。
3 结束语
未知雷达辐射源脉间PRI调制识别一直是电子侦察领域的热点和难点问题。本文针对雷达辐射源信号常见的7种脉间PRI调制方式特点,提取了零交叉密度、PRI二阶差分序列等多个特征量,在充分考虑脉冲丢失与虚假脉冲处理等实际应用的基础上,结合工程实践设计了一种基于多个特征量的综合识别算法。仿真实验表明,将该算法用于雷达辐射源脉冲序列PRI调制方式识别是可行和有效的。另外较之以往通过支持向量机及直方图统计的方法,该算法复杂程度更低,工程应用稳健性更强。
[1] 赵国庆. 雷达对抗原理[M]. 西安: 西安电子科技大学出版社, 1999:1-7.
[2] BROOKNER E. Phased Arrays and Radars Past, Present, and Future[J]. Microwave Journal, 2006, 49(1):22-46.
[3] 荣海娜, 张葛祥, 金炜东. 基于频率和形状特征的脉冲重复间隔调制识别[J]. 西南交通大学学报, 2007, 42(2):194-199.
[4] 胡国兵, 胥嘉佳, 李岳衡, 等. 雷达调制信号分析与处理技术[M]. 北京: 人民邮电出版社, 2014:34-49.
[5] 刘明. 一种改进的基于PRI参数的雷达信号分选算法[J]. 舰船电子工程, 2018, 38(2):65-68.
[6] 张葛祥, 荣海娜, 金炜东. 支持向量机在雷达辐射源信号识别中的应用[J]. 西南交通大学学报, 2006, 41(1):25-30.
[7] 杨朝, 何明浩, 韩俊, 等. 一种雷达信号特征参数评估的新方法[J]. 雷达科学与技术, 2018, 16(4):446-450.
YANG Zhao, HE Minghao, HAN Jun. A New Evaluation Method for Radar Signal Characteristic Parameters[J].Radar Science and Technology, 2018, 16(4):446-450.(in Chinese)
[8] 安琦. 信号侦收中的识别与分类理论与算法研究[D]. 成都: 电子科技大学, 2017.
[9] 王慧娟, 徐欣, 李霄. 雷达信号PRI抖动模式识别改进方法[J]. 指挥信息系统与技术, 2016, 7(1):69-72.
[10] 蔡丹凤, 林伟. 一种新的基于PRI的脉内调制信号分选算法[J]. 实验技术与管理, 2017, 34(4):59-63.
