0 引言
近年来，穿墙雷达成像(Through the Wall Radar Imaging, TWRI)一直以来都是超宽带技术应用研究的热点，它的主要目的是通过电磁波感知墙体或建筑物后态势。因此穿墙雷达成像在灾害救援、城市巷战等军事和民用领域具有广泛的应用。由于墙体与空气的介电常数存在巨大差异，电磁波在穿透墙壁的同时传播方向会发生折射、传播速度会发生改变、信号幅度也会发生衰减[1]。如何消除墙体杂波对目标信号造成的严重干扰，是TWRI需要解决的关键问题之一。
一种静止目标成像的经典方法是背景相消法，其利用背景先验信息能够很好地消除墙体杂波[2]。但在实际应用中，通常无法直接测量墙体后的背景环境。近年来，以奇异值分解(Singular Value Decomposition,SVD)、主元分析(Principal Component Analysis,PCA)等为代表的统计方法无需场景的先验知识[3]。其中SVD由于复杂度低、计算量小，应用较为广泛[4]，其主要是通过墙体杂波与目标回波信号能量之间的大小差异来确定墙体子空间，进而通过子空间投影方法抑制墙体杂波。常规成像模型通常都建立在天线阵列接近且平行于墙体的标准模式下。然而，在一些特殊场景中(如反恐、营救人质等)无法保证天线阵列与墙体平行，也无法将天线阵列紧贴墙体放置。近几年的一些研究表明，天线阵列与墙体之间的倾角会导致现有的子空间投影算法失效。从文献[5]中可知，当天线阵列倾斜，墙体反射存在于主奇异项的多维子空间中，导致墙体子空间与目标子空间发生混叠，无法判定墙体子空间与目标子空间的界限。此外，利用倾斜天线阵列接收的回波信号进行墙后场景图像的重建，会导致图像发生畸变甚至无法进行目标探测。可见，天线阵列的倾斜不仅会影响目标定位的准确性，也会对成像质量造成严重影响。针对上述问题，文献[6]通过回波时延估计墙体参数(墙体厚度、相对介电常数等)，然后对墙体回波信号进行电磁建模，利用相消法消除墙体杂波信号。然而，该算法需要在相同或相近的探测情况下，将墙体替换成金属板进行测量校准。文献[7]提出一种基于离散长椭球序列的新字典描述墙体回波信号，然后采用分块稀疏模型消除墙体杂波信号。该算法能够有效地抑制墙体杂波信号，且无须考虑天线阵列是否与墙体之间存在未知倾角，但是该算法在实际应用中会占用较多硬件资源。
本文针对以上问题，从目标产生偏移的原因出发，提出了基于时延校正和单边Jacobi奇异值分解的方法，以消除天线阵列倾斜于墙体造成的影响。对时延校正后的信号应用子空间投影法抑制墙体杂波。该方法求解出的矩阵奇异值具有较高的相对精度、奇异向量正交性好、数值稳定性强等优点，并且算法实现简单，有利于并行计算[8]。
1 穿墙雷达场景建模
本文利用基于FDTD的仿真软件GprMax2D/3D[9]，对穿墙雷达实验场景进行建模，验证本文提出的算法。在GprMax中，每个位置天线接收的一维时域信号称作A-scan，一条测量线上的A-scan组成的二维数据，称作B-scan。设B-scan为M×N维矩阵，行和列分别代表时间采样点数和天线个数。
假设天线阵列倾斜于墙体时的穿墙雷达探测模型如图1所示。本文采用单层均匀介质板代替实际墙体。设墙体厚度为d，相对介电常数为εr，电导率为σ。目标为圆形理想电导体，其半径为r，圆心与前墙体之间的垂直距离为δ。与常规建模不同，天线阵列沿着倾斜于墙体θ的测量线等间隔排列，对穿墙雷达成像场景进行N次扫描，且第一根天线与墙体之间的垂直距离为h。发射信号为Ricker子波，即一阶高斯脉冲信号取负，其表达式如下:
s(t)=-2ζ
(1)
式中，ζ
为中心频率，本文中取f0=1.5 GHz。
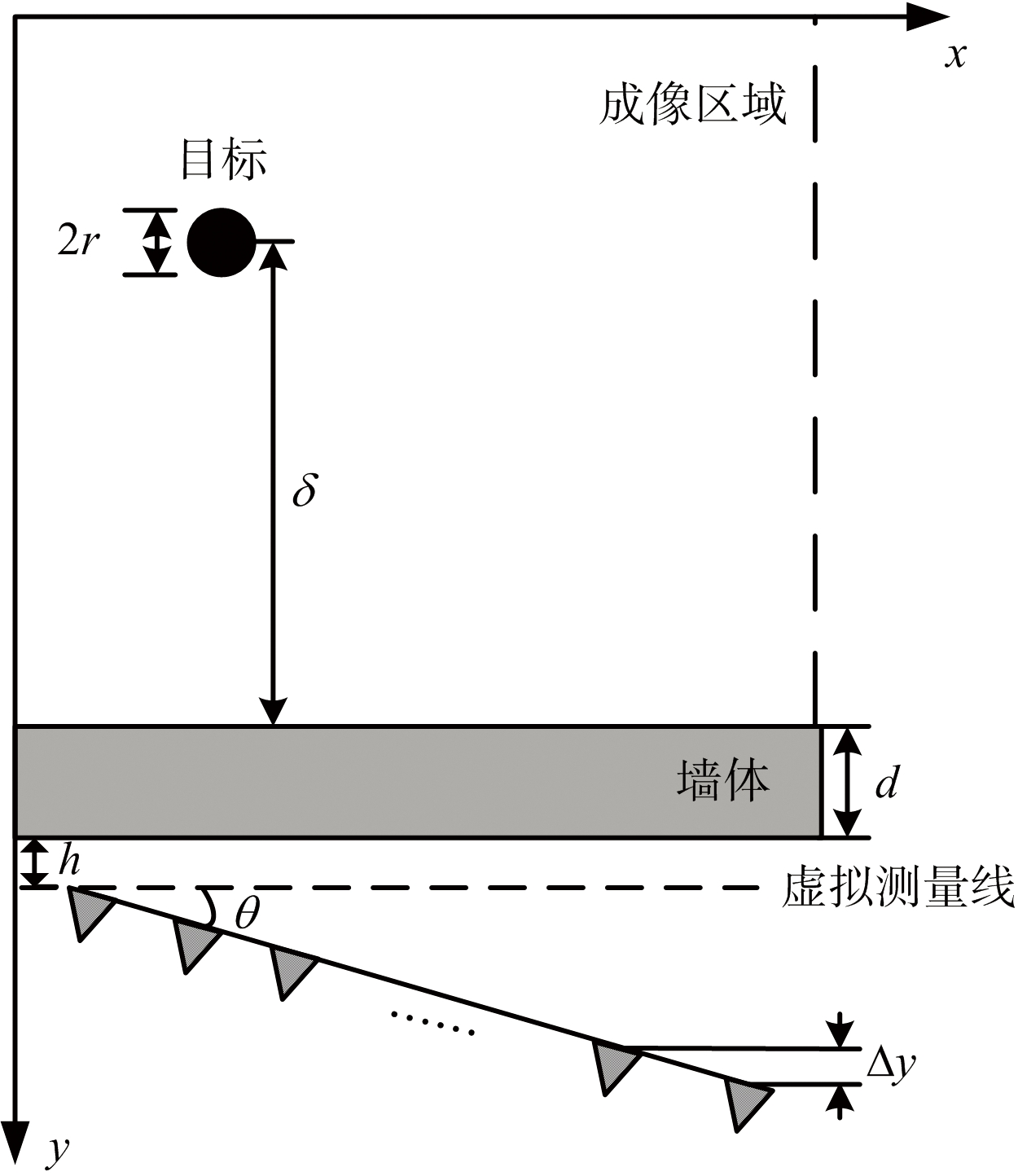
图1 倾斜天线阵列穿墙雷达模型
2 墙体杂波抑制算法
本文提出的墙体杂波抑制算法由两个阶段实现：在第一阶段，对回波信号进行时延校正，使其等效于天线阵列平行于墙体的情况；在第二阶段，将经过时延校正处理后的信号矩阵应用基于单边Jacobi奇异值分解算法抑制墙体杂波。
2.1 时延校正
在图1所示的模型中，成像时目标坐标会偏离实际位置，这是因为假设天线位于与墙体平行的测量线上，导致天线阵元与成像场景中每个像素点间的往返时间计算有误。天线阵元位置不同，到墙体的垂直距离也不同，因此天线与墙体间的往返时延与墙体的回波幅度也不同。根据上述分析，提出时延校正的思想，即将每个天线阵元的发射与接收时刻均校正到与墙体平行的虚拟测量线(如图1所示)上，去除掉每个天线阵元与虚拟测量线之间的往返时间。设τ(n)为第n个天线与虚拟测量线的往返时间：
τ(n)=2(n-1)Δy/vc
(2)
式中，Δy为相邻两个天线阵元在垂直方向上的移动步长，它可由任意两个天线阵元的接收时域回波信号计算得到，vc为电磁波速度。假设已知第k，l个天线发射信号到达墙体的时间分别为tk，tl，且k<l，则
(3)
则校正后的回波信号为
s′(t,n)=s(t+τ(n),n)
(4)
式中，s(t,n)为原始接收回波信号B-scan。
2.2 单边Jacobi奇异值分解
为去除整个天线阵列孔径的公共信号，即减少墙体的直接反射杂波以及发射天线与接收天线间耦合波的影响，需要先对雷达回波信号进行减均值的预处理[10]。令
为从B-scan回波信号矩阵S(S∈RM×N)的每列减去平均矢量得到的矩阵，即
(5)
式中，m为S各列的均值，eT=[1,1,…,1]为一个n维单位行向量。
接下来，用单边Jacobi方法对减均值后的矩阵
进行奇异值分解。1985年，Hestenes等人在经典双边Jacobi方法的基础上，提出单边 Jacobi方法[11]。具体Jacobi平面旋转变换的结构如式(6)所示：
J(i,j,α)=
(6)
它是在一个单位矩阵的基础上改变i行、j行与i列、j列四个交点上的值得到，c表示cos α，s表示sin α，α称为旋转角。不难证明JΤJ=I，即Jacobi旋转变换为一正交变换。由于在采用Jacobi方法求解矩阵奇异值时仅从一个方向对矩阵进行旋转变换，因此称之为单边Jacobi。该方法的步骤是先用一系列Jacobi平面旋转变换对进行正交化得到B[5]：
(7)
使得B中任意两列向量bi,bj满足
(8)
然后对Bm×n归一化得到
B=UΣ
(9)
因此
的奇异值分解有以下形式：
(10)
式中：V=J1J2J3…,它是由一系列Jacobi旋转变换矩阵相乘而得，所以V本身也是一个正交矩阵；U和V是由的左、右奇异向量构成的酉矩阵；T代表转置变换；Σ=diag(σ1,σ1,…,σn-1,σn)，是的奇异值矩阵，其中
在矩阵正交化的过程中，只有的i和j两列xi,xj的元素受到影响，具体的变换过程如下：
(11)
得到两个等式：
(12)
(13)
由式(14)计算参数c和s：
即可得
(15)
s=k×c
(16)
式中，
(17)
(18)
式中，sign(α)为符号函数：
(19)
在式(7)中，B的任意两个列向量都正交一次后，算法收敛，因此需要对进行n(n-1)/2次旋转变换后才能使矩阵所有列都彼此正交。由于单边Jacobi方法中平面旋转变换仅影响相应的两列元素，因此，通过合理的划分可以并行地对相互之间不存在依赖关系的列对进行变换。用于Jacobi的数据调度序列有很多种，它们各有优势。本文采用Ring序列，该序列不仅仅能够在最少的步骤(n-1)内产生所有的索引对，同时还能够保证列范数的有序排列[8]。本文用矩阵与计算得到的奇异值分解反推的矩阵之间的误差来衡量对奇异值分解的精度，定义如下:
(20)
误差E越小代表对回波信号奇异值分解越准确，精度更高。
信号在奇异值分解后采用文献[9]提出的奇异值差分谱法划分墙体子空间与目标子空间的界限，再利用子空间投影抑制墙体杂波。经上述处理后，利用后向投影方法(Back Projection, BP)重建成像场景。墙体杂波抑制的效果用图像的目标-杂波比(Target-to-Clutter Ratio, TCR)来评估，现定义如下[10]：
(21)
式中，I(·)为成像点所对应的归一化幅度值；At和Ac分别为目标区域和杂波区域，而Nt和Nc为各区域所对应的成像点数目。
3 实验与结果分析
根据图1所示的系统模型，建立仿真场景：全向天线阵列沿倾斜于墙体的测量线等间距扫描26次，倾斜角度为10°，且第一根天线距离墙体0.05 m，天线横向扫描范围为0.1～2.1 m。墙体是均匀介质，其厚度为d=0.2 m，相对介电常数为εr=6.4。目标为圆形的理想电导体，其圆心距离墙体δ=1.3 m，半径r=0.1 m。通过GprMax2D/3D软件仿真获取各个测量位置的回波信号。对回波信号应用传统的子空间投影法抑制墙体杂波，从奇异值幅值分布与成像方面证明倾斜阵列下本算法的失效。
对原始回波数据进行奇异值分解，归一化奇异值幅值分布如图2所示。可见，幅值下降得很平缓，不存在明显的突变点。这是因为不平行于墙体的天线阵列接收到的墙体回波信号跨越多维子空间，使得墙体子空间与目标子空间混叠。
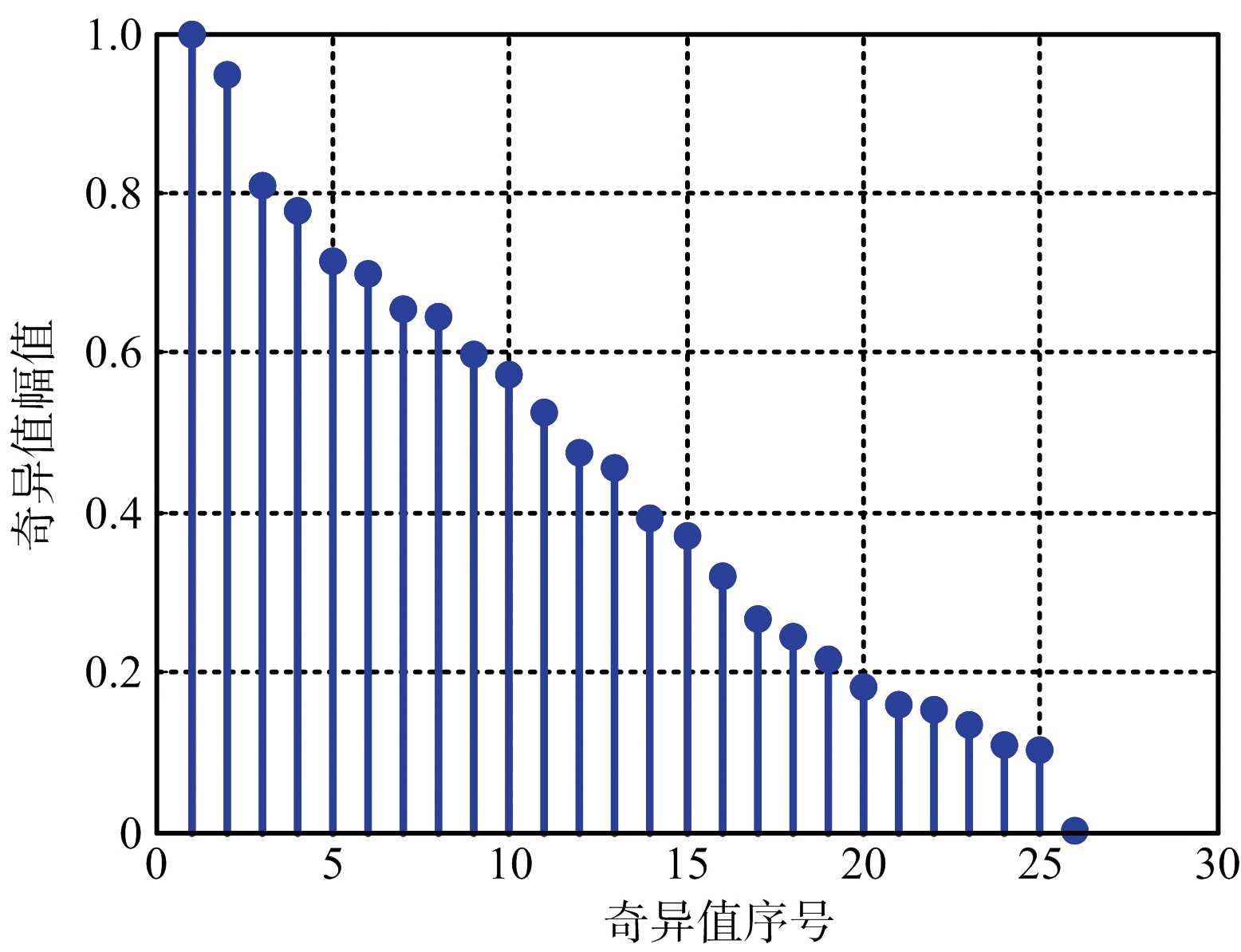
图2 归一化奇异值幅值分布
从成像方面来看，如图3(a)、(b)、(c)、(d)所示，比较去除前一、二、三、四个奇异项的成像结果，可以发现离墙体越远的天线接收到的墙体回波越难被去除，这是因为离墙体越远的天线接收到的回波越弱，从而越容易与强度弱的目标信号子空间混叠在一起，这使得利用奇异值差分谱判定墙体子空间与目标子空间边界的方法失效。且目标成像位置相比真实目标位置发生了明显的偏移，如图3(d)标出。以上分析表明，传统的基于子空间投影的墙体杂波抑制算法不能准确定位目标位置，且墙体回波信号不能被完全抑制。
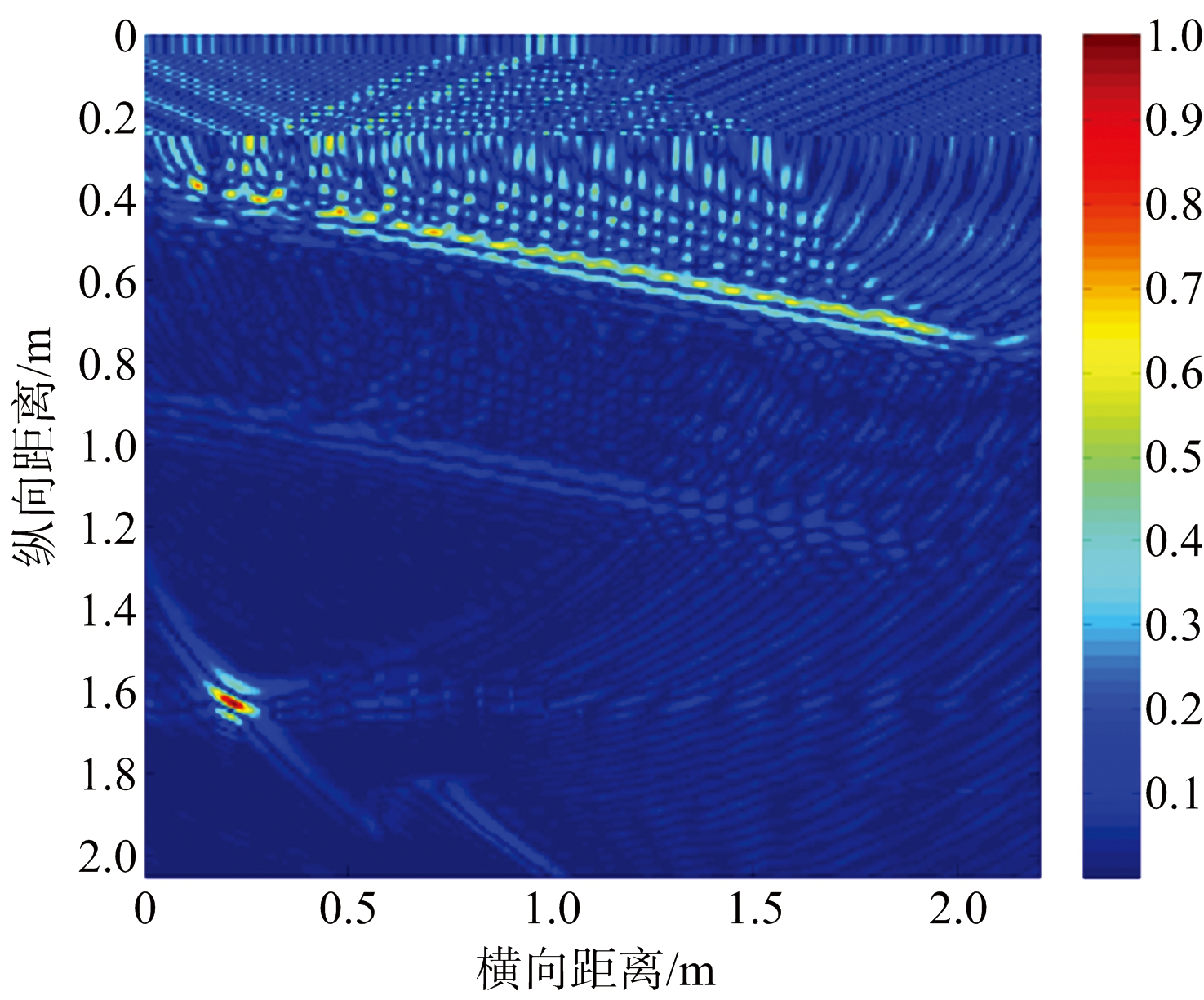
(a) 去除第一奇异项
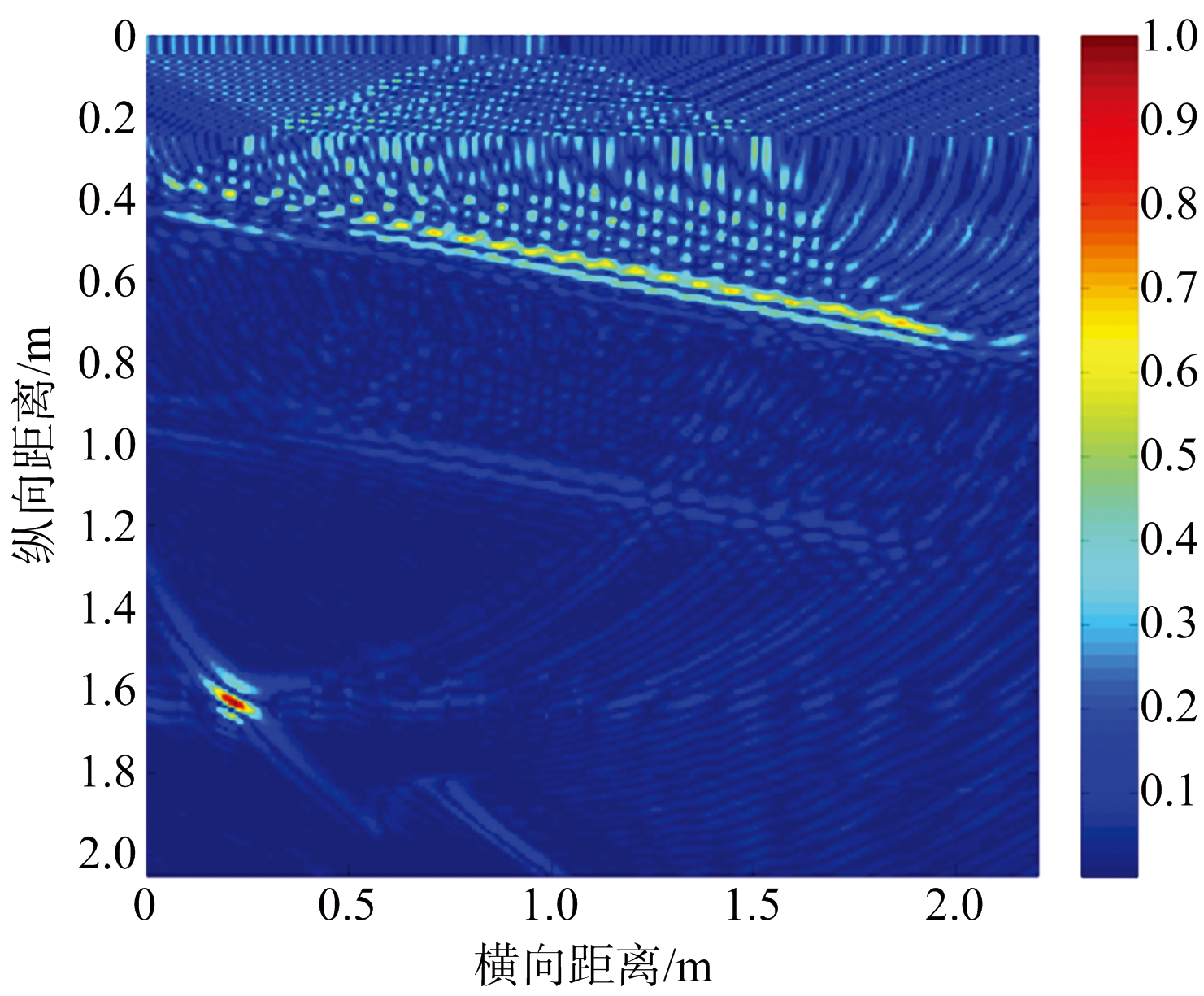
(b) 去除前两项奇异项
(c) 去除前三项奇异项
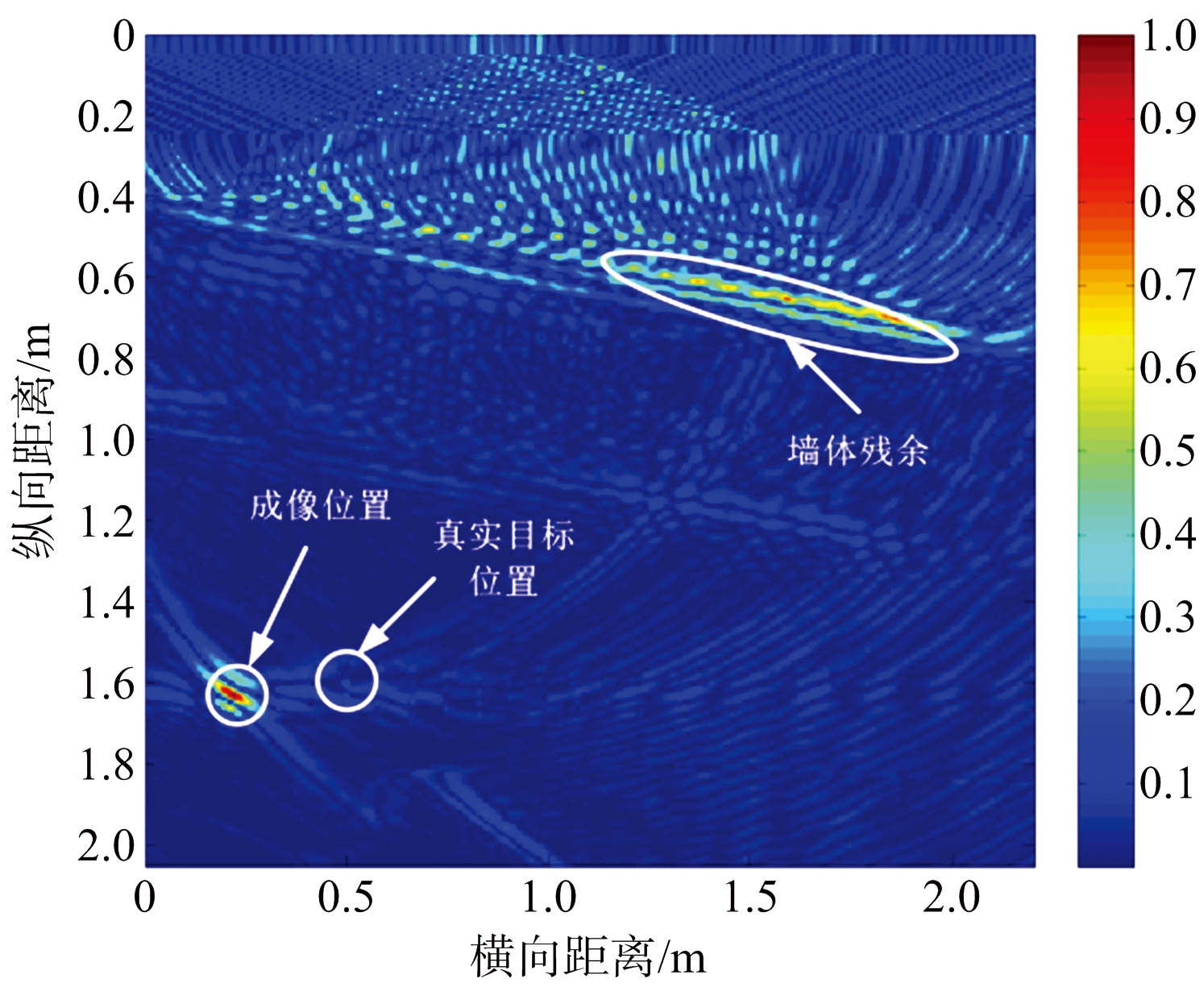
(d) 去除前四项奇异项
图3 去除不同奇异项的成像结果
为解决上述问题，在对原始接收回波信号进行子空间投影前运用本文提出的时延校正方法处理回波信号。任意选取两个不同位置的天线，图4给出了第1个与第26个天线接收的时域回波信号。从图中可以看出，墙体回波时延分别为t1=4.529 ns和t26=7.041 ns。根据式(3)计算可得垂直步长Δy=0.015 07 m，与真实值0.014 08 m相差0.000 99 m。因此，估计精度在可接受范围内，即证明了式(3)的正确性。估计得到垂直步长Δy后，再利用式(2)与式(4)将每个天线的发射与接收时刻校正到虚拟测量线上。图5为时延校正后第1个与第26个天线接收的时域回波信号，第26个天线时延校正后的墙体回波时延为4.694 ns，与第一个天线的墙体回波时延相差0.165 ns，可忽略为零。因此，可以将两根天线看作是在同一时刻接收到墙体回波信号。同理，所有天线的A-scan经过时延校正处理后，均在t1时刻附近接收到墙体回波，这与天线阵列平行于墙体模型下的特性相同。
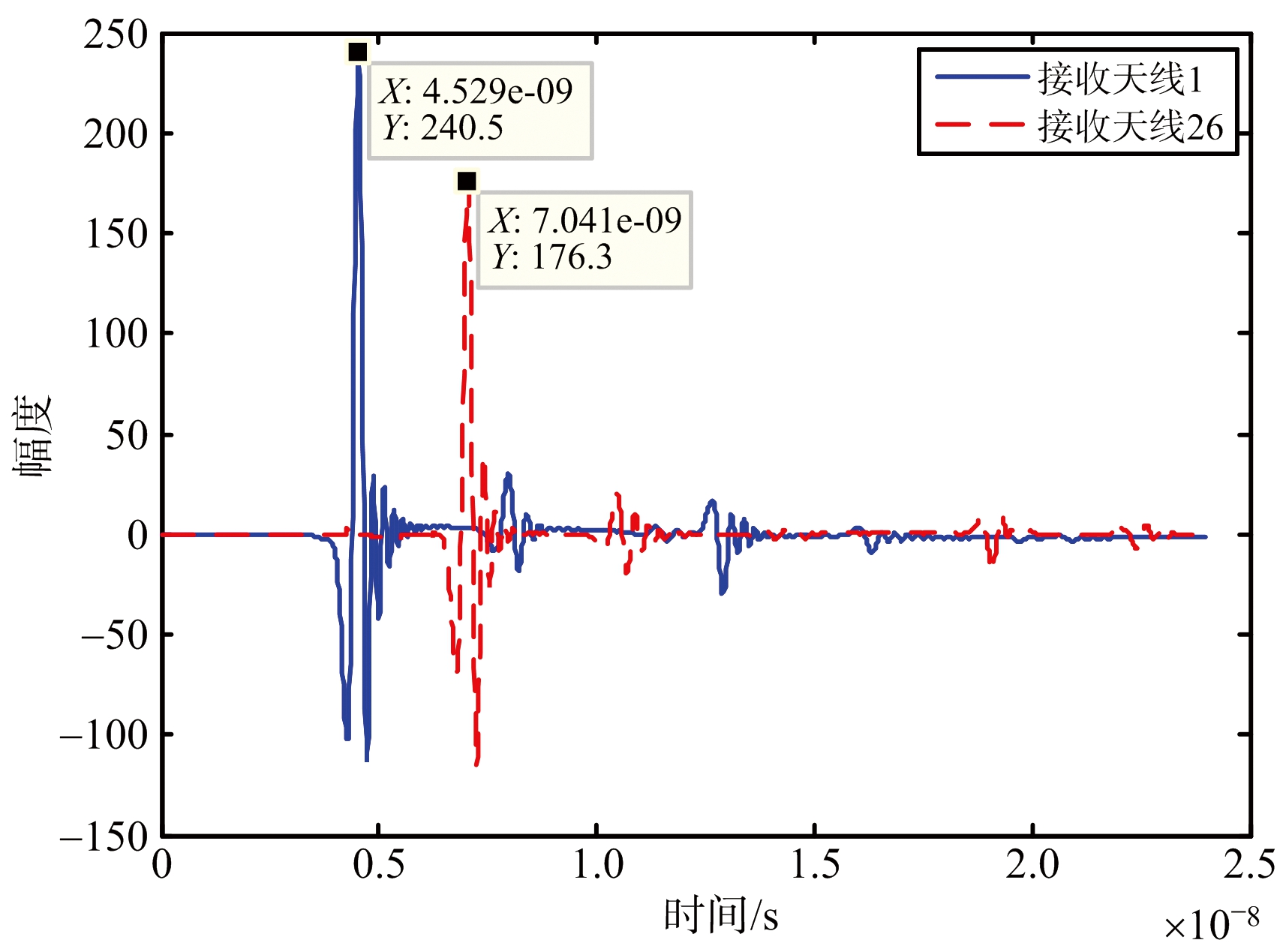
图4 接收天线1与26接收的回波信号
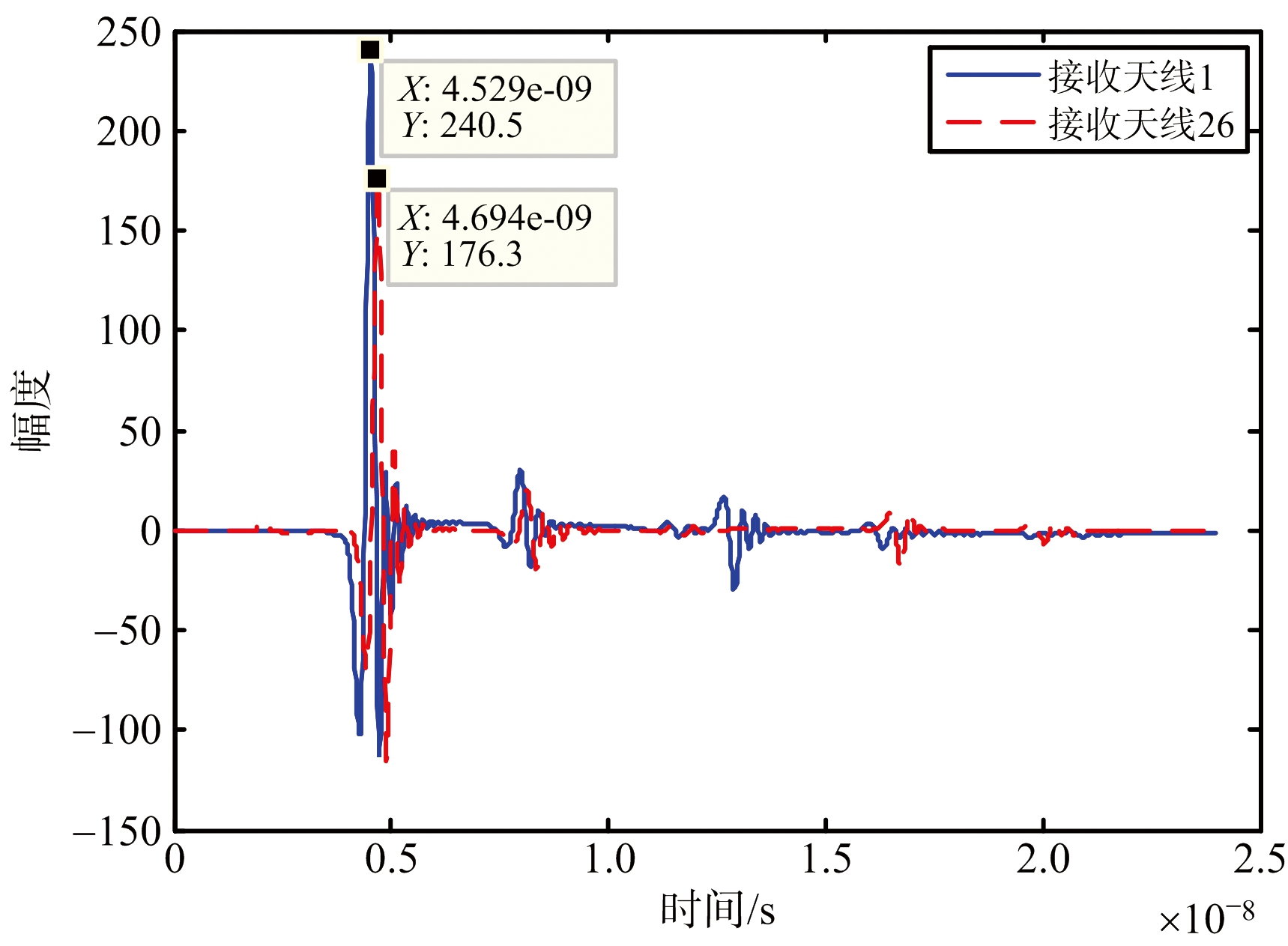
图5 时延校正后的接收回波信号
对上述经过时延校正后的B-scan进行单边Jacobi奇异值分解，图6给出了归一化奇异值幅值分布情况。可见，第一个奇异值与第二个奇异值差距较大，因此可通过计算奇异值差分谱得到墙体子空间与目标子空间的界限在第一个奇异值与第二个奇异值间取得，这表明墙体反射信号占据第一个奇异项。确定表征墙体的奇异项后，用子空间投影算法抑制墙体杂波。最后通过BP算法对其进行成像，结果如图7(a)所示。可以看出，墙体杂波几乎被完全滤除，这证明了墙体子空间与目标子空间未发生混叠。并且目标也被校正到正确位置。仿真结果证明时延校正消除了天线阵列倾斜于墙体所产生的影响。
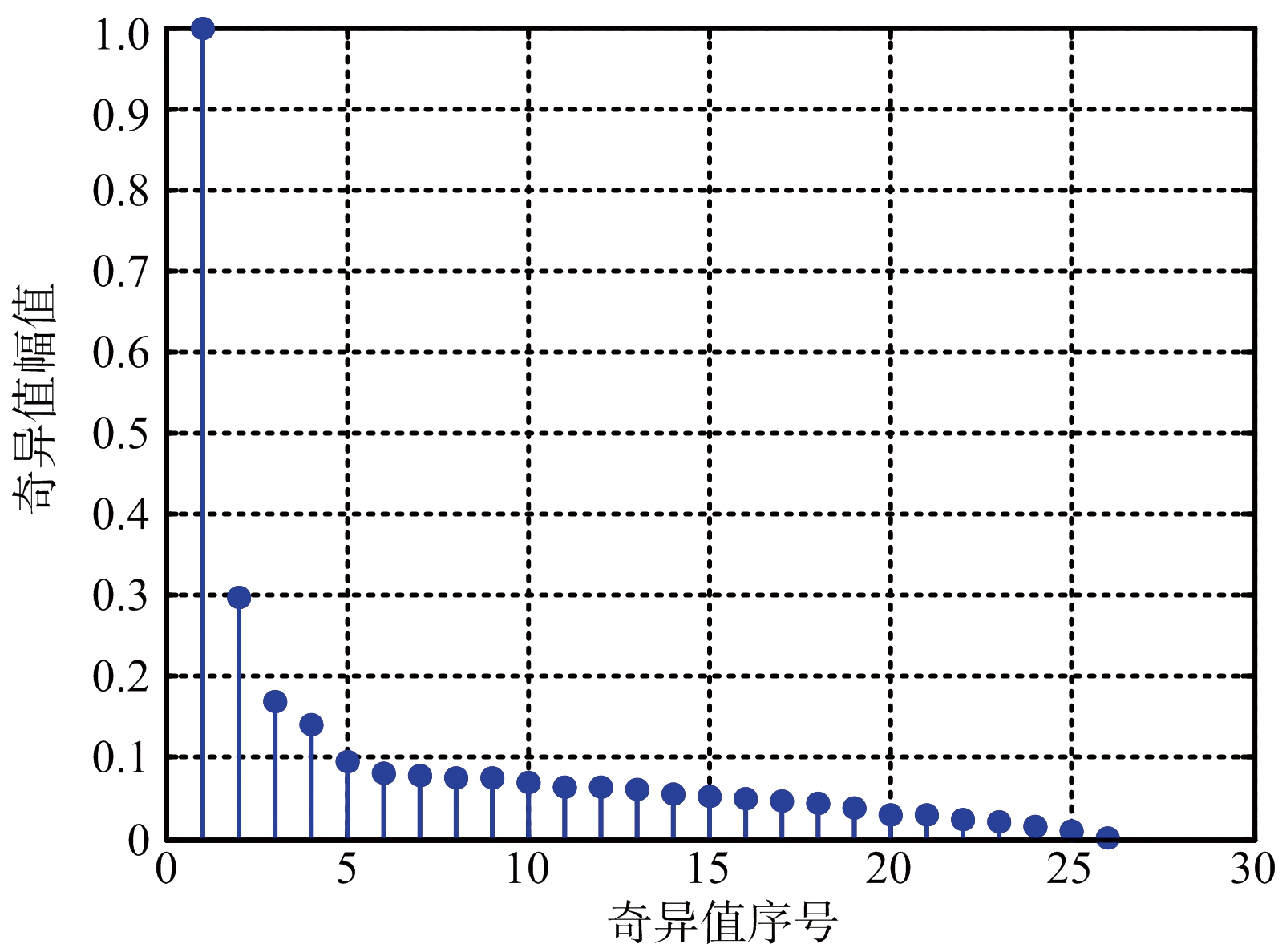
图6 时延校正后奇异值幅值分布
对经过时延校正后的信号矩阵分别应用单边Jacobi奇异值分解与原始奇异值分解，根据式(20)计算两者的误差，前者为1.03×10-12，后者为5.06×10-10。可见，相比之下单边Jacobi奇异值分解的精度更高。图7给出了应用两种不同奇异值分解的成像结果，可以看出图7(a)中成像效果要好于图7(b)，在图7(b)中还存在少许墙体杂波残余。
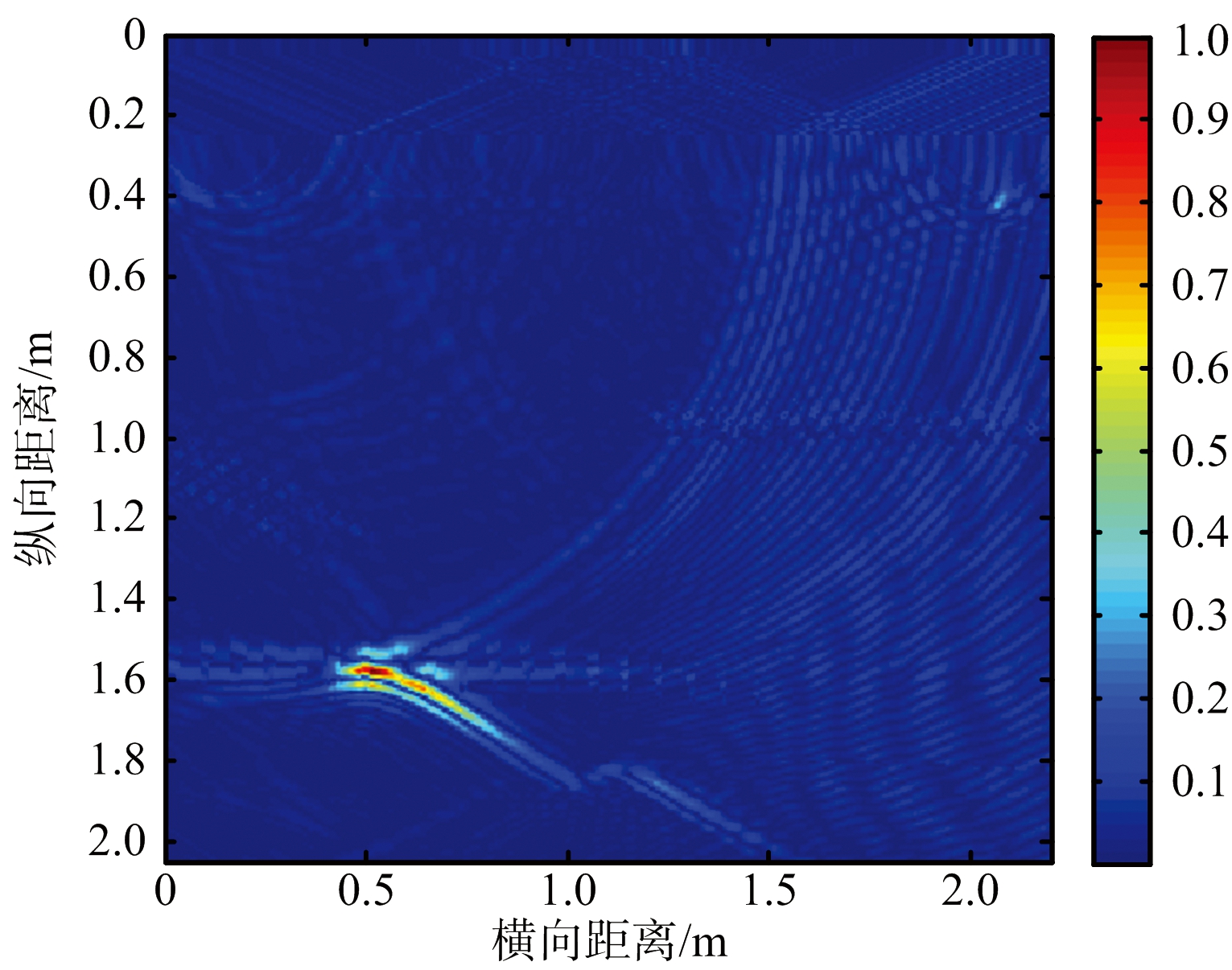
(a) 单边Jacobi实现奇异值分解
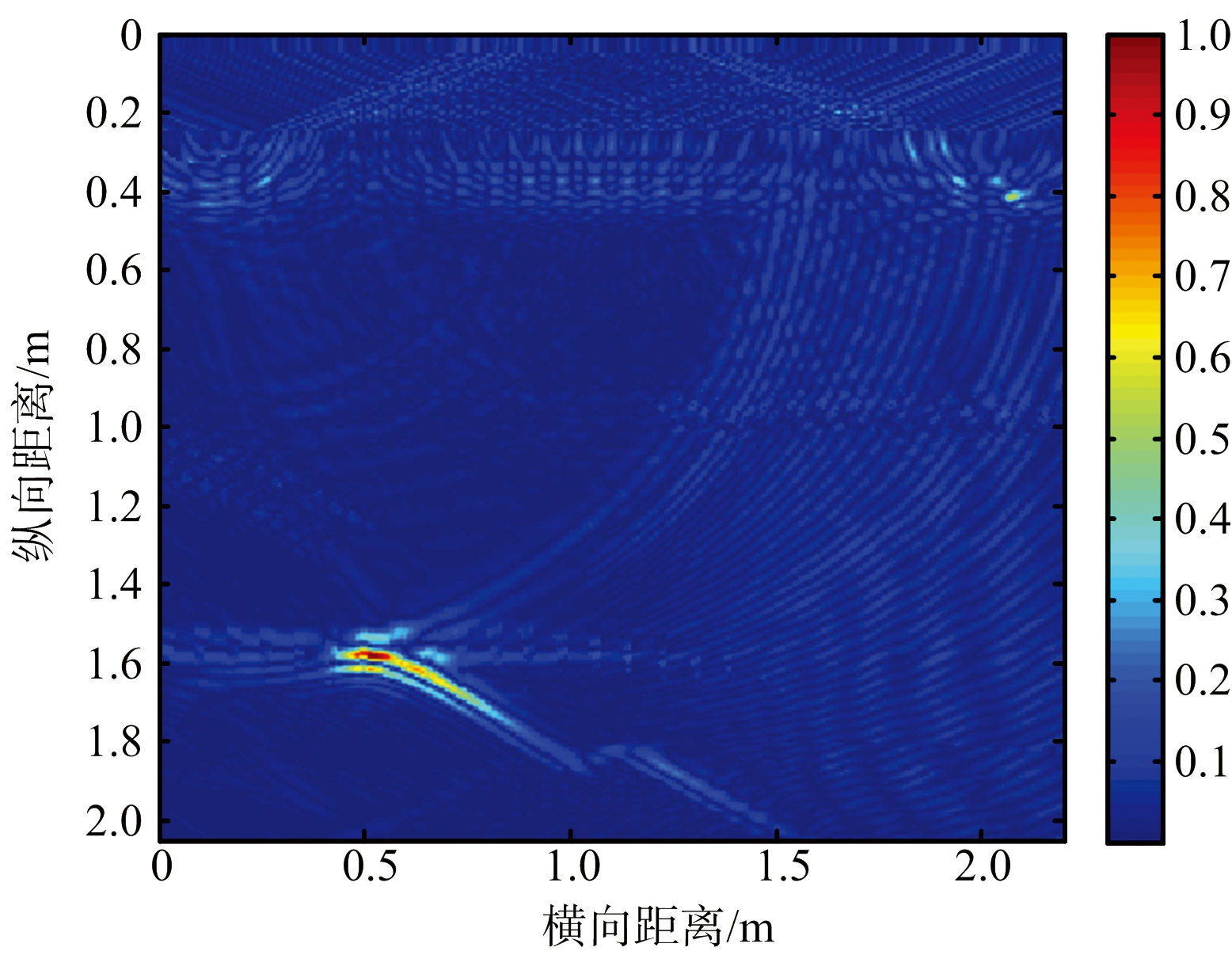
(b) 原始奇异值分解
图7 经过时延校正处理后应用不同奇异值分解的
成像结果
由于在实际系统中噪声不可避免，因此在回波信号中添加高斯白噪声模拟有噪情况，在不同信噪比的条件下重复穿墙雷达成像过程。表1给出不同信噪比下应用原始奇异值分解与Jacobi奇异值分解的输出目标图像信杂比。由表1中的数据可知，当信噪比SNR=-8 dB时，本文提出的单边Jacobi奇异值分解方法比原始奇异值分解的目标图像TCR提高了1.52 dB，且随着信噪比的增大，单边Jacobi奇异值分解的优势越明显。
表1 不同信噪比时的输出目标图像TCR比较
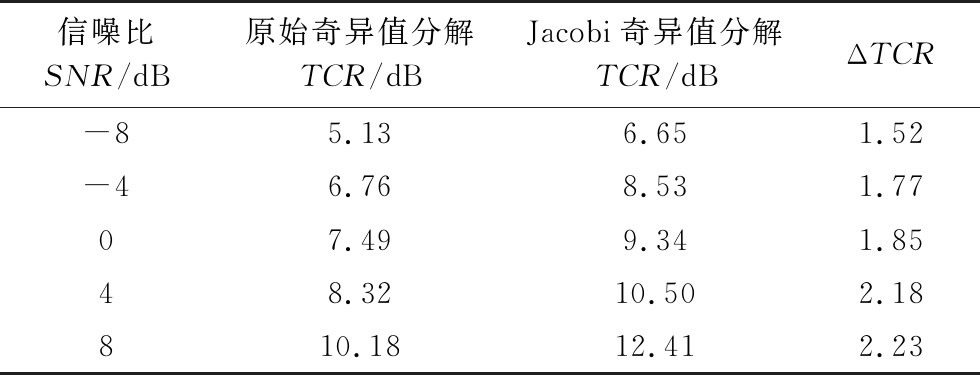
信噪比SNR/dB原始奇异值分解TCR/dBJacobi奇异值分解TCR/dBΔTCR-85.136.651.52-46.768.531.7707.499.341.8548.3210.502.18810.1812.412.23
4 结束语
为了解决天线阵列倾斜于墙体时基于奇异值分解的子空间投影杂波抑制算法失效、目标成像产生偏移的问题，本文提出了时延校正的基于Jacobi奇异值分解的墙体杂波抑制算法。即首先通过时延校正使各天线的发射与接收时刻校正到与墙体平行的等效测量线上。仿真结果表明采用时延校正方法对回波信号预处理，能够有效地实现墙后目标的准确定位，并且墙体子空间与目标子空间不再发生混叠，这使得墙体反射信号能够被完全滤除。与传统奇异值分解相比，单边Jacobi奇异值分解具有更高的精度，成像结果显示该算法的成像效果以及图像信杂比均优于原始奇异值分解。理论推导以及程序仿真实验充分说明了本文方法对于实际工程中墙体杂波抑制与成像具有一定的理论指导意义。
[1] 郑晨,席晓莉,宋忠国.基于延迟锁定环跟踪对消技术的穿墙雷达杂波抑制[J].电子学报,2018,46(9):2181-2187.
[2] ZHENG Chen, XI Xiaoli, SONG Zhongguo, et al. Multilevel Delay Lock Loop Approach for Wall Clutter Mitigation in Through-the-Wall Radar Imaging[J].IET Microwaves Antennas & Propagation, 2018,12(12):1986-1992.
[3] TIVIVEF H C,BOUZERDOUM A. An Improved SVD-Based Wall Clutter Mitigation Method for Through-the-Wall Radar Imaging[C]∥2013 IEEE 14th Workshop on Signal Processing Advances in Wireless Communications, Darmstadt, Germany:IEEE, 2013:430-434.
[4] 王芳芳,洪伟,张业荣,等.基于奇异值分解的墙杂波抑制[J].南京邮电大学学报(自然科学版),2017,37(3):52-59.
[5] TIVIVE F H C,AMINM G,BOUZERDOUM A. Wall Clutter Mitigation Based on Eigen-Analysis in Through-the-Wall Radar Imaging[C]∥2011 17th International Conference on Digital Signal Processing (DSP),Corfu,Greece:IEEE,2011:1-8.
[6] DEHMOLLAIAN M, SARABANDI K. Refocusing Through Building Walls Using Synthetic Aperture Radar[J]. IEEE Trans on Geoscience and Remote Sensing, 2008, 46(6):1589-1599.
[7] AHMAD F, QIAN J, AMIN M G. Wall Clutter Mitigation Using Discrete Prolate Spheroidal Sequences for Sparse Reconstruction of Indoor Stationary Scenes[J]. IEEE Trans on Geoscience and Remote Sensing, 2015,53(3):1549-1557.
[8] 郭强. 并行JACOBI方法求解矩阵奇异值的研究[D].苏州：苏州大学,2011.
[9] ALSHARAHI G, FAIZE A, MOSTAPHA A M M, et al. 2D FDTD Simulation to Study Response of GPR Signals in Homogeneous and Inhomogeneous Mediums[J]. International Journal on Communications Antenna and Propagation, 2016, 6(3):153.
[10] SUN Xin, LU Biying, JIN Tian, et al. Antenna Planes Based Wall-Clutter Mitigation in Through-Wall-Imaging Applications[J].Journal of Central South University, 2016, 23(10):2638-2646.
[11] AN Jianjing, WANG Dong. Efficient One-Sided Jacobi SVD Computation on AMD GPU Using OpenCL[C]∥2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu:IEEE,2016:491-495.
