0 引言
建筑物布局成像是穿墙雷达在实际中的重要应用,精确地获取建筑布局图像对于了解建筑物内部结构信息,获得室内目标的检测与定位,打击犯罪分子保护己方力量有重要的现实意义[1-2]。
文献[3]用传统的后向投影成像方法首先获得单视角建筑布局成像,然后融合单视角图像,形成较为完整的建筑布局全景图,但其高分辨率成像要求大带宽信号及长阵列孔径,产生的大量数据不易于存储和处理。为缓解数据处理瓶颈,文献[4]利用墙体结构的先验信息,构造出表示墙体位置的稀疏字典,考虑到墙体的镜面反射特性,该稀疏字典仅仅考虑了位于天线正前方的墙体,将场景用互不重叠的块来划分,因而恢复出的墙体呈块状不连续状态。文献[5]充分考虑了墙体回波信号的块稀疏性及连续性特点,在块稀疏贝叶斯算法的基础上,利用块稀疏信号块内前后稀疏系数之间的相关性及块间相关性,虽然较好地重构出墙体图像,但是却以花费大量的时间为代价。以上方法虽然能够恢复出简单的建筑物布局图像,但对于复杂场景并不适用,因为当场景内部存在多个目标时,这些目标对内部墙体成像影响较大,因此,要想准确地重构复杂建筑物场景的布局图像,必须考虑建筑物内部目标及墙角对墙体成像的影响。
由于墙体物理结构的连续性使得墙体回波矩阵成为一个低秩矩阵,而空间稀疏分布的多个目标使得这些目标的回波矩阵成为一个稀疏矩阵,因此,感兴趣的成像空间就视为一个低秩稀疏分解问题[6]。为得到清晰的墙体成像,本文首先采用快速迭代软阈值算法(FISTA)求解低秩稀疏约束下的凸优化问题来恢复墙体回波矩阵。在此基础上,采用交替迭代法结合非单调线性搜索法求解全变分(TV)约束下稀疏重构系数。这种联合低秩稀疏分解和全变分约束稀疏重建的方法可以有效去除场景内部目标、墙角以及杂波对墙体成像的影响,从而得到较为清晰的建筑物布局图像。
1 回波模型
如图1所示,使用一个包含M个收发共置天线单元的穿墙雷达系统对建筑物场景进行探测。以视角1为例,在第m个测试位置接收到的信号包括墙体回波![]() 目标回波
目标回波![]() 墙角回波
墙角回波![]() 和杂波噪声υm,即
和杂波噪声υm,即
(1)
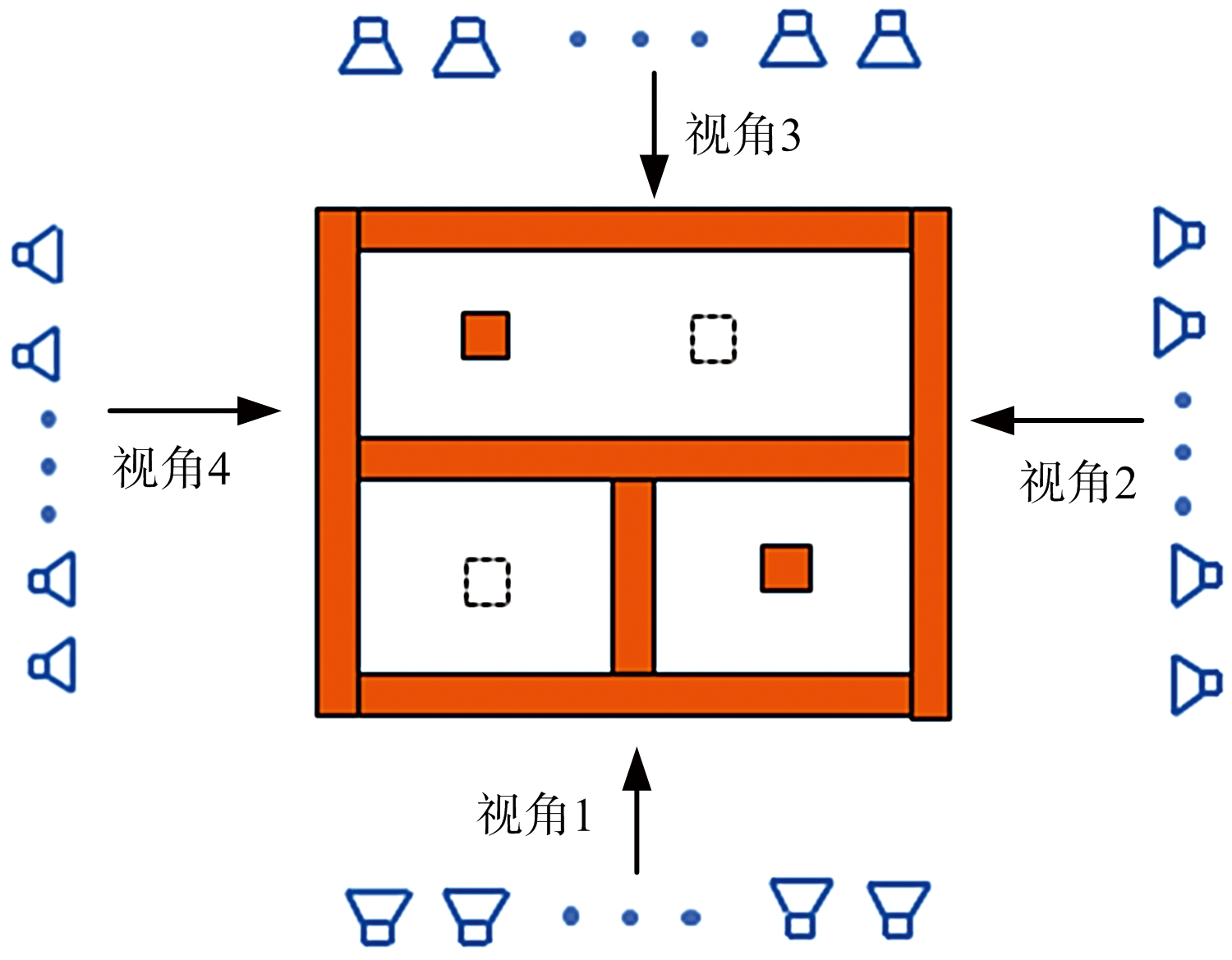
图1 建筑物场景探测图
将这M个测试点测得的所有数据构成矩阵,可得
Z=Zw+ZT+ZC+V
(2)
式中,![]() 以及V=[υm]。由于墙体物理结构的连续性及相关性使得墙体回波矩阵Zw为一个低秩矩阵,而目标及墙角的空间稀疏性使得目标回波矩阵ZT及墙角回波矩阵ZC均为稀疏矩阵,因此,求解墙体回波矩阵的问题就转化为从回波矩阵中恢复低秩矩阵的问题。
以及V=[υm]。由于墙体物理结构的连续性及相关性使得墙体回波矩阵Zw为一个低秩矩阵,而目标及墙角的空间稀疏性使得目标回波矩阵ZT及墙角回波矩阵ZC均为稀疏矩阵,因此,求解墙体回波矩阵的问题就转化为从回波矩阵中恢复低秩矩阵的问题。
2 Zw的求解
由式(2)可知,墙体回波矩阵Zw的恢复是建筑物布局成像的关键,必须消除ZT和ZC的影响。将ZT和ZC记为矩阵ZTC,ZTC是一个稀疏矩阵,由于秩的求解是一个非凸问题,求解比较困难,根据文献[7],矩阵的秩凸近似解就是其核范数,可用奇异值阈值算子进行求解,而稀疏成分通常用l1范数最小化模型求解,即

(3)
式中,![]() 表示核范数(矩阵奇异值之和),
表示核范数(矩阵奇异值之和),![]() 表示l1范数(矩阵所有元素的绝对值之和)。将约束问题式(3)转化为无约束的Lagrange正则化形式:
表示l1范数(矩阵所有元素的绝对值之和)。将约束问题式(3)转化为无约束的Lagrange正则化形式:
(4)
式中,λ为正则化参数,μ为惩罚项参数。文献[7]采用迭代软阈值算法(ISTA),通过二次近似,求解目标函数:
(5)
式中,tk为所选步长,Γλ为收缩算子,定义为
Γλ(x)i=(|xi|-λ)+sgn(xi)
(6)
尽管ISTA的简单性在求解线性逆问题时具备优势,但每次迭代涉及矩阵的奇异值分解,收敛速度缓慢。本文用一种快速迭代软阈值方法(FISTA)求解式(5),利用前两次迭代的结果作为下一次迭代的计算,并且动态地更新步长,加快了恢复算法的收敛速度。引入辅助变量矩阵G,Y,目标函数式(4)的求解改写为
(7)
(8)
式中,tk为步长,Z0为原始回波。通过奇异值软阈值算子与迭代软阈值方法交替收缩Zw的奇异值和ZTC的大小,从而得到Zw与ZTC。对![]() 进行奇异值分解,即
进行奇异值分解,即
(9)
这样,得到的墙体回波矩阵与目标回波矩阵分别为
(10)
(11)
式中,λ的取值为![]() 此外,辅助变量矩阵Y的更新为
此外,辅助变量矩阵Y的更新为
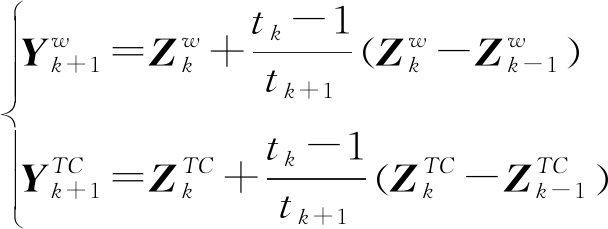
(12)
其中,步长tk+1更新为
(13)
综上所述,基于FISTA的Zw求解流程如表1所示。
表1 基于FISTA的Zw求解流程

初始化:令Zw0=Z0,ZTC0=0,YTC1=ZTC0,k=1,t1=1,λ=41.2,μ=2,ε=106,T=100;步骤1:根据式(7)、(9)、(10)更新Zwk;步骤2:由式(8)、(11)更新ZTCk;步骤3:由式(13)更新tk+1;步骤4:由式(12)更新Ywk+1;步骤5:若(Zwk+ZTCk2-Zwk-1+ZTCk-12)/Zwk-1+ZTCk-12>ε,或迭代次数小于T,则Zwk-1=Zwk,ZTCk-1=ZTCk,Ywk=Ywk+1,YTCk=YTCk+1;i=i+1,返回步骤1;否则,跳出循环;输出参数:输出重构结果Zwk
3 TV约束下稀疏系数的求解
将![]() 按列重新排成一个列向量,然后用测量矩阵Φ进行稀疏采样得到新的向量y。根据文献[4]建立y与墙体反射系数向量σ的关系为
按列重新排成一个列向量,然后用测量矩阵Φ进行稀疏采样得到新的向量y。根据文献[4]建立y与墙体反射系数向量σ的关系为
y=Φψσ=Aσ
(14)
式中,Ψ是大小为NM×NxNz的字典矩阵,与Φ满足不相关性,A=Φψ是感知矩阵。根据文献[9],全变分最小化模型具备保留图像的边缘细节信息方面的优势,使恢复图像轮廓更清晰。本文通过TV约束优化问题来恢复σ,即
(15)
式中,![]() 代表第i个像素的离散梯度,与距离向和方位向的梯度有关。用二次惩罚项将式(15)约束优化问题转化为无约束优化问题,即
代表第i个像素的离散梯度,与距离向和方位向的梯度有关。用二次惩罚项将式(15)约束优化问题转化为无约束优化问题,即
(16)
由于直接求解式(16)是困难的,因为惩罚项参数μ要达到无穷才能保证该式收敛,从数值上来说,这是个病态问题。通过引入新的松弛变量wi∈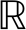 2来分裂变量Diσ,从而引入新的正则项使原来的不适定问题变为适定问题[10]:
2来分裂变量Diσ,从而引入新的正则项使原来的不适定问题变为适定问题[10]:
(17)
相应的增广拉格朗日形式为
L(σ,w,ν,δ)=
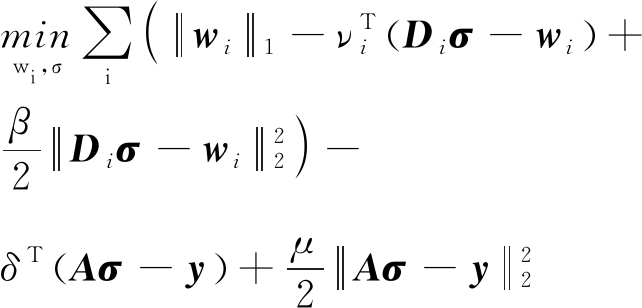
(18)
式中,ν,δ为拉格朗日乘子,μ,β为惩罚项参数。由于目标函数属于可分离结构,所以可以采用交替方向法结合非单调线性搜索法[10]求解,这样,将增广拉格朗日函数分解为如下的子问题进行求解:
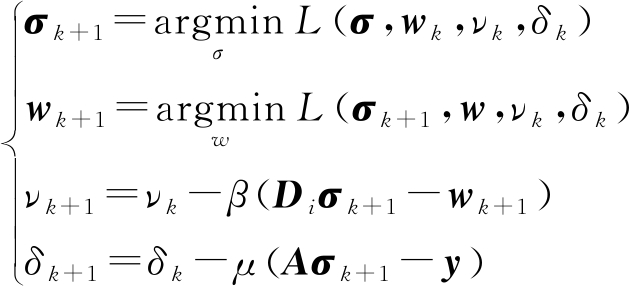
(19)
其中,在求解σk+1的过程中,可以忽略式(18)中与σk不相关项,用非单调线性搜索方法直接进行求解。同样地,求解wk+1的过程中也可忽略与wk不相关项,经过推导,用ISTA求解wk+1,即
(20)
式中,shrink(·)表示![]()
4 仿真与实测结果分析
4.1 仿真结果分析
建筑物仿真场景如图1,长宽尺寸为2 m×2 m的四面墙体由均匀介质材料构成,其墙厚、相对介电常数以及电导率分别是0.1 m,4.5和0.01 S/m。仿真数据由GprMax电磁仿真软件产生,GprMax的网格单元、时间步长和采样时间窗分别是0.01 m,23 ps和40 ns,仿真中发射的窄高斯脉冲信号的中心时刻和脉冲宽度均为1 ns。采用收发共置阵元距离墙体2 m处进行4个垂直视角的合成孔径探测,每隔0.1 m设置一个回波接收点,共有21个收发共置的天线单元合成线性阵列。
图2为文献[4]中的分块稀疏字典方法成像,图3为文献[5]中基于稀疏贝叶斯学习的块间耦合成像结果,图4为本文方法成像。可以看出,由于文献[4]考虑到墙体的镜面反射特性,将一个指示函数ζ与字典矩阵ψ相乘,作为新的字典矩阵。当天线在像素值(k,l)的正前方时,该指示函数ζ为1,否则为0。因此,该分块稀疏字典方法不能将内部目标与墙体分离,且恢复出的墙体不连贯,成像效果不佳。而文献[5]将稀疏信号的块间耦合系数引入到控制稀疏信号先验概率分布的超参数中,将稀疏信号的结构性转化为超参数之间的耦合关系,因此,该方法能有效去除内部目标对墙体成像的影响,所成墙体的外部轮廓较为清晰,但该方法所呈内部墙体轮廓特性不明显,且该方法在每个视角下成像所需时间长达1 200 s左右,不具有实时性。在本文方法的成像中,先是将内部目标和墙角与墙体分离,而后通过求解TV约束下的稀疏重构系数,滤除了杂波,所呈墙体前后表面连贯,轮廓较为清晰,对建筑物墙体的恢复较为完整。
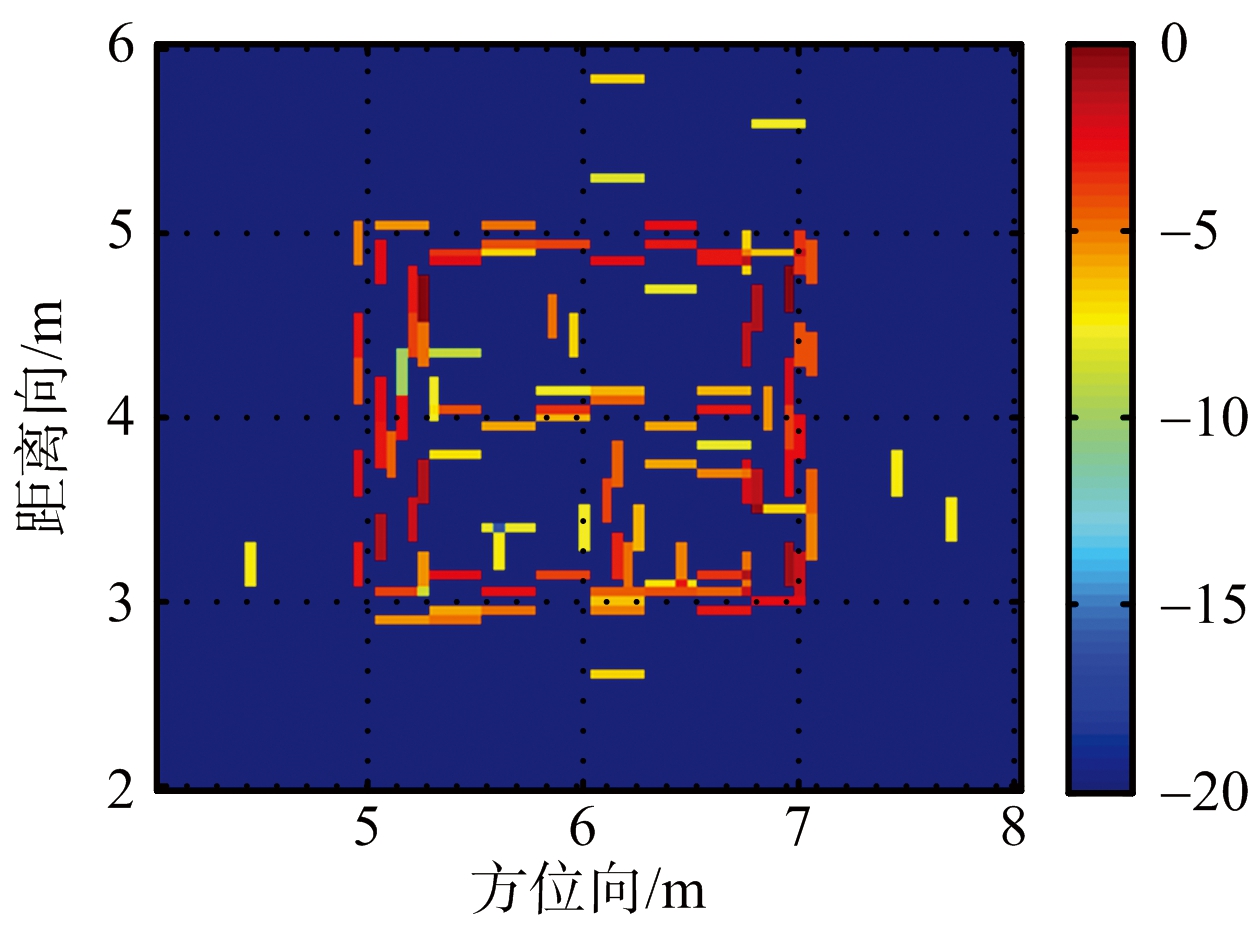
图2 文献[4]的方法
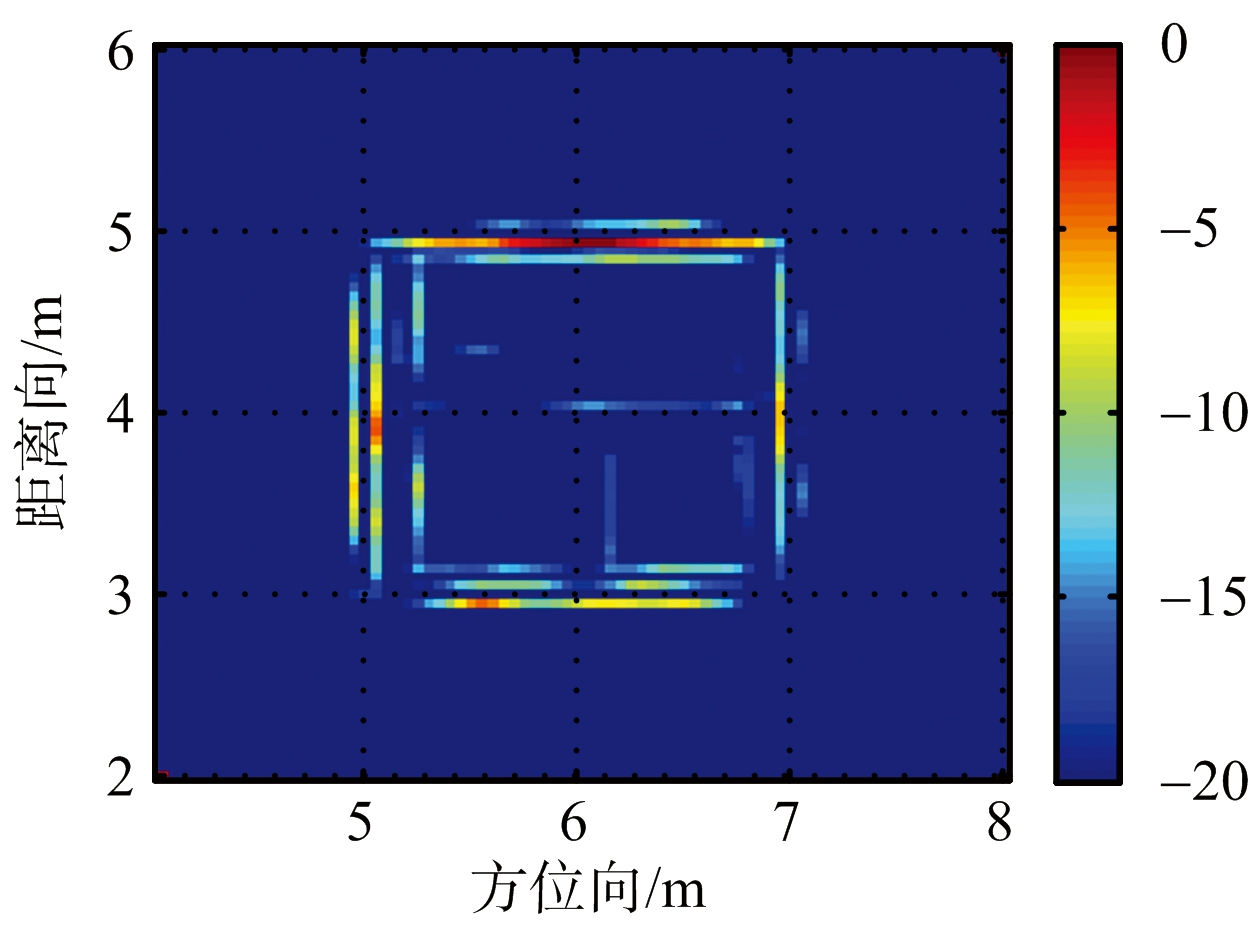
图3 文献[5]的方法
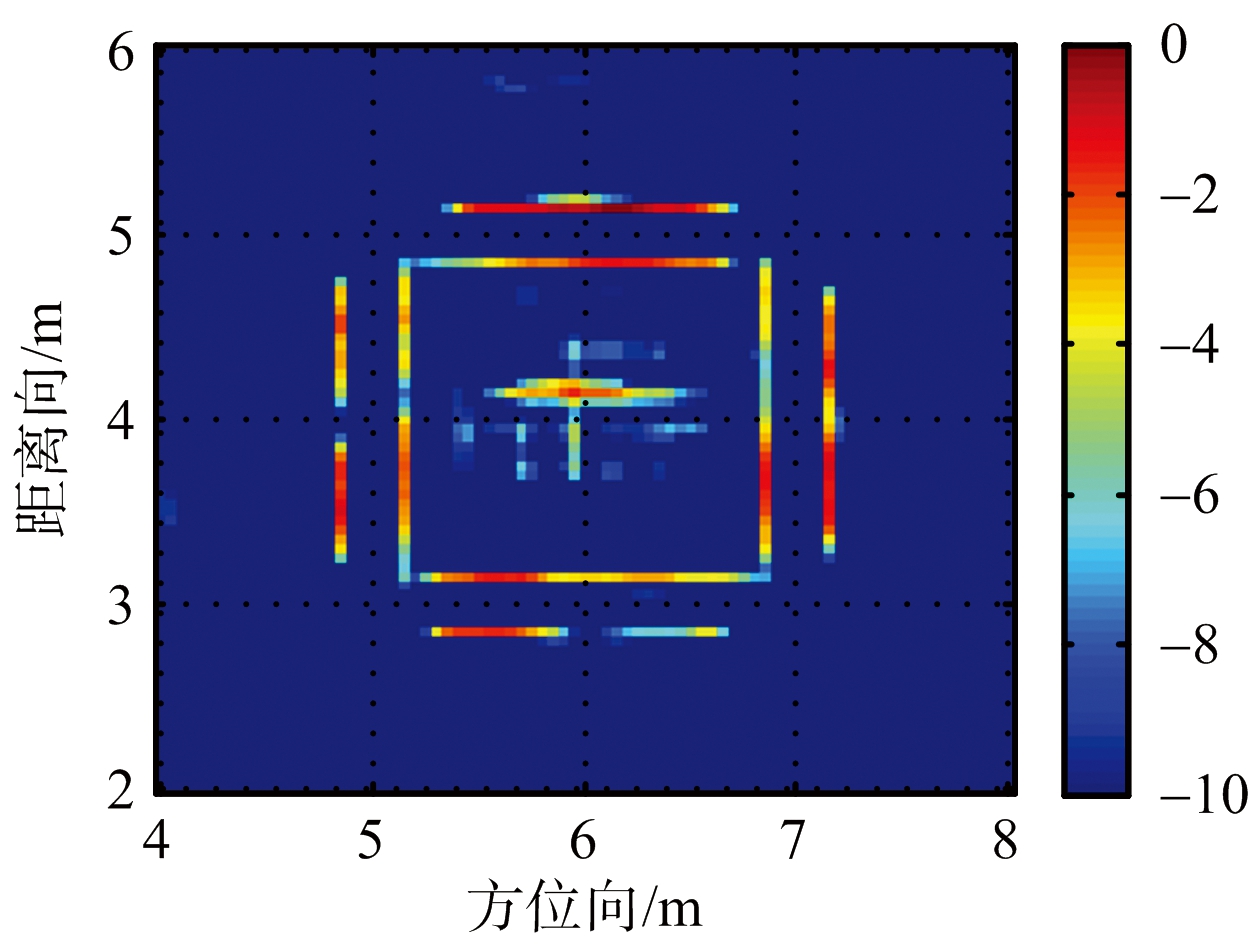
图4 本文方法
根据文献[12]的参数进行对比,结果如表2所示。从表中可以看出,3种算法的ENT值相同,说明图像整体复杂度相同;本文方法成像的MFOD和PRT最小,说明本文算法的计算量最少,成像也最平滑;文献[4]方法和文献[5]方法的PRT较大,说明算法较为复杂,文献[5]更是以PRT为代价获得较为清晰的成像;从MFOD和PRT值最佳说明本文算法较好地凸显了墙体目标,图像轮廓边缘明显且较为清晰。
表2 TCR、ENT、MFOD与PRT比较
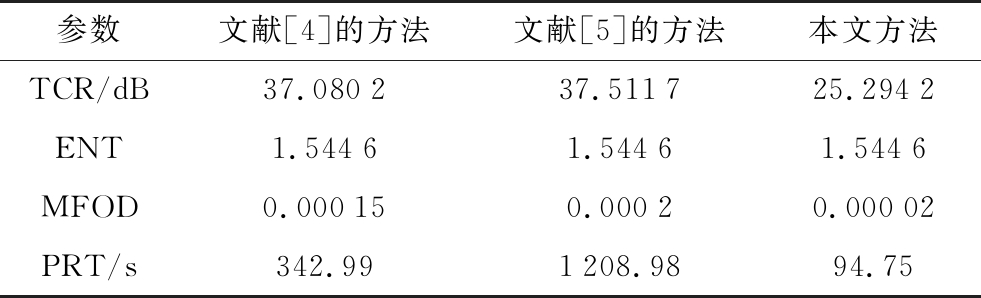
参数文献[4]的方法文献[5]的方法本文方法TCR/dB37.080237.511725.2942ENT1.54461.54461.5446MFOD0.000150.00020.00002PRT/s342.991208.9894.75
4.2 实测结果分析
实际建筑物探测场景如图5所示,场景大小为2.4 m×2.4 m,墙体厚度为0.2 m,介电常数为6.5,中间放置一个带有金属边缘的凳子。雷达探测系统是基于矢量网络分析仪的超宽带喇叭天线实验平台,采用一发五收的收发分置天线,频带为1~2 GHz,步进频率为5 MHz,从视角1和视角2两个视角进行探测,如图6和图7所示,两个视角下天线均距离墙体1 m,相邻喇叭天线之间的距离分别为0.27 m,0.275 m,0.325 m,0.28 m,0.27 m。
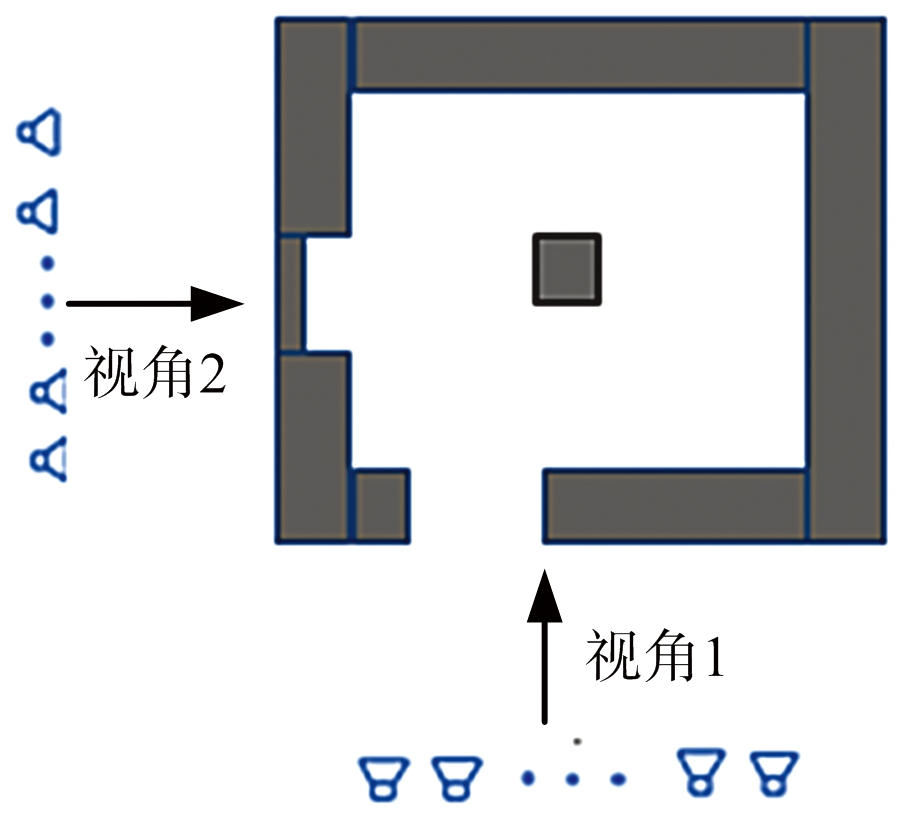
图5 实测场景图

图6 视角1探测

图7 视角2探测
图8到图10为实测数据经视角相加后的成像结果。图8为文献[4]中的块稀疏字典方法成像,图9为文献[5]中基于稀疏贝叶斯学习的块间耦合方法成像,图10为本文方法成像。可以看出,本文方法所呈墙体轮廓较为明显,不仅分离出了内部目标与墙角,使之减少对墙体成像的影响,也滤除了背景噪声,相较于文献[4]和文献[5]中的方法在成像质量上有所提高。

图8 文献[4]的方法

图9 文献[5]的方法
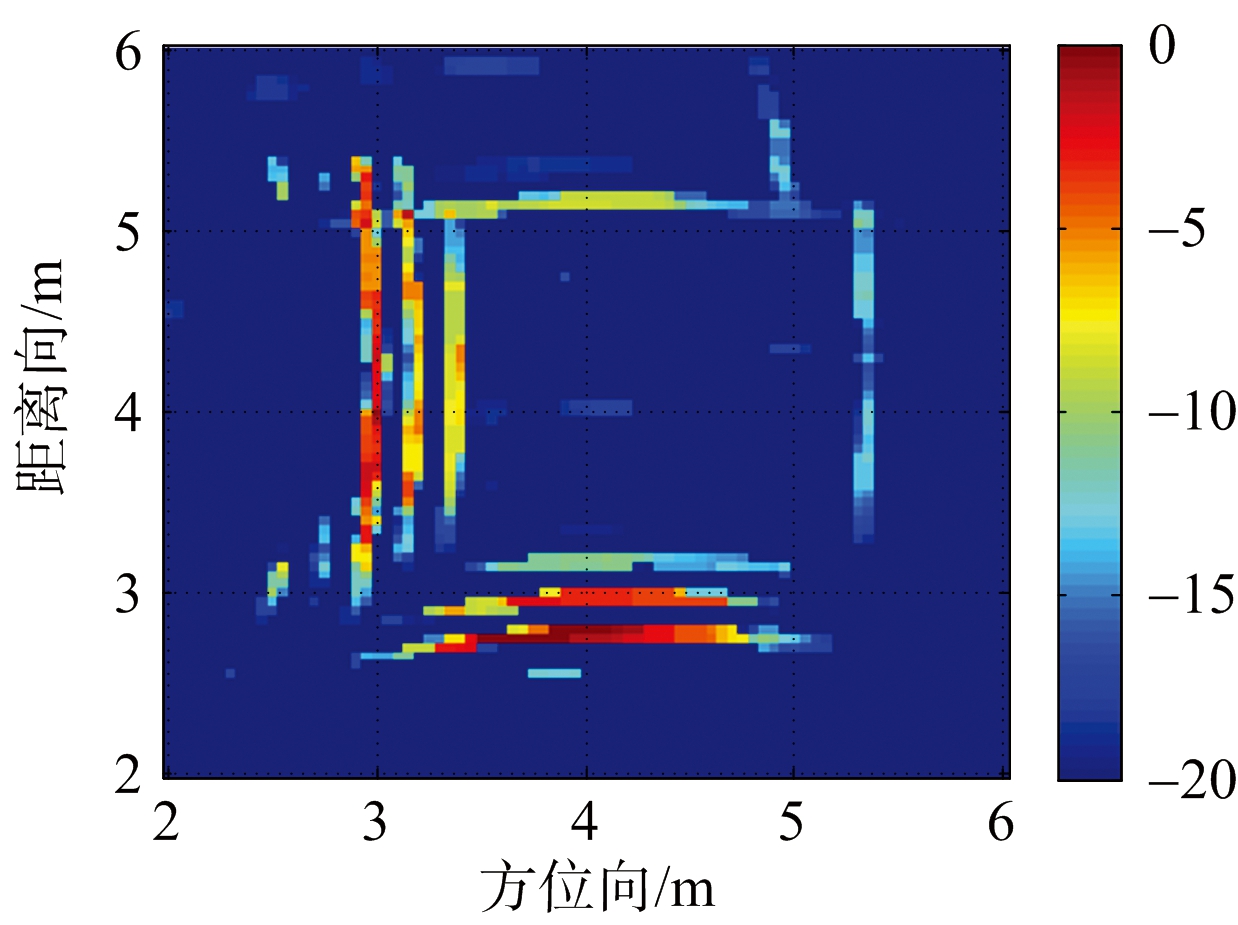
图10 本文方法
5 结束语
提出的基于低秩稀疏分解的TV约束下的稀疏成像方法有效将建筑物内部目标和墙角与墙体分离,保留墙体边缘轮廓的同时滤除了杂波噪声,解决了复杂场景的建筑物内部目标和墙角对墙体成像的影响。仿真结果和实测结果表明,所形成的建筑物布局全景图边缘轮廓较为清晰,成像质量比文献[4]和文献[5]明显提高,为下一步实现建筑物内部目标成像作重要参照。
[1] WANG Xueqian, LI Gang,LIU Yu, et al.Two-Level Block Matching Pursuit for Polarimetric Through-Wall Radar Imaging[J].IEEE Trans on Geoscience and Remote Sensing, 2018,56(3):1533-1545.
[2] QIU Lei,JIN Tian,HE Yuan, et al.Sparse and Low-Rank Matrix Decomposition Based Micro-Motion Target Indication in Through-the-Wall Radar[J].Electronics Letters, 2017,53(3):191-192.
[3] JIA Yong, CUI Guolong, KONG Lingjiang, et al.Multichannel and Multiview Imaging Approach to Building Layout Determination of Through-Wall Radar[J].IEEE Geoscience and Remote Sensing Letters, 2014, 11(5):970-974.
[4] LAGUNAS E, AMIN M G, AHMAD F, et al. Determining Building Interior Structures Using Compressive Sensing[J].Journal of Electronic Imaging, 2013, 22(2): 1-28.
[5] 晋良念,冯飞,刘庆华,等.利用块间耦合稀疏贝叶斯学习的建筑物布局成像方法[J].电子与信息学报,2018,40(4):853-859.
[6] TANG V H, BOUZERDOUM A,PHUNG S L.Multipolization Through-Wall Radar Imaging Using Low-Rank and Jointly-Sparse Representations[J].IEEE Trans on Image Processing, 2018, 27(4):1763-1776.
[7] TANG V H, BOUZERDOUM A,PHUNG S L, et al.Radar Imaging of Stationary Indoor Targets Using Joint Low-Rank and Sparsity Constraints[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, Shanghai:IEEE, 2016:1412-1416.
[8] LAGUNAS E, AMIN M G, AHMAD F, et al. Joint Wall Mitigation and Compressive Sensing for Indoor Image Reconstruction[J]. IEEE Trans on Geoscience and Remote Sensing,2013, 51(2):891-906.
[9] HANDA H, MANSOUR H, LIU D H, et al. Extended Target Localization with Total-Variation Denoising in Through-the-Wall-Imaging[C]∥IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP),Cancun, Mexico:IEEE,2015:445-448.
[10] YANG Junfeng, ZHANG Yin, YIN Wotao.A Fast Alternating Direction Method for TVL1-L2 Signal Reconstruction from Partial Fourier Data[J].IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2):288-297.
[11] MUQAIBEL A H. Efficient Reformulation of Image Reconstruction with Compressive Sensing[J].AEU-International Journal of Electronics and Communications, 2017,76:46-51.
[12] 晋良念,申文婷,钱玉彬,等.组合字典下超宽带穿墙雷达自适应稀疏成像方法[J].电子与信息学报,2016, 38(5):1047-1054.


