0 引言
与单站雷达相比，分布式雷达的空间分集特性可以有效克服目标雷达散射截面(Radar Cross Section,RCS)起伏对检测性能的影响，使之具有更好的检测能力和目标分辨能力[1-2]。但是这种空间分集特性获得的增益不足以提升微弱目标的信噪比，为提高分布式雷达场景下微弱目标的检测能力，通常使用检测前跟踪(Track Before Detect,TBD)技术。TBD技术通过对多帧信息联合处理实现微弱目标能量累积，并在多帧累积后同时完成目标检测与跟踪，是一种探测微弱目标的有效手段。
目前，基于TBD技术的分布式雷达微弱目标检测与跟踪已取得一定的成果。2009年，龚亚信等人研究了基于粒子滤波(Particle Filter,PF)的多传感器检测前跟踪算法，确定了多传感器融合粒子权重与单传感器局部粒子权重间的关系[3]。2012年空军雷达学院的冯讯等人将PF算法用于多输入多输出(Multiple Input Multiple Output，MIMO)雷达目标检测，解决了MIMO雷达在非线性非高斯杂波条件下无法得到似然比检测统计量的问题，但只用了单帧信息用于目标检测，没有充分利用接收信息中包含的有用信息，增益提升有限[4]。2016年，Kong等人在分布式雷达系统下研究了基于动态规划(Dynamic Programming,DP)的检测前跟踪算法，给出多帧联合似然比表达式，利用目标多帧信息，获得了较好的检测性能和较高的跟踪精度，但DP算法的适用范围有限[5]。
粒子滤波非参数化的特点在非线性非高斯系统中表现出的优越性，决定了它的适用范围非常广泛，本文主要研究分布式雷达场景下基于粒子滤波的目标检测与跟踪。在单帧内，利用分布式雷达的空间分集技术在空域上增强信号；多帧累积时，利用基于粒子滤波的检测前跟踪技术进行时域非相干累积，以提升分布式雷达系统的检测能力。针对粒子滤波固有的粒子样本贫化问题[6]，提出将一种多簇聚类粒子滤波算法用于分布式雷达目标检测，该算法利用聚类思想将粒子划分为多个粒子簇，然后对每个簇的粒子进行移动，使之朝着最大联合似然区域扩散，从而加快收敛速度，提高目标检测与跟踪能力。仿真结果表明，在分布式雷达目标检测跟踪中，多簇聚类粒子滤波算法比传统的粗化策略粒子滤波算法具有更高的跟踪精度，在相同虚警概率条件下，能更快地达到检测门限，从而更早地检测到目标。
1 分布式雷达检测前跟踪
1.1 分布式雷达信号模型
假设分布式雷达系统中包含M个发射站和L个接收站，多个雷达接收站从不同方向对探测区域进行监测。各发射站发射相互正交的信号，即满足条件：
(1)
式中，Si(t)，Sj(t)分别为第i个发射站和第j个发射站归一化的发射信号。假设多个雷达接收站距离足够远，目标回波信号满足不相关条件，则第l个雷达接收站的接收信号为
Zl(t)=
ej2πfm,l(t-τm,l)+φm,l+νl(t)
(2)
式中，am,l为第m个发射站到第l个接收站的目标反射信号强度，νl(t)为第l个雷达接收站的观测噪声，τm,l和fm,l分别为第m个发射站到第l个接收站的反射信号时延与多普勒频偏，φm,l为目标反射信号随机相移。如图1所示，v为目标速度矢量，Rl为目标到第l个雷达接收站的距离，em和el分别为第m个发射站到目标的单位方向向量和目标到第l个接收站的单位方向向量。
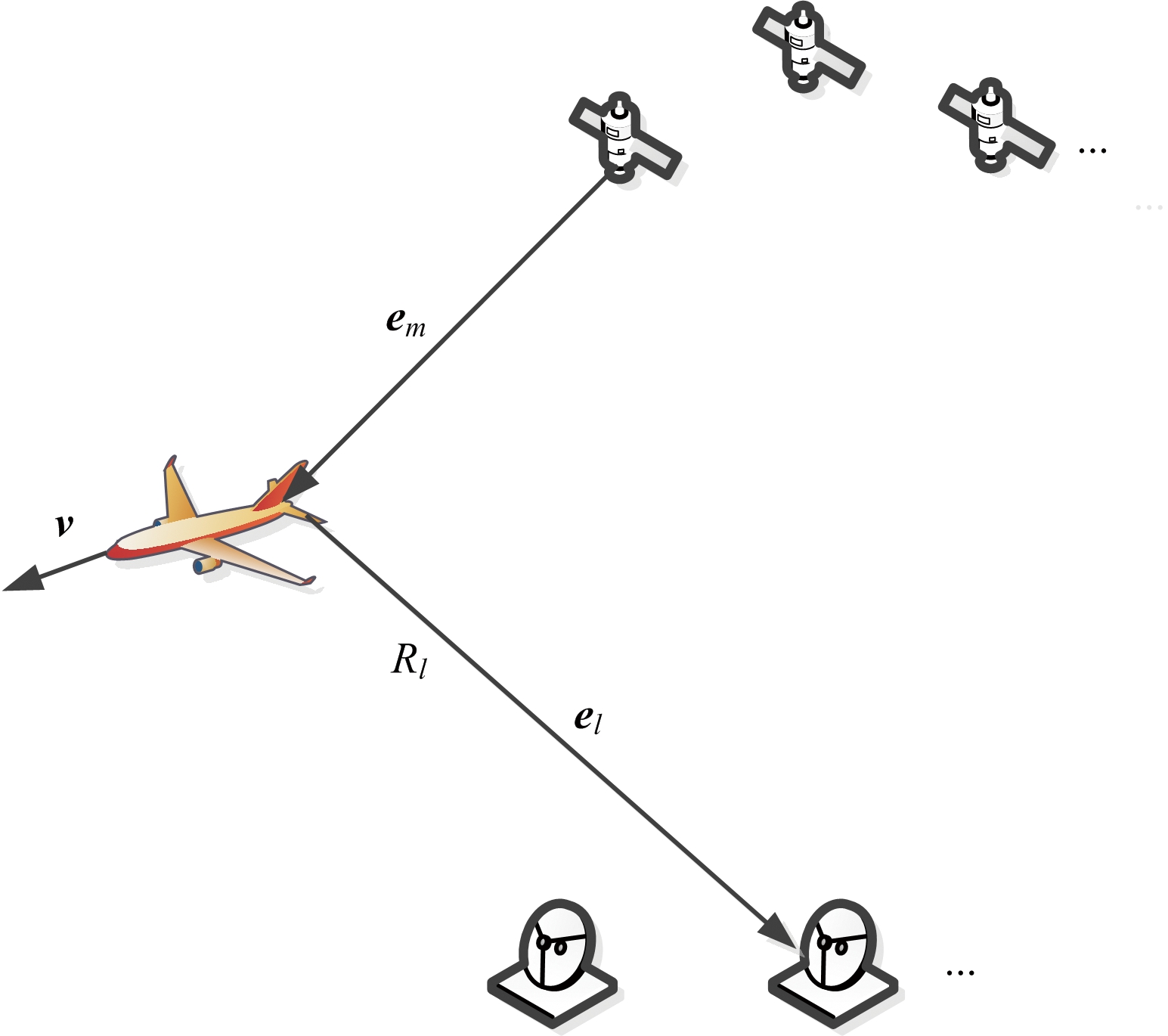
图1 发射站、目标与接收站位置关系
则时延和多普勒频偏计算公式如下：
τm,l=Rl(1-em·el)/c
(3)
fm,l=fc·(v·el-v·em)/c
(4)
在n时刻，将每个雷达接收信号分别与M个发射信号进行匹配滤波和相干累积后，可以得到M·L个空间分集通道的独立观测：
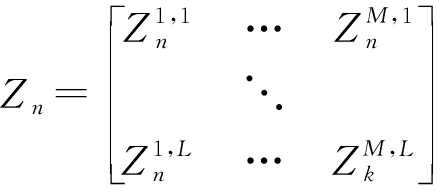
(5)
1.2 粗化策略PF算法
粒子滤波通过非参数化的蒙特卡洛方法实现递推贝叶斯滤波，根据最优贝叶斯理论，目标跟踪中的状态估计问题是根据已有观测数据Z1:n递推地计算出当前状态Xn的可信度，主要由预测方程和更新方程组成：
p(Xn|Z1:n-1)=
(6)
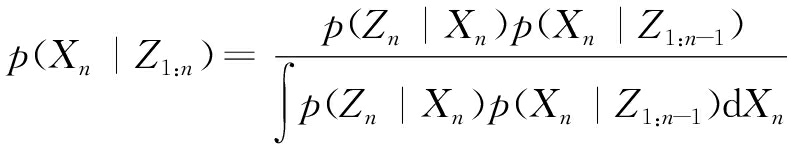
(7)
式中，p(Xn-1|Z1:n-1)为先验概率，p(Xn|Xn-1)为状态转移函数，p(Zn|Xn)为似然函数。对非线性非高斯模型，更新方程中的高维积分问题无法直接计算，需要利用蒙特卡洛方法从一个已知的提议分布q(Xn|Xn-1,Z1:n)中采样粒子进行离散化，将积分计算转化为求和计算，近似为
(8)
式中，Np为采样粒子数，δ(·)为狄拉克函数，
经序贯重要性采样(Sequential Importance Sampling, SIS)后，得到粒子权重的递推式：
(9)
SIS理论上给出了状态估计的递推公式，但随着时间的推移，存在着粒子权值退化问题，目前改善该问题的主流方法是重采样[7]。重采样解决了权值退化问题，但又引入了粒子样本贫化问题，导致粒子的多样性匮乏，影响估计性能。传统的粗化策略PF算法通过扩大过程噪声使粒子扩散，一部分粒子被重新分配到高似然区域。粗化策略PF粒子扩散过程为
(10)
传统的粗化策略使得粒子样本贫化问题得到改善，但由于扩散过程没有明确的方向，扩散过程具有盲目性，算法的效率不高。
1.3 基于PF算法的分布式雷达似然比检测
分布式雷达系统目标检测问题可以表示为二元假设检验问题：
有目标
(11)
无目标
(12)
式中，
和
分别为n时刻第m个发射信号
到第l个接收站的回波信号和噪声经匹配滤波和相干累积后的信号部分和噪声部分。则分布式雷达的单帧联合似然比为
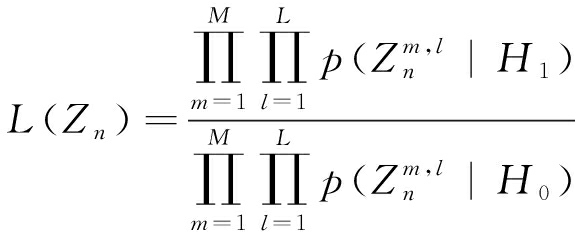
(13)
其中H1和H0条件下的似然分别为
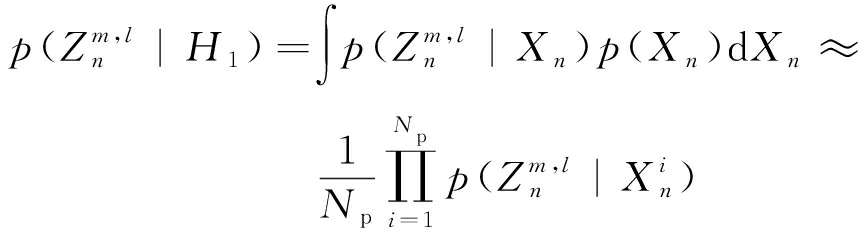
(14)
(15)
式中，
为噪声部分的概率分布。则n时刻分布式雷达联合似然比可以表示为
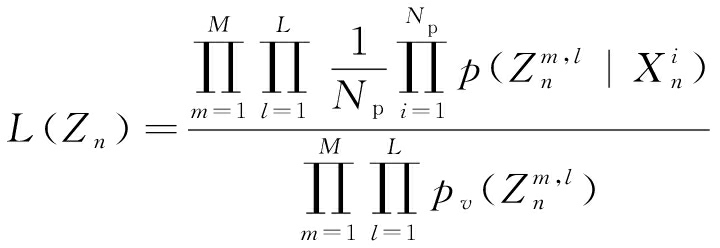
(16)
以上即单帧内分布式雷达的联合似然比表达式。检测前跟踪算法通过多帧累积提升微弱信号的信噪比。则多帧累积的联合似然比检测为
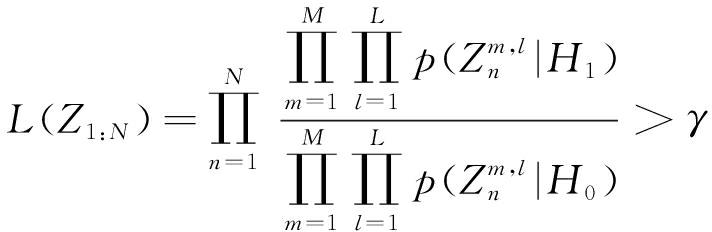
(17)
时判为H1，否则判为H0。其中γ由给定的虚警概率得到。实际操作中，通常对式(17)取对数处理，利用对数联合似然比进行检测判决。
2 多簇聚类PF算法
基于PF的分布式雷达检测前跟踪算法结合了分布式雷达的空间分集特性和时域非相干累积增益的优势，给微弱目标的探测提供了解决手段。但PF算法中粒子样本贫化问题的存在，仍然对检测性能有一定的影响，为进一步提高分布式雷达的检测跟踪能力，本文提出将一种多簇聚类PF算法用于分布式雷达目标检测与跟踪。
首先n时刻最大联合似然粒子状态定义为
argmax(p(Zn|Xn))=
(18)
然后对n时刻所有粒子使用改进的K-Means算法[8]进行聚类分析，粒子被划分为多个粒子簇。定义每个簇中的粒子状态均值为
(19)
聚类分析后共得到K个粒子簇，被划分到第k个簇的粒子共Nk个，满足
(20)
因此，可以得到n时刻每个簇的状态均值到最大联合似然粒子状态的向量差：
(21)
多簇聚类PF算法对每个粒子簇中粒子按如下规则进行移动：
(22)
多簇聚类PF算法利用粒子簇状态均值到最大联合似然粒子状态的向量差，将粒子朝着高联合似然区域移动，加快了粒子收敛速度。基于多簇聚类PF的分布式雷达检测前跟踪具体实现步骤如下：
Step1 初始化，0时刻在状态空间均匀采样产生Np个粒子；
Step2 n>0时刻，根据状态转移函数对粒子进行状态转移，按照式(10)的粗化策略在状态转移阶段同时对粒子进行状态扩散；
Step3 粒子权重计算，根据权重递推公式(9)计算每个粒子的权重信息；
Step4 指引粒子向高联合似然区域移动。对粒子进行聚类分析后，按照式(22)的规则移动粒子，并重新计算粒子的权重信息，计算单帧对数联合似然比；
Step5 重采样，按粒子的归一化权重对状态空间重新采样粒子；
Step6 对对数联合似然比累加，估计n时刻目标的状态信息，令n=n+1，转入Step2直至 n=N；
Step7 多帧累积联合似然比检验。根据虚警概率设定门限，对多帧累积后的对数联合似然比值进行判决完成目标检测。
3 仿真实验
本文针对一个拥有4个发射站、2个接收站的分布式雷达场景，分别利用多簇聚类PF算法和粗化策略PF算法实现检测前跟踪算法，验证多簇聚类PF算法在分布式雷达场景中跟踪性能和检测性能的优越性。图2为分布式雷达场景。
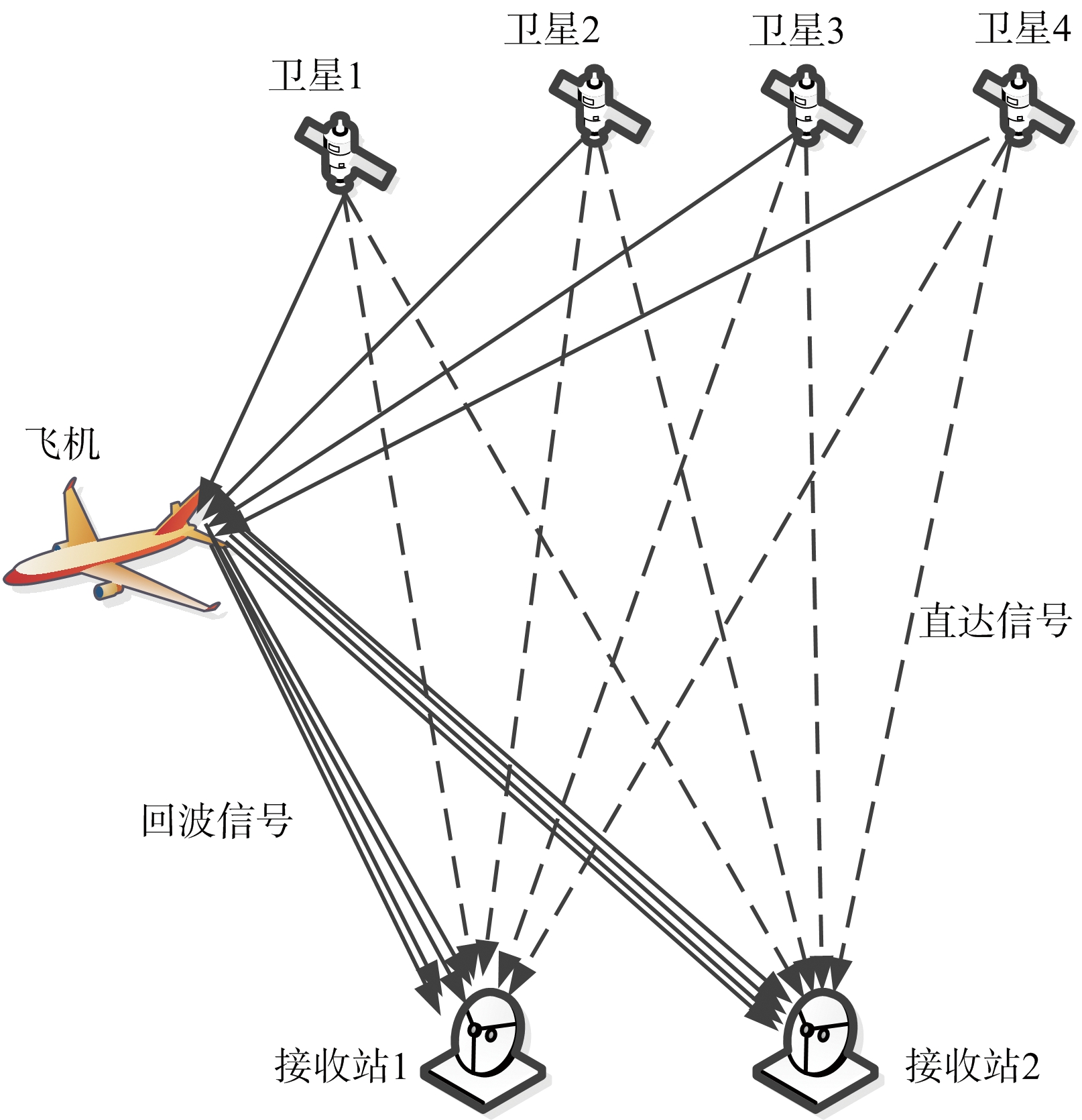
图2 分布式雷达场景
在该场景下，目标为一架均速运动的飞机。目标状态矢量
和
分别为目标在n时刻的二维位置和速度状态。目标的运动模型为
Xn=F·Xn-1+un-1, un-1～N(0,Q)
(23)
式中,F为状态转移矩阵，un-1为过程噪声，满足
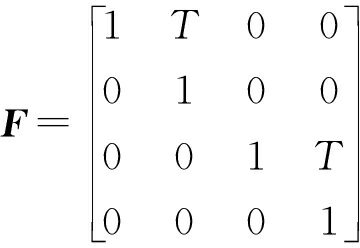
(24)
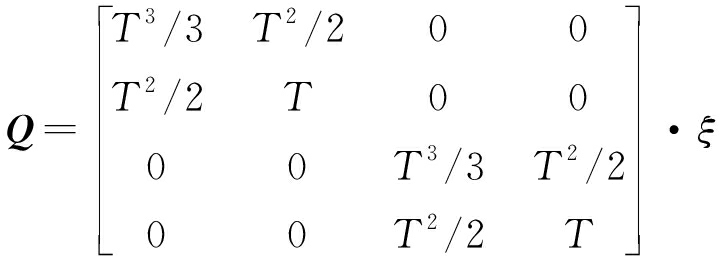
(25)
式中，ξ为噪声抖动强度，T为帧长。仿真中目标初始位置为(-1 000，2 800) m，初始速度为(163，10) m/s。状态空间范围为xn∈(-1 500,1 500)，
以4颗导航卫星信号作为发射信号，卫星信号发射站距离地面很远，认为两个雷达接收站相对于每一颗卫星发射站的方位角和俯仰角近似相等。卫星功率密度为-100 dBm/m2。4颗卫星的方位角为(39.73°，25.69°，-171.17°，-196.68°)，俯仰角为(19.32°，48.10°，36.80°，39.01°)。仿真中两个雷达接收站的位置分别为(-1 000，0)和 (1 000，0)，单位为m。粒子数为10 000，帧长取0.1 s，累积50帧。信号采样频率为20.46 MHz，接收天线增益为40 dB，噪声功率密度为-174 dBm/Hz，噪声抖动强度为500，平均RCS为10 dB，初始聚类中心个数为50个。
采用上述参数分别对多簇聚类PF算法和粗化策略PF算法进行单次仿真，得到的单次跟踪结果如图3所示，图3(a)为目标位置空间跟踪结果，图3(b)为速度空间跟踪结果。
从图3可以看出，跟踪开始的5帧内，两种算法跟踪结果都不理想，但是5帧之后，多簇聚类PF能够很快收敛到真实目标附近，而传统的粗化策略PF收敛速度缓慢，跟踪效果不如多簇聚类PF。
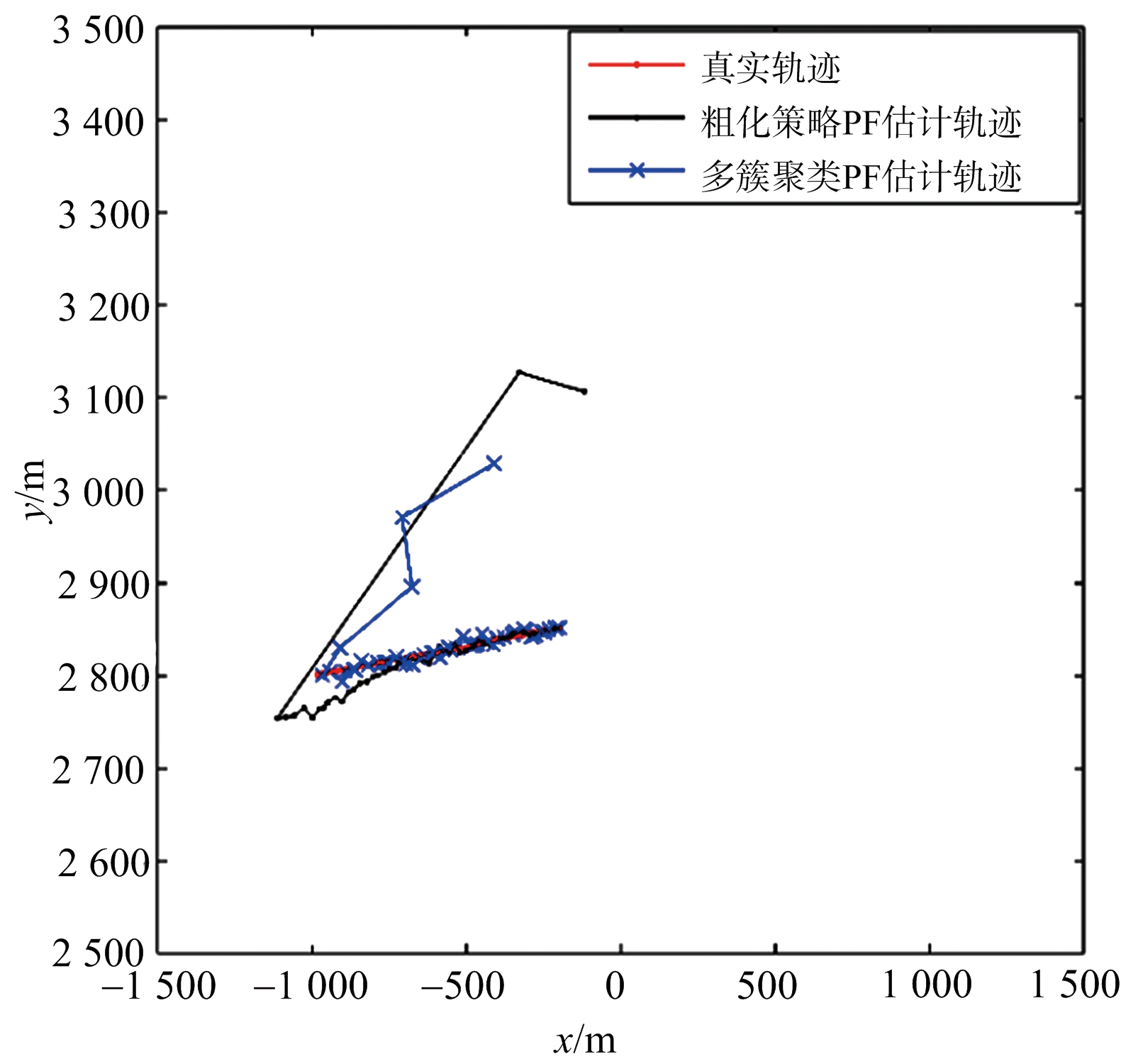
(a) 位置空间跟踪结果
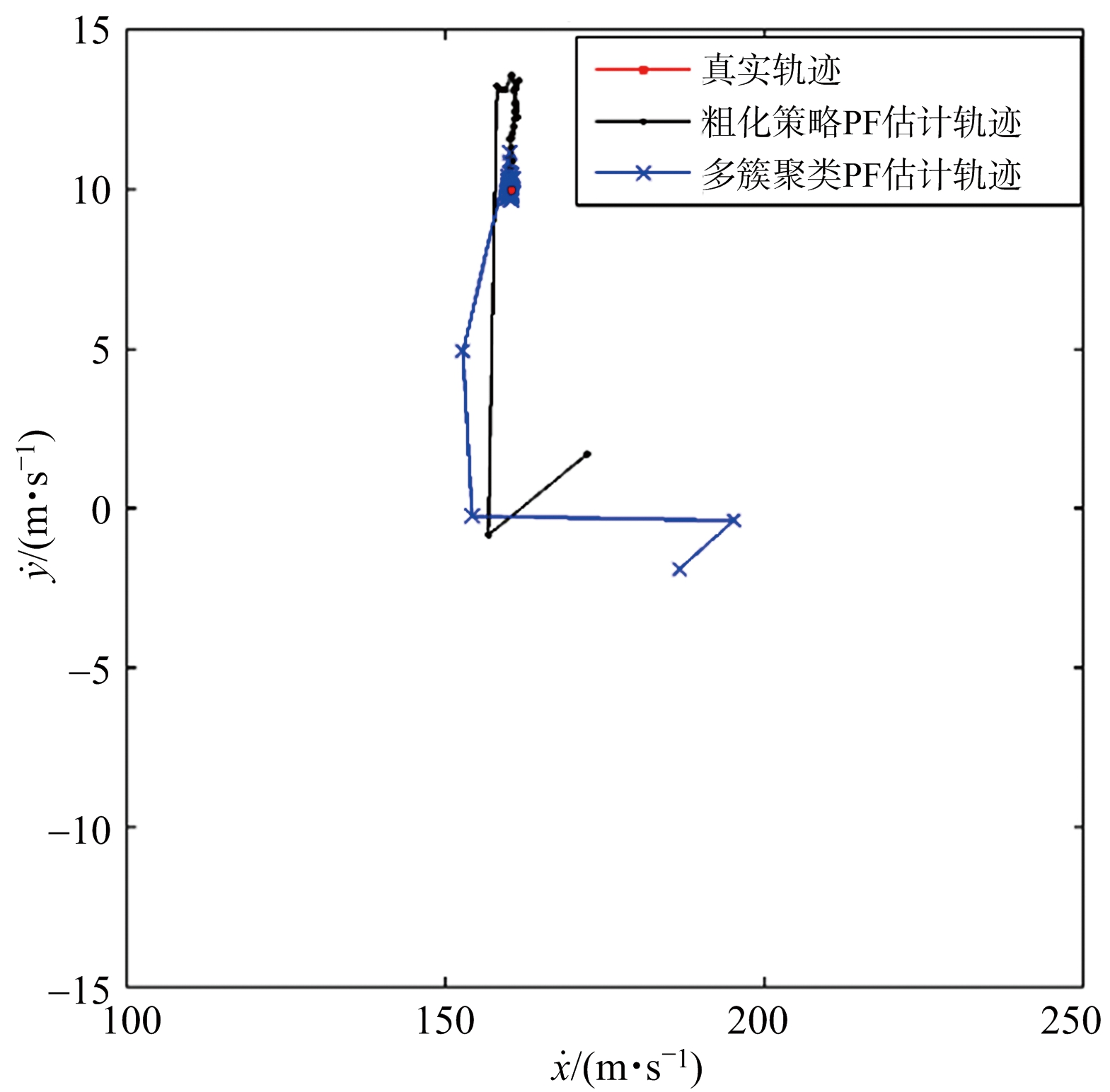
(b) 速度空间跟踪结果
图3 单次仿真目标跟踪结果
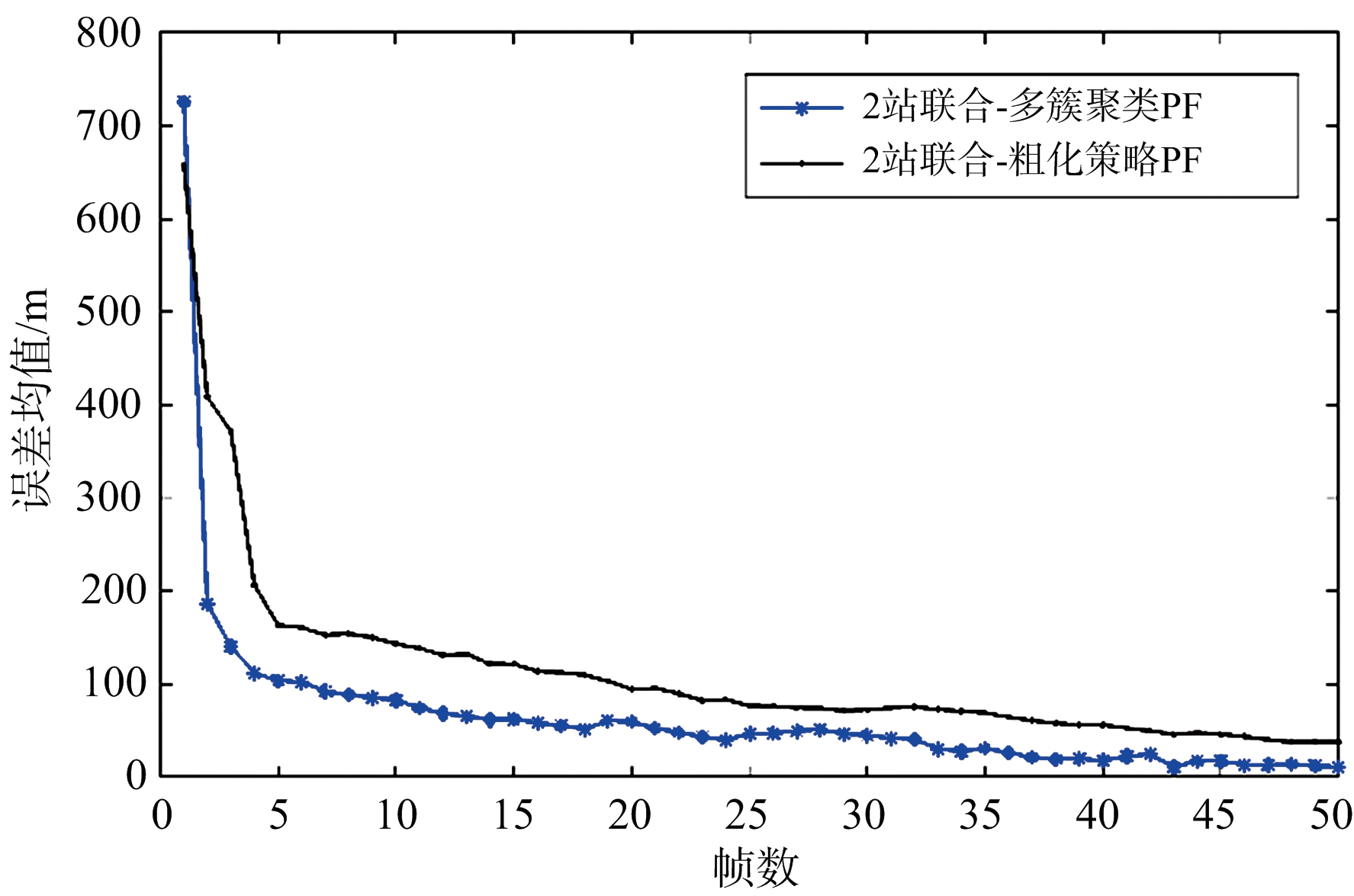
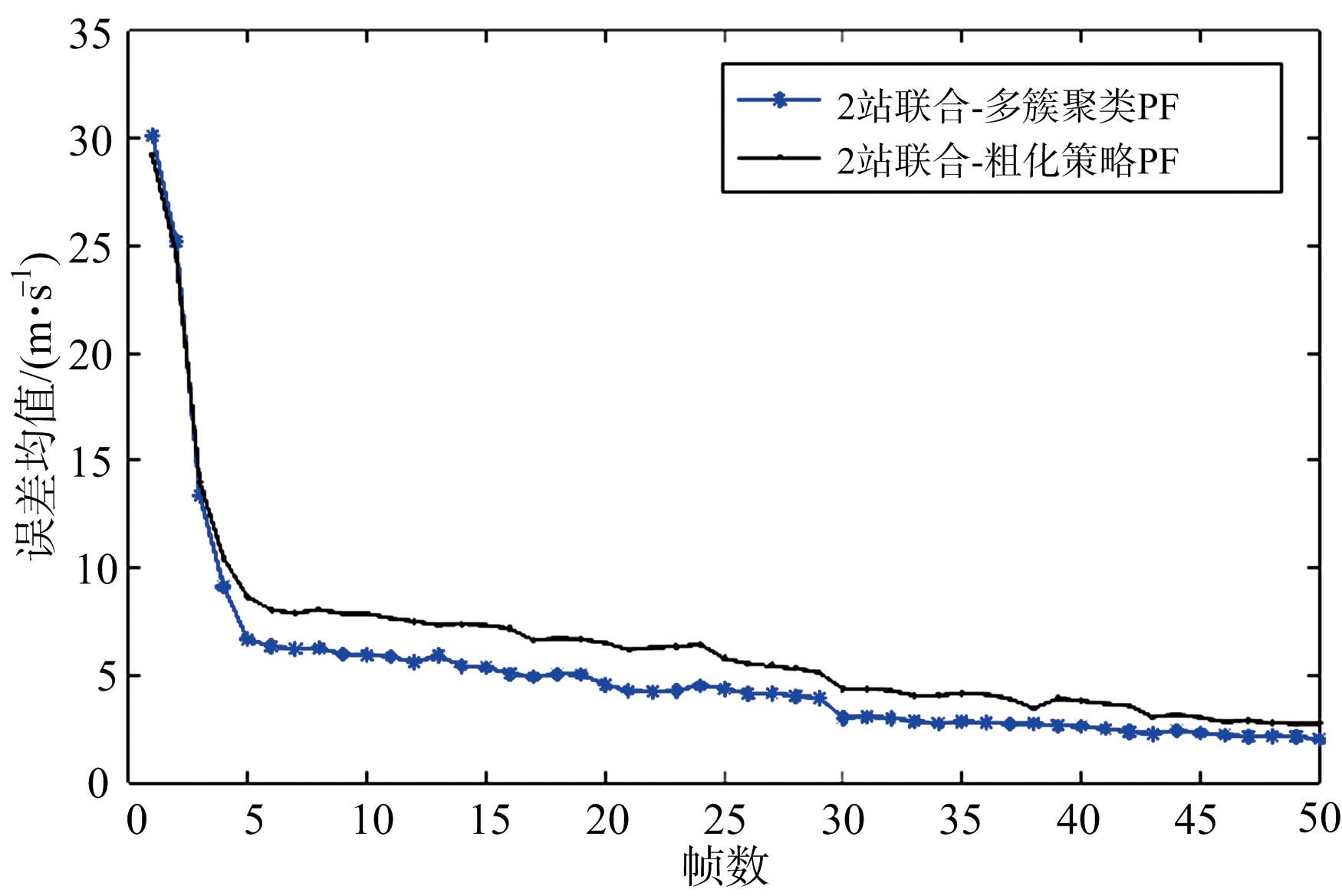
对两种算法分别进行30次独立蒙特卡洛仿真，对得到的跟踪结果进行误差分析。目标状态估计的均方根误差如图4所示，其中位置均方根误差如图4(a)所示，速度均方根误差如图4(b)所示。
从图4可以看出，在分布式雷达目标跟踪中，多簇聚类PF算法相比与传统的粗化策略PF算法具有更高的跟踪精度。从而证明多簇聚类PF算法在改善粒子贫化问题上有较好的效果。
(a) 位置空间均方根误差
(b) 速度空间均方根误差
图4 目标状态估计的均方根误差
多帧联合似然比累积结果如图5所示。从图中可以看出，分布式雷达场景中多簇聚类PF算法对数联合似然比累积速度更快。说明在相同的虚警概率条件下，多簇聚类PF算法能够更快地达到检测门限，更早地检测到目标。图中以粗化策略PF算法累积50帧的对数联合似然比值作为门限，多簇聚类PF算法仅需41.5帧就能达到检测门限，提前0.85 s检测到目标，比传统的粗化策略PF算法在检测时间上缩减了17%，证明多簇聚类PF算法在检测性能上的优越性。
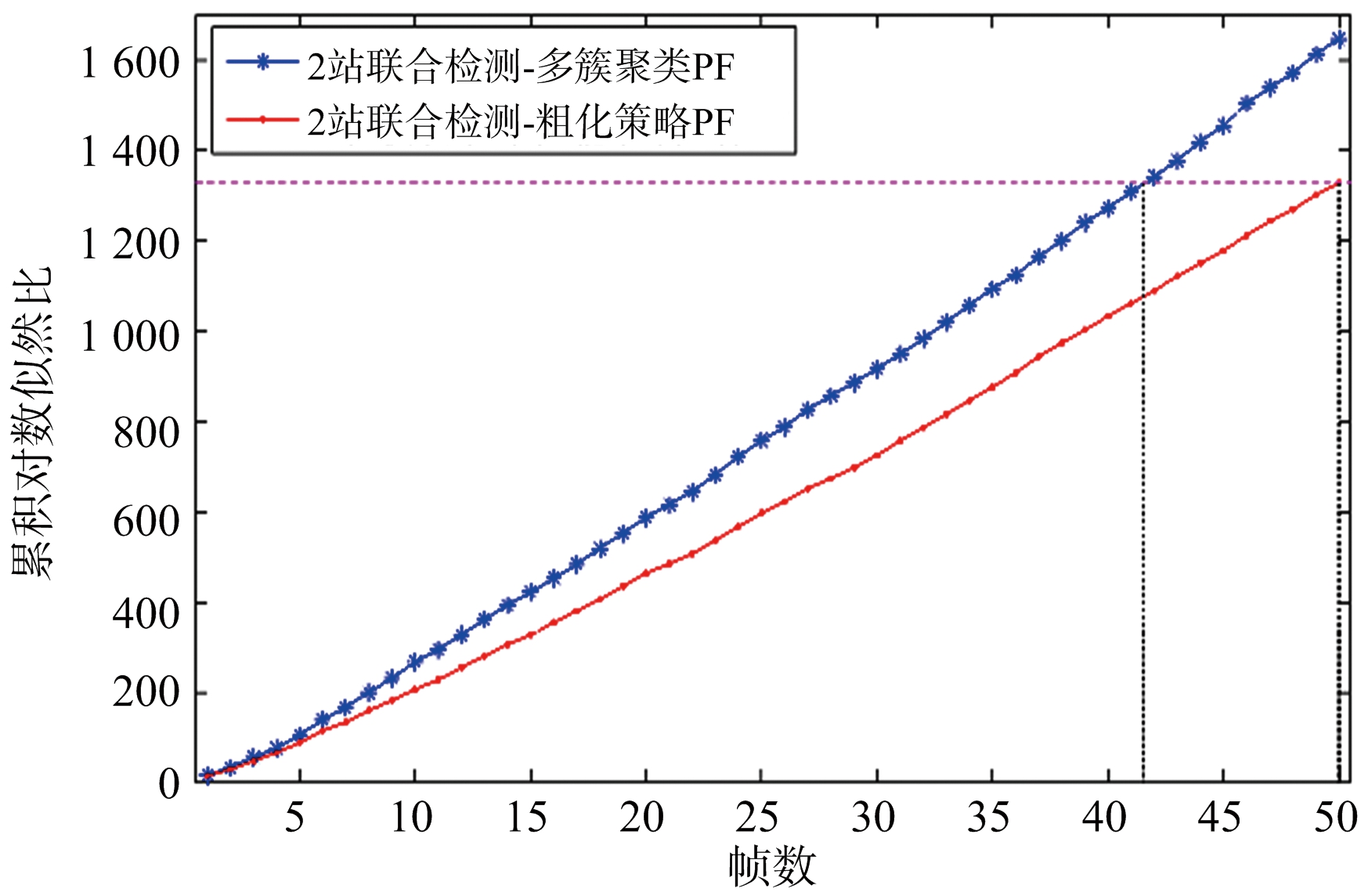
图5 对数联合似然比累积情况
4 结束语
本文主要研究了分布式雷达场景下基于粒子滤波的目标检测与跟踪算法，针对粒子滤波固有的粒子样本贫化问题，提出将一种多簇聚类PF算法用于分布式雷达目标检测与跟踪。该算法通过计算粒子簇状态均值到最大联合似然粒子状态的向量差，将粒子朝着高联合似然区域移动，从而加快了粒子收敛到真实目标的速度，同时也提高了目标的跟踪精度。仿真结果表明，本文所提方法具有更好的检测能力和更高的跟踪精度。
[1] NAZARI MAJD M, RADMARD M, CHITGARHA M M, et al. Diversity-Multiplexing Tradeoff in MIMO Radars[J]. IET Radar, Sonar & Navigation, 2017, 11(4):691-700.
[2] EDRICH M, HOFFMANN F. Transmitter Network Model and Diversity Experiments for a Multiband Passive Radar System[C]∥2017 IEEE Radar Conference, Seattle, WA：IEEE，2017:140-145.
[3] 龚亚信,杨宏文,胡卫东,等.一种改进的分布式弱目标检测前跟踪算法[J].信号处理,2009,25(11):1686-1693.
[4] 冯讯,王首勇,朱晓波.基于粒子滤波的MIMO雷达目标似然比检测方法[J].华中科技大学学报(自然科学版),2012,40(2):85-90.
[5] ZHANG Ziwei, YI Wei, KONG Lingjiang. Target Detection and Localization Using Multi-Frame Information for Noncoherent MIMO Radar[C]∥IET International Radar Conference, Hangzhou, China: IET, 2016.
[6] LI Tiancheng, SUN Shudong, SATTAR T P, et al. Fight Sample Degeneracy and Impoverishment in Particle Filters: A Review of Intelligent Approaches[J]. Expert Systems with Applications, 2014, 41(8):3944-3954.
[7] 于金霞, 刘文静, 汤永利. 粒子滤波重采样算法研究[J]. 微计算机信息, 2010, 26(16):44-45.
[8] 王泾燃,张志宏,张钟浩,等.一种基于传统粗化策略的改进粒子滤波算法[J].工业控制计算机,2018,31(7):76-78.
