0 引言
在现代战争中,以被动导引头为关键部件的反辐射武器成为雷达的主要威胁。近年来,一些新的被动导引头抗干扰技术的出现,使得对抗反辐射武器更加困难[1-2]。随着被动导引头在电磁战场上发挥的作用日益凸显,研究对其的干扰技术对提高雷达电子防御能力显得非常重要。
随着脉冲技术的发展,采用高重频脉冲信号对抗接收机的研究逐渐展开,文献[3]给出了高重频脉冲对雷达接收机的压制式干扰试验效果,初步证明了干扰的有效性。利用高重频脉冲对作为对抗反辐射武器的手段,计算其对导引头的有效压制区对干扰资源配置及战场决策部署具有重要意义,因而,本文首先分析干扰脉冲的作用机理,之后给出了干扰机有效压制区的计算方法,并讨论了决定压制区大小的因素,最终仿真得到了单站及多站干扰时的有效压制区。研究结果对高重频干扰的应用具有参考意义。
1 对被动导引头的干扰机理
1.1 高重频脉冲信号特征
高重频脉冲信号是一种重复频率极高的脉冲信号,脉冲宽度通常为几纳秒至几百纳秒,远小于雷达发射信号的脉冲宽度,具有超宽带的特性。其时域表达式为[4]
(1)
式中,A为脉冲幅度,τ为脉冲宽度,T为脉冲重复周期,N为脉冲数量,rect(·)为矩形函数。对式(1)进行傅里叶变换得到高重频脉冲的频域表达式为
J(f) =![]()
e-jπf(N-1)T
(2)
设PRFj为高重频干扰脉冲重复频率,当A=2 mV,τ=1 ns,N=1 000,PRFj=200 kHz时,高重频脉冲时域波形及频谱如图1所示。

(a) 时域波形
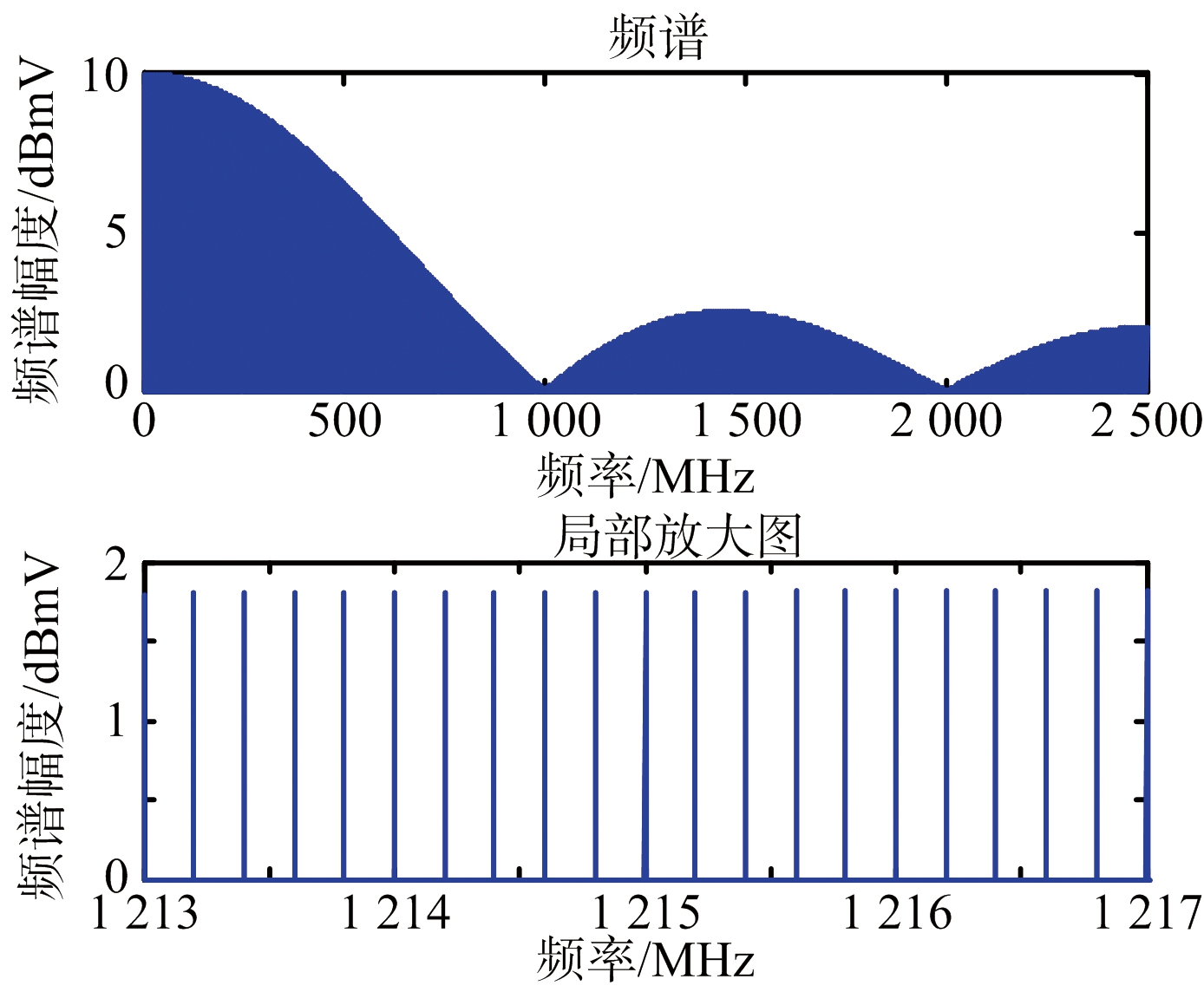
(b) 频谱
图1 高重频脉冲时域波形及频谱图
从图1可以看出,高重频脉冲的频谱由离散谱线组成,相邻谱线间隔为脉冲重复频率,谱线包络同sinc函数,频率覆盖范围极宽。从其独特的信号特征上来看,实施高重频干扰后,其宽频带特性将使干扰信号频域上能够完全覆盖导引头接收频带;脉冲宽度极窄使其可以渡越接收系统的保护电路,使前端模拟器件产生严重的瞬态响应,最终影响信号检测。
1.2 尖峰泄漏效应
干扰脉冲在被导引头天线接收后,首先将进入由限幅器、带通滤波器和放大器组成的微波前端,其作用是对接收信号进行滤波、放大和混频后送给中频组件处理。由于干扰脉冲经过前端带通滤波器后带宽变窄、脉宽变宽、脉冲前后沿变缓,将不再产生明显的瞬态响应,因此高重频脉冲产生的瞬态响应主要来源于限幅器。
对于PIN限幅器而言,其尖峰泄漏效应是造成自身工作特性受损的主要原因[5]。尖峰泄漏效应是指当干扰脉冲重复频率达到兆赫兹级甚至更高时,脉冲宽度将小于限幅器的响应时间(通常为几十纳秒),干扰脉冲将直接通过限幅器进入带通滤波器,即限幅器对干扰脉冲不发挥作用。这会导致干扰脉冲进入后级滤波器时,若脉冲重复周期小于滤波器响应时间,输出相邻脉冲前后沿相互叠加,将产生类噪声信号;当脉冲重复周期大于滤波器响应时间时,由于滤波器输出的干扰谱线频率与雷达信号载频非常接近,当两者频率差倒数接近雷达信号脉宽时,会产生近似噪声调幅干扰的效果。在不考虑后级电路失真影响下,功率足够的干扰脉冲在检波后会压制雷达信号,影响接收机检测。
1.3 压制效果仿真
根据前文分析,分两种情况对限幅器尖峰泄漏效应产生的压制效果进行仿真。
首先分析干扰脉冲重复周期小于滤波器响应时间的情况,此时设雷达信号脉冲宽度τs=11.2 μs,限幅器响应时间tx=10 ns,干扰信号脉宽τj=1 ns。这时限幅器将产生尖峰泄漏效应,设滤波器中心频率对准雷达载频,其响应时间为0.1 μs。当雷达信号功率Pt=500 W,PRFj=50 MHz,Ptj=50 kW时,带通滤波器输出干扰脉冲波形如图2(a)所示,干扰前后检波输出波形如图2(b)所示。
再分析干扰脉冲重复周期大于滤波器响应时间的情况,假设PRFj=0.5 MHz、Ptj=5 MW,其余参数不变,仿真结果如图3所示。

(a) 滤波器输出干扰波形

(b) 干扰前后检波器输出波形
图2 重频为50 MHz的压制干扰效果

(a) 滤波器输出干扰波形

(b) 干扰前后检波器输出波形
图3 重频为0.5 MHz的压制干扰效果
从图2可以看出,干扰脉冲重复频率为50 MHz时,由于脉冲重复周期小于滤波器响应时间,干扰信号滤波后前后沿脉冲叠加,检波后将雷达信号完全压制,已无法完成正常检测。从图3可以看出,干扰脉冲重复频率为0.5 MHz时,脉冲重复周期大于滤波器响应时间,干扰脉冲经过滤波器后相邻脉冲没有叠加,但由于噪声调幅干扰起遮盖作用的主要是旁频成分[6],干扰功率足够大时同样压制了雷达信号。
对比图2、图3的仿真结果可以发现,当尖峰泄漏效应发生时,即便干扰脉冲重复频率不同会导致不同的作用机理,但是足够功率时,干扰脉冲形成的类噪声信号会有效压制雷达信号。
2 有效压制区计算
在计算干扰机对导引头的有效压制区之前,首先必须确定干扰机的部署位置。而布阵的首要前提就是不能影响雷达的正常工作,此外,还要保证干扰机处于导引头视场范围,保证干扰脉冲能始终被导引头接收。导引头、雷达和干扰机三者的空间位置关系如图4所示。

图4 导引头、雷达、干扰机空间位置图
2.1 布阵临界距离
由于雷达普遍采用恒虚警检测技术,当虚警概率为Pfa时,检测概率Pd与检测信噪比r存在如下关系[7] :

(3)
式中,![]() 为信噪比,
为信噪比,![]() 为信号功率,
为信号功率,![]() 为噪声功率,I0(·)表示第一类一阶贝塞尔函数。在虚警概率一定的条件下,为保证一定的检测概率,接收机必须有足够高的检测信噪比。本文以此作为雷达正常工作的评判标准,并利用信噪比推算出干扰机与雷达的临界距离值,从而确定其部署位置。下面计算接收机检测信噪比。
为噪声功率,I0(·)表示第一类一阶贝塞尔函数。在虚警概率一定的条件下,为保证一定的检测概率,接收机必须有足够高的检测信噪比。本文以此作为雷达正常工作的评判标准,并利用信噪比推算出干扰机与雷达的临界距离值,从而确定其部署位置。下面计算接收机检测信噪比。
典型雷达接收机组成原理框图如图5所示,雷达接收到来自探测目标的回波信号功率为
(4)
式中,Pt为雷达发射功率,Gt为雷达天线增益,Rur为雷达与无人机之间的距离,σu为目标的雷达散射截面积,λ为雷达信号波长,Lur为信号传输过程中的路径总损耗。

图5 典型雷达接收机组成原理框图
将N部干扰机等间隔地部署在以雷达为圆心,Rjr为半径的同心圆上,且每部干扰机的参数设置相同。为最大限度减少对雷达的影响,应使干扰脉冲从副瓣进入,则雷达接收到的干扰功率为
(5)
式中,Ptj为干扰机发射功率,Gtj为干扰天线增益,Grj为雷达天线副瓣增益,Rjr为各干扰机与雷达之间的距离,γ为极化损耗因子,Br为雷达接收机带宽,Bj为干扰信号的有效频宽,其大小为[8]
Bj=2π/Pwj
(6)
由于前端滤波器带宽远小于干扰脉冲带宽,故近似认为落入通频带内的干扰谱线强度相等,均为滤波器中心频率对应的干扰谱线强度,则前端滤波器输出干扰功率为
(7)
式中,Bf为前端带通滤波器带宽,f0为滤波器中心频率,P(f0)为f0对应干扰谱线的功率,大小为

(8)
式中,JB(f0)表示带通滤波器输出的频率为f0的干扰谱线强度,大小为
JB(f0)=H(f0)J(f0)
(9)
式中,H(f)为带通滤波器传输特性,理想情况下有
(10)
式中,f1,f2为带通滤波器的起始频率和截止频率,即Bf=f1-f2。
干扰脉冲通过低噪声放大器时,还将产生三阶互调分量,其功率大小为
PJ2=3(PJ1·G)-2Q3
(11)
式中,G为放大器增益,Q3为放大器的三阶截交点,通常在放大器的技术指标中给定。
假设雷达接收机前端能确保不失真地传输回波信号,则中放输出的回波信号功率可近似为G·Pur。采用平方律检波,检波后输出功率为
(12)
式中,Kd为检波系数。
将干扰脉冲产生的类噪声信号近似为射频噪声,则检波器输出的干扰功率为[9]
(13)
式中,BI为中频滤波器带宽,PJ3是直接落入接收机中频通带的频率分量产生的干扰功率,其大小为
(14)
最后,截获信号(含回波信号和干扰脉冲)经过视频放大器时,将其视为线性系统,并考虑接收机热噪声,则接收机输出信噪比为
(15)
式中,PN0为接收机内部噪声功率,其大小为
PN0=kT0FBI
(16)
式中,k为玻耳兹曼常数,T0为接收机温度,F为噪声系数。
此外,雷达检测前还要进行脉冲压缩及相参积累等处理以改善信噪比,故最终接收机检测信噪比为
(17)
式中,D为脉冲压缩系数,I(n)为视频积累的信噪比改善因子,通常![]() 综上,即可在给定信噪比时得到干扰机与雷达的临界距离。
综上,即可在给定信噪比时得到干扰机与雷达的临界距离。
2.2 有效压制区计算
根据高重频脉冲的作用机理,依照功率准则评估其干扰效果,并采用压制系数Kj评估压制效果。压制系数Kj表示对导引头实施有效干扰(搜索状态下是指发现概率Pd下降到10%以下)时,接收机输入端所需的最小干信比[10],即
(18)
式中,Pj和Ps分别为导引头接收到的干扰功率和信号功率。对于干扰机而言,要有效干扰被动导引头,必须满足
(19)
通常,采用噪声信号对雷达导引头实施压制式干扰式要求压制系数Kj≥10[11],由于高重频干扰形成的并非完全意义上的高斯噪声,其压制效果较理想噪声存在差距,因此本文在评估干扰效果时要求Kj≥30。
导引头接收到的雷达信号功率为
(20)
式中,Gs为导引头接收天线增益,Rsr为雷达与导引头之间的距离,Lsr为信号传输过程中的路径总损耗。
导引头接收到的干扰信号功率为
(21)
式中,i=1,2,…,N,Prji为导引头收到的单部干扰机的干扰功率,其大小为
(22)
式中,Rji为导引头与单部干扰机之间的距离,Brs为导引头的接收机带宽,Ljr为信号的传输损耗。
3 仿真验证
3.1 仿真条件
在以雷达为原点的空间直角坐标系下,则雷达坐标为R(0,0,0),设导引头坐标为S(xs,ys,zs),干扰机坐标为J(xj,yj,0)。本文假设干扰脉冲始终能被导引头接收,各干扰波束对准导引头来袭方向。
仿真中各参数设置如下:雷达载频f=1 215 MHz,Pt=55 kW,Gt=30 dB,Grj=-10 dB,PRI= 2 000 μs,Br=100 MHz;以作战飞机为目标,设雷达对其探测距离为300 km,σ=2 m2;干扰机天线采用垂直极化,方向图用高斯函数表示,主波束宽度为60°,Gtj=35 dB;导引头高度为zs=3 000 m,天线采用圆极化,Gs=3 dB,放大器Q3=18 dBmW,G=18 dB;带通滤波器参数:fL=645 MHz,fH=655 MHz,k=1.38×10-23 J/K,T0=290 K,F=12 dB,Lsr=Lur=Ljr=15 dB,γ=30 dB。
3.2 单站干扰的压制区
根据式(3)可绘制不同虚警概率下接收机的检测特性曲线如图6所示。由图5可以看出,为保证雷达在虚警概率低于10-6的情况下检测概率大于0.8,接收机检测信噪比必须大于5.5 dB。

图6 接收机检测特性
当干扰脉冲功率为10 kW,重频为400 kHz,脉宽为20 ns时,计算出不同数量的干扰机与在部署时雷达的临界距离及部署距离如表1所示。
表1 干扰机部署距离

N/部临界距离/km部署距离/km114.715220.821325.526429.530
根据2.2节所述模型,计算单部干扰机情况下的有效压制区如图7所示。
由图7可以看出,压制区集中于导引头波束所指方向,距离雷达最近约为4 km,且压制区域关于干扰机与雷达连线对称。为分析不同干扰参数下有效压制区的变化情况,分别改变干扰机功率、重频和脉宽,观察有效压制区变化,结果如图8所示。

图7 有效压制区

(a) 干扰功率变为5 kW

(b) 干扰重频变为200 kHz

(c) 干扰脉宽变为10 ns
图8 改变干扰参数后的有效压制区
将图8与图7进行对比可以看出,当干扰机功率、重频和脉宽分别减小后,有效压制区域缩小,这是由于导引头收到的干扰脉冲平均功率有所减小而导致的。同时,当减小干扰脉冲参数时,干扰机与雷达的临界距离也相应减小。
3.3 多站协同时的压制区
根据表1所示的不同数量干扰机时的部署临界距离值,增加干扰机数量,其余干扰参数不变,得到有效压制区如图9所示。

(a) N=2

(b) N=3

(c) N=4
图9 不同数量干扰机时的有效压制区
从图9可以看出,随着干扰机数量的增加,对导引头的有效压制区在逐渐扩大,雷达暴露区逐渐减小,压制区仍主要集中于干扰机波束所指方向。当2部或3部干扰机协同干扰时,仅在雷达周围约13 km或26 km范围内具备全方位压制能力,仍存在较大面积的暴露区,当4部干扰机协同干扰时,在雷达周围约100 km范围内实现了对雷达全方位的有效保护。由此可见,多部干扰机的压制效果更理想,但必须以不影响雷达的正常检测为前提。
4 结束语
本文从分析高重频脉冲的信号特征出发,验证了其对导引头产生的压制效果,接着考虑布阵时干扰机与雷达的电磁兼容问题,以此计算干扰机部署时与雷达的临界距离,最终给出了有效压制区的计算方法。结果表明,干扰机可在反辐射武器来袭方向形成有效压制区,压制区的大小与干扰参数和干扰机数量等有关。从仿真结果看,单部干扰机还不足以对雷达实施全方位的有效保护,在干扰资源充足、安全系数足够高的条件下,增大干扰机数量将达到更好的效果。
[1] 晁淑媛,邓磊,马亮,等.全极化雷达导引头抗干扰技术[J].制导与引信,2016,37(3):1-7.
[2] 陈志坤,乔晓林,李风从.基于极化波束形成的相控阵雷达导引头抗干扰技术研究[J].航空兵器,2016(6):16-20.
[3] 孙龙祥,羌洪发.高重频脉冲干扰技术探索[J].中国电子科学研究院学报,2006,1(2):147-151.
[4] 赵宇姣.基于高重频超宽带脉冲的雷达干扰技术研究[D].成都:电子科技大学,2015.
[5] 汪海洋,李家胤,周翼鸿,等.PIN限幅器PSpice模拟与实验研究[J].强激光与粒子束,2006,18(1):88-92.
[6] 邵国培.电子对抗作战效能分析[M].北京:解放军出版社,1998:86-87.
[7] 林象平.雷达对抗原理[M].西安:西安西北电讯工程学院出版社,1985:244-245.
[8] 曾禹村,张宝俊,沈庭芝,等. 信号与系统[M].3版.北京:北京理工大学出版社, 2010:119-120.
[9] 赵国庆.雷达对抗原理[M].西安:西安电子科技大学出版社,1999:128-131.
[10] 刘家祺,欧阳中辉,王董静.被动雷达导引头抗干扰性能评估[J].科学技术与工程,2013,13(3):721-725.
[11] 孟跃宇,吴华,程嗣怡,等.对雷达导引头干扰效能多级模糊综合评估[J].火力与指挥控制,2015,40(11):58-61.
