0 引言
OFDM信号波形具备波形捷变、抗干扰、低截获的性能优势，同时有应用于雷达通信一体化、分布式一体化电子信息系统等新体制雷达的潜力，具有广阔的应用前景，是现阶段各国关于雷达波形的研究热点之一。但同时，OFDM信号波形在实际应用上存在着两大主要缺陷[1]：1)发射波形的包络峰均比(PMEPR)较高，导致射频放大器功率效率低。OFDM信号包络是时变的，由于雷达发射机的功率放大器一般都不是线性的，且其动态范围有限，当 OFDM 信号这种变化范围较大的信号通过非线性部件(例如进入放大器的非线性区域时)，信号会产生非线性失真，产生谐波，造成较明显的频谱扩展干扰以及带内信号畸变，从而导致整个雷达系统性能的下降，而且同时还会增加 A/D 和 D/A 转换器的复杂度并降低它们的准确性。2)对OFDM的模糊函数研究表明，大多数OFDM 雷达信号具有图钉状模糊函数，这就意味着 OFDM 雷达同时具备距离高分辨和多普勒高分辨，不存在距离多普勒耦合。然而，图钉状的模糊函数也使 OFDM 雷达信号成为“多普勒敏感”信号，在回波处理时如果匹配滤波器存在细微的多普勒失配，将导致滤波器性能迅速下降。大量的研究围绕解决这两个问题展开，其中，研究适当的OFDM信号调制码字是解决这两个问题的一种重要手段。
ZC作为码字调制的OFDM信号被广泛地用于4G通信中，用作时频同步序列。文献[2-4]均说明了ZC序列作为码字调制的OFDM符号具有良好的相关特性。文献[2]通过比较在不同信噪比条件下ZC序列调制的OFDM符号与PN序列调制的OFDM符号、通信符号自身CP和修正过的CP四种符号序列作为时频同步序列进行同步的同步精度，说明了ZC序列调制的OFDM符号在低信噪比条件仍能保持较高的同步精度；文献[3]比较了在不同信噪比条件下分别利用PN序列调制的OFDM符号和ZC序列调制的OFDM符号作为同步序列进行通信情况下的通信误码率，说明了在信噪比从-10 dB到15 dB的条件下，ZC序列调制的OFDM符号作为同步序列进行通信的通信误码率明显要低于PN序列调制的OFDM符号作为同步序列进行通信的通信误码率；文献[4]比较了在信噪比从-10 dB到4 dB的条件下，ZC序列调制的OFDM符号作为同步序列进行通信的通信误码率明显要低于Gold序列调制的OFDM符号作为同步序列进行通信的通信误码率。
仅仅基于用于通信同步的相关性无法说明ZC序列调制的OFDM信号作为雷达信号的探测性能，文章重点研究了ZC序列调制的OFDM信号的峰均比特性和匹配特性以及多普勒容限特性，并比较了ZC序列调制的OFDM信号波形与线性调频信号波形的模糊函数特性，论证了ZC序列调制的OFDM信号作为雷达探测信号的可行性。
1 ZC序列的定义及其相关性质
ZC序列(又名Zadoff-Chu序列)的定义[5]如下：
Zμ(k)=
k=0,1,2,…,N-1
(1)
式中,WN=e-j2π/N ,N为序列的长度，μ∈N+为序列的根序列，μ和N满足gcd(μ,M)=1。可改写为如下形式：
Zμ(k)=
k=0,1,2,…,N-1
(2)
式中，cf=Nmod 2，q∈Z为参数。
OFDM信号的调制方式提供了一种在频域上设计信号波形的办法。OFDM信号的数学表达式为
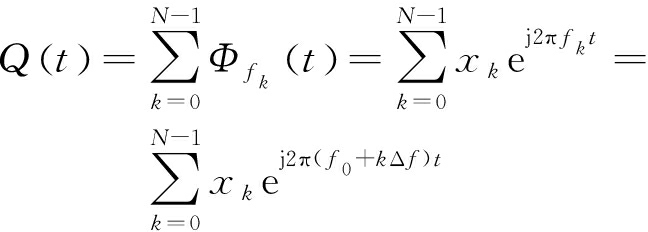
(3)
式中，fk=f0+kΔf，f0为起始频率，Δf为频率间隔。欲表示信号的采样信号，对式(3)以Ts(1/fs)为间隔周期进行采样，令t=nTs，有
(4)
若令起始频率f0=0，则频率间隔为Δf=1/NTs=fs/N，即频率间隔为采样频率的1/N，则得OFDM信号的采样信号序列表达式：
(5)
式(3)、(4)、(5)表达了调制序列xk与OFDM信号的采样信号Qn的离散傅里叶变换关系，也表达了调制序列xk的特性，即OFDM信号的频域特性。
1.1 ZC序列的傅里叶不变性
ZC序列经离散傅里叶变换和离散傅里叶逆变换后仍然是ZC序列。对ZC序列
进行傅里叶变换有
zμ(n)=
n=0,1,2,…,N-1
(6)
注意到文献[6]：
ejπ(μ×(μ-1n)×(μ-1n+cf+2q))/N×
e-jπ[μ(k+μ-1n)(k+μ-1n+cf+2q)]/N
(7)
式中，μ-1为μ关于1模N的乘法逆元，即满足 μ×μ-1≡1mod N。因此ZC序列Zμ(k)的傅里叶变换可写作[7]：
zμ(n)=
n=0，1,2，…，N-1
(8)
有
(9)
所以有
zμ(n)=
n=0,1,2,…,N-1
(10)
结合式(6)、 (7)、 (8)、 (9)、 (10)可得ZC序列经过傅里叶变化后仍然是ZC序列，且经过傅里叶变换后的ZC序列的根植μ-1与原ZC序列的根植μ满足μ×μ-1≡1mod N。同理，ZC系列经过逆傅里叶变换也有同样的性质。表1给出了在N=67，cf+2q=1情况下，ZC序列的部分根植和其对应的傅里叶变化后的根植。
表1 ZC序列原始根植与傅里叶变换后序列根植对应表
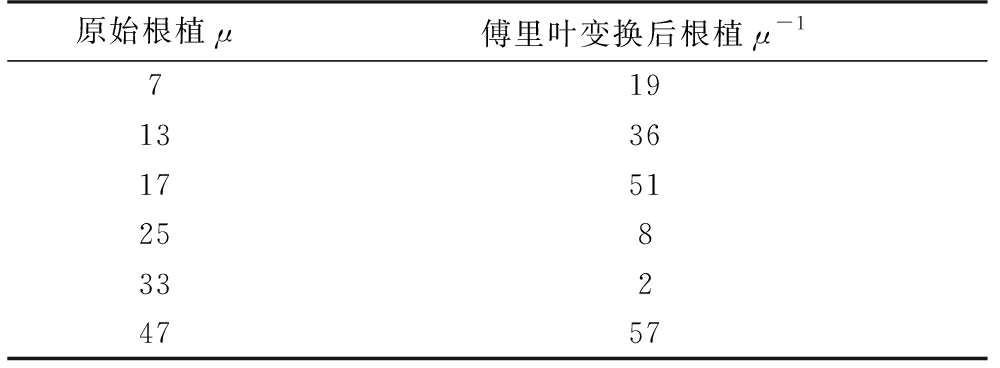
原始根植μ傅里叶变换后根植μ-1719133617512583324757
根据ZC序列的傅里叶不变性和OFDM信号中调制序列和OFDM信号采样序列之间的关系可得：基于ZC序列调制的OFDM信号的采样序列仍然是ZC序列，ZC序列的特性即OFDM信号的时域特性和频域特性。
1.2 ZC序列的循环相关性
定义ZC序列的循环自相关函数：
rn=
n=1,2,3,…,N-1
(11)
经公式推导[8]有
r0=N,rn=0,n=1,2,3,…,N-1
(12)
对N=60,cf+2q=0,μ=7的ZC序列的循环自相关函数仿真如图1所示。
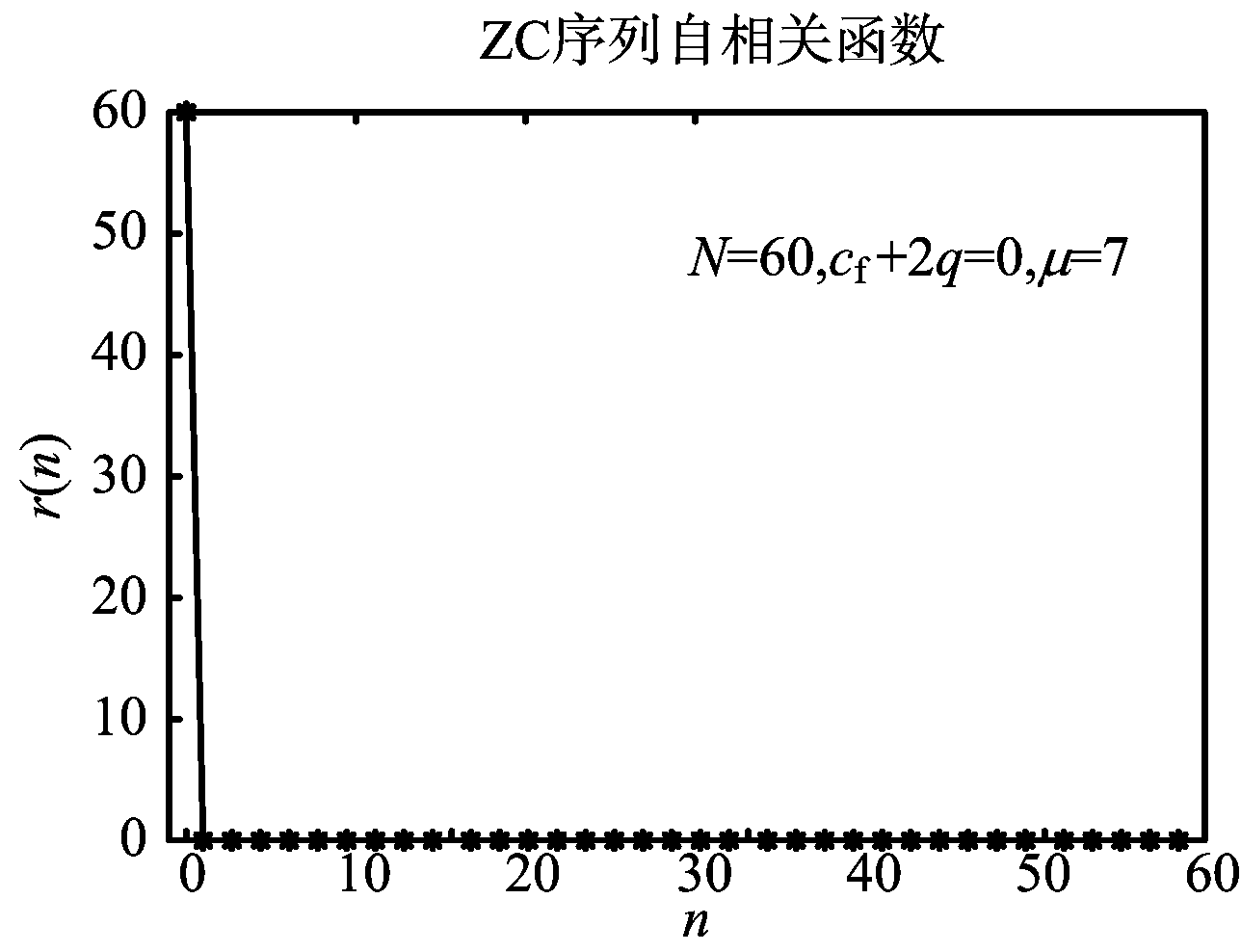
图1 ZC序列的循环自相关函数仿真
1.3 ZC序列的低峰均比特性
将ZC序列的定义式用欧拉公式展开可得
Zμ(k)=e-jπμk(k+cf+2q)/N=
cos(πμk(k+cf+2q)/N)-
jsin(πμk(k+cf+2q)/N)
j2=-1
(13)
对ZC序列的实部和虚部进行峰均比PAR(real)、PAR(imag)计算：
PAR(real)=
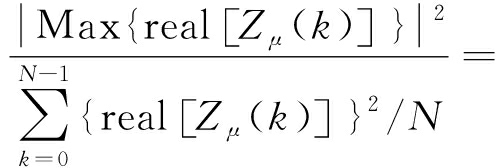
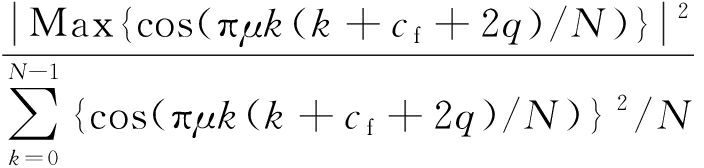
0≤k≤N-1
PAR(imag)=
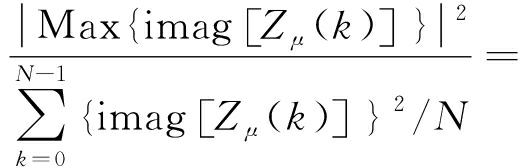
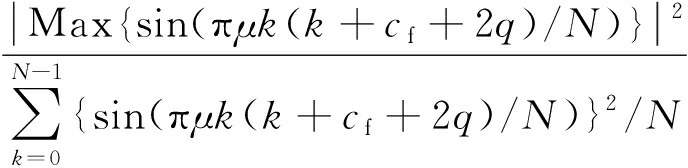
0≤k≤N-1
(14)
易得
Max{cos(πμk(k+cf+2q)/N)}≈
Max{sin(πμk(k+cf+2q)/N)}≈1
(15)
注意到文献[9]：
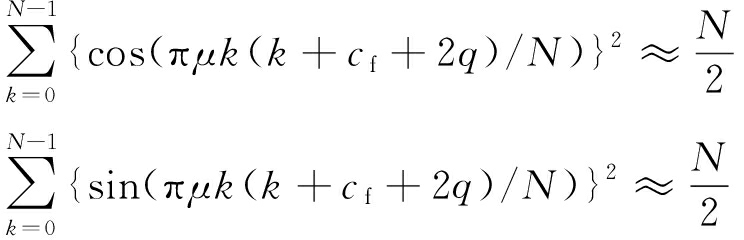
(16)
由式(15)、 (16)可得
PAR(real)≈PAR(imag)≈2=3 dB
(17)
仿真如图2所示。
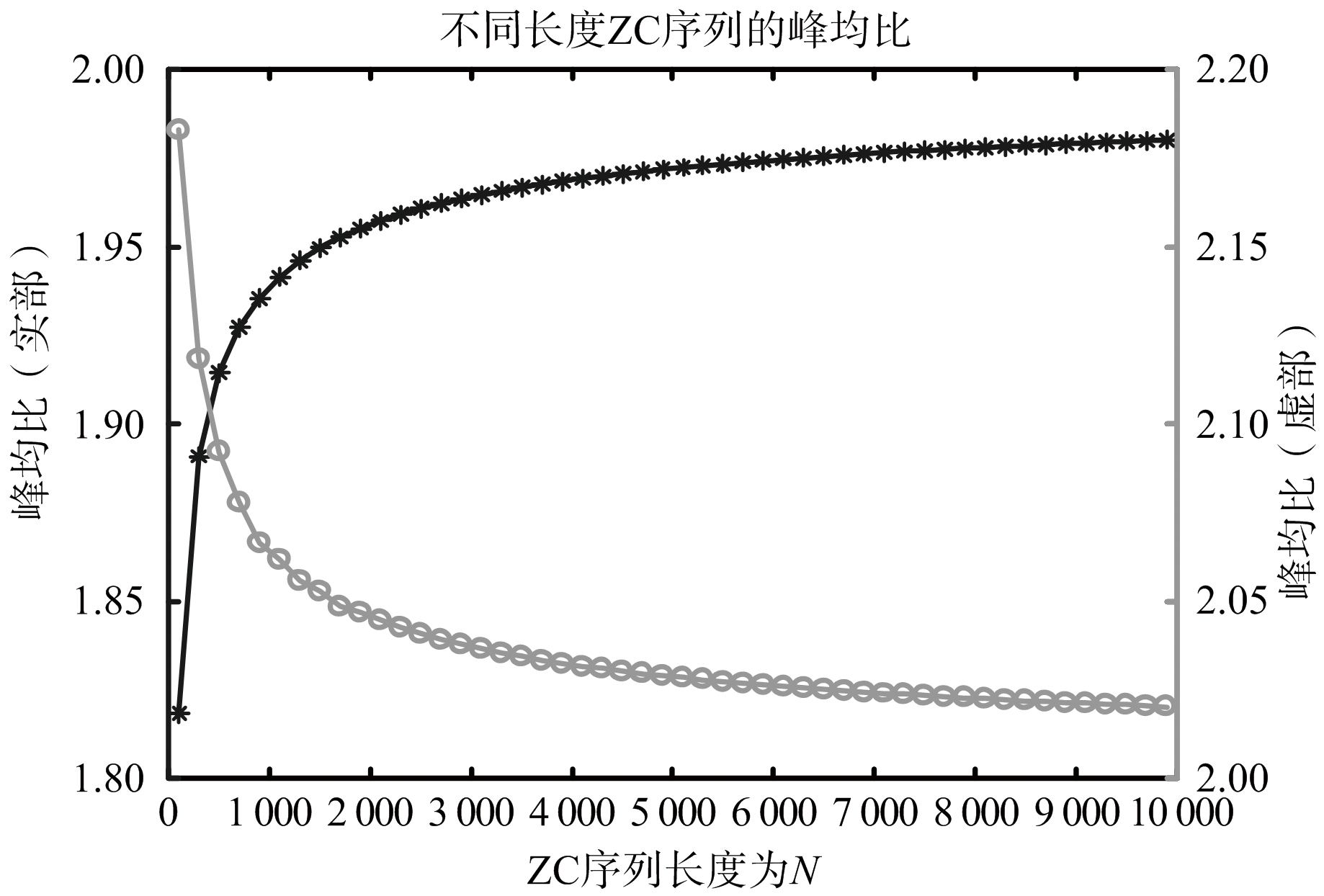
图2 不同长度ZC序列的峰均比
1.2节和1.3节分别说明了ZC序列的循环自相关特性和低峰均比特性，又根据1.1节有ZC序列的特性既反映ZC序列调制的OFDM信号波形的频域特性又反映其频域特性，可以得出ZC序列调制的OFDM信号波形具有1.2节和1.3节所得出的循环自相关特性和低峰均比特性。
2 ZC序列调制的OFDM信号波形的探测特性研究
为充分论证ZC序列调制的OFDM信号的探测特性，将ZC序列调制的OFDM信号和线性调频信号的模糊函数、距离分辨特性、频率分辨特性进行对比分析，并提出匹配特性检测算法和多普勒容限特性检测算法，用以对比分析ZC序列调制的OFDM信号波形和线性调频信号波形的匹配特性和多普勒容限特性。
线性调频信号的数学表达式为
G(t)=ej(2πfct+πkt2)
(18)
式中，f0为起始频率，k为频率调制斜率，k=B/t。定义其复包络信号为
(19)
2.1 ZC序列调制的OFDM信号波形的模糊函数分析
由式(3)，ZC序列调制的OFDM信号波形的复包络信号:
(20)
作为探测回波，在雷达接收处，信号波形表现为时延特性和因探测目标的径向运动导致的多普勒特性。现假设信号波形的时延为τ，探测目标有径向速度为υ，电磁波传播速度为c,c=3×108 m/s，信号在传播过程中信号衰减为原来的A倍，则信号回波可表示为
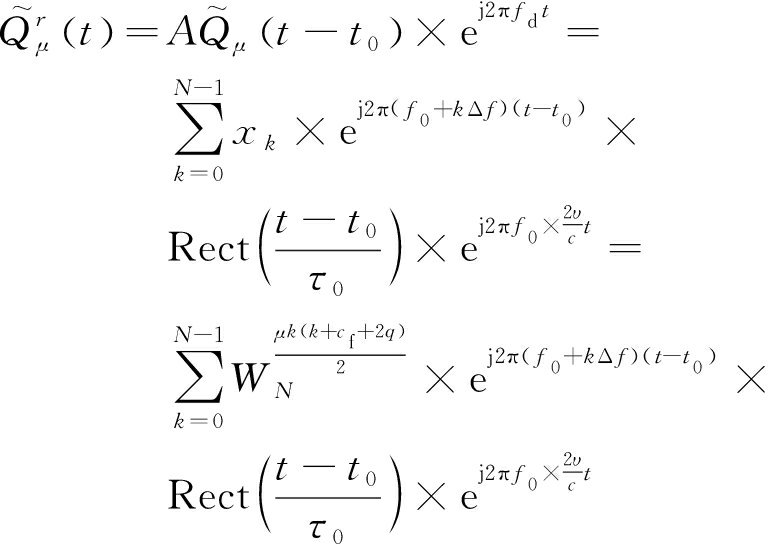
(21)
模糊函数作为雷达探测波形分析的重要工具，它可以刻画波形与相应匹配滤波器的特征，通过分析波形的模糊函数，可以得到雷达系统在采用最优匹配滤波处理时的距离分辨率、速度分辨率与多普勒容限特性。连续时间信号的模糊函数的定义为[10]
(22)
式中，E为信号的总能量。利用傅里叶变换性质，式(22)可得到一种等效的表示形式：
(23)
式中，X(f)为x(t)的傅里叶变换,其值为
由此可得到信号x(t)的模糊函数与其频域X(f)的模糊函数之间的关系为
u(τ,fd)=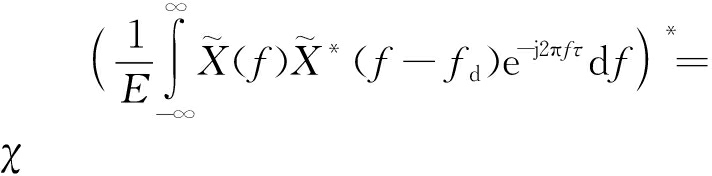
U*(fd,-τ)
(24)
对于离散时间序列，即雷达的码字序列，模糊函数定义为[11]
式中，
为采样率，N为采样点数。同理，离散序列c(n)的模糊函数与其频域序列
的模糊函数存在对应关系：
(26)
由于OFDM信号的离散序列是其调制序列的离散傅里叶逆变换，也即调制序列就是OFDM离散序列所对应的频域序列，可得ZC序列调制的OFDM信号波形模糊函数为
(27)
线性调频信号和ZC序列调制的OFDM信号波形和线性调频信号波形的模糊函数仿真如图3(a)和图3(b)所示。
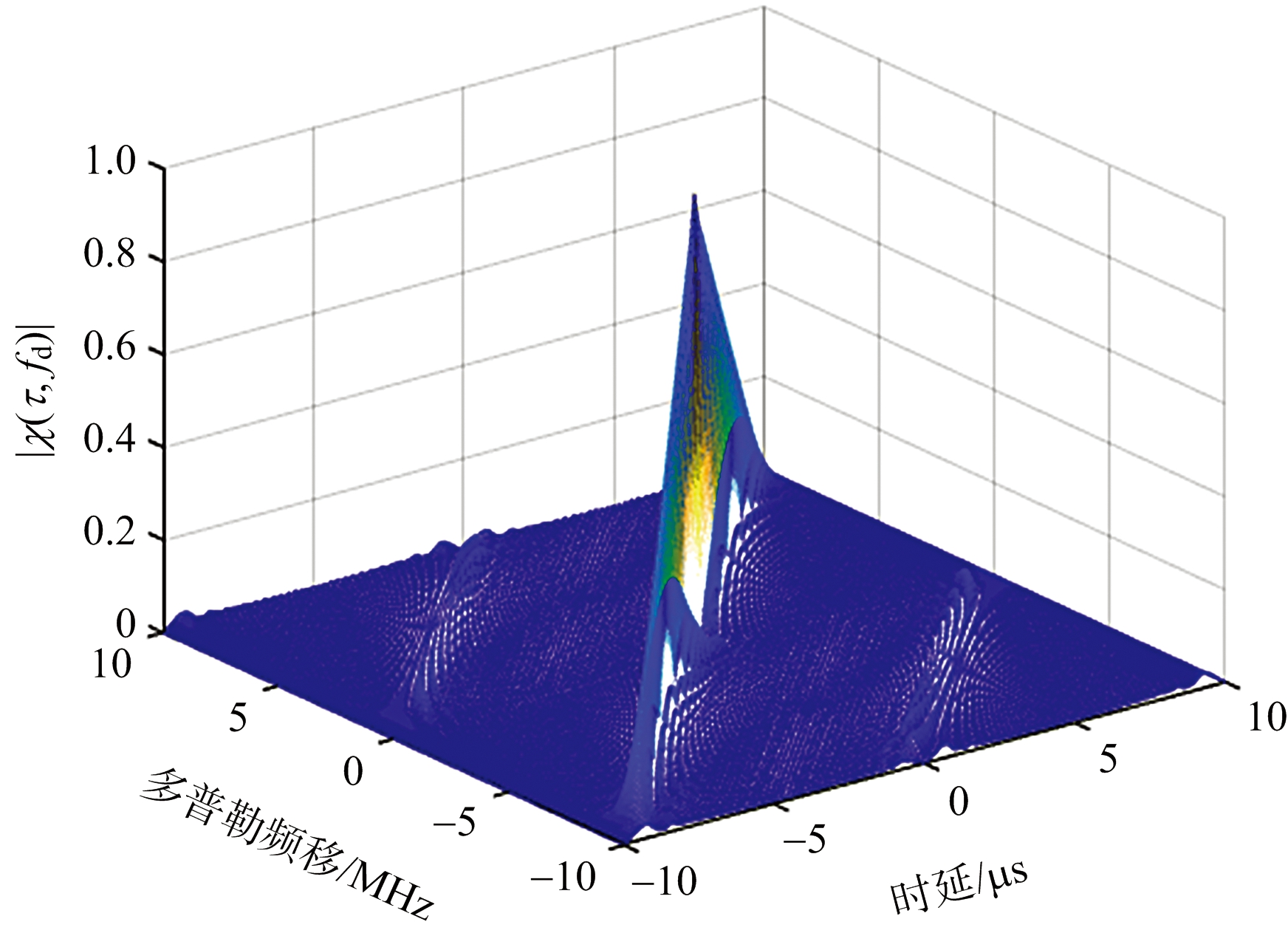
(a) ZC序列调制的OFDM信号的模糊函数
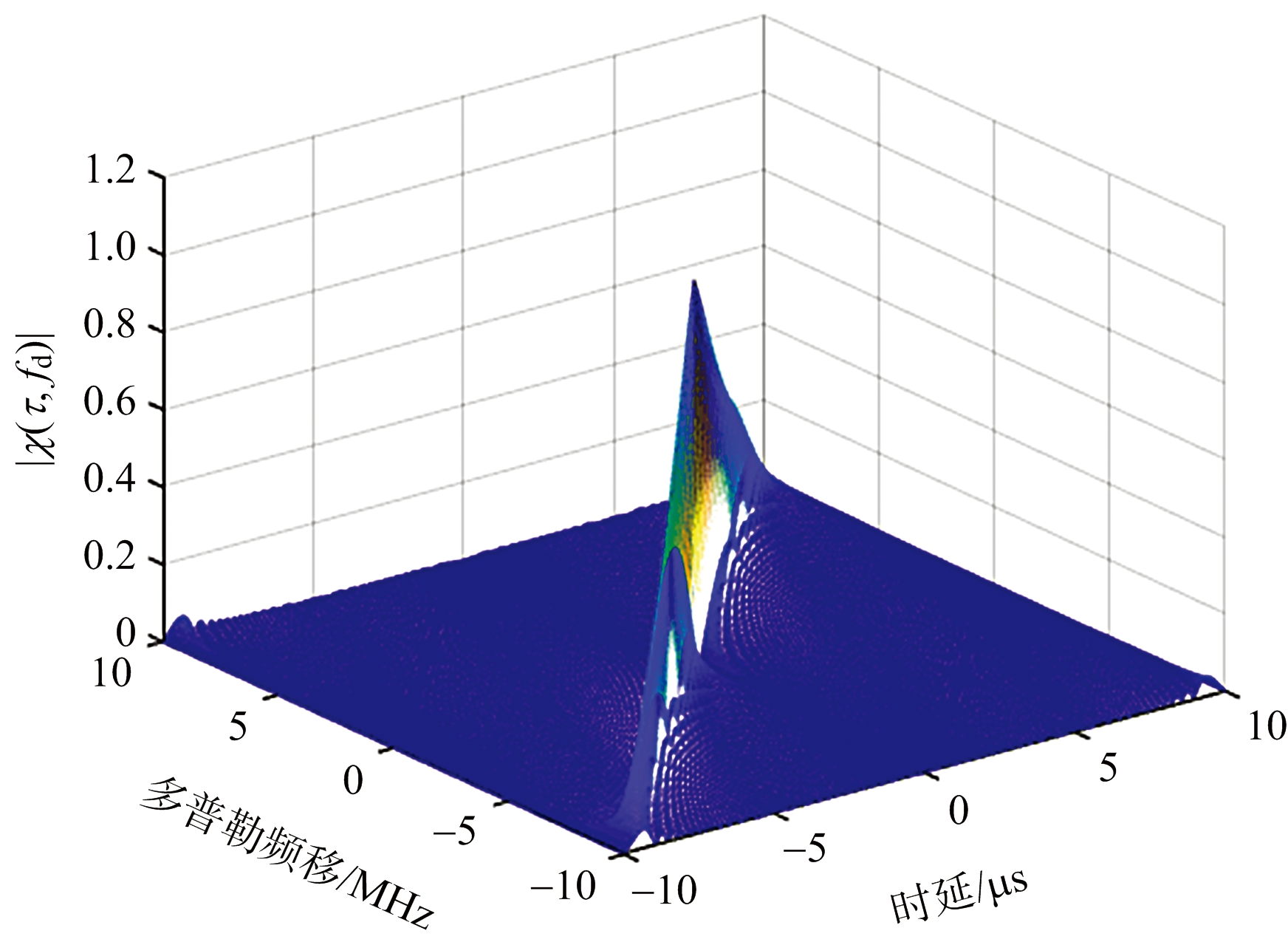
(b) 线性调频信号的模糊函数
图3 ZC序列调制的OFDM信号和线性调频信号的模糊函数图
由图3可以看出，ZC序列调制的OFDM信号波形的模糊函数和线性调频信号波形的模糊函数呈现相同的“斜刀刃”特性。
2.2 匹配特性检测算法以及ZC序列调制的OFDM信号波形的匹配特性研究
雷达信号回波处理时通常采用脉冲压缩的方法进行处理，良好的探测信号具有回波脉冲压缩处理后主副瓣比大的特点。定义信号波形在噪声环境下经过脉冲压缩处理后主副瓣比的特性为信号波形的匹配特性。定义匹配性检测函数rp(Δt)：
(28)
式中，n(t)为与
信噪比SNR=σ的高斯白噪声信号，B为信号带宽。 对式(28)两边以Ts(1/fs)为间隔周期进行采样，令t=nTs，有
rp(Δt)=
(29)
可得离散匹配性检测函数rp(n)：
(30)
由采样定理可得时长t是采样时间间隔长度Ts与采样点数M的乘积，反之有
M=Ts×fs
(31)
为比较同等时宽、带宽条件下ZC序列调制的OFDM信号和线性调频信号的探测特性，不妨设信号采样率为fs=20 MHz、带宽为B=10 MHz，时宽长度为t=10 μs，根据式(31)有M=200。由式(4)和式(5)可得调制序列的长度N为
N=B×t
(32)
ZC序列的OFDM信号时宽为t=10 μs,带宽B=10 MHz，可得N=100。按照同等的时宽和带宽参数设置的线性调频信号基带信号[13]参数为f0=0，k=B/t=1(MHz/μs)。
在噪声σSNR(m)=10 dB的情况下，根据式(30)，对μ=1，M=100的ZC序列调制的OFDM信号和线性调频信号的自身匹配特性分析如图4和图5所示。
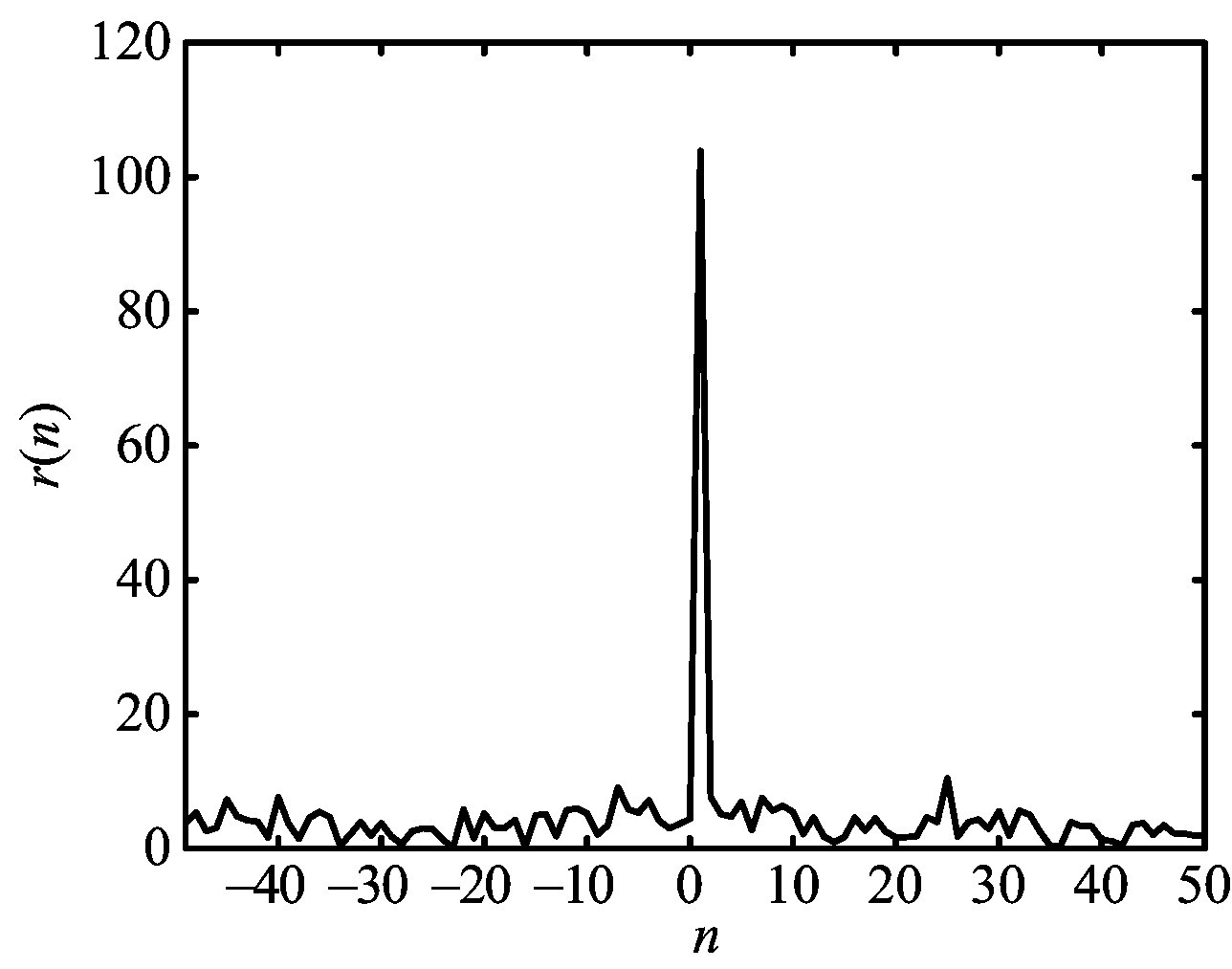
(a) ZC序列调制的OFDM信号的匹配性检测函数
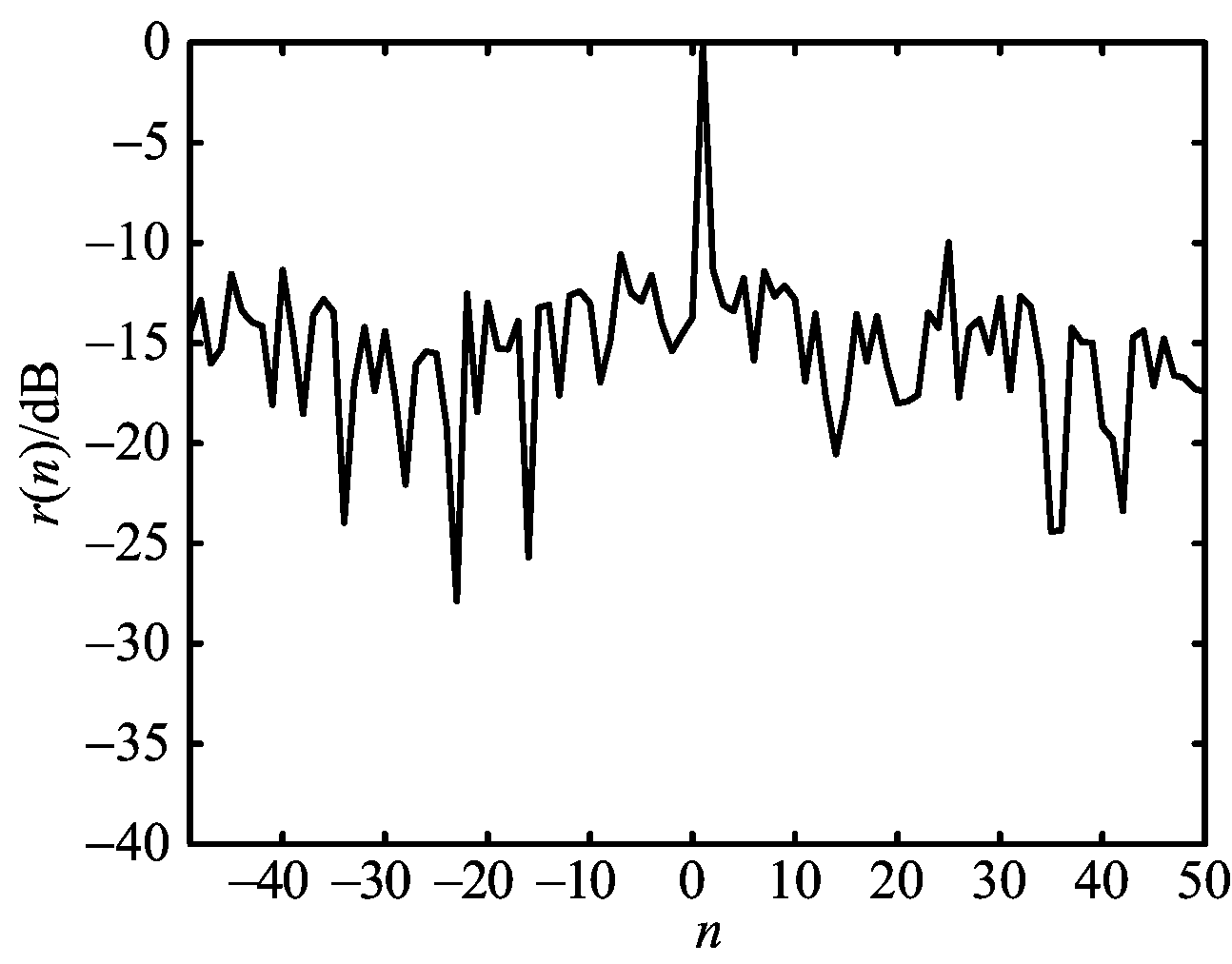
(b) ZC序列调制的OFDM信号的匹配性检测函数(归一化)
图4 噪声σSNR(m)=10 dB的情况下ZC序列调制的OFDM信号的匹配特性
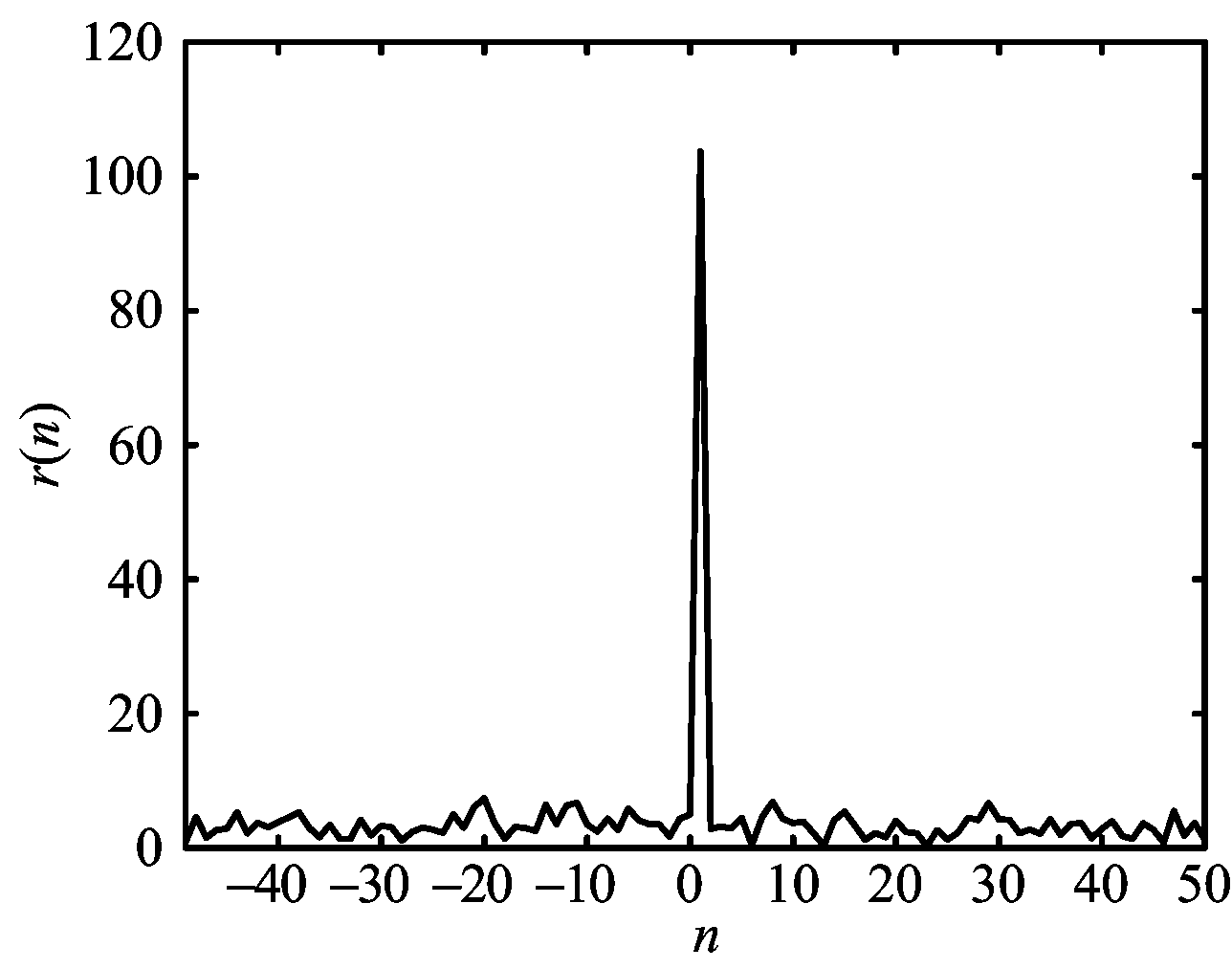
(a) 线性调频信号的匹配性检测函数
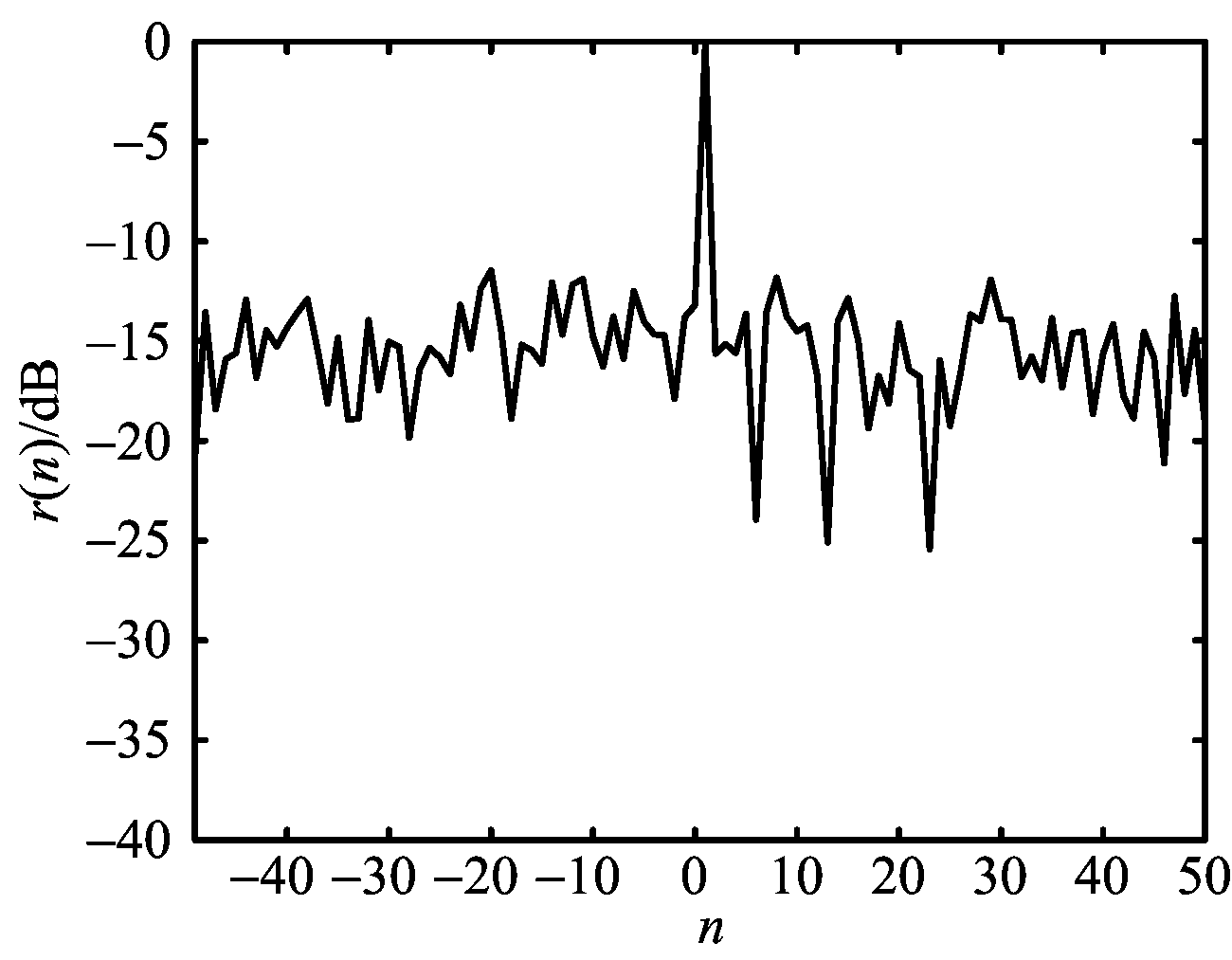
(b) 线性调频信号的匹配性检测函数(归一化)
图5 噪声σSNR(m)=10 dB的情况下线性调频信号的匹配特性
信号的噪声σSNR(m)从1 dB到20 dB情况下，ZC序列调制的OFDM信号和线性调频信号的自身匹配性检测函数的最小主副瓣比[14]比较如图6所示。
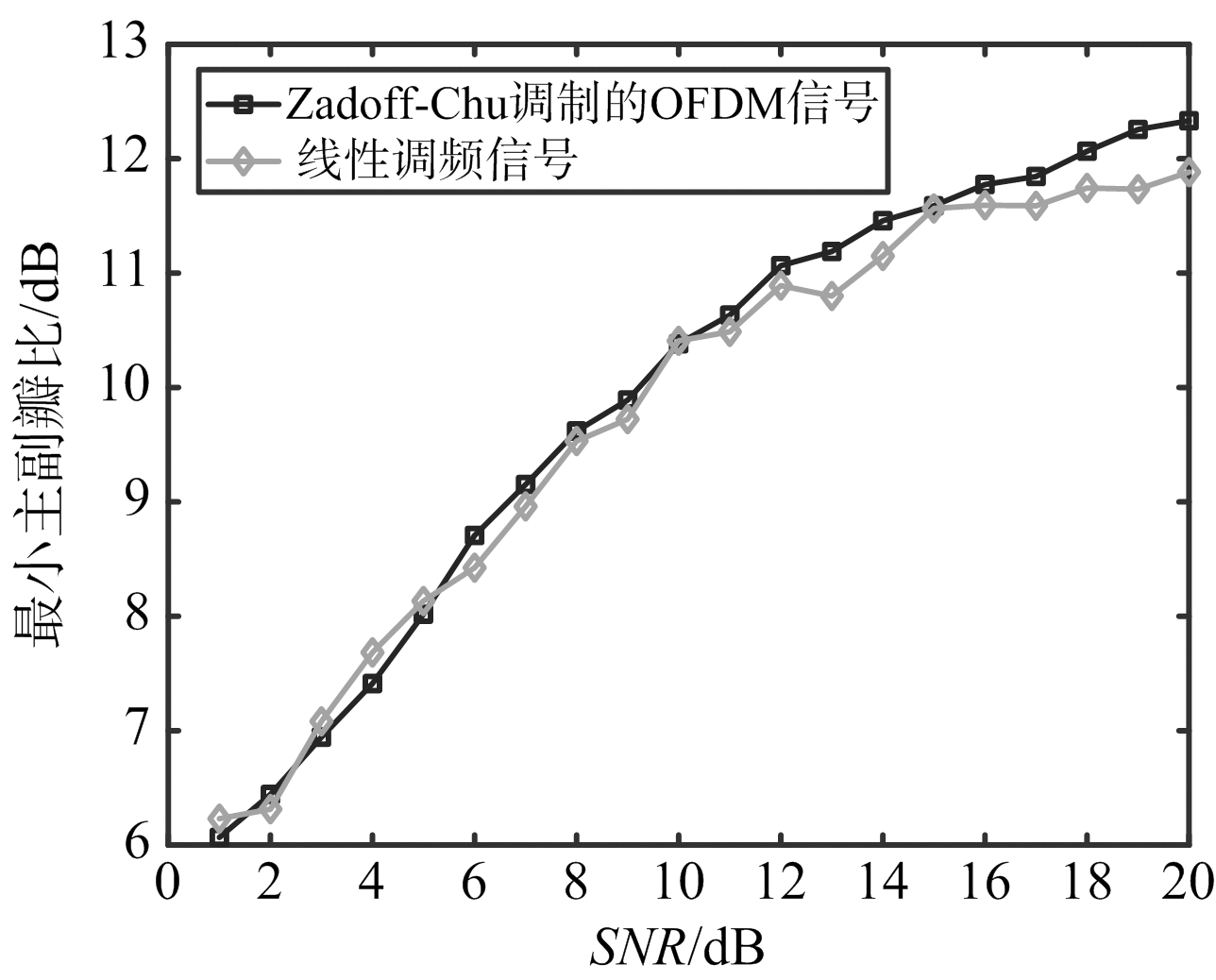
图6 不同信噪比下ZC序列调制的OFDM信号和线性调频信号的匹配性检测函数的最小主副瓣比
从图6可以看出，在噪声信噪比从1 dB到20 dB情况下,ZC序列调制的OFDM信号与线性调频信号有几乎相同的优良匹配特性，优良的匹配特性决定了在雷达波形能量在相同情况下可以获得较远的探测距离。
2.3 多普勒容限检测算法以及ZC序列调制的OFDM信号的多普勒容限特性研究
定义雷达探测信号受多普勒效应影响后，其回波在进行脉冲压缩处理后的最大峰值能量为其多普勒容限特性。多普勒容限检测函数为
(33)
同理，对式(33)两边以Ts(1/fs)为间隔周期进行采样，令t=nTs，有
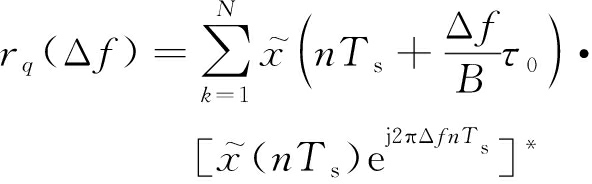
(34)
可得离散多普勒容限检测函数rq(m)：
(35)
根据式(35)，在同等采样率fs=20 MHz、带宽B=10 MHz、时宽长度t=10 μs的条件下，对ZC序列调制的OFDM信号的多普勒容限特性和线性调频信号的自身多普勒容限特性分析如图7所示。
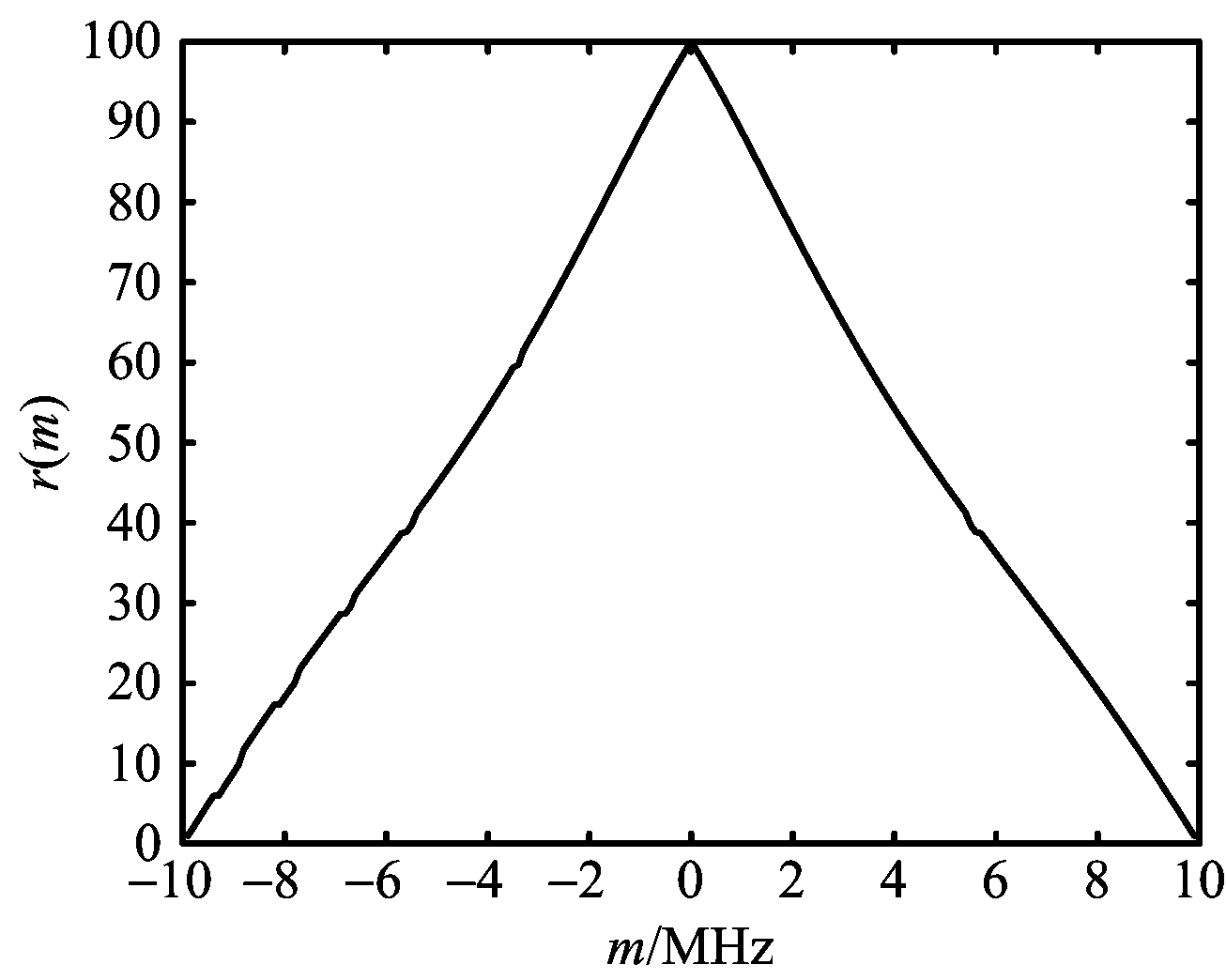
(a) ZC序列调制的OFDM信号的多普勒容限特性
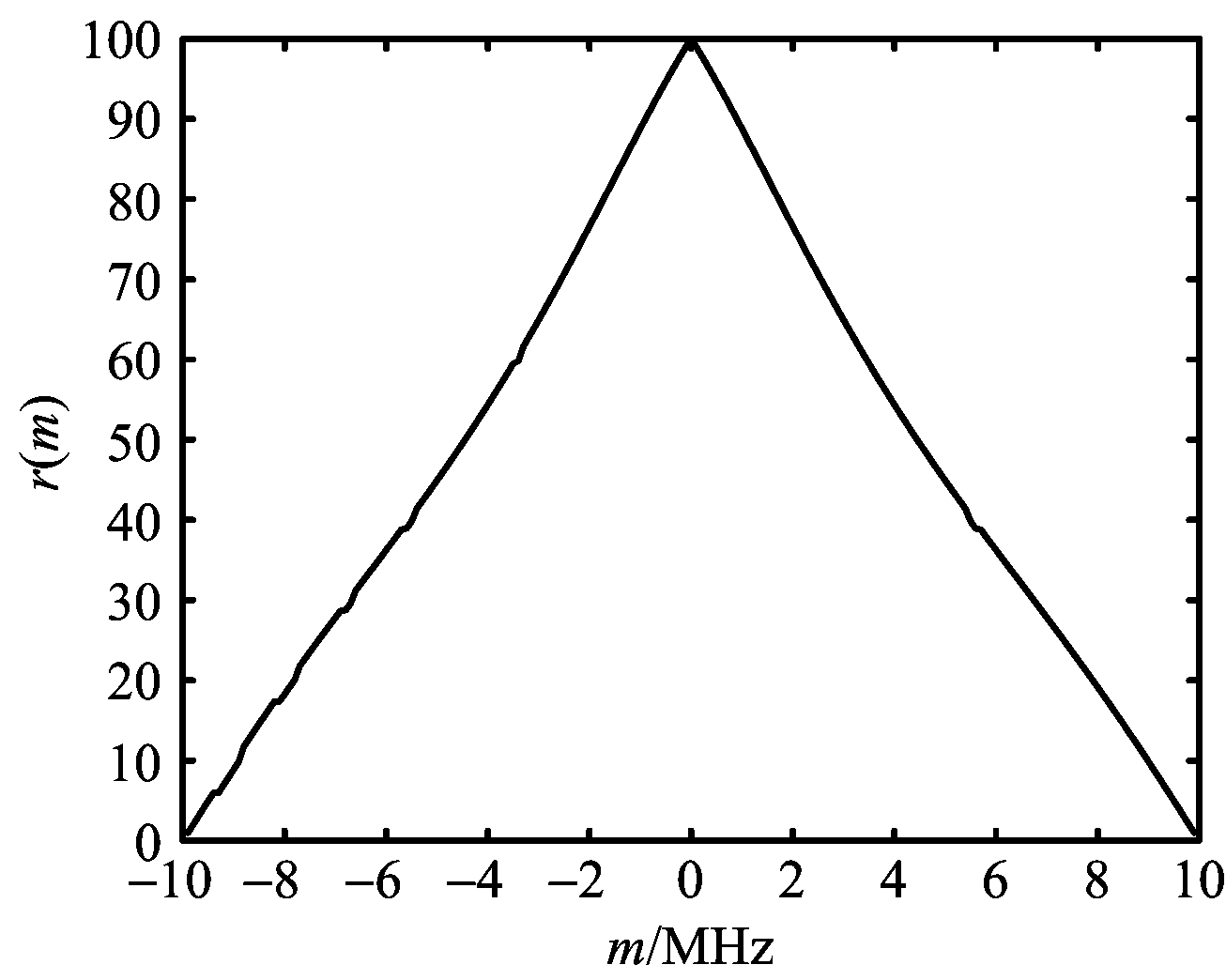
(b) 线性调频信号的多普勒容限特性
图7 ZC序列调制的OFDM信号和线性调频信号的多普勒容限特性分析
仿真结果表明，ZC序列调制的OFDM信号和线性调频信号拥有相同的多普勒容限特性。
2.4 多普勒估计
2.3节研究结果表明，ZC序列调制的OFDM信号具有和线性调频信号相似的多普勒容限特性，但多普勒频移的存在会对脉冲压缩过程产生峰偏移
的影响。因此，为了克服此种影响需要对多普勒频移作估计并对其频偏进行补偿。多普勒频偏可以采取频域相关出峰的方式对其估计。时长为τ0的回波零中频信号经过采样率为Fs后可得到长度为N=τ0×Fs的信号序列，将同等长度的零中频信号匹配样本按同样采样频率采样后得到同等长度的匹配序列。信号序列和匹配序列经过FFT变换后作相关，峰值点的位置即对应着信号频偏值。这里需要指出的是，由于ZC序列的傅里叶不变性以及OFDM信号的调制特性，ZC序列调制的OFDM信号的频域仍具有ZC序列相同的强相关性。
3 结束语
文章证明了ZC序列码调制的OFDM信号具有低峰均比特性、宽多普勒容限特性，克服了大多数OFDM信号所面临的峰均比过大导致信号放大失真、多普勒敏感导致匹配滤波器失效的两大难题。通过对ZC序列码调制的OFDM信号和线性调频信号的对比研究分析，得到ZC序列码调制的OFDM信号具有和线性调频信号相同的 “斜刀刃型”的模糊函数特性以及不亚于线性调频信号的高距离分辨率特性、高速度分辨率特性和良好的匹配特性的结论。但同时，由于ZC序列码调制的OFDM信号拥有“斜刀刃型”的模糊函数特性，因此该信号存在着距离和多普勒频移耦合的现象；并且该信号的匹配滤波器输出压缩脉冲包络仍近似为sinc(x)函数，需要采取数字加权的办法并以增大主瓣宽度为代价来降低副瓣，这在一定程度上也降低了系统的灵敏度。
[1] 霍凯, 赵晶晶. OFDM新体制雷达研究现状与发展趋势[J]. 电子与信息学报, 2015, 37(11):2776-2789.
[2] CAO Yunhe, XIA Xianggen. IRCI-Free MIMO-OFDM SAR Using Circularly Shifted Zadoff-Chu Sequences [J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(5):1126-1130.
[3] TENG C F, LIAO C C, CHENG H Y, et al. Reliable Compressive Sensing (CS)-Based Multi-User Detection with Power-Based Zadoff-Chu Sequence Design [C]∥IEEE International Workshop on Signal Processing Systems, Lorient, France: IEEE, 2017:1-5.
[4] JACOB N M, MATHEWS L, PILLAI S S. Transmit Precoding with Encoding Using Zadoff-Chu Sequence for MIMO-OFDM System [C]∥ International Conference on Communication Systems and Networks, Thiruvananthapuram, India: IEEE, 2017:76-80.
[5] POPOVIC B M. Generalized Chirp-Like Polyphase Sequences with Optimum Correlation Properties [J]. IEEE Trans on Information Theory, 1992, 38(4):1406-1409.
[6] PICCINNI G, AVITABILE G, COVIELLO G. A Novel Distance Measurement Technique for Indoor Positioning Systems Based on Zadoff-Chu Sequences [C]∥15th IEEE International New Circuits and Systems Conference, Strasbourg, France: IEEE, 2017:337-340.
[7] POPOVIC B M. Efficient DFT of Zadoff-Chu Sequences [J]. Electronics Letters,2010,46(7):502-503.
[8] CHU D. Polyphase Codes with Good Periodic Correlation Properties (Corresp.) [J].IEEE Trans on Information Theory, 1972, 18(4):531-532.
[9] SARWATE D. Bounds on Crosscorrelation and Autocorrelation of Sequences (Corresp.) [J]. IEEE Trans on Information Theory, 1979, 25(6):720-724.
[10] HYDER M, MAHATA K. Zadoff-Chu Sequence Design for Random Access Initial Uplink Synchronization
in LTE-like Systems [J]. IEEE Trans on Wireless Communications, 2017, 16(1):503-511.
[11] 林茂庸, 柯有安. 雷达信号理论[M]. 北京：国防工业出版社, 1984.
[12] PROAKIS J G, MANOLAKIS D G. Digital Signal Processing: Principles, Algorithms and Applications[M].4th ed. New York: Macmillian Publishing Company, 1992.
