0 引言
在实际中,警戒雷达因低分辨雷达体制的局限性及雷达探测过程中背景杂波的影响,其飞机目标的分类识别率较低从而限制了其应用[1],针对常规低分辨雷达体制下飞机目标的分类辨识,许多研究人员开展了研究,并取得了一定的研究成果。概括来讲,低分辨雷达飞机目标的分类特征可概括为以下3类:飞机回波的波动特性(雷达截面积、幅相的波动特性、二维灰度图等)、飞机的运动特性(高度、速度和加速度等)和喷气引擎调制(JEM)特征[2-3]。综合3类特征提取方法,JEM特征占较大比重[4]。由于常规雷达性能和体制等方面的限制,在常规雷达体制下提取飞机目标的JEM特征具有一定的困难[5]。对螺旋桨飞机、直升机和喷气式飞机来讲,从时域提取的信号周期和从多普勒域提取的频谱间隔可以较好地区分这3类飞机目标,然而这种分类识别方法对脉冲重复频率和目标观测时间有较高要求。分数阶Fourier变换(FRFT)是在时-频域分析信号,且具有可逆性,可借助快速傅里叶变换实现,计算复杂度较低[6]。 Yu等人借助于FRFT在强杂波背景下进行动目标检测和延时估计,并获得较理想的实验结果[7];杜兰等人引入FRFT提取喷气式飞机、螺旋桨飞机和直升机的特征,并结合线性相关向量机对3类飞机目标进行分类辨识,分类识别率较传统的特征提取方法有一定程度的提高[8]。飞机目标回波和背景杂波具有多重分形特性[9-11],李秋生等人通过分形理论研究了螺旋桨飞机、喷气式飞机和直升机的多重分形特性,并通过支持向量机验证了飞机目标分类方法的有效性[12-14],以上表明FRFT和分形都可提高低分辨雷达飞机目标的分类识别率。结合这两种方法,顾智敏等人以海杂波为研究对象,在FRFT域分析有、无目标时海杂波的多重分形特性,并进行了海上动目标检测[15],李秋生等人在FRFT域对民航机和战斗机回波数据进行了分形判定和无标度区间估计[16]。
本文通过FRFT处理低分辨雷达飞机目标回波并研究飞机目标回波在最优FRFT域的多重分形特性,并借助支持向量机,分析了FRFT域多重分形方法和时域多重分形方法的飞机目标分类识别性能,研究FRFT域多重分形方法在不同信噪比下的分类情况。
1 理论基础1.1 分数阶Fourier变换
FRFT保留了傅里叶变换的固有特性,并且也具有许多特殊的性质,文献[17]对比分析了FRFT和傅里叶变换在自适应滤波方面的优越性。FRFT通过逆时针旋转信号的时间轴α度得到另一新的坐标轴u轴。信号f(t)的p阶FRFT定义如下:
fp(u)=![]() Kp(u,t)f(t)dt
Kp(u,t)f(t)dt
(1)
式中,fp(u)为经FRFT在对应的FRFT域得到的变换信号。FRFT的核函数表示为Kp(u,t),其定义为
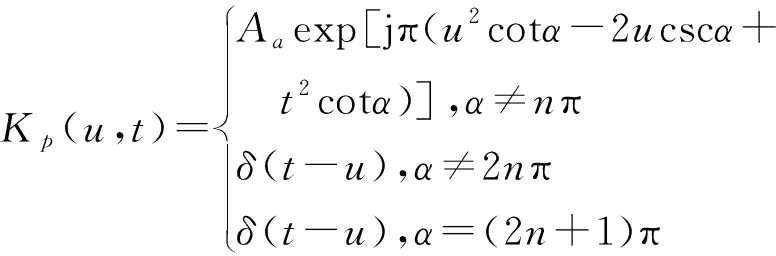
(2)
式中,![]()
在实际数字信号处理中,通常需要离散形式的FRFT,例如直接采样方法和快速方法。本文使用的方法是将FRFT转换为信号卷积的形式,从而可得到如式(3)所示的离散形式的FRFT,详细推导过程可参见文献[18]。
![]()
![]()
(3)
式中,1/Δx为时域的采样间隔,n为时域的采样点,m为FRFT域的采样点,N为时域采样点的总数。若信号f(t)为线性调频函数,其分数阶Fourier变换fp(m/2Δx)将在最优FRFT域形成冲激函数,从而最大化地聚集信号的能量,提高信噪比,利于信号处理和分析。
1.2 多重分形的理论基础和参数估计
多重分形主要是用来刻画分形体在不同分形尺度下的生长过程。分形体作为一个整体,可被划分为许多小的分形生长区域,每一小区域的面积记为ε,小区域总数记为Nε,并将第i个小区域的生长概率记为Pi(ε)。不同分形小区域的生长概率Pi(ε)和其面积ε之间的关系为
pi(ε)∝εσi,i=1,2,…,N
(4)
其中,σi体现不同面积的分形区域生长概率的差异,被称为局部分形维(LFD)或奇异指数,其值表征了各分形小区域生长概率的差异。对于不同面积的分形区域,局部分形维数若不相同,该分形体可被称为多重分形几何体;如果不同面积的分形区域,局部分形维数相同或相近,该分形体被称为单一分形几何体。对式(4)取q次方并相加,可得配分函数Γ(q,ε),如式(5)所示:
Γ(q,ε)=![]()
![]()
(5)
一般来讲,对分形体内部结构的描述程度不同,分形间隔也应不相同,因此,在实际应用中,可根据实际需求确定q的取值范围。在式(5)中,如果q≫1,分形体中生长概率较大的子集将发挥主要作用;如果q≪1,分形体中生长概率较小的子集将起主要作用。若式(5)右半部分成立,配分函数Γ(q,ε)和分形小区域面积ε之间存在幂律关系,配分函数取对数后与分形面积ε之间的变化率记为τ(q),称为质量指数。假定质量指数和q之间满足线性关系,该分形几何体称为单一分形体;假定质量指数是q的凸函数,该分形几何体呈现出多重分形特性,称为多重分形体。多重分形谱 f(σ)定义为具有相同奇异指数的分形子集的分形维数,可用对应于不同奇异指数σ的多重分形谱的序列来表示整个分形体的分形维数,从整体上进一步反映分形体生长分布概率的特性。文献[4]表明,τ(q)~q和f(σ)~σ之间是Legendre变换的关系,因此对质量指数τ(q)进行Legendre变换可得多重分形谱f(σ)。
1.3 飞机目标回波数学模型
若忽略由飞机目标回波的非刚性颤动、姿态角变换和JEM调制等产生的背景杂波和电磁干扰,在单个雷达脉冲信号扫描周期内(20~100 ms),回波信号之间可认为具有相关性,飞机目标可被当作点目标进行处理[19]。常规低分辨雷达回波数据应由3部分组成,噪声分量、机身分量及JEM分量,如式(6)所示。
s(t)=as(t)[casa(t)+cjemsjem(t)]+cnsn(t)
(6)
式中:as(t)表示雷达天线扫描系统对雷达回波数据的综合影响,as(t)=at(t)aa(t)ar(t),at(t)为发射信号模型的影响因子,aa(t)为扫描天线本身的影响因子,ar(t)为接收信号模型的影响因子; sn(t), sa(t)和sjem(t)分别表示噪声分量、机身分量和JEM分量;cn, ca和cjem分别表示对应噪声分量、机身分量和JEM分量的强度系数。具体来讲,假定存在一架飞机,飞机有M个发动机,距离雷达的远场距离为R0, 方位角为α, 俯仰角为β,在飞机目标被雷达激励的观测时间内,其基频机身分量表示为
sa(t)=![]()
t0≤t≤t0+T
(7)
式中:u为调频斜率,u=2a0/λ,a0表示飞机目标加速度a在雷达-目标视线方向的投影,λ表示雷达工作波长;fd=2vf/λ表示机身多普勒频率,vf为机身速度在雷达-目标视线方向的投影;飞机的飞行速度表示为v,vf=vcosφ,φ为飞机飞行速度v相对于雷达-目标视线方向的斜率;T表示飞机目标总的观测时间。
常规雷达工作波长一般要远小于飞机目标的尺寸,因此飞机目标的散射处于光学区。处于光学区的各个散射中心之间的相互作用较弱,飞机目标的旋转部件的桨叶可被看作是等效的散射中心,散射过程被称为线性局部过程,多个独立的散射回波的线性叠加形成飞机目标总的散射回波,JEM散射分量是由旋转部件所有桨叶散射回波的线性叠加[5],JEM分量如式(8)所示:
sjem(t)=![]()

(8)
式中:v(α,β′,p)表示可见函数,可以描述飞机目标旋转部件在雷达-目标视线方向的遮挡问题,其中,飞机类型用参数p表示,β′的取值与飞机目标的飞行方向及飞机表面的旋转有关,当旋转平面和飞机飞行轨迹平行时,β′=β;当旋转平面和飞机飞行轨迹垂直时,β′=π/2-β。Nm, ωrm, L1m和L2m分别表示第m组旋转部件的叶片数、旋转速度、桨叶中心到桨叶尖的距离及桨叶中心到桨叶根的距离;θkm = θ0 + 2πk/Nm, k = 0, 1,…,Nm - 1, 其中θ0表示第0片桨叶的初始相位。对于第m组旋转部件,相邻调制谱线之间的间隔为fTm = Nmωrm/2π,相邻调制谱线之间的间隔由Nm和ωrm确定,谱线的幅值Cm,k由Nm, λ, β′, L1m, L2m,θ0及贝塞尔函数共同确定。N1m是单边谱线的数量,B1m是单边信号的带宽,N1m和B1m如式(9)、式(10)所示:
N1m=8πL2mcosβ′/(Nmλ)
(9)
B1m=4ωrmL2mcosβ′/λ
(10)
2 多重分形特征提取方法
在引入了多重分形及FRFT理论知识的基础上,以上述的常规雷达回波数据模型为依托,利用FRFT域多重分形方法进行常规雷达飞机目标的分类识别研究。根据上述分析,常规雷达飞机回波数据包括噪声分量、JEM分量和机身分量,下面以常规雷达飞机回波数据模型为基础,结合实验说明FRFT域多重分形方法的实现过程。不同类型的飞机目标结构之间存在较显著差异,对于直升机,其主旋翼相对于尾翼来讲,直径大、转速低,其JEM分量主要受主旋翼影响,实验设计中,主旋翼直径为尾翼直径的3倍,主旋翼速度减小为尾翼速度的1/3,在尾翼和主旋翼之间产生随机转角差拍,以保证实验的鲁棒性。螺旋桨飞机和直升机装有两个发动机,飞机桨叶的结构和旋转速度相近,同样在两个桨叶之间存在随机距离和随机转角差拍。在飞机目标被雷达激励的观测时间内,目标可认为是点目标,其机身分量为式(7)所示的单频信号。飞机目标的雷达截面积符合斯威林模型,其中螺旋桨飞机和直升机符合斯威林III型,喷气式飞机符合斯威林 I型。在以下实验中,雷达的工作波段为L波段,雷达的脉冲重频fr=600 Hz,雷达工作波长λ=0.3 m,信噪比为10 dB,飞机目标的观测时间为50 ms,其飞机目标的结构参数和旋转速度如表1所示,飞机目标探测的场景参数如表2所示。飞机目标的结构参数和场景参数摘自文献[20]。
表1 3类25种飞机目标的结构参数和旋转速度
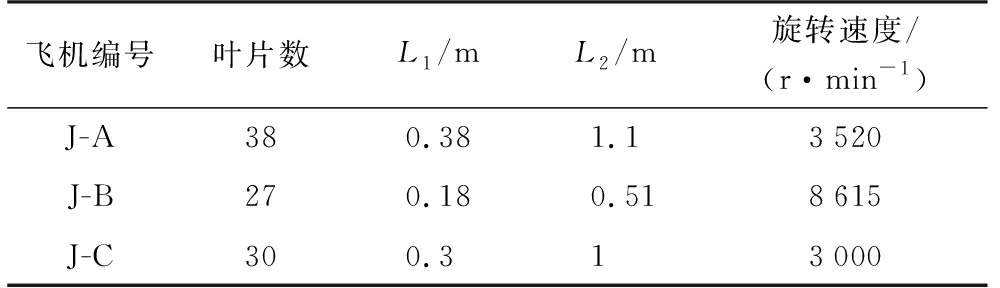
飞机编号叶片数L1/mL2/m旋转速度/(r·min-1)J-A380.381.13520J-B270.180.518615J-C300.313000
续表1
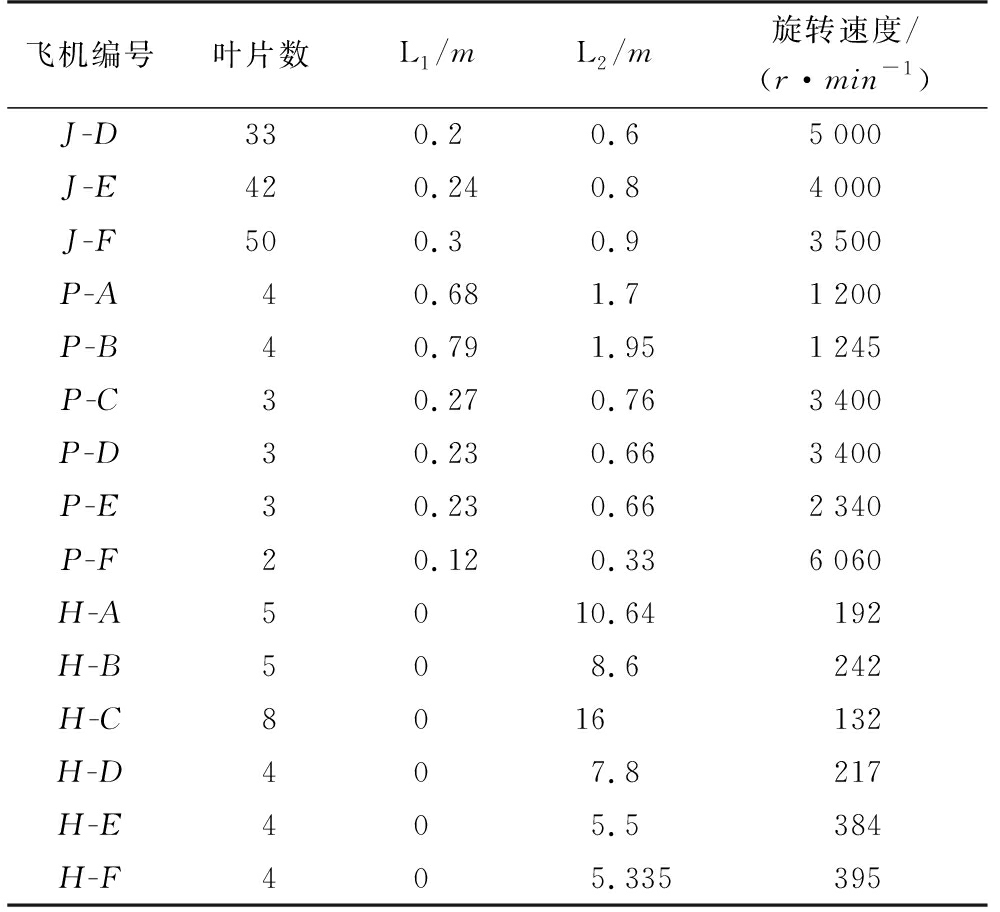
飞机编号叶片数L1/mL2/m旋转速度/(r·min-1)J-D330.20.65000J-E420.240.84000J-F500.30.93500P-A40.681.71200P-B40.791.951245P-C30.270.763400P-D30.230.663400P-E30.230.662340P-F20.120.336060H-A5010.64192H-B508.6242H-C8016132H-D407.8217H-E405.5384H-F405.335395
注:‘J’ 代表喷气式飞机,‘P’ 代表螺旋桨飞机,‘H’ 代表直升机。
表2 3类25种飞机目标的典型场景参数和飞行速度
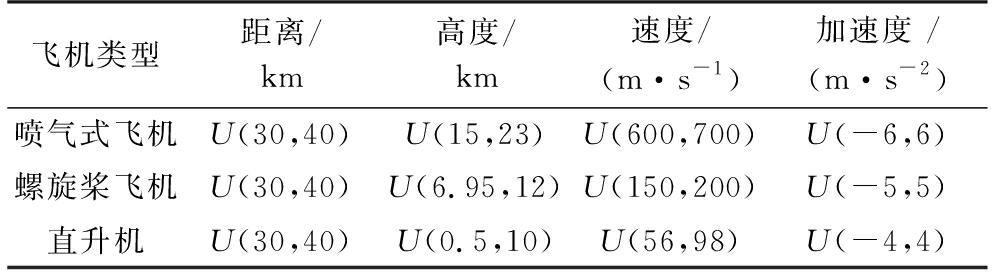
飞机类型距离/km高度/km速度/(m·s-1)加速度 /(m·s-2)喷气式飞机U(30,40)U(15,23)U(600,700)U(-6,6)螺旋桨飞机U(30,40)U(6.95,12)U(150,200)U(-5,5)直升机U(30,40)U(0.5,10)U(56,98)U(-4,4)
注:U(a, b) 表示数据在区间[a,b]内服从均匀分布。
2.1 最优FRFT域的判定
飞机目标回波能量可得到最大程度的聚集的分数域是最优FRFT域,相对应的在最优FRFT域杂波能量相对分散,有利于目标的检测。因此,在特征提取之前,使用FRFT处理飞机目标回波找到最优FRFT域,最优FRFT阶数popr所对应的分数域称为最优FRFT域。熵值可以衡量信号的不稳定程度,熵值越小,表明信号的能量聚集性越好,在文献[21]中用熵值来衡量信号的稳定性,进而对常规低分辨雷达体制下的战斗机和民航机进行分类。分数域多重分形方法通过熵值体现回波信号能量在某分数域的聚集程度,三阶Renyi信息熵可以有效地衡量飞机目标回波信号的能量聚集能力,最优FRFT域对应飞机目标回波三阶Renyi信息熵的最大值。
三阶Renyi信息熵的定义如式(11)所示:
(11)
不同类型飞机目标的结构等参数一般不同,其三阶Renyi信息熵也不相同;对于同种类型飞机,飞机目标回波的三阶Renyi信息熵同样受飞机目标的速度、加速度、姿态角及环境等因素的影响。不同的三阶Renyi信息熵通常对应不同的FRFT变换的最优阶数,因此,每组飞机目标回波都需要计算其三阶Renyi信息熵。FRFT的变换阶数p的范围为[0,2],阶数p的计算步长为0.01,分别计算直升机、螺旋桨飞机和喷气式飞机的三阶Renyi信息熵,我们可以确定飞机目标回波的最优FRFT域。以喷气式飞机为例,飞机目标回波的典型三阶Renyi信息熵如图1所示。
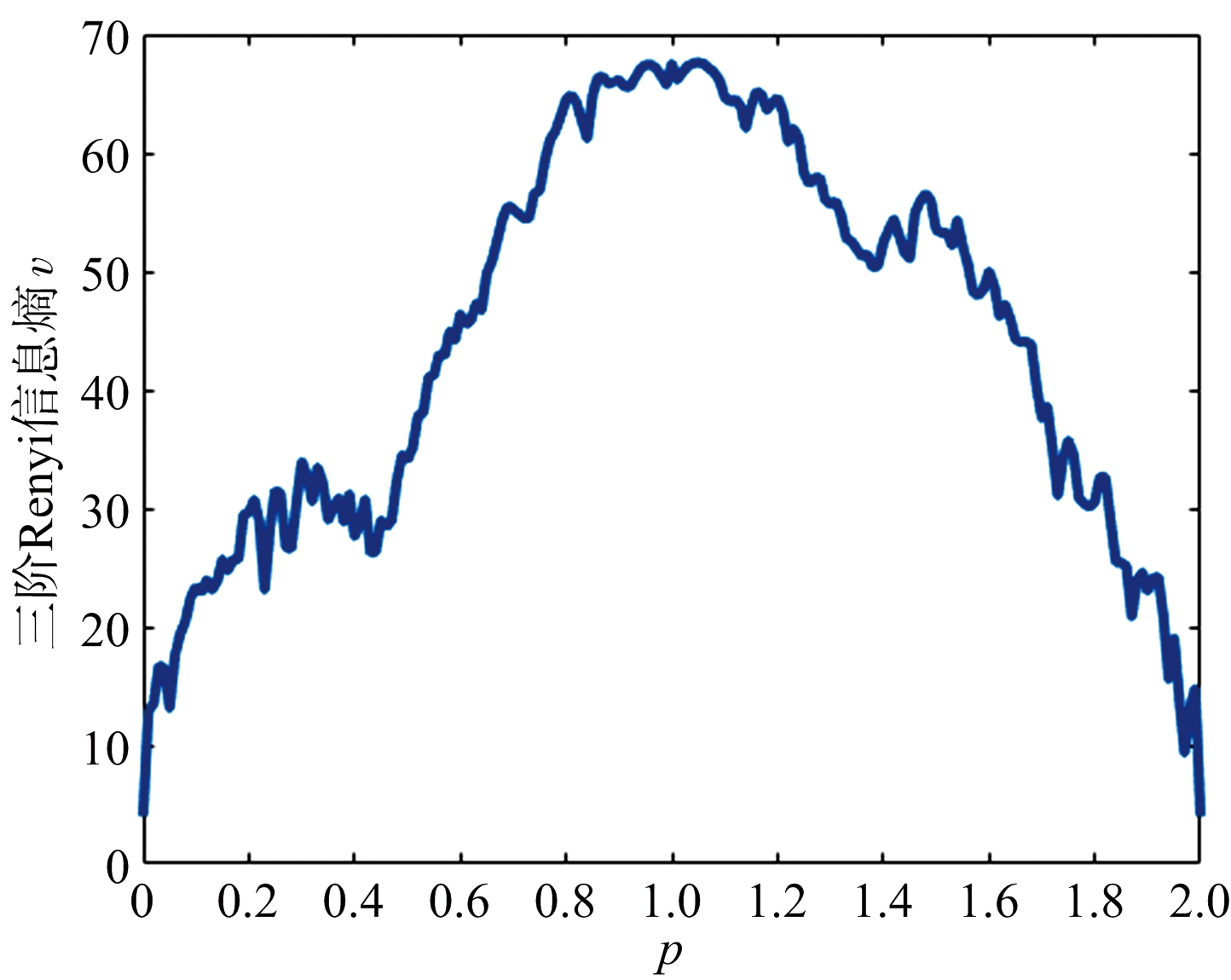
图1 喷气式飞机的三阶Renyi信息熵
2.2 最优FRFT域多重分形特性分析与特征提取
分形理论建立在分形体具有自相似性的基础上,因此,分数域多重分形方法首先要判定在最优FRFT域飞机目标回波是否体现出多重分形特性,在无标度区间内分析其多重分形特性。雷达的工作波段是L波段,雷达工作波长为0.3 m,雷达的脉冲重复频率为600 Hz,信噪比为10 dB,飞机目标的观测时间为50 ms,飞机目标的结构参数和旋转速度如表1所示,飞机目标探测的场景参数如表2所示。分析最优FRFT域下雷达回波数据的多重分形特性,实验结果如图2~图4所示。
(a) 未进行FRFT
(b) 进行FRFT
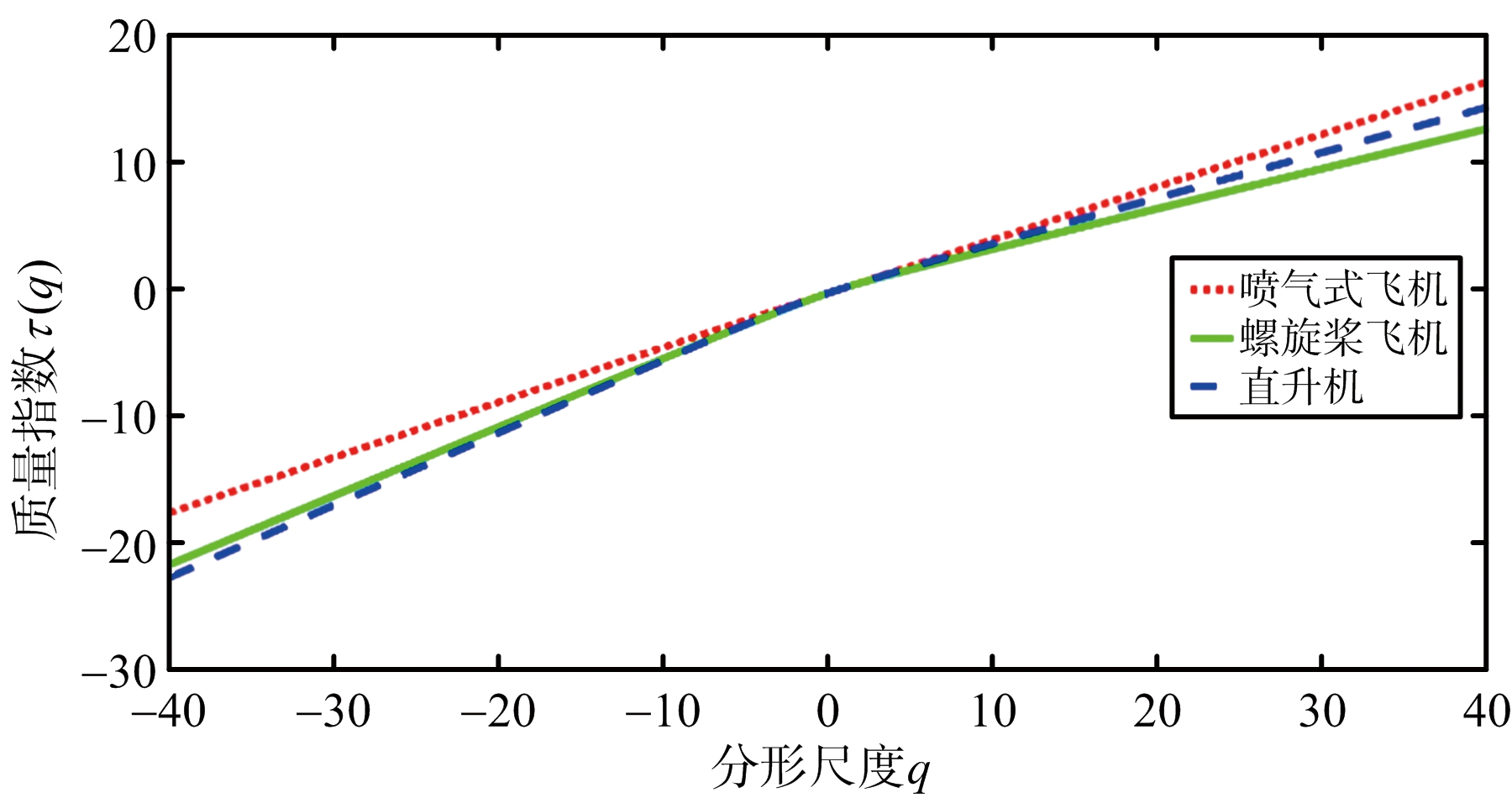
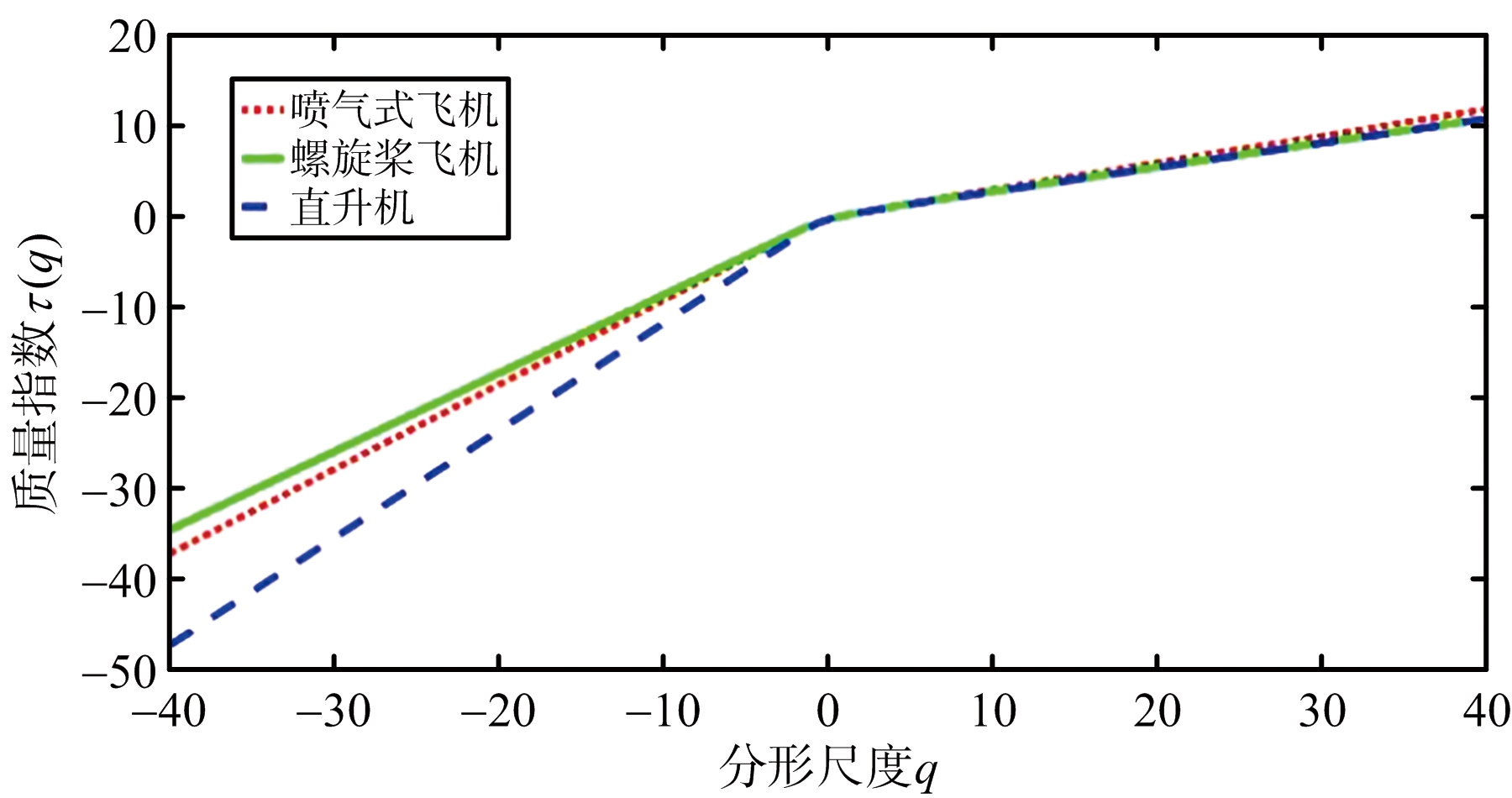
图2 3类飞机目标的质量指数曲线

(a) 未进行FRFT
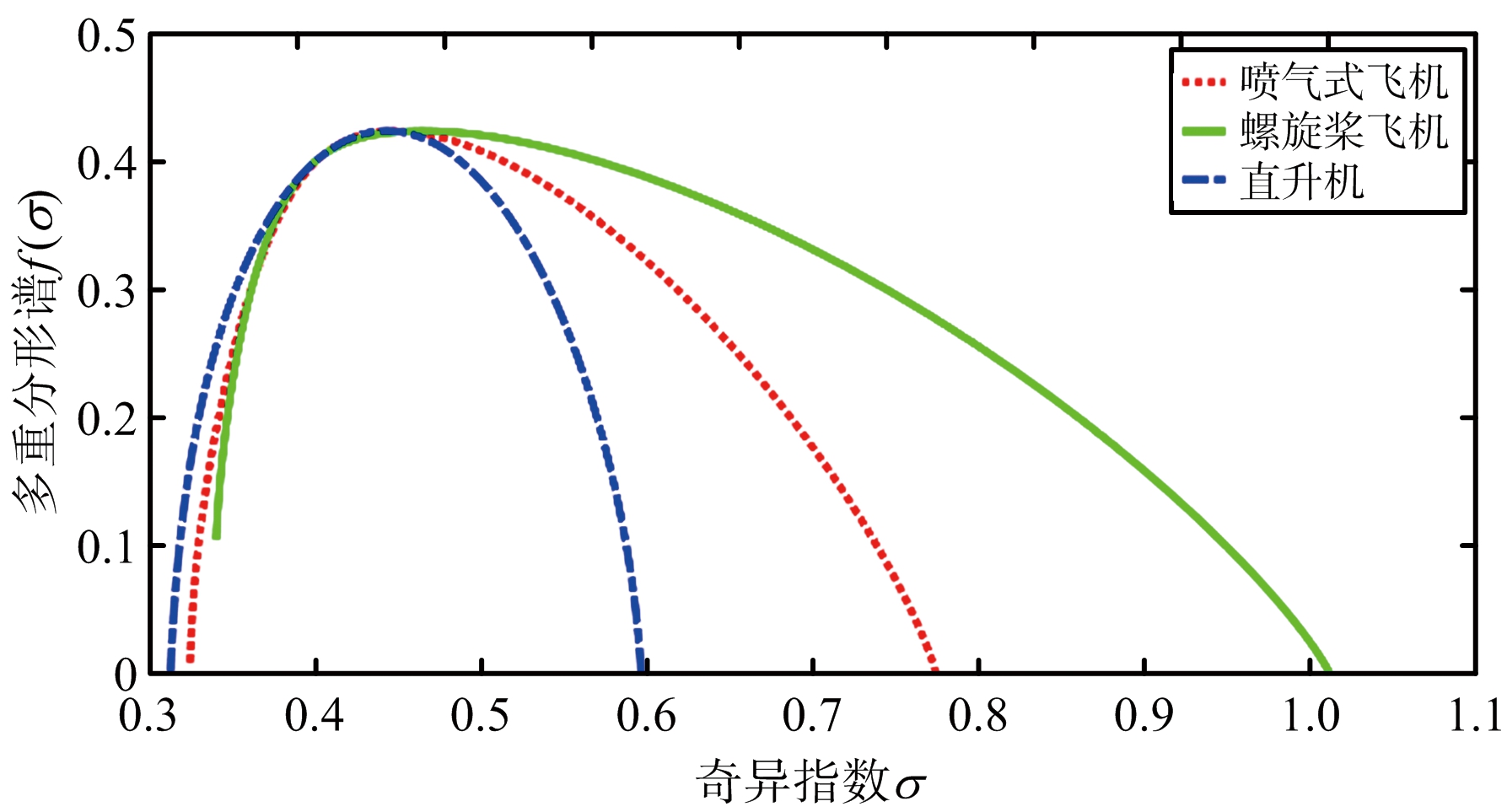
(b) 进行FRFT
图3 3类飞机目标的多重分形谱
从图2(a)可以看出,在进行FRFT之前,直升机和喷气式飞机的质量指数曲线近似为线性函数,多重分形特性不明显;经FRFT后,在最优FRFT域分析雷达回波数据的质量指数曲线,如图2(b)所示,3类飞机目标的质量指数呈现出凸函数的特性,多重分形特性均可以得到增强,尤其是直升机。喷气式飞机和直升机的奇异指数的分布范围较小,多重分形特性不明显,如图3(a)所示,这也进一步证实了在图2(a)中其质量指数曲线近似服从线性关系;从图3(b)可以看出,在最优FRFT域,3类飞机目标回波数据的奇异指数的分布范围均增大,其中直升机增幅最大。分析在时域和最优FRFT域下,不同分形尺度下分形维数之间的差异性,实验结果如图4所示。在图4(a)中,不同分形尺度下,喷气式飞机和直升机的分形维数基本保持不变,多重分形特性不明显;经FRFT后,如图4(b)所示,不同分形尺度下,分形维数的变化明显,多重分形特性得到增强。
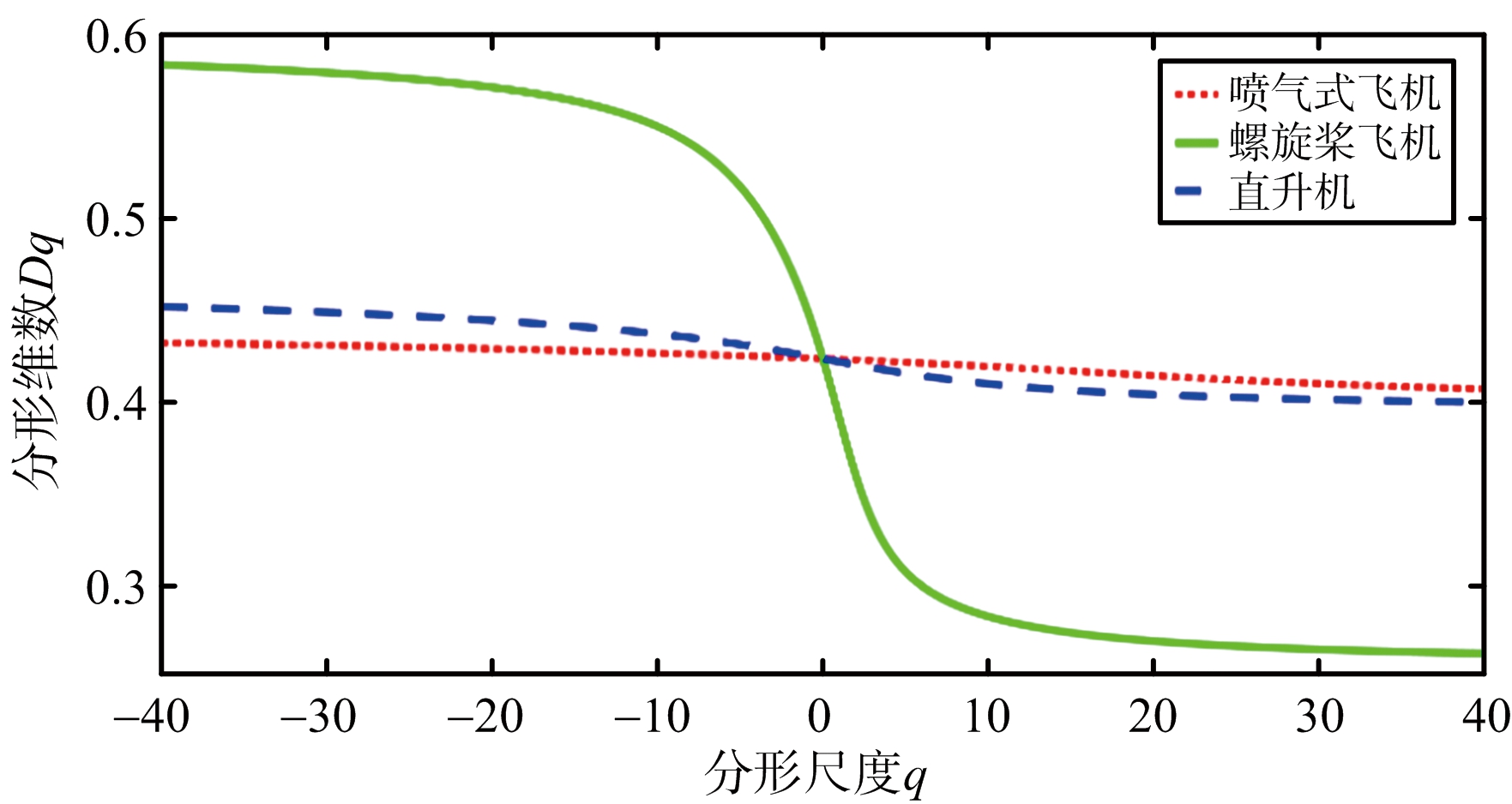
(a) 未进行FRFT
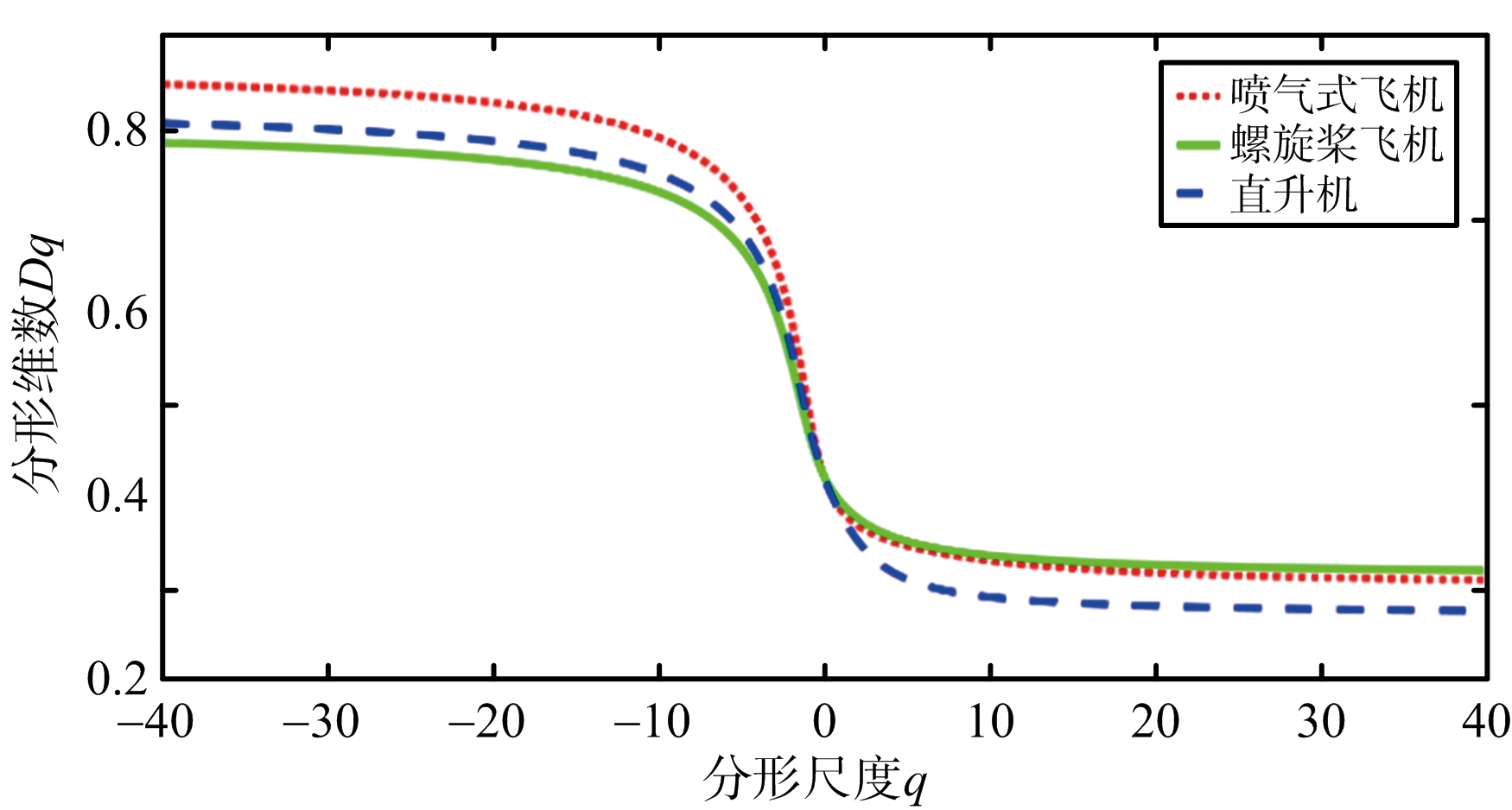
(b) 进行FRFT
图4 3类飞机目标的分形维数谱
随着飞机目标观测时间的增加,3类飞机目标回波数据的多重分形特性会更明显。实验结果表明,首先,3类飞机目标回波数据在最优FRFT域具有多重分形特性;其次,飞机目标回波的多重分形特性可被增强。从图2中的质量指数曲线及图3中的多重分形谱可以看出,3类飞机目标多重分形曲线的形状存在显著差异,因此,利用多重分形曲线形状之间的差异性定义多重分形特征来实现3类飞机目标之间的分类识别。多重分形特征定义如下:
1) 多重分形谱宽度Δσ
Δσ=σmax-σmin
(12)
2) 质量指数曲线截距d
d=min (τ(q))
(13)
3) 多重分形谱一阶导数f′(σ)
(14)
多重分形谱宽度衡量局部分形维数的分布范围,对于某具体的分形体来讲,可认为局部分形维数的范围越大,多重分形特性越明显;质量指数曲线截距表示质量指数曲线的最小值;多重分形谱一阶导数衡量多重分形谱的变化率。在提取飞机目标回波多重分形特征的过程中,雷达的工作参数、飞机目标的工作参数和场景参数及观测时间等条件保持不变,机身分量零补偿。喷气式飞机、螺旋桨飞机和直升机的3个多重分形特征的概率密度分布曲线如图5所示。从图5可以看出,3类多重分形特征对喷气式飞机均具有较强的分类识别能力;图5(c)中,多重分形谱一阶导数对直升机也具有较强的分类识别能力。尽管所提取的多重分形特征在一定范围内存在重叠,但综合利用这3个特征有可能获得较好的分类识别性能。
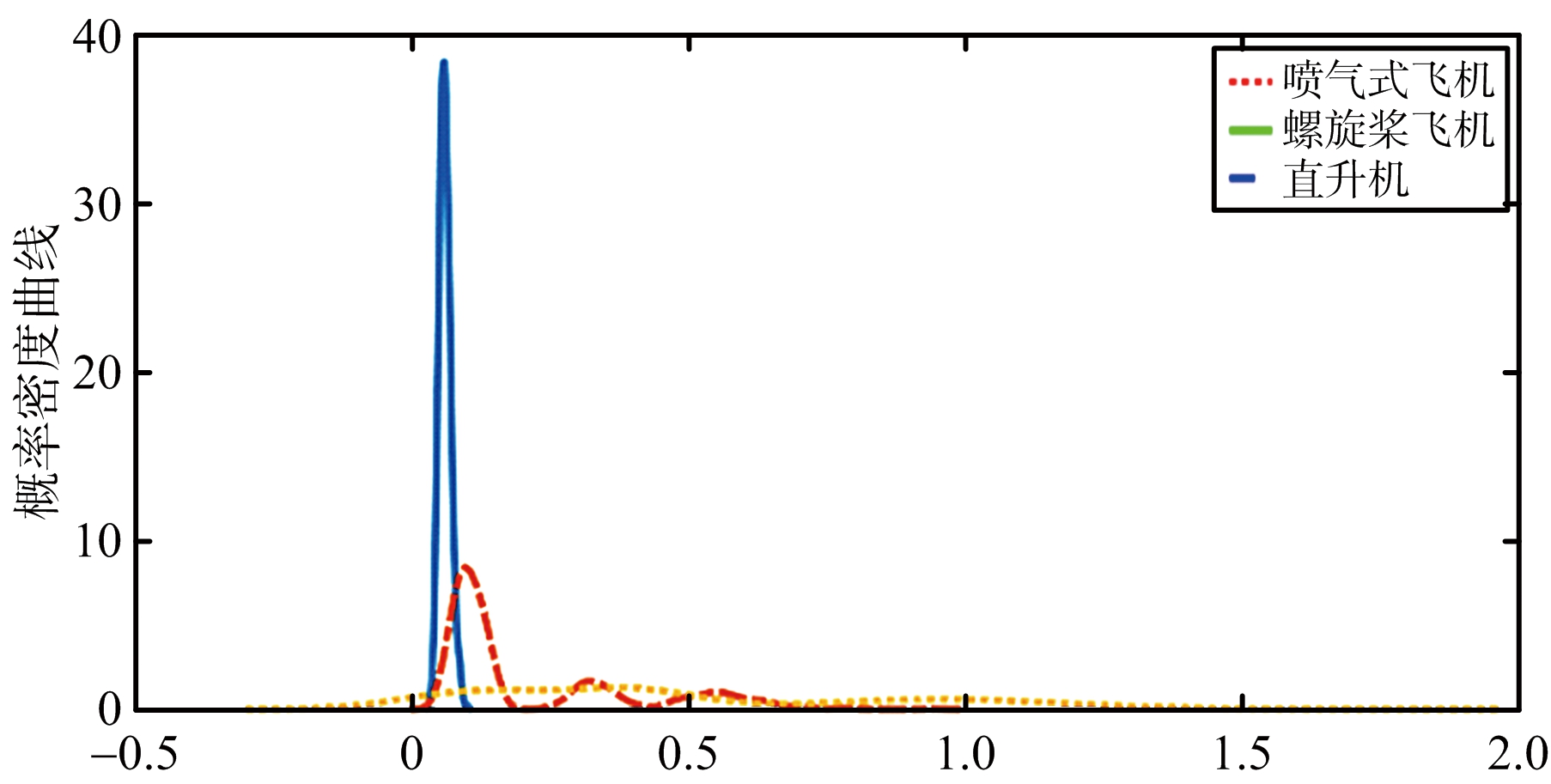
Δσ
(a) 多重分形谱宽度
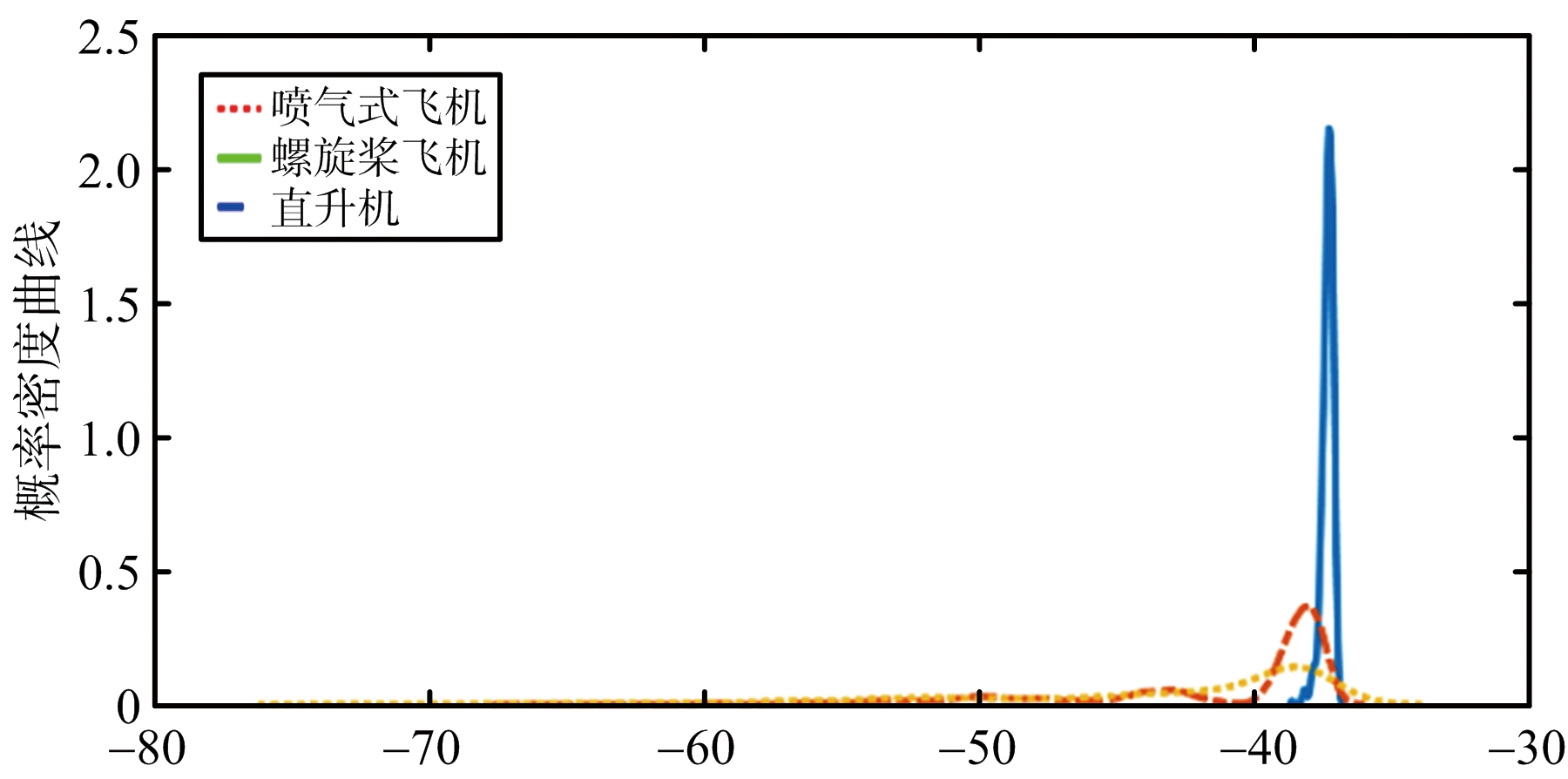
d
(b) 质量指数曲线截距
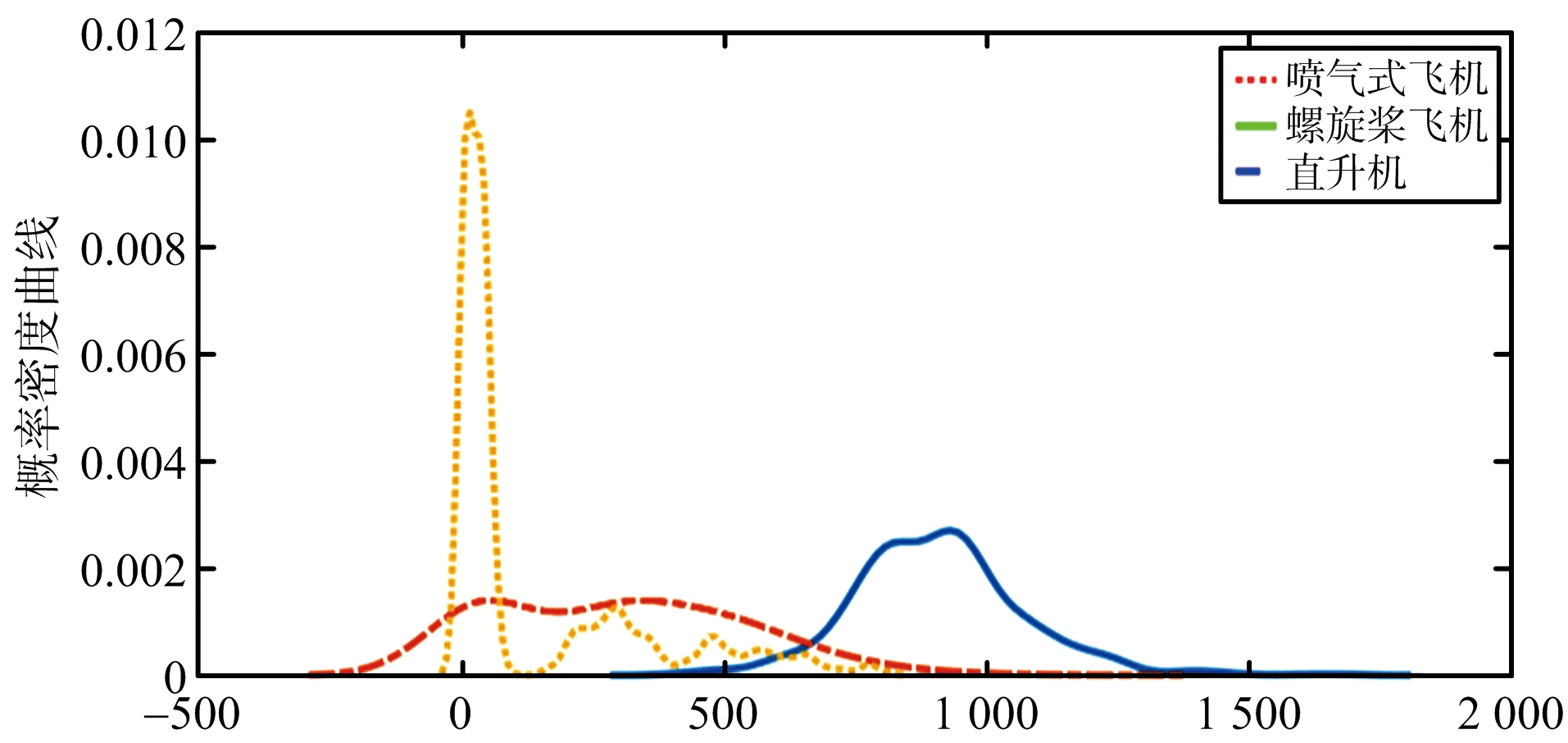
f′(σ)
(c) 多重分形谱一阶导数
图5 多重分形特征的概率密度分布曲线
3 飞机目标分类实验
文献[4]提出了一种时域多重分形飞机分类识别方法,并借助该方法对喷气式飞机、螺旋桨飞机和直升机进行分类识别,结果表明,基于时域多重分形特征的飞机目标正确分类识别率要优于基于特征谱散布特征的飞机目标正确分类识别率。文献[22]采用幅度调制特征和频域熵作为分类特征并结合支持向量机对喷气式飞机、螺旋桨飞机和直升机进行分类,该算法的分类识别率要低于文献[4]提出的基于时域多重分形特征的分类识别率。因此,为探究分数域多重分形方法的有效性,将该方法与文献[4]中所述的时域多重分形分类方法进行对比分析。支持向量机具有较强的泛化能力和收敛速度,因此低分辨雷达飞机目标的分类实验采用支持向量机作为分类器。在实验中,SVM采用高斯核函数,K(xi,xj)= exp(-‖xi-xj‖2/σ2), 目前还没有衡量核函数参数σ2性能的先验知识,因此,在下面的实验研究中,我们会在计算复杂度允许的范围内,多次选择核函数参数σ2通过比较获得较理想的飞机目标分类识别效果。以下实验所得的正确分类识别率均是在合理选择高斯核函数参数基础上得到的。
雷达的工作参数保持不变,飞机目标的结构参数和旋转速度如表1所示,飞机目标探测的场景参数如表2所示。在该实验中,以直升机、喷气式飞机和螺旋桨飞机为例,分析FRFT域多重分形方法和时域多重分形方法的飞机目标分类识别能力,每种类型的飞机有600组回波数据,其中300组回波数据作为测试数据,300组回波数据作为训练数据。两种方法的飞机目标正确分类识别率如表3所示。
表3 不同分类方法飞机目标的分类识别结果
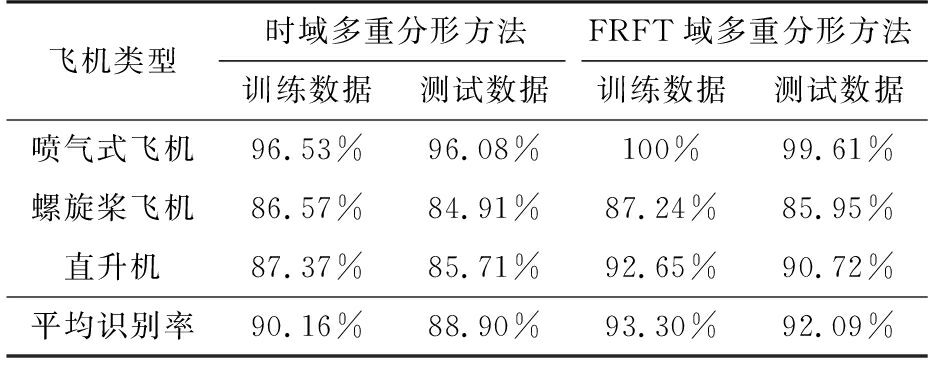
飞机类型时域多重分形方法FRFT域多重分形方法训练数据测试数据训练数据测试数据喷气式飞机96.53%96.08%100%99.61%螺旋桨飞机86.57%84.91%87.24%85.95%直升机87.37%85.71%92.65%90.72%平均识别率90.16%88.90%93.30%92.09%
从表3可以看出,对于上述3类飞机目标,FRFT域多重分形方法的飞机目标正确分类识别率要高于时域多重分形方法,其中,直升机的分类识别率增幅最大;FRFT域多重分形方法的平均正确分类识别率要高于时域多重分形方法的平均正确分类识别率;同样条件下,不论是采用FRFT域多重分形方法还是时域多重分形方法,螺旋桨飞机的分类识别率最低。
在上述实验的基础上,为进一步探究分数域多重分形方法在低信噪比下飞机目标分类识别效果,我们进行了以下实验。雷达的工作参数、飞机目标的工作参数及场景参数保持不变,同样以上述3类飞机目标为研究对象,每种类型的飞机有600组回波数据,其中300组回波数据作为训练数据,300组回波数据作为测试数据。在该实验中分类器采用SVM,SVM采用高斯核函数,且合理选择核函数参数,分析在不同信噪比下分数域多重分形方法的飞机目标分类识别效果,3类飞机目标测试数据的平均正确分类识别率如表4所示。表4说明,信噪比降低,飞机目标的平均正确分类识别率减小,即使在低信噪比的条件下,分数域多重分形方法也可实现3类飞机目标的粗分类。随着观测时间和脉冲积累数的增加,飞机目标的分类识别率会增加。
表4 不同信杂比条件下的分类识别结果
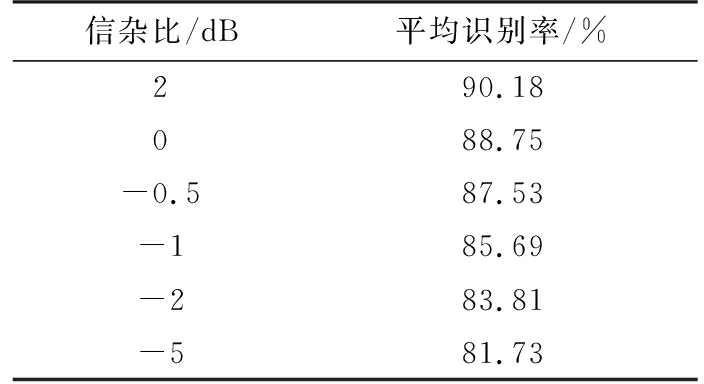
信杂比/dB平均识别率/%290.18088.75-0.587.53-185.69-283.81-581.73
上述实验表明,FRFT域多重分形方法具有较理想的分类识别效果,究其原因主要是因为该方法是在最优FRFT域分析雷达回波数据的多重分形特性,首先,在最优FRFT域,雷达回波数据的噪声能量被抑制,有效回波能量较大,可提高信号的信噪比,有利于飞机目标的分类识别;其次,所提取的多重分形特征对飞机目标均具有较强的分类能力。
4 结束语
从最优FRFT域提取飞机目标的多重分形特征为常规低分辨雷达飞机目标的分类辨识提供了新的分类方法。在本文中,我们首先用三阶Renyi信息熵计算飞机目标回波的最优FRFT阶数,并确定雷达回波数据的最优FRFT域;在最优FRFT域分析飞机目标回波的多重分形特性并提取多重分形特征;借助SVM作为分类器对飞机目标进行分类辨识。实验表明,直升机、喷气式飞机和螺旋桨飞机的雷达回波数据不仅在最优FRFT域具有多重分形特性,且其多重分形特性经FRFT后得到增强;采用FRFT域多重分形方法,3类飞机目标的分类识别率及平均分类识别率都要高于时域多重分形方法;在低信噪比的条件下,FRFT域多重分形方法也可实现飞机目标的粗分类。由于低分辨雷达体制存在的局限性,尽管飞机目标的分类识别率在一定程度上得到了提高,本文所述方法只能对不同类型的飞机目标实现粗分类。
[1] 丁建江.防空雷达目标识别技术[M]. 北京: 国防工业出版社,2008:44-66.
[2] YONG Y W, HOON P J, WOO B J, et al. Automatic Feature Extraction from Jet Engine Modulation Signals Based on an Image Processing Method[J]. IET Radar, Sonar and Navigation , 2015, 9(7):783-789.
[3] 邵云, 王恒立, 张何建, 等.低分辨率雷达基于波形特征的目标识别[J]. 舰船电子对抗, 2015, 38(4):62-65.
[4] 李秋生, 谢维信.基于多重分形特征的防空雷达目标分类方法[J]. 计算机应用研究, 2013, 30(2):405-409.
[5] 丁建江, 张贤达.常规雷达JEM特征分析与目标分类的研究[J]. 电子与信息学报, 2003,25(7):956-962.
[6] 谢岱玲, 陈泽宗, 洪羽萌, 等.利用分数阶Fourier变换抑制高频地波雷达中线性调频干扰[J]. 电讯技术, 2016, 56(3):313-318.
[7] YU Ge, PIAO Shengchun, HAN Xiao. Fractional Fourier Transform-Based Detection and Delay Time Estimation of Moving Target in Strong Reverberation Environment[J]. IET Radar, Sonar and Navigation, 2017, 11(9):1367-1372.
[8] 杜兰, 史蕙若, 李林森, 等.基于分数阶傅里叶变换的窄带雷达飞机目标回波特征提取方法[J]. 电子与信息学报, 2016, 38(12):3093-3099.
[9] 范一飞, 罗丰, 李明, 等.海杂波AR谱多重分形特性及微弱目标检测方法[J]. 电子与信息学报, 2016, 38(2):455-463.
[10] 金丹, 察豪, 左雷, 等.海杂波的多重分形消除趋势波动分析[J]. 海军工程大学学报, 2017, 29(5):29-33.
[11] LI Qiusheng, XIE Weixin, LUO Cheng. Identification of Aircraft Targets Based on Multifractal Spectrum Features[C]∥2012 IEEE 11th International Conference on Signal Processing, Beijing: IEEE, 2012:1821-1824.
[12] 李秋生, 刘小燕, 陈建萍.常规雷达飞机回波的分形建模与目标分类研究[J]. 赣南师范学院学报, 2015, 36(3):34-39.
[13] 李秋生, 袁新娣, 管立新.常规雷达飞机目标回波多重分形特性分析[J]. 安徽大学学报(自然科学版), 2012, 36(5):47-54.
[14] LI Q, XIE X, LU Q. Generalized Dimension Spectrum Features Based Classification Method for Aircraft[C]∥2016 CIE International Conference on Radar, Guangzhou, China: IEEE, 2016.
[15] 顾智敏, 张兴敢, 王琼. FRFT域内的海杂波多重分形特性与目标检测[J]. 南京大学学报(自然科学版), 2017, 53(4):731-737.
[16] 李秋生, 谢晓春, 朱红, 等.分数阶Fourier域低分辨雷达飞机回波的分形特性分析与目标分类[J]. 计算机应用研究, 2018, 35(9):2869-2872.
[17] ELGAMEL A S, CLEMENTE C, SORAGHAN J J. Radar Matched Filtering Using the Fractional Fourier Transform[C]∥Sensor Signal Processing for Defence,London, UK:IET,2010:1-5.
[18] 邵岩.分数阶傅里叶变换算法的应用研究[D].哈尔滨:哈尔滨理工大学, 2016.
[19] 陈辉, 丁宇, 焦小辉, 等.基于广义模糊函数的低分辨雷达目标识别[J]. 舰船电子对抗, 2016, 39(5):46-49.
[20] LI Q S, XIE W X. Target Classification with Low-Resolution Surveillance Radars Based on Multifractal Features[J]. Progress in Electromagnetics Research B, 2012,45:291-308.
[21] LI Q S, ZHANG H X, LU Q, et al. Research on Analysis of Aircraft Echo Characteristics and Classification of Targets in Low-Resolution Radars Based on EEMD[J]. Progress in Electromagnetics Research M, 2018, 68:61-68.
[22] 宋新景.低分辨雷达的目标分类识别研究[J]. 雷达科学与技术, 2016, 14(3):286-290.
SONG Xinjing.Target Identification for Low Resolution Radar[J].Radar Science and Technology, 2016, 14(3):286-290.(in Chinese)
