0 引言
目标角度估计是雷达探测的一项重要任务,单脉冲测角技术因其原理简单且易于工程实现,被广泛应用于各类雷达系统[1-2]。在干扰环境下,采用自适应数字波束形成(ADBF)技术可有效抑制干扰,然而对干扰的抑制会使阵列方向图产生扰动,尤其当干扰靠近主瓣时,自适应和差方向图严重畸变,自适应单脉冲鉴角曲线与静态鉴角曲线失配,导致角误差估计性能严重恶化。
针对该问题,目前已有的自适应单脉冲测角方法大致可以分为三大类:第一类是和、差波束同时置零技术,这是一种开环处理方法,要求干扰方向已知,其自适应能力较差;第二类是基于最大似然方法的广义单脉冲测角技术,最早由Davies等[3]针对等距线阵模型提出,Nickel[4-6]将该方法推广到任意结构的两维阵列上去,但该方法实际是一种二维方向信息联合一阶逼近算法,测角精度不高;第三类是基于自适应方向图保形技术,即通过采用约束的方法来进行自适应方向图保形[7-8],使得在抑制干扰的同时使鉴角曲线特性尽可能保持不变。这类方法通常都采用线性约束,当存在近主瓣干扰时,鉴角曲线还是会恶化严重,影响测角精度[9-10]。文献[11-12]提出了一种多点约束自适应单脉冲测角方法,能在抑制主瓣干扰的同时较好地保持鉴角曲线特性,但该方法只适用于一维线阵,局限性较大。
本文在此基础上提出了一种适用于二维面阵的约束自适应单脉冲测角方法,该算法首先通过约束条件对二维方向信息去耦合,然后在各方向维上分别应用多点约束进行鉴角曲线拟合,最后采用广义单脉冲测角技术进行角度估计。仿真实验证实了该方法的有效性
1 单脉冲测角问题分析
通常雷达系统中主瓣干扰与旁瓣干扰的区分以和方向图主瓣3 dB波束宽度或第一零点为基准,文章针对干扰靠近主瓣时角误差估计问题,首次给出近主瓣干扰定义:即当干扰从旁瓣进入到差方向图3 dB波束宽度(即图1中A点)开始,到干扰进入和方向图3 dB波束宽度(B点)结束,这中间一段间隔称之为“近主瓣”(A点到B点),在这段间隔内出现的干扰称其为“近主瓣干扰”。
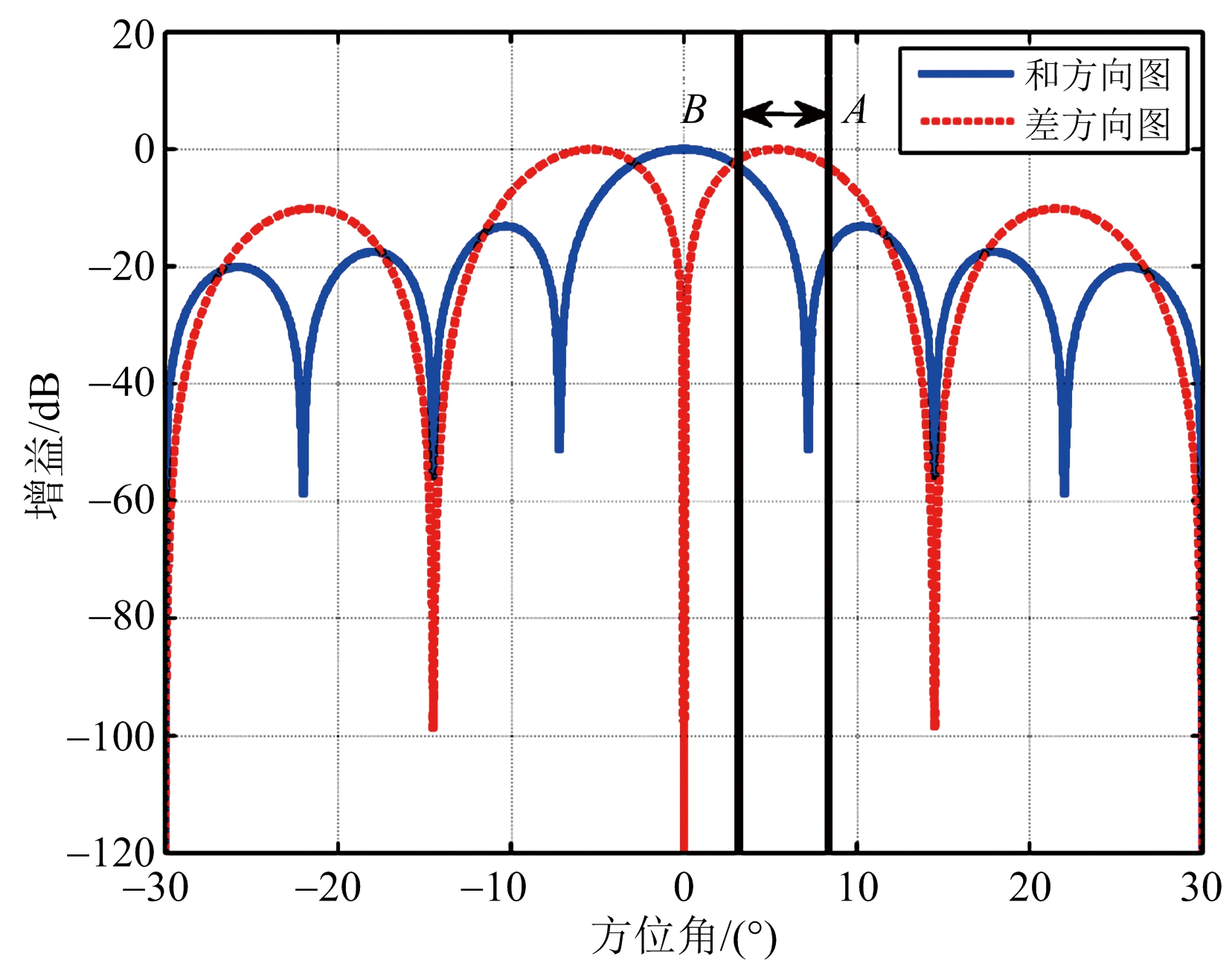
图1 和差方向图
假设空间有一窄带信号及干扰,则阵列输出信号可以表示为
z(t)=a(ut,vt)St+Ajsj+n
(1)
式中:ut=cosθtsinφt,vt=sinθt分别为信号入射方向参数,φt,θt分别为目标方位角和俯仰角; a(ut,vt)为目标信号导向矢量;St为目标信号;Aj为干扰信号导向矢量矩阵;sj为干扰信号矢量;n为阵列高斯白噪声,并设噪声相互独立且噪声与信号互不相关。
阵列和、差波束分别为![]() 其中w和dα为和、差波束对应的权矢量。则静态单脉冲比为[10]
其中w和dα为和、差波束对应的权矢量。则静态单脉冲比为[10]
gα=real(Δα/Σ),α=u,v
(2)
当存在干扰时,若采用常规的自适应波束形成方法,得到的和差波束权矢量为w′=R-1w, d′α=R-1dα,其中,R为包括干扰和噪声的接收信号的协方差矩阵,由此得到的自适应单脉冲比为
g′α=real((d′α)Hz/w′Hz),α=u,v
(3)
考虑一个16阵元的均匀线阵,阵元间距为半波长,对应图1中A,B点分别为θA=8.4°和θB=3.2°。当干扰角度θj从旁瓣慢慢靠近主瓣时,其自适应鉴角曲线与静态鉴角曲线的对比如图2所示。图中实线表示无干扰存在时的静态鉴角曲线,虚线表示不同干扰下的自适应鉴角曲线。当干扰角度θj临近θA时,观察到自适应鉴角曲线明显偏离静态鉴角曲线,开始发生畸变,且干扰越靠近θB畸变越明显。
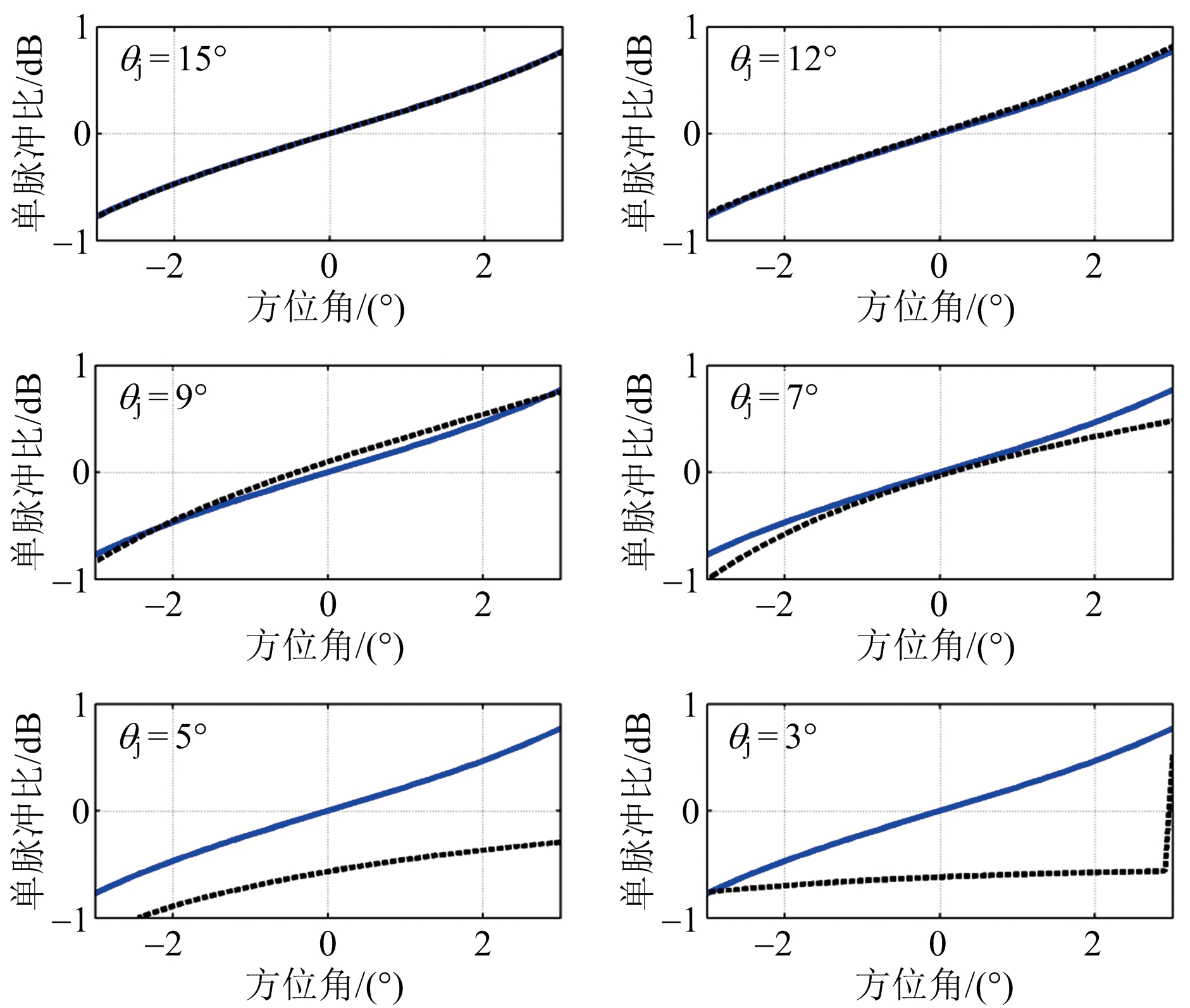
图2 自适应鉴角曲线
由以上分析可知,当存在近主瓣干扰时,常规自适应单脉冲测角性能将急剧下降,因此需要研究新的单脉冲测角方法。
2 平面阵约束自适应单脉冲测角方法
针对近主瓣干扰引起的自适应单脉冲测角失效问题,本文提出一种平面阵约束自适应单脉冲测角算法,该方法首先形成无约束的自适应和波束,其次在形成自适应差波束时增加相应约束,保证抑制干扰的同时鉴角曲线基本不失真,最后应用广义单脉冲测角算法进行角误差估计,得到角度估计值。具体算法如下:
步骤1 根据雷达接收回波数据,利用自适应波束形成算法,形成无约束的自适应和波束权w′=R-1w,其中R为干扰加噪声协方差矩阵。
步骤2 根据相应的约束条件形成约束自适应差波束权。
根据线性约束最小方差(LCMV)自适应波束形成算法[7]:

(4)
式中,Sα为约束条件矩阵,Gα为约束条件矩阵Sα对应的响应。式(4)解为
(5)
本算法采用以下约束条件来形成差波束:
1) 二维去相关约束:约束二维自适应单脉冲角误差在主波束内近似一阶互不相关,即
α,β=u,v,α≠β
(6)
式中,B为和波束宽度。该式可化为

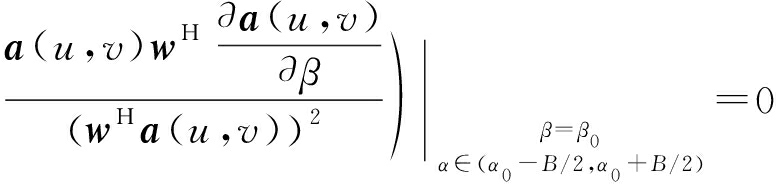
α,β=u,v,α≠β
(7)
2) 零点约束:使自适应差波束在波束指向上为零点,即
(8)
式中,a(u0,v0)为波束指向方向(u0,v0)的导向矢量。
3) 线性约束:在鉴角曲线线性区域保持斜率不变,即
(9)
(10)
式中:(u±Δu,v),(u,v±Δv)分别为方位、俯仰鉴角曲线线性区域两个对称的约束点;ku,kv分别为方位、俯仰静态单脉冲比斜率常数。
4) 非线性点约束:在非线性区域选取点约束
(11)
(12)
式中:(u±Δu1,v),(u,v±Δv1)分别为非线性区域选取的约束点;Ju,Jv分别为约束点处静态单脉冲比绝对值。
约束条件1)是平面阵二维方向信息去耦合条件,可在主波束内选择几个点进行约束,条件2)和3)常见于线阵的自适应单脉冲测角算法,条件4)是针对存在近主瓣干扰时鉴角曲线畸变的情况增加的点约束,可进行鉴角曲线拟合。由此得到约束条件矩阵和响应矩阵为
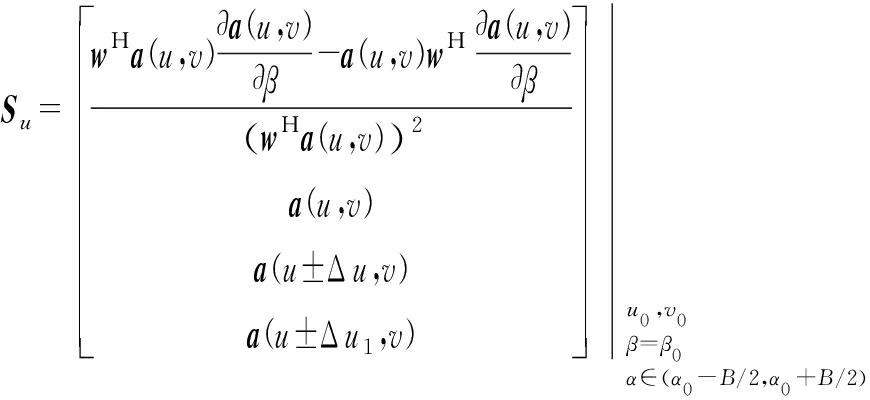
(13)

Sv和Gv与上面类似,这里不再赘述。代入式(5),即可解得约束自适应单脉冲测角的差波束权系数du,dv。
步骤3 应用广义单脉冲原理得到角度估计值ut,vt。
广义单脉冲原理是基于最大似然估计推导得到的更为实用的阵列雷达单脉冲角度测量方法,可适用于特殊的和差波束加权,例如低副瓣加权、自适应加权等,其计算公式为[3]
(15)
式中,g′α=real((d′α)Hz/w′Hz)为求得的方位向和俯仰向单脉冲比,![]() 为单脉冲比的斜率修正矩阵,
为单脉冲比的斜率修正矩阵,![]() 为偏差修正量,且
为偏差修正量,且
(16)
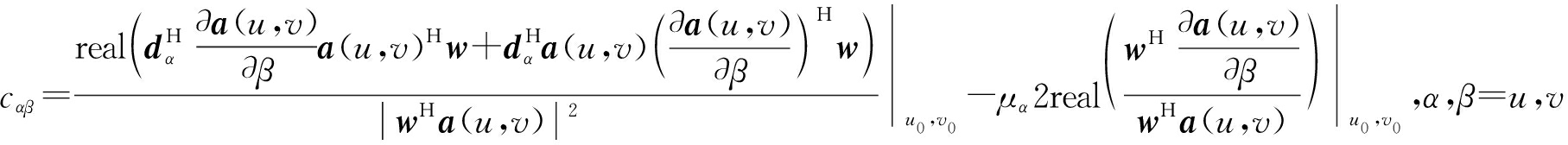
(17)
将步骤3得到的du,dv代入式(15),即得到角度估计值ut,vt。
3 仿真实验
下面通过两个仿真实验分别对新方法的鉴角曲线特性和测角性能进行仿真。
实验1: 鉴角曲线对比
考虑一个30×15的平面阵,相邻阵元间距为半波长,其方位和俯仰向3 dB的波束宽度分别为φ3 dB=7.3°,θ3 dB=3.5°。设波束指向为(φ0,θ0)=(0°,0°),目标角度为(φt,θt)=(0.5°,0.5°),存在一个近主瓣干扰(φj,θj)=(4°,0°),干噪比为50 dB,约束条件1)选取点(φ0,θ0),(φ0±1°,θ0),(φ0,θ0±1°),约束条件4)选取点(φ0±2°,θ0),(φ0,θ0±2°),噪声为高斯白噪声。
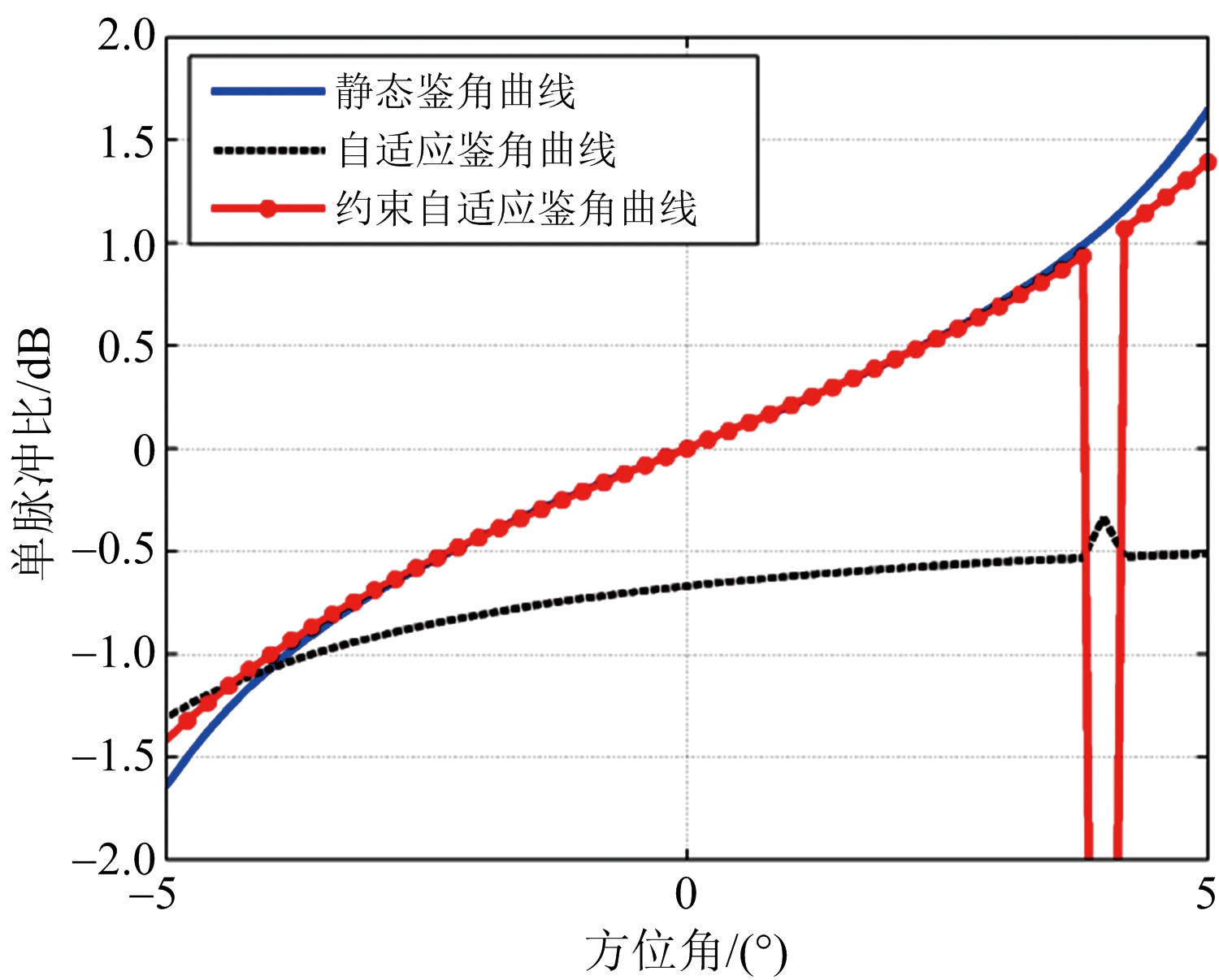
(a) 方位鉴角曲线
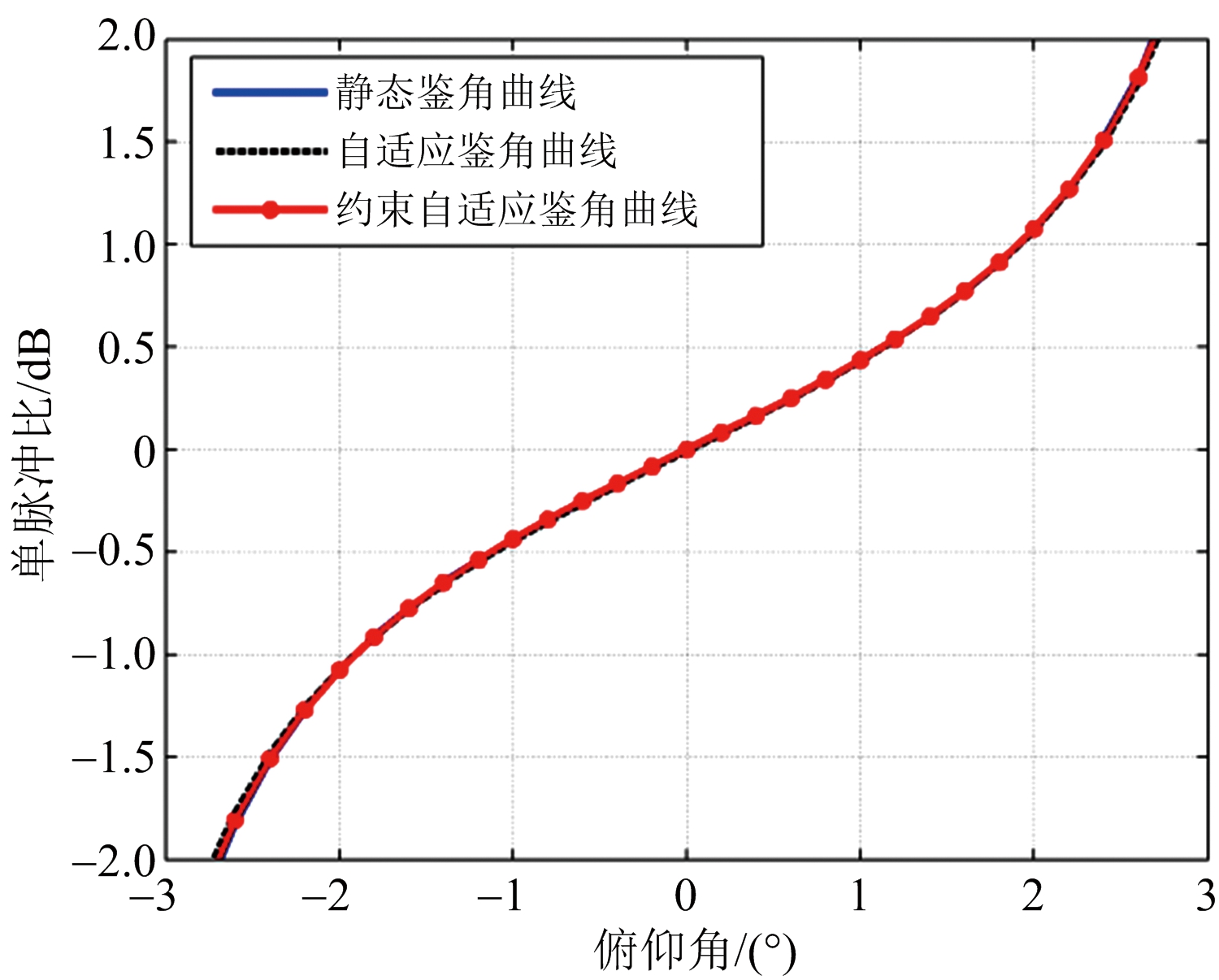
(b) 俯仰鉴角曲线
图3 近主瓣干扰下鉴角曲线
图3分别给出了方位和俯仰两个方向的静态、常规自适应和约束自适应鉴角曲线。无干扰时直接采用静态鉴角曲线进行角误差估计;在近主瓣干扰情况下,由于和差方向图在干扰方向产生自适应零陷,导致常规自适应鉴角曲线失配严重,在波束指向附近的零点特性和线性特性丧失,难以完成角误差估计;而约束自适应鉴角曲线,在近主瓣干扰环境下,除干扰方向曲线畸变外,其他区域基本能够保持静态鉴角曲线特征,因此单目标出现在该区域内,依然能够较准确完成目标角误差估计。该仿真结果有效验证了约束自适应单脉冲测角算法在抑制近主瓣干扰的同时能基本保持自适应鉴角曲线不失真。
实验2: 单脉冲测角性能对比
仍采用实验1所用阵列及基本参数,在方向图主瓣区域均匀固定25个目标,分别对不同干扰场景下的自适应单脉冲角误差估计性能进行仿真分析。
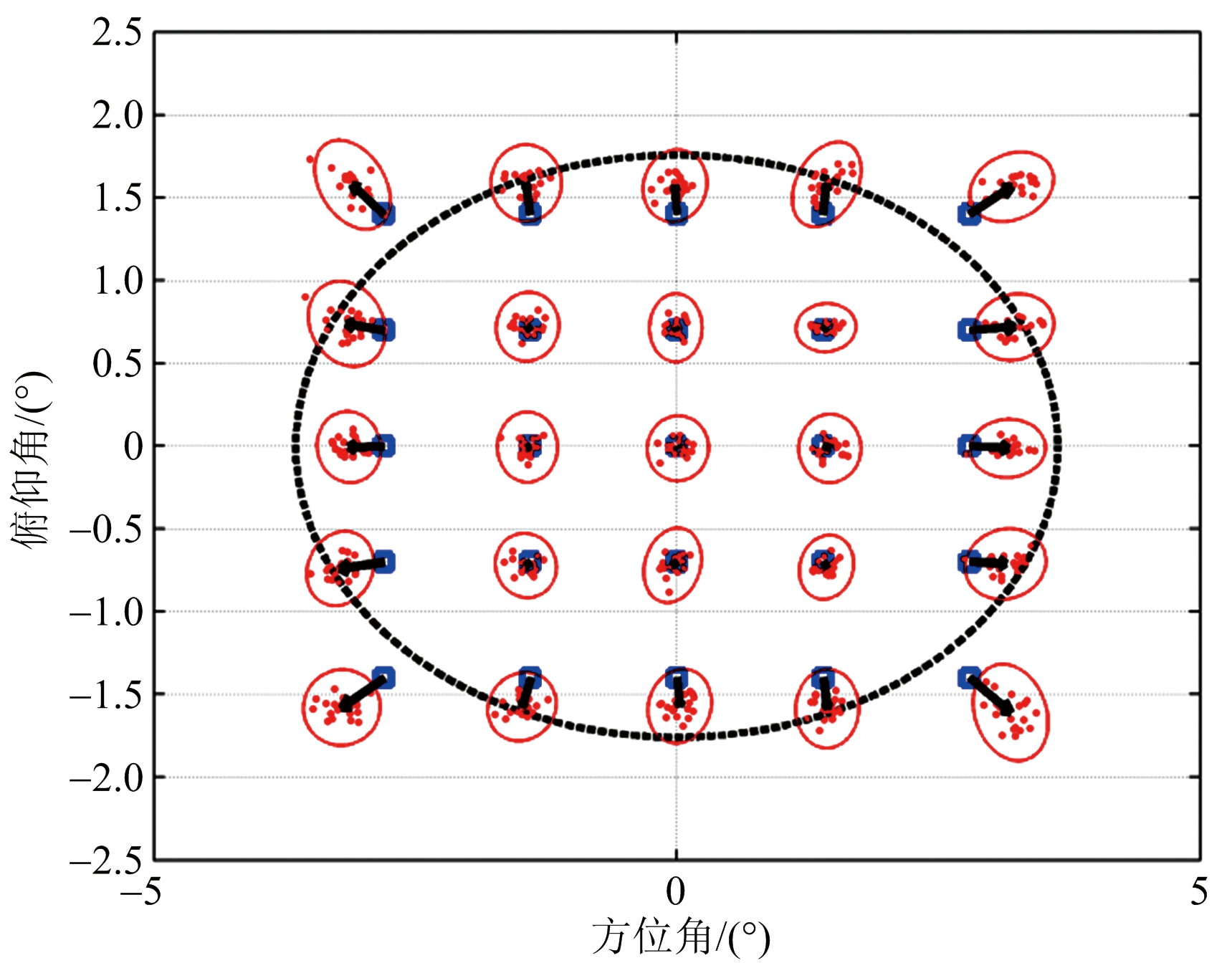
图4 无干扰时单脉冲角度估计
图4给出了无干扰时和波束主瓣内的常规单脉冲测角性能示意图,和波束的3 dB主瓣在图中用近似为圆的虚线表示。针对每个所设定的目标位置(图中用“□”表示)进行20次仿真,每次角度测量值在图中用点表示,实线椭圆为20次角度估计的标准差椭圆,直观地反映了角度测量值的分布情况,真实值与估计均值之间用箭头连接,箭头长短反映了测角偏差的大小。
1) 干扰场景1: 旁瓣干扰(20°,0°)
场景1为旁瓣干扰,其自适应单脉冲估计性能如图5所示,常规自适应和差波束基本无畸变,所以两种自适应单脉冲技术的测角性能与无干扰时基本相当。

(a) 常规自适应单脉冲
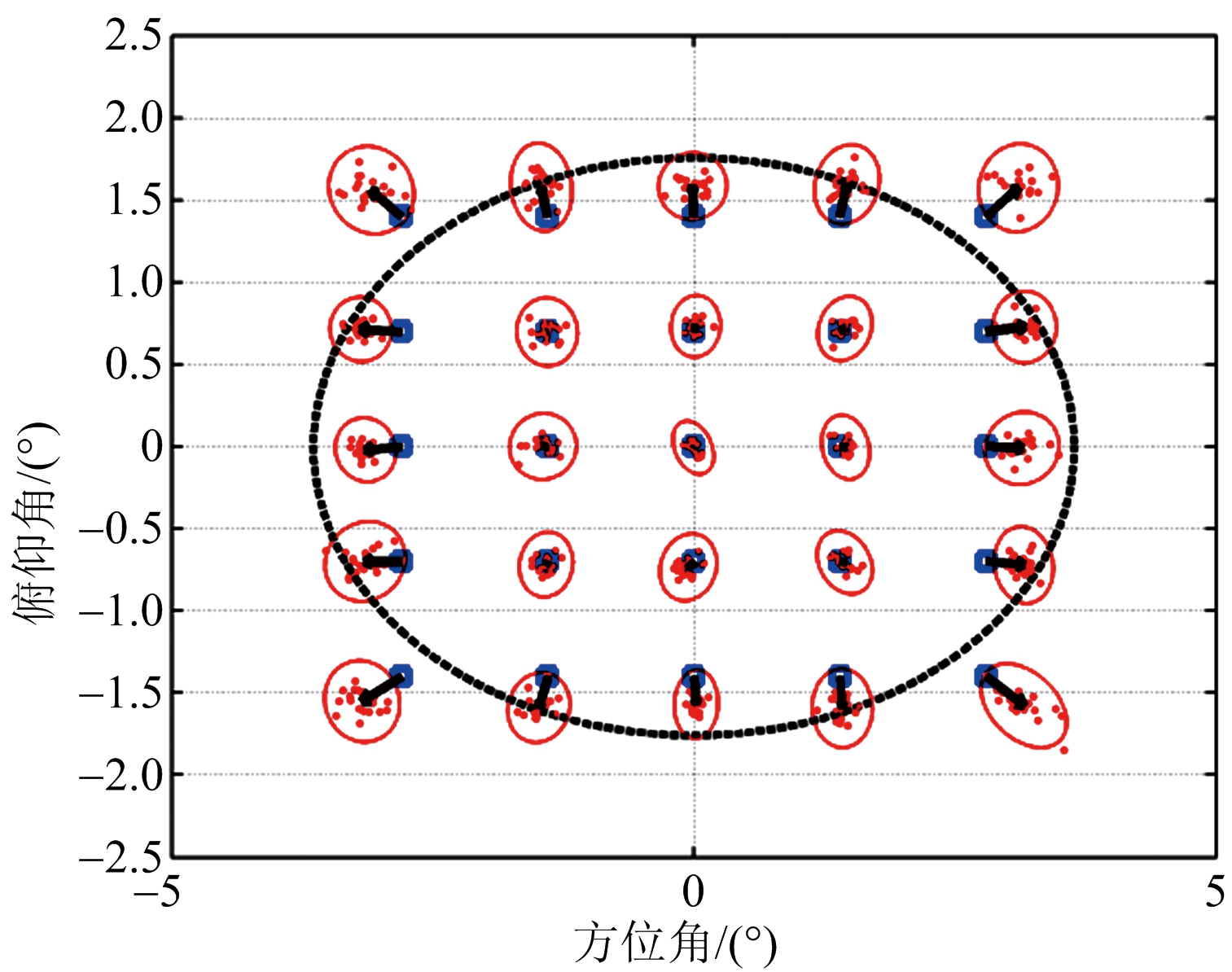
(b) 约束自适应单脉冲
图5 干扰场景1单脉冲角度估计
2) 干扰场景2: 近主瓣干扰(4°,2°)
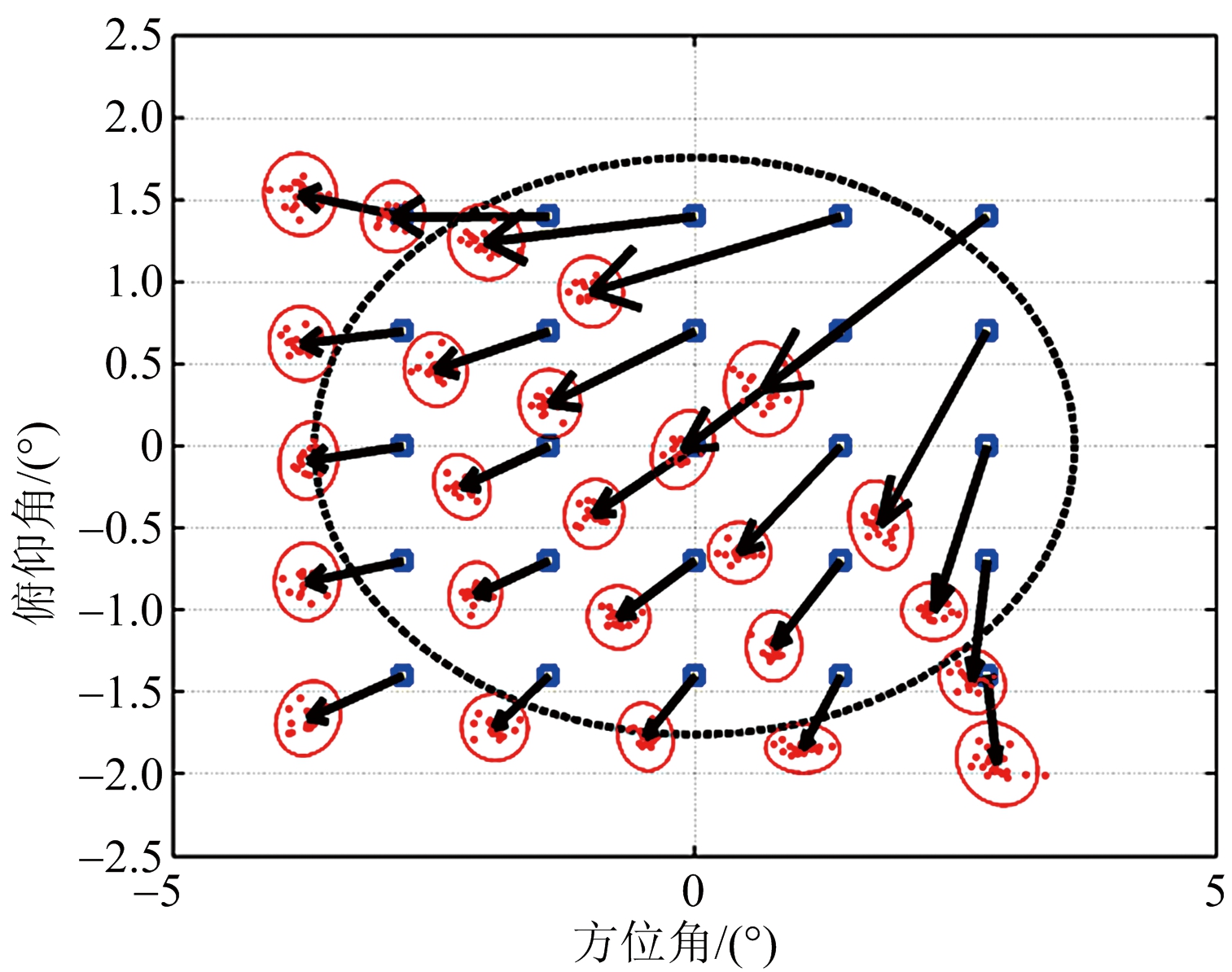
(a) 常规自适应单脉冲
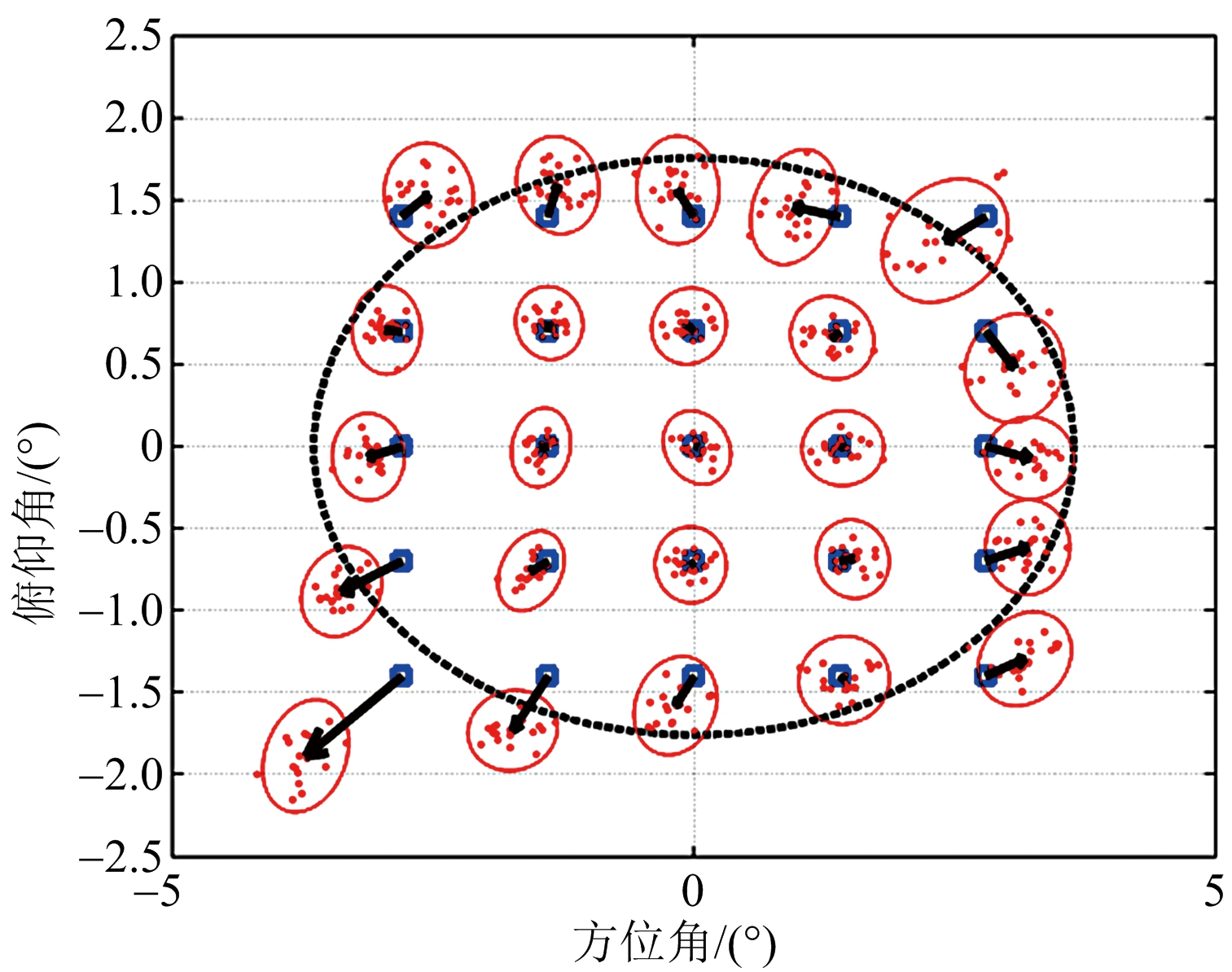
(b) 约束自适应单脉冲
图6 干扰场景2单脉冲角度估计
场景2为近主瓣干扰,其自适应单脉冲估计性能如图6所示。此时干扰已进入差方向图3 dB波束主瓣,其自适应和差波束已出现畸变,因此常规自适应单脉冲的测角性能已出现严重恶化,而约束自适应单脉冲测角性能还可保持相对较高的精度,证明了约束自适应单脉冲具备较好的近主瓣干扰角度估计性能。
4 结束语
本文针对存在近主瓣干扰时,采用常规自适应波束形成技术会导致鉴角曲线严重恶化的情况,提出了一种适用于二维面阵的约束自适应单脉冲测角算法。该方法首先通过二维方向信息去耦合约束,将二维角度联合估计转化为一维;然后,在两个方向维上分别选取多个点约束,得到带约束的自适应和、差方向图,来保证近主瓣干扰存在时自适应鉴角曲线基本不失真;最后,应用广义单脉冲算法得出角度估计值。仿真实验验证了该算法能在抑制干扰的同时保证鉴角曲线基本不失真,具有较高的测角精度。
[1] 李军, 王珍, 张娟娟, 等. MIMO雷达比幅单脉冲测角精度分析[J]. 系统工程与电子技术,2015,37(1):55-60.
[2] YU Kaibo. Advanced Monopulse Processing of Phased Array Radar[C]∥2015 IEEE Radar Conference, Arlington, VA:IEEE, 2015:174-179.
[3] DAVIES R C, BRENNAN L E, REED L S. Angle Estimation with Adaptive Arrays in External Noise Fields[J]. IEEE Trans on Aerospace and Electronic Systems, 1976,12(2):179-186.
[4] NICKEL U L.Monopulse Estimation with Subarray-Adaptive Arrays and Arbitrary Sum and Difference Beams[J]. IEE Proceedings of Radar, Sonar and Navigation, 1996, 143(4):232-238.
[5] NICKEL U L. Overview of Generalized Monopulse Estimation[J].IEEE Aerospace and Electronic Systems Magazine, 2006,21(6):27-57.
[6] NICKEL U L, CHAUMETTE E, LARZABAL P. Statistical Performance Prediction of Generalized Monopulse Estimation[J]. IEEE Trans on Aerospace and Electronic Systems,2011, 47(1):381-405.
[7] 刘宏伟, 张守宏. 平面阵线性约束自适应单脉冲测角算法[J]. 电子与信息学报, 2001, 23(3):275-279.
[8] 徐伟. 线性约束自适应单脉冲测角算法约束条件研究[J]. 火控雷达技术, 2005,34(1):38-42.
[9] 张忠传, 邰新军, 孟庆昌, 等. 主/旁瓣干扰对单脉冲测角的影响分析[J]. 雷达科学与技术, 2012,10(2):207-211.
ZHANG Zhongchuan, TAI Xinjun, MENG Qingchang, et al. Analysis on the Effect of Main/Side Lobe Jamming on Monopulse Angle Estimate[J].Radar Science and Technology, 2012,10(2):207-211.(in Chinese)
[10] ZHENG Zhe, ZHAI Jiahuan, JIA Dongrui, et al. The Principle and Implementation of Monopulse Antenna Angle Error Signal Simulator[C]∥IEEE International Conference on Communication Software and Networks, Beijing:IEEE,2016:249-253.
[11] RAO Cao, LI Rongfeng, DAI Lingyan. Monopulse Estimation with Multipoint Constrained Adaptation in Mainlobe Jamming[C]∥Proceedings of 2011 IEEE CIE International Conference on Radar, Chengdu:IEEE,2011:1054-1057.
[12] 饶灿, 李荣峰.主瓣干扰下多点约束自适应单脉冲测角方法[J]. 雷达科学与技术, 2011, 9(3):232-236.
