0 引言
定位精度是被动定位能否发挥其探测效能的关键因素[1]。多机测角被动定位系统的定位精度除了与雷达角度测量误差、平台位置误差有关外，还和协同编队与辐射源目标相对位置有关[2]。雷达测量误差与平台位置误差受到传感器装备发展的制约，很难在短时间内有大幅提升。因此要提高系统的定位精度，重点需要从协同编队与辐射源目标相对位置方面考虑。
目前大部分研究成果都集中在对协同编队的运动轨迹进行实时控制与规划方面，其中文献 [3-4]对多机测角被动定位载机编队轨迹优化进行了研究，文献[5-6]对多机时差被动定位载机编队轨迹优化进行了研究。上述研究对提高系统定位精度有较好的效果，但载机的运动受到控制与规划，约束了飞行员的空战战术。另外，在低速数据链条件下，机间通信能力受到较大限制，参与目标位置解算的协同平台数目是有限的，因此低速数据链条件下载机运动无约束的被动定位精度提升方法的研究具有现实的意义。
本文提出了一种基于低速数据链的多机测角被动定位协同平台自适应选取方法，可根据协同平台与目标空间态势的实时变化，动态选取参与目标位置解算的协同平台，在保证协同平台数目不大于设定值的条件下，使多机测角被动定位系统的性能最优，同时该方法对载机的运动也没有约束。
1 问题描述
如图1所示，在平面二维情况下，x轴向北， y轴向东，方位角以x轴为起始边，顺时针为正。
表示k时刻协同平台i(i=1,…,n)的坐标，
表示k时刻目标的坐标；θi(k)表示k时刻协同平台i测得的目标方位角。协同平台自适应选取问题就是根据k时刻协同平台与目标空间态势位置相对关系，从n个协同平台中，实时选取m(m≤n)个协同平台参与目标位置解算，使k时刻多机测角被动定位系统的静态定位误差最小。其中，k时刻协同平台i的位置坐标
由平台惯导系统提供，目标位置坐标由多机角度信息融合估计得到。在新的观测数据到达之前，由目标预测状态可以确定下一时刻的目标位置，并重新开始下一时刻的递推循环。
图1 系统协同平台k时刻位置分布图
2 协同平台自适应选取函数
如图1所示，已知k时刻平台i(i=1,…,n)的坐标
测得的目标方位角θi(k)，则有下列关系成立：
(1)
式中：xt(k)，yt(k)分别表示目标北向位置与东向位置；
分别表示平台i北向位置与东向位置；θi(k)表示平台i测得的目标方位角。
由式(1)，对目标位置、方位角和平台位置取微分(用符号Δ表示)，可得
Δθi=
(2)
式中，
由式(2)组成的定位误差方程矢量形式为
dV=CdX+dXs
(3)
式中,观测误差矢量
目标位置误差矢量
与载机位置有关的误差矢量：
(4)
系数矩阵：
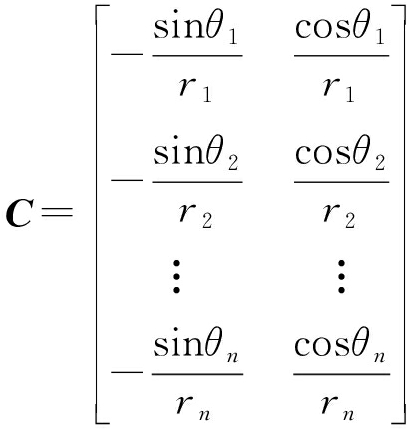
(5)
由式(3)可得目标位置误差矢量为
dX=(CTC)-1CT(dV-dXs)
(6)
相应的误差协方差矩阵为
(7)
系统定位误差的圆概率误差值(CEP)可表示为
(8)
以两平台为例，推导系统定位误差的圆概率误差值(CEP)的具体表达式，设
其中
为雷达角度测量误差方差，
为平台位置误差方差，则
(9)
(10)
Pdx=
(11)
式中，
两平台系统定位误差的圆概率误差值(CEP)具体表达式为
(12)
3 协同平台自适应选取设计与计算步骤
协同平台自适应选取的基本思想是将系统定位圆概率误差值作为优化设计指标，寻求协同平台数目不大于设定值的条件下，系统定位性能最优，即考虑协同平台中采用哪个子集参与目标位置解算。
3.1 自适应选取模型
假设空中存在n个平台，参与目标位置计算的协同平台数目不超过m个，则协同平台编队组成的样本空间为
S=
it≠il∀t,l}
(13)
将系统圆概率误差值(CEP)写成一个与样本空间S相关的函数，即σR(CEP)=f(S)。将其作为目标函数进行优化设计，协同平台自适应选取系统优化设计模型描述为
(14)
式中：Sc表示约束参数集，为S的子集，当存在某种约束时Sc⊆S，对无约束情形Sc=S；Sopt为优化后的最优参数；
表示在约束参数集Sc使用不同的算法求使目标函数最优的参数集。系统优化设计框图如图2所示。
图2 系统优化设计框图
3.2 穷举优化算法
本文所要求解的问题为具有约束条件的最优化问题，可描述为
(15)
由于协同平台编队组成的样本空间的参数元素是有限的，因此拟采用穷举法求解该优化问题，具体步骤为：
1) 根据动态网络拓扑平台数目，计算获取协同平台编队组成的样本空间S；
2) 在样本空间编队组合元素中任意两平台基线距离需小于设定值的约束条件，统计满足约束条件的集合元素，得到约束参数集；
3) 根据式(14)计算优化函数值，保留函数最小值，同时记录相应的协同平台编队组合元素。
4 仿真条件及结果分析4.1 仿真条件
各平台观测器角度测量误差为0.3°，符合零均值高斯分布，采样时间T=0.1 s，目标辐射源的初始位置为(200 km,200 km)，位置导航误差为100 m，符合零均值高斯分布，目标辐射源蛇形机动，径向速度200 m/s，切向速度200 m/s，转弯半径5 km，航向角-90°。协同平台菱形编队、倒T形编队与倒Y形编队时，参与目标位置计算的协同平台数目不超过3个；协同平台正三角形编队与倒三角形编队时，参与目标位置计算的协同平台数目不超过2个。各协同平台编队初始运动状态信息描述如下：
1) 菱形编队，各平台初始运动状态信息分别为(0,0,200,200)，(20,0,200,200)，(0,20,200,200)，(20,20,200,200)；
2) 倒T形编队，各平台初始运动状态信息分别为(0,0,200,200)，(14.1,-14.1,200,200)，(-14.1,14.1,200,200)，(14.1,14.1,200,200)；
3) 倒Y形编队，各平台初始运动状态信息分别为(0,0,200,200)，(0,-20,200,200)，(-20,0,200,200)，(24.1,24.1,200,200)；
4) 正三角形编队，各平台初始运动状态信息分别为(0,0,200,200)，(5.17,-19.31,200,200)，(-19.31,-5.17,200,200)；
5) 倒三角形编队，各平台初始运动状态信息分别为(0,0,200,200)，(19.31,5.17,200,200)，(5.17,19.31,200,200)。
上述平台运动状态信息矢量分量分别为北向位置、东向位置、北向速度和东向速度；单位分别为km，km，m/s和m/s。
各协同平台构型如图3～图7所示。
图3 菱形编队
图4 倒T形编队
图5 倒Y形编队
图6 正三角形编队
图7 倒三角形编队
4.2 仿真结果与分析
图8～图12分别给出了5种不同平台编队距离跟踪误差曲线。相比较而言，在参与目标位置计算的协同平台数目相同的条件下，采用平台自适应选取技术对参与目标位置计算的平台选取后，其组合滤波的距离跟踪精度误差结果要小于其他固定编队组合的滤波误差结果。
表1 距离跟踪误差百分比比较表 %
编队构型固定组合1固定组合2固定组合3固定组合4自适应法菱形0.830.890.970.640.63倒T形0.730.861.110.720.69倒Y形1.131.501.361.410.96正三角2.843.252.32-1.34倒三角1.452.091.05-0.84
图8 菱形编队距离跟踪误差曲线
图9 倒T形编队距离跟踪误差曲线
图10 倒Y形编队距离跟踪误差曲线
图11 正三角形编队距离跟踪误差曲线
图12 倒三角形编队距离跟踪误差曲线
5 结束语
本文紧密结合工程应用背景，针对多机测角被动定位精度提升问题，提出了一种低速数据链条件下载机运动无约束的协同平台自适应选取方法。仿真结果表明，本文提出的协同平台自适应选取方法能够针对不同场景，根据敌我双方空间态势，动态选取参与目标位置解算的协同平台，大大提高了多机被动定位系统的定位精度。
[1] 方海，白琳，陈显舟.空中运动目标无源定位测速精度
分析[J].空间电子技术，2015,12(3):59-63.
[2] 张永利，周荣坤，计文平，等.舰载机协同无源定位系统精度比较分析[J].兵工自动化，2017，36(2):41-45.
[3] RUI Liyang，XU Zhen. A Fast Global Node Selection Algorithm for Bearings-only Target Localization[J]. Chinese Journal of Aeronautics，2008，21(1):61-70.
[4] 顾晓婕，王新民，李俨.机载雷达组网多站测角被动跟踪轨迹优化研究[J].计算机仿真，2012，29(5)：14-18.
[5] 顾晓婕，王新民，李文超. 多站时差无源定位探测器位置优化[J].传感技术学报，2011，24(1)：93-99.
[6] 曲长文，王昌海，冯奇，等. 时差无源定位系统多机编队动态布站优化[J].舰船电子工程，2017,37(3)：38-43.
