0 引言
空时自适应处理是一种重要的杂波和干扰抑制方法，并广泛应用于雷达、声呐、地震探测和通信领域[1-3]中。在这些领域，通常由于干扰或杂波在时空域中与目标信号耦合，所以需要进行空时自适应处理。
STAP需要准确估计CUT的杂波协方差矩阵[4-12]。在当前的STAP中，CCM完全通过与CUT相似的训练样本[8-10]或者与CUT的CCM相似的样本[11-12]来估计。其中，文献[9]选择和CUT具有较大相关系数的样本作为训练样本来估计CCM。文献[10]选择与CUT的时域波形相似的样本来估计CCM。但是由于完全不相似的样本也可能具有相同的协方差矩阵，所以文献[9-10]中的方法可能会丢弃一些有用的样本。为解决这个问题，文献[11-12]选择与CUT的协方差矩阵相似的样本来估计CCM。其中，文献[12]提出了一种基于系统识别的样本选择方法。它直接选择与CUT的杂波协方差矩阵相似的样本来估计杂波协方差矩阵。
上述方法在估计CUT的CCM时，CUT的所有频率通道的杂波都用选取的训练样本来估计。我们注意到CUT有自身的先验知识：CUT中只有待检测的频率通道可能含有目标信号，其他频率通道都是CUT的杂波，因此CUT的大部分频率通道的杂波是不需要用训练样本来估计的。
考虑到上述先验知识，本文提出基于CUT自身知识的STAP杂波抑制算法。该方法将CUT的杂波分成两部分来重建：第一部分是待检测频率通道的杂波，部分杂波可能混有目标信号，因此需要通过训练样本来估计；第二部分杂波是除了待检测频率通道以外的其他频率成分的杂波，这部分杂波直接采用CUT的杂波，无须估计。
针对高频雷达[13-15]，处理结果表明：1)与文献[8-10]基于CUT相似性的方法相比，所提方法的输出SCNR提高了7 dB以上; 2)与文献[11-12]基于CCM相似性的方法相比，所提方法的输出SCNR提高了5 dB以上。
1 STAP处理的基本原理
设雷达接收天线为N个阵元的线阵，阵元间距为d；一个CPI内有K个脉冲；第l个距离环的数据表示为xl，xl∈C1×NK。于是有
xl=alsws,wt+cl+nl
(1)
式中，cl，nl分别为杂波和噪声，sws,wt为目标的空时导向向量，al为目标信号幅值。
sws,wt=swt⊗sws
(2)
式中,swt为时域导向矢量，swt=[1 ej2πwt … ej(K-1)2πwt]，wt为归一化的多普勒频率；sws为空域导向矢量，sws=[1 ej2πws…ej(K-1)2πws]，ws为空间频率；⊗表示Kronnecker乘积。
设待检测的第l0个距离单元是CUT，则该CUT单元的STAP权向量为
(3)
在式(3)中，sws,wt是待检测频率通道的导向向量，是已知的，而CUT的杂波协方差矩阵Rl0是未知的。目前STAP方法用CUT以外的其他参考单元来估计CUT的Rl0，Rl0的估计值记为
(4)
式中，Ω表示选择的训练样本空间，xl表示第l个训练样本的数据。
2 所提基于CUT自身知识的STAP方法
目前的STAP方法在估计CUT杂波协方差矩阵时，CUT的所有频率通道的杂波都用训练样本来估计。我们注意到CUT中只有待检测频率通道可能混有目标信号，因此只有该频率通道的杂波需要用训练样本来估计；而CUT的其他频率通道都是准确的杂波，不需要用训练样本进行估计。基于该特点，本节给出了基于CUT自身知识的STAP算法。所提方法在重构CUT的杂波时，只有待检测频率通道的杂波用训练样本估计，其他频率通道的杂波用CUT自身的杂波。由于所提方法利用了CUT自身的准确的杂波信息，因此估计的杂波协方差矩阵更准确，从而提高了STAP的性能。
下面将CUT的杂波分成两部分来重建：第一部分是待检测频率通道的杂波重建；第二部分是除了待检测频率以外的其他频率成分的杂波，这部分杂波直接从CUT中提取。最后由重建的杂波来计算CUT的杂波协方差矩阵。
2.1 待检测频率通道的杂波重建
检测CUT的第i个频率通道时，由于该频率通道中的杂波可能混有目标信号，因此需要用训练样本来估计该频率通道的杂波:
(5)
式中，
为CUT中第i个频率通道的杂波幅度的估计值，si为第i个频率通道的导向向量，xl为选取的第l个训练样本的信号，
是第l个训练样本的第i个频率通道的杂波幅度。
2.2 CUT的杂波重构
设CUT的信号为xCUT，则CUT的第i个频率通道(待检测频率通道)的幅度为
xCUT，其中si表示该频率通道的导向矢量。设重构的杂波为
则
(6)
式中：ρisi表示CUT单元中第i个待检测的频率通道的成分，由于该频率通道可能混有目标信号，因此该频率通道的杂波需要由训练样本来估计；
表示用训练样本估计的CUT的第i个频率单元的成分，其中，由式(5)估计；xCUT-ρisi表示CUT单元中除了第i个待检测频率通道以外的其他频率通道的成分，这些频率通道的成分是CUT的杂波成分，无须估计。
2.3 CUT杂波协方差矩阵的估计
用重构的杂波
估计CUT的杂波协方差矩阵：
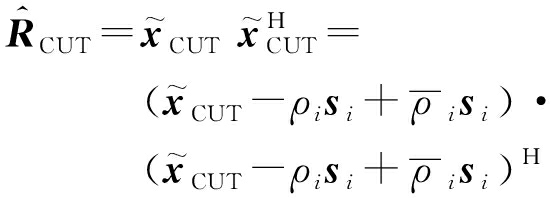
(7)
令
将式(7)估计的杂波协方差矩阵代入到式(3)中，则得到本文所提的基于CUT自身知识的STAP方法。
3 仿真分析
本节中，处理结果表明: 1)与文献[8-10]基于CUT相似性的方法相比，所提方法的输出SCNR提高了7 dB以上; 2)与文献[11-12]基于CCM相似性的方法相比，所提方法的输出SCNR提高了5 dB以上。
雷达工作频率为f0，雷达CPI内有N个脉冲，脉冲间隔为T。在第370个距离单元内，有一个多普勒频率为0.813 8 Hz的弱目标。
3.1 对比分析
第370个距离单元的回波信号的原始频谱如图1(a)所示。从图1(a)可以看出，弱目标回波信号被强杂波掩盖。从图1(a)中截取目标所在方位角的频谱如图1(b)所示。
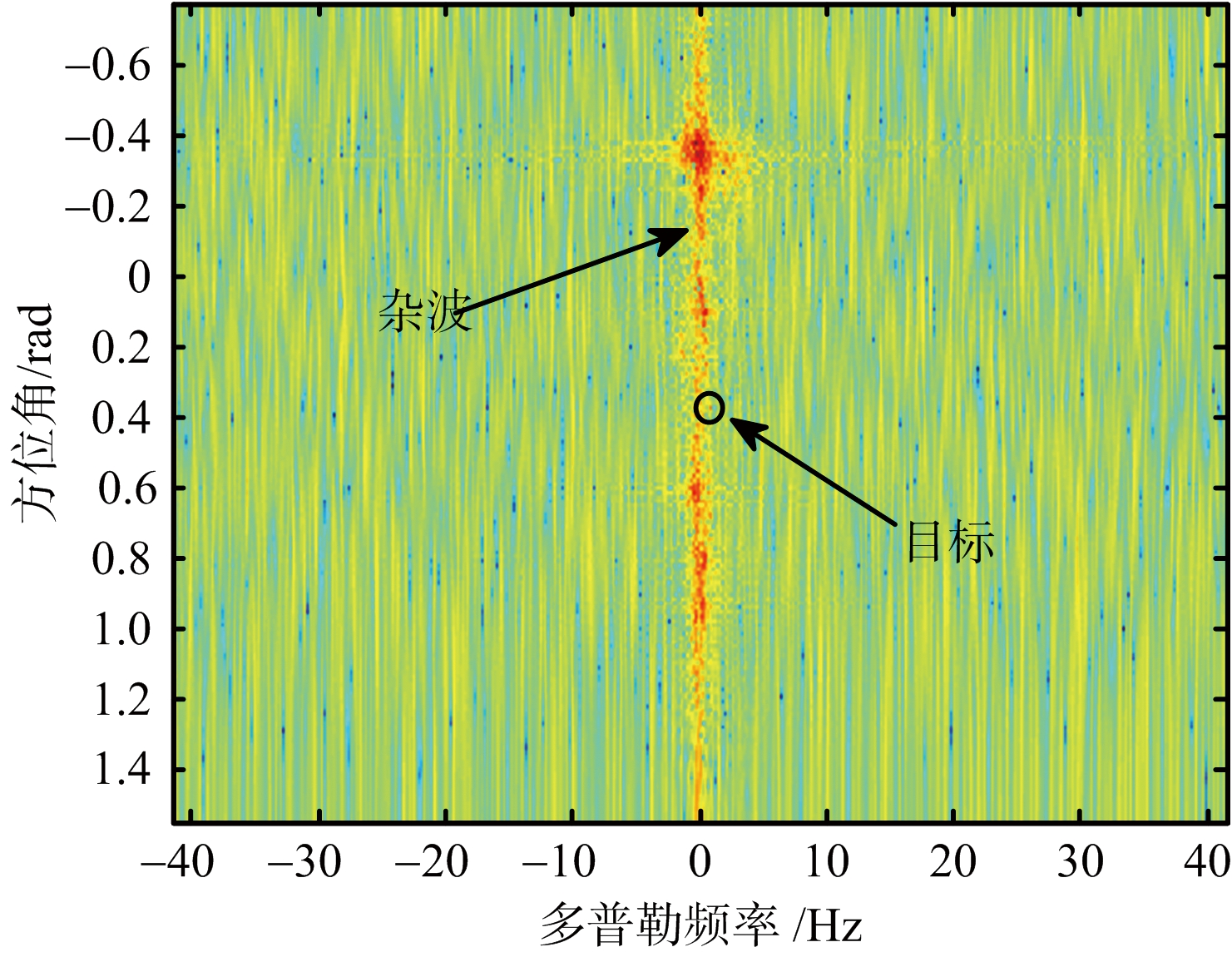
(a) 第370个距离单元的信号频谱
(b) 目标所在方位角的信号频谱
图1 探测信号的频谱
图2(a)是文献[8-10]方法的处理结果，其选择与CUT相似的样本; 图2(b)是文献[11-12]方法的处理结果，其选择与CCM相似的样本。图2(c)是本文提出方法的处理结果。
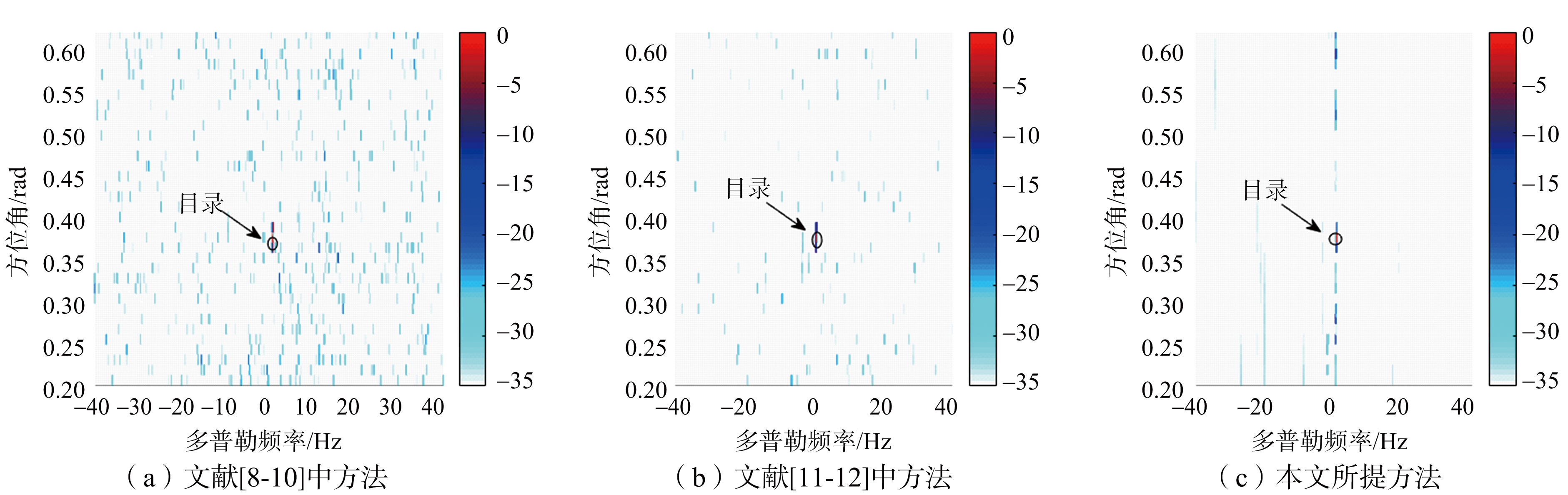
图2 STAP结果
在图2(a)中，残余杂波很强; 图2(b)中的残余杂波明显减弱，在图2(c)中，剩余杂波进一步减弱。图2显示了文献[11-12]选择与CCM相似的样本的方法比文献[8-10]选择与CUT相似的样本方法的杂波抑制性能更好。而所提出方法的杂波抑制性能比文献[11-12]中的方法更好。
为了更清楚地对比上述3种方法的性能，我们截取图2中目标所在方位角的频谱作对比分析，如图3所示。
图3 截取图2中目标所在方位角的处理结果
图3(a)是文献[8-10]方法的处理结果，最大残余杂波是-10.1 dB。图3(b)是文献[11-12]方法的处理结果，最大残余杂波为-12.46 dB。图3(c)是所提方法的处理结果，最大残余杂波为-17.46 dB。比较上述结果，所提方法的性能相比文献[8-10]的方法提高了7.36 dB，相比文献[11-12]的方法提高了5 dB。
3.2 性能对比分析
下面的仿真分析中，我们在雷达的海杂波中加入目标信号，输出为归一化的SCNR。仿真结果如图4所示。这里，SCNR定义如下：
(8)
式中，Es为信号能量，Ecn为杂波和噪声能量。
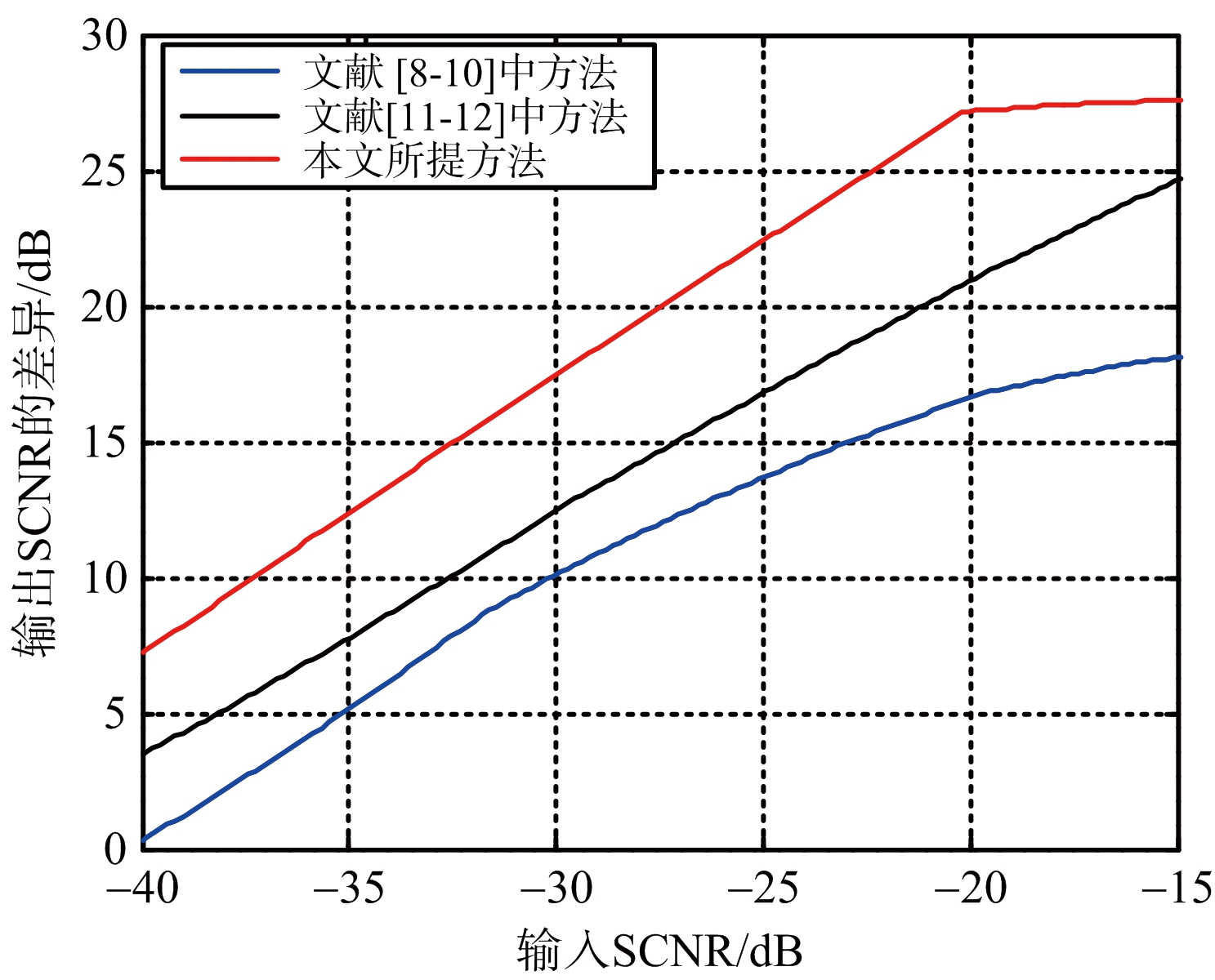
图4 3种STAP方法的性能对比
图4是不同输入SCNR下3种STAP方法的性能表现，纵轴是归一化的输出SCNR。图4显示相比文献[8-10]中选择与CUT相似样本的方法，所提方法的性能提高了7 dB以上；相比文献[11-12]中选择与CUT的CCM相似样本的方法，所提方法性能提高了5 dB以上。
4 结束语
本文提出了一种基于CUT自身先验知识的STAP方法，该方法把CUT的杂波分成两部分来重建：待检测频率通道的杂波用训练样本来估计，而其他频率的杂波则直接从CUT中抽取。处理结果表明，所提算法有效提高了STAP性能。
[1] WANG X R, ABOUTANIOS E, AMIN M G. Reduced-Rank STAP for Slow-Moving Target Detection by Antenna-Pulse Selection[J]. IEEE Signal Processing Letters, 2015, 22(8):1156-1160.
[2] WANG P, LI H, HIMED B. A Bayesian Parametric Test for Multichannel Adaptive Signal Detection in Nonhomogeneous Environments[J]. IEEE Signal Processing Letters, 2010, 17(4):351-354.
[3] LIM C H, MULGREW B. Prediction of Inverse Covariance Matrix (PICM) Sequences for STAP[J]. IEEE Signal Processing Letters, 2006, 13(4):236-239.
[4] NEUMANN D,JOHAM M, UTSCHICK W. Covariance Matrix Estimation in Massive MIMO[J]. IEEE Signal Processing Letters, 2017, 99:1-5.
[5] UPADHYA K, VOROBYOV S A. Covariance Matrix Estimation for Massive MIMO[J]. IEEE Signal Processing Letters,2018,25(4):546-550.
[6] ZHANG Zhenyu, LIU Wei, LENG Wen, et al. Interference-plus-Noise Covariance Matrix Reconstruction via Spatial Power Spectrum Sampling for Robust Adaptive Beamforming[J]. IEEE Signal Processing Letters, 2016, 23(1):121-125.
[7] DAI B, WANG T, WU J, et al. Adaptively Iterative Weighting Covariance Matrix Estimation for Airborne Radar Clutter Suppression[J]. Signal Processing, 2015, 106(1):282-293.
[8] ANGELO C. Regularized Covariance Matrix Estimation via Empirical Bayes[J]. IEEE Signal Processing Letters, 2015, 22(11):2127-2131.
[9] WANG Pu, LI Hongbin, HIMED B. Moving Target Detection Using Distributed MIMO Radar in Clutter with Nonhomogeneous Power[J]. IEEE Trans on Signal Processing, 2011, 59(10):4809-4820.
[10] WU Yifeng，WANG T, WU Jianxin, et al. Robust Training Samples Selection Algorithm Based on Spectral Similarity for Space-Time Adaptive Processing in Heterogeneous Interference Environments[J]. IET Radar, Sonar & Navigation, 2015, 9(7):778-782.
[11] WU Yifeng，WANG T, WU Jianxin, et al. Training Sample Selection for Space-Time Adaptive Processing in Heterogeneous Environments[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(4):691-695.
[12] LI Huiyong, BAO Weiwei, HU Jinfeng, et al. A Training Samples Selection Method Based on System Identification for STAP[J]. Signal Processing, 2017,142:119-124.
[13] HU Jinfeng, CAO Jian, CHEN Zhuo, et al. Knowledge-Aided Ocean Clutter Suppression Method for Sky-Wave Over-the-Horizon Radar[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(3):355-358.
[14] HU Jinfeng, CHEN Hanwen, LIN Zhirong, et al. Radio Frequency Interference Suppression Algorithm Based on SOCP in OTHR[J]. Circuits Systems and Signal Processing, 2017, 36(6):2459-2472.
[15] HU Jinfeng, AI Hui, XUE Changpiao, et al. Ionospheric Decontamination Based on Sparse Reconstruction for Skywave Radar[J]. Journal on Advances in Signal Processing, 2016,93:1-10.
