0 引言
在阵列信号处理中，波达方向(Direction of Arrival,DOA)估计算法被广泛应用于雷达、声呐和无线通信等领域，基于均匀线阵(Uniform Linear Array，ULA)的DOA估计技术成熟且阵列结构简单，是最常用的阵列DOA估计方法[1-2]。近年来，由于互质阵列在相同阵元数下较均匀阵列有更大的孔径，由于其出色的性能引起了广泛的关注[3]。然而，由于互质阵列的非均匀性，该阵列相应的DOA估计算法较均匀线阵更难实现，故互质阵列DOA估计算法具有一定研究意义。将互质阵列通过某种方式拓展成虚拟阵列，虚拟阵列阵元数比实际的阵元数多，在一定程度上可以增加自由度(Degrees-of-Freedom，DOF)。由互质阵拓展得到的虚拟阵列由于缺失阵元而不是线性均匀阵列，运用传统的DOA估计方法无法得出准确的波达方向。为了解决这个问题，利用虚拟阵列的最大连续阵元的信息进行空域平滑的DOA估计，但该方法会损失不连续阵元的信息，影响DOA估计的自由度和分辨率[4]。文献[5]通过将组成互质阵中的较小均匀线阵的个数加倍，用虚拟阵列的最大连续阵元的信息进行空域平滑的DOA估计提高了自由度和分辨率，但实际阵元数的增加会占用更多的空间资源。本文提出的算法在保持实际阵元数不变的情况下，通过阵列内插的方式将虚拟阵列缺失的阵元补齐从而达到线性均匀的虚拟阵列，重构协方差矩阵并优化相关的元素进行DOA估计，提高了自由度和分辨率。
1 信号模型
图1给出了互质阵的阵列结构。该阵列由图1(a)中的两个稀疏均匀线阵(ULA)嵌套构成，记为子阵1和子阵2，互质阵中子阵1和子阵2的第1个阵元相互重合。子阵1有M个阵元，阵元间距为Nd，子阵2有N个阵元，阵元间距为Md，M和N为互质的整数，d=λ/2，λ一般为半波长。由于M和N的互质性，除了第一个阵元，该互质阵列其他阵元不会相互叠加，阵元数为M+N-1。
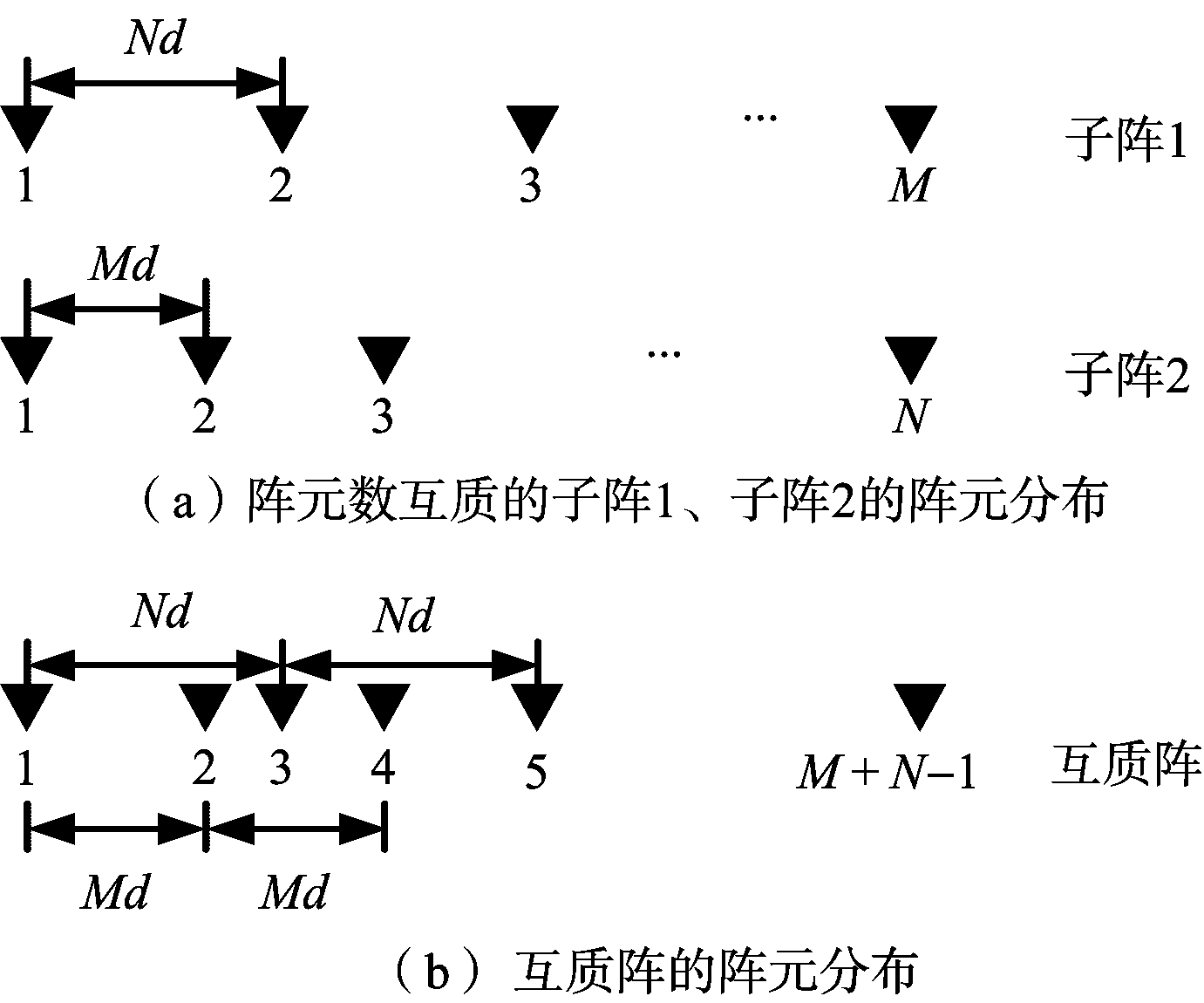
图1 互质阵的阵列结构
假设有K个远场非相干窄带信号从不同入射角θ=[θ1,θ2,…,θK]以功率
发射并被该互质阵列接收，互质阵列接收信号可以表示为
x(t)=
A(θ)s(t)+n(t)
(1)
式中：s(t)为信源矢量；A(θ)为阵列流型矩阵，由图1中互质阵列可知A(θ)=[a(θ1),a(θ2),…, a(θK)]，其中a(θk)=[1,e-jπl2dsin(θk),…,e-jπlM+N-1dsin(θk)]T为第k个信号源的方向向量,
表示矩阵转置运算，互质阵列中第i个阵元的位置位于lid ( i=1,2,…,M+N-1 )；n(t)为加性高斯白噪声
表示Hermitian转置运算。
计算互质阵列接收信号x(t)的协方差矩阵如式(2):
Rx=E(x(t)xH(t) )=
(2)
由于Rx在实际应用中无法直接获得，在经典DOA估计中，其值通常由样本协方差矩阵代替为[6]
(3)
式中,T表示快拍数。
2 互质阵列DOA估计
目前利用互质阵列进行DOA估计的方法主要有两种[7]，一是利用互质阵的子阵列进行DOA估计，联合两个子阵列的估计结果进行角度的解模糊，但该方法对信源分辨的个数小于子阵列的个数；二是对互质阵列接收信号的协方差矩阵矢量化后构造虚拟阵元，然后利用该虚拟阵列进行DOA估计。为了充分利用互质阵列的信息，更大地提高其自由度，本文采用方法二进行分析。
2.1 互质阵列的虚拟阵元拓展方式
将互质阵列拓展成虚拟阵列是提高算法自由度的关键，虚拟阵元的位置与物理阵元的位置差相关，如图2所示。为了方便叙述，考虑含有N个整数的集合S={di,i=1,2,…,N}，将集合S上的差分集定义为Sdiff=
。易知，该差分集是一个关于原点对称的集合，且有重复元素存在。为了充分利用互质阵列的稀疏特性，提取数据协方差矩阵中差集拓展的虚拟阵元信息并进行排列，通过协方差矩阵的向量化建立起互质阵列和虚拟阵列的统计关系：
(4)
式中，Av为虚拟阵列的导向向量组成的矩阵，Av=
表示共轭运算，vec(·)表示矢量化运算，⊗表示克罗内克积运算。
向量化后的矢量v中的元素代表每一个虚拟阵元的相关信息，其中包括重复元素，对应差分集中重复的元素，即重复的阵元。假设虚拟阵元位于Ld={li,i=1,2,…,M+N-1}d，Ldiff为实际阵元的位置集合的差分集，即Ldiff={li-lj|i,j=1,2,…,M+N-1}。故矢量v中的元素对应差分集Ldiff，但此差分集重复的虚拟阵元存在，因此取重复阵元位置元素的均值。重复阵元位置取均值后的集合为
Ldiff1={±(Mn-Nm)|n=0,1,…,N-1,
m=0,1,…,M-1}
(5)
该差分集对应的矢量
(6)
式中，C1为位于Ldiff1d的互质虚拟阵列的导向矢量构成的矩阵，i1表示iv中取出重复阵元后的阵列对应的元素。
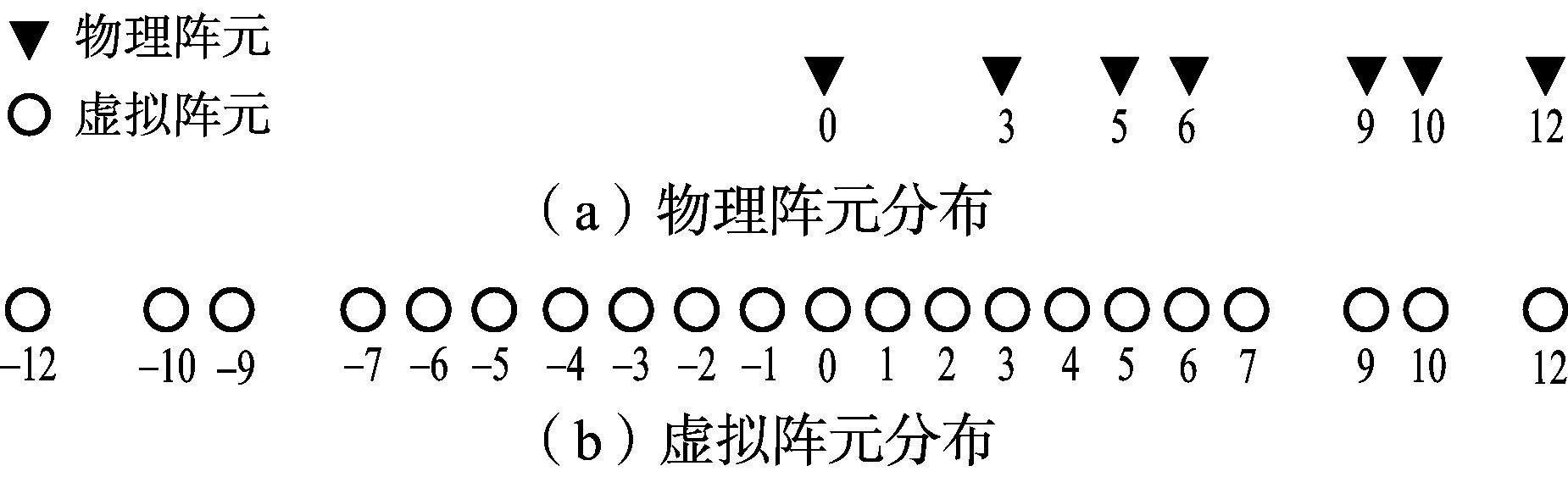
图2 互质阵列以及拓展的虚拟阵列
现以子阵1阵元数M=3,子阵2阵元数N=5为例，对互质阵列的虚拟阵元拓展以及虚拟阵列的DOA估计进行分析，则实际阵元的位置为{0,3,5,6,9,10，12}。由此集合得到具有重复元素的差分集L1为{0,-3,-5,-6,-9,-10,-12,3,0,-2,-3,…,1,0,-2,12,9,7,6,3,2,0}，重复阵元位置的元素取均值并进行重排处理得到差分集L2为{-12,-10,-9,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,9,10,12}，如图2(b)所示。虽然图2(b)中的阵列相对于互质阵列阵元数增加，但在位置{-11,-8,8,11}处存在虚拟阵元的缺失，导致该虚拟阵列是一个非均匀阵列。
2.2 最大连续虚拟阵列空域平滑DOA估计
为了解决虚拟阵列的不均匀性带来的问题，一般的方法为先将该不均匀阵列中最大的连续虚拟阵列取出，然后在最大连续虚拟阵列进行空域平滑，最后进行DOA估计。如图3所示为阵元数M=3,N=5时的最大连续虚拟阵列，在矢量v中取出最大连续虚拟阵列，令其对应差分集为L3，差分集L3中的元素连续，对应矢量
为最大连续虚拟阵列的导向矢量构成的矩阵，i2表示iv中最大连续虚拟阵列对应的元素。由于v2是矢量，其秩为1，无法分辨多个信号源，故需要进行空域平滑[5]。
如图3所示，将该阵列分解成L=(|L3|+1)/2个相互重叠的均匀子线阵，|·|表示集合的基数，每一个均匀子线阵包含L个连续虚拟阵元，v2,p，l=1,2,…,L分别为L个子阵的矢量信息。进行空域平滑得到矩阵：
(7)
最后利用子空间类算法对矩阵Rv进行特征分解，张成对应的子空间，从而实现DOA估计。
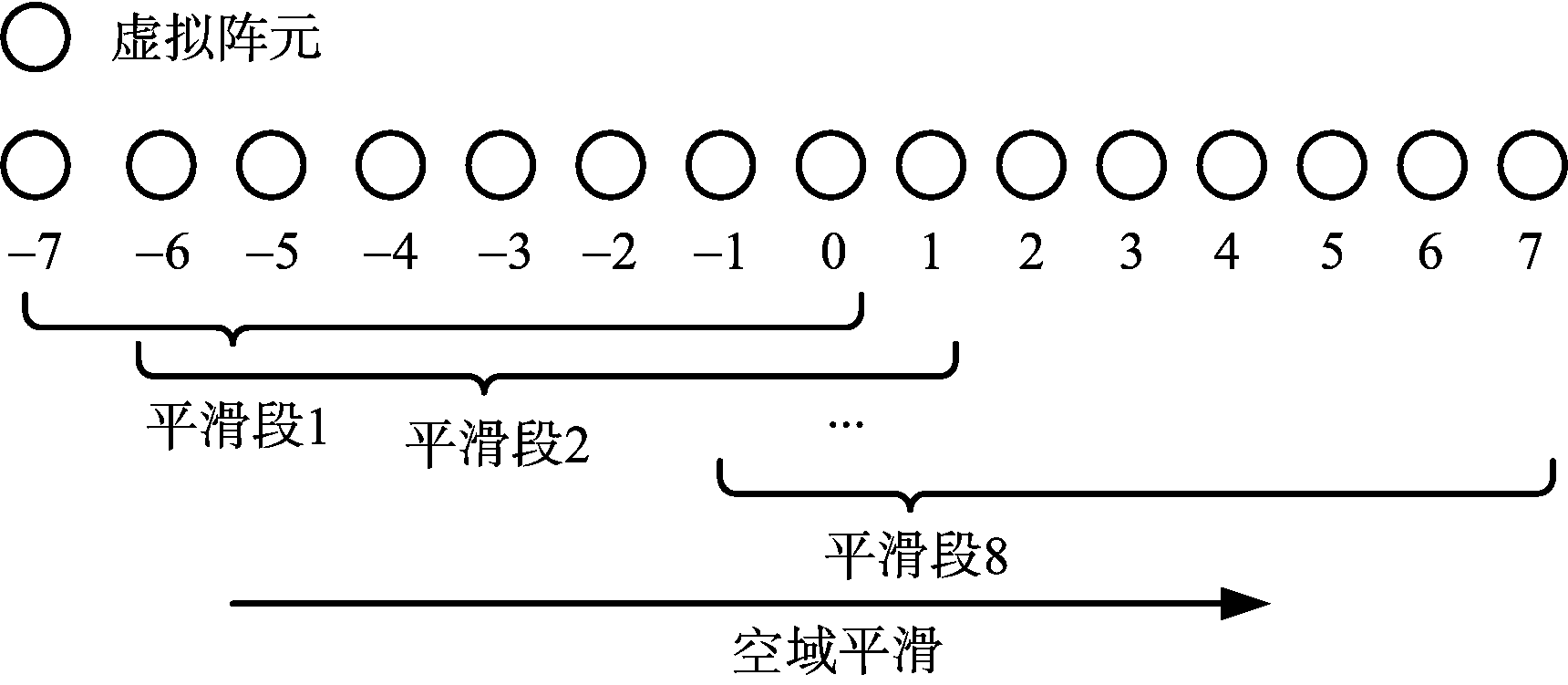
图3 最大连续虚拟阵元的空域平滑
2.3 基于虚拟阵列内插的协方差矩阵重构DOA估计
利用最大连续虚拟阵元的矢量信息进行DOA估计的方法会造成部分接收信号信息的丢失，从而影响后续DOA估计的精度并降低自由度。为了充分利用虚拟阵元的信息，我们引入了阵列内插的思想来构造一个包含L1中所有虚拟阵元的均匀阵列，形成如图4所示的虚拟阵列L4。建立L4的向量化协方差矩阵v3和L1向量化协方差矩阵v1之间的关系，原虚拟阵元的等效信号不变，插入阵元接收到的信号为0[9]:
(8)
同理，v3是一个秩为1的向量，无法直接分辨多个信号源，需要通过图4空域平滑来解决。由于v3关于原点对称，利用式(9)简化初始的协方差矩阵，该矩阵包含了线性虚拟阵元中的全部信息，故省略空间平滑过程，即
R2=T(v3+)
(9)
式中，T(v3+)表示以向量v3+为第一列的厄米特托普利兹矩阵，v3+=〈v3〉i,0≤i≤L1，L1=(|L4|+1)/2，R2是一个满秩矩阵。矩阵重构的目的是要恢复内插虚拟阵列的协方差矩阵，当矩阵含丢失元素时，可以根据矩阵的低秩结构来恢复矩阵的所有信息[11]。建立一个寻找低秩矩阵T的优化问题，T(z)为以向量z为第一列的厄米特托普利兹矩阵，约束条件为该矩阵的平方与
的差值的Frobenius范数最小[10],即
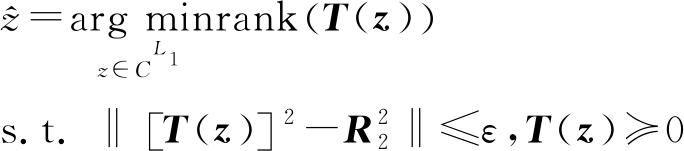
(10)
式中，ε为协方差矩阵拟合误差，rank(·)为矩阵的秩。
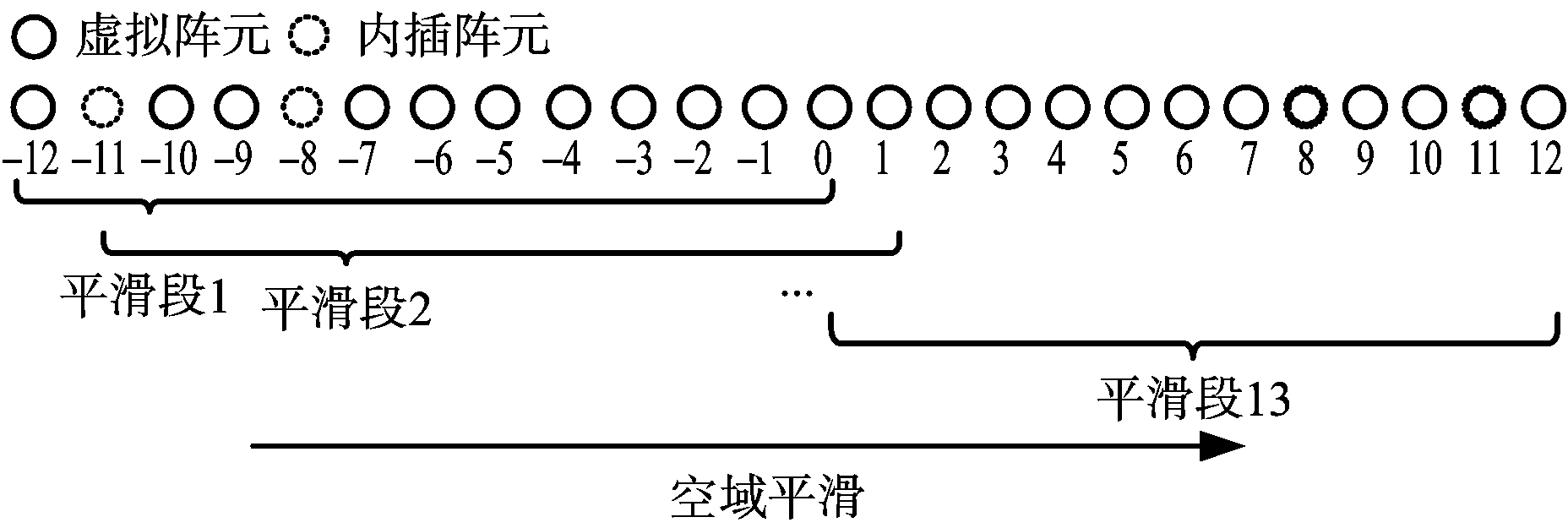
图4 内插虚拟阵列空域平滑
为简化式(10)中的优化问题，定义与矩阵R2相同维度的投影矩阵P，矩阵R2与P中的元素均与图4的内插均匀阵列的矢量元素对应，但矩阵P对应内插阵元的元素值为0，其余为1。引入矩阵的迹，将式(10)中的优化问题转化为凸优化问题[10]：
s.t. T(z)
0
(11)
式中,τ为正则化参数，‖·‖F表示计算Frobenius范数。在计算以向量z为第一列的厄米特托普利兹矩阵时，由于z是由复数元素组成的向量，该向量的第一个元素无法进行共轭拓展，故先将向量z的第一个元素定义为实数，并且在完成向量z的整体优化后再单独优化向量z的第一个元素。最后利用子空间类算法对优化重构后的矩阵T(z)进行特征分解，张成对应的子空间，进行谱峰搜索，得到波达方向。
2.4 算法步骤总结
根据上述分析过程，将基于虚拟阵列内插的协方差矩阵重构DOA估计算法的主要步骤归纳如下：
步骤1： 根据互质阵模型以及预设入射角，求解接收信号的协方差矩阵，如式(3)并对协方差矩阵进行向量化处理，如式(4)，初步构造虚拟阵列模型，如式(6)；
步骤2： 对不连续的虚拟阵列进行内插，在构造的均匀虚拟阵列的基础上初始化协方差矩阵，如式(8)、式(9)；
步骤3： 利用初始化的协方差矩阵进行凸优化，初步重构协方差矩阵，如式(11)，然后优化矢量z的第一个元素以完成矩阵T(z)的重构；
步骤4： 对重构后的矩阵T(z)进行特征值分解，依据信号子空间和噪声子空间的正交性，进行谱峰搜索，最终得到DOA估计结果。
3 实验和结果分析
为了验证算法的性能，分别对最大连续虚拟阵列(Maximum Continuous Virtual Array，MCVA)DOA估计算法和协方差矩阵重构(Covariance Matrix Reconstruction，CMR)DOA估计算法进行仿真对比分析。基于上述阵列模型和算法进行了仿真分析,其中两组互质的稀疏均匀阵列的阵元数分别为M=3,N=5，由这两组阵列组成的非均匀阵列的阵元数为M+N-1=7，分别位于{0,3d,5d,6d,9d,10d,12d}，d=λ/2。正则化参数τ的取值为2.2×10-5，步骤3对矢量z第一个元素最后的优化值为6.0。
实验1 不同信源数时算法的检测性能仿真实验
为了验证两种算法的检测能力，设置仿真条件：信噪比SNR=5 dB,快拍数K=1 000,来波分布在-50°～50°之间，对信源数为K=7和K=9作了仿真。图5给出在多目标情况下利用MCVA算法和CMR算法计算出的空间谱，竖线为所设置的信号源入射角。当M=3,n=5时，是式(7)中MCVA算法空域平滑计算出的矩阵Rv的最大秩为8，故该算法最多能分辨7个不同方向的信号源。由图5可知，MCVA算法和CMR算法均能分辨7个不同方向信号源，且CMR算法可分辨9个不同方向信号源，故CMR算法具有更大的自由度。
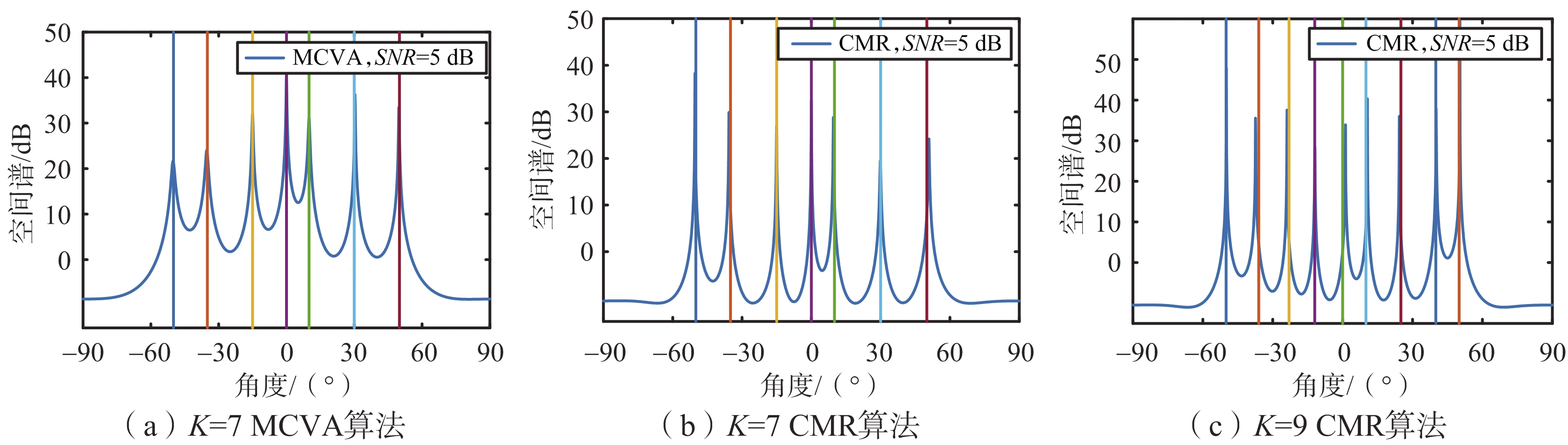
图5 不同信源数K下MCVA算法和CMR算法的空间谱
实验2 算法的分辨率性能仿真实验
分辨率表征了算法对相邻信号源的谱峰的分辨能力。设置仿真条件：信噪比SNR=5 dB,快拍数K=1 000,研究两种算法在相邻信号源方向分别为θ1=-3°,θ2=3°，θ1=-2°,θ2=2°，θ1=-1.5°,θ2=1.5°的情况下的分辨情况，实验结果如图6所示，竖线表示信号源入射方向。由图6可知，MCVA算法在θ1=-2°,θ2=2°时无法分辨两个目标，在θ1=-3°,θ2=3°可分辨两个目标，而CMR算法在θ1=-1.5°,θ2=1.5°和θ1=-2°,θ2=2°均能分辨两个目标，故CMR算法的分辨率较高。
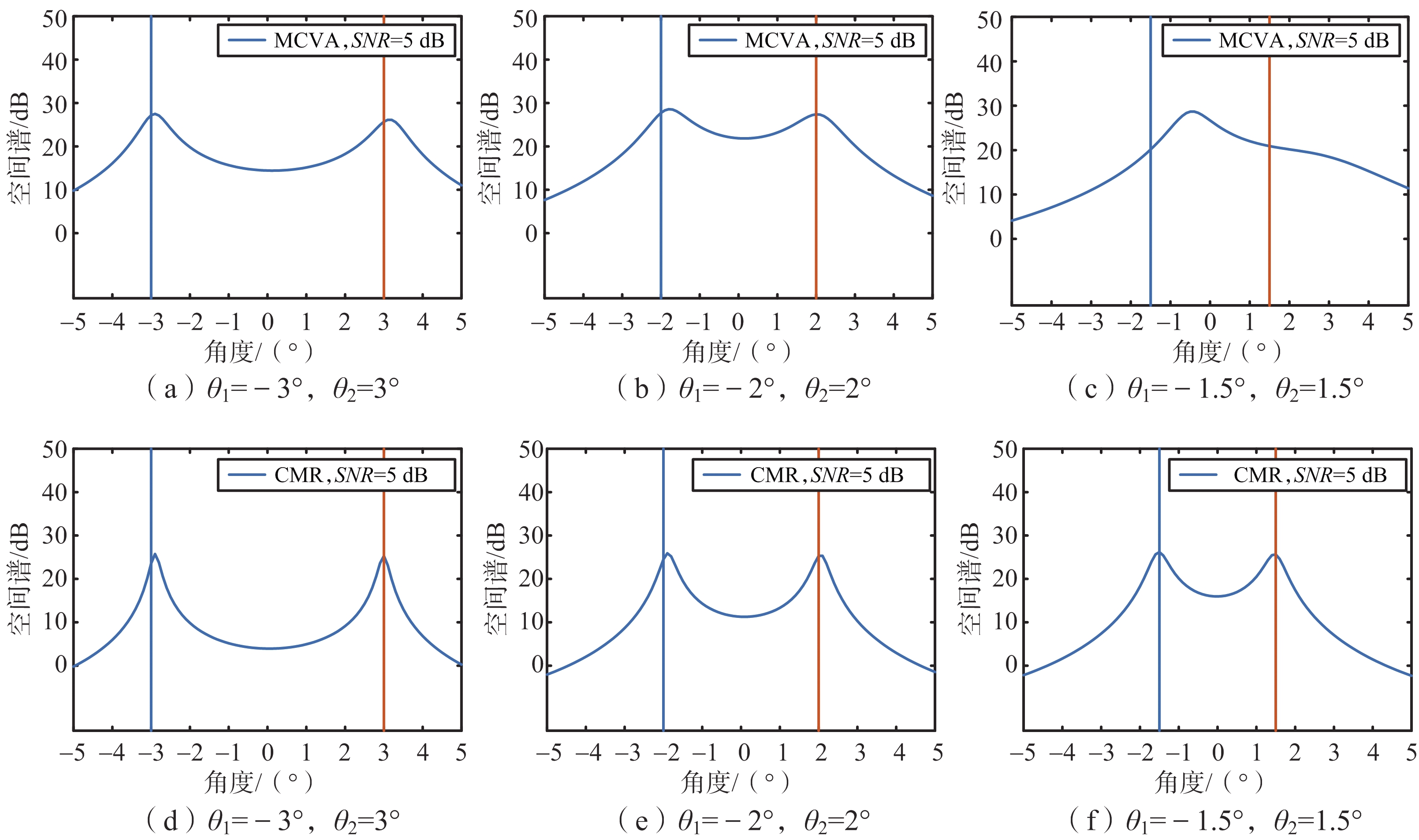
图6 算法在相邻目标θ1,θ2下的空间谱
实验3 算法的估计精度仿真实验
为了衡量算法的检测精度，定义均方根误差(Root Mean Square Error,RMSE)的数学表达式如式(12)：
(12)
式中，
为在第p次Monte-Carlo试验中第k个信号源θk所估计出的波达方向，P为Monte-Carlo试验次数，K为总信号源个数。如图7(a)所示信源方向为θ1=-30°,θ2=30°，快拍数为1 000时，MCVA算法和CMR算法在不同信噪比下的均方根误差的实验结果，其中Monte-Carlo试验次数为P=30。如图7(b)所示为信源方向为θ1=-30°,θ2=30°,SNR=5 dB时，MCVA算法和CMR算法在不同快拍数下的均方根误差的实验结果，其中Monte-Carlo试验次数为P=30。由图可知，CMR算法的性能优于MCVA算法。
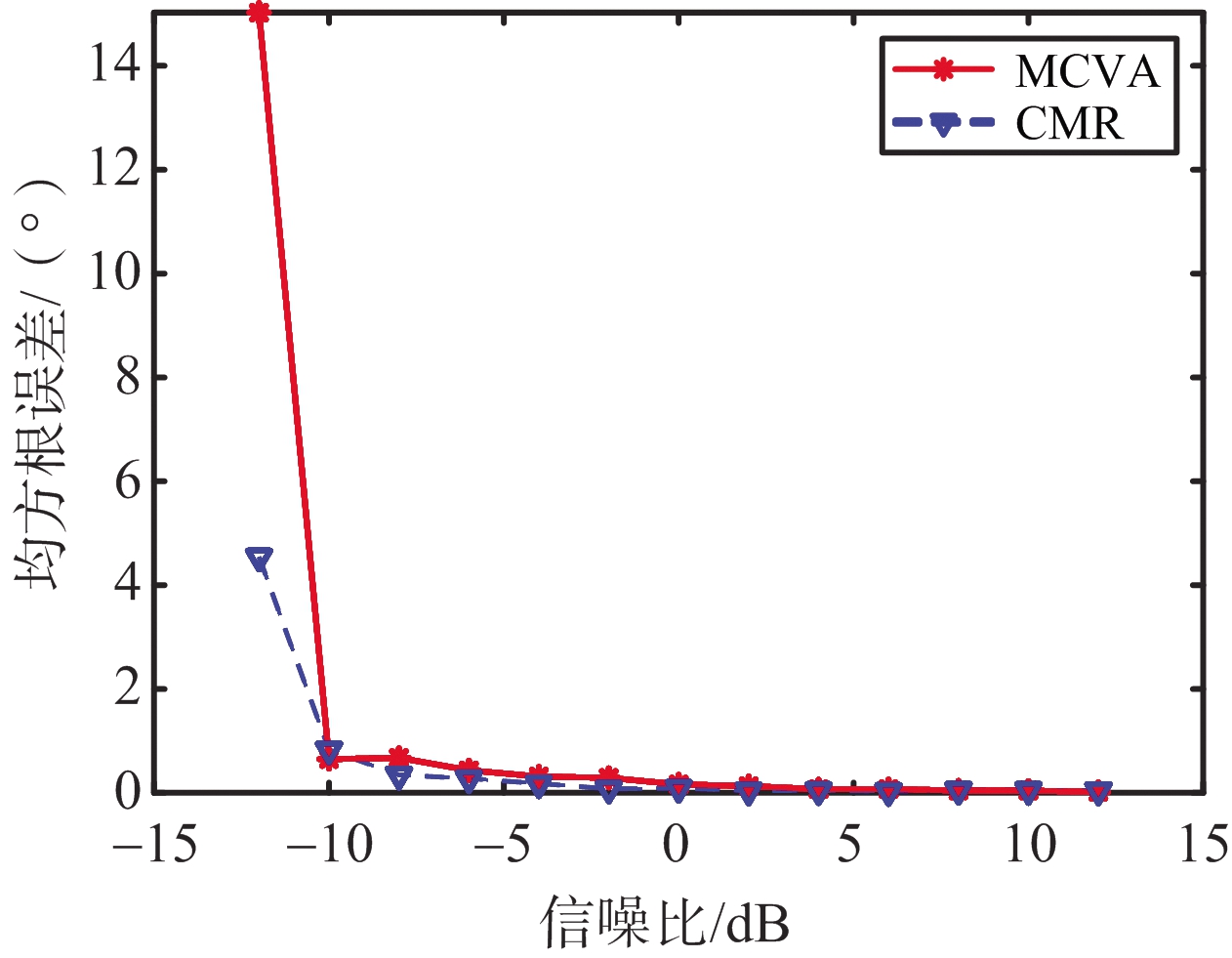
(a) 不同信噪比
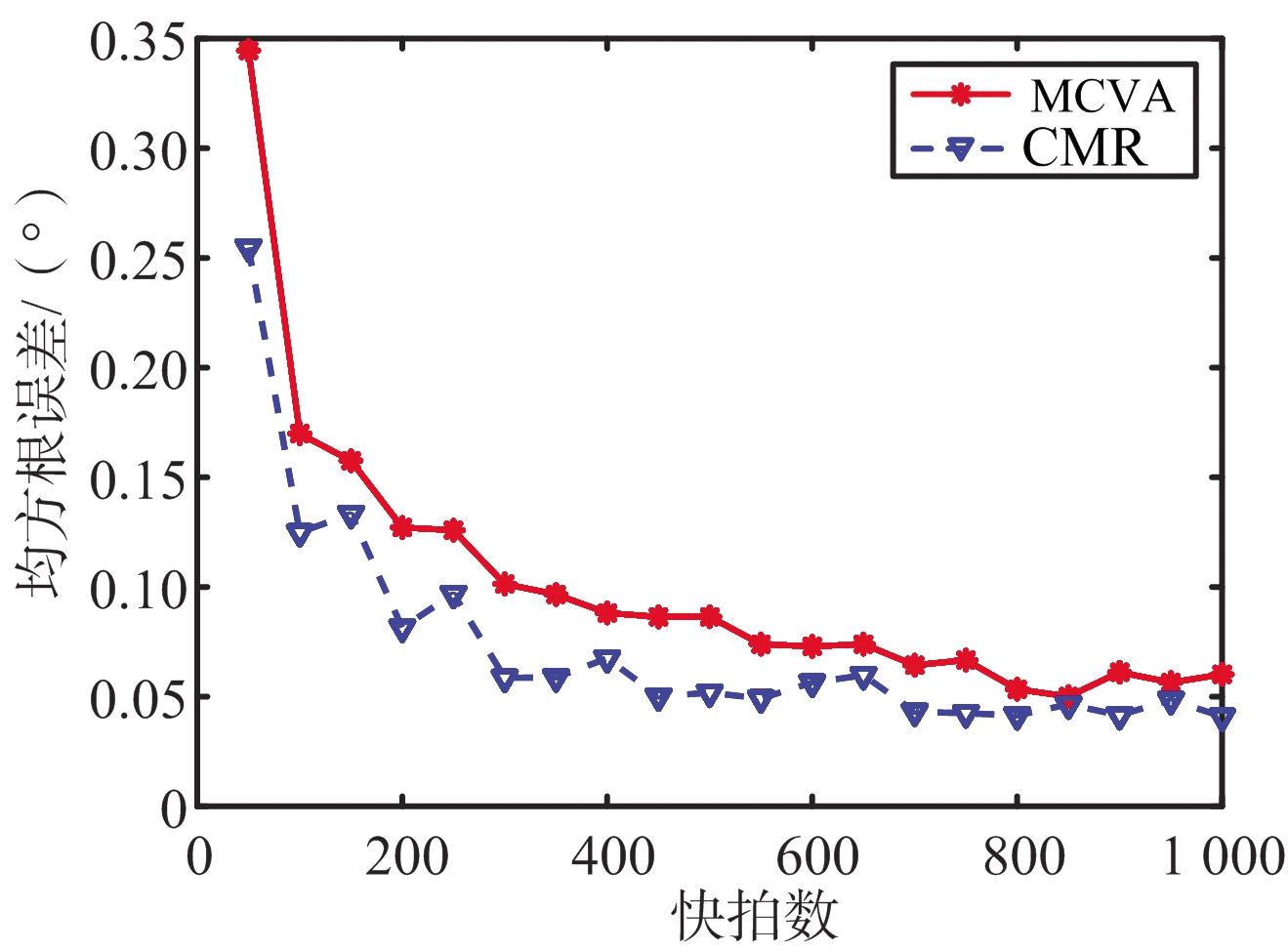
(b) 不同快拍数
图7 算法在信源数K=2下的均方根误差
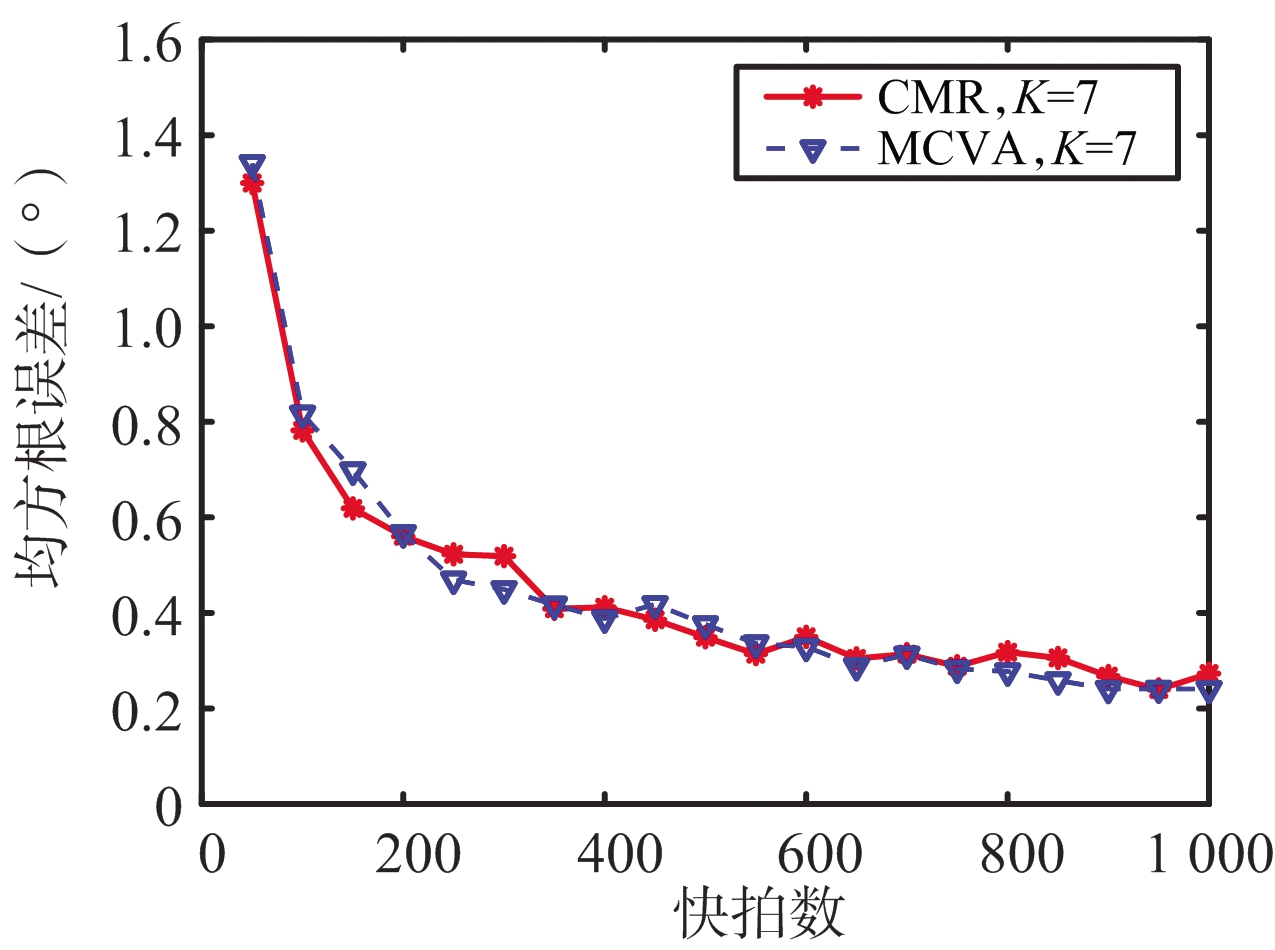
(a) 信源数K=7
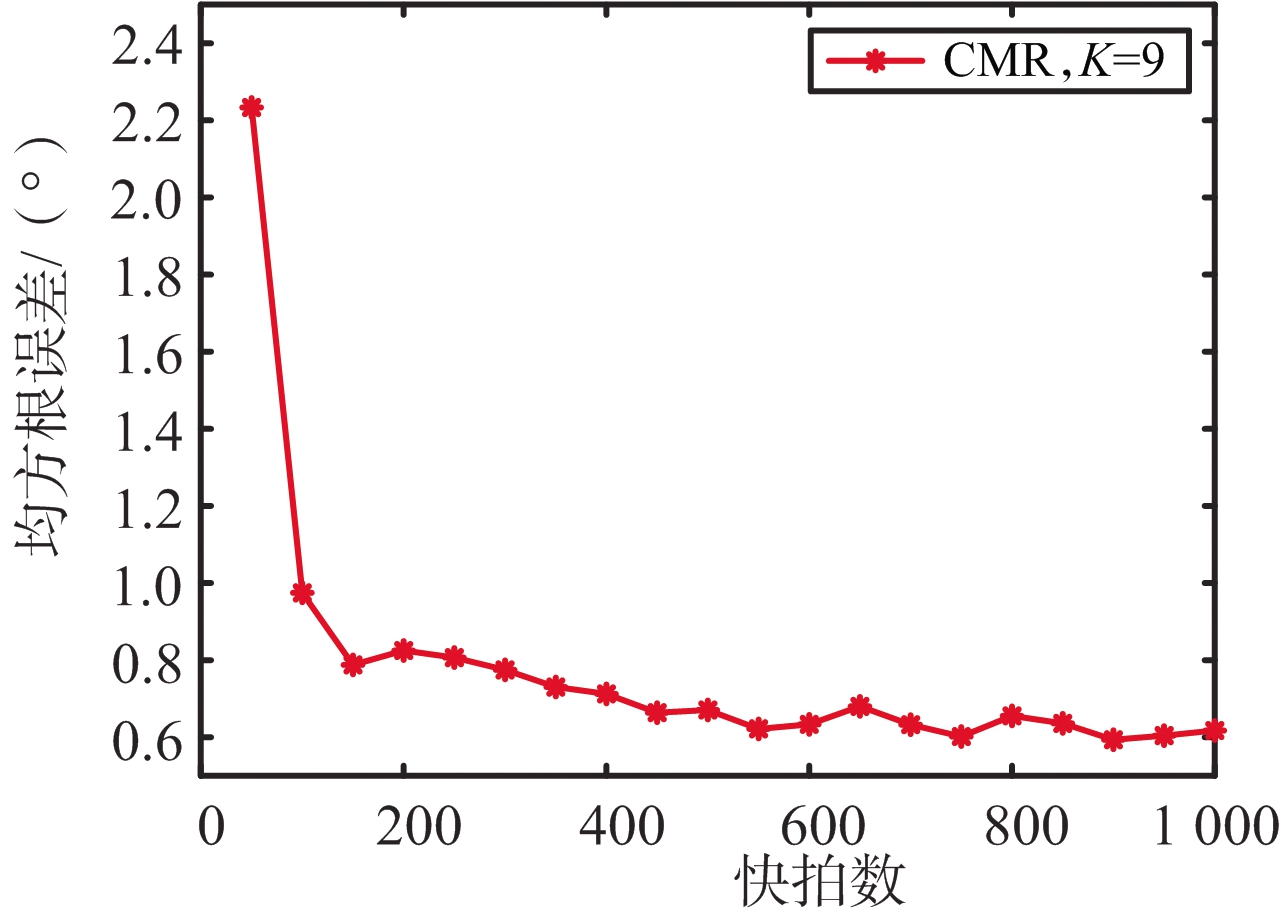
(b) 信源数K=9
图8 多信源数下算法在不同快拍数下的性能
如图8(a)所示为信源数K=7,方向为θ= [-50°,-35°,-15°,0°,10°,30°,50°]，信噪比SNR=5 dB，Monte-Carlo试验次数为P=30下MCVA算法和CMR算法在不同快拍数下的RMSE的实验结果；如图8(b)所示为信源数K=9,方向为θ= [-50°,-36°,-23°,-12°,0°,10°,25°,40°,50°],信噪比SNR=5 dB，Monte-Carlo试验次数为P=30下CMR算法在不同快拍数下的RMSE的实验结果。由图可知，随着快拍数的增加，RMSE随之减小，最后趋于平稳，说明算法鲁棒性较好。
4 结束语
本文提出了一种基于虚拟阵列插值的矩阵重构DOA估计算法，该算法通过阵列插值的方式将互质阵列的虚拟阵列拓展成虚拟均匀线阵，利用均匀虚拟线阵等效信息初始化协方差矩阵，最后通过并优化协方差矩阵的相应矢量的首个元素，利用重构的低秩协方差矩阵进行DOA估计，充分利用了互质阵列拓展的虚拟阵列的信息。将本文算法与最大连续虚拟阵元的空间平滑协方差矩阵DOA估计算法进行对比，在不同信源数时算法的检测空间谱、分辨率性能和不同信源数下的均方根误差进行了仿真实验，结果表明，该算法可实现更大的自由度和更高的分辨率，并呈现出较好的鲁棒性。
[1] 张小飞，汪飞,徐大专.阵列信号处理的理论和应用[M].北京：国防工业出版社，2010:1-20.
[2] SHI J, HU G, ZHANG X, et al. Generalized Co-Prime MIMO Radar for DOA Estimation with Enhanced Degrees of Freedom[J]. IEEE Sensors Journal, 2018, 18(3):1203-1212.
[3] VAIDYANATHAN P P, PAL P. Sparse Sensing with Co-Prime Samplers and Arrays[J]. IEEE Trans on Signal Processing, 2011, 59(2):573-586.
[4] PIYA P. Correlation Awareness in Low-Rank Models: Sampling, Algorithms, and Fundamental Limits[J]. IEEE Signal Processing Magazine, 2018, 35(4):56-71.
[5] SHI Z, ZHOU C, GU Y, et al. Source Estimation Using Coprime Array: A Sparse Reconstruction Perspective[J]. IEEE Sensors Journal, 2017, 17(3):755-765.
[6] ZHOU Chengwei, SHI Zhiguo, GU Yujie, et al. Doa Estimation by Covariance Matrix Sparse Reconstruction of Coprime Array[C]∥ IEEE International Conference on Acoustics,Speech and Signal Processing,Brisbane, QLD, Australia :IEEE,2015.
[7] 张小飞,林新平,郑旺,等.互质阵中空间谱估计研究进展[J].南京:南京航空航天大学学报,2017,49(5):635-644.
[8] 张彦奎,许海韵,巴斌,等.基于互质阵列重构的高维波达方向估计算法[J].电子学报,2018,46(12):2923-2929.
[9] ZHOU Chengwei, GU Yujie, ZHANG Yimin, et al. Coarray Interpolation-Based Coprime Array Doa Estimation via Covariance Matrix Reconstruction[C]∥2018 IEEE International Conference on Acoustics, Speech and Signal Processing,Calgary, AB, Canada:IEEE,2018:3479-3483.
[10] FAN Xing, ZHOU Chengwei, GU Yujie, et al. Toeplitz Matrix Reconstruction of Interpolated Coprime Virtual Array for DOA Estimation[C]∥2017 IEEE 85th Vehicular Technology Conference,Sydney, NSW, Australia:IEEE,2017:1-5.
[11] 史加荣,郑秀云,魏宗田,等.低秩矩阵恢复算法综述[J].计算机应用研究,2013,30(6):1601-1605.
