0 引言
波束形成技术在雷达、声呐以及麦克风语音领域的阵列信号处理中应用广泛。实际环境下,信号协方差矩阵是通过采样信号获取,有限的采样快拍数会导致训练数据中包含期望信号。此外,基阵位置偏差、阵元幅相误差等因素会产生角度失配问题,从而无法精确获得导向矢量,导致Capon波束形成器性能急剧下降。
针对上述标准Capon波束形成器存在的问题,文献[1-5]提出一类重构协方差矩阵的方法。其中文献[1]将空域分成干扰和信号两个互不重叠的大区域,通过对干扰区域积分获得干扰协方差矩阵,接着对信号区域积分得到信号协方差矩阵,将信号协方差矩阵特征值分解,以分解后特征向量作为导引向量估计,实验表明效果良好,然而该方法在获取干扰加噪声协方差矩阵以及导向矢量时计算量过大,不适合实际工程中应用。除了上述的方法,对角加载算法[6-9]也是经常使用的方法。其中文献[6]根据协方差矩阵的不同特征值选择不同的加载因子,可以有效地抑制干扰并消除角度失配的影响,但自适应的加载因子难以确定,加载因子过大或者过小都会带来不利影响。针对以上两种方法的不足,不确定约束集的稳健波束形成[10-13]被提出,如文献[13]提出的改进的双约束稳健波束形成算法,该方法对噪声子空间附加两个约束条件,通过辅助约束条件,把问题转化为单约束问题,和普通双约束稳健波束形成方法比,运算量有所降低,但和其他类算法相比,该算法运算量依然巨大。文献[14]提出了根据不同导向矢量误差获取对应的加载量,同样,最优加载值的求解方法运算量大且收敛速度也慢。此外,文献[14-16]中运用到一些专门解最优问题工具箱,用来解决二次规划二次约束问题,此类算法可在较少快拍以及低输入信噪比(Signal-to-Noise Ratio, SNR)环境中保持一定性能,但巨大的计算量限制了这类算法的实际应用。
针对上述算法存在的问题,依据标准Capon波束形成器,提出一种基于加权空间平滑与导向矢量估计相结合的稳健波束形成算法。算法对阵列信号进行两次平滑,其中第一次平滑时阵列的子阵数等于第二次平滑时阵列子阵的阵元数,目的是为了使加权矩阵中的元素与平滑矩阵一一对应。充分利用子阵输出的自相关性与互相关性,以此获得更加精确的协方差矩阵,采用不确定范围约束期望导向矢量来估计获得真实导向矢量。由于加权空间平滑后的协方差矩阵精度更高,故而导向矢量也更加准确,算法的鲁棒性也得到提高。
1 阵列信号模型
假设阵列为均匀线阵,阵元数为M,相互独立的信源同时入射到阵列,则第k个快拍时接收到的信号为
x(k)=xs(k)+xj(k)+n(k)
(1)
式中,xs(k)为期望信号,xj(k)为干扰信号,n(k)为独立于信源的噪声。
阵列接收信号的理想协方差矩阵可表示为
Rx=E{x(k)x(k)H}=Rs+Ri+σ2I
(2)
式中,Rs表示期望信号协方差矩阵,Ri表示干扰信号协方差矩阵,σ2表示噪声功率,I表示单位矩阵。
自适应波束形成对阵列接收信号x(k)进行加权处理,阵列信号输出为
y(k)=wHx(k)
(3)
式中,加权矢量w=[w1,w2,w3,…,wM],根据最小方差无失真响应(即标准Capon波束形成),保证输出中的噪声和干扰总功率最小,并且期望信号不会失真,转化为数学模型为
(4)
该约束条件下的寻优问题可用拉格朗日乘子法求解,得到
(5)
实际的工程应用中,Ri+n无法直接获得,通常用采样协方差矩阵Rs来代替,K个快拍的采样协方差矩阵为
(6)
2 本文算法
2.1 前后向空间平滑
考虑阵元数为M的均匀线阵,取子阵阵元数为m,子阵数为p,则接收到的信号前向空间平滑的数据矢量可表示为
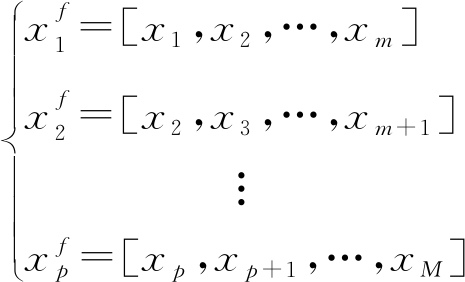
(7)
数据的协方差矩阵为
(8)
则前向平滑的协方差矩阵为
(9)
同理可知后向空间平滑的数据矢量可表示为
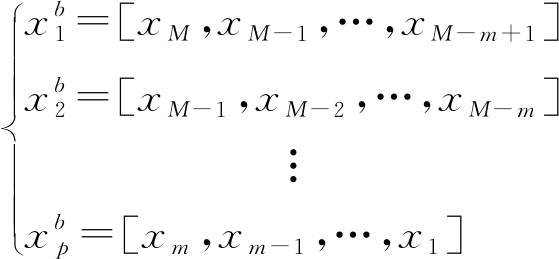
(10)
此时数据的协方差矩阵为
(11)
则后向平滑的协方差矩阵为
(12)
将二者取平均后可得到前后向平滑的协方差矩阵
(13)
2.2 改进的加权前后向空间平滑
由于普通的前后向空间平滑只利用了子阵自相关协方差矩阵,此处提出一种改进的加权前后向空间平滑算法,同时利用子阵的自相关协方差矩阵与互相关协方差矩阵,更好地消除回波信号中的相干性,获取更为精准的协方差矩阵。此外,本方法不需知道信源的先验位置,也不需预估信源方向,适用于信源信息未知情况下的协方差矩阵解相干。算法构造两次特殊结构的子阵划分形式,使第一次子阵阵元数与第二次子阵数相等,此做法是为了保证加权元素总数能够一一对应到加权空间平滑矩阵上。第一次划分后得到的前后向平滑协方差矩阵中的元素作为加权因子,将这些加权因子对应与第二次划分后的协方差矩阵相乘即可得到加权后的协方差矩阵。由于两次划分时,都是均匀选取大小相同的子阵,加权元素也都是一一对应到平滑矩阵上,故加权平滑后的协方差矩阵不会出现整体偏离。
在取子阵阵元数为m,子阵数为p时,由式(14)可知第一次划分得到的协方差矩阵为Rfb,此时加权矩阵W为
W=(Rfb)+
(14)
第二次划分时,取子阵阵元数为p,子阵数为m,利用上式求得的W加权到此时得到的协方差矩阵
Rwf=![]()
式中,wij为W中的元素,Rij为第二次划分后得到的信号协方差矩阵中的元素,J为转置矩阵。
2.3 导向矢量估计
针对低信噪比情况下,信号子空间包含期望信号少,估计得到的导向矢量会指向干扰方向,从而导致波束形成的主瓣指向发生偏差的问题,提出一种根据导向矢量不确定范围加以约束条件来搜索信号子空间,估计阵列真实导向矢量的方法。
通过将期望导向矢量对Rwf进行特征分解得到投影Ts,则真实导向矢量可表示为
(16)
假设期望与导向矢量之间的有限误差,则二者之间的关系可表示为
(17)
式中,ε0为约束因子,由系统中的各种实际误差造成,可以估计得到。将式(17)代入式(18)可得
(18)
化简后可得
(19)
式(20)指期望导向矢量主要集中在该子空间,当式(20)不成立时,表明期望导向矢量在噪声子空间中分量较大,此时需要重新搜索子空间,定义不同维度的子空间函数为
(20)
式中,![]() 为N×k维的子空间。
为N×k维的子空间。
将Rwf分解后特征值从大到小排列,令k在特征值对应的特征向量内由小到大依次搜寻,直到满足条件
f(k)≤ε0
(21)
满足上式得到的子空间中存在大量期望导向矢量,将期望导向矢量向此处搜寻到的子空间投影可估计获得的真实导向矢量满足式(22)的约束条件。
把式(16)得到的信号协方差矩阵Rwf与此处得到的真实导向矢量![]() 代入式(6)可知
代入式(6)可知
(22)
为更方便理解整体算法过程,将算法主要步骤列出,如表1所示。
表1 主要算法步骤

初始化:接收信号数据x(t)1) 根据式(6)得到k个快拍数下接收信号数据的采样协方差矩阵Rs2) 对采样协方差矩阵作第一次平滑,平滑后的协方差矩阵为Rfb,由式(14)可得加权矩阵W3) 通过加权矩阵W作第二次平滑,此时可得到协方差矩阵Rwf4) 根据真实导向矢量与期望导向矢量之间的关系,设定二者之间的约束因子ε0,约束因子取值为0.15) 将满足式(21)约束条件的真实导向矢量与加权平滑后的协方差矩阵Rwf代入式(5)获得Wopt
3 仿真实验
采用以下实验仿真来验证算法的性能。仿真中假设阵列为16阵元的均匀线阵,阵列之间的间距固定为半波长,入射信号为一个期望信号以及两个干扰信号,期望信号的来波角度为80°,信号的真实来波方向为78°,两个干扰信号来波角度分别为60°和105°,干噪比为30 dB,为了验证算法的性能,将本文算法分别与对角加载波束形成(Diagonal Loading Beamforming,DLB)、特征子空间鲁棒波束形成(Eigen Space Robust Beamforming,ESRB)以及最差性能最优波束形成(Worst-Case Optimal Beamforming,WCOB)方法进行对比。
仿真实验1:采用几种算法的归一化波束图对比,取快拍数为100,期望信号来波方向为80°,假设期望信号来波方向存在误差,误差角度为-2°,即真实来波方向为78°,期望信号的信噪比设置为0 dB,图1为几种算法对应的波束图。
由图1可见,本文算法拥有较低的旁瓣,且在两个干扰方向形成了最低的零陷,主瓣方向也指向了真实的期望信号的来波方向。DLB方法对导向矢量的偏差过于敏感,导致主瓣所指方向与真实期望信号方法产生偏差,并且该方法对旁瓣的抑制有限,对干扰的零陷也较浅。WCOB方法能够有效地对干扰产生零陷,但对导向矢量存在偏差的情况过于敏感,并且抑制旁瓣的效果不够理想。ESRB方法主瓣波束指向80°,无法保持真实信号的最大增益。从以上对比可说明本文算法能够有效降低旁瓣,抑制干扰信号并且在期望信号导向矢量存在偏差时能够识别出真实的来波方向。
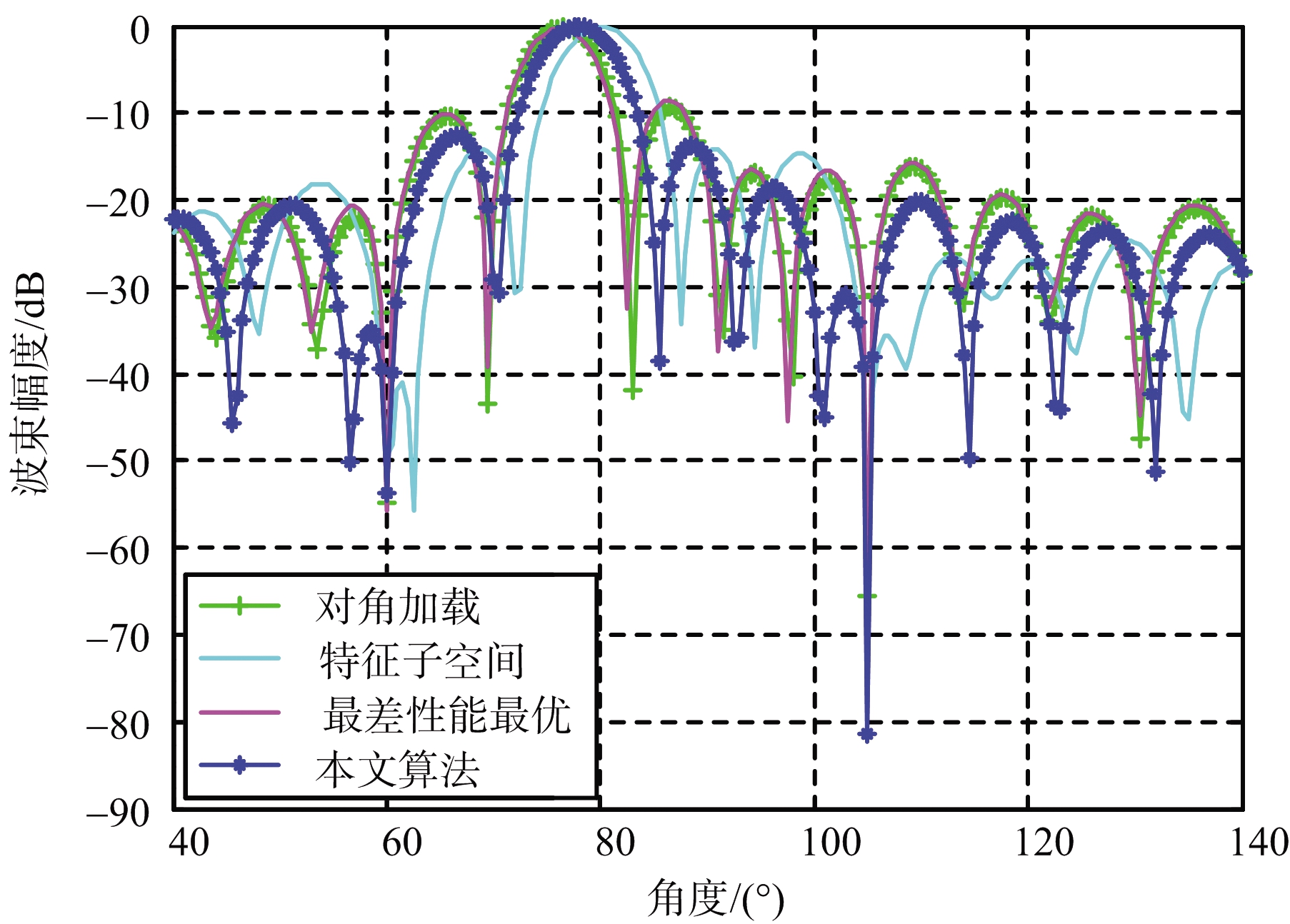
图1 导向矢量存在误差时的波束图
仿真实验2:验证算法在低SNR环境下的性能。假设两个干扰来波方向分别为60°和105°,信号来波的期望方向为80°,真实方向为78°,设置快拍数为100,输入期望信号SNR为-20 dB,图2为几种算法在低SNR下的波束图。
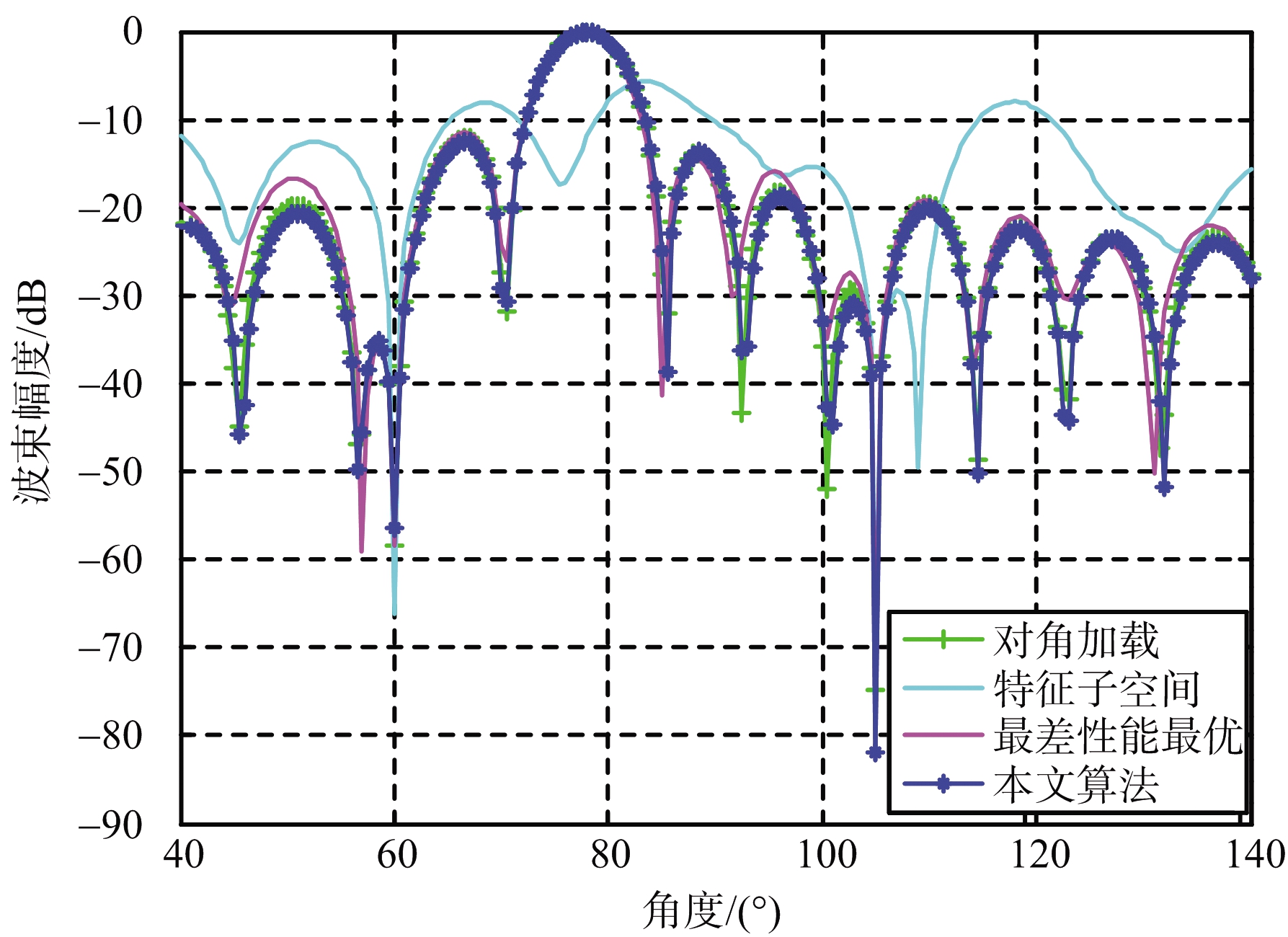
图2 低信噪比下几种算法的波束图
从波束仿真图可以看出,本文提出的方法在波束指向、旁瓣高度以及对干扰的零陷都无明显变化。DLB方法会出现抑制期望信号的现象,即出现了信号相消的问题。ESRB方法出现主瓣降低,旁瓣升高的问题,严重的角度会出现旁瓣高度接近主瓣高度。WCOB方法出现了旁瓣指向角度失配问题,算法性能下降较多。
仿真实验3:验证算法在高SNR环境下的性能。假设两个干扰来波方向分别为60°和105°,信号来波的期望方向为80°,真实方向为78°,设置快拍数为100,输入期望信号SNR为50 dB,图3为几种算法在高SNR下的波束图。
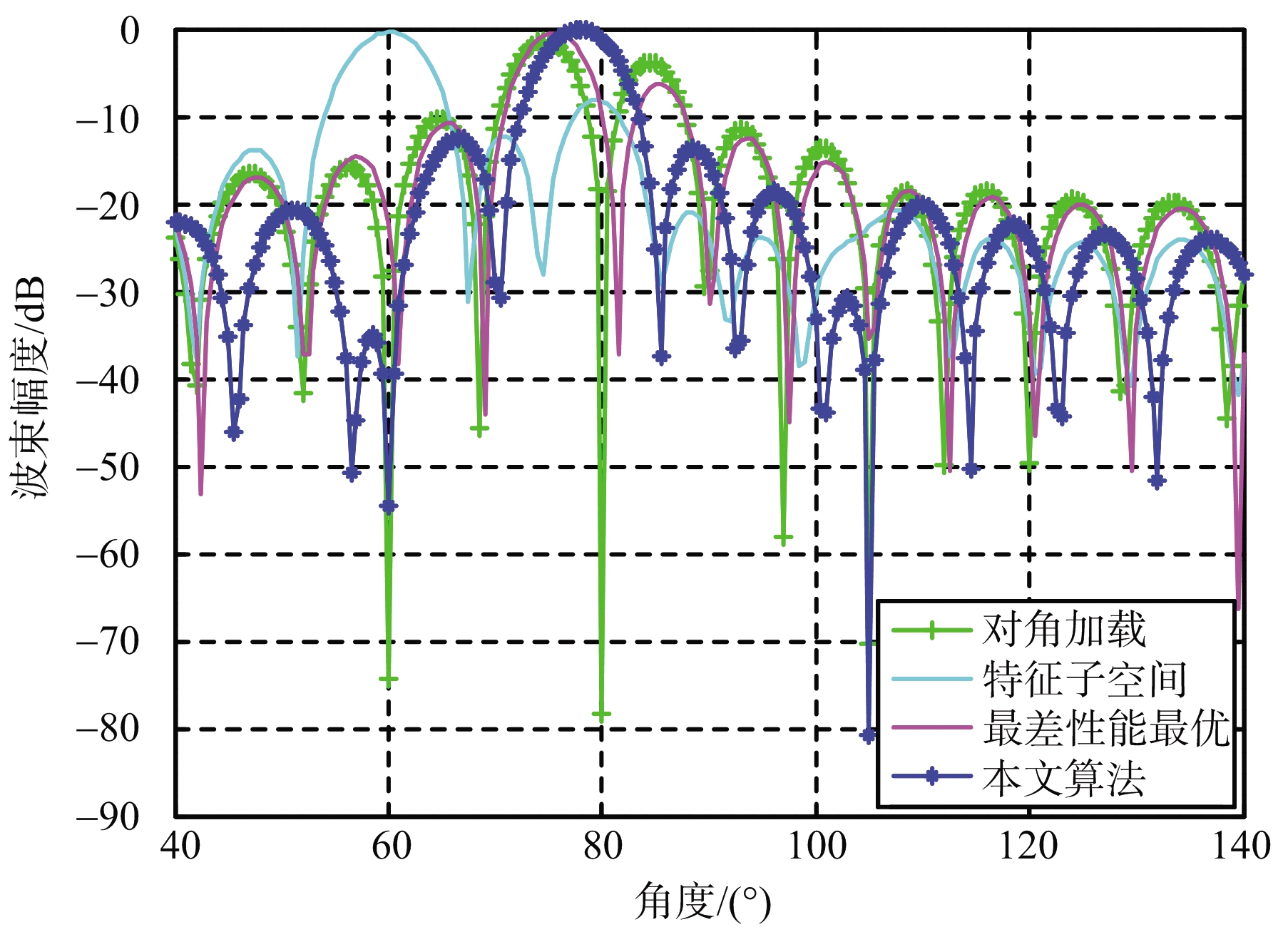
图3 高信噪比下几种算法的波束图
由波束仿真图可以看出,除了本文算法外,其余几种算法主瓣指向均发生偏差,此外,DLB算法的旁瓣过高,且出现了错将期望信号当成干扰信号进行零陷的信号相消现象。WCOB算法除了旁瓣过高外,已经无法识别出105°处的干扰。ESRB算法出现了旁瓣高于主瓣的情况,算法性能急剧下降。
仿真实验4:验证算法的输出信干噪比(Signal to Interference-plus-Noise Ratio,SINR)随输入SNR变化关系。假设两个干扰来波方向分别为60°和105°,信号来波的期望方向为80°,真实方向为78°,设置快拍数为100,两个干扰的干噪比(Interference-plus-Noise Ratio,INR)设置为30 dB。图4为几种算法输出SINR随输入SNR的变化关系。
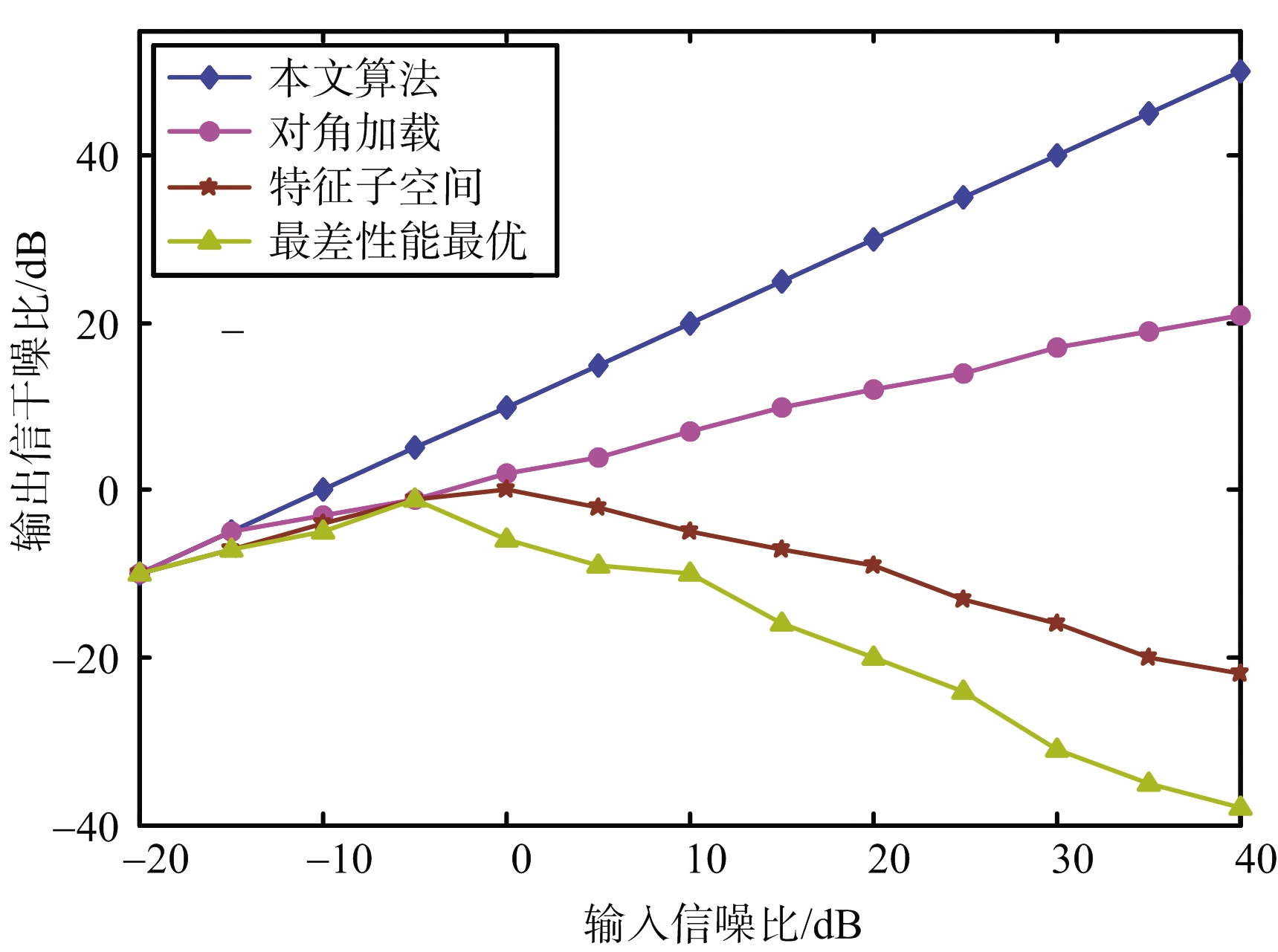
图4 几种算法输出SINR随输入SNR变化对比
DLB算法的输出SINR会随着输入SNR的增加而增加,且输出SINR相对较高。WCOB算法由于期望信号会产生相消现象,因此在曲线中会出现输出SINR降低的现象。ESRB算法效果优于算法WCOB,但是由于算法中对角加载值本身的限制,其依然会出现信号相消现象。
仿真实验5:此处研究快拍数对输出SINR的影响。假设两个干扰来波方向分别为60°和105°,信号来波的期望方向为80°,真实方向为78°期望信号的SNR为0 dB。
从图5可以看出,本文算法收敛速度最快,并且收敛于最优输出SINR。除此之外,DLB算法收敛速度较慢,但输出SINR相对较高,另外两种算法的输出SINR相对较低。
仿真实验6:实验6研究输出SINR随误差角度的变化关系。假设空间存在两个干扰,来波方向分别是60°和105°,期望信号来波方向为80°,INR为30 dB,SNR为25 dB,真实信号与期望信号的角度误差为0°到5°,快拍数取100,图6为几种算法二者关系的关系图。
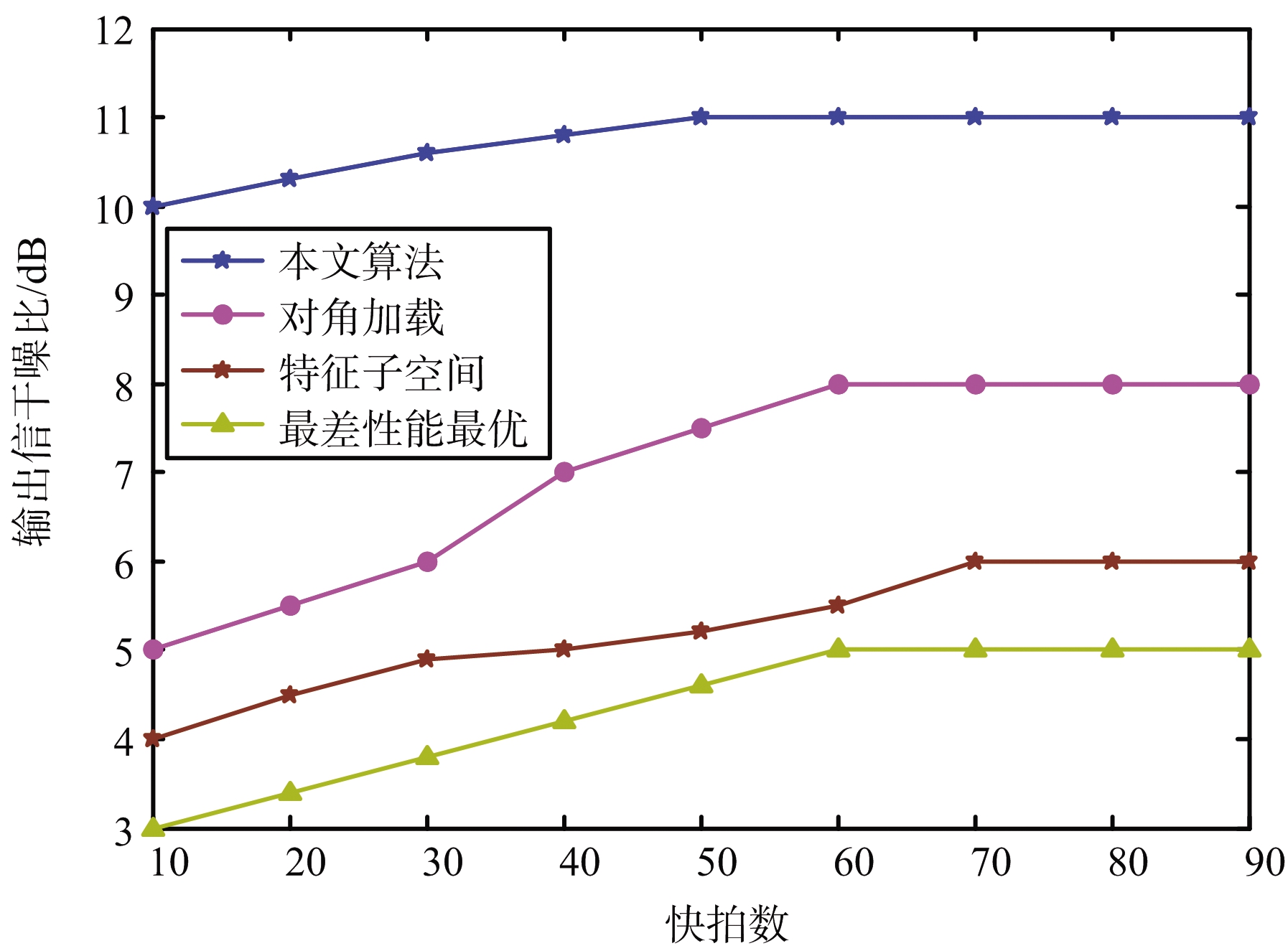
图5 几种算法输出SINR随快拍数变换关系
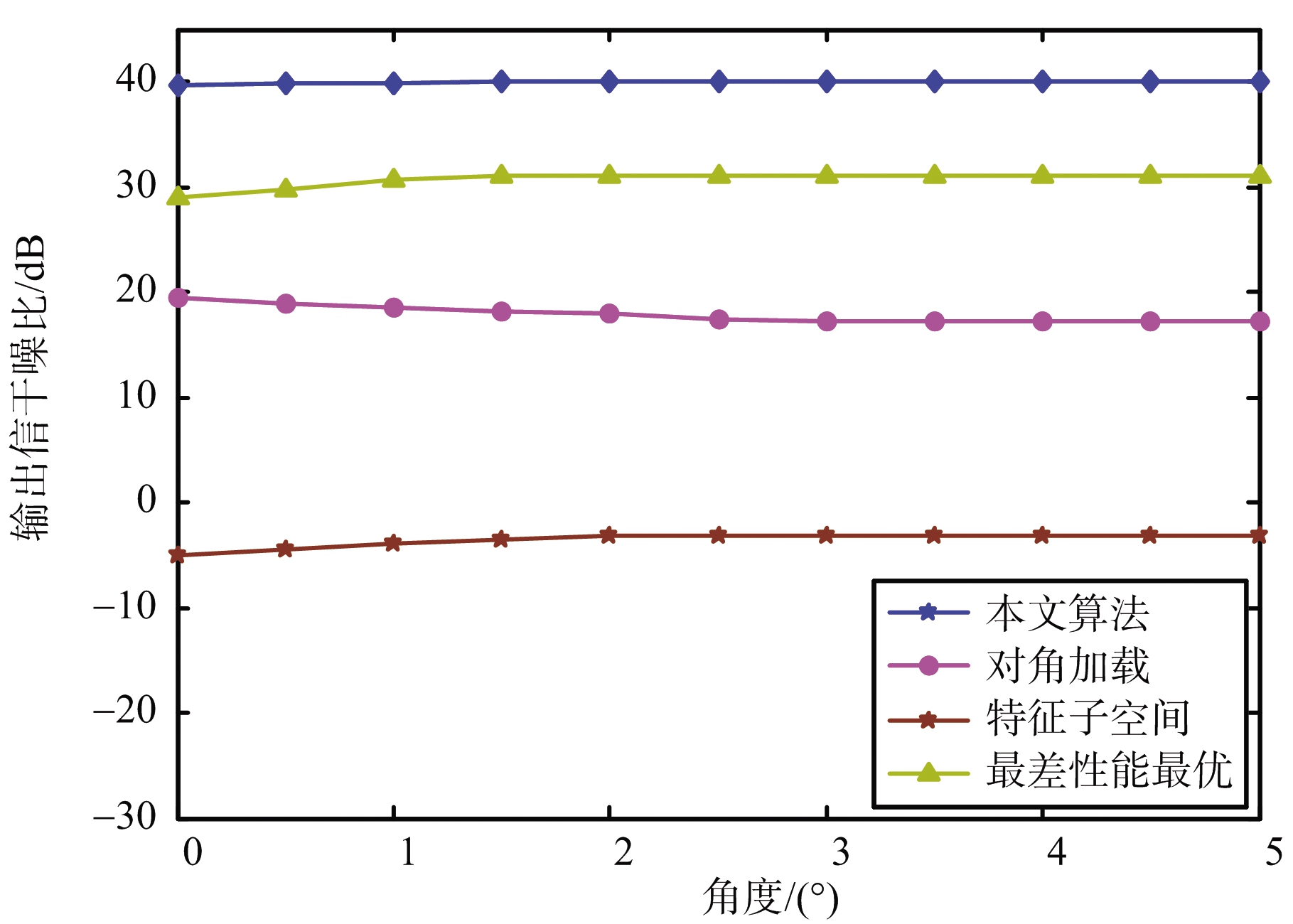
图6 几种算法输出SINR随误差角度变化图
由图6可见,DLB算法随着误差角度变大,输出SINR有略微下降,这是由于误差角度变大时会产生信号相消的现象。ESRB算法性能与算法WCOB和算法DLB比较差,本文算法随着误差角度变化表现稳定且维持较高的输出SINR,由此可见,本文算法在存在角度失配时有较高鲁棒性。
为了更方便比较各算法间差异,列出表2对各算法进行对比。从表中可知,从对真实来波方向估计、主瓣宽度、旁瓣高度以及对干扰抑制效果综合来看,本文算法有着很明显的优越性。
表2 各算法对比

算法真实来波方向估计主瓣宽度旁瓣高度对干扰抑制对角加载存在误差最窄较高较高特征子空间存在误差较宽较低较低最差性能最优存在误差较窄较高较高本文算法准确较窄最低最低
4 结束语
针对标准Capon波束形成中导向矢量失配情况下,算法性能急剧下降的问题,提出了本文算法。算法首先使用加权空间平滑对信号协方差矩阵进行平滑,获得更加精确的协方差矩阵,然后利用导向矢量不确定集方法获得真实导向矢量,接着利用范数约束提高算法鲁棒性。理论分析与仿真实验表明本文算法能够有效对干扰进行零陷同时降低旁瓣高度,在快拍数低的情况下保持高输出SINR。此外,导向矢量存在失配时算法能保持对期望信号的最大增益。从算法的计算量上来说,本文提出的算法运算量为O(5N3),DLB算法的运算量为O(N3),ESRB算法的运算量为O(8N3),WCOB算法的运算量为O(ρN3),其中ρ为迭代次数,一般取值为10以上的数,本文的算法总体计算量偏低。综上,本文算法是一种理论意义与实际价值兼备的鲁棒性波束形成算法。
[1] 王昊,马启明.协方差矩阵重构的稳健自适应波束形成算法[J].声学学报,2019,44(2):170-176.
[2] 陈沛,赵拥军,刘成城.基于稀疏重构的共形阵列稳健自适应波束形成算法[J].电子与信息学报,2017,39(2):301-308.
[3] SHEN Feng, CHEN Fengfeng, SONG Jinyang. Robust Adaptive Beamforming Based on Steering Vector Estimation and Covariance Matrix Reconstruction[J]. IEEE Communications Letters, 2015,19(9):1636-1639.
[4] MOHAMMADZADEH S, KUKRER O. Robust Adaptive Beamforming Based on Covariance Matrix and New Steering Vector Estimation[J]. Signal Image and Video Processing, 2019,10(8):131-157.
[5] HUANG Lei, ZHANG Jing, XU X, et al. Robust Adaptive Beamforming with a Novel Interference-Plus-Noise Covariance Matrix Reconstruction Method[J]. IEEE Trans on Signal Processing, 2015, 63(7):1643-1650.
[6] DENG Zhenghong, XU Jiwei, LI Xueqiang,et al. Robust Adaptive Beam-Forming Optimization Method Based on Diagonal-Loading and MSE Criterion[J].Chaos, Solitons and Fractals,2018,108(7):87-93.
[7] SERRA J, NAJAR M. Asymptotically Optimal Linear Shrinkage of Sample LMMSE and MVDR Filters[J]. IEEE Trans on Signal Processing, 2014, 62(14):3552-3564.
[8] ZHANG Ming, ZHANG Anxue, YANG Qingqing. Robust Adaptive Beamforming Based on Conjugate Gradient Algorithms[J]. IEEE Trans on Signal Processing, 2016, 64(22):6046-6057.
[9] YANG L,MCKAY M R,COUILLET R.High-Dimensional MVDR Beamforming:Optimized Solutions Based on Spiked Random Matrix Models[J].IEEE Trans on Signal Processing,2018,66(7):1933-1947.
[10] 刘骐玮,马彦恒,李根,等.基于空时频输出矩阵的盲波束形成算法[J].雷达科学与技术,2019,17(1):44-48.
[11] GONG Xiangwu, LONG Hong, YIN Hao, et al. Robust Amplify-and-Forward Relay Beamforming for Security with Mean Square Error Constraint[J]. IET Communications, 2015, 9(8):1081-1087.
[12] SOMASUNDARAM S D. Linearly Constrained Robust Capon Beamforming[J]. IEEE Trans on Signal Processing, 2012, 60(11):5845-5856.
[13] 李立欣,白童童,张会生,等.改进的双约束稳健Capon波束形成算法[J].电子与信息学报,2016,38(8):2014-2019.
[14] WANG Yasen, BAO Qinglong, CHEN Zengping. Robust Adaptive Beamforming Using IAA-Based Interference-Plus-Noise Covariance Matrix Reconstruction[J]. Electronics Letters, 2016, 52(13):1185-1186.
[15] GU Y, GOODMAN N A, HONG S, et al. Robust Adaptive Beamforming Based on Interference Covariance Matrix Sparse Reconstruction[J]. Signal Processing, 2014, 96(1):375-381.
[16] ZHANG Zhenyu, LIU Wei, LENG Wen, et al. Interference-plus-Noise Covariance Matrix Reconstruction via Spatial Power Spectrum Sampling for Robust Adaptive Beamforming[J]. IEEE Signal Processing Letters, 2016, 23(1):121-125.

