0 引言
无源定位系统被广泛应用于环境监测、医疗和军事等领域，其基本原理是通过测量目标辐射源的发射信号，对目标进行定位。常用的无源定位技术有：基于到达时间(Time of Arrival , TOA)、到达时间差(Time Difference of Arrival, TDOA)、到达角度(Angle of Arrival, AOA)、到达频率差(Frequency Difference of Arrival,FDOA)等[1]。其中，TDOA技术因其较高的定位精度得到广泛的研究和应用。当定位技术确定时，影响定位精度的主要因素有基站布局、时差测量误差、布站误差等[2]。本文主要研究在不同时差测量误差影响下的TDOA定位系统的最优布站方法。
目前研究各种无源定位系统布站方法的文献中，大多是使用解析法，假设TDOA测量误差为恒定高斯分布，理论推导后得到基站在一些特定位置时的布站方法，其求解较复杂且不具有普遍适用性。如文献[3]通过半正定规划的方法研究了传感器网络中最优定位节点的选择。文献[4]研究了直线、梯形、平行四边形、长方形、菱形、倒三角、正方形和Y形八种规则布站时的定位误差，指出Y形布站覆盖范围最大，各个方向定位精度较好。文献[5]通过对克拉美罗下界的迹的表达式推导得到：当接收站包围目标并呈等角布站时布站最优。文献[6]通过改变规则图形布站的基线长度和基线指向，研究了不规则布站的布站策略。文献[7]将TDOA系统布站问题转化为最优化问题进行求解，使用遗传算法(Genetic Algorithm , GA)来求解最优布站，具有普遍适用性，但是该方法仍然是假设TDOA测量误差为恒定高斯分布，未考虑基站和目标的位置、目标信号带宽、接收机噪声带宽等因素对TDOA测量误差的影响，而且遗传算法调节参数较多，收敛速度较慢，需要较多次迭代才能解得最优布站位置。
针对以上问题，本文以TDOA无源定位系统为研究对象，求解出更符合实际情况的TDOA测量误差，并在此基础上用粒子群算法(Particle Swarm Optimization，PSO)求解指定范围内的最优布站位置。
1 三维空间TDOA定位模型
假设在三维空间中，待定位目标辐射源位置为x=[x,y,z]T，接收基站位置si=[xi,yi,zi]T， i=0,1,…,n，表示为向量形式为s=[s0,s1,…,sn]T，辐射源到接收站的欧氏距离为ri=‖x-si‖，i=0,1,…,n。设定s0为主接收基站，辐射源信号传播速度为c，可得式(1)：
ri0=cti0=Δri0+cni0,i=1,2,…,n
(1)
式中，ri0为实际测得的第i号基站与主站到目标辐射源距离的差值，ti0为实际测得的第i号基站与主站到目标辐射源的时差，Δri0为第i号基站与主站在不含测量误差情况下到目标辐射源距离的差值，ni0为第i号基站与主站的实际时差测量误差。
将式(1)表示为向量形式：
z=h(x)+e
(2)
式中，z=[r10,r20,…,rn0]T，e=[cn10,cn20,…,cnn0]T,h(x)=[r1-r0,r2-r0,…,rn-r0]T。
三维空间TDOA定位即是在已知接收站的位置和测量时差的基础上，对目标的位置u进行求解。
2 不同TDOA测量误差下定位精度的CRLB分析
在无源时差定位问题中，目标的定位误差会存在CRLB。CRLB的迹表示了无偏的目标位置估计量在各个维度上方差的和，工程中一般以它来衡量目标定位性能。在定位方法一定时，TDOA测量误差的计算方式不同，会影响CRLB的求解。
假设x的无偏估计量为
则估计误差的方差矩阵的下界为[8]
(3)
F为Fisher信息矩阵：
F=E{[
xlnp(z|h(x))][xlnp(z|h(x))]T}
(4)
当各基站时间测量误差相互独立，服从均值为零，标准差为σi的高斯分布，即
时，
此时定位误差的CRLB为[8]
CRLB=F-1=(QTR-1Q)-1
(5)
式中，
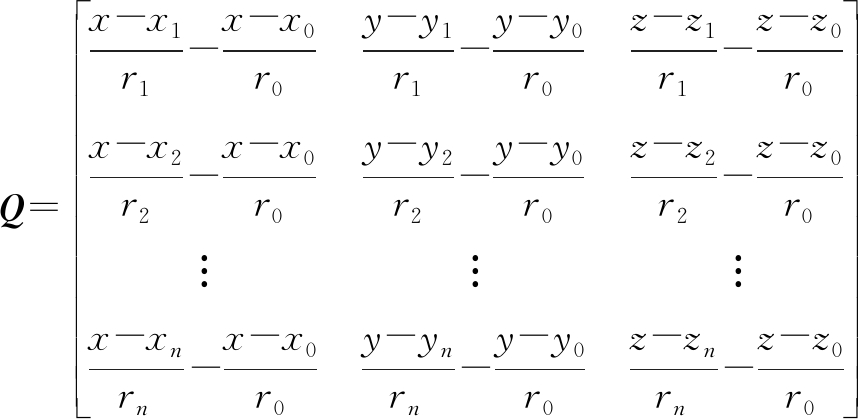
(6)
R=cov(e·eT)=
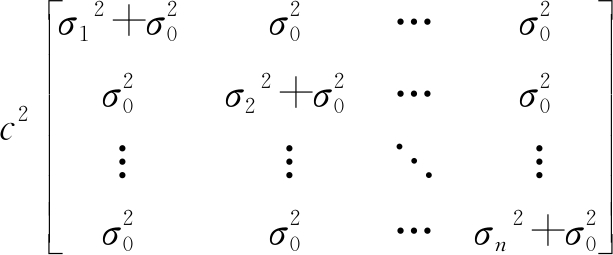
(7)
假设σ0=σ1=…=σn=σs时，
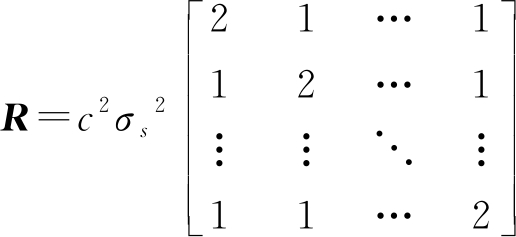
(8)
实际应用中，基站的观测性能受多种因素的影响，此时可将TDOA测量误差的方差视为由目标信号参数、信噪比和传播距离等决定的一个函数，表示为：ni0～(0,σ2(x)),i=1,2,…,n，因此提出一种更接近实际情况的计算CRLB的方法。假设三维空间TDOA定位模型在视距环境中，则第i个基站接收信号的功率可由电磁波在自由空间的传播损耗模型来确定[9]：
(9)
式中，Pt为发射信号功率，
为第i个基站接收信号功率，Gt为发射天线增益，Gr为接收天线增益，λ为传输信号载波波长，ri为信号到第i个基站的传播距离，L为馈线损耗。假设噪声信号功率相等，则定位基站和参考节点处接收信噪比的比值为
(10)
SNR为某一参考距离r处的信噪比，则第i个定位基站处接收信号的信噪比可以表示为
(11)
由TDOA测量相关理论可知，当多种可用技术用于测量TDOA时，该估计将是无偏的而且其方差可以达到时差测量的CRLB[10]。利用互相关法测量信号时间差的精度极限可以表示为[11]
(12)
式中，B为接收信号的均方根等效带宽，Bn为噪声信号的均方根等效带宽，T为信号相对于采样周期的时间长度，SNRi0为相关后信号对噪声的功率比，两者都是无单位的比值。SNRi0可表示为
SNRi0=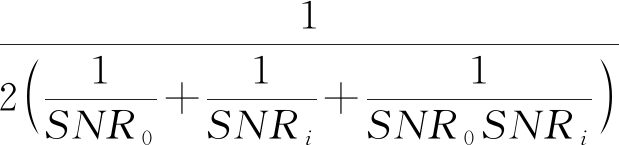
i=1,2,…,n
(13)
式(11)和式(13)代入式(12)中可得第i号基站和主站所测辐射源信号的TDOA下界为
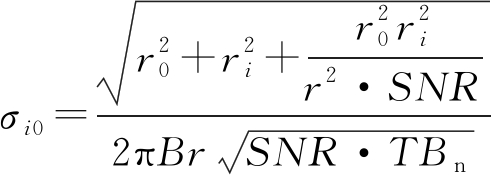
(14)
由式(14)可以看出,TDOA测量误差与目标辐射源和基站间的距离、目标信号带宽，目标信号累积时间、接收机的噪声带宽、参考距离及其对应信噪比有关。
此时假设主站和不同基站间的TDOA测量误差相互独立，则测量向量z的似然函数为
(15)
此时，距离误差的协方差矩阵为
R(x)=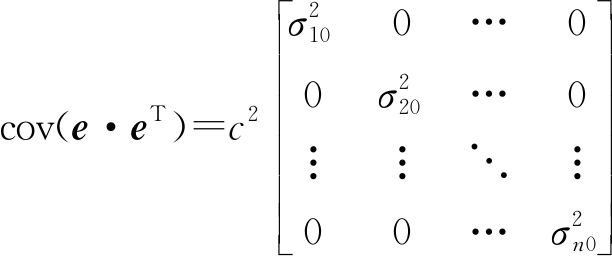
(16)
将式(15)代入式(4)中，可得F的各个元素为
Fij=(QTR(x)-1Q)ij+
(17)
其中，Q可以用式(6)来表示。则有
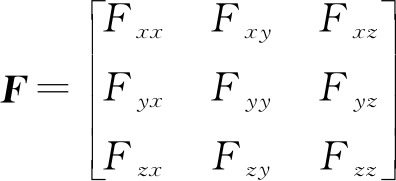
(18)
则CRLB的迹为
J=tr(CRLB)=tr(F-1)
(19)
3 基于粒子群算法的最优布站方法
在求解最优布站位置时，辐射源目标的具体位置是未知的，为确保目标区域的整体定位精度，本文采用的方法是将目标区域离散化，目标区域的整体定位精度可以表示为
(20)
式中，θ=[x0,y0,z0,x1,y1,z1,…,xn,yn,zn]为参与定位的n+1个基站的位置，N为目标区域内的辐射源目标个数。则在基站指定布站区域内，用粒子群算法对目标函数f(θ)迭代寻优，使函数f(θ)的值最小时的变量θ即为基站的最优布站位置。粒子群算法求解最优布站流程为：
1) 种群初始化：随机产生规模为M个粒子的种群，设定迭代次数、在布站区域内初始化粒子θ中每个基站的三维坐标位置和坐标移动速度。
2) 根据目标函数f(θ)计算每个粒子的定位误差，获取粒子个体的历史最佳位置、种群的历史最佳位置、个体最佳适应度、种群最佳适应度。粒子定位误差越小，其适应度越高，布站位置越好。
3) 按粒子群算法粒子更新公式[12]更新粒子位置和速度，继续执行流程2)，直到迭代到指定次数。迭代后所求得的适应度最高的粒子即为最优布站位置，其对应的函数值即为定位误差。
4 算法仿真和结果分析
本节主要是采用粒子群算法，对三维空间中不同TDOA测量误差下最优布站位置和布站性能进行仿真和分析。仿真参数设置为：
1) 定位系统参数：定位基站个数为4，基站区域为R1:{x∈[-25,25],y∈[-25,25],z∈[0,5]}，目标区域为R2:{x∈[-100,200],y∈[0,200],z∈[5]}，单位为km。信号等效带宽 B=500 kHz，噪声等效带宽Bn=1 MHz，时间长度T=1 000，参考距离r=100 m处的信噪比为30 dB，即SNR=1 000。
2) 粒子群算法参数：种群规模为200，最大迭代次数为200次，变量维数为12，自我学习因子 c1=1.5，群体学习因子c2=1.5，惯性权重ω取0.9～0.4，随迭代次数的增加线性递减。
假设目标在定位区域内出现的概率相等，根据本文分析，现有两种计算定位精度的方法： 1) TDOA测量误差为恒定高斯分布时计算得到的定位精度，此时，令距离测量误差协方差矩阵R内
测量误差为关于目标信号参数、信噪比和传播距离等的函数时测得的定位精度。基于方法1)，用PSO算法和GA算法求解最优布站；基于方法2)，用粒子群算法(PSO-NEW)求解最优布站，得到仿真图如图1～图3所示。
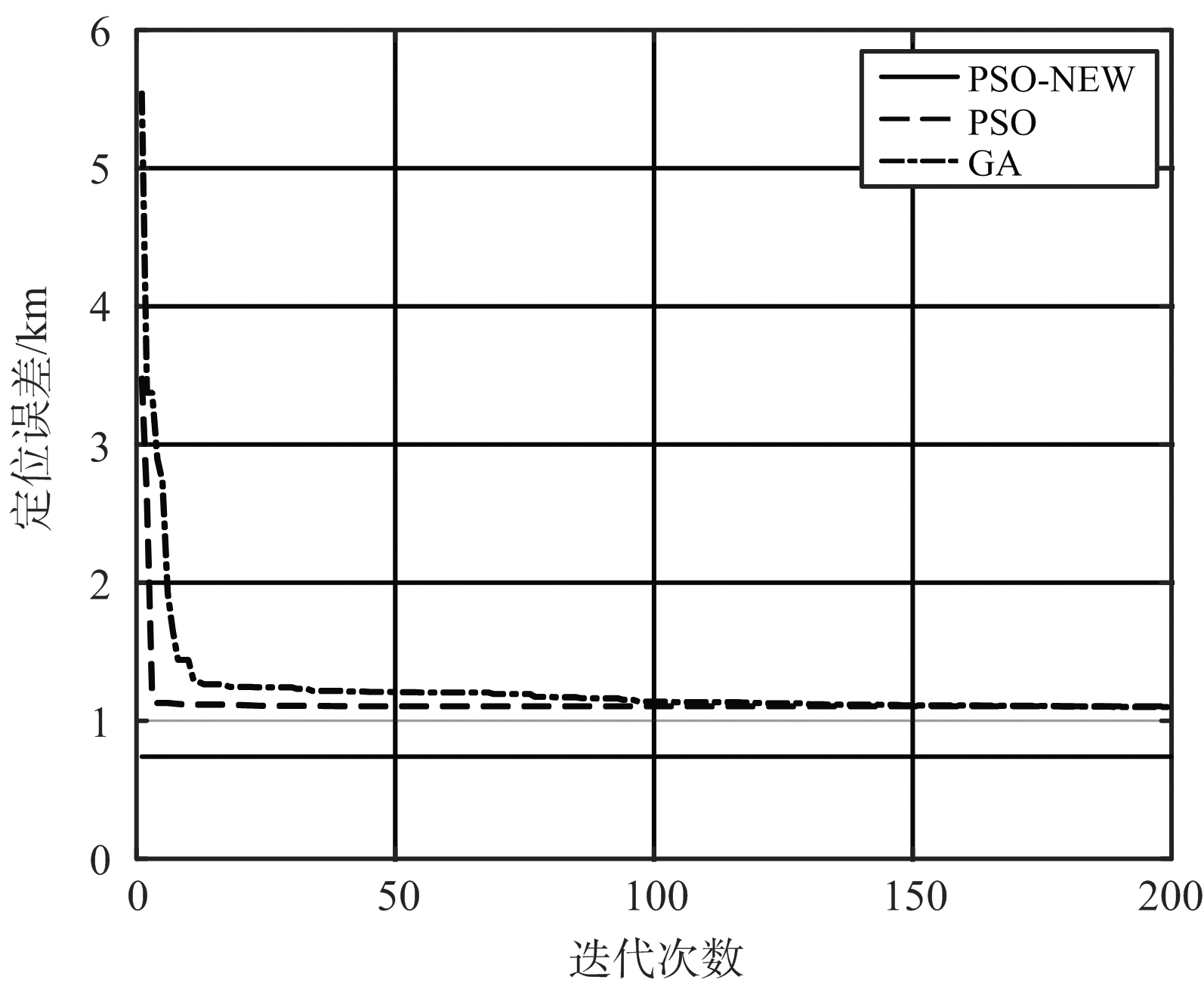
图1 不同迭代次数后基站最优布站时的定位误差
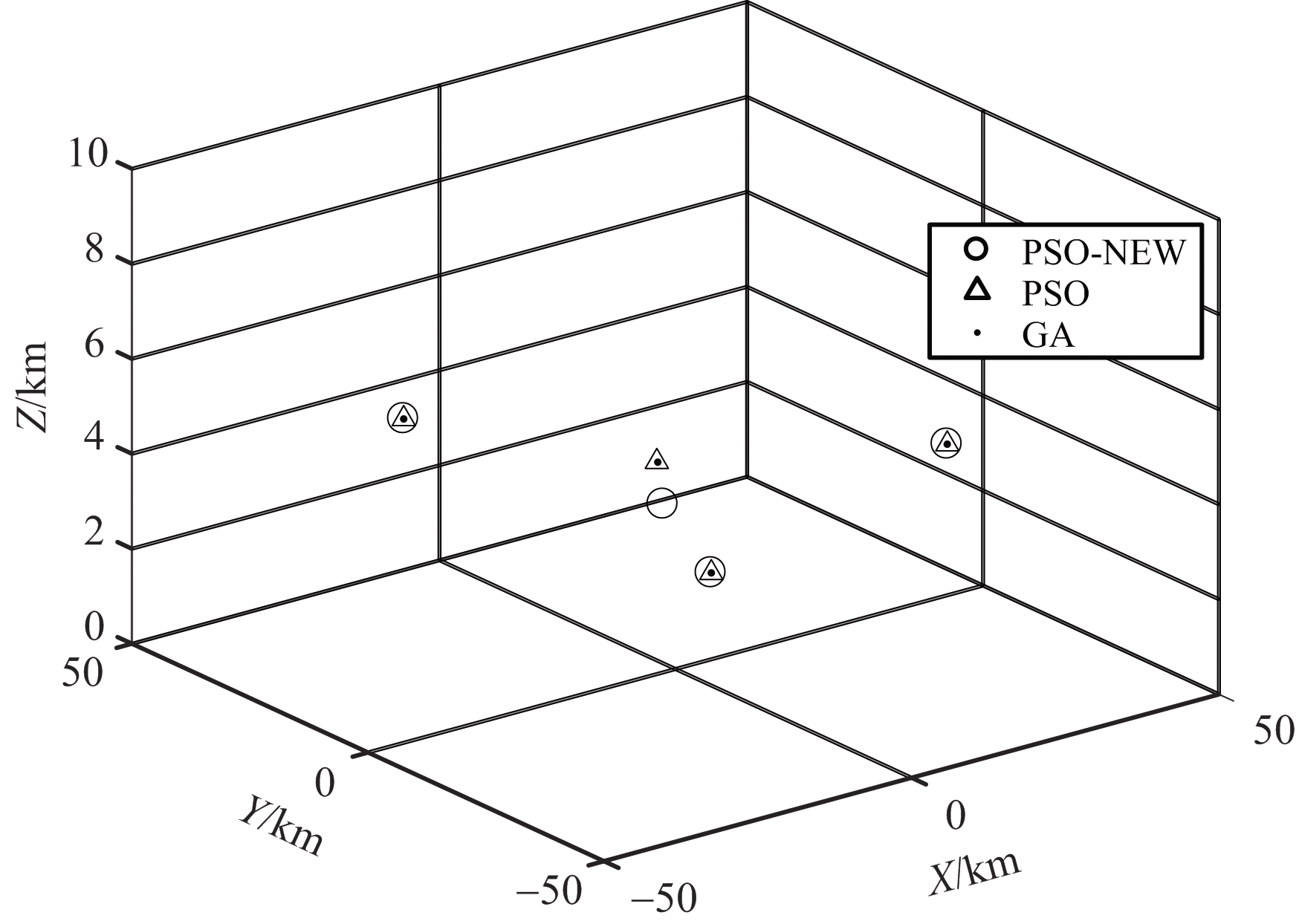
图2 迭代200次后最优布站的位置
图3 PSO-NEW算法最优布站时定位误差等高线图
图1为随迭代次数的增加，3种算法求解得到的基站最优布站对目标区域的定位误差。图2为迭代200次后，3种算法求解后得到的最优布站三维坐标图，不同算法求解得到的基站位置用不同形状的图形来区分。从图1可以看出：当TDOA测量误差为恒定高斯分布时，粒子群算法(PSO)比遗传算法(GA)收敛速度更快，更适用于需要快速作出反应的无源定位环境，两者定位精度基本相同。从图2可以看出：当TDOA测量误差为恒定高斯分布时，PSO算法和GA算法求解的最优布站位置基本相同。从图1还可以看出：当TDOA测量误差为多种因素综合影响的函数时，用PSO算法求得最优布站所对应的定位误差与TDOA测量误差为恒定高斯分布时相比，定位误差由1.092 5 km下降到0.529 81 km，说明此时求解的最优布站位置更好，可以实现对目标区域更高精度的定位。
图3为PSO-NEW算法200次迭代后求得的最优布站位置所对应的定位误差CRLB的等高线图，从图中可以看出，目标区域R2内，定位误差以布站区域为中心向四周逐渐递增，目标区域的定位误差基本都在2 km以内，进一步证明本文所提算法求得的布站位置对目标区域的整体定位性能良好。
5 结束语
本文研究了三维时差定位系统模型，提出了一种更符合实际情况的TDOA测量误差的计算方法，并推导出在不同时差测量误差影响下，目标区域定位误差的CRLB。本文以定位误差CRLB的迹的平均值最小为优化目标，用粒子群算法求解最优布站。仿真结果表明：本文所提算法求解的最优布站位置，与假设TDOA测量误差为恒定高斯分布时相比，其定位误差明显减小，目标区域整体定位性能良好；与用遗传算法求解的最优布站位置相比，其收敛速度快且调节参数少，更适用于需要快速作出反应的侦察定位场合；同时，本文所提算法无需像解析法中那样针对特定情况推导最优布站位置，在理论上可以求解在任意布站区域内的最优布站，求解简单且具有普遍适用性。
[1] GIACOMETTI R, BAUSSARD A, CORNU C, et al. Accuracy Studies for Tdoa-Aoa Localization of Emitters with a Single Sensor[C]∥2016 IEEE Radar Conference，Philadelphia, PA, USA：IEEE, 2016:1-4.
[2] WANG Zhenyong, MA Ming, LI Dezhi, et al.
Analysis on Positioning Accuracy Based on Joint TDOA and FDOA for Single Satellite Passive Location[C]∥International Conference in Communications, Signal Processing, and Systems, Singapore:Springer,2017:2625-2633.
[3] 郝本建,王林林,李赞,等.面向TDOA被动定位的定位节点选择方法[J].电子与信息学报,2019,41(2):462-468.
[4] LEI Yanping, GONG Fengxun, MA Yanqiu. Optimal Distribution for Four-Station TDOA Location System [C]∥2010 3rd International Conference on Biomedical Engineering and Informatics,Yantai,China:IEEE,2010:2858-2862.
[5] 周成,黄高明,高俊.时差定位最优布站方法研究[J]. 西安电子科技大学学报,2016,43(4):123-127.
[6] 王瀚,钟丹星,周一宇. 不规则布站时差定位系统定位精度分析[J]. 现代电子技术,2007，30(7):19-21.
[7] 闫青丽,陈建峰.分布式声源定位系统节点最优布局方法及性能研究[J]. 电子学报,2018,46(5):1186-1193.
[8] FOWLER M, HU X. Signal Models for TDOA/FDOA Estimation[J]. IEEE Trans on Aerospace and Electronic Systems, 2008, 44(4):1543-1550.
[9] 丁鹭飞,耿富录.雷达原理[M].西安：西安电子科技大学出版社，2002：4-5.
[10] 田中成,刘聪锋. 无源定位技术[M].北京：国防工业出版社,2015:275-277.
[11] 胡来招.无源定位[M].北京：国防工业出版社，2004：190-191.
[12] ABED A K, ABDEL-QADER I. Access Point Selection Using Particle Swarm Optimization in Indoor Positioning Systems[C]∥NAECON 2018-IEEE National Aerospace and Electronics Conference,[S.l.]:IEEE, 2018:403-410.
